文章信息
- 李练兵, 宋清翔, 张文煜, 杨海跃
- LI Lianbing, SONG Qingxiang, ZHANG Wenyu, YANG Haiyue
- 仅逆变器侧电流反馈的改进有源阻尼方法
- Improved active damping method with inductive current feedback on inverter side only
- 中国测试, 2024, 50(8): 180-188
- CHINA MEASUREMENT & TEST, 2024, 50(8): 180-188
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022100104
-
文章历史
- 收稿日期: 2022-10-22
- 收到修改稿日期: 2023-03-20
2. 国网冀北张家口风光储输新能源有限公司,河北 张家口 075000;
3. 国网河北省电力公司衡水供电公司,河北 衡水 053000
2. State Grid Hebei Zhangjiakou Scenic Storage and Transportation New Energy Co., Ltd., Zhangjiakou 057000, China;
3. Hengshui Power Supply Company of State Grid Hebei Electric Power Company, Hengshui 053000, China
随着分布式发电机(distributed generation, DG)的普及,并网逆变器作为新能源并网的关键设备得到了广泛的应用。LCL型滤波器因其优越的高频谐波衰减能力而广泛安装在并网逆变器与电网的连接中[1]。然而,传统的LCL滤波器存在高频谐振风险,需要适当的阻尼方案来进行谐振抑制[2]。与PD技术通过阻尼装置来实现谐振抑制相比,AD技术具有无需添加阻尼装置即可实现谐振抑制且不会导致附加能量损耗的优点。因此,有源阻尼谐振抑制技术成为当前研究的热点。
针对有源阻尼谐振抑制方法,国内外研究形成了两类主要的方法。第一类方法为前向通道串联校正法[3-5],即通过在系统前向回路中串联陷波滤波器实现对谐振峰的补偿。文献[3]提出采用比例-谐振(proportional resonance, PR)控制串联陷波器的方法抑制LCL谐振峰值。虽然避免了复杂的反馈控制设计,但是随着电网电感变化,陷波器的调频设计难度增加,这不利于LCL滤波器的鲁棒性设计;对此文献[4]中提出一种基于傅里叶分析的陷波器自调试设计方法,减小了陷波器调频难度,但是由于傅里叶变换的引入增加了控制器运算压力,不利于工程实现。文献[5]提出一种陷波器设计方法,通过设计谐振频率与陷波器频率点的偏差构成谐振漂移裕度,在一定程度上提高了系统鲁棒性。串联校正方法虽然能有效抑制LCL谐振峰,但陷波器参数设计过于复杂,不利于此类方法的推广。
第二类为基于状态变量的反馈方法,即通过传感器采样将电流、电压等状态变量反馈至控制环路[4-6],对控制输出信息进行校正,从而实现谐振抑制。根据状态变量的不同,可以分为网侧电流电容电压[7]、电容电流[6]、逆变侧电流及多状态组合反馈控制。其中电容电压反馈控制、电容电流反馈控制、多状态组合反馈控制均需添加额外的传感器来对状态变量进行采样[8],如文献[6]提出结合电容电流反馈与串联超前校正的附加有源阻尼设计方法,通过将电容电流根据阻抗模型参数反馈至控制器输出,来抑制中低频谐振,但存在高频相位裕度不足的情况;文献[7]提出电容电压全反馈方案,可以抑制由电网电压引起的并网电流失真,但二阶微分的引入对噪声进行了放大也将影响系统稳定;文献[9]提出一种逆变器侧电流反馈结合电网电压反馈的控制策略,减少了并网电流谐波,但是该方法控制器结构复杂,算法实现困难。
上述文献所提方法均需添加额外的传感器来对反馈变量进行采样,由于系统对采样传感器的精度要求较高,系统设计成本也随之增加。网侧电流反馈[10-11]和逆变器侧电流反馈控制[12]能解决这一问题,文献[10]提出基于网侧电流反馈的有源阻尼设计方法,可以完成谐振抑制。但是当电网阻抗变化时,需重新选择延时补偿系数,在电网电压畸变及阻抗变化迅速情况下适用能力减弱;文献[11]针对网侧电流反馈方案在弱电网下对电网阻抗变化较为敏感的问题设计了一种满足输出阻抗超宽范围变化的控制策略,但该策略下系统响应速度变慢,不利于对快速变化的输入信号进行跟踪。文献[12]针对逆变器侧电流提出了基于阻尼系数的比例反馈设计方法,能有效实现并网电流的稳定控制,但该方法下控低频增益不足,不利于进行并网控制。
本文在文献[12]方法的基础上进行推导,提出基于PI控制下的改进逆变侧电流反馈有源阻尼(improved inverter-side current feedback active damping, IICFAD)设计方法,首先,通过对PI控制结构下系统传递函数的推导,结合等效电路进行对比分析,得到IICFAD阻尼方法下的反馈增益函数;其次,结合控制系统稳定性判据给出控制参数优化计算方法;最后,通过Simulink仿真和30 kW样机实验验证了方法的有效性。
1 并网逆变器控制与建模 1.1 并网逆变器控制图1所示为LCL型电压源逆变器(VSI)结构,采用逆变器侧电流反馈控制。其中udc为直流母线电压,vpcc为三相逆变器输出与电网连接节点电压,L1、L2分别为逆变器滤波电感,C为滤波电容,Lg为电网等效电感。

|
| 图 1 逆变侧电流反馈并网结构 |
如图1所示,忽略L1、L2、C和Lg的等效串联阻抗即可抵消所有PD影响。VSI通过LCL滤波器与电网相连,其中LCL滤波器固有谐振频率可记为ωr,如式(1)所示;逆变侧电流控制采用PI控制,其传递函数如式(2)所示;此外数字控制的并网VSI存在1.5个采样周期的计算和脉宽调制延时Gd(s),其传递函数如式(3)所示[13]。
| $ {\omega _r} = \sqrt {\frac{{{L_1} + {L_2} + {L_{\text{g}}}}}{{{L_1}\left( {{L_2} + {L_{\text{g}}}} \right)C}}} $ | (1) |
| $ {G_{{\text{PI}}}}(s) = {K_p} + \frac{{{K_i}}}{s} $ | (2) |
| $ {G_d}(s) = {{\text{e}}^{ - 1.5s{T_s}}} $ | (3) |
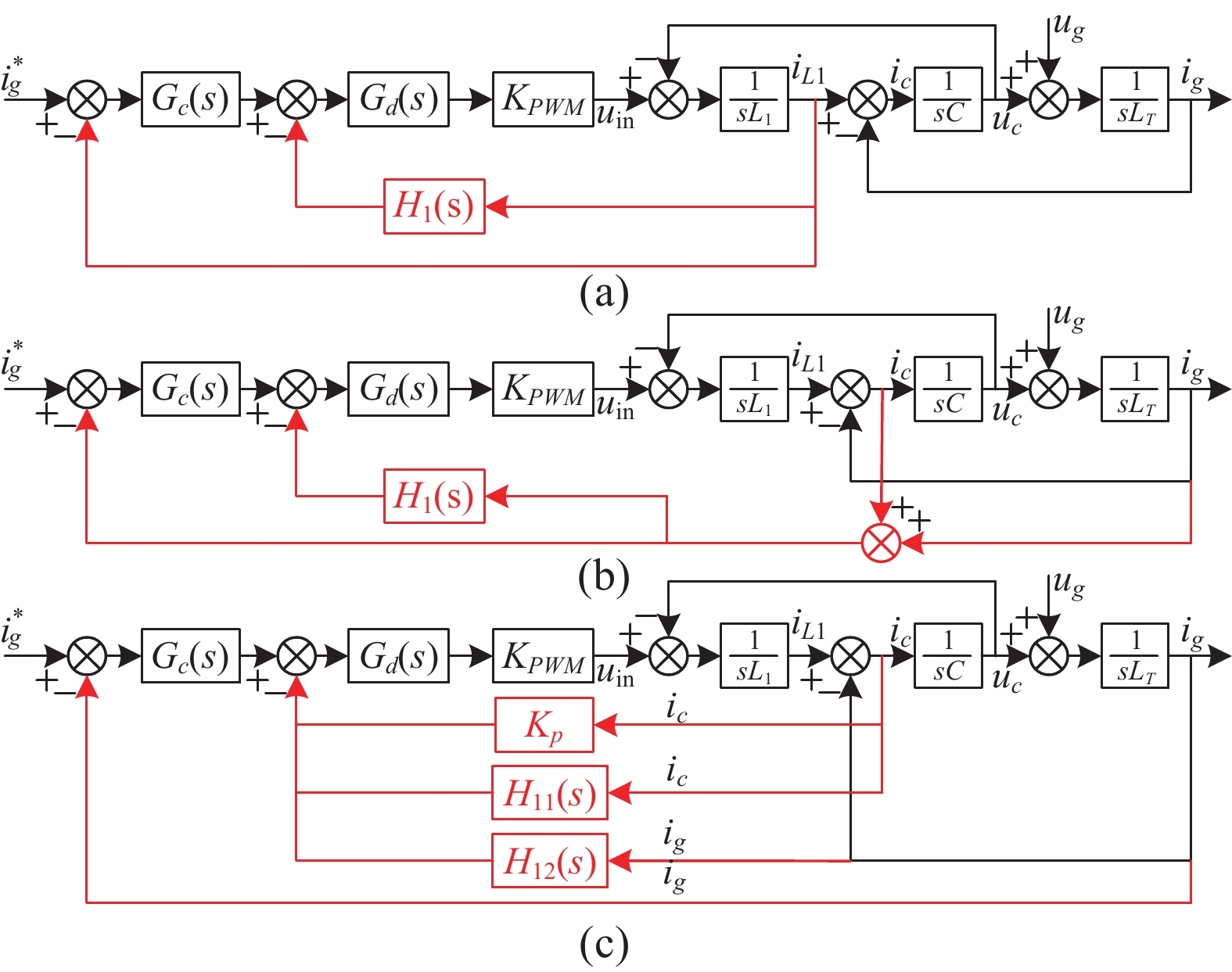
结合上一节所述,在abc三相静止坐标系下,可将LCL型并网VSI的控制框图等效为图2(a)所示,其中KPWM为数字控制下逆变器输出电压的调制增益,LT为滤波电感L2与电网电感Lg之和。考虑到并网电流稳定性是评价逆变器运行稳定性的标准,可将逆变侧电流等效为并网电流ig与电容支路电流ic之和,由此控制框图可等效为图2(b)所示。此时由于PI控制的积分分量对高频段信号的影响较小可忽略不计,由此对电容电流反馈可仅考虑比例分量影响,此外将电感电流反馈增益分解为电容电流等效增益H11(s)和并网电流等效增益H12(s)可将控制框图等效为图2(c)所示。
|
| 图 2 并网控制器等效结构 |
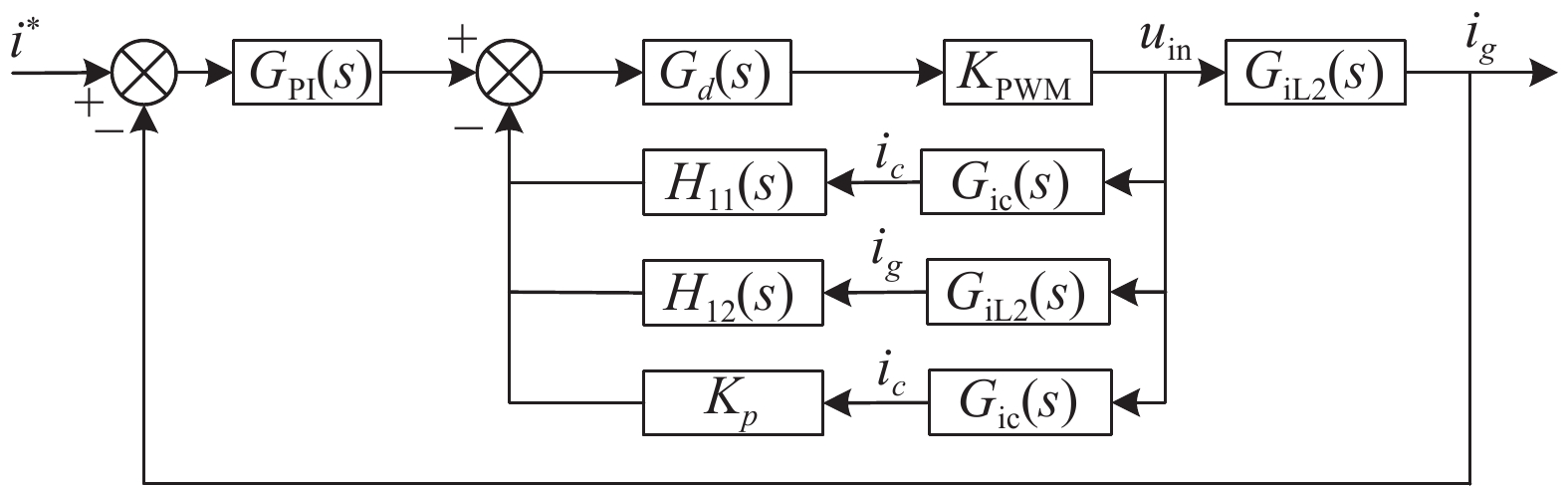
再次对并网VSI控制器结构进行等效变换。根据LCL滤波器中状态的传递函数,可以得到控制框图如图3所示。其中GiL2(s)和Gic(s)分别为逆变器输出侧电压到电网侧电流ig和到电容器电流ic的传递函数,分别可表示为式(4)和(5)。
|
| 图 3 并网控制器等效结构 |
| $ {G_{{\text{ic}}}}(s) = \frac{s}{{{L_1}\left( {{s^2} + \omega _r^2} \right)}} $ | (4) |
| $ {G_{{\text{iL2}}}}(s){\text{ }} = \frac{1}{{{L_1}{L_T}Cs\left( {{s^2} + \omega _r^2} \right)}} $ | (5) |
此外,给出电容电流等效增益H11(s)和并网电流等效增益H12(s)的传递函数表达式如式(6)和(7)所示。
| $ {H_{11}}(s) = {K_{{\text{H1}}}} $ | (6) |
| $ {H_{{\text{12}}}}(s) = {L_T}C{K_{{\text{H2}}}}{s^2} $ | (7) |
其中:KH1和KH2分别为电容电流增益系数和并网电流增益系数。
由图3结合梅森计算公式可以得到,系统等效闭环传递函数Ф(s)为式(8),定义逆变器输出电压到电网侧电流的开环传递函数GLCL(s)可表示为式(9)。
| $ \begin{split} &\varPhi (s) = {G_{{\text{PI}}}}(s){G_d}(s){K_{{\text{PWM}}}}{G_{{\text{iL2}}}}(s)/ \\ &\left\{ \begin{gathered} 1 + {K_{{\text{PWM}}}}{G_d}(s) \\ \left( {{H_{11}}(s){G_{{\text{ic}}}}(s) + {H_{12}}(s){G_{{\text{iL2}}}}(s) + {K_p}{G_{{\text{ic}}}}(s)} \right) \\ \end{gathered} \right\} \end{split}$ | (8) |
| $ \begin{split} &{G_{{\text{LCL}}}}(s) = {G_{{\text{iL2}}}}(s)/ \\ &\left\{ \begin{gathered} 1 + {K_{{\text{PWM}}}}{G_d}(s) \\ \left( {{H_{11}}(s){G_{{\text{ic}}}}(s) + {H_{12}}(s){G_{{\text{iL2}}}}(s) + {K_p}{G_{{\text{ic}}}}(s)} \right) \\ \end{gathered} \right\} \end{split}$ | (9) |
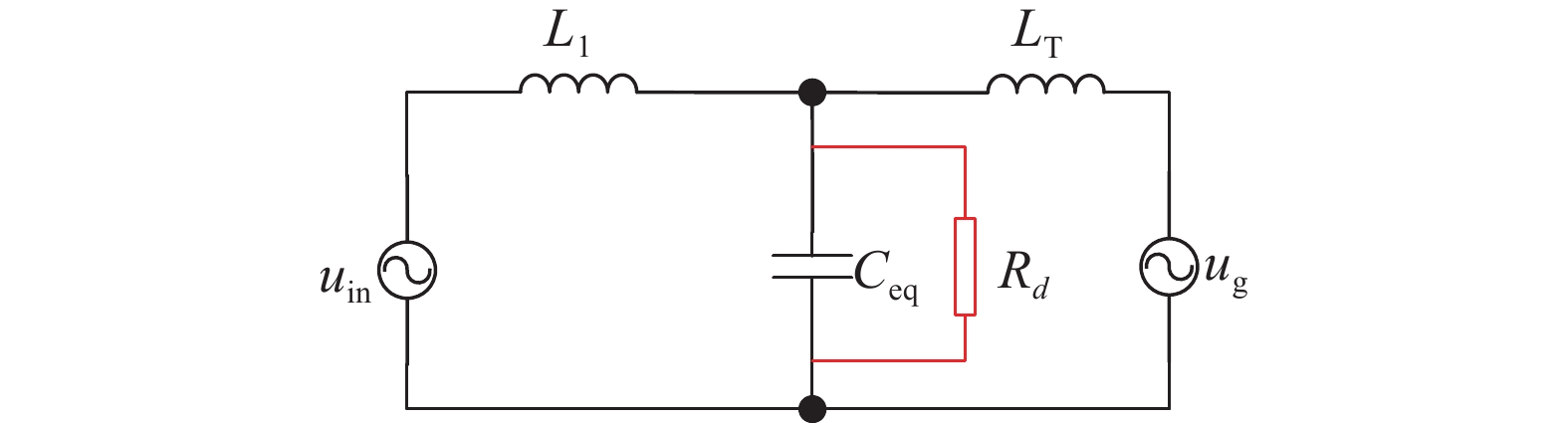
为进一步理解有源阻尼系数,对比分析无源阻尼与有源阻尼方法。参考文献[14]中的分析,当逆变侧电容并联电阻器时,能够提供更好的阻尼效果,且能够避免串联电阻器时导致LCL滤波器低频增益降低或电感并联电阻器导致的高频衰减能力降低的问题[14]。为满足更好的谐振抑制效果的同时保证低频增益,本文以滤波电容并联电阻器进行对比分析。滤波电容并联电阻器结构如图4所示,其等效开环传递函数GLCL_R(s)可表示为(10)[14]。
|
| 图 4 并网控制器等效结构 |
| $ {G_{{\text{LCL\_R}}}}(s) = \frac{1}{{{L_1}C{L_T}{s^3} + {L_1}{L_T}/{R_d}{s^2} + \left( {{L_1} + {L_T}} \right)s}} $ | (10) |
其中:Rd为并联的阻尼电阻器。
结合(1)及自动控制原理可以得到阻尼系数ζ计算表达式(11)。
| $ \zeta {\text{ }} = \frac{1}{{2C{R_d}{\omega _r}}} = \frac{1}{{\sqrt {\dfrac{{4{R_d}^2({L_1} + {L_T})C}}{{{L_1}{L_T}}}} }} $ | (11) |
由此(10)可简化为(12):
| $ G(s) = \frac{1}{{{L_1}C{L_T}s}}\frac{1}{{{s^2} + 2\zeta {\omega _r}s + {\omega _r}^2}} $ | (12) |
通过比较PD和AD之间G(s)的表达式来推导IICFAD的等效电路。通过将式(1)和(4)~(7)代入(9)可以得到IICFAD控制方法下LCL滤波器的等效开环传递函数GLCL_II(s)可由下式表示。
| $ {G_{{\text{LCL\_II}}}}(s) = 1/\left\{ \begin{gathered} {L_1}C{L_T}{s^3} + {L_T}C{K_{{\text{PWM}}}}{G_d}(s)K{s^2} + \\ \left( {{L_1} + {L_T}} \right)s \\ \end{gathered} \right\} $ | (13) |
其中:
| $ K = {K_{{\text{H1}}}} + {K_{{\text{H2}}}} + {K_P} $ | (14) |
与无阻尼系统相比,IICFAD有三个阻尼源,即一个固有阻尼和两个附加阻尼,分别体现在Kp、KH1和KH2中,为了保证基于IICFAD方法的系统和基于滤波电容并联电阻器无源阻尼系统具有相同的极点,式(13)与(10)应当分母相同。因此在不考虑延时影响的情况下,总阻尼增益K和等效阻尼电阻Rd之间的关系可以导出为(15)。
| $ {R_d} = \frac{{{\omega _r}}}{{{K_{{\text{PWM}}}}K}} $ | (15) |
考虑延时影响时,分母中的二次项将引入指数项因子,改变系统的开环极点分布,因此可将具有延时环节的IICFAD等效为电容器并联阻抗Zeq(s),可表示为(16)。
| $ {Z_{{\text{eq}}}}(s) = \frac{{{R_d}}}{{{{\text{e}}^{ - 1.5s{T_s}}}}} $ | (16) |
结合欧拉公式及s=jω有:
| $ \begin{split} {Z_{{\text{eq}}}}(s) = &\frac{{{R_d}}}{{\left[ {\cos (1.5\omega {T_s}) - {\rm j}\sin (1.5\omega {T_s})} \right]}}\triangleq \\ & {R_{{\text{eq}}}}(\omega )//{\rm j}{X_{{\text{eq}}}}(\omega ) \end{split}$ | (17) |
| $ {R_{{\text{eq}}}}(\omega ) = \frac{{{R_d}}}{{\cos (1.5\omega {T_s})}} $ | (18) |
| $ {X_{{\text{eq}}}}(\omega ) = \frac{{{R_d}}}{{\sin (1.5\omega {T_s})}} $ | (19) |
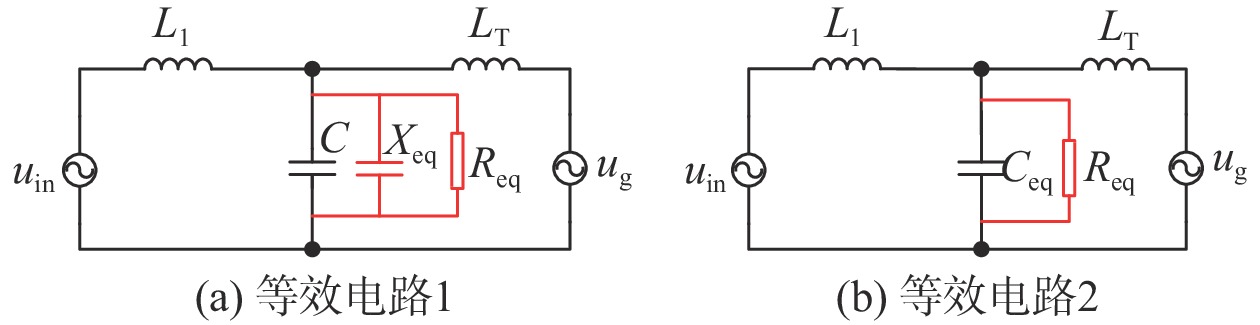
由此可以得到如图5(a)所示等效电路,将Zeq(s)与电容器并联可得出图5(b)所示等效电路,其中Ceq可由(20)表示,对应的谐振频率记为
|
| 图 5 IICFAD等效电路 |
| $ {C_{{\text{eq}}}}(\omega ) = \frac{{{\rm j}{X_C}//{\rm j}{X_{{\text{eq}}}}}}{\omega } = \frac{C}{{1 - \omega C{X_{{\text{eq}}}}}} $ | (20) |
| $ {\omega }_{r}'=\sqrt{\frac{{L}_{1}+{L}_{T}}{{L}_{1}{L}_{T}{C}_{\text{eq}}}} $ | (21) |
将(20)代入(21)可以得到表示等效容抗的计算式(22),再如图5(b)所示,结合(10)和(11)可以得到阻尼系数ζ1和等效电路下的开环传递函数GLCL(s)表达式分别为(23)(24)。
| $ {X_{{\text{eq}}}}(\omega _r^{'}) = \frac{{\omega {{_r^{'}}^2} - {\omega _r}^2}}{{{\omega _r}^2\omega _r^{'}C}} $ | (22) |
| $ {\zeta _1}{\text{ }} = \frac{1}{{2{C_{{\text{eq}}}}{R_{{\text{eq}}}}\omega _r^{'}}} = \sqrt {\frac{{4{R_{{\text{eq}}}}^2({L_1} + {L_T}){C_{{\text{eq}}}}}}{{{L_1}{L_T}}}} $ | (23) |
| $ {G_{{\text{LCL}}}}(s) = \frac{1}{{{L_1}{C_{{\text{eq}}}}{L_T}{s^3} + {L_1}{L_T}/{R_{{\text{eq}}}}{s^2} + \left( {{L_1} + {L_T}} \right)s}} $ | (24) |
对比式(24)和(13)可以知道,两个表达相等,可实现相互转换。
2.2 控制效果优化将(15)和(19)代入(22)可以得到总阻尼增益K与等效电路下的谐振频率
| $ K = \frac{{\left( {{L_1} + {L_T}} \right)\omega _r^{'}{\omega _r}}}{{{L_1}{L_T}{K_{{\text{PWM}}}}\left( {\omega {{_r^{'}}^2} - {\omega _r}^2} \right)\sin (1.5\omega {T_S})}} $ | (25) |
将(15)、(18)~(20)代入(24)可以得到总阻尼增益下的阻尼系数计算式(26),结合系统传递函数及阻尼系数特性,可以知道阻尼果,
| $ {\zeta _1}(\omega _r^{'}) = \frac{{\cos (1.5\omega _r^{'}{T_S})\left( \begin{gathered} {K_{{\text{PWM}}}}K\sin (1.5\omega _r^{'}{T_S}) - \\ {\omega _r}C\omega _r^{'} \\ \end{gathered} \right)}}{{2{\omega _r}C\omega _r^{'}}} $ | (26) |
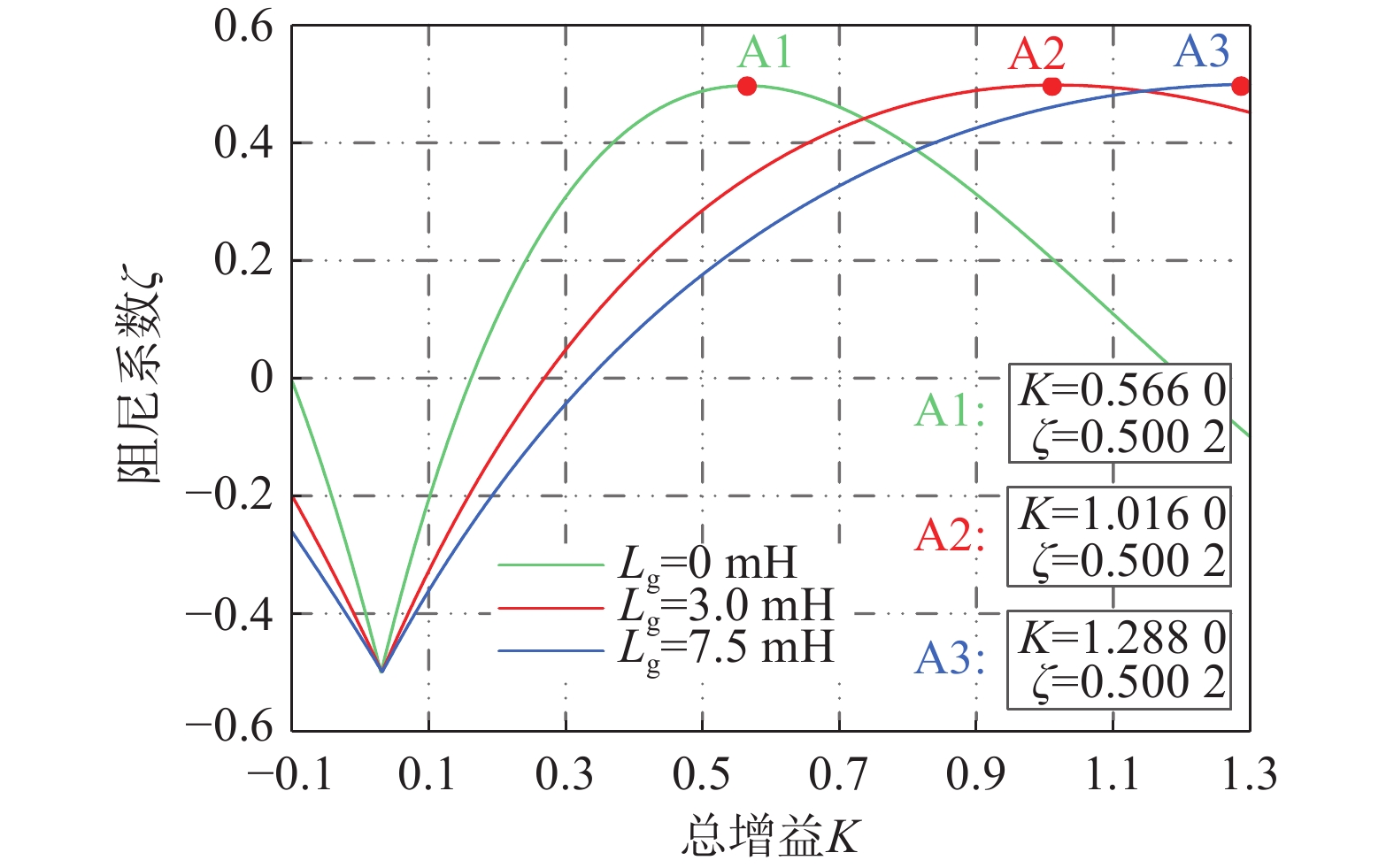
由式(26)结合如表1所示系统电路参数,可以得到阻尼系数与总增益K之间关系如图6所示。
| 参数 | 值 | 参数 | 值 |
| 电感L1 | 3.50 mH | 母线电压 | 600 V |
| 电感L2 | 1.75 mH | 逆变增益 | 200 |
| 电感Lg | 6.00 mH | 开关频率 | 10 kHz |
| 电容C | 47.0 μF | 采样频率 | 50 kHz |
| 电网电压vg/fg | 220 V(RMS)/50 Hz |
|
| 图 6 不同电网下阻尼因子与K的关系图 |
由图可知,电网特性不同时,阻尼系数随K值变化的总体趋势相同,在低阻尼增益情况下,存在负阻尼区域;随着总阻尼增益K的增大,可以达到最优阻尼,而超出最优阻尼后,继续增大K值,系统总阻尼将会减小,可定义阻尼大于0小于最优阻尼的状态为欠阻尼状态。由此结合图示曲线可知在不同电网条件下均存在最优阻尼ζ=
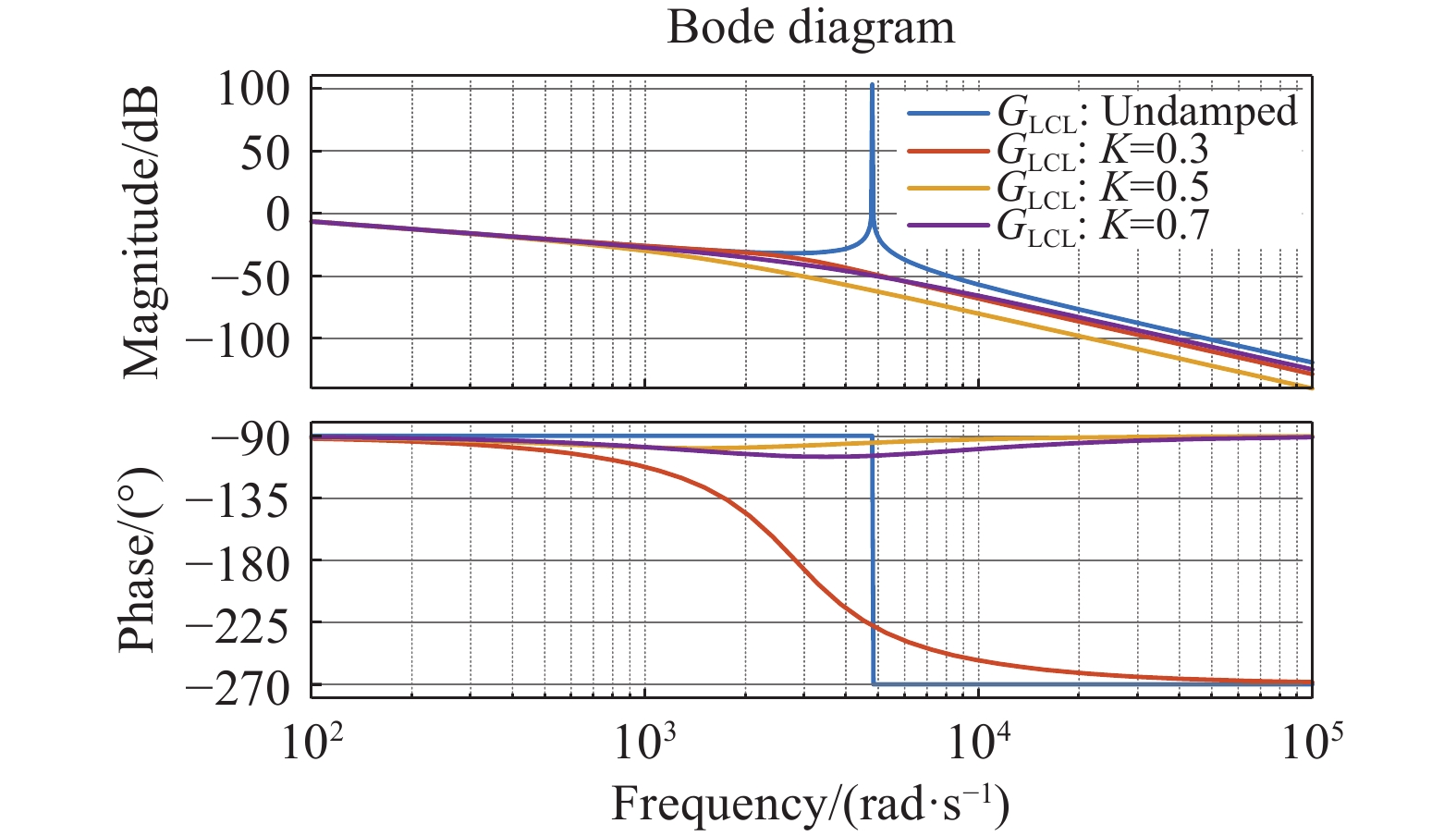
根据式(24)绘制并网逆变器电流反馈增益变化时的开环传递函数伯德图如图7所示,其中Lg=3.0 mH。
|
| 图 7 不同K值下IICFAD方法开环伯德图 |
由图对比无阻尼增益K和任意阻尼增益K的曲线可知,当采用IICFAD反馈控制时,能有效抑制LCL谐振。进一步对系统进行幅频和相频分析如下:对比总阻尼增益K取值为0.3、0.5和0.7三种情况下的幅频曲线可知,当总阻尼增益小于最优阻尼增益时,低频段随着总阻尼增益的增大会出现增益降低的情况,但会随着总阻尼增益实现最优阻尼而得到改善,而高频段在欠阻尼区域时即可实现较高的高频谐波抑制,随着总阻尼增益的增大,高频谐波衰减能力将会减小,但总体上仍优于无增益系统的高频衰减能力。此外对比其相频曲线可知,随着总阻尼增益K的增大,相频曲线将不再穿越-180°,可见随着K值的增大,系统将具有较好的相角裕度。根据内奎斯特稳定判据,此时系统稳定性可由幅值裕度直接确定。
为进一步说明IICFAD方法,结合(4)~(7)得到H1(s)的表达式如(27)所示,其中比例系数(KH1+KH2)揭示了逆变侧电感电流比例反馈增益,二阶积分环节揭示了逆变侧电感电流反馈的积分补偿。
| $ \begin{split} {H_1}(s) = &\frac{{{H_{11}}(s){G_{{\text{ic}}}}(s) + {H_{12}}(s){G_{{\text{iL2}}}}(s)}}{{{G_{{\text{ic}}}}(s) + {G_{{\text{iL2}}}}(s)}}= \\ & ({K_{{\text{H1}}}} + {K_{{\text{H2}}}}) - \frac{{{K_{{\text{H1}}}} + {K_{{\text{H2}}}}}}{{1 + {L_T}C{s^2}}} \end{split} $ | (27) |
如式(27)所示,其中控制参数为(KH1+KH2)可由总控制增益进行计算,满足式(28)。
| $ ({K_{{\text{H1}}}} + {K_{{\text{H2}}}}) = K - {K_p} $ | (28) |
实际运行时,电网参数变化对系统稳定性作用非常重要,因此有必要分析包含IICFAD的系统在电网参数变化情况下的稳定特性。
考虑刚性电网情况,取Lg=0 mH和Lg=3.0 mH,由图6和图7可知,随着电网感抗增加,K的稳定阈值增大,最优阻尼系数保持在
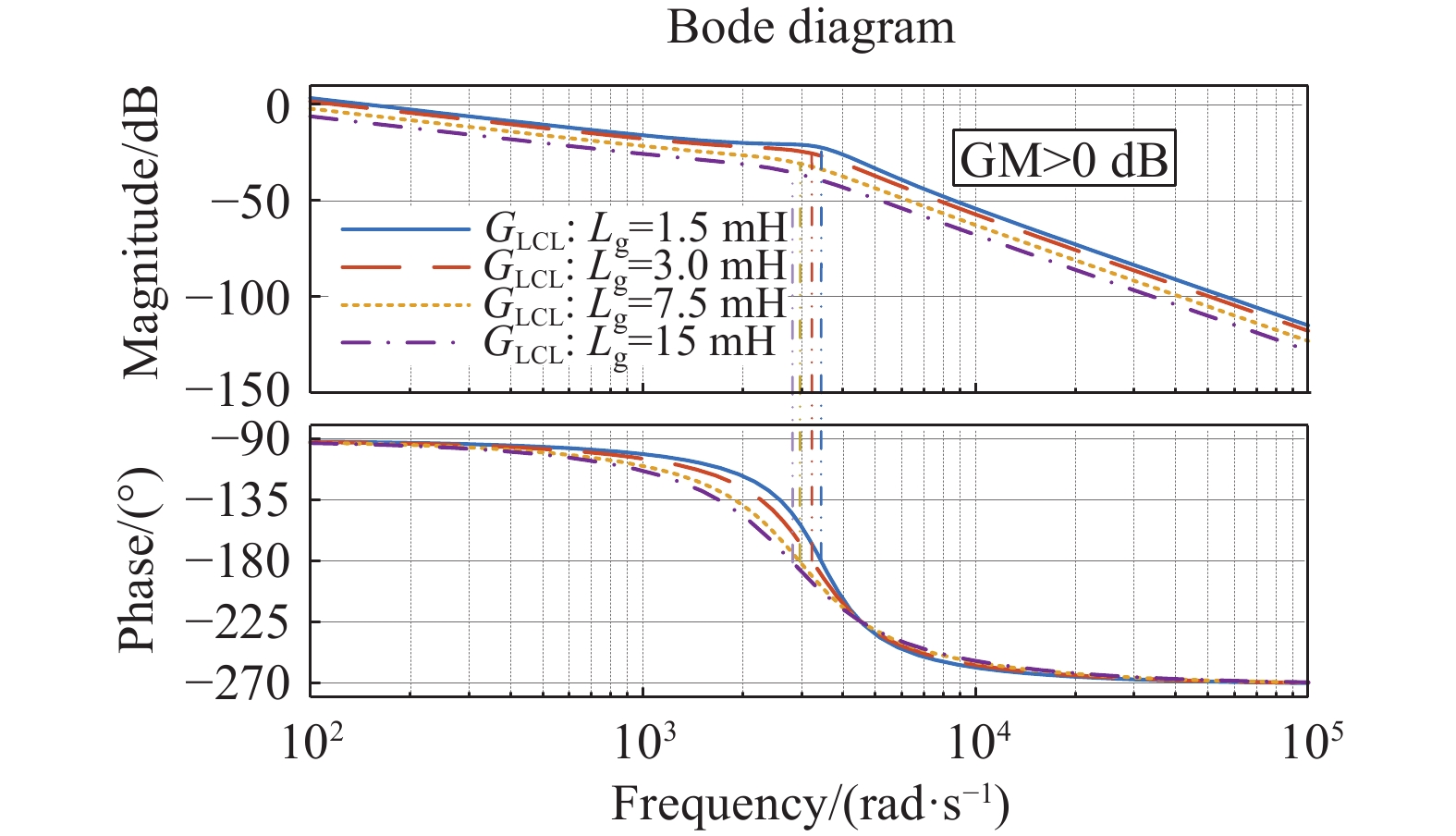
为验证本文所提方法在弱电网下也具有较好的性能,绘制系统增益为Lg=15 mH的最优阻尼增益时,电网参数从刚性电网到弱电网变化的系统Bode图如图8所示。
|
| 图 8 不同电网条件下系统开环伯德图 |
对比图中电网电感Lg=1.5、3.0、7.5、15 mH下的曲线可知,LCL谐振峰变得平滑,这表明阻尼因子增大。此外,随着电网性能的减弱,系统低频特性逐渐减小,其截止频率和穿越频率均在减小,同时系统幅值裕度GM>0,根据奈奎斯特稳定判据可知,最优阻尼参数在弱电网也可实现稳定并网,单独计算弱电网Lg=15 mH下的幅值裕度和相角裕度分别为:55 dB和89°,可见弱电网下系统仍具有较高的稳定裕度。
3 实验验证为验证所提方法的有效性,本文设计仿真实验和30 kW样机实验如下[15]。
3.1 仿真验证仿真实验采用Simulink平台,搭建LCL型并网逆变器模型,就文献[12]所提控制方法和本文所提控制方法进行对比分析。系统参数由表1给出。
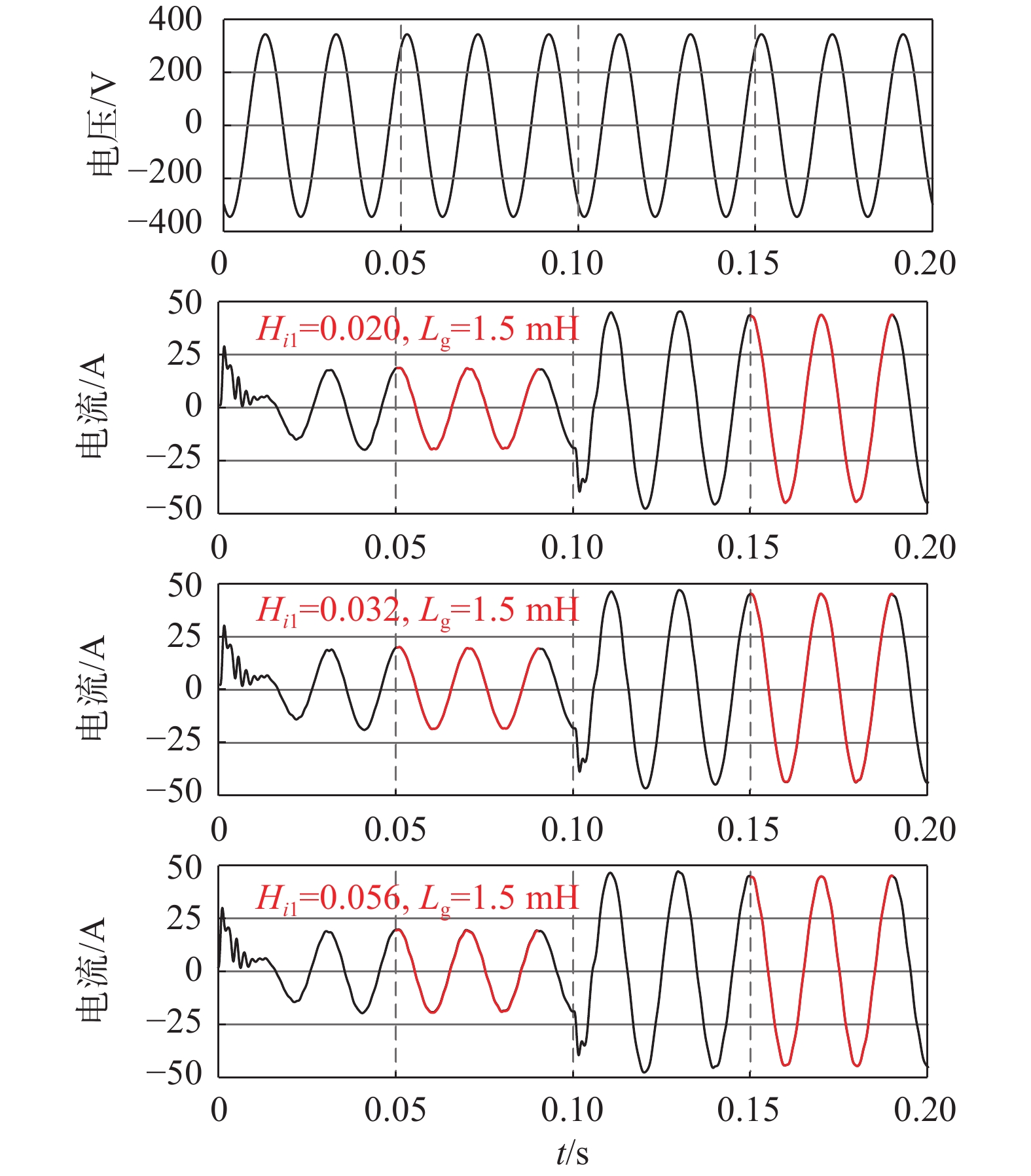
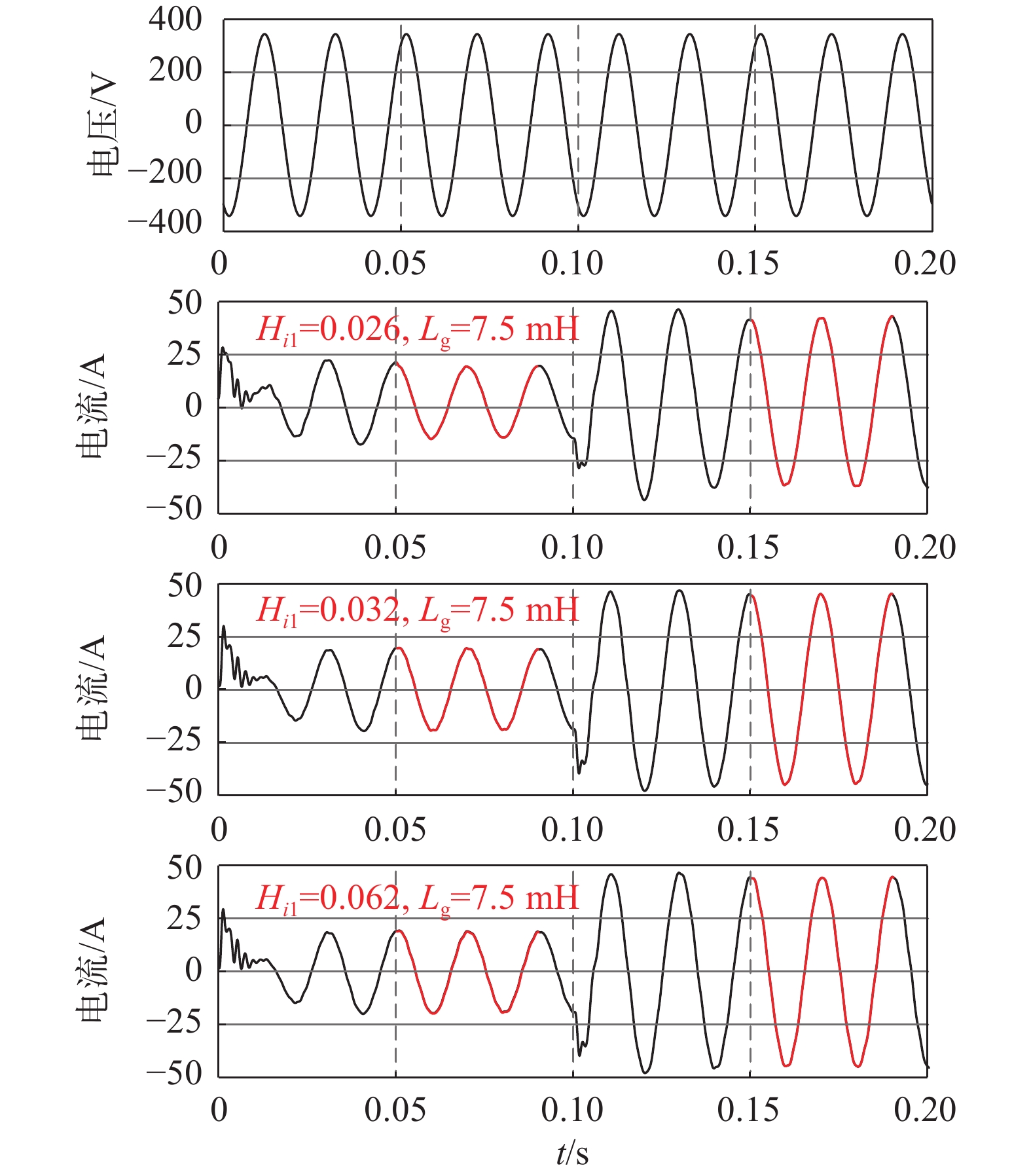
采用文献[12]所述方法。在0.1 s时给定并网电流由20 A到45 A突变,获取刚性电网和弱电网下并网电压和电流波形分别如图9和图10所示。
|
| 图 9 刚性电网:ICFAD方法仿真波形 |
|
| 图 10 弱电网:ICFAD方法仿真结果 |
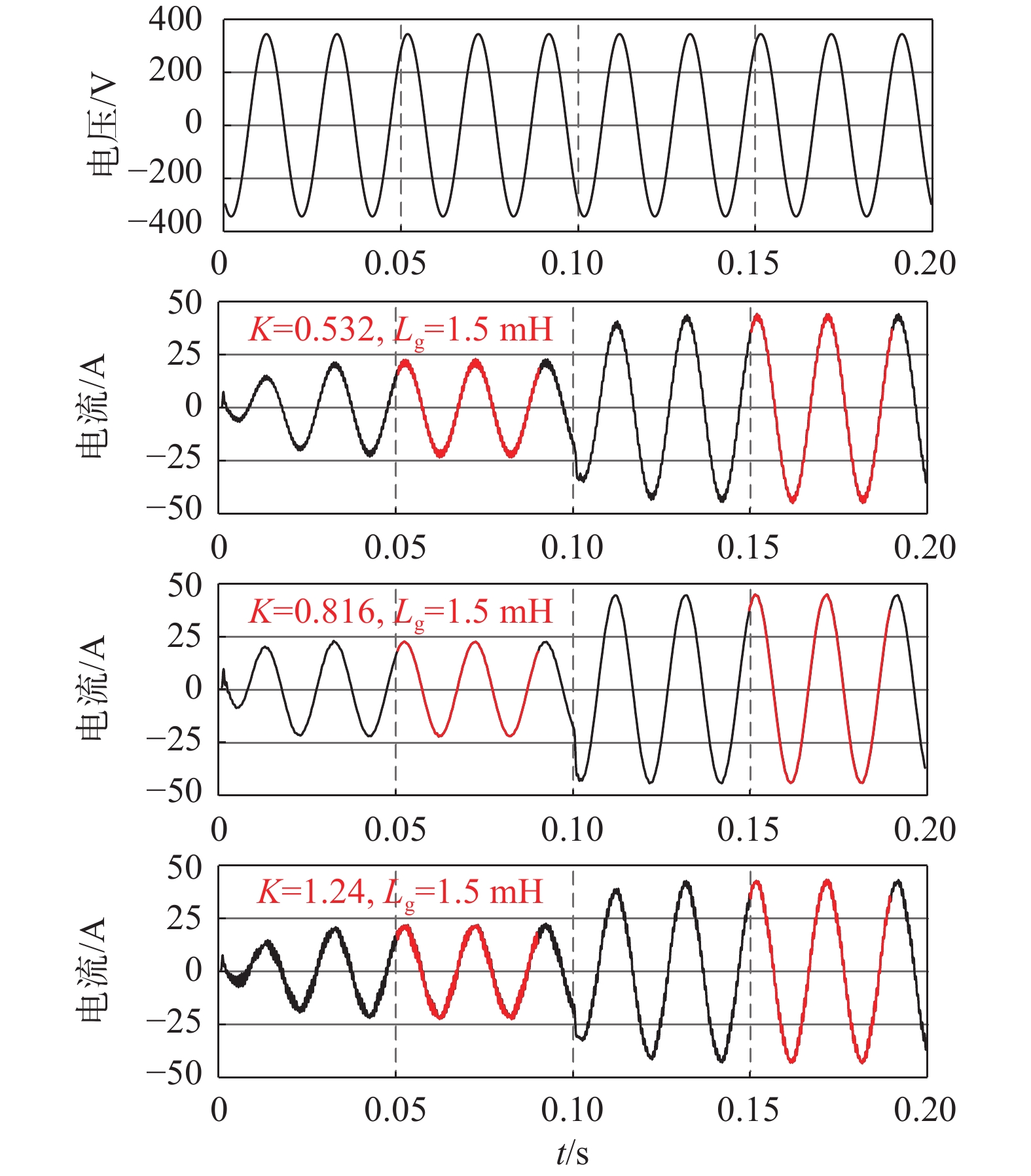
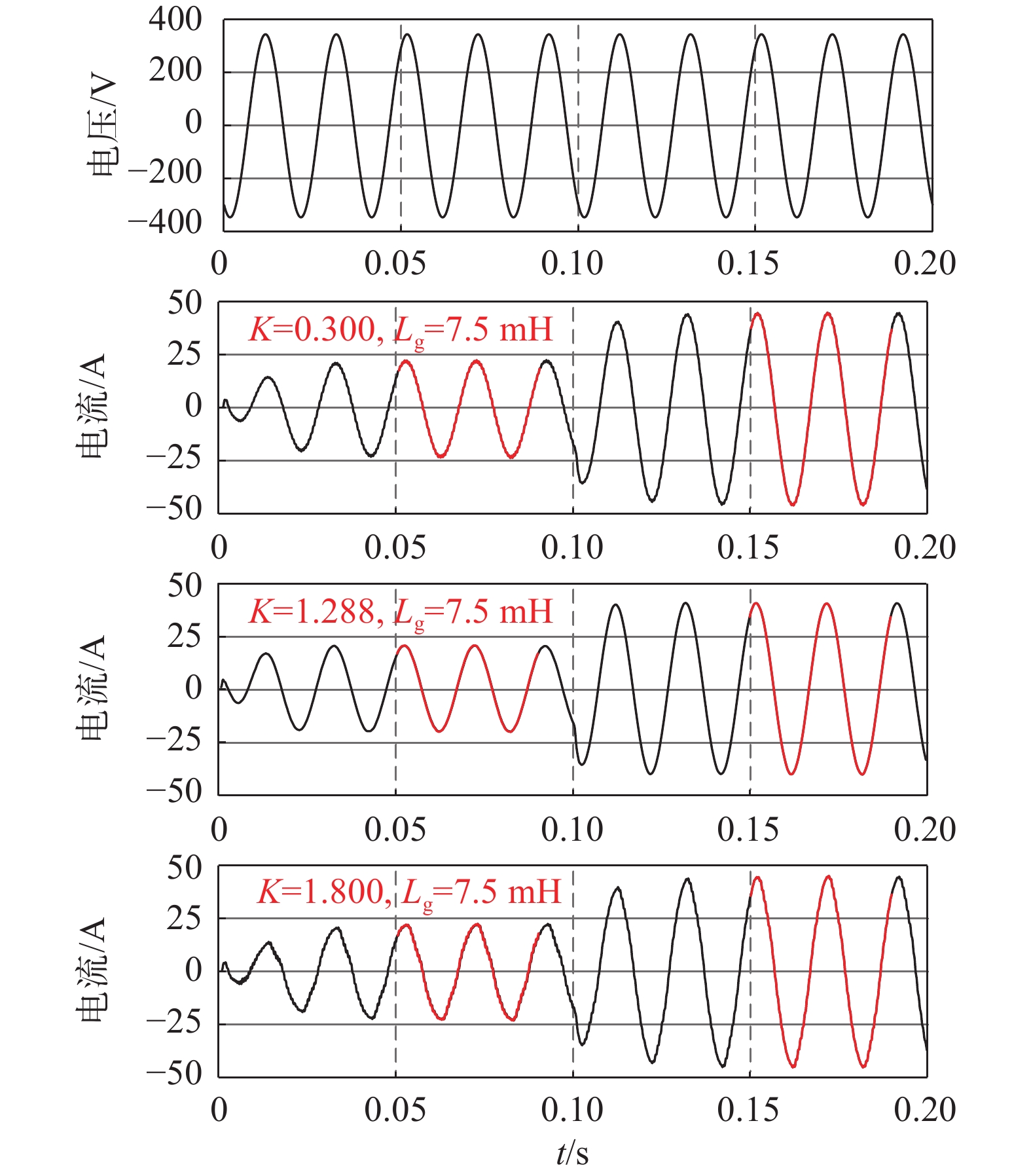
由本文所述IICFAD方法搭建仿真模型。同理,给出电网电流给定值从20A到45A突变时刚性电网和弱电网的并网电流波形分别如图11和图12所示。其中,K值分别为当前电网条件时的欠阻尼、最优阻尼情况。
|
| 图 11 刚性电网:IICFAD方法仿真结果 |
|
| 图 12 弱电网:IICFAD方法仿真结果 |
截取图中电流波形稳态周期进行谐波分析得到并网电流谐波和基波参数分别如表2和表3所示。
| % | |||||||
| 方法 参数 |
ICFAD | IICFAD | |||||
| Lg=1.5 mH | 0.020 | 8.29 | 3.78 | 0.532 | 1.98 | 1.09 | |
| 0.032 | 1.04 | 0.65 | 0.816 | 1.32 | 0.94 | ||
| 0.056 | 13.14 | 6.49 | 1.240 | 2.53 | 1.72 | ||
| Lg=7.5 mH | 0.026 | 2.82 | 1.16 | 0.300 | 3.72 | 1.48 | |
| 0.032 | 0.56 | 0.31 | 1.288 | 1.68 | 0.89 | ||
| 0.062 | 5.24 | 2.55 | 1.800 | 3.44 | 1.47 | ||
| % | |||||||
| 方法 参数 |
ICFAD | IICFAD | |||||
| Lg=1.5 mH | 0.020 | 18.06 | 43.11 | 0.532 | 18.97 | 44.17 | |
| 0.032 | 19.09 | 43.93 | 0.816 | 19.75 | 44.83 | ||
| 0.056 | 17.04 | 42.11 | 1.240 | 18.93 | 43.89 | ||
| Lg=7.5 mH | 0.026 | 19.16 | 44.30 | 0.300 | 19.53 | 44.52 | |
| 0.032 | 19.38 | 44.31 | 1.288 | 19.67 | 44.80 | ||
| 0.062 | 18.53 | 43.88 | 1.800 | 19.52 | 44.52 | ||
结合图9、图10和表2参数分析可知,ICFAD方法在刚性电网和弱电网情况下的最优控制效果分别可用增益参数为0.032时0.05 s和0.15 s开始的两个周期内谐波含量来表示,其谐波含量分别为1.04%,0.65%,0.56%,0.31%,总谐波含量较低,但是通过对系统的增益参数进行调节,系统稳定性变化较大,当增益参数为0.056和0.062时,刚性电网与弱电网的总谐波含量已不满足并网需求,可见此时该方法高频谐波抑制能力减弱。
结合图11、图12和表2参数分析可知,IICFAD方法在刚性电网和弱电网情况下的最优控制效果分别可用增益参数为0.816和1.288两种情况下的从0.05 s和0.15 s开始的两个周期内谐波含量来表示,其谐波含量分别为1.32%,0.98%,1.68%,0.89%,总谐波含量较低。此外调节阻尼增益取值,当K取较小值时,分析其谐波含量分别为:1.98%,1.09%,3.72%,1.48%;当K=1.8时谐波含量分别为2.53%,0.72%,此当K取较大值时,分析其谐波含量分别为:2.53%,1.72%,3.44%,1.47%可见,随着K的增大,谐波含量由大减小再增大,满足上述不同电网下的最优阻尼增益分析,且均满足并网需求。
对比图9、图11和图10、图12可知:IICFAD方法具有更宽的控制参数设计范围和更优异的阻尼控制效果,与前文理论分析一致;再结合表3数据,本文所提方法在相同的系统参数下具有更好的控制跟随特性,尤其在基波频率附近其基波含量更接近给定值,可见低频增益效果较好。
3.2 实验验证为进一步验证本文所提方法的有效性,搭建30 kW并网逆变器实验样机,如图13所示。通过样机实验完成本文方法的验证,整个实验将三相两电平逆变器通过三相LCL滤波器与三相调压器相连,即进行低压并网实验完成验证。

|
| 图 13 样机实验平台 |
不考虑三相电网不平衡情况[15],以A相为例,设计刚性电网下恒定电流、电流突变并网实验和弱电网下的恒电流并网实验如下。
实验一:刚性电网下,通过调压器调节电网电压为150 V,进行给定电流1 A进行最优阻尼增益恒电流并网实验。实验波形如图14所示。
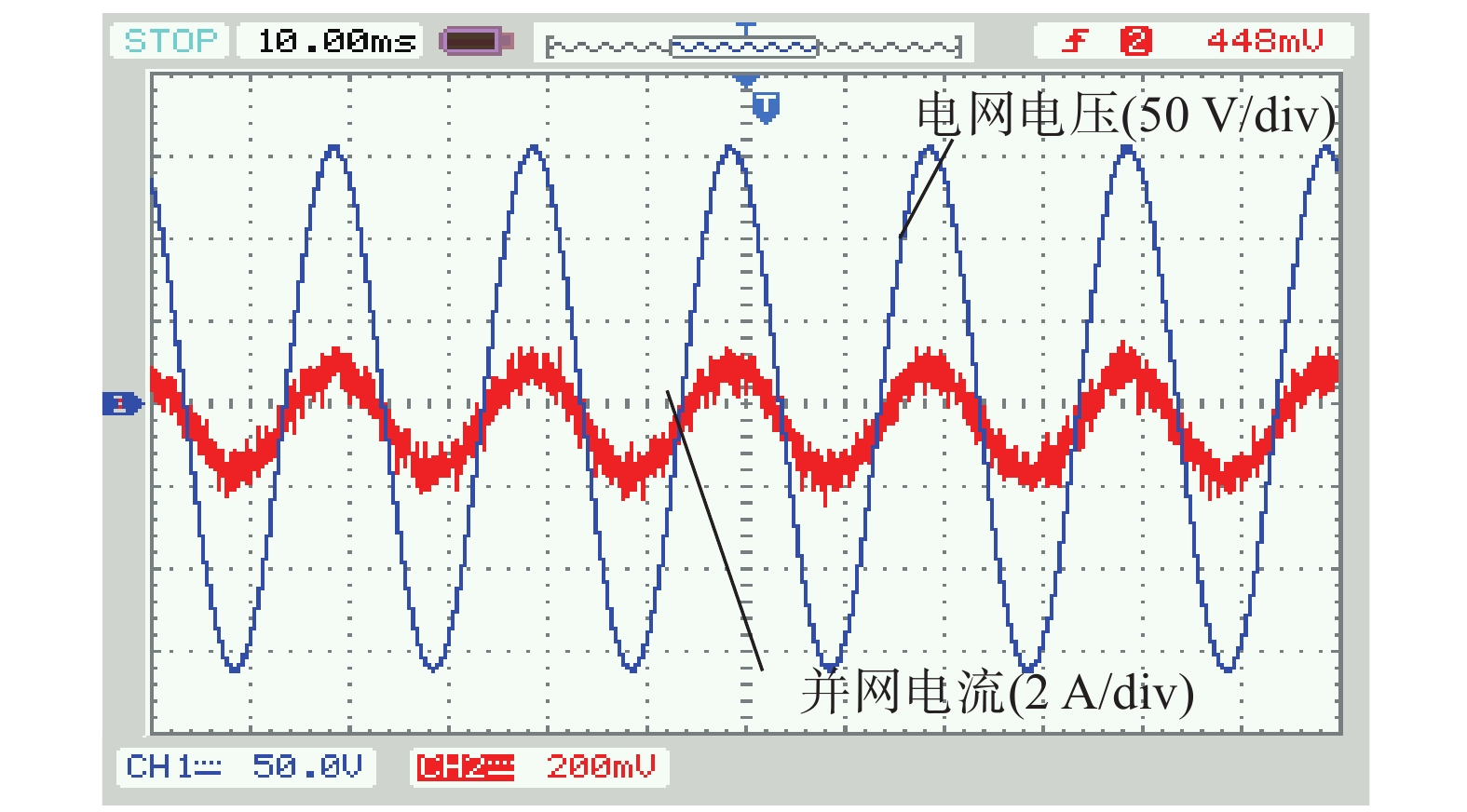
|
| 图 14 刚性电网:恒电流并网 |
实验二:刚性电网下,通过调压器调节电网电压为150 V,将并网电流给定值由1 A突变为2 A,进行最优阻尼增益变电流并网实验。实验波形如图15所示。

|
| 图 15 刚性电网:变电流并网 |
实验三:弱电网下,通过调压器调节电网电压为150 V和100 V,给定电流2A分别进行欠阻尼增益和最优阻尼增益实验。实验波形如图16和图17所示。
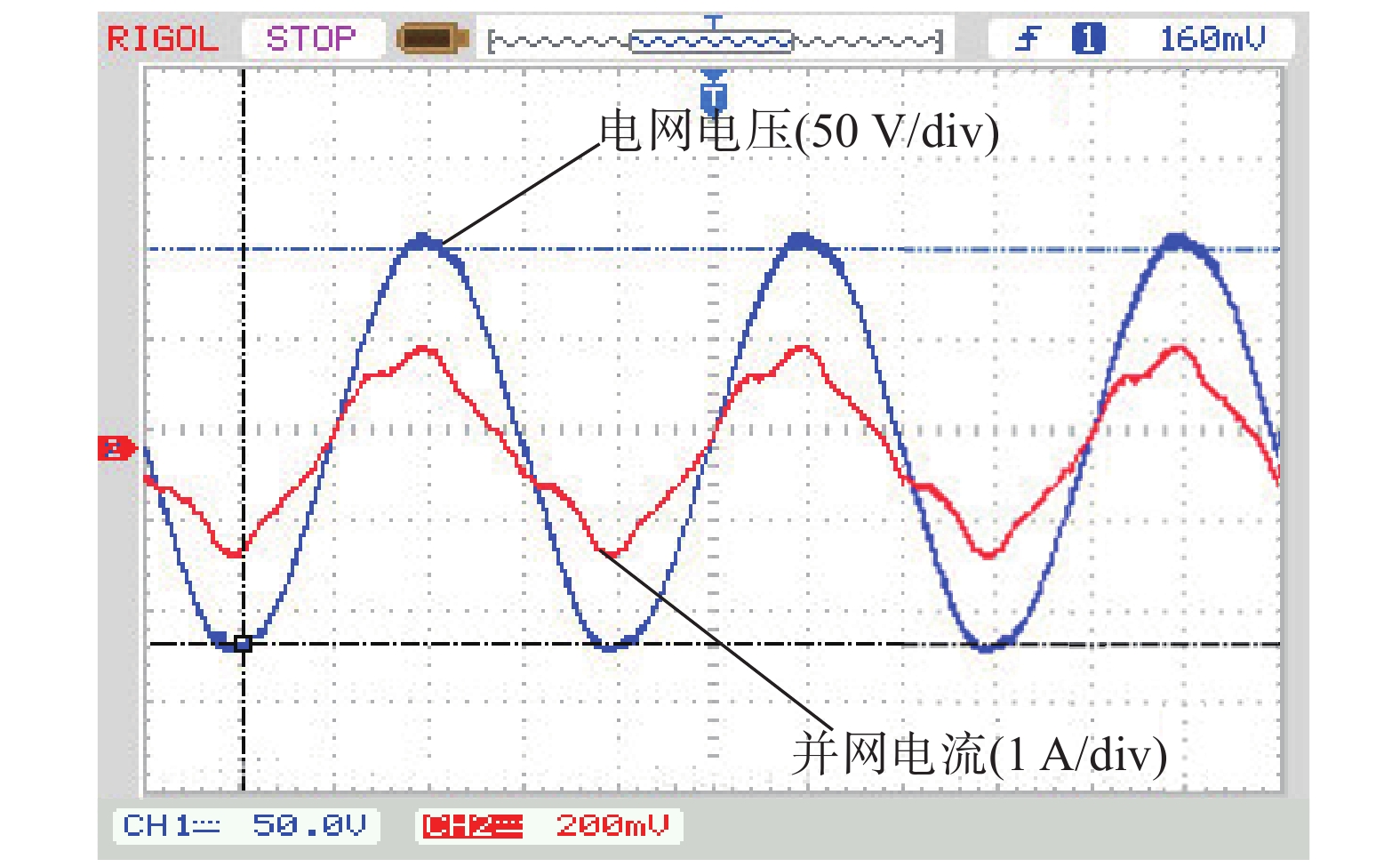
|
| 图 16 弱电网:欠阻尼恒电流并网 |
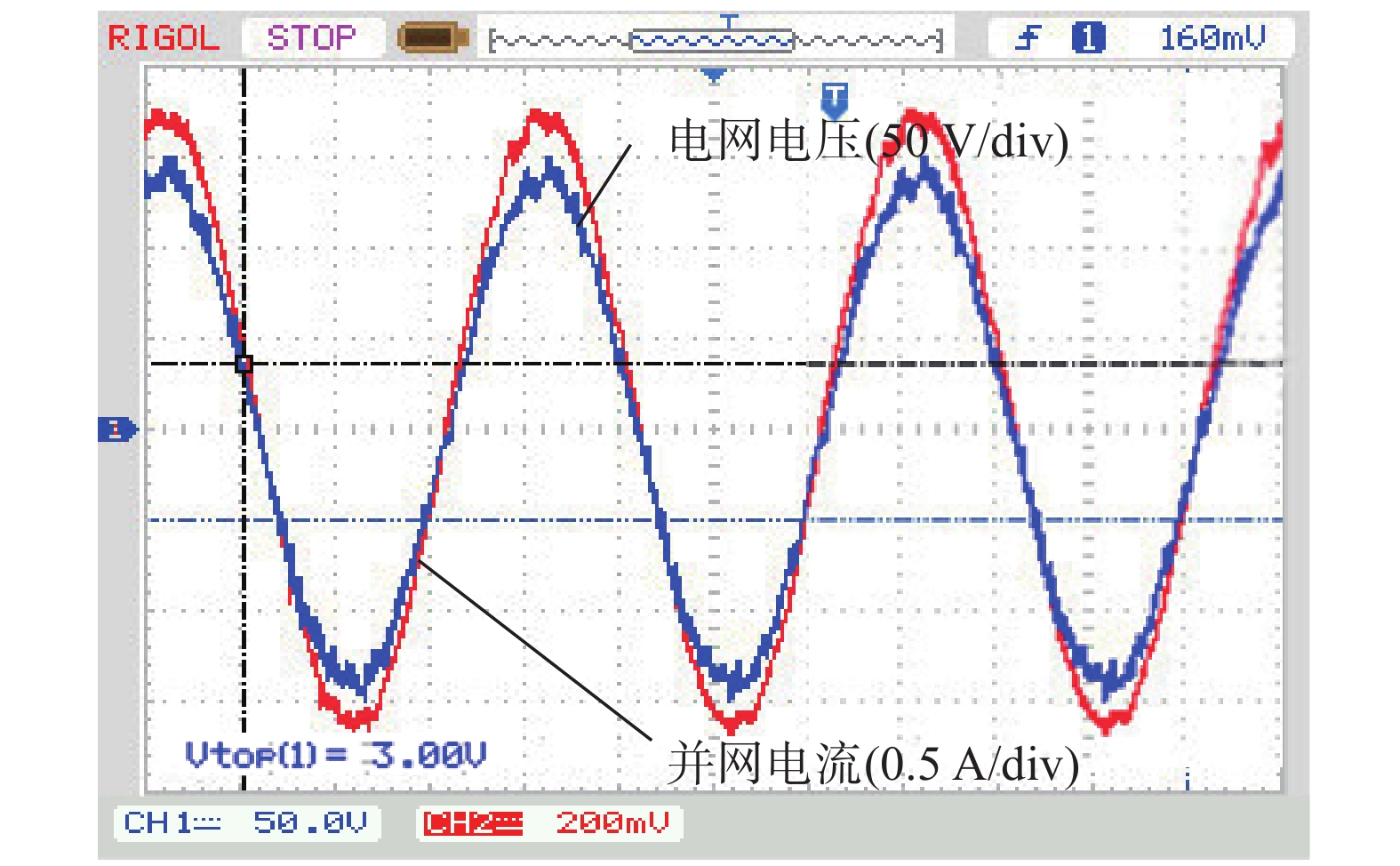
|
| 图 17 弱电网:最优阻尼恒电流并网 |
结合样机实验可知,本文所提方法在刚性电网下能够较好的完成恒定电流和变电流并网运行,系统动态和稳态性能良好。弱电网下,欠阻尼增益时并网电流波形杂乱,系统稳定性较差;但在最优阻尼增益情况下并网电流波形较好,并网电流谐波含量降低,能够实现稳定并网。
4 结束语本文针对并网逆变器使用LCL滤波器存在谐振影响逆变器并网稳定性的问题,通过对现有谐振抑制方法的分析,指出AD和PD谐振抑制方法固有特点,并就有源阻尼谐振抑制方案出发,提出一种仅逆变侧电感电流反馈的谐振抑制方法。基于等效电路和系统稳定性分析,指出逆变侧电流反馈环节参数设计方案,借助Matlab/Simulink平台和30 kW实验样机,通过仿真及实验得出以下结论。
1) 所提出的控制算法解决了ICFAD方法低频增益不足的问题,同时得到可进行更宽范围取值的控制参数。
2) 所提方法直接控制逆变侧电流,受电网阻抗变化影响小,可实现高质量并网电流波形。
3) 所提方法采用逆变侧电感电流进行反馈控制,无需添加信号传感器,降低成本的同时,也实现了对并网逆变器的注入功率控制、过流保护和谐振抑制等功能。
本文所提控制方法为高性能、中小功率并网逆变器的研制提供了有效的解决方案。
| [1] |
BOSCH S, STAIGER J, STEINHART H. Predictive current control for an active power filter with LCL-filter[J] IEEE Transactions on Industrial Electronics, 2018 65(6): 4943-4952.
|
| [2] |
周成虎, 黄明明, 高振东, 等. 三相LCL/P补偿无线充电系统设计与建模分析[J].
中国测试, 2022, 48(8): 86-93.
ZHOU C H, HUANG M M, GAO Z D, et al. Design and modeling analysis of three-phase LCL/P compensation wireless charging system[J].
China Measurement & Test, 2022, 48(8): 86-93.
|
| [3] |
李彦哲, 保婷婷. 三相LCL光伏并网逆变器的新型入网控制策略[J].
控制工程, 2018, 25(8): 1511-1515.
LI Y Z, BAO T T. A novel grid connection control strategy for three-phase LCL photovoltaic grid connected inverters[J].
Control Engineering of China, 2018, 25(8): 1511-1515.
|
| [4] |
ALZOLA R P, LISERRE M, BLAABJERG F, et al. Self-commissioning notch filter for active damping in three phase LCL-filter based grid converters[A]. 2013 15th European Conference on Power Electronics and Applications (EPE), 2013: 1-9.
|
| [5] |
YAO W L, YANG Y H, ZHANG X B, et al. Design and analysis of robust active damping for LCL filters using digital notch filters[J].
IEEE Transactions on Power Electronics, 2017, 32(3): 2360-2375.
DOI:10.1109/TPEL.2016.2565598 |
| [6] |
王渝红, 叶葳, 宋瑞华, 等. 基于阻抗分析法的三相LCL型并网逆变器附加有源阻尼设计[J].
高电压技术, 2021, 47(8): 2645-2656.
WANG Y H, YE W, SONG R H, et al. Design of additional active damping for three-phase LCL grid connected inverters based on impedance analysis method[J].
High Voltage Engineering, 2021, 47(8): 2645-2656.
|
| [7] |
ZHANG H, RUAN X B, LIN Z H, et al. Capacitor voltage full feedback scheme for LCL-Type grid-connected inverter to suppress current distortion due to grid voltage harmonics[J].
IEEE Transactions on Power Electronics, 2021, 36(3): 2996-3006.
DOI:10.1109/TPEL.2020.3014338 |
| [8] |
梁文科, 苏淑靖, 梁东飞, 等. 一种逆变器并网电流采集与过流检测方法[J].
电子测量技术, 2021, 44(13): 11-16.
LIANG W K, SU S J, LIANG D F, et al. A method for collecting grid connected current and detecting overcurrent in inverters[J].
Electronic Measurement Technology, 2021, 44(13): 11-16.
|
| [9] |
吴云亚, 谢少军, 阚加荣, 等. 逆变器侧电流反馈的LCL并网逆变器电网电压前馈控制策略[J].
中国电机工程学报, 2013, 33(6): 54-60.
WU Y Y, XIE S J, KAN J R, et al. LCL grid connected inverter grid voltage feedforward control strategy based on inverter side current feedback[J].
Proceedings of the CSEE, 2013, 33(6): 54-60.
|
| [10] |
贺诗明, 熊健. 基于牛顿插值的LCL型并网逆变器机侧电流反馈延时补偿策略[J].
电网技术, 2020, 44(12): 4766-4772.
HE S M, XIONG J. A delay compensation strategy for machine side current feedback in LCL grid connected inverters based on newton interpolation[J].
Power System Technology, 2020, 44(12): 4766-4772.
|
| [11] |
边志维, 何远彬, 吴圆圆, 等. 一种提高LCL型并网逆变器无源性及抗扰性的网侧电流控制策略[J].
中国电机工程学报, 2022, 42(6): 2175-2186.
BIAN Z W, HE Y B, WU Y Y, et al. A grid side current control strategy to improve the passivity and disturbance immunity of LCL type grid connected inverters[J].
Proceedings of the CSEE, 2022, 42(6): 2175-2186.
|
| [12] |
CHEN W, ZHANG Y, TU Y M, et al. Active damping control for LCL filters with inverter-side current feedback only[J].
IEEE Transactions on Power Electronics, 2022, 37(9): 10065-10069.
DOI:10.1109/TPEL.2022.3159229 |
| [13] |
薛家祥, 张坤, 郑照红. 光伏离网逆变器并联控制系统研究[J].
中国测试, 2017, 43(3): 63-68.
XUE J X, ZHANG K, ZHENG Z H. Research on parallel control system of photovoltaic off grid inverters[J].
China Measurement & Test, 2017, 43(3): 63-68.
DOI:10.11857/j.issn.1674-5124.2017.03.013 |
| [14] |
CHKIOUA A, HMAD J, ABID H, et al. Design and performance analysis of different resonance passive-damping solutions for LCL filter-based grid-interfaced DG inverter[A]. 2019 19th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), 2019: 435-441.
|
| [15] |
陈峻峰, 郎宝华, 张宏鹏. 新型Z源并网逆变器的研究[J].
国外电子测量技术, 2020, 39(12): 54-59.
CHEN J F, LANG B H, ZHANG H P. Research on new Z-source grid connected inverters[J].
Foreign Electronic Measurement Technology, 2020, 39(12): 54-59.
|
 2024, Vol. 50
2024, Vol. 50