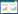文章信息
- 何太碧, 何风成, 杜文, 袁伟杰, 贾瑞, 韩锐
- HE Taibi, HE Fengcheng, DU Wen, YUAN Weijie, JIA Rui, HAN Rui
- 埋地输氢管道泄漏扩散规律研究
- Research on the leakage and diffusion law of buried hydrogen pipeline
- 中国测试, 2024, 50(8): 171-179
- CHINA MEASUREMENT & TEST, 2024, 50(8): 171-179
- http://dx.doi.org/10.11857/j.issn.1674-5124.2024060043
-
文章历史
- 收稿日期: 2024-06-12
- 收到修改稿日期: 2024-07-19
2. 西华大学材料科学与工程学院,四川 成都 610039
2. School of Materials Science and Engineering, Xihua University, Chengdu 610039, China
高压气氢输送是主要的运氢方式,有着充放速度快、成本低的优点[1],同时管道运输是氢能产业链中重要的一环,是实现氢气大规模、长距离输运的重要方式之一,具有效率高、能耗低、经济效益好等优点,是未来运氢的终极方向。根据相关规划,截至 2030 年,我国氢气长输管道总里程将达到
目前,国内外已有众多学者对埋地管道的泄漏扩散进行了一系列研究。陈一鸣等人[3]将声比拟法(FW-H)与计算流体动力学(CFD)理论相结合,对管道泄漏声场进行仿真模拟,以计算泄漏声场气动噪声源的类型与声强信号。结果表明,埋地管道发生泄漏后,管外土壤中泄漏流体的速度变化梯度较大,泄漏声场的声波强度与管道内压、泄漏口直径大小呈正相关。胡玮鹏[4]、罗宗林[5]等人将气体泄漏等效为在大气中添加稳定排出气体的小孔,研究其扩散情况。Sun等人[6]将管路等效为电路,根据电学公式推导出了计算管道泄漏率和泄漏处上下游压力等参数的公式,且与实验结果吻合度良好。Zhang等人[7]研究了埋地输氢管道的渗漏孔、土体类型、管道压力、管道直径对氢气泄漏扩散的影响。Wang等人[8]对管廊中混氢天然气的泄漏与扩散特性进行了研究,并提出了一种新的扩散系数模型,评估了影响气体泄漏和扩散规律的因素。Bagheri等人[9]基于优化理念,建立了全面的土壤分类模型来估算埋地天然气管道的渗漏率。钟明杉等人[10]则是通过使用卷积神经网络对管道的泄漏进行检测和定位。
综上所述,现有针对埋地管道的研究多为天然气管道或天然气掺氢管道,对埋地输氢管道的研究较少。因此本文基于Fluent建立了包括管道、土壤、大气的完整泄漏扩散模型,以求在氢气不同土壤条件、泄漏孔径、管道压力等因素下的扩散规律。
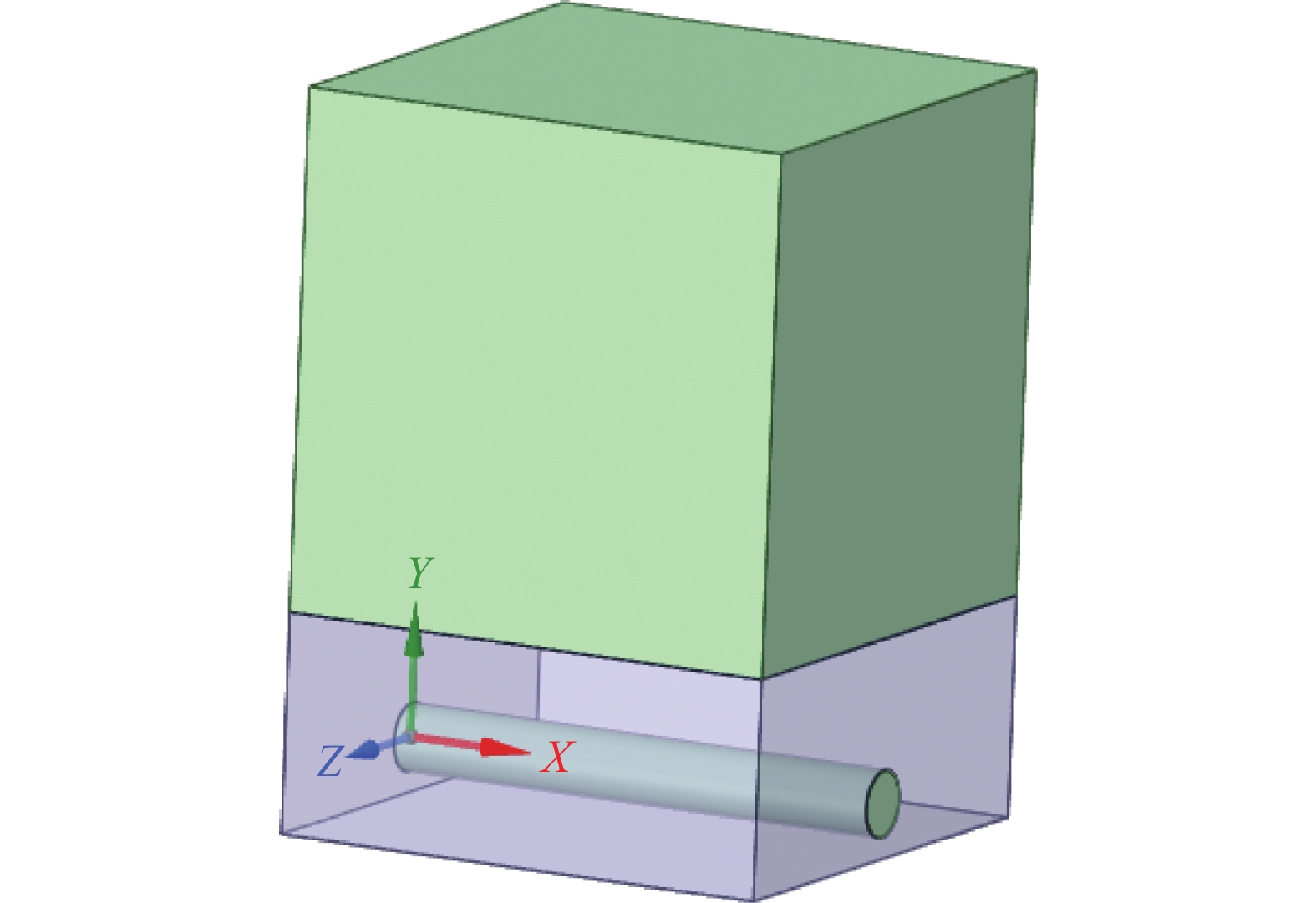
1 模型建立 1.1 流体域模型选取埋地输氢管道为研究对象,建立如图1所示完整流体域模型,该模型包括了管道、土壤、大气三个部分。为监测氢气在土壤和大气中的扩散情况,在该模型的土壤和大气中共设置如图2所示的4个监测点,其中监测点1、2位于土壤内,监测点3位于土壤大气的界面、监测点4位于大气中。
|
| 图 1 模型示意图 |
|
| 图 2 监测点示意图 |
1.2 数学模型 1.2.1 组分输运方程
由于本文旨在计算氢气在空气中的扩散情况,涉及到组分运输问题,需要利用组分运输方程对其扩散过程进行描述。
| $ \frac{{\partial \left( {\rho {c_s}} \right)}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_j}{c_s}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{D_s}\frac{{\partial \left( {\rho {c_s}} \right)}}{{\partial {x_j}}}} \right) $ | (1) |
式中:cs——组分s的体积分数;
uj——j 方向的速度,m/s;
Ds——组分s的扩散,m2/s。
1.2.2 湍流方程氢气在管道中的流动往往以湍流状态进行,因此需要利用湍流模型对该过程进行描述。
湍流动能控制方程k为:
| $ \frac{\partial }{{\partial {x_j}}}\left( {\rho k{u_j}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {\mu _t}\frac{{\partial {u_i}}}{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \rho \varepsilon$ | (2) |
耗散率的控制方程ɛ为:
| $ \begin{split} \frac{\partial }{{\partial {x_j}}}\left( {\rho \varepsilon {u_j}} \right) =& \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\ & {C_{1\varepsilon }}\frac{\varepsilon }{k}{\mu _t}\frac{{\partial {u_i}}}{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} \end{split}$ | (3) |
式中:k——湍流动能;
ɛ——动能的耗散率。
1.2.3 多孔介质模型土壤是一种天然多孔介质,由沙粒相互堆积形成固体骨架和沙粒之间的内部孔隙组成[11]。因此,本次计算将采用多孔介质模型描述土壤对氢气扩散的阻碍效应,模型如下:
| $ S_u=\left(-D_u\mu u\right)+\left(-C_u\frac{1}{2}\rho\left|u\right|u\right)$ | (4) |
式中:Du——粘性阻力系数;
Cu——惯性阻力系数。
1.3 边界条件设置 1.3.1 边界条件将管道入口设置为质量流入口,出口设置为压力出口。边界条件的改变会对管道的稳定流动产生影响[12],因此为得到合理的管道出口压力等边界条件,本文基于Sun等人[6]的研究成果,利用Visual Studio 编写了用于计算出口压力和上下游流量的计算器。向该计算器输入环境压力、入口压力等相关参数后,能得到对应工况下的管道出口压力、上下游流量等参数,计算器界面和部分计算结果如表1所示。其余面根据其所处位置分别设置为对称面和压力出口。
Fuller 公式在计算二元气体扩散系数时有较好的精度[13],为了得到合理的氢气扩散系数,本文基于Fuller公式编写了用于计算氢气扩散系数的udf(用户自定义函数)并嵌入Fluent中。Fuller公式表达式为:
| $ {{D_{ab}} = \frac{{0.0101{T^{1.75}}\sqrt {\dfrac{1}{{{M_a}}} + \dfrac{1}{{{M_b}}}} }}{{{p_{ab}}{{\left(v_a^{\frac{1}{3}} + v_b^{\frac{1}{3}}\right)}^2}}}} $ | (5) |
式中:Dab——由 a、b 两种气体组成的二元气体扩散系数,m2 /s;
pab——二元气体的总压,Pa;
T——二元气体的温度,K;
Ma、Mb——组分a、b的摩尔质量,g/mol;
va、vb——组分a、b的摩尔体积,cm3 /mol。
1.3.2 土壤参数为讨论不同土壤对氢气扩散的影响,本文选取了三种典型的土壤类型作为土体材料。在查阅相关资料后,现将土壤物性参数整理如表2所示。
| 土壤类型 | 粘性阻力系数/m–2 | 惯性阻力系数/m–1 |
| 砂土 | 8.07×109 | 1.36×105 |
| 黏土 | 1.07×1012 | 1.40×106 |
| 壤土 | 3.05×1011 | 5.21×105 |
2 埋地输氢管道数值模拟 2.1 管道压力对氢气扩散的影响
为研究不同管道压力对氢气扩散的影响规律,本文选取了2、3、4、5 MPa四种工况,计算结果如图3、图4所示。与管道在大气中泄漏时所产生的射流不同,埋地管道发生泄漏后由于氢气扩散受到土壤的阻碍,氢气迅速在泄漏口附近产生堆积,后在管道上方出现球状气云,并持续向四周扩散。由云图可知,在仅改变管道工作压力的情况下,氢气分布总体关于泄漏口对称,且随着管道压力的增大,管道泄漏后产生的气云半径也呈增大的趋势,在同一时间点上,高压力管道的氢气扩散范围也更大。

|
| 图 3 不同管道压力下管道轴向的氢气体积分数 |

|
| 图 4 不同管道压力下管道径向的氢气体积分数 |
氢气体积分数在远离泄漏孔的区域有着较小变化梯度,因此在该区域中氢气的扩散主要依靠浓度差进行。同时,由图3、图4可知越远离泄漏孔的区域,氢气体积分数的等值线越稀疏,说明越远离泄漏孔的区域氢气体积分数增长速率越慢,氢气的扩散速率也越缓慢。
图5为发生泄漏后的30 s内,各监测点的氢体积分数随时间变化的曲线图。由图5可知,各监测点的浓度同管道的工作压力呈正相关,说明由高压管道泄漏出的氢气有更大的扩散速度。当工作压力为5 MPa时,监测点1处的氢气体积分数在3 s达到了0.5,而工作压力降为2 MPa后,氢气体积分数仅为0.23,由于监测点1靠近泄漏口,其氢气体积分数也为所有监测点中最高的一点。

|
| 图 5 各监测点下氢气体积分数变化 |
监测点1、2位于土壤内,因氢气的扩散受到土壤的阻碍,其氢气体积分数的变化曲线大致可分为快速提升、缓慢回落和缓慢回升三个阶段,其中快速提升阶段为泄漏口附近气云形成的时段,缓慢回落和缓慢回升两阶段则是氢气向四周扩散的过程。监测点1与监测点2的体积分数曲线在各阶段的时间分布大致相同,两监测点下的共八条曲线均在4 s左右结束快速提升阶段,在15 s左右开始缓慢提升。
监测点3位于大气和土壤的界面上,在不同的管道工作压力下,监测点3均在0.75 s左右检测出氢气的存在,随后各工况下的氢气体积分数会以相同的速度出现短暂的快速升高,随后再以不同的速度均匀增加,这种增长速度与管道工作压力呈正相关。监测点4位于大气中,在不同的管道工作压力下,监测点4均在1.3 s左右检测出氢气的存在,随后氢气体积分数直接以不同速度均匀升高,与监测点3所得规律相似,管道压力越高其增速越大。
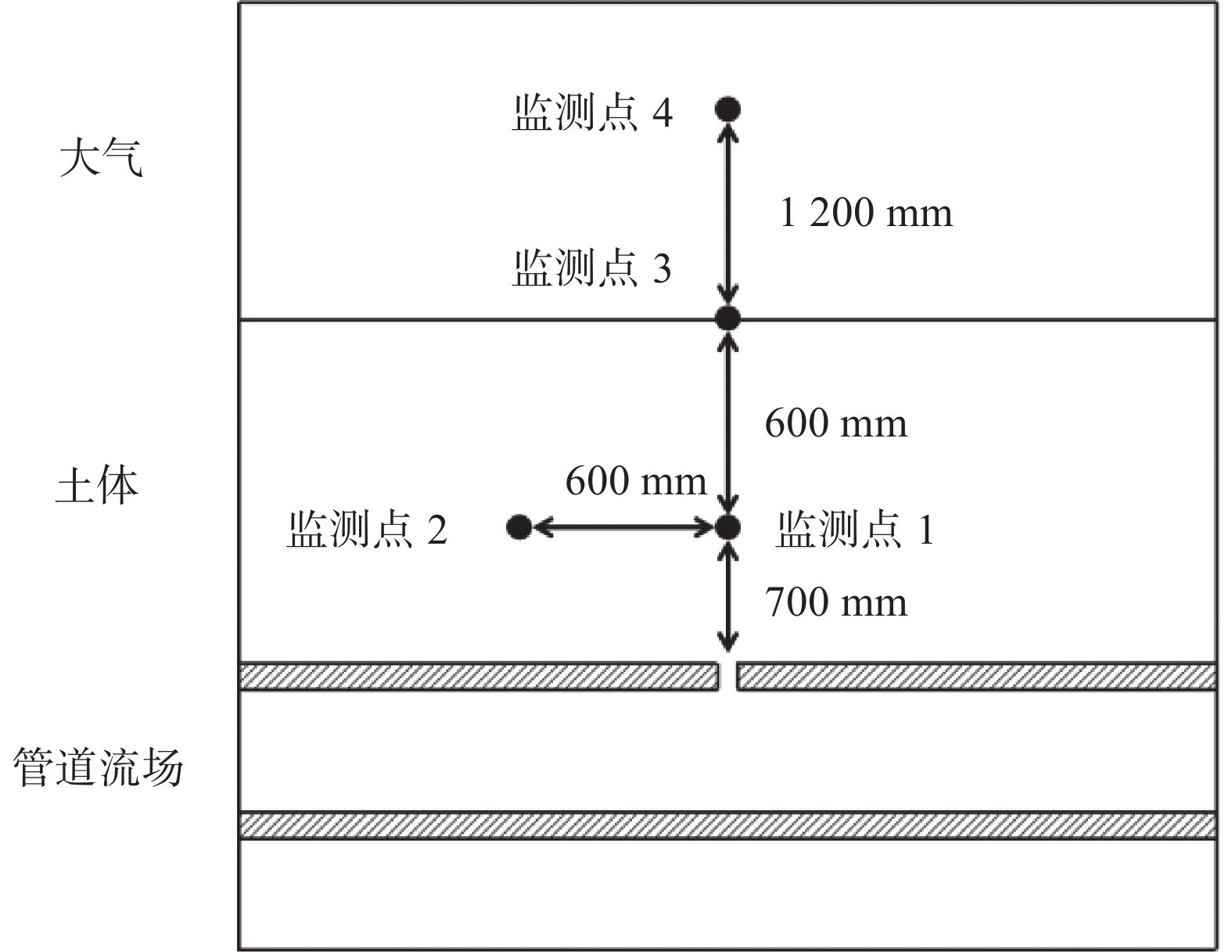
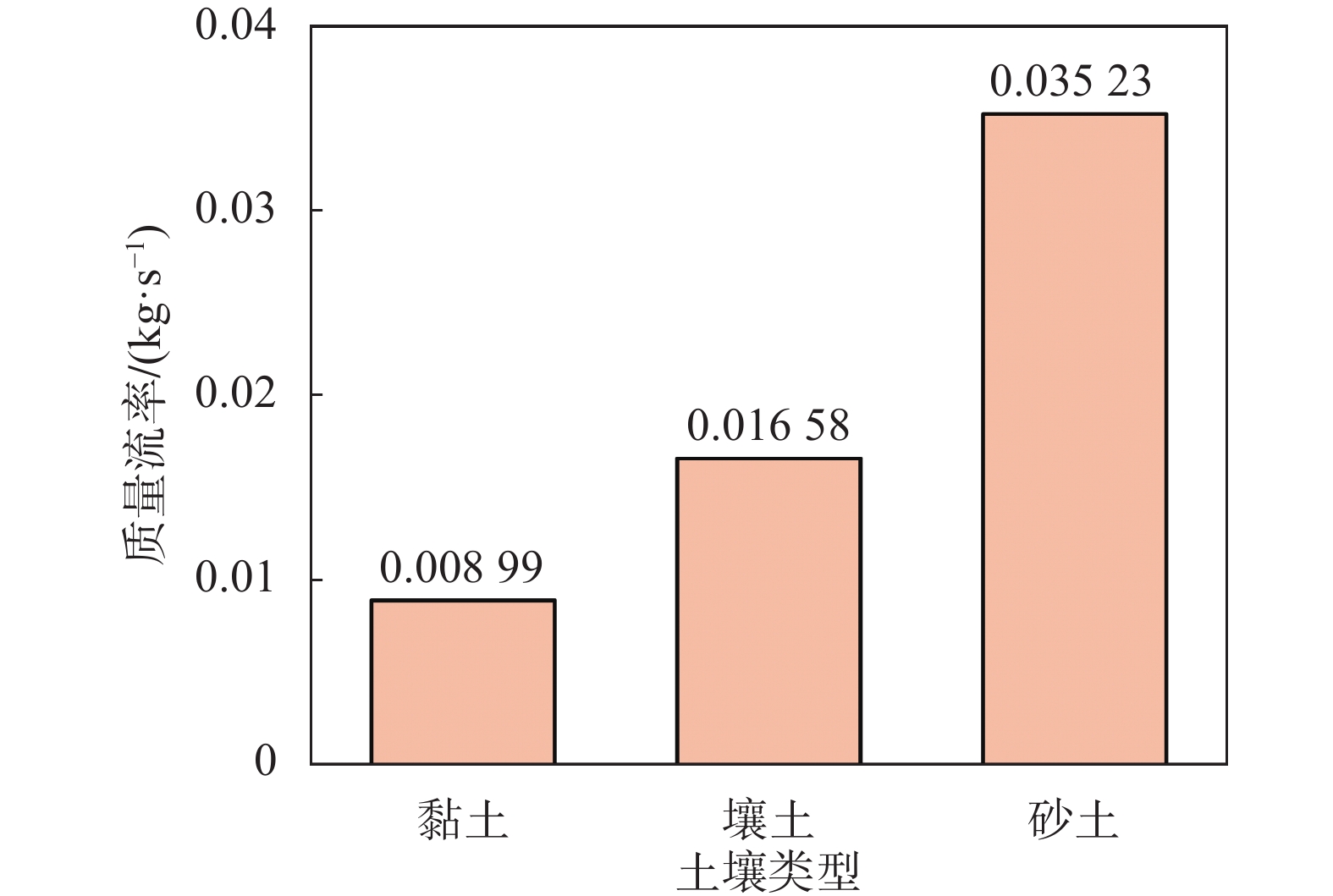
2.2 土壤类型对氢气扩散的影响为研究不同土壤类型对氢气扩散的影响,本节选取了砂土、黏土、壤土三种典型的土壤进行数值模拟计算。图6所示为在发生泄漏30 s时管道轴向和径向的氢气浓度分布情况,在不同的土壤类型下氢气的扩散有着显著差异,氢气在砂土中产生的气云直径和扩散范围远大于其他两种土壤条件下的工况,同时壤土工况又大于黏土工况,因此氢气泄漏后形成的气云直径和扩散范围与土壤的阻力系数呈反比关系。由图7可知土壤的阻力系数越大会导致气体扩散量越小,当管道泄漏稳定后管道在砂土中的泄漏量是壤土的1.8倍,是黏土的40倍左右,综上所述,输氢管道在砂土中泄漏扩散的危险系数高于壤土,壤土又高于黏土。
|
| 图 6 不同土壤类型下的氢气体积分数 |
|
| 图 7 不同土壤下的质量流率 |
图8给出了各监测点的氢气体积分数在不同土壤种类中随时间的变化情况。位于土壤中的监测点1和2的氢气体积分数在砂土工况下于14 s左右进入缓慢升高阶段,早于壤土工况下的24 s和黏土工况下的29 s。同时砂土工况下氢气的体积分数也始终高于其他两种工况,在30 s的计算范围内,监测点1在砂土工况下的氢气体积分数最高达到了30%,远大于黏土的13%,这是由于砂土的黏性阻力系数和惯性阻力系数远小于壤土和黏土,因此氢气会有更大的扩散动量和泄漏量。位于大气中的监测点3、4的氢气体积分数则是呈均匀上升的趋势,其中砂土工况最早监测出氢气出现,并且后续增速远大于其他两种工况,其增速同土壤阻力系数呈反比关系。当管道在砂土环境中发生泄漏后,地面在0.7 s检测出氢气浓度,并在11 s左右达到氢气的燃烧浓度下限4%,两个时间点均远早于黏土和壤土两种工况。

|
| 图 8 各监测点下氢气体积分数变化 |
2.3 泄漏孔径对氢气扩散的影响
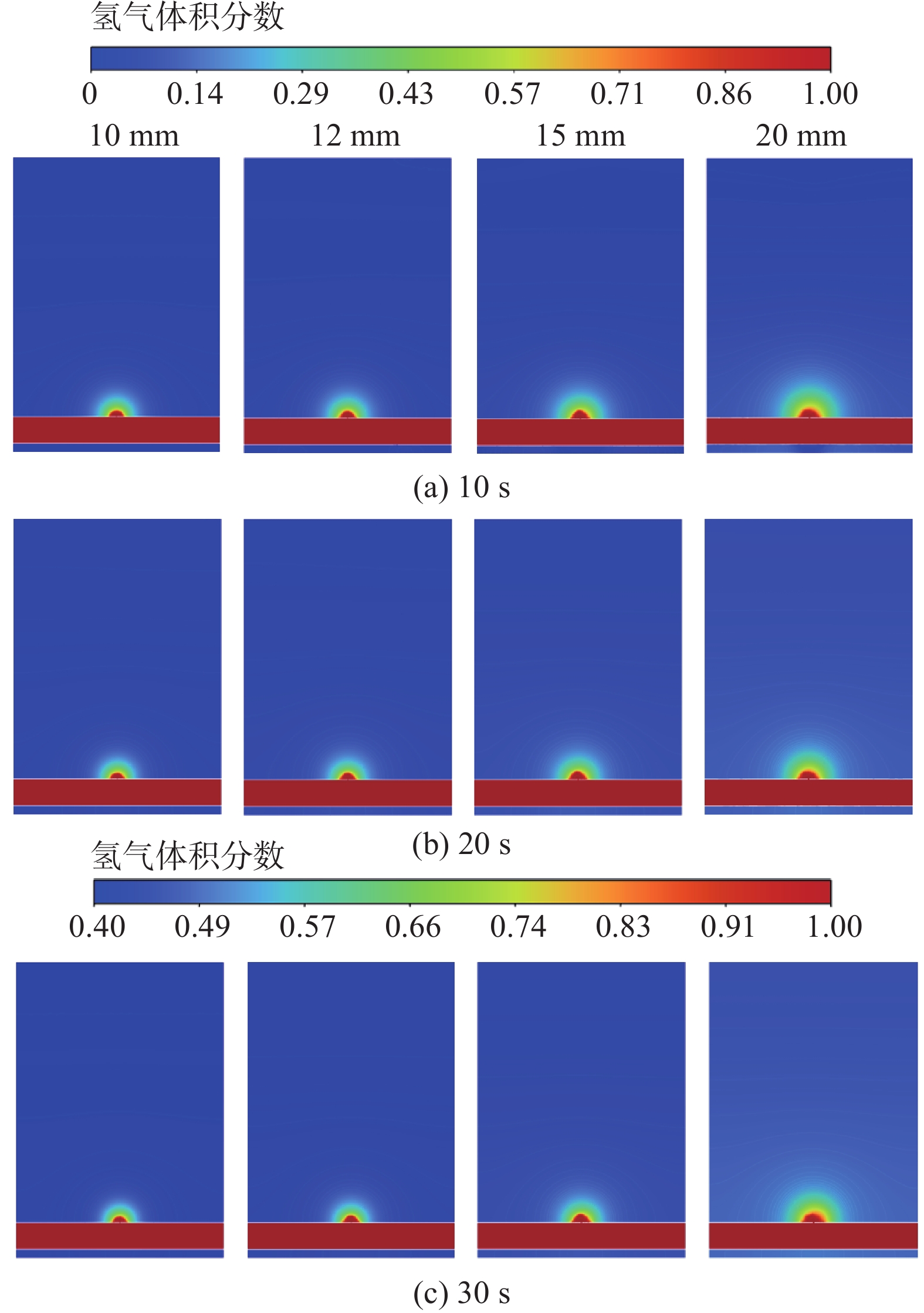
对不同泄漏孔孔径下的氢气扩散情况进行了研究,选取了10、12、15、20 mm四种泄漏孔径。不同孔径下各时间点的氢气分布如图9所示,由云图可知随着管道泄漏孔径的增大,泄漏孔上方的氢气气云半径呈现增大的趋势。在氢气分布上,随着孔径的提升,计算域内氢气浓度也有着明显提升,说明当管道发生泄漏后,气体的扩散速率和泄漏量与管道泄漏孔孔径呈正相关的关系。
|
| 图 9 不同泄漏孔径下管道径向的氢气体积分数 |
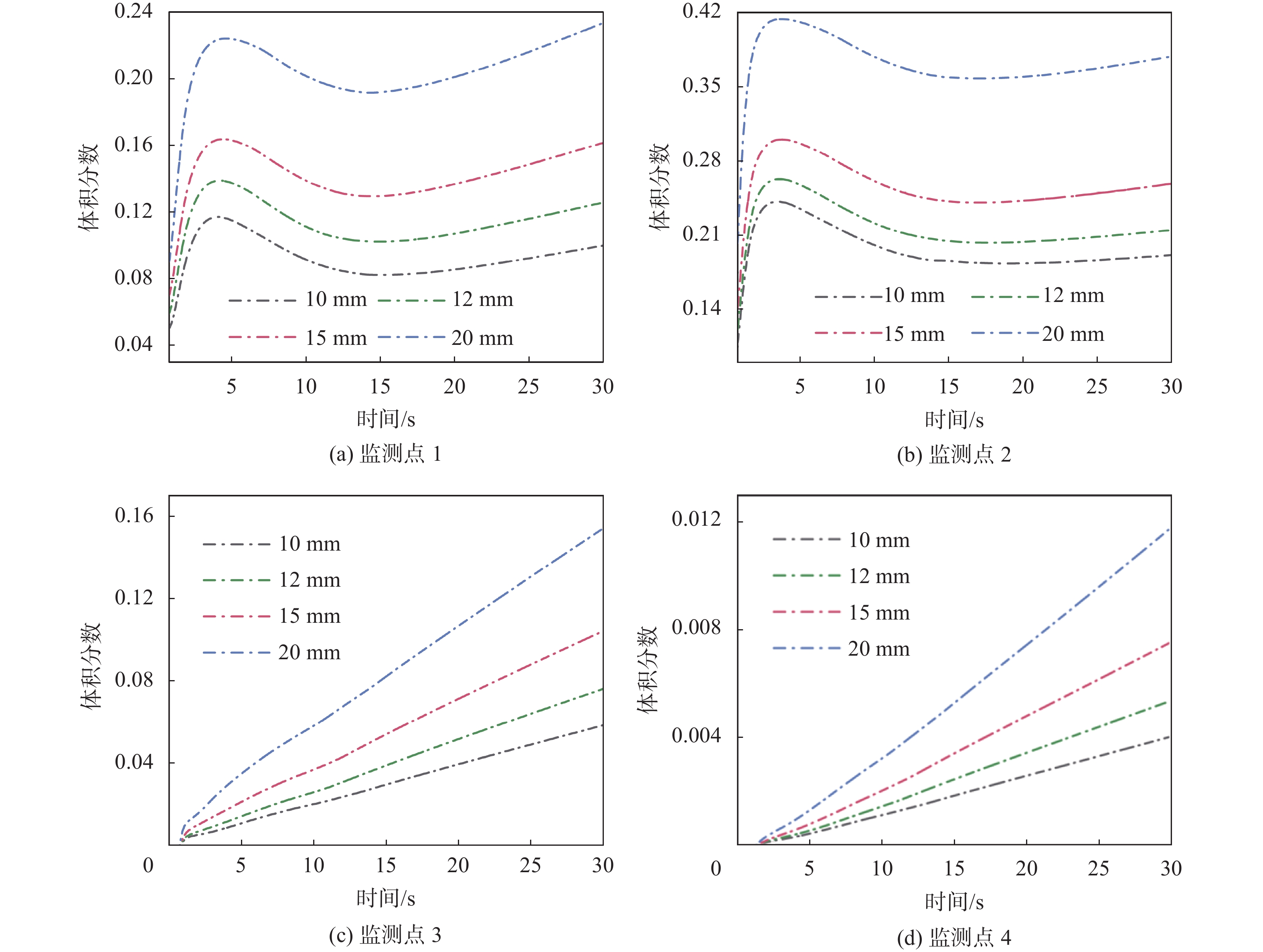
各监测点氢气体积分数随时间变化的曲线如图10所示。由体积分数曲线图可知在0~30 s时间内,各监测点的氢气体积分数与泄漏孔孔径呈正相关。监测点3、4检测出氢气浓度的时间受泄漏孔径的影响较小,监测点3的各工况均在0.7 s检测出氢气,随后氢气体积分数开始以不同速度均匀升高,泄漏孔径越大体积分数增速越大。监测点4的各工况均在1.3 s检测出氢气,同监测点3规律相似,后续时间里氢气体积分数开始以不同速度均匀升高,增速同孔径呈正比关系。
|
| 图 10 各监测点下氢气体积分数变化 |
3 基于GA-BP神经网络模型的危险时间预测 3.1 神经网络模型的选取
BP神经网络是一种多层前馈人工网络,利用误差反向传播,持续不断优化神经网络权值与阈值,最终获得高精度拟合数据模型,是目前应用最广泛的神经网络模型之一。与其他算法相比,BP 神经网络在处理高维、非线性或复杂的数据集时有着较高的精准度,因此常用于图像识别、语音识别、文本分类等场景。但由于该模型使用的梯度下降算法本身存在一定局限性,使得传统的BP学习算法通常存在收敛速度慢、容易陷入局部极小值等缺点[14]。
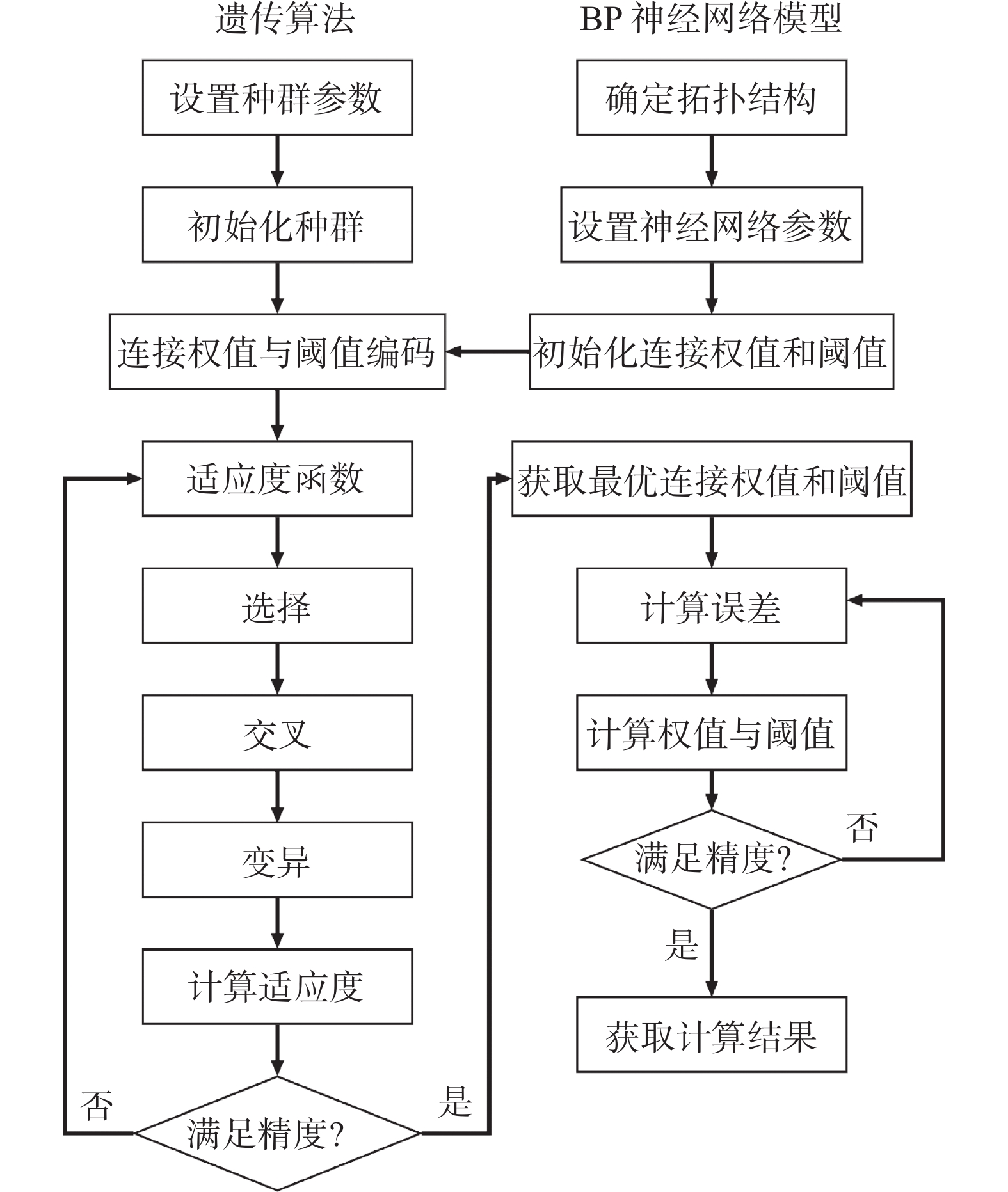
遗传算法是一种模拟生物进化相关过程的算法,该算法可以通过不断迭代优化计算结果,使其无限接近于全局最优解。BP神经网络初始阈值和权值的合理选取是决定模型精度的一个重要因素,选取不合理的初始阈值和权值容易使得神经网络模型陷入局部最优的情况。因此将遗传算法和BP神经网络模型结合,即利用遗传算法对BP神经网络模型初始权值和阈值进行寻优选取,能够大大提高BP模型的计算效率和准确度,优化后的算法流程图如图11所示。基于此,本文将采用GA-BP神经网络,对输氢管道在不同工况下发生泄漏后地面氢气浓度达到燃烧下限的时间进行预测。
|
| 图 11 GA-BP算法流程图 |
3.2 GA-BP 神经网络模型的构建与性能评价指标
本文共取40组数据作为样本,其中32组数据作为训练集用于神经网络模型的拟合,8组数据作为验证集进行误差计算。BP 神经网络相关参数设置如下:训练函数采用trainlm,训练次数设置为
完成模型构建后,为对其性能进行合理评估,本文采用决定系数(r2)、平均绝对百分比误差(MAPE)、平均绝对误差(MAE)及均方根误差(RMSE)对GA-BP模型进行评价,
计算公式如下:
| $ {{r^2} = 1 - \frac{{\displaystyle \sum \limits_{i = 1}^n {{\left( {{x_{{\text{sim}}}} - {x_i}} \right)}^2}}}{{\displaystyle \sum \limits_{i = 1}^n {{\left( {\overline {{x_i}} - {x_i}} \right)}^2}}}} $ | (6) |
| $ {{R_{{\text{MAPE}}}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^n \left| {\frac{{{x_i} - {x_{{\text{sim}}}}}}{{{x_i}}}} \right|} $ | (7) |
| $ {{R_{{\text{MAE}}}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^n |{x_{{\mathrm{sim}}}} - {x_i}|} $ | (8) |
| $ {{R_{{\text{RMSE}}}} = \sqrt {\frac{{\displaystyle \sum \limits_{i = 1}^n {{\left( {{x_{{\text{sim}}}} - {x_i}} \right)}^2}}}{n}} } $ | (9) |
式中:
在完成GA-BP模型的构建后,将40组样本数据导入模型进行多次计算,预测结果如表3所示,表中各项评价指标均表明该模型有较好的性能。
| 实验 序号 |
决定 系数 |
平均绝对百 分比误差 |
平均绝对 误差 |
均方根 误差 |
最小 误差 |
| 1 | 0% | ||||
| 2 | 1.47% | ||||
| 3 | 2.92% | ||||
| 4 | 2.81% | ||||
| 5 | 0.01% | ||||
| 6 | 0.11% |
为证明优化后的GA-BP模型有较高的精准度,将传统BP模型和GA-BP模型的预测值与真实值绘制成如图12所示的曲线图。由图可知,传统的BP模型的误差为8%左右,远大于GA-BP模型的误差,因此后者的预测精度更高,表明优化后的模型能对氢气泄漏的问题进行准确预测。
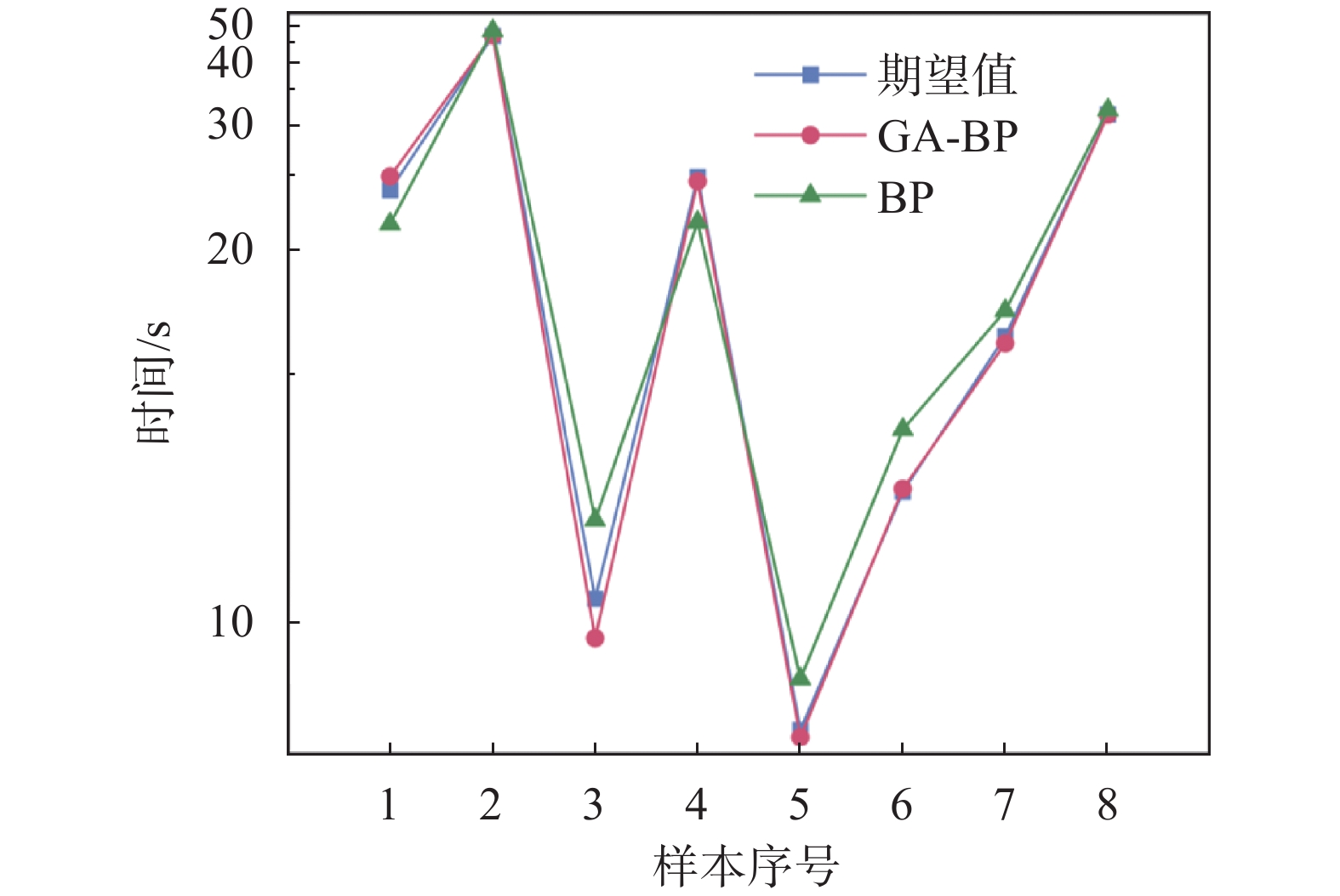
|
| 图 12 预测曲线对比图 |
4 结束语
本研究主要探究了土壤性质、泄漏孔径、管道压力对埋地输氢管道泄漏的影响,并利用GA-BP模型对相关问题进行了预测,主要结论总结如下:
1)以砂土为例,当管道发生泄漏后,管内氢气的扩散为:当管道发生泄漏后,氢气迅速在泄漏口附近产生球状气云,后续由于受到土壤的阻碍,氢气开始缓慢向四周扩散,扩散以泄漏点为中心且关于水平方向对称。氢气的扩散范围同管道压力和泄漏速度呈正比关系。
2)本文讨论了砂土、壤土与黏土对氢气泄漏扩散的影响,发现黏土对氢气扩散的阻碍效果最大,壤土其次,砂土最小。土壤的阻力系数与管道的泄漏量呈反比关系,在管道泄漏稳定后管道在砂土中的泄漏量是壤土的1.8倍,是黏土的40倍左右。
3)使用了GA-BP神经网络模型对地面氢气浓度到达燃烧浓度下限的时间进行了预测,预测结果证明GA-BP在该问题上表现出较好的预测性能,预测精准度高传统BP神经网络模型。
| [1] |
何润民, 赵莉, 黄星, 等. 川渝地区天然气产业与氢工业融合发展路径[J].
天然气工业, 2023, 43(9): 162-173.
HE R M, ZHAO L, HUANG X, et al. Integrated development path of natural gas industry and hydrogen industry in Sichuan-Chongqing area[J].
Natural Gas Industry, 2023, 43(9): 162-173.
|
| [2] |
沈晓波, 章雪凝, 刘海峰. 高压氢气泄漏相关安全问题研究与进展[J].
化工学报, 2021, 72(3): 1217-1229.
SHEN X B, ZHANG X N, LIU H F. Research and progress on safety issues related to high-pressure hydrogen leakage[J].
Acta Chemologica Sinica, 2021, 72(3): 1217-1229.
DOI:10.11949/0438-1157.20200874 |
| [3] |
陈一鸣, 王博, 刘宏达, 等. 基于声比拟法的埋地输气管道泄漏数值模拟[J].
西安石油大学学报(自然科学版), 2023, 38(5): 85-91.
CHEN Y M, WANG B, LIU H D, et al. Numerical simulation of buried gas pipeline leakage based on acoustic analogy method[J].
Journal of Xi 'an Shiyou University (Natural Science Edition), 2023, 38(5): 85-91.
|
| [4] |
胡玮鹏, 陈光, 齐宝金, 等. 埋地纯氢/掺氢天然气管道泄漏扩散数值模拟[J].
油气储运, 2023, 42(10): 1118-1127.
HU W P, CHEN G, QI B J, et al. Numerical simulation of leakage and diffusion in a buried pure hydrogen/hydrogen-doped natural gas pipeline[J].
Oil and Gas Storage and Transportation, 2023, 42(10): 1118-1127.
DOI:10.6047/j.issn.1000-8241.2023.10.005 |
| [5] |
罗宗林, 张甜甜, 谭羽非, 等. 土壤-大气耦合下直埋燃气管道泄漏扩散模拟[J]. 煤气与热力, 2021, 41(9): 36-42.
LUO Z L, ZHANG T T, TAN Y F, et al. Simulation of leakage and diffusion of direct buried gas pipeline under soil-atmosphere coupling[J]. Gas & Heat, 2021, 41(9): 36-42.
|
| [6] |
SUN L. Mathematical modeling of the flow in a pipeline with a leak[J]. Mathematics and Computers in Simulation, 2012, 82(11): 2253-2267.
|
| [7] |
ZHANG W, ZHAO G. Leakage and diffusion characteristics of underground hydrogen pipeline[J/OL]. Petroleum, 2023[2024-06-04]. https://www.sciencedirect.com/science/article/pii/S2405656123000378. DOI: 10.1016/j.petlm.2023.06.002.
|
| [8] |
WANG K, LI C, JIA W, et al. Study on multicomponent leakage and diffusion characteristics of hydrogen-blended natural gas in utility tunnels[J]. International Journal of Hydrogen Energy, 2024, 50: 740-760.
|
| [9] |
BAGHERI M, SARI A. Study of natural gas emission from a hole on underground pipelines using optimal design-based CFD simulations: Developing comprehensive soil classified leakage models[J]. Journal of Natural Gas Science and Engineering, 2022, 102: 104583.
|
| [10] |
钟明杉, 李兆飞, 张奕杰, 等. 基于一维卷积神经网络的天然气管道泄漏检测模型[J]. 国外电子测量技术, 2023, 42(5): 62-68.
ZHONG M S LI Z F, ZHANG Y J, et al. Based on one-dimensional convolutional neural network of natural gas pipeline leak detection models [J]. Foreign Electronic Measurement Technology, 2023, 42 (5) : 62-68.
|
| [11] |
金龙, 陈樑, 王海燕, 等. 不同土壤对输气管道泄漏扩散影响模拟分析[J].
石油与天然气化工, 2020, 49(04): 101-108.
JIN L, CHEN L, WANG H Y, et al. Simulation analysis of effects of different soils on leakage and diffusion of gas pipelines[J].
Oil & Gas Chemical Industry, 2020, 49(04): 101-108.
|
| [12] |
吴森林, 王秋良, 甘杜芬, 等. 双弯弯管水力特性数值模拟分析[J].
中国测试, 2024, 50(5): 19-28.
WU S L, WANG Q L, GAN D F, et al. Numerical simulation of hydraulic characteristics of double bend pipe[J].
China China Measurement & Test, 2024, 50(5): 19-28.
|
| [13] |
李长俊, 刘雨寒, 贾文龙. 多组分非理想气体扩散系数的改进[J].
油气储运, 2019, 38(3): 297-302.
LI C J, LIU Y H, JIA W L. Improvement of diffusivity of multi-component nonideal gas[J].
Oil and Gas Storage and Transportation, 2019, 38(3): 297-302.
DOI:10.6047/j.issn.1000-8241.2019.03.009 |
| [14] |
YU F, XU X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network[J]. Applied Energy, 2014, 134: 102-113.
|
 2024, Vol. 50
2024, Vol. 50