文章信息
- 王宽田, 覃琴, 罗梦霞, 梁世华
- WANG Kuantian, QIN Qin, LUO Mengxia, LIANG Shihua
- 考虑电磁干扰的差动式电容力矩传感器动态校准方法
- Dynamic calibration method of differential capacitive torque sensor considering electromagnetic interference
- 中国测试, 2024, 50(8): 164-170
- CHINA MEASUREMENT & TEST, 2024, 50(8): 164-170
- http://dx.doi.org/10.11857/j.issn.1674-5124.2023050072
-
文章历史
- 收稿日期: 2023-05-17
- 收到修改稿日期: 2023-08-29
2. 桂林理工大学信息科学与工程学院,广西 桂林 541004
2. College of Information Science and Engineering, Guilin University of Technology, Guilin 541004, China
差动式电容力矩传感器属于一体式设计,可以同时测量多个方向以及力矩分量的传感器,具有体积小以及结构紧凑等优势,在科学实验以及工业生产中取得了十分广泛的应用。差动式电容力矩传感器主要通过压电元件的压电效应完成对模型力矩的测量,刚度和固有频率的取值都十分高,特别适用于动态测量[1-2],但是仍然存在静态特性差和技术不成熟等缺点,在应用过程中主要以特殊场合需求定制为主。随着技术的不断发展和工业自动化要求的不断提升,越来越多的场合需要展开动态力的测量,同时对测量精度的要求也就越来越高。虽然已经在传感器中加入了全新的技术替换应变桥测量软件,但是仍然无法克服动态特性比较差的问题,所以研究差动式电容力矩传感器动态校准具有十分重要的研究意义。
国内外相关专家针对上述内容展开了大量研究,高猛等[3]对传感器展开频率特性分析,构建子弹构型和加载信号带宽两者之间的关系,利用斜端面对传感器展开三轴同步冲击校准。王东颖等[4]分析传感器的工作原理和组成,引入电测法对传感器校准处理。劳嫦娟等[5]采用基于环境参量测量的激光波长实时补偿作为标准位移发生器,以此为依据完成位移动态校正。RASPOPOV等[6]研究了角速度传感器模式下的科里奥利振动陀螺仪的调谐和校准方法。但是该方法主要针对的是整体结构的调谐和校准,传感器自身运行时受干扰影响较大,从而导致调谐效果不理想。VARZHITSKII等[7]比较了用于测量位移、变形和振动参数的非接触传感器在不同物理性质的工作原理下的特性。在漫反射模型中,证实了光耦合器在非接触式振动位移传感器开发中的效率。提出了一种振动信号数字处理算法,在宽动态和频率范围内研究传感器计量精准性。但是该方法受混合噪声干扰,导致计量精度下降,且该方法侧重计量,未对其计量后的数据进行校准。LIU等[8]提出了一种基于粒子群优化的两阶段校准方法,该方法充分利用了地球磁场矢量的振幅不变性和方向不变性,设计两阶段适应度函数。第一阶段:利用地球磁场的振幅不变性设计粒子群的适应度函数,根据适应度函数输出的初步误差矩阵和偏置误差,补偿了三轴磁传感器测量误差。但是由于粒子群算法计算体量较大的问题,导致校准效率较低。
在以上几种方法的基础上,本文设计并提出一种考虑电磁干扰的差动式电容力矩传感器动态校准方法。经实验测试结果证明,采用所提方法可以更好完成传感器动态校准。
1 差动式电容力矩传感器动态校准 1.1 基于小波变换的电磁干扰抑制电磁干扰是信号处理中一种十分常见的干扰,特别是在工业环境中。其干扰源包括电源线的噪声、电机的干扰、无线通信设备等,这些干扰源可以对传感器的输出信号产生干扰,并影响力矩测量的准确性。为此,本文采用小波变换[9-10]对差动式电容力矩传感器电磁干扰信号进行去噪,以获取更平稳的信号。
函数
| $ C_{\rm wt}\left( {a,b} \right) = \int\limits_E {x\left( t \right)} \left\{ {{{\tilde \psi }_{a,b}}} \right\}{\text{d}}t\left| {\frac{{t - b}}{a}} \right| $ | (1) |
式中:
在实际应用过程中,必须对连续小波离散化处理[11-12],同时设定小波变换中不同参数的取值,进而获取对应的小波系数,如下式所示:
| $ {\psi _{a,b}}\left( t \right) = {\left| {\frac{{t - b}}{a}} \right|^2}\left\{ {{{\tilde \psi }_{a,b}}} \right\} \times x\left( t \right) $ | (2) |
其中,
通过式(2)得到的小波函数就是离散小波,则对应的离散小波变换可以表示为:
| $ C_{\rm wt}\left( {a,b,c} \right) = \frac{{{{\left| {\dfrac{{t - b}}{a}} \right|}^2}\left\{ {{{\tilde \psi }_{a,b}}} \right\} \times x\left( t \right)}}{{\left\{ {{{\tilde \psi }_{a,b}}} \right\}\left| {\dfrac{{t - b}}{a}} \right|}} $ | (3) |
展开小波分析可以得到最优的时空域分辨率[13-14],但是得到的小波基不是非连续函数,所以获取的频域分辨率也并不是十分理想。在混合噪声干扰下,需要对小波展开三层分解处理,同时获取对应的峰值信噪比
| $ \mathrm{PSNR}=10\mathrm{l\mathrm{g}}\frac{\left(s_{\max}-s\right)}{\dfrac{1}{n}\displaystyle\sum\limits_{t=1}^{\mathrm{\mathit{T}}}\left[x\left(t\right)-x\left(t+1\right)\right]} $ | (4) |
式中:
对于一个随机信号而言,离散小波变换的第一步是将含有噪声的信号划分为两个部分,分别为:1)近似部分,主要用来描述不同信号的主要特征;2)低频部分,对低频部分展开相似运算,经过处理,得到最佳尺度因子。
通过上述分析,利用图1给出电磁干扰抑制的详细操作流程[15]。
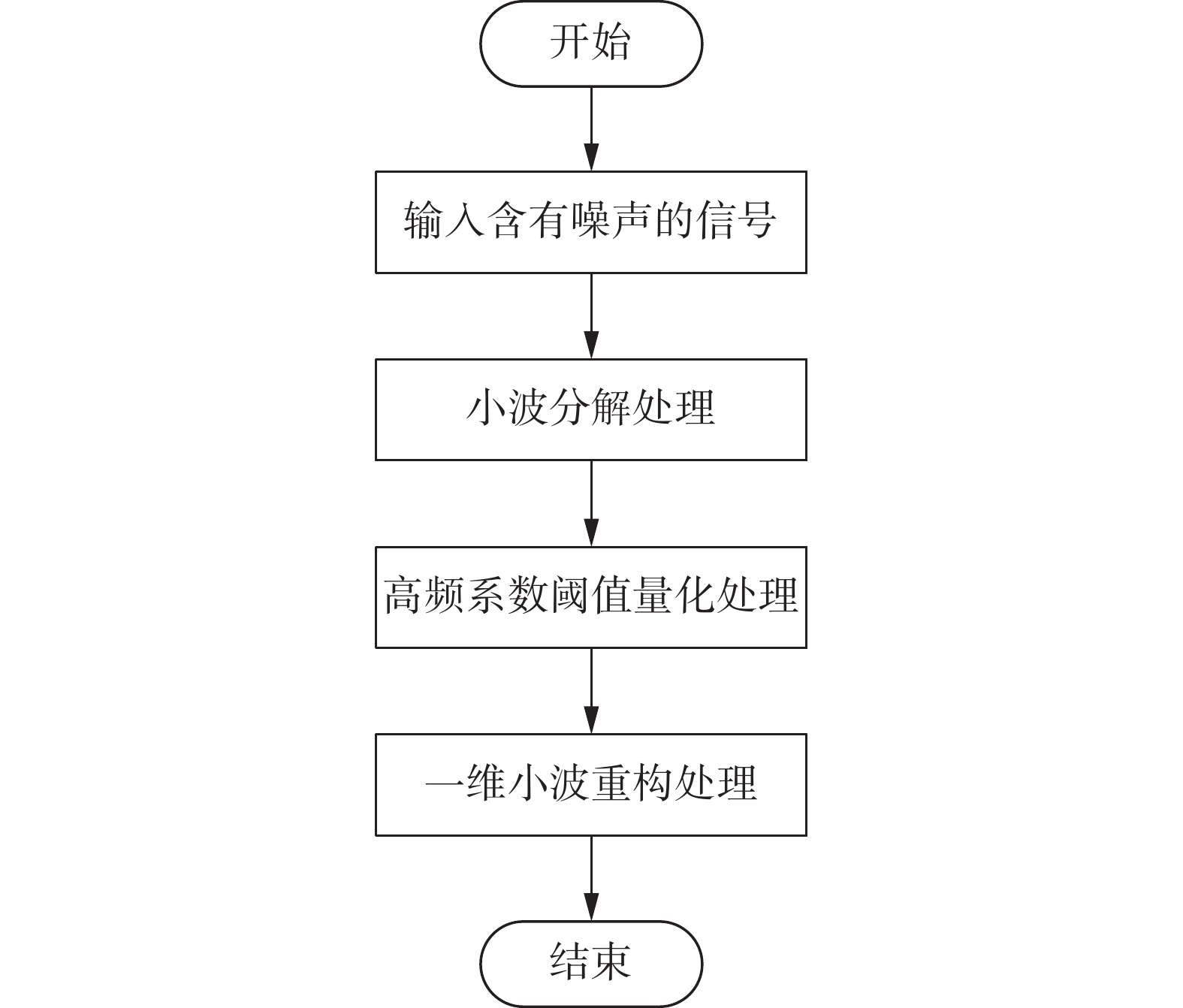
|
| 图 1 差动式电容力矩传感器电磁干扰抑制流程图 |
1.2 差动式电容力矩传感器动态校准
在电磁干扰得到有效抑制后,为了有效展开动态特性分析,将差动式电容力矩传感器近似为二阶模型。由于压电材料具有较大的弹性和阻尼特征,在力
| $ \left\{ \begin{aligned} {p_1}\frac{{{d}{{\textit{z}}_1}\left( t \right)}}{{{t^2}}} =& S\left( t \right) - k\left[ {{{\textit{z}}_1}\left( t \right) - {{\textit{z}}_2}\left( t \right)} \right] + \\ & f\left[ {\frac{{{d}{{\textit{z}}_1}\left( t \right)}}{{{t^2}}} - \frac{{{d}{{\textit{z}}_2}\left( t \right)}}{{{t^2}}}} \right] \\ {p_2}\frac{{{d}{{\textit{z}}_2}\left( t \right)}}{{{t^2}}} =& k\left[ {{{\textit{z}}_1}\left( t \right) - {{\textit{z}}_2}\left( t \right)} \right] + f\left[ {\frac{{{d}{{\textit{z}}_1}\left( t \right)}}{{{t^2}}} - \frac{{{d}{{\textit{z}}_2}\left( t \right)}}{{{t^2}}}} \right] \end{aligned} \right. $ | (5) |
式中:
在设定时间内,需要使质量块
| $ N\left( t \right) = {{\textit{z}}_1}\left( t \right) - {{\textit{z}}_2}\left( t \right) $ | (6) |
将式(5)和式(6)两者联立,同时对微分方程展开拉式变换处理,则对应的计算式如下:
| $ \left\{ \begin{gathered} {Z_1}\left( s \right){s^2} = \frac{{r\left( s \right) - \left[ {{{\textit{z}}_1}\left( t \right) + {{\textit{z}}_2}\left( t \right)} \right]}}{{{p_1}W\left( s \right)}} \\ {Z_2}\left( s \right){s^2} = \frac{{r\left( s \right) + f\left( s \right)}}{{{p_2}W\left( s \right)}} \\ \end{gathered} \right. $ | (7) |
式中:
f(s)——相对位移长度为s时的阻尼系数。
对电压静态标定结果求解处理
| $ W{\left( s \right)_{x,y}} = \frac{{\left[ {r\left( s \right) + f\left( s \right)} \right]S\left( t \right)}}{{{Z_1}\left( s \right){Z_2}\left( s \right)}} $ | (8) |
经过上述分析,深入分析差动式电容力矩传感器的组成结构,进而构建参数化数学模型,如下式所示:
| $ G\left( s \right) = \left[ {r\left( s \right) - f\left( s \right)} \right] \times \frac{{W{{\left( s \right)}_{x,y}}{Z_1}\left( s \right){Z_2}\left( s \right)}}{{k\left[ {{{\textit{z}}_1}\left( t \right) - {{\textit{z}}_2}\left( t \right)} \right]}} $ | (9) |
其中,
通过式(9)构建的模型可以获取动态激励和结构响应两者之间的频域传递关系,也就是差动式电容力矩传感器的频率特性,对应的计算式如下:
| $ \left\{ \begin{gathered} {\textit{z}}\left( \tau \right) = \frac{{t\left( {{p_1},{p_2}} \right)}}{{\sqrt {{p_1}{p_2}} + r\left( s \right) + f\left( s \right)}} \\ s\left( \tau \right) = \arctan \frac{{\left( {{p_1} - {p_2}} \right) \times W\left( s \right)}}{{\left( {{p_1} + {p_2}} \right) \times N\left( t \right)}} \\ \end{gathered} \right. $ | (10) |
其中,
利用最小二乘法分析传递函数的频域几何关系,详细的操作步骤如下所示:
1)通过EOV模态的类型确定对应参数的取值范围。
2)确定待校正频带以及曲线中随机两个极值的频率值
| $ w\left( {\tau ,t} \right) = \frac{{y\left( {d,t} \right) \times s\left( \tau \right) \times {\textit{z}}\left( \tau \right)}}{{r\left( s \right) + f\left( s \right)}} $ | (11) |
其中,
3)在确定等待补偿的范围内,随机选择多个参数,同时计算各个参数对应的极值频率。
4)引入最小二乘法计算每组的离散频率点以及幅值信息,则对应的计算式如下:
| $ \left\{ \begin{gathered} \alpha \left( {\tau ,t} \right) = \frac{{w\left( {\tau ,t} \right)\left[ {r\left( s \right) - f\left( s \right)} \right] - G\left( s \right)}}{{\left[ {W{{\left( s \right)}_{x,y}} \times {Z_1}\left( s \right) \times {Z_2}\left( s \right)} \right]}} \times \left[ {{{\textit{z}}_1}\left( t \right) + {{\textit{z}}_2}\left( t \right)} \right] \\ q\left( {\tau ,t} \right) = \frac{{{\textit{z}}\left( \tau \right) \times t\left( {{p_1},{p_2}} \right)}}{{f\left( {\dfrac{{{d}{{\textit{z}}_1}\left( t \right)}}{{{t^2}}} - \dfrac{{{d}{\textit{z}_2}\left( t \right)}}{{{t^2}}}} \right)}} \times {{\textit{z}}_1}\left( t \right){{\textit{z}}_2}\left( t \right) \\ \end{gathered} \right. $ | (12) |
其中,
5)在满足设定条件下的基础上,通过式(13)的准则选择一组最佳参数,将其作为差动式电容力矩传感器二次补偿的参数解。
| $ h\left( {\tau ,t} \right) = m\left( {\tau ,t} \right) + f\left( {\frac{{{d}{{\textit{z}}_1}\left( t \right)}}{{{t^2}}} - \frac{{{d}{{\textit{z}}_2}\left( t \right)}}{{{t^2}}}} \right) \times \left\{ {r\left( s \right) + f\left( s \right)} \right\} $ | (13) |
式中:
通过上述分析,进一步对传感器展开动态解耦和动态补偿操作,详细的操作流程如图2所示。
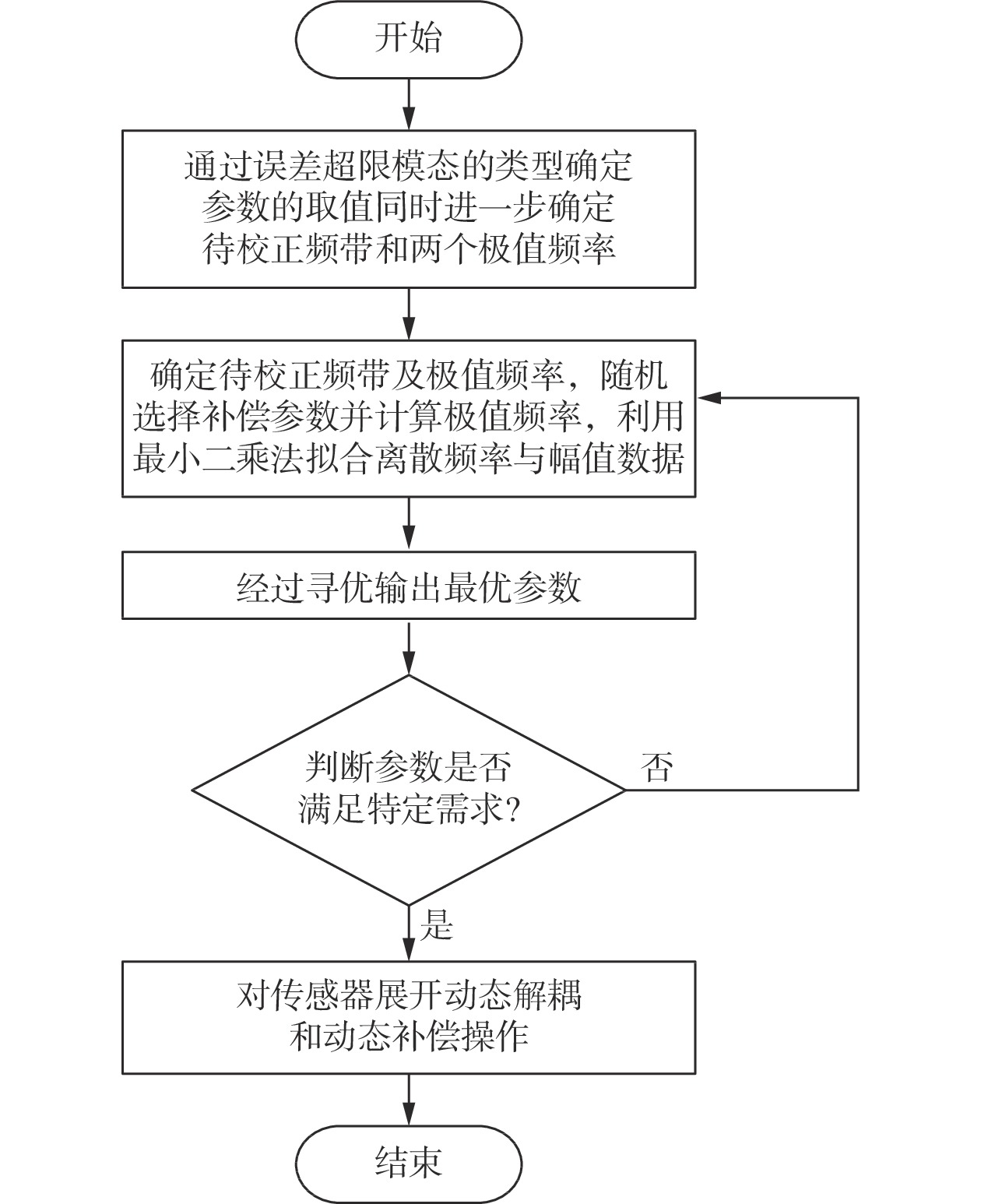
|
| 图 2 差动式电容力矩传感器解耦和动态补偿操作流程图 |
同时引入预矩阵改变耦合矩阵在固定频率点的幅值,对应的预矩阵
| $ {\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {{q_{11}}}&{{q_{12}}}& \cdots &{{q_{1n}}} \\ {{q_{21}}}&{{q_{22}}}& \cdots &{{q_{2n}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{q_{m1}}}&{{q_{m2}}}& \cdots &{{q_{mn}}} \end{array}} \right] $ | (14) |
其中,
在满足收敛性的条件下,可以采用迭代的方式获取差动式电容力矩传感器的迭代解耦,为了进一步得到实际的解耦结果,需要对解耦处理后的不同通道数据展开动态补偿处理,对应的计算式如下:
| $ p\left( {s,\tau } \right) = \frac{{\left| {{{\textit{z}}_1}\left( t \right) + {{\textit{z}}_2}\left( t \right)} \right|w\left( {\tau ,t} \right) \times \left[ {r\left( s \right) - f\left( s \right)} \right]}}{{{\textit{z}}\left( \tau \right)s\left( \tau \right)}} $ | (15) |
其中,
| $ \left| {p\left( {s,\tau ,\omega } \right)} \right| = \frac{{h\left( {\tau ,t} \right)m\left( {\tau ,t} \right)}}{{1 + \dfrac{{w\left( {\tau ,t} \right)}}{{{\textit{z}}\left( \tau \right)s\left( \tau \right)}} + 4\dfrac{{s\left( \tau \right)}}{{{\textit{z}}\left( \tau \right)}}}} \times \left[ {r\left( s \right) - f\left( s \right)} \right] $ | (16) |
通过冲击剪断装置形成的力矩信号对传感器展开动态标定处理,详细的操作步骤如下所示:
1)设定预矩阵的取值范围以及待校正频带,假设原始的谱半径大于设定值,则确定频带的取值范围;反之,则说明存在多个待校正的频带。
2)确定耦合矩阵展开预处理操作产生的影响和对应频段信息。
3)确定影响列对应的影响频率取值
| $ {\lambda}_{xy}=\left|\begin{array}{*{20}{c}}\lambda_{11} & \lambda_{12} & \cdots & \lambda_{1n} \\ \lambda_{21} & \lambda_{22} & \cdots & \lambda_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \lambda_{x1} & \lambda_{x2} & \cdots & \lambda_{xy}\end{array}\right| $ | (17) |
4)在确定
5)将步骤3)和步骤4)两者有效结合,进而确定影响列的陷波器,计算各个影响频率对应的谱半径。
6)引入冲击剪断装置对差动式电容力矩传感器展开分析,根据形成的力矩信号对传感器动态标定处理。
在完成差动式电容力矩传感器的标定处理之后,需要采用检测电路测量阶跃信号校准标定结果,进而实现差动式电容力矩传感器动态校准处理。
2 实 验 2.1 实验条件为了验证所提考虑电磁干扰的差动式电容力矩传感器动态校准方法的有效性,在图3所示的环境中进行测试。

|
| 图 3 实验测试环境 |
如图3所示的实验测试环境中使用的电脑为Windows 10操作系统,Intel Core i7处理器,16 GB RAM;数据采集软件为LabVIEW;使用型号为JN-DN3的力矩传感器,相关参数如表1所示。
通过离散小波变换,可以将获取到的差动式电容力矩传感器的信号划分为近似部分和低频部分:
近似部分:近似部分主要用来描述信号的整体特征,即对整体力矩的近似描述。用来反映力矩信号的整体趋势和变化。
低频部分:低频部分对低频内容展开相似运算,经过处理后,可以获得最佳尺度因子,即与缓慢变化的扭矩成分相关的信息。通过分析低频部分,了解到力矩的稳态响应和缓慢变化特征。
通常情况下,差动式电容力矩传感器的刚度可以达到108 N/m以上,等效的阻尼系数的取值范围在103~104 kg/s,鉴于传感器自身的工作特性和使用领域,可以将传感器传递函数的近似值
| $ K\left( {x,y,\tau } \right) = h\left( {\tau ,t} \right)m\left( {\tau ,t} \right) \times \frac{{{\lambda _{xy}} \times q\left( {\tau ,t} \right)}}{{G\left( s \right)}} $ | (18) |
根据式(18)计算后,可得差动式电容力矩传感器的脉冲速度以及加速度信号如图4所示。
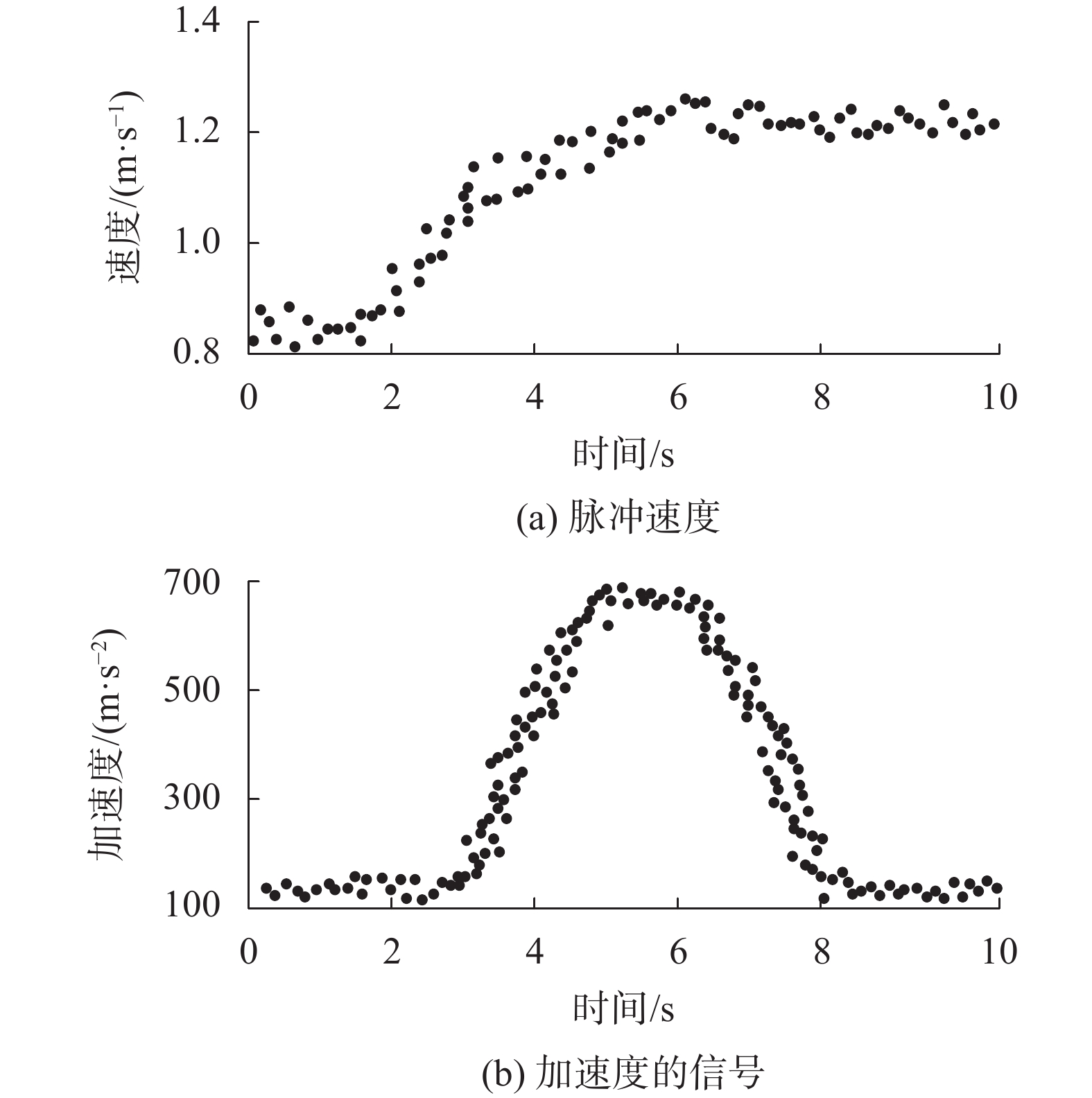
|
| 图 4 脉冲速度以及加速度信号变化情况 |
2.2 实验结果及分析
1)误差校正系数测定
经过上述分析,可得差动式电容力矩传感器在不同增益档位对应的误差校正系数测定结果如表2所示。
| 增益档位 | 基准电阻/Ω | 最大量程/(N·m) | 测量误差校正系数 |
| 1 | |||
| 2 | |||
| 4 | |||
| 8 | |||
| 16 | |||
| 32 | |||
| 64 | |||
| 128 | 895 | ||
| 256 | 533 | ||
| 512 | 328 |
分析表2中的实验数据可知,增益档位为1时,测量误差校正系数为
2)校准处理后的绝对误差测试
为了更进一步验证各个差动式电容力矩传感器动态校准方法对智能节电电阻测量精度的提升效果,分析各个方法校准处理后的绝对误差变化情况,详细的实验测试结果如图5所示。
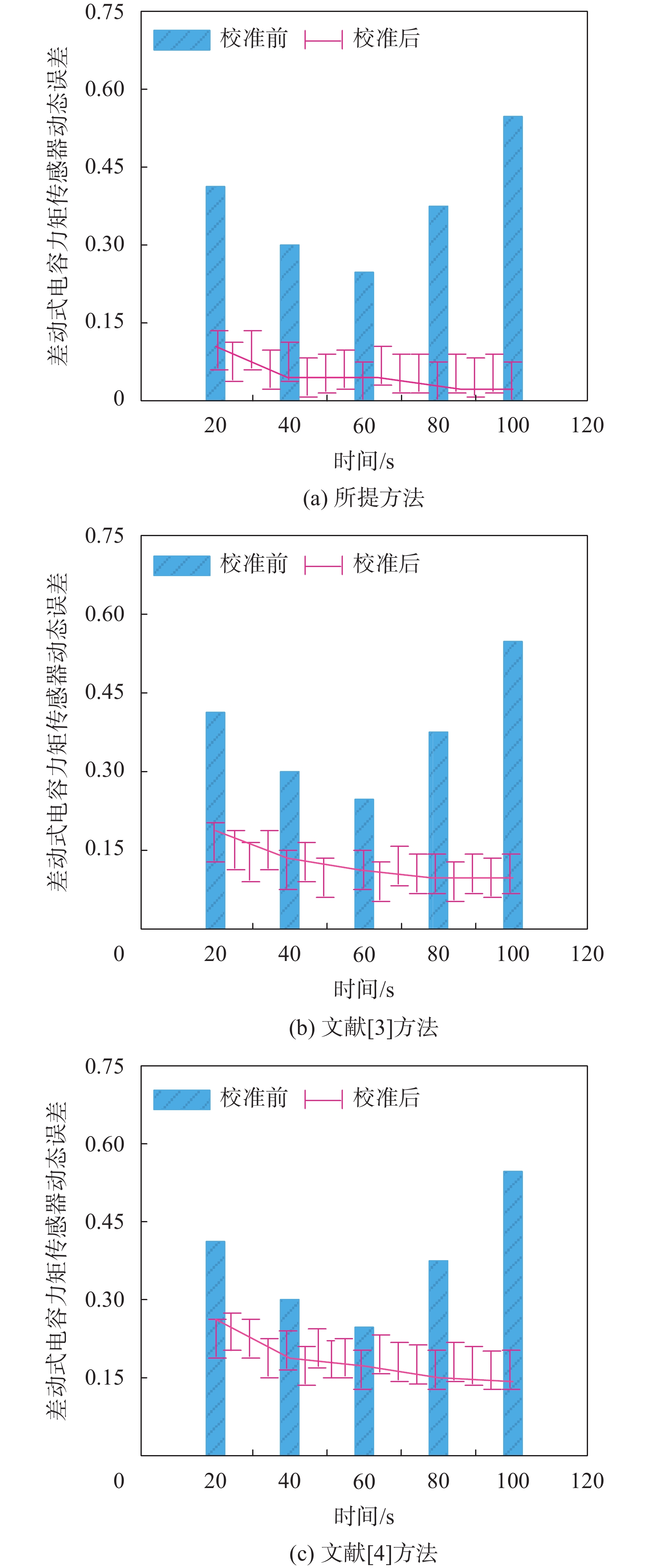
|
| 图 5 不同方法校准后的绝对误差对比结果 |
对于智能节电电阻测量来说,精确测量电路中的电阻值是实现节能目标的关键。如果力矩传感器的输出存在误差,那么根据力矩计算所得的电阻值也会有相应的误差。通过使用差动式电容力矩传感器动态校准方法,提高力矩传感器的测量精度,从而得到更准确的电阻值测量结果。分析图5中的实验数据可知,所提方法在有效抑制电磁干扰之后,时间分别为20、40、60 s时,绝对误差为0.11、0.52、0.5;利用文献[3]方法,时间分别为20、40、60 s时,绝对误差为0.17、0.14、0.13;利用文献[4]方法,时间分别为20、40、60 s时,绝对误差为0.25、0.18、0.17。所提方法的差动式电容力矩传感器动态误差明显小于文献[3]方法和文献[4]方法。其本文在抑制差动式电容力矩传感器电磁干扰的基础上,基于最小二乘法分析动态激励和结构响应两者之间的频域传递关系的频域几何关系式,实现了传感器动态解耦和动态补偿,并利用通过校准标定结果,优化了差动式电容力矩传感器动态校准效果。
综上分析可知,所提方法在有效抑制电磁干扰之后,可以更好完成差动式电容力矩传感器动态校准,且校准性能明显优于另外两种方法。
3 结束语针对差动式电容力矩传感器动态校准性能较差的问题,设计并提出一种考虑电磁干扰的差动式电容力矩传感器动态校准方法。经过试验测试结果表明,采用所提方法可以更好完成传感器动态校准方法。随着动态测试场合的不断增加,还需要进一步对差动式电容力矩传感器动态校准方面展开更加深入的研究。
| [1] |
卢涛, 王勇, 肖飞云. 基于双姿态传感器的关节运动角度测量方法[J].
合肥工业大学学报(自然科学版), 2021, 44(6): 738-742.
LU T, WANG Y, XIAO F Y. A method for measuring joint motion angle based on dual-attitude sensor[J].
Journal of Hefei University of Technology(Natural Science), 2021, 44(6): 738-742.
|
| [2] |
李志宇, 林嘉睿, 孙岩标, 等. 一种基于线结构光传感器的圆位姿测量方法[J].
光学学报, 2020, 40(15): 105-114.
LI Z Y, LIN J R, SUN Y B, et al. A method for measuring circular pose based on line structured light sensor[J].
Acta Optica Sinica, 2020, 40(15): 105-114.
|
| [3] |
高猛, 徐宇珩, 巨荣博, 等. 冲击力传感器灵敏度系数的三轴同步校准方法研究[J].
仪器仪表学报, 2021, 41(8): 34-43.
GAO M, XU Y H, JU R B, et al. Research on the triaxial synchronous calibration method of sensitivity for the impact force sensor[J].
Chinese Journal of Scientific Instrument, 2021, 41(8): 34-43.
|
| [4] |
王东颖, 杜文斌, 雷强, 等. 一种高频响拉杆式位移传感器设计与校准研究[J].
火炮发射与控制学报, 2020, 41(2): 82-86.
WANG D Y, DU W B, LEI Q, et al. The design and calibration of a high frequency response rod-type eddy current displacement sensor[J].
Journal of Gun Launch & Control, 2020, 41(2): 82-86.
|
| [5] |
劳嫦娟, 曹洁, 孙骏栖, 等. 基于激光干涉比长的大范围线位移动态校准系统研究[J].
中国测试, 2021, 47(S1): 12-18.
LAO C J, CAO J, SUN J X, et al. Research on dynamic calibration system of large range linear displacement based on laser interference comparator[J].
China Measurement & Test, 2021, 47(S1): 12-18.
|
| [6] |
RASPOPOV V Y, ALALUEV R V, LADONKIN A V, et al. Tuning and calibration of a coriolis vibratory gyroscope with a metal resonator to operate in angular rate sensor mode[J]. Gyroscopy and Navigation, 2020, 11(1): 34-40.
|
| [7] |
VARZHITSKII L A, CHERTYKOVTSEVA N V, TARASOV E M. Improvement and possibilities of application of calibration methods for optoelectronic vibration displacement sensor [J]. Measurement Techniques, 2020, 63(9): 713-721.
|
| [8] |
LIU Y X, HU Z K, FANG J J. Two-step calibration method for three-axis magnetic sensor error based on particle swarm optimization[J].
Sensor Review, 2020, 40(5): 577-583.
DOI:10.1108/SR-01-2020-0013 |
| [9] |
马星河, 孔卫东, 李自强, 等. 一种基于S_VMD与Sdr_SampEn的局部放电信号去噪方法[J].
电力系统保护与控制, 2022, 50(18): 29-38.
MA X H, KONG W D, LI Z Q, et al. A denoising method for a partial discharge signal based on S_VMD and Sdr_SampEn[J].
Power System Protection and Control, 2022, 50(18): 29-38.
|
| [10] |
张锐, 钱超. 基于RFDA小波阈值的心电信号去噪算法[J].
计算机仿真, 2022, 39(8): 373-376.
ZHANG R, QIAN C. ECG signal denoising algorithm based on RFDA wavelet threshold[J].
Computer Simulation, 2022, 39(8): 373-376.
DOI:10.3969/j.issn.1006-9348.2022.08.071 |
| [11] |
程龙, 张方华. 用于混合储能系统平抑功率波动的小波变换方法[J].
电力自动化设备, 2021, 41(3): 100-104.
CHENG L, ZHANG F H. Wavelet transform method for hybrid energy storage system smoothing power fluctuation[J].
Electric Power Automation Equipment, 2021, 41(3): 100-104.
|
| [12] |
朱林, 芦翔, 祁升龙, 等. 基于自适应阈值调整小波去噪法和HT-LMD的电流幅值时滞检测方法[J].
中国测试, 2022, 48(7): 37-41.
ZHU L, LU X, QI S L, et al. Current amplitude delay detection method based on adaptive threshold adjusted wavelet denoising method and HT-LMD[J].
China Measurement & Test, 2022, 48(7): 37-41.
|
| [13] |
韩微, 乔玉龙. 基于时间—顶点谱图小波变换的动态纹理分类方法[J].
信号处理, 2021, 37(6): 1008-1016.
HAN W, QIAO Y L. Dynamic texture classification method based on spectral time-vertex wavelet transform[J].
Journal of Signal Processing, 2021, 37(6): 1008-1016.
|
| [14] |
明勇, 甘晓敏, 杨帆. 基于时空域及高阶矩的红外弱目标检测算法[J].
国外电子测量技术, 2021, 40(12): 1-6.
MING Y, GAN X M, YANG F. Infrared weak target detection algorithm based on space-time domain and high-order moment[J].
Foreign Electronic Measurement Technology, 2021, 40(12): 1-6.
|
| [15] |
卢中昊, 徐军, 林铭团. 电磁辐射发射现场测试中基于空域对消的背景电磁干扰抑制方法[J].
系统工程与电子技术, 2020, 42(7): 1433-1438.
LU Z H, XU J, LIN M T. Background electromagnetic interference suppression method based on spatial cancellation for on-site test of electromagnetic radiation emission[J].
Systems Engineering and Electronics, 2020, 42(7): 1433-1438.
DOI:10.3969/j.issn.1001-506X.2020.07.01 |
 2024, Vol. 50
2024, Vol. 50


 ,
,