文章信息
- 于瑞红, 姚振静, 罗青山, 王妍, 罗鑫, 邱忠超
- YU Ruihong, YAO Zhenjing, LUO Qingshan, WANG Yan, LUO Xin, QIU Zhongchao
- 面向低频振动测量的双光纤光栅加速度传感器研究
- Research on double fiber grating acceleration sensor for low frequency vibration measurement
- 中国测试, 2024, 50(8): 157-163
- CHINA MEASUREMENT & TEST, 2024, 50(8): 157-163
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022110028
-
文章历史
- 收稿日期: 2022-11-06
- 收到修改稿日期: 2023-01-25
2. 河北省地震灾害仪器与监测技术重点实验室,河北 三河 065201
2. Hebei Key Laboratory of Seismic Disaster Instrument and Monitoring Technology, Sanhe 065201, China
低频振动测量对地震海啸等灾害预警、地质勘探和能源开发等领域具有重要意义[1-2]。加速度传感器是测量低频振动的关键部件,传统加速度传感器主要包括压电式、电阻式和电容式等,它们具有成本低、技术较为成熟等优点,但存在易受外界磁场干扰、接线繁琐、远距离传输时信号衰减严重等缺点[3-4]。基于光纤布拉格光栅(fiber Bragg grating, FBG)的加速度传感器由于具有抗电磁干扰、耐腐蚀、体积小、质量轻和准分布式等独特优点而受到广泛关注[5-6]。
近年来,国内外学者对低频FBG加速度传感器开展了一系列研究。乔学光等[7]开发了一种紧凑型光纤加速度计,机械振动元件是采用3D打印技术制作的六角形结构,可以将垂直振动转化为纵向定位的光纤结构的周期性变形,并通过反射光谱的波长位移来建立振动加速度与波长位移之间的关系。测量的灵敏度为421.4 pm/g,工作范围10~210 Hz。梁磊等[8]提出了一款基于柔性铰链结构的小型FBG加速度计,采用柔性铰链作为弹性体,工作频带可达20~400 Hz,悬弧结构实现了加速度计的小型化,适用于航空航天等领域狭窄空间的中低频振动监测,然而灵敏度较低,为26.962 pm/g。乔学光等[9]研制出一种基于多级柔性铰链的低频高灵敏度光纤加速度计,加速度计在1~60 Hz的工作区间内拥有927.21 pm/g的较高灵敏度。Udos等[10]提出了一种新型的悬臂梁FBG加速度传感器,其采用磁铁作为质量块,并构成磁阻尼器结构,在一定程度上拓展了工作频带范围,但是灵敏度相对较低。戴玉堂等[11]提出一种新型弯曲弹簧片FBG加速度计,两个对称弯曲的弹簧板作为弹性元件对称放置,使FBG产生大小相等但方向相反的轴向应变,进而使FBG频移加倍,传感器固有频率为46 Hz,在0.7~20 Hz频率范围内有较好的线性响应。尽管前期研究已取得了一系列丰硕成果,然而,低频振动测量时灵敏度低一直是阻碍FBG加速度传感器应用于工程实际的瓶颈问题。
为了提高低频振动测量时FBG加速度传感器的灵敏度,提出一种高灵敏度低频双FBG加速度传感器。采用十字簧片作为拾振结构,理论分析传感器的振动响应特性,给出传感器的谐振频率和灵敏度公式。建立传感单元的数学模型,对传感单元结构参数进行优化,并利用有限元仿真验证理论分析结果,最后制作传感器实物并对其进行性能测试。
1 传感器结构设计与理论分析 1.1 传感器结构建模FBG加速度传感器由两根FBG、刚性梁、十字簧片、基座、L形底座和一个质量块组成,如图1所示。由四个簧片构成两个对称的十字簧片结构,减小横向串扰和摩擦力的不利影响。当FBG加速度传感器受到外界振动激励时,其自由端的质量块会随惯性力发生垂直偏转,刚性梁作为一个平移结构,将质量块的垂直挠度转化为FBG的轴向挠度[12]。质量块绕十字簧片中心微幅振动,使FBG产生应变,从而影响其反射光的中心波长。反射光中心波长的漂移量与质量块的线性位移量正相关,同时也与加速度正相关,因此测量反射光中心波长的漂移量即可获得加速度大小,实现对振动的测量[13]。
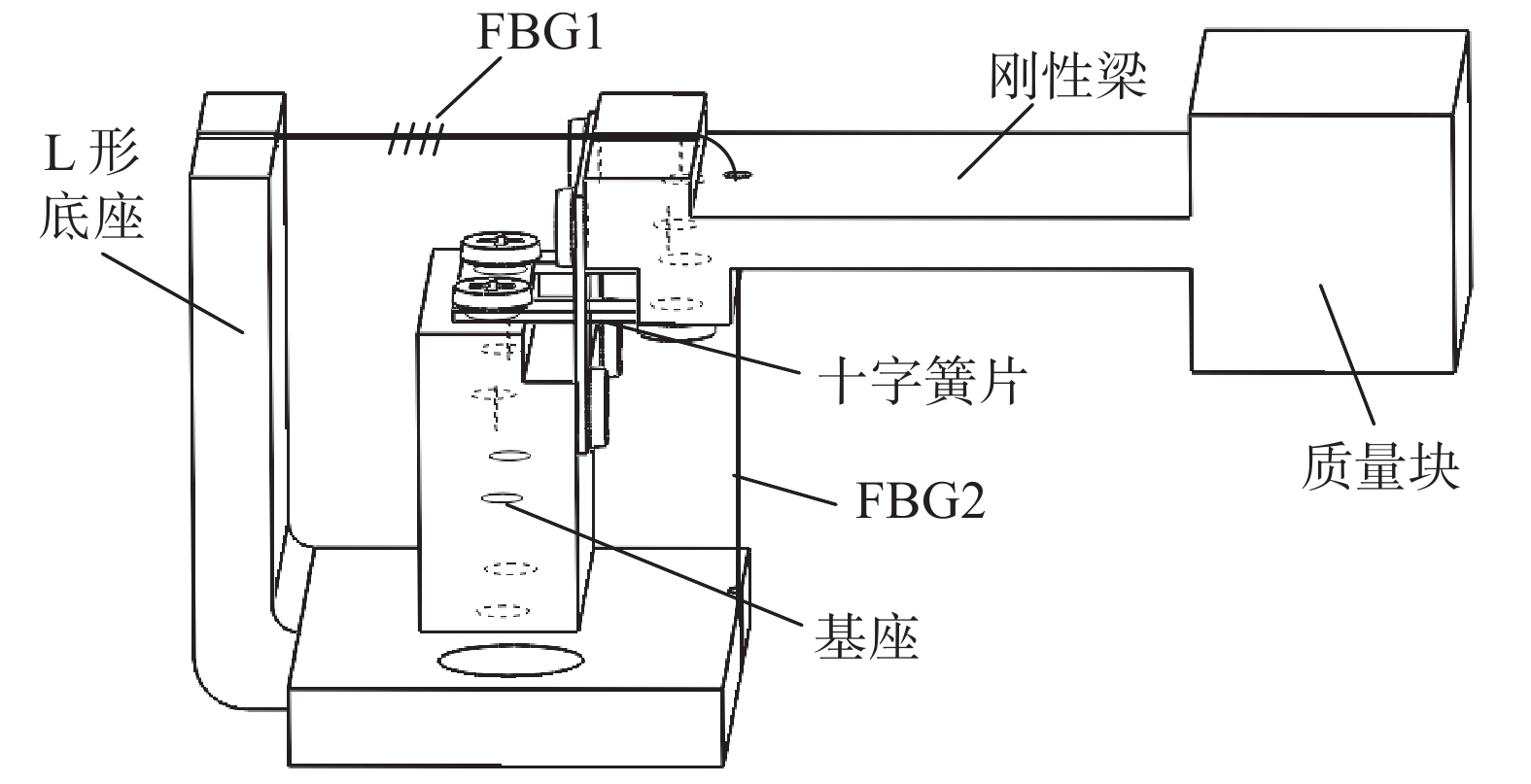
|
| 图 1 传感器结构示意图 |
1.2 理论分析
传感器结构振动模型如图2所示,振动时由于物体惯性力的存在,基座会带动连接有十字簧片的质量块做自由单摆运动。当加速度方向垂直向下时,质量块向下移动,FBG1与FBG2做等量的拉伸应变和压缩应变。在上述振动过程中,FBG中心波长会随应变的改变而产生相应变化,且二者的变化呈现一定的规律,FBG中心波长数值与受到加速度数值成正相关关系。
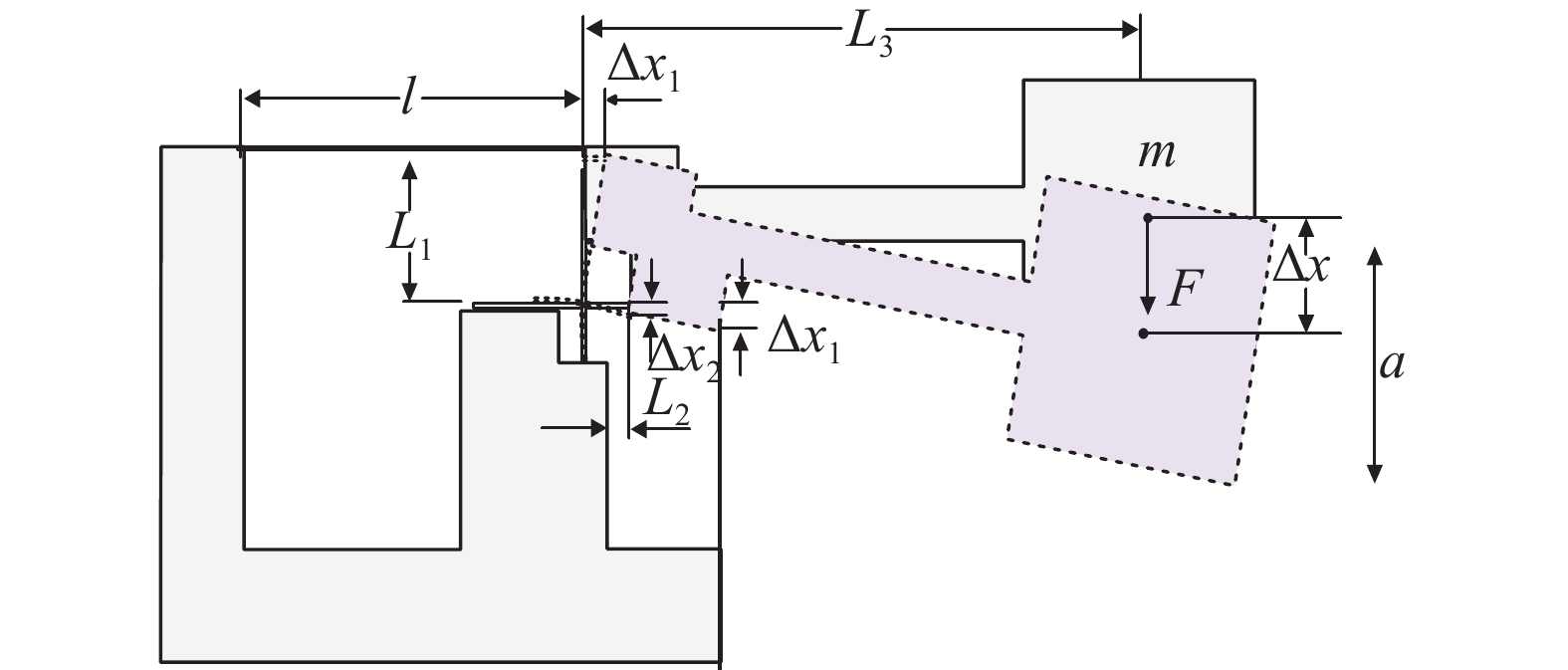
|
| 图 2 传感器结构振动模型 |
设每根光纤刚度为
| $ K = 2 {\left( {\frac{{{L_1}}}{{{L_3}}}} \right)^2}{k_1} + 4 {\left( {\frac{{{L_2}}}{{{L_3}}}} \right)^2}{k_2} $ | (1) |
固有频率为
| $ f = \frac{1}{{2\pi }}\sqrt {\frac{K}{m}} = \frac{1}{{2\pi }}\sqrt {\frac{{2{{({L_1}/{L_3})}^2}{k_1} + 4{{({L_2}/{L_3})}^2}{k_2}}}{m}} $ | (2) |
在式(2)中,设质量块的质量为
在方向垂直向上合力的作用下,设质量块相对于底座的位移为
| $ \Delta {x_{\text{1}}} = \frac{{{L_1}}}{{{L_3}}}\Delta x = \frac{{{L_1}}}{{{L_3}}} \cdot \frac{{ma}}{K} $ | (3) |
得光纤产生的应变
| $ \Delta \varepsilon = \frac{{\Delta {x_1}}}{l} = \frac{{({L_1}/{L_3})ma}}{{2l{{({L_1}/{L_3})}^2}{k_1} + 4l{{({L_2}/{L_3})}^2}{k_2}}} $ | (4) |
该传感器两根FBG的波长变化受应变和温度变化的共同影响,可表示为
| $ \Delta {\lambda _{{\mathrm{B}}{\text{1}}}} = {\lambda _{{\mathrm{B}}{\text{1}}}}\left[ {({a_\Lambda } + {a_{\mathrm{n}}})\Delta T + (1 - {P_{\mathrm{e}}})\Delta \varepsilon } \right] $ | (5) |
| $ \Delta {\lambda _{{\mathrm{B}}{\text{2}}}} = {\lambda _{{\mathrm{B}}{\text{2}}}}\left[ {({a_\Lambda } + {a_{\mathrm{n}}})\Delta T - (1 - {P_{\mathrm{e}}})\Delta \varepsilon } \right] $ | (6) |
式中,
| $ \Delta {\lambda _{{\mathrm{B}}1}} - \Delta {\lambda _{{\mathrm{B}}2}} = 2{\lambda _{\mathrm{B}}}(1 - {P_{\mathrm{e}}})\Delta \varepsilon $ | (7) |
由式(3)和(7)可计算该FBG传感器的灵敏度
| $ S = \left| {\frac{{\Delta {\lambda _{{\mathrm{B}}1}} - \Delta {\lambda _{{\mathrm{B}}2}}}}{a}} \right| = \frac{{2{\lambda _{\mathrm{B}}}(1 - {P_{\mathrm{e}}})({L_1}/{L_3})m}}{{2l{{({L_1}/{L_3})}^2}{k_1} + {\text{4}}l{{({L_{\text{2}}}/{L_3})}^2}{k_{\text{2}}}}} $ | (8) |
基于上述分析,可知差分结构可以实现FBG加速度传感器的温度自补偿效果,减小测量误差,同时可以通过优化结构参数来降低传感器的固有频率和提高灵敏度。
2 仿真分析 2.1 结构参数分析固有频率和灵敏度是衡量FBG加速度传感器的两个重要评定指标。对式(2)和(8)分析可知,传感器的质量块质量
由低频振动测量的工程实际可知,低频振动传感器的工作频带一般在2~50 Hz之间[14],在同时考虑到传感器的尺寸和质量,采用单一变量法对结构参数优化,结果如表1所示。
| 结构参数 | 数值 |
| 光纤有效长度 | 15 mm |
| 十字簧片中心到光纤的距离 | 5.8 mm |
| 十字簧片中心到刚性梁的距离 | 3.35 mm |
| 十字簧片中心到质量块中心距离 | 28.2 mm |
| 质量块质量 | 10 g |
| 十字簧片长度 | 4.4 mm |
| 十字簧片宽度 | 2 mm |
| 十字簧片厚度 | 0.4 mm |
| FBG中心波长 | |
| 光纤横截面积 | 1.23×10–8 m2 |
| 光纤有效弹光系数 | 0.22 |
2.2 COMSOL仿真分析
采用COMSOL对传感器进行静应力分析与模态仿真分析,如图3所示。在静应力分析过程中,将L型底座固定,沿Y轴方向施加1 g(9.8 m/s2)的加速度,质量块最大位移量约为0.07 mm,刚性梁粘光纤处位移量为0.012 mm,表明传感器能够较好采集外界振动信号,同时粘贴光纤光栅位置的形变位移量足够小,可以保证光纤光栅的物理特性不受影响,确保结构的稳定性。同理,沿Z轴方向施加1 g的加速度可得横向等效位移图,刚性梁粘光纤处位移量为2.26×10–5 mm。计算可知,相同大小加速度条件下,传感器光纤横向位移仅为纵向的0.19%,说明该传感器在敏感方向的振动可视为一种单自由度振动。
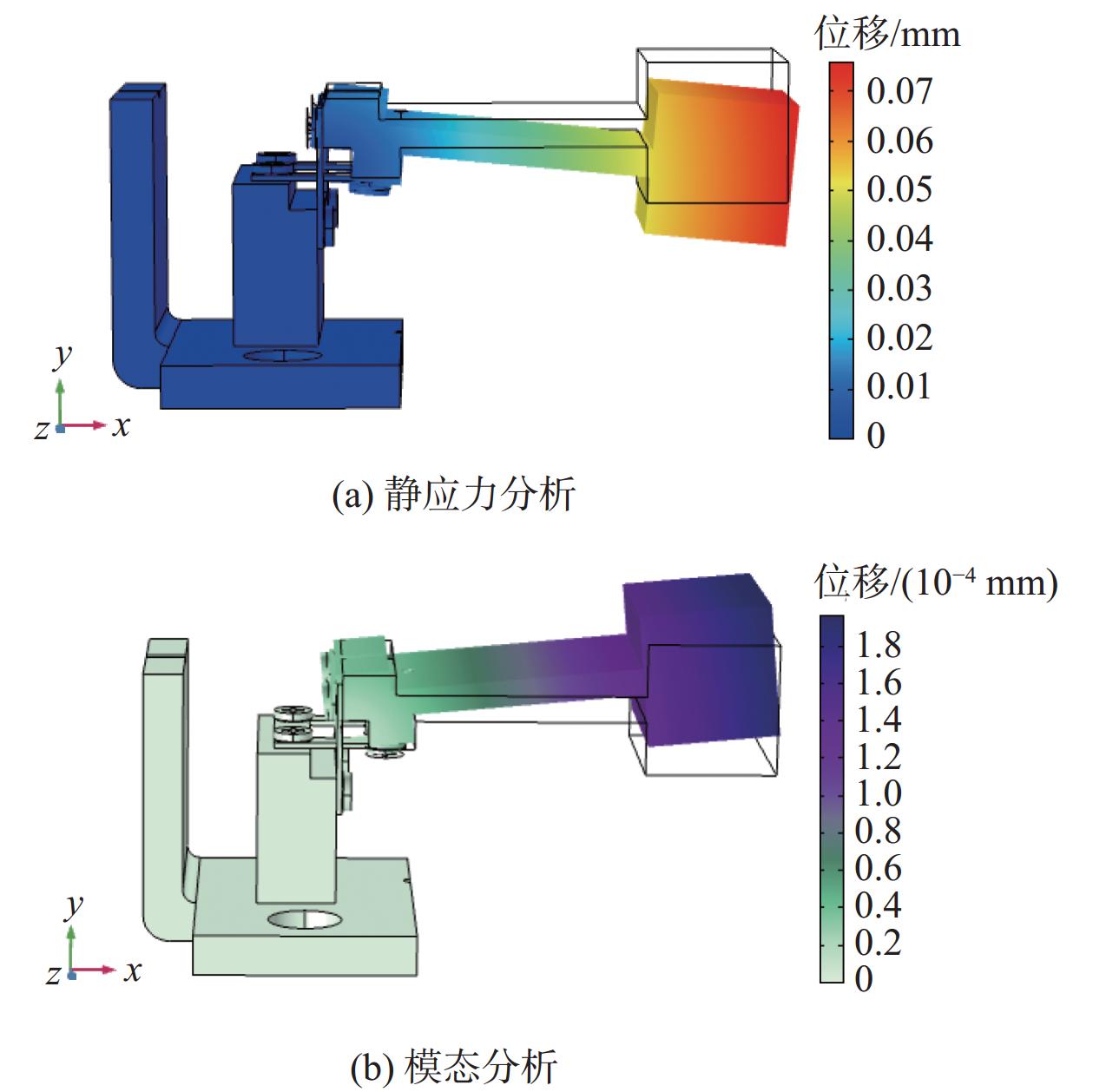
|
| 图 3 结构仿真分析 |
对模型的前四阶模态分析可得,一阶、二阶、三阶、四阶模态频率分别为65.22 Hz、
测试系统由振动系统和传感系统两部分组成,如图4所示,其中振动系统由信号发生器、功率放大器、电磁激振台等部分组成,传感系统由传感器、调制解调器与计算机等部分组成。根据结构参数优化与仿真结果研制FBG加速度传感器,采用两点粘贴法并施加适当的预应力粘贴FBG,以避免FBG的栅区产生不均匀应变而导致啁啾现象。

|
| 图 4 传感器测试系统 |
3.1 输出响应特性
对传感器的输出响应特性进行测试,保持振动台的加速度值为1 m/s2,得到频率为20 Hz和40 Hz时的响应曲线如图5所示。

|
| 图 5 传感器输出响应曲线 |
由图5可知,传感器能够较好地获取外界输入的正弦激励,表明FBG所受的应力均匀,无啁啾与多峰现象。在输入相同加速度时,不同频率值时测得的时域曲线幅值相近,说明传感器在工作频段内响应是平坦的。
3.2 幅频特性在幅频特性测试中,设定加速度为1.5 m/s2,信号发生器输出频率为3~110 Hz的正弦信号,并且每隔5 Hz改变其频率,当频率临近仿真得到的固有频率时,每隔2 Hz改变频率,得到幅频特性曲线如图6所示。
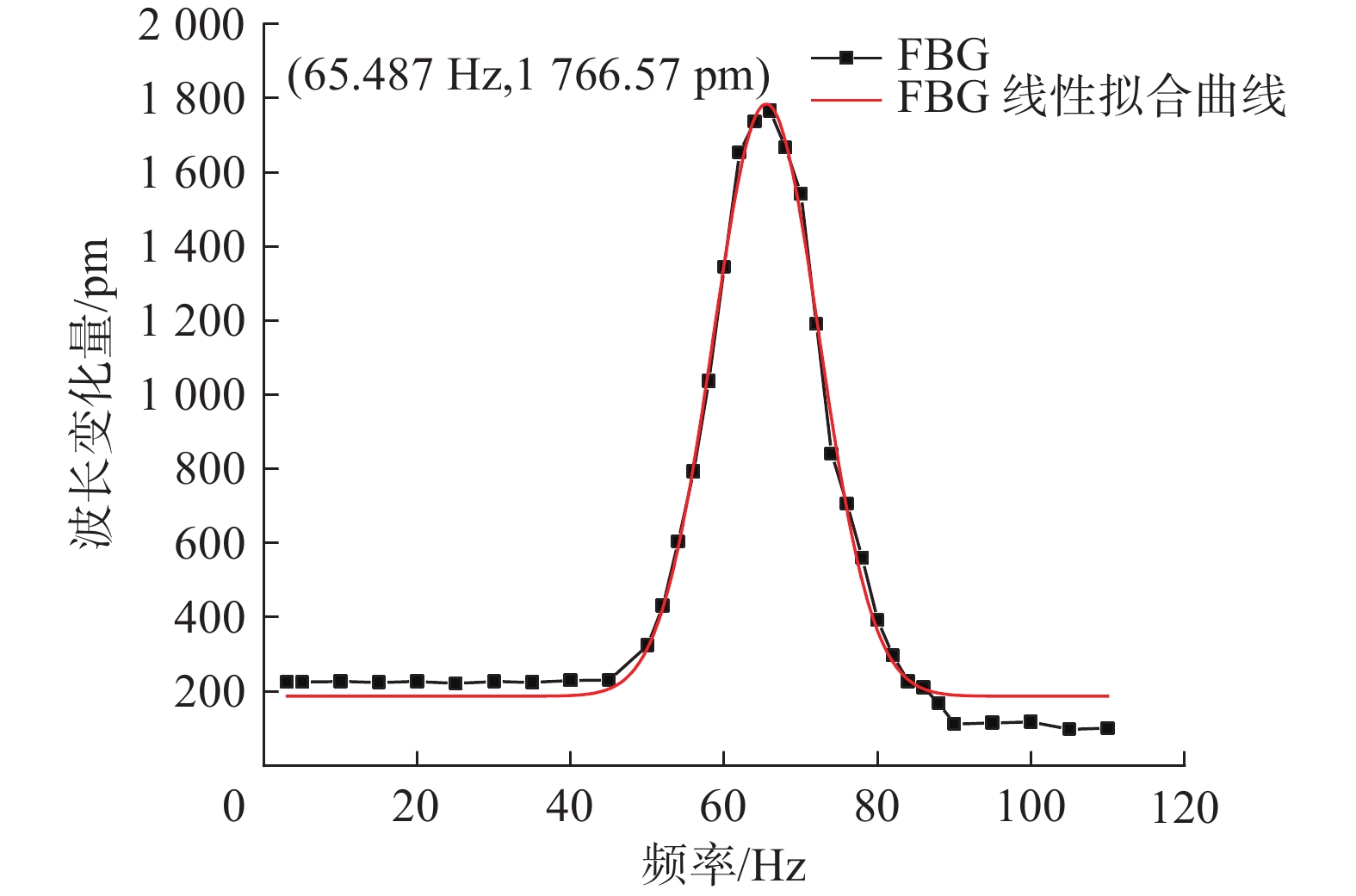
|
| 图 6 传感器幅频特性 |
由图6可知,传感器固有频率为65.487 Hz,与仿真分析的理论值65.22 Hz接近,频率值在3~45 Hz内曲线区域趋于平坦,可作为传感器的工作范围,其中3 Hz为实验采用的电磁激振式振动台可测量的最小振动频率。
3.3 灵敏度与线性度测试以步长为10 Hz将振动频率由10 Hz增加到40 Hz,同时将加速度由0.5 m/s2增加到3 m/s2,可得光纤光栅波长变化量随加速度的变化曲线,如图7所示。

|
| 图 7 线性度拟合曲线图 |
由图7可知,输入频率在10 Hz、20 Hz、30 Hz、40 Hz时加速度传感器的灵敏度依次为
动态范围(DR)是评估FBG振动传感器传感特性的一个关键参数,通常反映了传感器接收强信号和弱信号的能力。根据振动加速度与波长之间的关系,可以通过以下公式表示:
| $ {R_{\mathrm{D}}} = 20\lg \left(\frac{{{\lambda _{\max }}}}{{{\lambda _{\min }}}}\right) $ | (9) |
在振动输入信号为零时,即系统处于静态时,FBG中心波长漂移量为1 pm,在振动信号频率为10 Hz,加速度超过30 m/s2时,满足在工作频带的线性度范围内,FBG中心波长的最大漂移量为
相较于激振信号,冲击信号是一个非稳态的瞬时信号且包含丰富的振动信息,能够充分反应加速度传感器的响应特性,同时还可以通过频域变换来验证该传感器的固有频率[15]。冲击响应实验时,将3个质量为20 g的砝码从20 cm高度做自由落体运动,模拟产生随机的冲击信号,时域冲激响应和傅里叶频谱分析结果如图8所示。
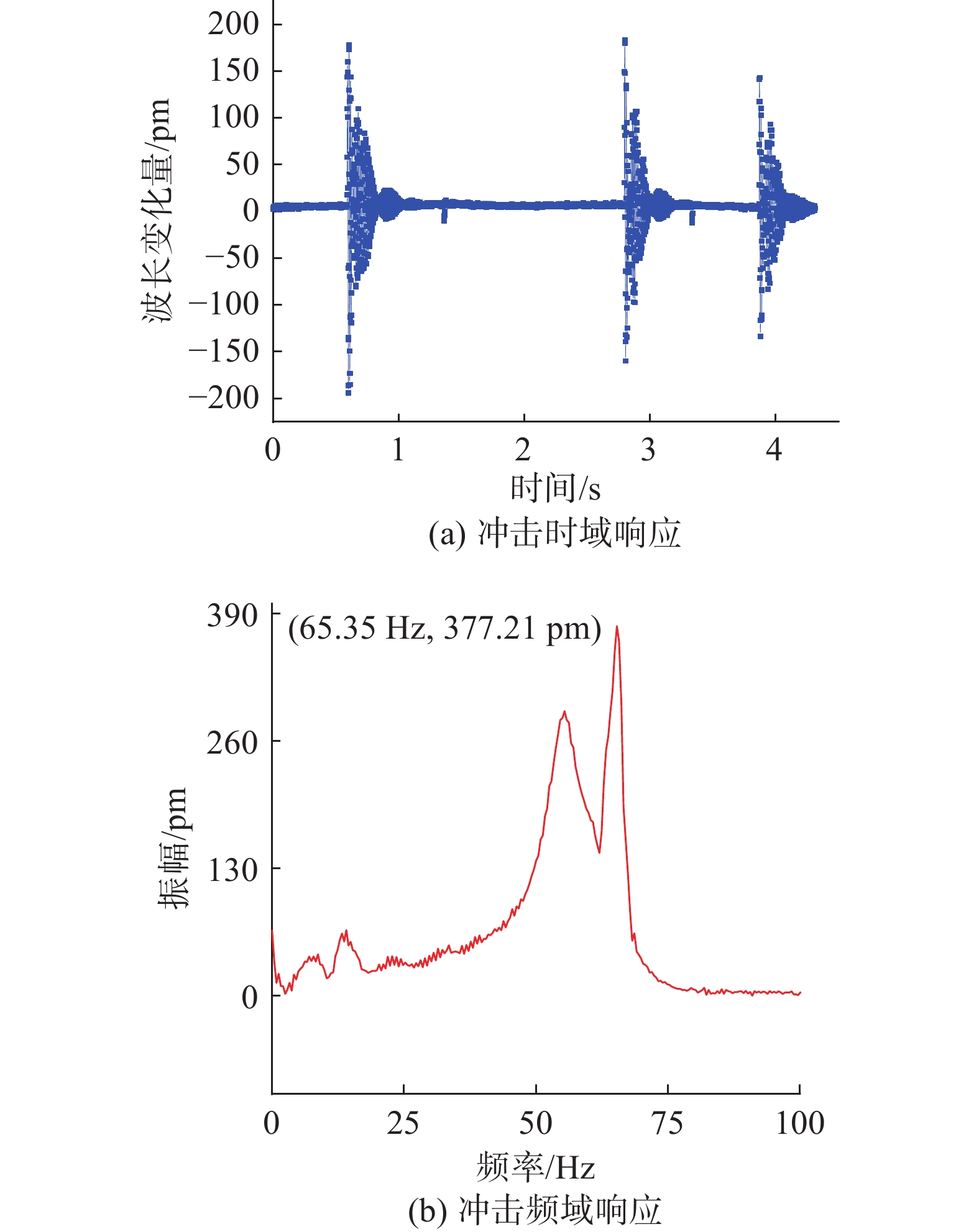
|
| 图 8 冲击响应曲线 |
由图8可知,FBG加速度传感器能够有效反映冲击激励,通过对该时域数据做快速傅里叶变换可得传感器的频谱图,如图8(b)所示。在幅值最大处对应的频率值为65.35 Hz,进一步验证了传感器的固有频率约为65.35 Hz,与仿真结果和传感器幅频响应实验结果吻合。
3.6 横向抗干扰测试横向干扰度为相同频率下加速度激励信号作用于横轴方向时FBG中心波长漂移量与作用于主轴方向时FBG中心波长漂移量的对数比。为了验证传感器的横向抗干扰特性,将传感器分别纵向和横向固定在振动台上,设定频率为40 Hz的正弦激励信号,加速度为1.5 m/s2,记录两种不同振动情况时的FBG中心波长漂移量,如图9所示。传感器的纵向响应与横向响应分别为227.25 pm和4.54 pm,得横向串扰为–33.99 dB,说明传感器能够有效抑制横向干扰的影响。
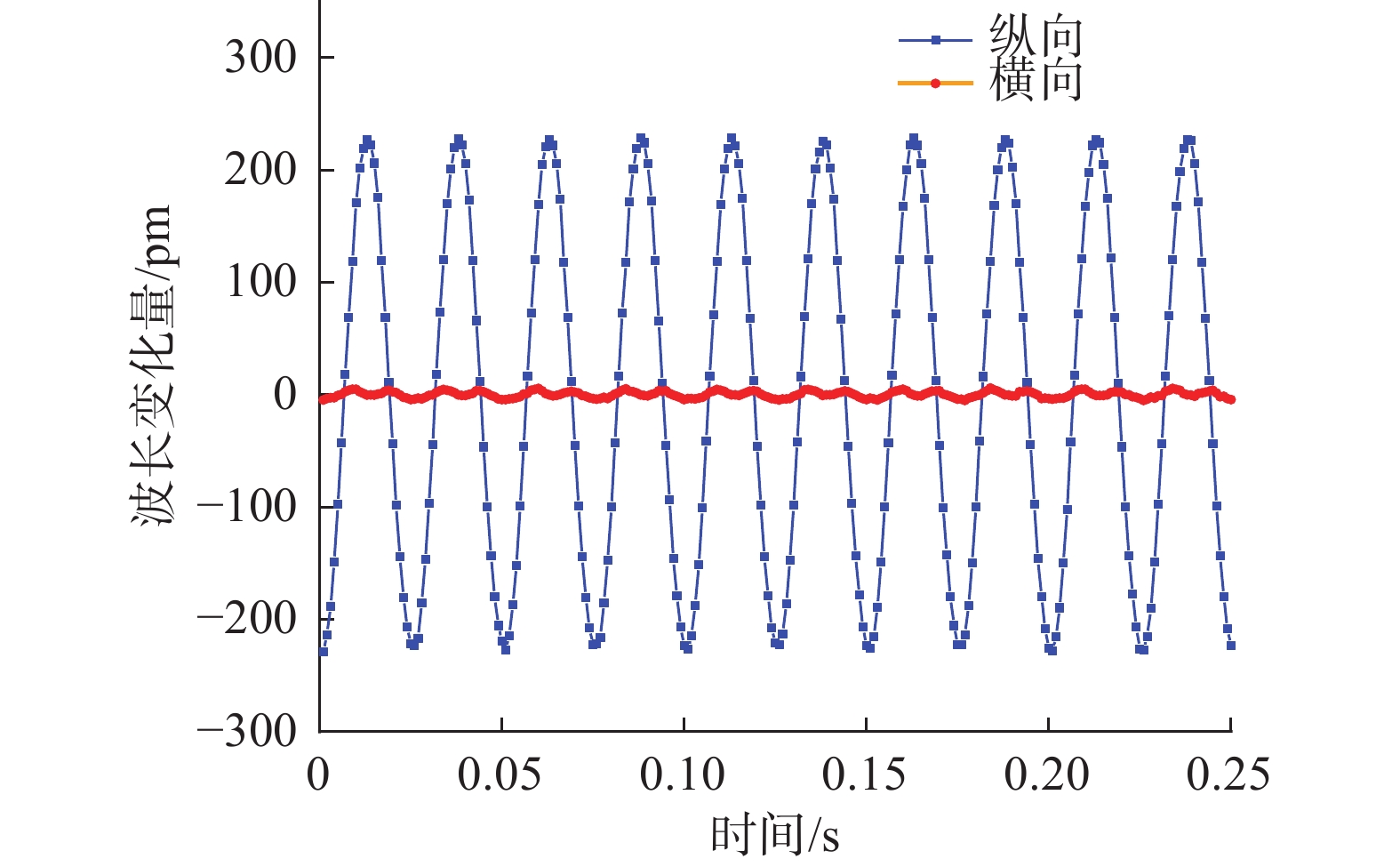
|
| 图 9 横向抗干扰测试 |
3.7 温度干扰测试
为了研究传感器的温度响应特性,需要使用温度测试系统,该系统由传感器、宽带光源、温度控制箱和光谱仪组成,如图10所示。当宽带光源发出的光通过环形器传输到温控设备里的传感器时,传感器会感知温控箱内的温度变化,将漂移后的FBG中心波长再通过环形器传输到光谱仪中对中心波长进行解调,实现对温度的测量。通过这种方式,可以探究双FBG差分结构在不同温度下的响应特性。
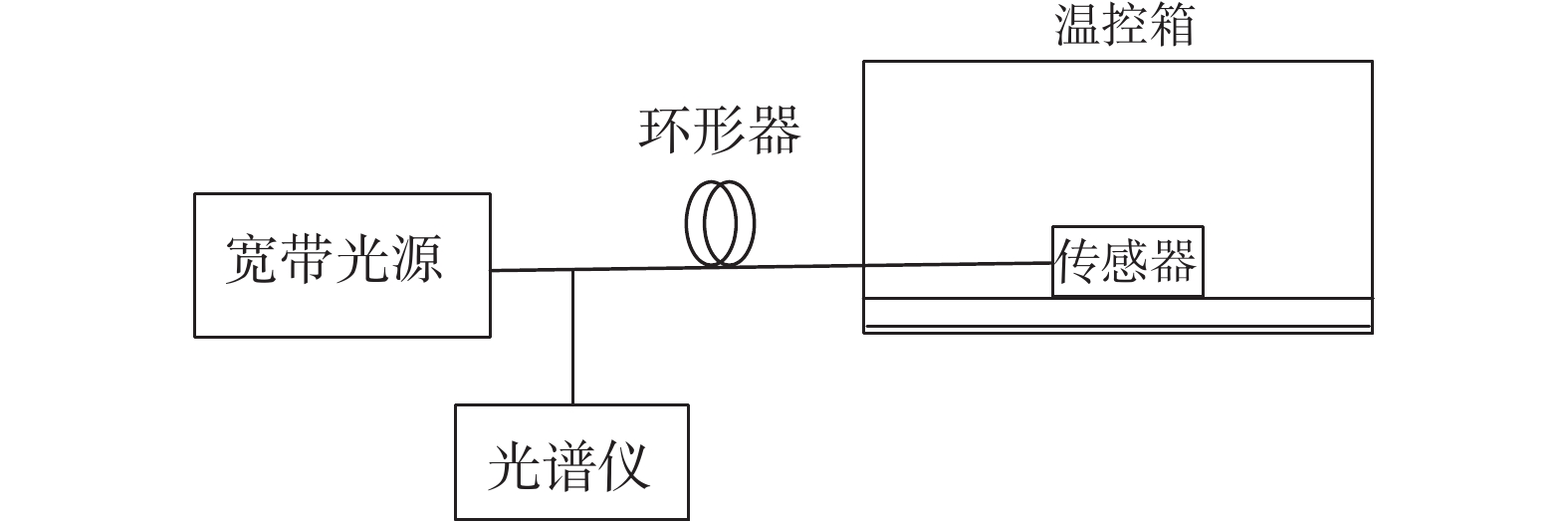
|
| 图 10 温度测试系统 |
温度测试曲线如图11所示,由图可知,单根FBG的温度漂移量为10.3 pm/℃,在60 ℃时,中心波长的漂移量高达510 pm,因此在振动监测中必须消除或者减小温度的影响以提高测量的准确性和精度。而双FBG差分结构能够显著改善测量环境温度对FBG加速度传感器的影响,其温度漂移量仅为0.18 pm/℃,约为单根FBG影响的1.75%。因此,双FBG差分结构可以实现对环境温度变化的自补偿,从而提高FBG加速度传感器的测量精度和准确性。
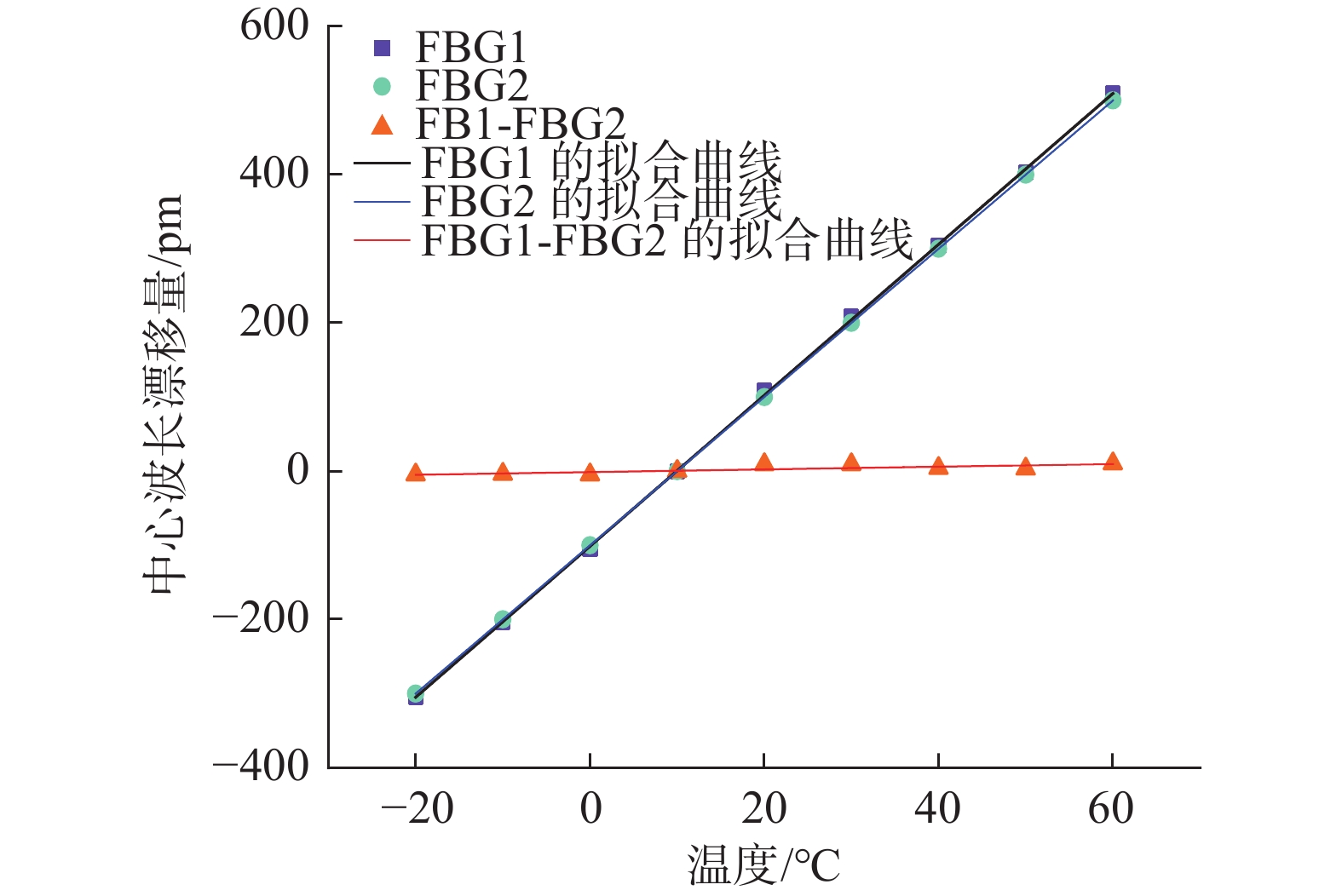
|
| 图 11 温度测试曲线 |
将传感器的关键性能指标与引言中介绍的典型FBG加速度传感器的性能进行比较,如表2所示。由表2可知,本文所设计的基于十字簧片结构的光纤光栅加速度传感器具有灵敏度高、低频性能好的特点,且能够实现3~45 Hz范围内低频振动测量。
4 结束语
针对低频振动测量时灵敏度低的问题,提出一种基于悬臂梁的高灵敏度低频双FBG加速度传感器。采用十字簧片作为拾振结构,理论分析传感器的振动响应特性,给出传感器的谐振频率和灵敏度公式。建立传感单元的数学模型,对传感单元结构参数进行优化,并利用有限元仿真验证理论分析结果,最后制作传感器实物并对其进行性能测试。结果表明,研制的低频FBG加速度传感器固有频率为65 Hz,在3~45 Hz内响应平坦,灵敏度达到
| [1] |
黄哲. 面向油气钻井振动测量的空间三轴加速度传感器阵列研究[J].
电子测量技术, 2021, 44(8): 155-160.
HUANG Z. Method of drilling vibration measurement based on spatial array of accelerometers[J].
Electronic Measurement Technology, 2021, 44(8): 155-160.
|
| [2] |
魏鹤鸣, 车嘉炜, 侯林嵩, 等. 高精度光纤光栅振动解调系统研究与应用[J].
国外电子测量技术, 2023, 42(1): 82-88.
WEI H M, CHE J W, HOU L S, et al. Research and application of high-resolution fiber Bragg grating vibration demodulation system[J].
Foreign Electronic Measurement Technology, 2023, 42(1): 82-88.
|
| [3] |
张晟, 龚涛波, 王鲁康, 等. 用于运动姿势捕捉的可穿戴MEMS微型化加速度计研制[J].
中国测试, 2021, 47(1): 82-87.
ZHANG S, GONG B T, WANG L K, et al. Development of a wearable MEMS miniaturized accelerometer for motion gesture capture[J].
China Measurement & Test, 2021, 47(1): 82-87.
DOI:10.11857/j.issn.1674-5124.2020100001 |
| [4] |
张明跃, 房立清, 郭德卿, 等. MEMS传感器数据漂移抑制技术研究[J].
电子测量技术, 2022, 45(11): 99-103.
ZHANG M Y, FANG L Q, GUO D Q, et al. Research on random drift suppression technology of MEMS sensor[J].
Electronic Measurement Technology, 2022, 45(11): 99-103.
|
| [5] |
张晓飞, 吕中虎, 杨秀元, 等. 弱反射光栅滑坡监测系统的研究与应用[J].
电子测量技术, 2022, 45(6): 119-123.
ZHANG X F, LV Z H, YANG X Y, et al. Research and application of landslide monitoring system based on weak-reflection fiber grating sensing network[J].
Electronic Measurement Technology, 2022, 45(6): 119-123.
|
| [6] |
陈光, 丁克勤, 种玉宝, 等. 大型原油储罐罐壁变形应变监测试验研究[J].
中国测试, 2022, 48(9): 164-170.
CHEN G, DING K Q, ZHONG Y B, et al. Experimental study on deformation and strain monitoring of large crude oil storage tank wall[J].
China Measurement & Test, 2022, 48(9): 164-170.
|
| [7] |
GUO T, ZHANG T X, LI Y Z, et al. Highly sensitive FBG seismometer with a 3D-printed hexagonal configuration[J].
Journal of Lightwave Technology, 2020, 38(16): 4588-4595.
DOI:10.1109/JLT.2020.2991667 |
| [8] |
LIANG L, WANG H, LI Z C, et al. Miniature bending-resistant fiber grating accelerometer based on a flexible hinge structure[J].
Optics Express, 2022, 30(19): 33502-33514.
DOI:10.1364/OE.465453 |
| [9] |
LI H D, GAO H, FAN W, et al. Development of low frequency and high sensitivity fiber optic accelerometer based on multi-stage flexure hinges[J].
Optical Fiber Technology, 2022, 73: 10308.
|
| [10] |
UDOS W, LEE Y S, LIM K S, et al. Signal enhancement of FBG-based cantilever accelerometer by resonance suppression using magnetic damper[J].
Sensors and Actuators A: Physical, 2020, 304: 111895.
DOI:10.1016/j.sna.2020.111895 |
| [11] |
LIU F F, DAI Y T, KARANJA J M, et al. A low frequency FBG accelerometer with symmetrical bended spring plates[J].
Sensors, 2017, 17: 206.
DOI:10.3390/s17010206 |
| [12] |
PARIDA O P, NAYAK J, ASOKAN S. Design and validation of a novel high sensitivity self-temperature compensated fiber Bragg grating accelerometer[J].
IEEE Sensors Journal, 2019, 19(15): 6197-6204.
DOI:10.1109/JSEN.2019.2909186 |
| [13] |
LI T L, GUO J X, TAN Y G, et al. Recent advances and tendency in Fiber Bragg Grating-based vibration sensor: A Review[J].
IEEE Sensors Journal, 2020, 20(20): 12074-12087.
DOI:10.1109/JSEN.2020.3000257 |
| [14] |
张文涛, 李慧聪, 黄稳柱, 等. 光纤地震仪研究进展[J].
应用科学学报, 2021, 39(5): 821-842.
ZHANG W T, LI H C, HUANG W Z, et al. Research progress of optical fiber seismograph[J].
Journal of Applied Sciences, 2021, 39(5): 821-842.
DOI:10.3969/j.issn.0255-8297.2021.05.008 |
| [15] |
王宇, 刘铁根, 刘丽娜, 等. 合金钢封装光纤Bragg光栅传感器传感特性的研究[J].
光学技术, 2006(6): 923-925.
WANG Y, LIU T G, LIU L N, et al. Study on fiber Bragg grating sensor encapsulated by the alloyed steel[J].
Optical Technique, 2006(6): 923-925.
DOI:10.3321/j.issn:1002-1582.2006.06.033 |
 2024, Vol. 50
2024, Vol. 50
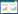


 ,
,