文章信息
- 梅善瑜, 陶为戈, 侯虎
- MEI Shanyu, TAO Weige, HOU Hu
- 永磁同步电机模糊控制和前馈补偿研究
- Research on fuzzy control and feedforward compensation for permanent magnet synchronous motor
- 中国测试, 2024, 50(8): 151-156
- CHINA MEASUREMENT & TEST, 2024, 50(8): 151-156
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022110030
-
文章历史
- 收稿日期: 2022-11-06
- 收到修改稿日期: 2023-02-18
永磁同步电机因其结构简单、体积小、质量轻、损耗小、效率高等优点被广泛应用在各种工业领域[1-2]。随着工业技术的飞速发展,对永磁同步电机控制性能的要求也越来越高[3],目前永磁同步电机在位置跟踪时多采用常规PID进行控制[4],但常规PID因其固定参数对位置信息的变化响应不及时,导致跟踪位置曲线波动较大,难以满足精确定位和快速响应的要求。
为提高永磁同步电机位置控制的精度和响应速度,国内外学者提出了滑模控制[5]、前馈控制[6]以及模糊控制[7]等控制方法。唐红雨等[8]提出了一种滑模自抗扰控制器的位置环控制方法,设计了滑模面和滑模控制率,把转动惯量和负载作为扰动量,把电机转子角度作为状态量,通过状态观测器观测,进行电机转子角度修正补偿,提高了系统的稳定性,但滑模自抗扰的非线性特征,导致状态观测器参数整定复杂,整体设计过程较复杂。蔚世超等[9]在位置跟踪时采用前馈控制算法,同时设计了一种新型扰动观测器,对负载转矩观测结果进行补偿,该方法有效降低了稳态误差和扰动造成的超调,改善了系统的跟踪性能,但仍难实现超低调。周萍等[10]将常规PID算法和模糊算法相结合,并设计了模糊控制器,该控制器通过对位置误差及其变化率进行判断,选择合理控制策略,可以降低超调,提高定位精度,但位置环响应速度有待提高。
针对上述方法的局限性,本文设计了新型位置环控制器,将比例P算法和模糊控制算法相结合,并引入前馈补偿算法用于位置跟踪控制,利用模糊控制算法降低位置跟踪的超调量,提高定位精度,利用前馈补偿控制提高位置环控制系统的响应速度。在Matlab/Simulink仿真平台上搭建仿真模型,通过对电机空载和带负载两种状态进行仿真对比分析,验证了此方法的可行性。
1 永磁同步电机的矢量控制原理矢量控制原理就是通过坐标变换的方法,将三相定子电流分解成控制励磁和转矩的两部分电流,实现对励磁和转矩单独的控制,以达到直流电机的控制效果。
永磁同步电机常见的矢量控制方法包括弱磁控制法、最大转矩法、恒功率因数控制法以及
经过坐标变换,永磁同步电机的
| $ {T_{\rm m}} = 1.5{P_{\rm n}}\left[ {{\psi _{\rm f}}{i_q} + ({L_d} - {L_q}){i_q}{i_d}} \right] $ | (1) |
| $ {T_{\rm m}} - {T_{\rm L}} = \frac{1}{{{P_{\rm n}}}}B\omega + \frac{1}{{{P_{\rm n}}}}J\frac{{{\text{d}}\omega }}{{{\text{d}}t}} $ | (2) |
当
| $ {T_{\rm m}} = 1.5{P_{\rm n}}{\psi _{\rm f}}{i_q} $ | (3) |
式中:
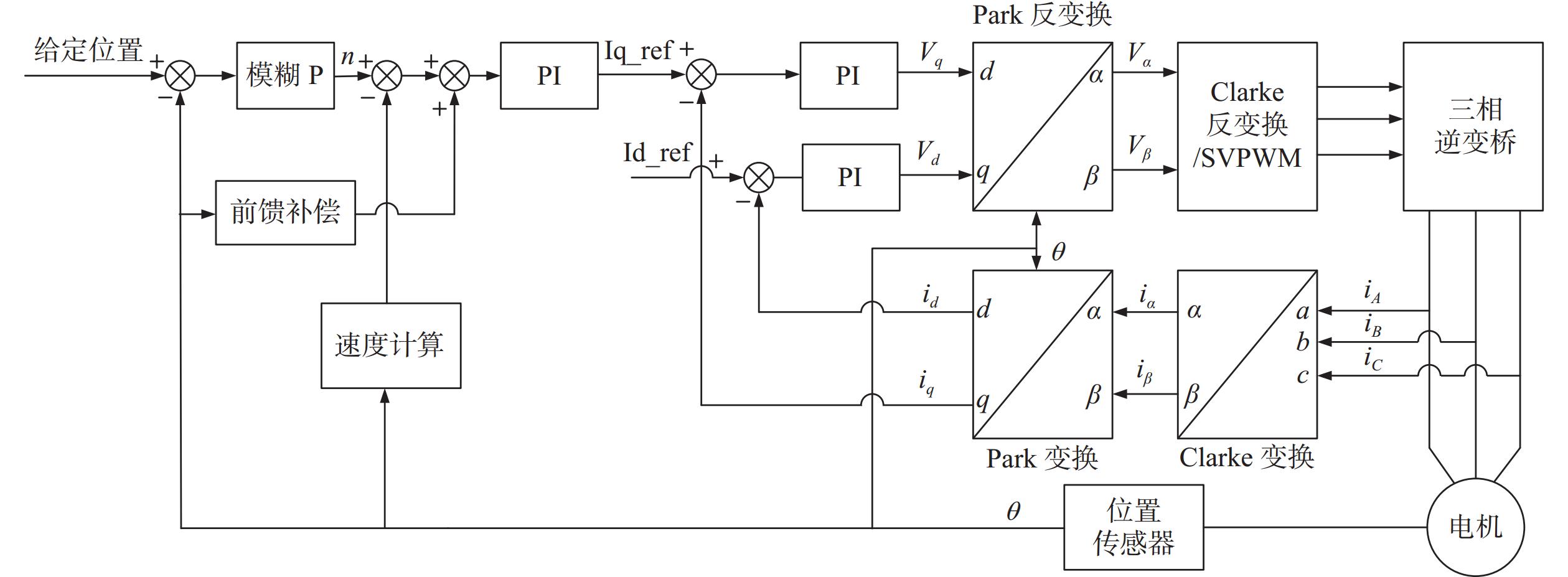
永磁同步电机三闭环控制系统如图1所示。三闭环包括位置环、速度环和电流环[12],位置环是三闭环矢量控制的最外环,主要作用是将电机的目标位置与实际位置的差值整定为速度信息,使电机准确跟随目标位置。速度环和电流环是位置控制的基础,在进行位置控制前,需要把此双环系统性能调节至最佳,因此电流环和速度环采用常规PI控制,选取适当的PI参数,保证系统的动态跟踪性能和静态精度。位置环采用模糊P控制器,并引入前馈补偿器,进一步提高系统的控制性能。
|
| 图 1 永磁同步电机三闭环控制系统结构图 |
2 位置环模糊控制器设计
模糊控制是一种模仿人的思维推理和逻辑决策的智能控制算法,不需要对控制对象精确建模,可以感知参数的变化并进行修正,适合控制永磁同步电机多变量、强耦合、非线性的系统。
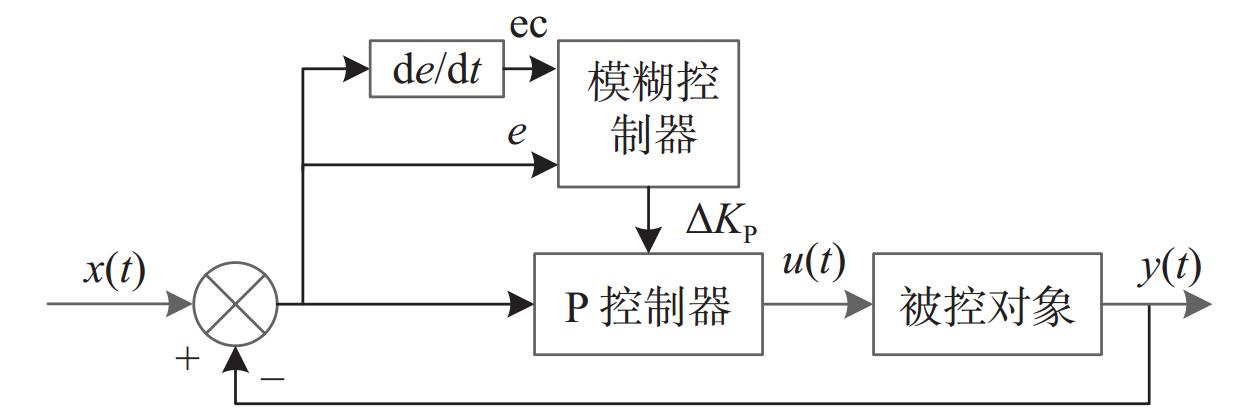
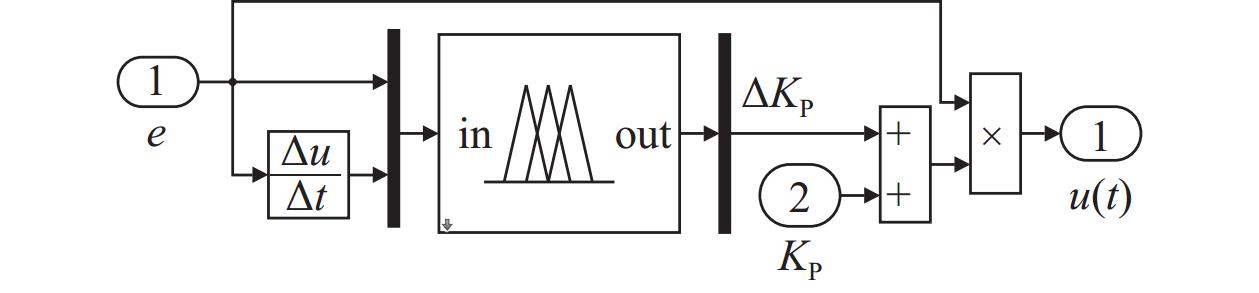
模糊P控制器一般结构如图2所示,仿真模型如图3所示。模糊P控制算法是在常规P算法的基础上增加了模糊控制器,模糊控制器将给定的位置信息
|
| 图 2 模糊P控制器结构图 |
|
| 图 3 模糊P控制器仿真模型图 |
经分析测试,选取
模糊规则制定是否合理决定了模糊控制器性能的好坏。文献[14]将速度环的模糊规则用于位置环中,速度环的模糊规则注重快速响应,对速度超调没有要求,而位置环要求位置跟随时,要实现无超调,毕竟对位置环来说,超调量越大,意味着位置控制精度越差,位置环的模糊规则注重控制精度,两组模糊规则存在明显差异。根据位置环高精度和无超调的控制要求,设定模糊规则如下:当误差
| e | ec | ||||||
| NB | NM | NS | Z | PS | PM | PB | |
| NB | NB | NM | NS | NS | Z | PS | PS |
| NM | NM | NS | NS | NS | NS | Z | Z |
| NS | NM | NS | NS | Z | Z | PS | PS |
| Z | NS | NS | Z | Z | PS | PS | PM |
| PS | NS | Z | Z | PS | PS | PM | PM |
| PM | NS | Z | PS | PS | PM | PM | PM |
| PB | PS | PS | PS | PM | PM | PM | PB |
3 前馈补偿控制器设计
在伺服控制系统中,大多数控制器的输入都是被控对象给定值和实际反馈值的偏差,这种控制方式是在被控对象出现偏差之后才开始动作,以修正扰动对被控对象的改变,控制作用总是滞后扰动作用,响应速度慢。前馈补偿控制器可以在被控对象改变前,补偿扰动对被控对象的影响。前馈补偿控制可以很好提高控制系统对指令信号的响应速度,减小跟踪误差。
位置前馈补偿器一般结构如图4所示。

|
| 图 4 位置前馈补偿器结构图 |
图4中,位置闭环前馈补偿控制系统的闭环传递函数为:
| $ G=\frac{q(t)}{p(t)}=\frac{F(s)H_1H_2+K_{\rm P}H_1H_2}{1+K_{\rm P}H_1H_2} $ | (4) |
由公式(4)可知,只有
| $ {H_1} = \frac{{{K_{\rm V}}}}{{{T_{\rm V}}S + 1}} $ | (5) |
| $ {H_2} = \frac{{{K_{\rm M}}}}{S} $ | (6) |
式中:
已知公式(5)、(6)可推出
| $ F(s) = \frac{1}{{{K_{\rm V}}{K_{\rm M}}}}S + \frac{{{T_{\rm V}}}}{{{K_{\rm V}}{K_{\rm M}}}}{S^2} $ | (7) |
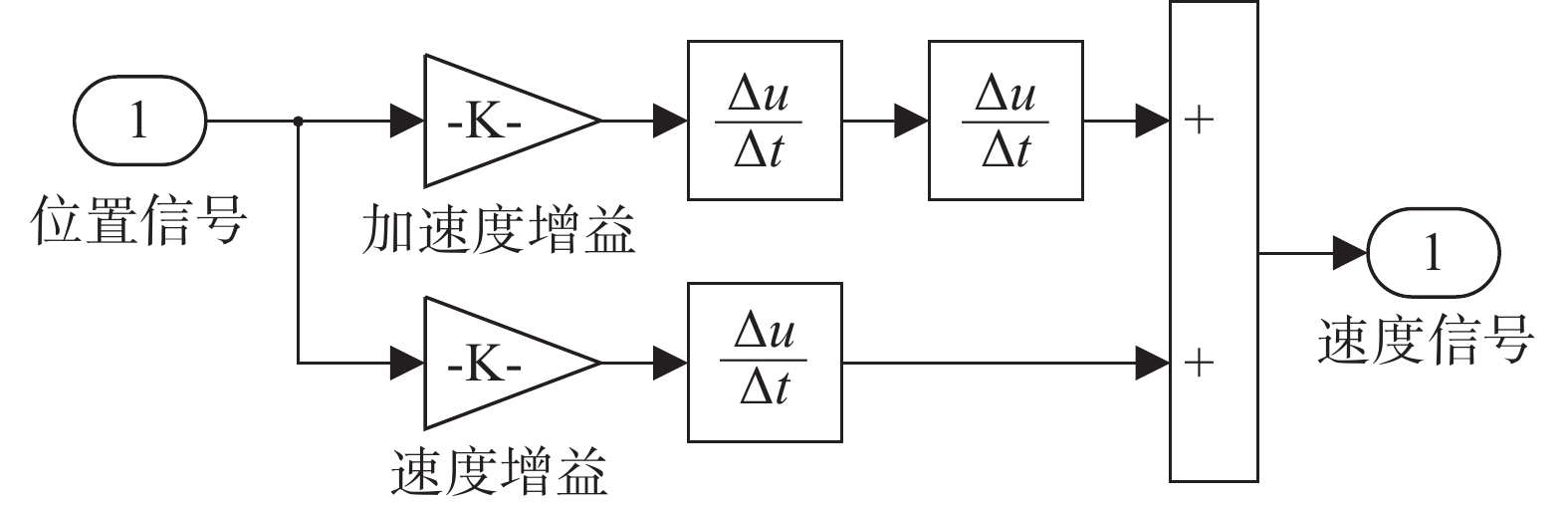
由公式(7)知,前馈补偿控制器的传递函数中包含了速度前馈补偿以及加速度前馈补偿函数,通过对速度和加速度的补偿实现补偿位置信号的目的。位置前馈补偿控制仿真模型如图5所示。
|
| 图 5 位置前馈补偿仿真模型图 |
4 仿真结果分析
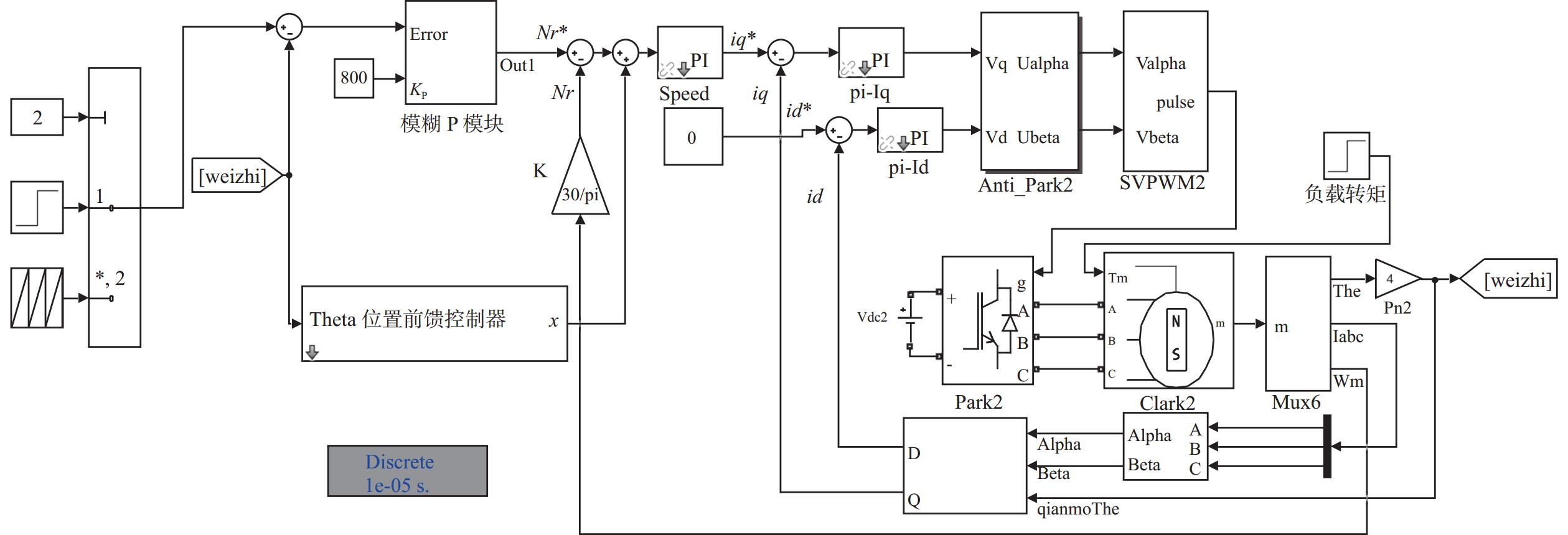
在Matlab/ Simulink上搭建永磁同步电机位置控制仿真模型,整体仿真模型如图6所示。
|
| 图 6 永磁同步电机位置控制仿真模型图 |
图6中永磁同步电机的电气参数为:电压

|
| 图 7 输入阶跃位置信号仿真结果图 |
|
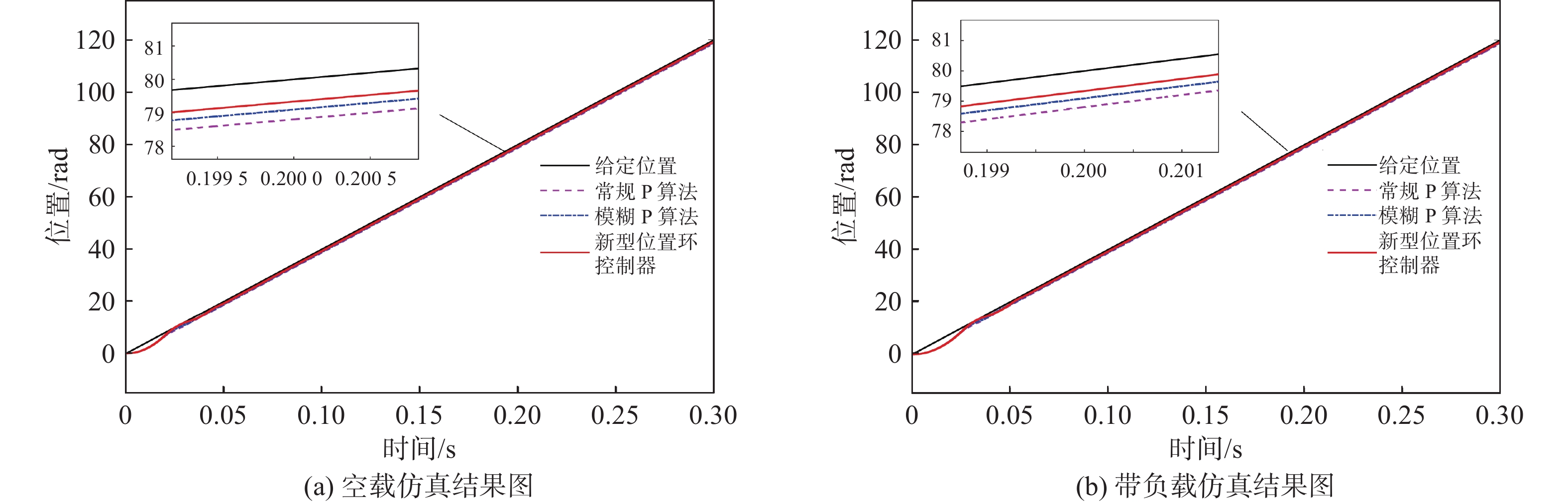
| 图 8 输入斜坡位置信号仿真结果图 |
由图7(a)和图7(b)可知,电机在空载和带负载状态下,输入阶跃信号进行位置跟踪时,使用常规P算法的系统超调量分别为5.6%和4.3%,使用模糊P算法的系统,能够抑制超调现象的发生,使用新型位置环控制器的系统,实际位置更接近给定值,跟踪误差更小。同时,新型位置环控制器控制的系统相较常规P和模糊P算法的系统,空载时,响应速度分别提高了25%和10%;带负载时,响应速度分别提高了24%和9.5%。
由图8(a)和图8(b)可知,电机在空载和带负载状态下,输入斜坡信号进行位置跟踪时,三种算法控制的系统都未出现超调现象,使用新型位置环控制器的系统,实际位置更接近给定值,相较常规P和模糊P算法的系统,空载时,误差分别减小了26.7%和42.7%;带负载时,误差分别减小了26.9%和44.5%。
综上所述,在永磁同步电机进行位置跟踪时,使用新型位置环控制方法可以消除常规P算法产生的超调量,又可以提高模糊P算法控制系统的跟踪精度和响应速度。
5 结束语本文将模糊P算法和前馈补偿控制应用于永磁同步电机位置环控制中,设计了新型位置环控制器,基于Matlab/Simulink平台搭建了永磁同步电机仿真模型,在电机空载和带负载两种状态下,与常规P和模糊P算法控制的系统对比仿真。从仿真结果可以看出,新型位置环控制器控制的系统,位置跟踪误差更小、响应速度更快,控制效果更优,具有良好的控制性能。
| [1] |
李英春, 侯金明, 王培瑞. 基于改进扩展卡尔曼滤波的PMSM在线参数辨识[J].
中国测试, 2022, 48(11): 47-53.
LI Y C, HOU J M, WANG P R. PMSM online parameter identification method based on improved extended Kalman filter[J].
China Measurement & Test, 2022, 48(11): 47-53.
|
| [2] |
熊凯强, 余银犬, 黄鹏程, 等. 永磁同步电机匝间短路不平衡磁力分析[J].
磁性材料及器件, 2023, 54(6): 43-49.
XIONG K Q, YU Y Q, HUANG P C, et al. Analysis of unbalanced magnetic force of permanent magnet synchronous motor with turn-to-turn short circuit[J].
Journal of Magnetic Materials and Devices, 2023, 54(6): 43-49.
|
| [3] |
ZHONG C Q, WANG L, XU C F. Path tracking of permanent magnet synchronous motor using fractional order fuzzy PID controller[J].
Symmetry, 2021, 13(7): 1118-1118.
DOI:10.3390/sym13071118 |
| [4] |
HYUNG W L, DAE H C, KYO B L. Rotor position estimation over entire speed range of interior permanent magnet synchronous motors[J].
Journal of Power Electronics, 2021, 21(4): 693-702.
DOI:10.1007/s43236-021-00217-9 |
| [5] |
闫宏亮, 张嘉楠, 龙虎林. 基于改进滑模趋近律和非线性干扰观测器的PMSM位置跟踪[J].
电子测量技术, 2022, 45(13): 104-108.
YAN H L, ZHANG J N, LONG H L. PMSM position tracking based on improved sliding mode reaching law and nonlinear disturbance observer[J].
Electronic Measurement Technology, 2022, 45(13): 104-108.
|
| [6] |
戴卫力, 张晓峰. 永磁同步伺服电机的变结构与前馈复合控制[J].
科学技术与工程, 2019, 19(4): 131-137.
DAI W L, ZHANG X F. Compound control of variable structure and feedforward for permanent magnet synchronous servo motor[J].
Science Technology and Engineering, 2019, 19(4): 131-137.
|
| [7] |
王嘉, 范蟠果. PMSM伺服系统位置环的PI-模糊混合控制器研究[J].
微电机, 2020, 53(7): 33-36.
WANG J, FAN P G. Research on PI-fuzzy hybrid controller for position loop of PMSM servo system[J].
Micromotors, 2020, 53(7): 33-36.
|
| [8] |
唐红雨, 刘贤兴. 基于滑模自抗扰控制器的永磁同步电机位置环控制研究[J].
微电机, 2015, 48(5): 90-94.
TANG H Y, LIU X X. Position loop control study of permanent magnet synchronous motor based on sliding ADRC control[J].
Micromotors, 2015, 48(5): 90-94.
|
| [9] |
尉世超, 杨振强. 基于前馈控制的高精度伺服系统[J].
组合机床与自动化加工技术, 2022(6): 134-137.
YU S C,YANG Z Q. High precision servo system based on feed-forward control[J].
Modular Machine Tool & Automatic Manufacturing Technique, 2022(6): 134-137.
|
| [10] |
周萍, 曹阳, 缪子繁. 模糊PID在永磁同步电机驱动的无阀液压系统中的应用[J].
机床与液压, 2020, 48(9): 70-74.
ZHOU P, CAO Y, MIAO Z F. Application of fuzzy PID in valveless hydraulic system driven by PMSM[J].
Machine Tool & Hydraulics, 2020, 48(9): 70-74.
|
| [11] |
陈昱昊, 郑宾. 基于模糊PI控制的永磁同步电机矢量控制性能研究[J].
国外电子测量技术, 2022, 41(7): 75-81.
CHEN Y H, ZHENG B. Research on vector control performance of permanent magnet synchronous motor based on fuzzy PI control[J].
Foreign Electronic Measurement Technology, 2022, 41(7): 75-81.
|
| [12] |
YANG Y S, PING Z W, SONG Y, et al. Experimental output regulation of permanent magnet synchronous motor position servo system: An internal model based two step control approach[J].
Transactions of the Institute of Measurement and Control, 2022, 44(1): 153-161.
DOI:10.1177/01423312211030241 |
| [13] |
吴伟, 曾庆军, 王阳, 等. 水下机器人多电机协同模糊滑模控制研究[J].
中国测试, 2021, 47(11): 101-106.
WU W, ZENG Q J, WANG Y, et al. Research on fuzzy sliding mode control of multi motor cooperative underwater robot[J].
China Measurement & Test, 2021, 47(11): 101-106.
|
| [14] |
翁红, 王邦继, 杨喆, 等. 适应于微型直流电机的模糊PID控制器FPGA实现[J].
电力电子技术, 2022, 56(9): 50-53.
WENG H, WANG B J, YANG Z. Implementation of fuzzy PID controller based on FPGA for micro DC motor[J].
Power Electronics, 2022, 56(9): 50-53.
|
| [15] |
游奇峰, 唐强, 米良, 等. 基于位置偏差调速的激光跟踪运动控制方法[J]. 中国测试, 2024, 50(2): 155-160.
YOU Q F, TANG Q, MI L,et al. Laser tracking motion control method with speed regulation based on position deviation[J]. China Measurement & Test, 2024, 50(2): 155-160.
|
 2024, Vol. 50
2024, Vol. 50


 ,
,