文章信息
- 罗瑛, 朱杨洋, 王宗平, 殷国富
- LUO Ying, ZHU Yangyang, WANG Zongping, YIN Guofu
- 基于多视数据重构损失标定的叶片型面光学检测
- Optical measurement of blade profile based on multi-view data reconstruction loss calibration
- 中国测试, 2024, 50(8): 118-124
- CHINA MEASUREMENT & TEST, 2024, 50(8): 118-124
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022120068
-
文章历史
- 收稿日期: 2022-12-13
- 收到修改稿日期: 2023-02-11
2. 四川大学机械工程学院,四川 成都 610065
2. School of Mechanical Engineering,Sichuan University, Chengdu 610065, China
叶片是航空发动机中数量最多的核心部件,起气流导向和能量转换的作用,其型面精度直接影响航空发动机的工作性能[1]。因此开展叶片型面高精度测量对提高叶片加工质量、保证航空发动机性能具有重要意义。当前叶片型面检测主要由基于接触式测量原理的三坐标测量机对型面上特定截面处型线的测量来完成[2]。然而,三坐标测量成本高、检测效率低,常被用于叶片型面精加工后的终检,且其在微小结构特征测量方面存在较大限制[3]。近年来,对叶片加工、维修等全生命周期检测的需求进一步提高,基于非接触式光学测量的叶片型面检测新方法因其高效性、易达性等特点受到广泛关注[4]。
基于光学测量的叶片型面检测方法受限于传感器视野范围及测量范围,完整的叶片型面数据通常需要传感器从多个工位获取。因此,多视数据的精准重构是实现叶片型面精确检测的关键[5-7]。目前围绕多视数据重构,研究人员进行了广泛的探索。Li等[8]通过3个标准球解决了光学传感器与转动平台间的标定问题,实现了将叶片多视测量数据表示在同一坐标系下。刘浩浩等[9]引入圆柱标定物,利用采集数据完成截面圆拟合,通过圆心坐标对齐实现了多视数据的重构。Sun等[10]采用标准量块标定回转中心,完成了叶片型面多视数据的重构。此外,标定板[11]、圆锥体[12]等也被用于叶片型面光学检测中。然而额外标定物的引入会增加检测系统的误差传递链长度和测量结果的不确定度[13]。此外,不同的被测叶片需要不同的标定物,导致检测方法通用性较差。鉴于此,郑昊天等[4]基于叶片自身前缘特征完成了回转中心的标定,实现了多视数据的重构。欧登荧等[14]利用叶片自身侧边基准面完成了回转中心的标定,得到了完整的叶片三维轮廓数据。虽然基于叶片自身特征进行回转中心标定提高了检测方法的通用性,但对采集数据进行特征描述方法的实用性常受方法鲁棒性的限制。
面向叶片全生命周期检测需求,结合叶片型面检测标准,本文首先开发了一套基于线激光器的叶片型面检测平台。基于本团队的研究基础,完成了线激光器与叶片相对位姿的校准。在此基础上,本文建立Z向测量基准,实现了叶片型面特定截面处型线数据的多视采集;最终提出了一种基于多视数据重构损失标定回转中心的型线重构方法,实现了多视数据坐标系的统一。相比三坐标测量机,本文方法降低了检测平台的搭建成本,基于光学测量原理提高了检测效率及灵活性;多视数据重构损失标定回转中心避免了额外标定物的引入及对数据特征描述,进一步降低了实验成本、保证了方法的鲁棒性。以两种典型燃气轮机导向叶片为检测对象,相关实验表明了所提出方法的可行性。
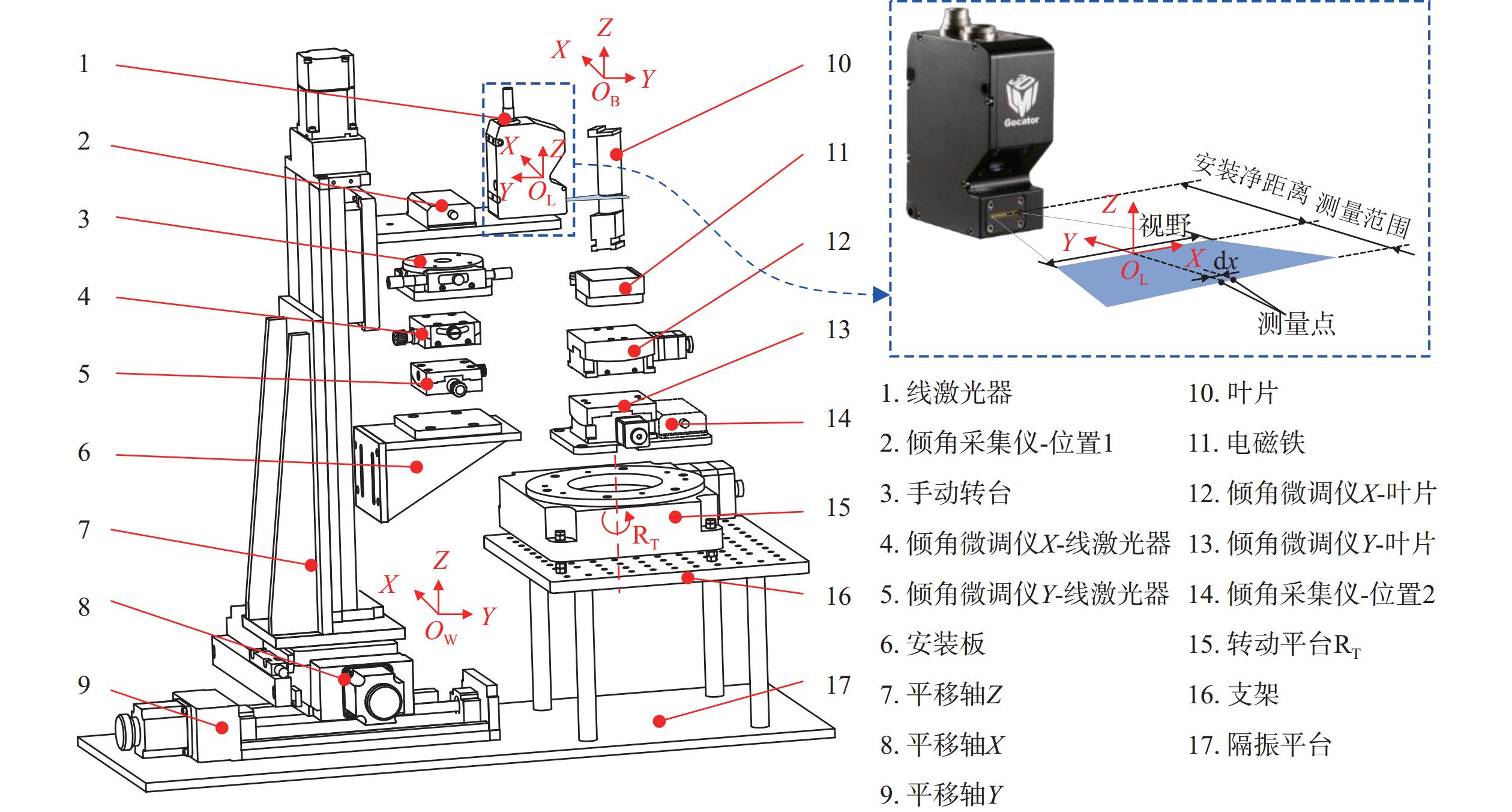
1 基于线激光器的叶片型面检测平台在当前叶片型面检测标准中,叶片型面检测通过三坐标测量机对型面上特定截面处型线的检测来完成。本文开发一套基于线激光的叶片型面检测平台如图1所示,以实现对叶片型面上特定截面处型线的测量,进而完成对叶片型面检测。
|
| 图 1 基于线激光器的叶片型面检测平台 |
该检测平台主要由一个线激光器、一个转动平台
此外,为保证检测平台所采集的数据是真实所需测量的特定截面处的型线数据,线激光器与叶片之间的相对位姿关系需得到严格保证。因此,如图1所示,可通过倾角采集仪、手动转台和倾角微调仪,结合校准方法[9]完成线激光器与叶片相对位姿的精确校准,最终保证线激光器坐标系
完成对线激光器和叶片相对位姿的校准后,叶片轴线保持竖直,且激光平面垂直于叶片轴线。一个转动平台
|
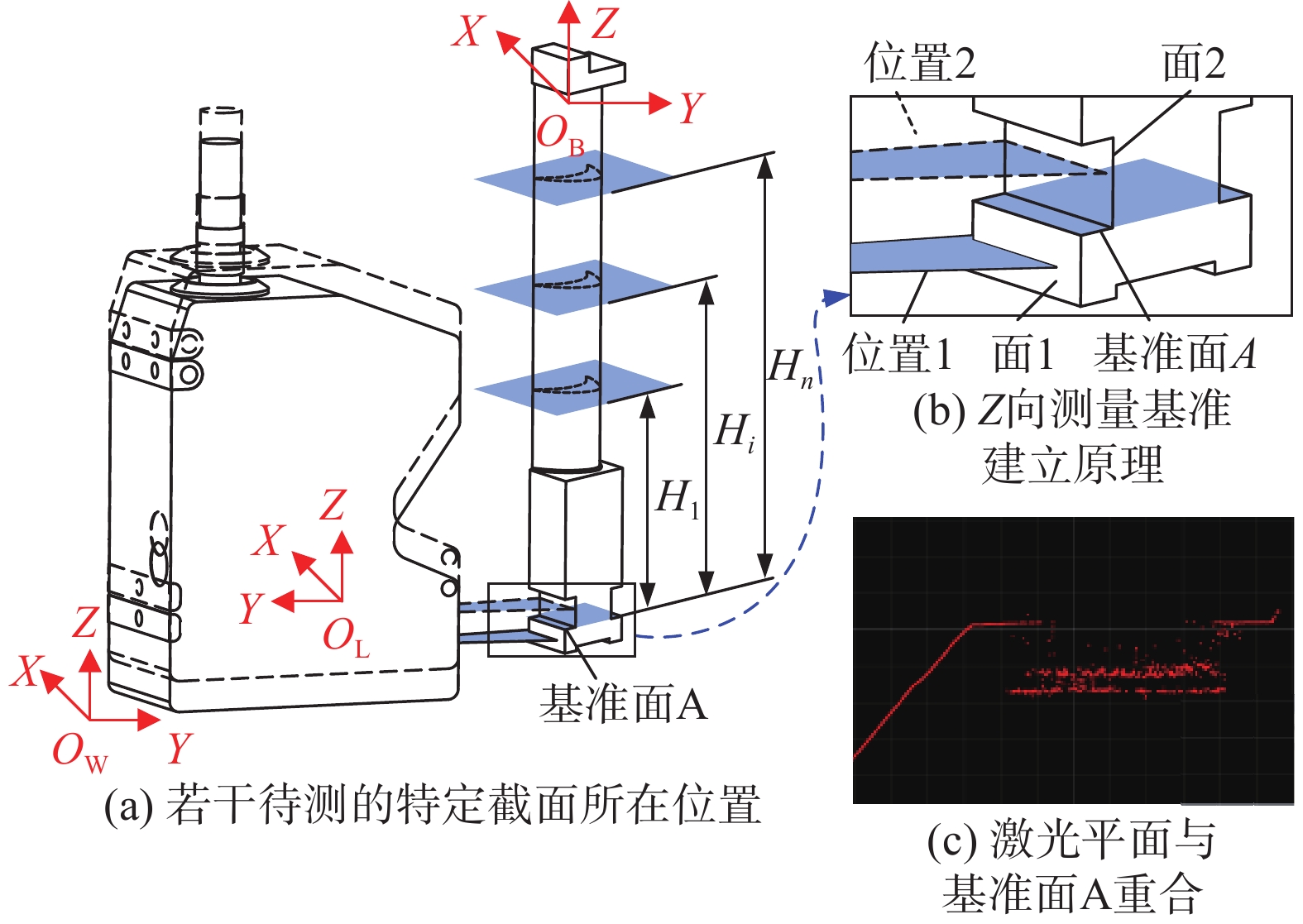
| 图 2 Z向测量基准建立 |
建立基于基准面A的Z向测量基准的本质是使激光平面与基准面A重合,然后将Z向坐标置零。Z向测量基准建立过程如下:首先调节平移轴X/Y,使叶片处于线激光器的有效测量范围内;接着调节转动平台
此部分完成叶片型面特定截面处型线数据的采集;结合型线多视数据间的关联,提出一种基于多视数据重构损失标定回转中心的方法,以完成型线多视数据重构。
3.1 叶片型线多视数据采集基于通过基准面A建立的Z向测量基准,并结合特定截面与基准面A之间的相对距离H,调节平移轴Z使线激光器沿着Z向移动距离H。此时线激光器激光平面所在位置即为特定截面所在位置。由于线激光器在单工位测量时视野范围及测量范围有限,因此测量过程中结合平移轴X/Y及转动平台
1) 将平移轴X/Y的位置参数
2) 调节平移轴X/Y及转动平台
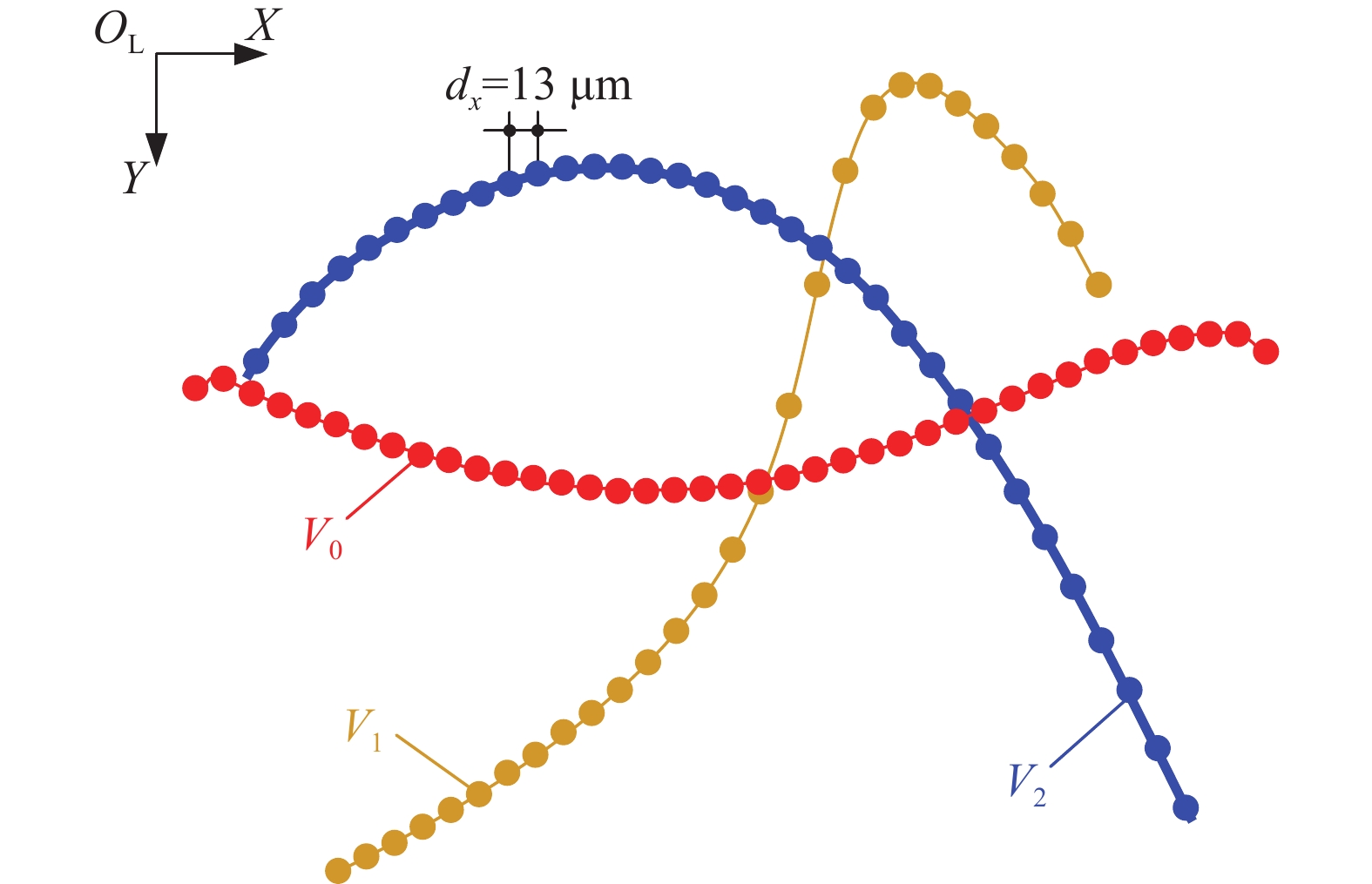
如图3所示为某叶片特定截面处型线的多视原始采集数据,其每个测量工位下采集的型线数据均是基于各自工位下线激光器自身坐标系
|
| 图 3 某叶片型线多视原始采集数据 |
3.2 叶片型线多视数据重构
本节首先通过选取型线上对应点来说明两视场间的转换关系;基于视场间的转换关系,本文提出一种基于多视数据重构损失标定回转中心的方法,进而实现型线多视数据重构。
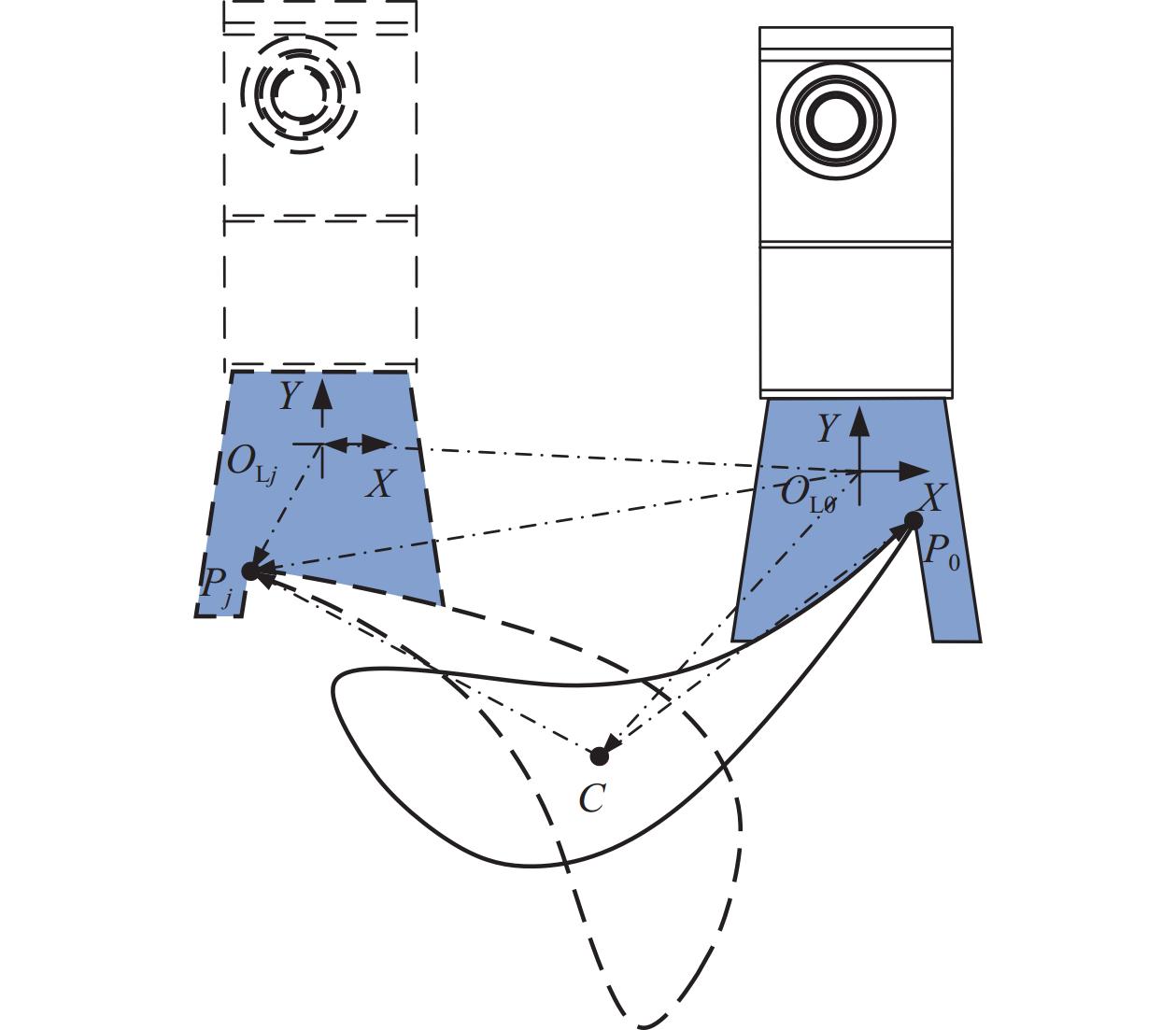
如图4所示为线激光器在初始位置
|
| 图 4 型线多视数据间的转换关系 |
| $ \overrightarrow {C{P_0}} = \overrightarrow {C{P_j}} \otimes {{{\boldsymbol{R}}}}\left( {{\theta _j}} \right) $ | (1) |
式中
基于上述分析,一旦实现对回转中心
| $ {V_{j \to C}} = \left( {{V_j} + \left( {{X_j},{Y_j}} \right) - \left( {x_0^c,y_0^c} \right)} \right) \otimes {\boldsymbol{R}}\left( {{\theta _j}} \right) $ | (2) |
其中
|
|
图 5
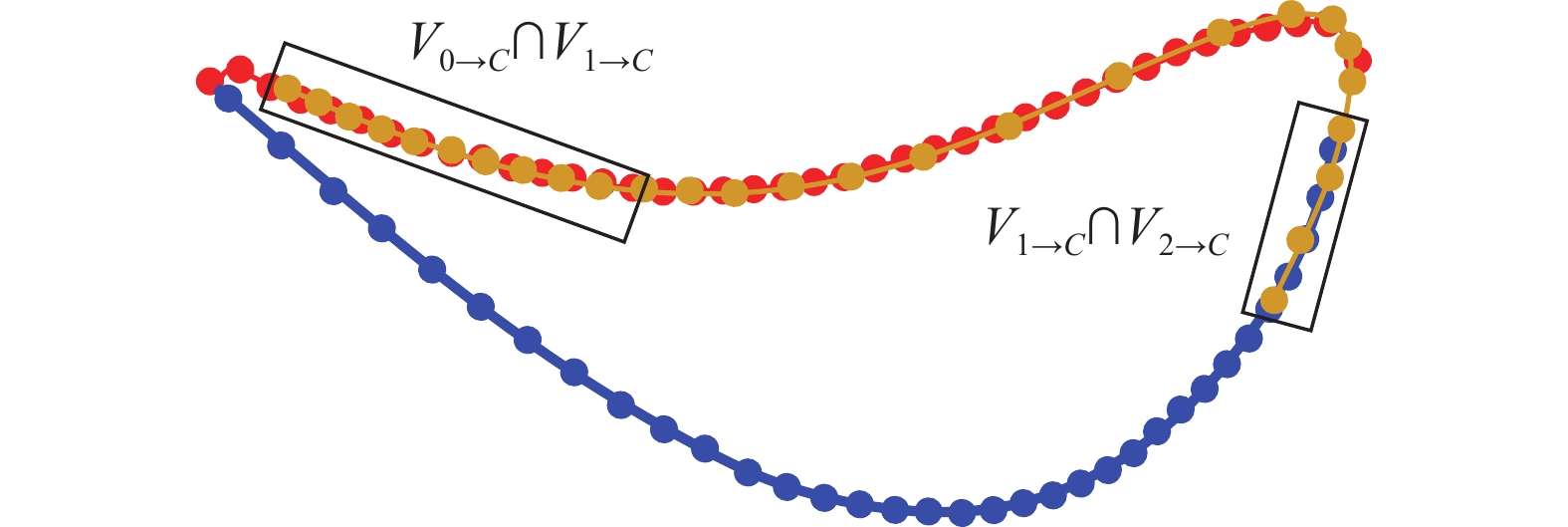
型线多视数据统一到以回转中心 |
由于相邻视场采集的型线数据仅存在部分重叠,且线激光器的数据保存具有有序性,因此可寻找第
| $ f\left( {x_0^c,y_0^c} \right) = \sum\limits_{j = 0}^n {\left( {\sum\limits_{i = 1}^{q\left( j \right)} {\min {{{\left( {\left( {x_{j \to C}^i,y_{j \to C}^i} \right) - {V_{\left( {j - 1} \right) \to C}}} \right)}^2}}} } \right)} $ | (3) |
式中
算法1 粒子群算法实现回转中心
输入:线激光器采集的型线数据
3) for
4) 返回
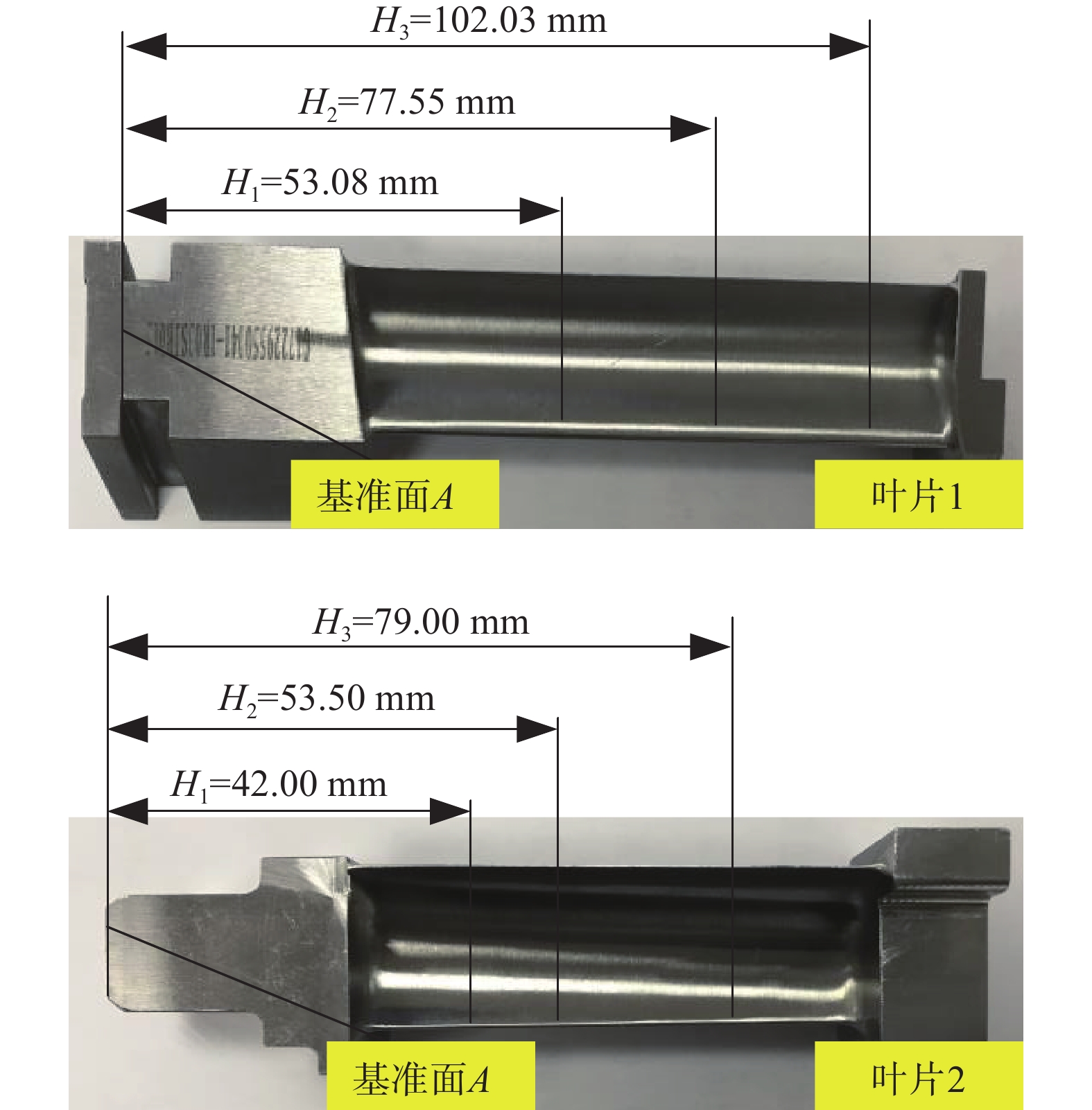
本文采用两种典型燃气轮机导向叶片作为实验对象。如图6所示,作为行业标准检测手段的三坐标测量机对该两种叶片的型面检测是通过测量其各自三个特定截面处型线的轮廓度是否在公差允许范围内,来判断叶片型面是否符合质量要求。本文实验设计将提出方法的实际测量结果与三坐标测量机的实际测量结果进行对比,当两种测量手段具有较好一致性时,便可验证本文所提出方法的可行性。
|
| 图 6 两种典型待检叶片的三个特定截面 |
4.1 叶片截面轮廓度检测结果对比
为验证本文提出的检测方法的可行性,将本文对该两种叶片型面上三个特定截面处型线的测量结果与三坐标测量机的测量结果进行对比,其截面轮廓度检测定性偏差图如图7所示,截面轮廓度检测定量偏差如表1所示。

|
| 图 7 本文方法与三坐标测量机对特定截面轮廓度检测结果定性偏差 |
| mm | ||||
| 叶片编号 | 截面高度 | 平均绝对偏差 | 标准偏差 | RMS估计 |
| 叶片1 | H1 | |||
| H2 | ||||
| H3 | ||||
| 叶片2 | H1 | |||
| H2 | ||||
| H3 | ||||
由表1可知,本文方法与三坐标测量机对两种叶片特定截面轮廓度的检测结果相比,最大平均绝对偏差为
叶片截面主要包括弦长、最大弦长、前/后缘半径及最大厚度等特征参数。这些特征参数是叶片加工较难保证的地方,它们对叶片的性能有着非常重要的影响。此处进一步将本文方法所获得的测量数据主要特征参数与三坐标测量机的测量结果进行对比,偏差结果如表2所示。
| mm | |||||
| 叶片编号 | 截面高度 | 特征参数 | 测量值 | 偏差 | |
| 三坐标机 | 本文方法 | ||||
| 叶片1 | H1 | 弦长 | 0.01 | ||
| 最大弦长 | |||||
| 前缘半径 | |||||
| 后缘半径 | |||||
| 最大厚度 | |||||
| H2 | 弦长 | – | |||
| 最大弦长 | –0.012 | ||||
| 前缘半径 | – | ||||
| 后缘半径 | |||||
| 最大厚度 | – | ||||
| H3 | 弦长 | ||||
| 最大弦长 | |||||
| 前缘半径 | 0.0 | ||||
| 后缘半径 | – | ||||
| 最大厚度 | 0.02 | ||||
| 叶片2 | H1 | 弦长 | –0.024 | ||
| 最大弦长 | – | ||||
| 前缘半径 | |||||
| 后缘半径 | |||||
| 最大厚度 | – | ||||
| H2 | 弦长 | ||||
| 最大弦长 | – | ||||
| 前缘半径 | |||||
| 后缘半径 | – | ||||
| 最大厚度 | |||||
| H3 | 弦长 | – | |||
| 最大弦长 | – | ||||
| 前缘半径 | – | ||||
| 后缘半径 | |||||
| 最大厚度 | |||||
由表2可知,本文方法与三坐标测量机对两种叶片特定截面特征参数的检测结果相比,弦长最大偏差为
针对三坐标测量机执行叶片型面检测成本高、效率低,结合现行的叶片型面检测标准,本文开发了一套基于线激光器的叶片型面光学检测平台,提出了一种基于多视数据重构损失标定回转中心的型线重构方法以实现叶片型面高效、高精检测。以两种典型燃气轮机导向叶片为检测对象,所提出方法的检测数据与三坐标测量机检测数据的对比结果表明,轮廓度检测平均绝对偏差在0.022 mm以内,最大标准偏差为
此外,可以发现平移轴X和Y的平移精度和转动平台
| [1] |
夏桂书, 吴虹星, 魏永超, 等. 旋转状态下的航空发动机叶片形变测量[J].
中国测试, 2022, 48(12): 40-44.
XIA G S, WU H X, WEI Y C, et al. Deformation measurement of aero-engine blades under rotating state[J].
China Measurement & Test, 2022, 48(12): 40-44.
|
| [2] |
黄智, 李超, 李凯, 等. 航空叶片型面三坐标检测技术现状及发展趋势[J].
航空制造技术, 2017(540): 73-79.
HUANG Z, LI C, LI K, et al. Status and prospect of detection technology of coordinate measuring machine for blade surface of aeroengine[J].
Aeronautical Manufacturing Technology, 2017(540): 73-79.
|
| [3] |
PENG W, WANG Y, MIAO Z, et al. Viewpoints planning for active 3-D reconstruction of profiled blades using estimated occupancy probabilities (EOP)[J].
IEEE T IND ELECTRON, 2020, 68(5): 4109-4119.
|
| [4] |
郑昊天, 殷鸣, 王宗平, 等. 基于前缘特征标定的叶片型面光学检测[J].
组合机床与自动化加工技术, 2022(4): 74-78.
ZHENG H T, YIN M, WANG Z P, et al. Optical measurement for blade profile based on leading edge feature calibration[J].
Modular Machine Tool & Automatic Manufacturing Technique, 2022(4): 74-78.
|
| [5] |
XIE L, ZHU Y, YIN M, et al. Self-feature-based point cloud registration method with a novel convolutional Siamese point net for optical measurement of blade profile[J]. MECH SYST SIGNAL PR, 2022, 178: 109243.
|
| [6] |
YIN M, ZHU Y, YIN G, et al. Deep feature interaction network for point cloud registration, with applications to optical measurement of blade profiles[J]. IEEE Transactions on Industrial Informatics, 2023, 19(8): 8614-8624.
|
| [7] |
WANG Z P, YIN M, DONG J, et al. Multi-view point clouds registration method based on overlap-area features and local distance constraints for the optical measurement of blade profiles[J]. IEEE-ASME Transactions on Mechatronics, 2022, 27(5): 2729 - 2739.
|
| [8] |
LI W, WU A, LI Z, et al. A new calibration method between an optical sensor and a rotating platform in turbine blade inspection[J].
MEAS SCI TECHNOL, 2017, 28(3): 035009.
DOI:10.1088/1361-6501/aa50df |
| [9] |
刘浩浩, 殷鸣, 王宗平, 等. 基于线结构光的叶片型面特征检测方法研究[J].
中国测试, 2021, 47(2): 6-12.
LIU H H, YIN M, WANG Z P, et al. Research on feature detection method of blade surface based on line structured light[J].
China Measurement & Test, 2021, 47(2): 6-12.
DOI:10.11857/j.issn.1674-5124.2020060104 |
| [10] |
SUN B, LI B. A rapid method to achieve aero-engine blade form detection[J].
SENSORS-BASEL, 2015, 15(6): 12782-12801.
DOI:10.3390/s150612782 |
| [11] |
HE W T, ZHONG K, LI Z W, et al. Accurate calibration method for blade 3D shape metrology system integrated by fringe projection profilometry and conoscopic holography[J]. Optics and Lasers in Engineering, 2018(110): 253-261.
|
| [12] |
傅屈晨, 谢核, 贺峥嵘, 等. 三维测量系统中基于圆锥拟合的旋转台轴线标定新方法[J]. 装备制造技术, 2018(6): 176-180.
FU Q C, XIE H, HE Z R, et al. A turntable calibration method based on conic-fitting for 3D measurement system[J]. Equipment Manufacturing Technology, 2018(6): 176-180.
|
| [13] |
WANG Z P, YIN M, OU D Y, et al. Optical measurement method for blade profiles based on blade self-features[J].
IEEE Transactions on Industrial Electronics, 2022, 69(2): 2067-2076.
DOI:10.1109/TIE.2021.3062213 |
| [14] |
欧登荧, 殷鸣, 王宗平, 等. 基于侧边基准面标定的叶片型面光学检测[J].
组合机床与自动化加工技术, 2022(1): 98-102.
OU D Y, YIN M, WANG Z P, et al. Research on optical inspection method of blade profile based on side datum plane calibration[J].
Modular Machine Tool & Automatic Manufacturing Technique, 2022(1): 98-102.
|
| [15] |
冯田, 冯志辉, 南亚明, 等. 基于特征向量提取的点云配准算法[J].
电子测量技术, 2022, 45(15): 57-62.
FENG T, FEN Z H, NAN Y M, et al. Point cloud registration algorithm based on feature vector extraction[J].
Electronic Measurement Technology, 2022, 45(15): 57-62.
|
 2024, Vol. 50
2024, Vol. 50


 ,
,