文章信息
- 李晓光, 张普锦, 周春雷, 赵亮, 李远
- LI Xiaoguang, ZHANG Pujin, ZHOU Chunlei, ZHAO Liang, LI Yuan
- 硐室岩壁过渡型破坏模式及最大线应变理论分析研究
- Theoretical analysis and research on transitional failure mode and maximum linear strain of cave wall
- 中国测试, 2024, 50(8): 109-117
- CHINA MEASUREMENT & TEST, 2024, 50(8): 109-117
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022100091
-
文章历史
- 收稿日期: 2022-10-19
- 收到修改稿日期: 2023-04-19
2. 北京科技大学顺德创新学院,广东 佛山 528399;
3. 中国铁建房地产集团有限公司,北京 100043;
4. 中央军委机关事务管理总局工程代建管理办公室,北京 100082
2. Shunde Innovation School, University of Science and Technology Beijing, Foshan 528399, China;
3. China Railway Construction Real Estate Group Co., Ltd., Beijing 100043, China;
4. Engineering Construction Management,General Administration of Central Military Commission Organs Affairs Management Office, Beijing 100082, China
在过去的40年中,随着隧道工程、石油工程、煤炭开采工程的建设,深部脆性硬岩的变形和破坏特征得到了广泛的调查与研究。受到煤层及深部硬岩的开采扰动,上覆岩体发生移动、破坏甚至垮塌对诱发采动裂隙及地表剥落起着重要影响[1]。BRACE W F等[2]研究了脆性岩石压缩脆剪破裂的全过程,提出脆性岩石的破坏过程可划分为以下阶段:孔隙裂隙压密;弹性变形裂隙稳定发展;非稳定破裂发展;破坏;峰后行为。岩石裂隙初始应力(
硐室围岩受到深部应力环境的影响,在开挖过程中,往往未达到其单轴抗压强度便出现片帮岩爆等低强度破坏现象,硐室岩壁发生了脆性破坏向剪切破坏过渡的现象,硐室岩壁的脆剪过渡式破坏在工程中较为常见[10]。因此,了解深部硐室围岩的物理力学特性是实现岩土工程开挖设计和决策科学化的必要前提。随着应力水平的增大,岩体逐渐表现为显著的非线性变形特征,事实表明,硐室岩壁往往达不到实验室所测单轴抗压强度,深部硐室围岩破坏与浅层岩体不同,破坏模式随着深度的增加而发生转化。目前针对硐室围岩破坏的研究多采用常规三轴进行试验,隧道硐室开挖需对岩石发生渐进破坏的过程进行分析,研究硐室岩壁脆剪过渡破坏模式,但缺乏通过一次试验分析硐室岩壁多种破坏模式的相关仪器。因此,研究深部硐室围岩的破坏模式对深部开挖具有重要意义,需要研发实验室水平的双向应力状态下岩石表面破坏分析仪器,模拟围岩实际应力状态,进而观察监测岩石的破坏进程。
硐室岩壁单元可分为三个方向应力构成:岩壁切向方向压应力
硐室岩壁脆剪过渡式破坏模拟仪参考Kao研发的表面不稳定仪设计思路[11],通过试验测试,改进缺陷,完善功能,授权发明专利(专利名称:硐室岩壁脆剪过渡式破坏模拟仪;专利号:ZL201711099093.8)[12]。硐室岩壁脆剪过渡式破坏模拟仪综合考虑了硐室围岩表面的几何因素(平面形状)和围岩表面岩石的双向应力状态,结合内窥激光散斑技术、LVDT技术、数字图像技术和声发射技术等对试验试样的内部、外部变形和破坏进行测量和定位。相对于真三轴试验,破坏模拟仪模拟的是渐进破坏,涉及破坏模式转化的研究,考虑几何因素,并具有一定延伸度的测量,不同于岩块,也不同于物理模拟,可获取轴线位移量、表面位移场,内部位移场,破裂声信号,压力数据等多种信息。破坏模拟仪配合压力机试验,能够模拟深部硐室岩壁的应力状态,监测岩体在单临空面双向应力状态下加载变形和开裂破坏过程。
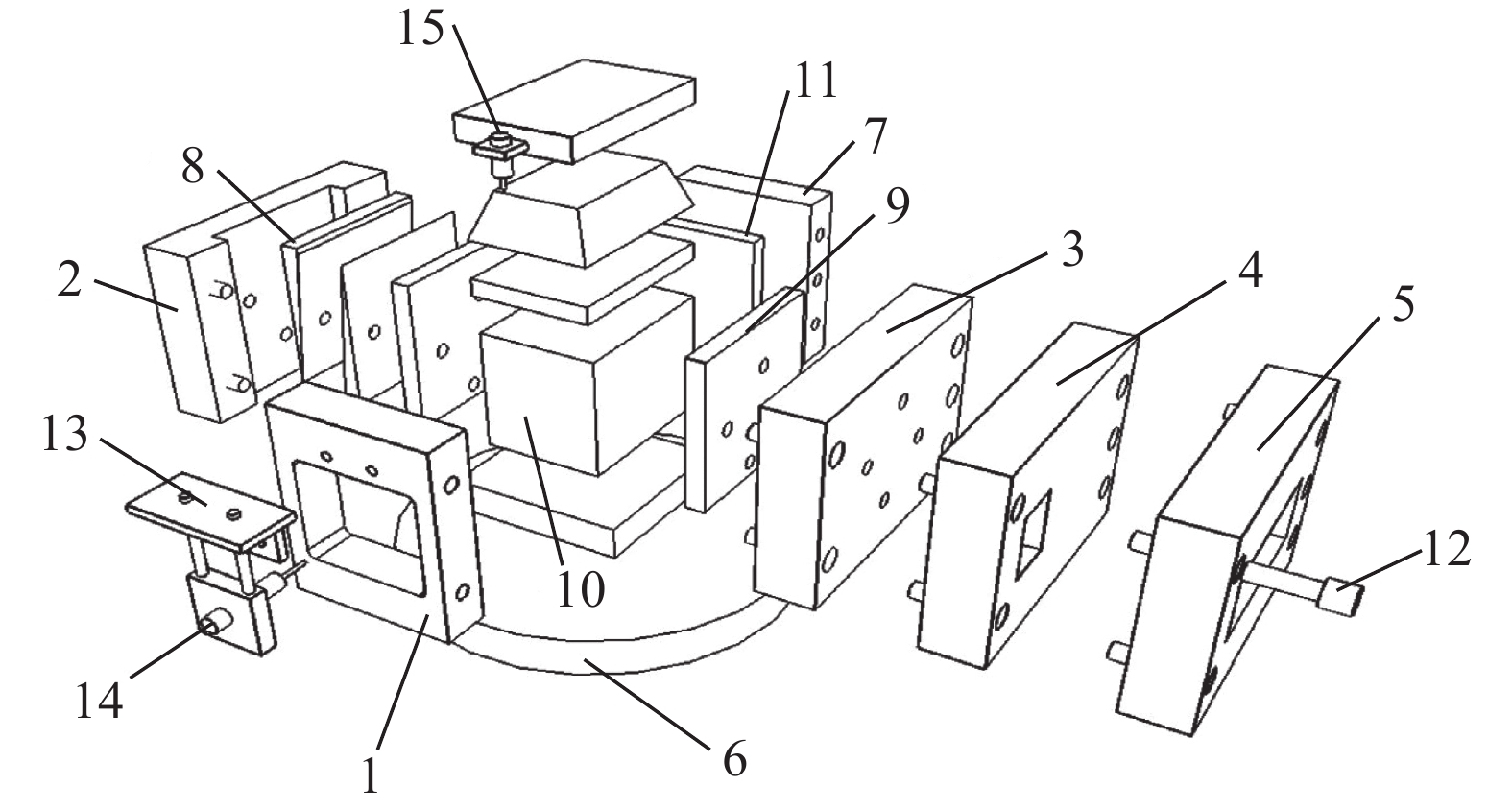
硐室岩壁脆剪过渡式破坏模拟仪如图1所示,包括前腹板1、左腹板2、匹配腹板(带孔腹板3、半窗腹板4、全窗腹板5其中之一)、底座6、后腹板7、楔形板8、亚克力垫板9、方形试样10、后楔形板垫板11、高强度螺栓12、传感器支架13、横向LVDT传感器14、竖向LVDT传感器15。
|
| 图 1 硐室岩壁脆剪过渡式破坏模拟仪示意图 |
1.2 设备参数
研发的硐室岩壁脆剪过渡式破坏模拟仪匹配腹板有三种,分别是带孔腹板、半窗腹板、全窗腹板。带孔腹板主要用于强度和刚度较高的试样,垫板采用普通钢垫板亦可,预留孔道是用来安装声发射设备,监测试样内部破裂位置;半窗腹板和全窗腹板主要是用来通过VIC-3D系统监测试样侧面的变形位移。因此垫板需要采用透明度和刚度较好的亚克力板。
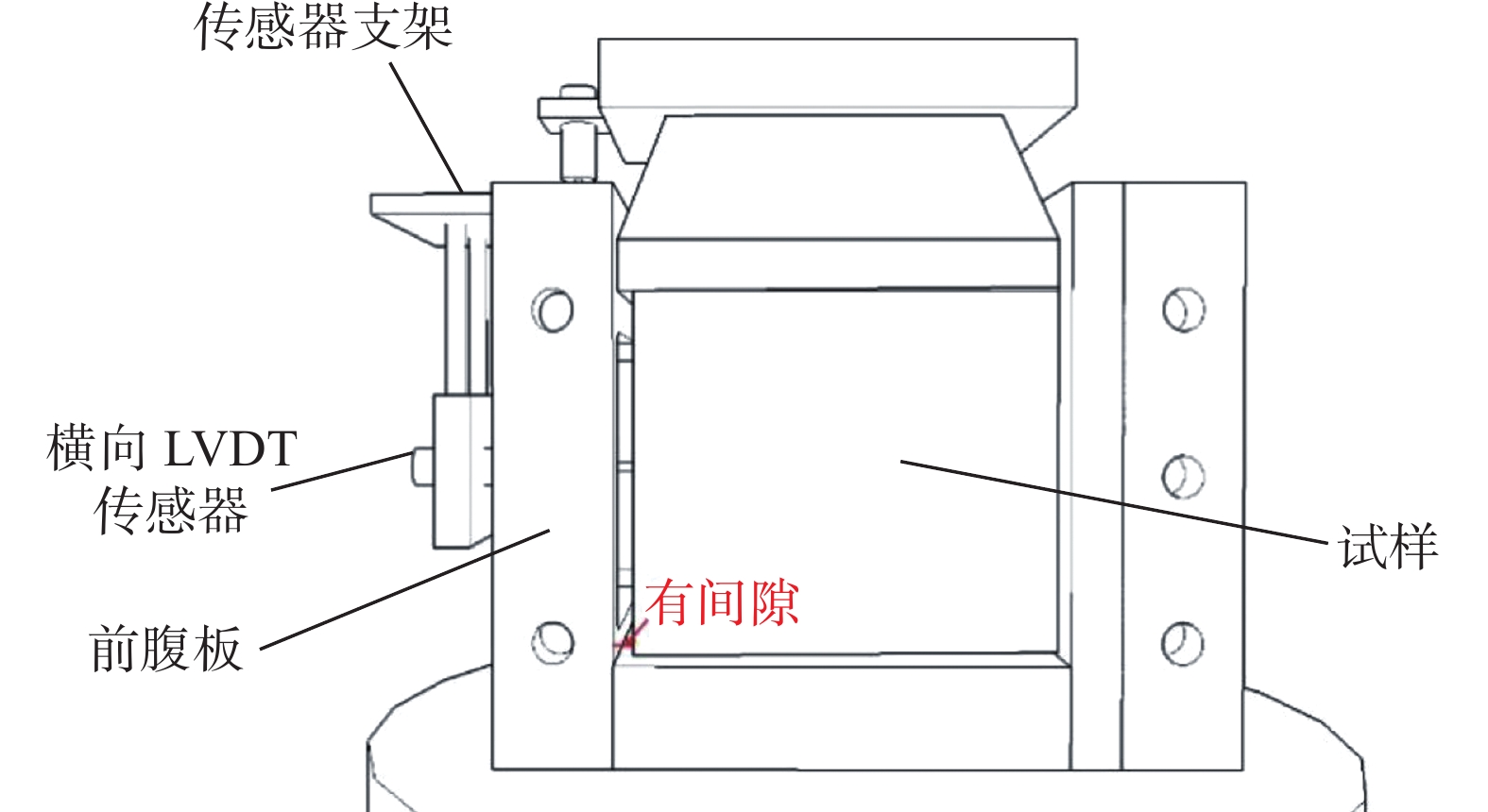
前腹板所在位置要比试样稍微靠前,给出试样足够的变形空间,前腹板窗口略小于试样自由面高度,防止试样因为突然破坏射出带来危险,如图2所示。
|
| 图 2 前腹板与试样位置示意图 |
破坏模拟仪所采用的LVDT传感器为改装回弹式传感器[13],由马克罗公司生产的CD-375系列微型LVDT位移传感器,量程为±2.5 mm,线性误差为±0.25%,灵敏度为63 mV/V/mm,LVDT传感器可记录试样加载过程中不同方向上的变形情况。
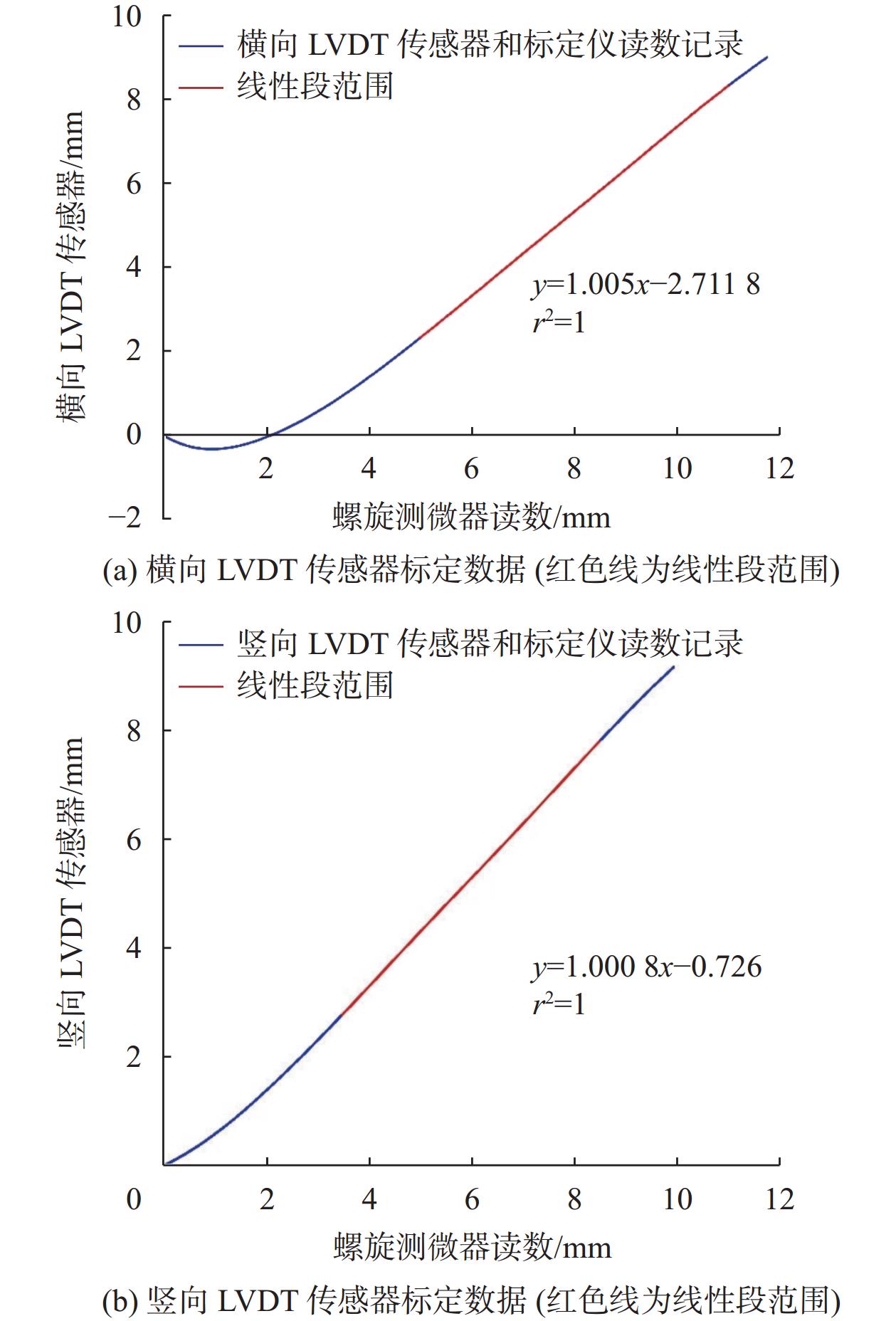
1.3 LVDT传感器及VIC-3D系统标定为保证测量精确,需要对LVDT传感器进行标定,将LVDT传感器安装到专用的螺旋测微器支架上,如图3所示。LVDT传感器与试验机传感器接收盒连接,传感器读数通过电脑test软件获取,根据螺旋测微器和LVDT传感器读数绘制标定曲线,得到约为5 mm测量线性段范围,并将此部分作为试验中的测量范围,如图4红色线所示。

|
| 图 3 LVDT标定装置安装示意图 |
|
| 图 4 LVDT传感器标定数据 |
VIC-3D系统对试样进行位移测量前,首先要进行相对位置计算和感光度标定,标定采用特制的标定板,如图5所示。将标定板放在靠近测量面的位置,图像采集器拍摄不同的角度和位置30~40张图像后,使用VIC-3D系统自带算法进行分析学习,自动完成标定。

|
| 图 5 VIC-3D系统标定板标定 |
2 硐室岩壁破坏模拟试验 2.1 试样制备
试验所用加载设备为长春市朝阳试验仪器有限公司生产的TAW-2000型微机控制电液伺服岩石三轴试验机,轴向最大试验力为
试验所用试样材料为四川黄砂岩(尺寸为80 mm×90 mm×110 mm,试样编号分别为S8090110-1、S8090110-2、S8090110-3、S8090110-4、S8090110-5)以及花岗岩试样(80 mm×90 mm×60 mm编号为H809060-1),如图6所示。并用硬脂酸或凡士林润滑剂均匀涂抹试样表面减小摩擦。

|
| 图 6 砂岩与花岗岩试样 |
2.2 硐壁破坏模拟试验前准备
VIC-3D设备使用前需采用随机印章法制作斑点图像[5]。试样的斑点面在试验中需要与亚克力板接触并产生中间主应力

|
| 图 7 试样随机印章法散斑图像 |
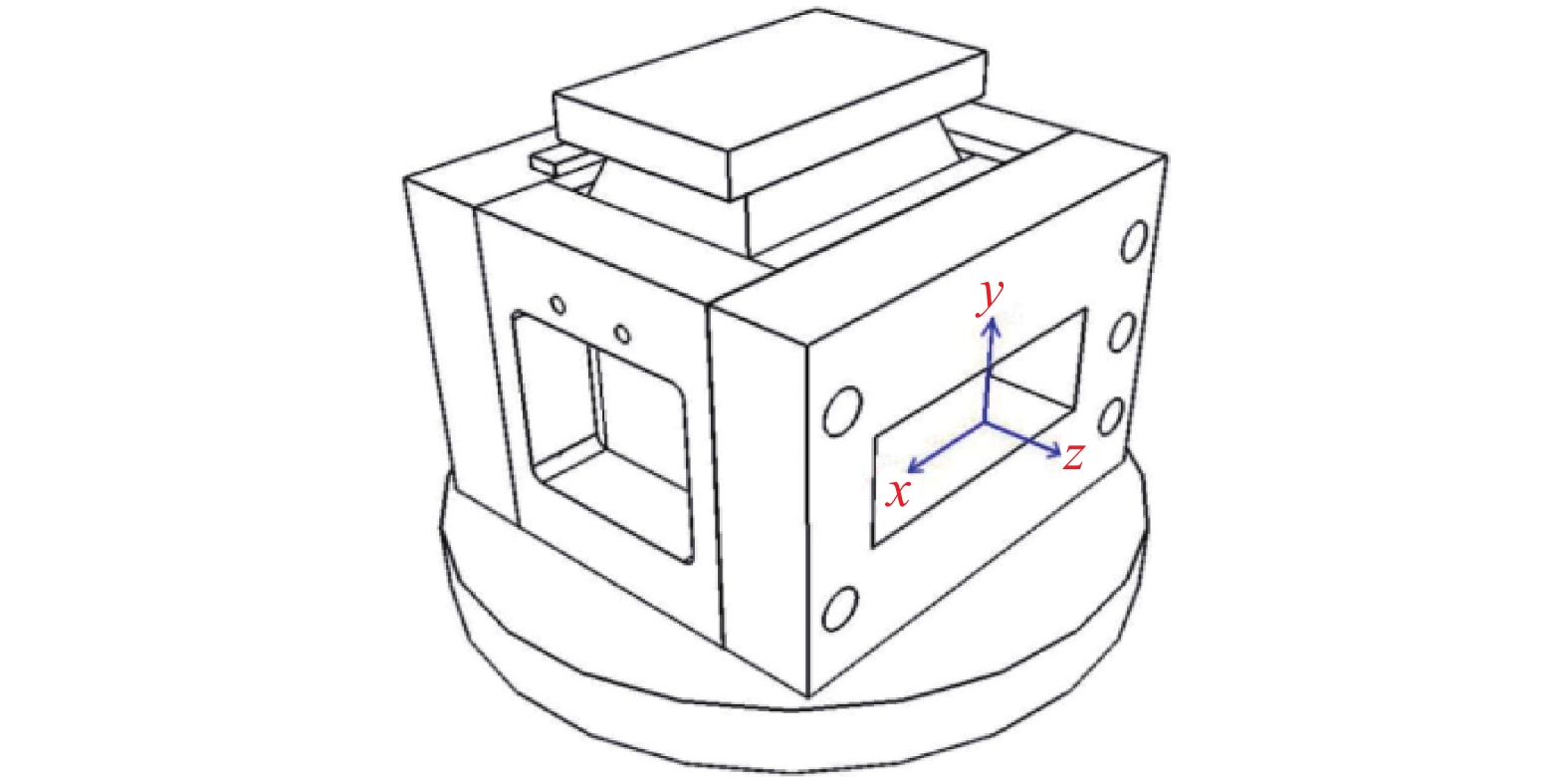
|
| 图 8 VIC-3D系统方向定义 |
2.3 硐壁破坏模拟试验方法
1)在试样表面均匀涂抹硬脂酸或凡士林润滑剂,将试样放置在底座,其余各面用相应的上垫块及腹板贴合,拧紧螺栓,放入楔形板,分别将横向和竖向回弹式LVDT传感器安装至对应位置。
2)试验加载前进行预加载——卸载循环,挤出过量的硬脂酸或凡士林润滑剂,并形成一层均匀的薄膜,循环加载以2 kN/s速率加载至100 kN,然后卸载至1 kN,进行两次循环加卸载。
3)设置好VIC-3D系统摄像头成像角和焦距,开启VIC-3D系统,设置图像采集器拍摄帧率为1帧/秒,直至试验结束,破坏模拟试验如图9所示。

|
| 图 9 破坏模拟过程 |
4)试验加载分为两步:①使用负荷控制0.5 kN/s加载至试样单轴抗压强度的30%;②控制模式改为0.01 mm/min的横向LVDT传感器控制,直到试样破坏后仍继续,出现多道裂缝停止。
3 破坏模拟试验结果与分析 3.1 试样加载破坏后裂隙扩展图像分别对80 mm×90 mm×110 mm长方体砂岩和80 mm×90 mm×60 mm长方体花岗岩进行加载,其试样加载结果见图10。图像中试样右侧是临空面。

|
| 图 10 破坏模拟试验试样加载结果 |
由图10可以看出,试样在双向应力状态下加载破坏首先发生在自由面端的近垂直劈裂,随后裂纹向着深部延伸扩展,裂缝角度越来越大,间距越来越大。
S8090110-3、S8090110-4、S8090110-5的DIC处理临界破坏时成像结果(拉应变为正,压应变为负)见图11,破坏时拉伸应变分别为2.157×10–3、2.423×10–3、2.401×10–3。

|
| 图 11 DIC处理临界破坏时成像结果(拉应变为正,压应变为负,单位:cm) |
由DIC图像可知,随着压力的增大,试样临空面侧下方变形首先达到极限值,裂隙首先出现在此处,随后,裂隙从临空面侧下方开始发育扩展,直至贯通整个试样发生破坏。
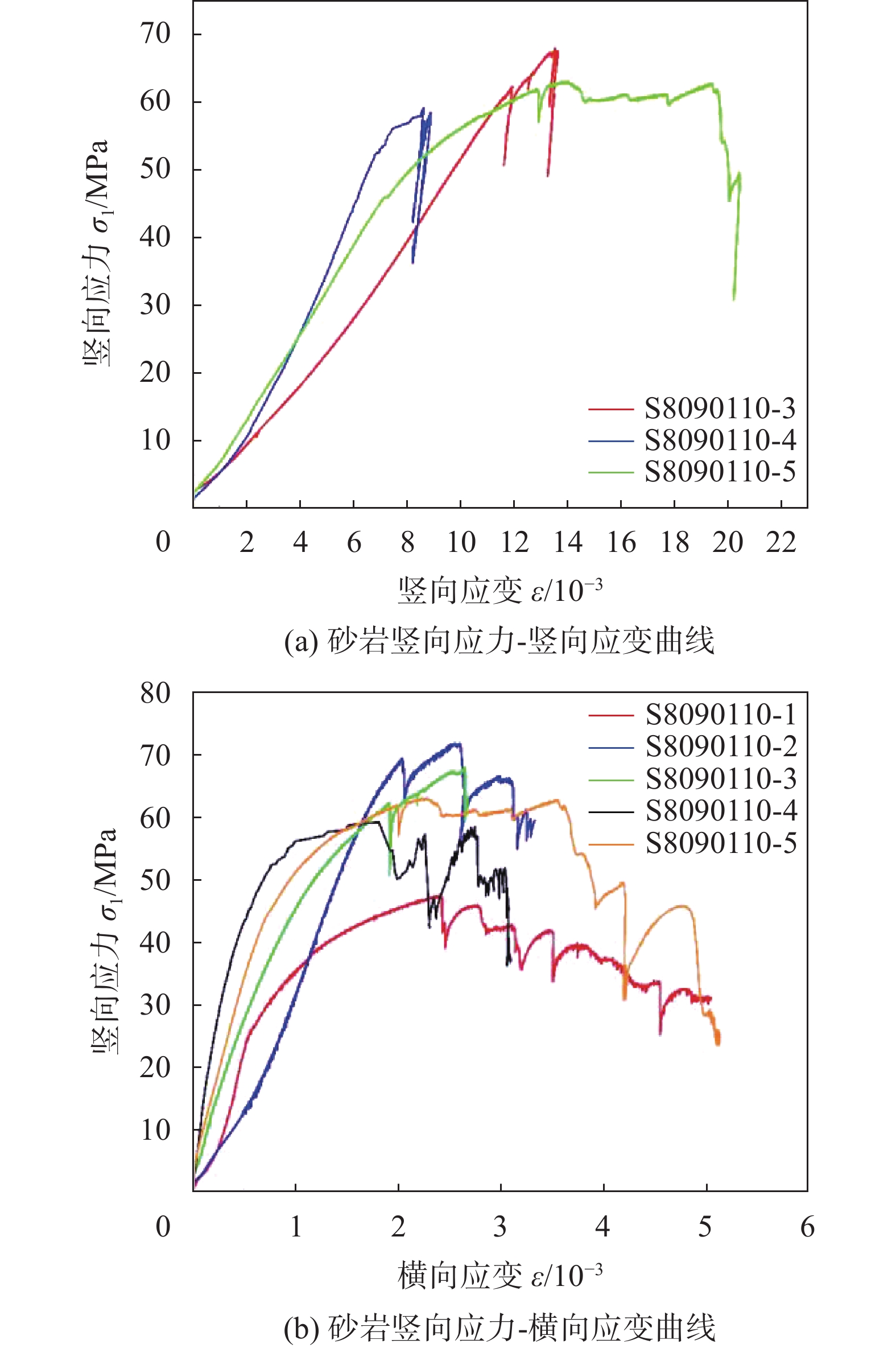
3.2 试样第一主应力与竖向、横向应变关系长方体砂岩试验加载破坏竖向应力-竖向应变曲线试验结果和竖向应力-横向应变曲线试验结果如图12所示。
|
| 图 12 长方体砂岩表面破坏模拟试验加载曲线 |
由图12可以发现砂岩试样破坏均发生在横向应变达到2×10–3处,且第一次开裂后,强度仍会继续上升,甚至超过第一次开裂时的应力。结合图10可以发现,岩石破坏面的开裂角度平行于最大主应力加载方向,表现为伸长型破坏。由于装置刚度限制,岩石表面破坏过程中发生应力降现象。随着应力继续加载,岩石破坏逐渐向内部发展,破坏模式由拉伸破坏向剪切破坏过渡。此时,岩石达到其峰值强度。随后,在峰后加载过程中,岩石发生连续破坏,其强度逐渐下降,直至到达残余强度。
长方体花岗岩试验加载破坏竖向应力-竖向应变曲线试验结果和竖向应力-横向应变曲线试验结果如图13所示。

|
| 图 13 长方体花岗岩表面破坏模拟试验加载曲线 |
由图13可以发现长方体花岗岩试样破坏时竖向应力在175 MPa左右,符合花岗岩破坏强度范围,说明硐室岩壁脆剪过渡式破坏模拟仪具备一定的普适性。同时花岗岩试样第一次开裂破坏发生后强度会再次增加,甚至超过第一次开裂时的应力。结合图10可以发现,岩石破坏面的开裂角度平行于最大主应力的加载方向,表现为伸长型破坏,随着应力的增加将宏观破坏模式从脆性转变为延性。岩石发生了脆剪过渡式破坏,其破坏失效机制根据应力水平的不同呈现出一种过渡特征[14]。
4 最大线应变理论分析及试验验证试样在单轴压缩或者双向应力状态下,其破坏模式是以拉伸破坏为主,而不是剪切破坏为主,所以比Mohr-Coulomb准则预测的实际值要低。试样在双向应力或者单轴压缩应力条件下,拉伸破坏垂直面上并没有张拉应力,Brace[2]、Gramberg[15]首次提出解释这种现象是由拉伸应变引起的拉伸破坏,Stacey[8]利用最大线应变理论试图预测南非深层块状石英岩的脆性破坏机制,结果表明,对于显示线性变形行为的材料,破坏发生可能考虑与拉伸应变有关。
由于硐壁围岩表面破坏模式是拉伸破坏,Mohr-Coulomb准则具有局限性,根据Stacey[8]和Barton等[9]的研究,提出了最大线应变理论,遵循“考虑初始拉伸应变”的思路,将岩石的破坏过程解释为是由于达到最大伸长线应变从而引起了岩石张拉破坏,即
| $ \left\{ \begin{gathered} {\varepsilon _1}{\text{ or }}{\varepsilon _{\text{2}}}{\text{ or }}{\varepsilon _{\text{3}}} = {\varepsilon _c} \\ {\varepsilon _3} = \frac{1}{E}\left[ {{\sigma _3} - \mu \left( {{\sigma _1} + {\sigma _2}} \right)} \right] \\ {\varepsilon _2} = \frac{1}{E}\left[ {{\sigma _2} - \mu \left( {{\sigma _1} + {\sigma _3}} \right)} \right] \\ {\varepsilon _1} = \frac{1}{E}\left[ {{\sigma _1} - \mu \left( {{\sigma _3} + {\sigma _2}} \right)} \right] \\ \end{gathered} \right. $ | (1) |
式中:
E——弹性模量。
立足于图8中x、y、z方向,
根据广义胡克定律,在xy平面上,垂直于xy平面的应变为0,即
| $ {\sigma _2} = \mu \left( {{\sigma _1} + {\sigma _3}} \right) $ | (2) |
通过式(2)对式(1)迭代,可以得到:
| $ {\varepsilon _3} = \frac{1}{E}\left[ {\left( {1 - {\mu ^2}} \right){\sigma _3} - \mu \left( {1 + \mu } \right){\sigma _1}} \right] $ | (3) |
试样发生拉伸破坏的条件是拉伸应变超过临界应变,即
| $ {\sigma _1} = \frac{{1 - \mu }}{\mu }{\sigma _3} - \frac{{E{\varepsilon _c}}}{{\mu \left( {1 + \mu } \right)}}\left( {{\varepsilon _c} < 0} \right) $ | (4) |
在破坏模拟试验中,由于试样是双向应力状态,即临空面上
| $ {\sigma _1} = - \frac{{E{\varepsilon _c}}}{{\mu \left( {1 + \mu } \right)}} $ | (5) |
根据砂岩加载试验,可以得到试样的力学性能参数见表1。
将砂岩试样测试结果代入式(5)可以得到
而应用广泛的Mohr-Coulomb准则如下式所示。
| $ \left\{ \begin{gathered} {\sigma _1} = {N_\phi }{\sigma _3} + 2c\sqrt {{N_\phi }} \\ {N_\phi } = \frac{{1 + \sin \phi }}{{1 - \sin \phi }} \\ \end{gathered} \right. $ | (6) |
式中:c——岩石的黏聚力;
ϕ——岩石的内摩擦角。
Mohr-Coulomb准则公式(6)和最大线应变强度分析式(4)均为
Hoek-Brown强度理论是经验型准则,准则公式如下:
| $ {\sigma _1} = {\sigma _3} + {\sigma _{{\mathrm{ci}}}}{\left( {m\frac{{{\sigma _3}}}{{{\sigma _{{\mathrm{ci}}}}}} + s} \right)^{0.5}} $ | (7) |
式中:
m和s——常数。
取决于岩石性质和承受破坏应力前岩石已破裂的程度,对于受强烈扰动的岩体,m=0.001,对于完整坚硬岩体,取m=25;对于破碎岩体,s=0,对于完整岩体,s=1。
最大线应变理论也适用于单轴应力下拉伸线应变破坏。李远等[16]提出脆-剪混合强度准则,认为岩体破坏是脆断和剪切破坏,提出系数b用来描述围压不断变化引起的整体破坏从脆断破坏向剪切破坏的过渡,其强度曲线形同H-B准则,拟合情况较好,其混合强度公式为:
| $ {\sigma _1} = b\left( {{C_1}{\sigma _3} + {C_2}} \right) + \left( {1 - b} \right)\left( {{D_1}{\sigma _3} + {D_2}} \right) $ | (8) |
式中:
b——表征脆性破坏向剪切破坏过渡的转变系数,取0~1。
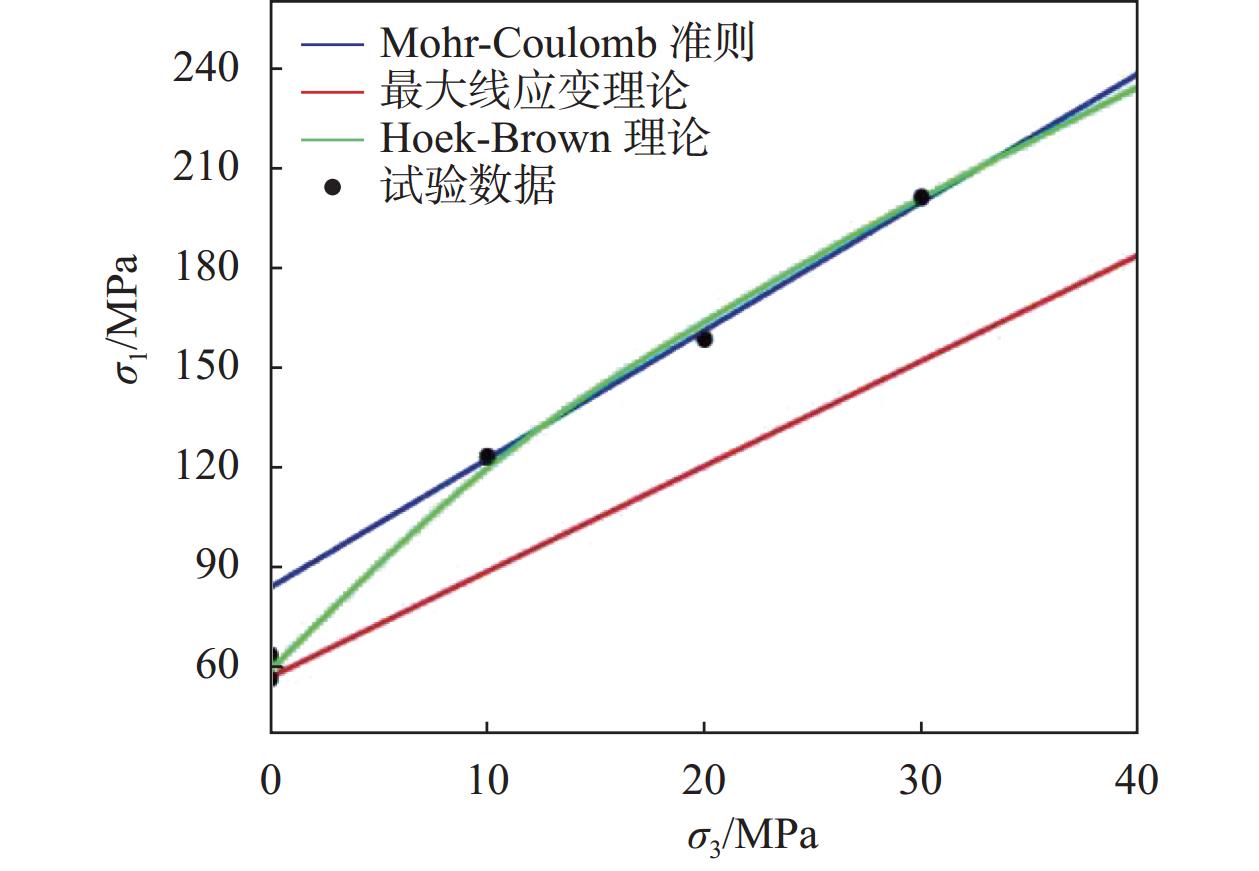
将最大线应变理论、Mohr-Coulomb准则和Hoek-Brown强度准则绘制在同一坐标系下,如图14所示。
|
| 图 14 Mohr-Coulomb准则和最大线应变理论曲线 |
对于试验用的80 mm×90 mm×110 mm砂岩试样,通过Mohr-Coulomb准则在
由此可知,由于试样在单轴情况下不只是剪切破坏,当使用Mohr-Coulomb准则预测岩石单轴情况下的强度值偏高。而考虑到双向应力状态下平面应变问题,尤其是硐室岩壁上的强度特征问题时,考虑到试样破坏是由拉伸破坏引起的,从而最大线应变理论更符合实际情况。
从图9~图13所示的裂缝发育角度、间距、破坏发生位置以及应力-应变关系曲线等方面可知,试样第一道裂缝产生在自由面端,是拉伸破坏造成的,随后压力继续上升,继而发生剪切破坏。裂缝充分发展后,发现从岩壁到深部发生了拉伸破坏到剪切破坏的过渡型破坏模式,试验模拟了岩石在双向应力状态下应力应变特性,还原在原位硐室岩壁的受力状态。在实验室单轴和三轴试验中,试样破坏是拉剪混合型破坏模式,而模拟硐壁岩石在双向应力状态下发生的第一次破坏是拉伸破坏,剪切破坏占比较低,第一次破坏之后随着裂缝深度增大,逐渐向剪切破坏过渡。因此,对于硐室岩壁强度低于室内单轴抗压强度,甚至低于预测强度值的解释有可能是因为没有考虑到岩壁破坏是拉伸破坏,导致预测强度值偏高。
5 结束语通过对试样表面不稳定性开展双向应力状态试验研究,研发出一套符合硐室岩壁过渡面破坏的室内模拟仪器,通过对长方体试样的双向应力加载试验,分析试样损伤和裂隙发展过程,表征了破坏模式转变的应力应变规律,得出以下结论:
1)硐室岩壁破坏是拉伸破坏向剪切破坏过渡的破坏模式。室内试验中发现,试样在双向加载条件下,拉伸破坏形成的裂缝首先出现在自由面末端,随后发生的是剪切破坏,裂缝充分发展后,试样从岩壁到深部发生了拉伸破坏到剪切破坏的过渡型破坏模式,试验模拟了岩壁在双向应力状态下应力应变特性,这种现象同样适用于花岗岩,解释了硐室岩壁强度低于室内强度的主要原因。
2)应用最大线应变理论解释试样的拉伸破坏。试样在双向应力状态下,两个方向约束,一个方向自由,基于广义胡克定律和拉伸破坏理论,推导出最大线应变强度分析公式,此外使用试验数据验证了最大线应变理论解释试样拉伸破坏的正确性。
3)硐室岩壁过渡型破坏模式导致强度准则适用性不同。最大线应变理论更适用于解释硐室内表面的过渡式破坏现象,此时破坏面角度和最大主应力方向平行。随着破坏向深处扩展,破坏模式从拉伸破坏逐渐过渡为剪切破坏,此时最大线应变理论可能不再适用,Mohr-Coulomb准则或者其他破坏准则可以更合理解释岩石的后续破坏过程。
| [1] |
王晓蕾. 工作面覆岩裂隙演化测试技术发展趋势[J].
中国测试, 2022, 48(5): 22-30.
WANG X L. Development trend of test technology for overburden fracture evolution in working face[J].
China Measurement & Test, 2022, 48(5): 22-30.
|
| [2] |
BRACE W F, BOMBOLAKIS E G. A note on brittle crack growth in compression[J].
Journal of Geophysical Research, 1963, 68(12): 3709-3713.
DOI:10.1029/JZ068i012p03709 |
| [3] |
HOEK E,MARTIN C D. Fracture initiation and propagation in intact rock – A review[J].
Journal of Rock Mechanics and Geotechnical Engineering: English Edition, 2014, 6(4): 14.
|
| [4] |
PATERSON M S. Experimental deformation and faulting in wombeyan marble[J].
Geological Society of America Bulletin, 1958, 69(4): 465-467.
|
| [5] |
米红林, 纳曼·麦麦提, 色麦尔江·麦麦提玉苏普, 等. 基于现代测试技术的危岩力学性能实验研究[J].
中国测试, 2021, 47(6): 38-44.
MI H L, NAMAN M, SEMERJAN M, et al. Experimental study on mechanical properties of dangerous rock based on modern testing technology[J].
China Measurement & Test, 2021, 47(6): 38-44.
DOI:10.11857/j.issn.1674-5124.2021020085 |
| [6] |
TARASOV B G, RANDOLPH M F. Frictionless shear at great depth and other paradoxes of hard rocks[J].
International Journal of Rock Mechanics and Mining Sciences, 2008, 45: 316-328.
DOI:10.1016/j.ijrmms.2007.06.001 |
| [7] |
MAKAROV V V, GUZEV M A, ODINTSEV V N, et al. Periodical zonal character of damage near the openings in highly-stressed rock mass conditions[J].
Journal of Rock Mechanics and Geotechnical Engineering, 2016, 8(2): 164-169.
DOI:10.1016/j.jrmge.2015.09.010 |
| [8] |
STACEY T R. A simple extension strain criterion for fracture of brittle rock[J].
International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1981, 18(6): 469-474.
|
| [9] |
BARTON N, SHEN B T. Risk of shear failure and extensional failure around over-stressed excavations in brittle rock[J].
Journal of Rock Mechanics and Geotechnical Engineering, 2017, 9(2): 210-225.
DOI:10.1016/j.jrmge.2016.11.004 |
| [10] |
PANTHI K K. Methods applied in the prediction of brittle failure in tunnels and underground caverns[J].
Hydro Nepal Journal of Water Energy & Environment, 2018, 22: 5.
|
| [11] |
KAO C S. Surface instability as damage evolution in rock[J]. Dissertations & Theses-Gradworks, 2011:162.
|
| [12] |
张普锦, 李远, 乔兰, 等. 硐室岩壁脆剪过渡式破坏模拟仪[P]. 北京: CN107907402B, 2020-08-11.
ZHANG P J, LI Y, QIAO L, et al. A brittle shear transition failure simulator for cave walls [P]. Beijing: CN107907402B, 2020-08-11.
|
| [13] |
马春庭, 谭业双, 李江波, 等. 基于LVDT传感器的测径仪研究[J].
国外电子测量技术, 2014, 33(10): 72-75.
MA C T, TAN Y S, LI J B, et al. Research on diameter measuring instrument based on LVDT sensor[J].
Foreign Electronic Measurement Technology, 2014, 33(10): 72-75.
DOI:10.3969/j.issn.1002-8978.2014.10.021 |
| [14] |
JIANG Q, YANG B, YAN F, et al. New method for characterizing the shear damage of natural rock joint based on 3D engraving and 3D scanning[J].
International Journal of Geomechanics, 2020, 20(2): 1-15.
|
| [15] |
GRAMBERG J. The axial cleavage fracture 1 Axial cleavage fracturing, a significant process in mining and geology[J].
Engineering Geology, 1965, 1(1): 31-72.
DOI:10.1016/0013-7952(65)90006-2 |
| [16] |
李远, 乔兰, 隋智力, 等. 岩石材料脆性剪切破坏模式下的强度分析[J].
北京科技大学学报, 2012, 34(12): 1364-1370.
LI Y, QIAO L, SUI Z Z, et al. Strength analysis of rock materials under brittle shear failure mode[J].
Journal of Beijing University of Science and Technology, 2012, 34(12): 1364-1370.
|
 2024, Vol. 50
2024, Vol. 50


 ,
,