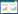文章信息
- 胡成放, 丁昊昊, 陈德君, 张岩, 刘启跃, 王文健, 郭俊, 林强
- HU Chengfang, DING Haohao, CHEN Dejun, ZHANG Yan, LIU Qiyue, WANG Wenjian, GUO Jun, LIN Qiang
- 基于双目视觉的列车轮对表面缺陷及型面参数检测方法
- Inspection method for surface defect and shape parameter of train wheelset based on binocular vision
- 中国测试, 2024, 50(8): 101-108
- CHINA MEASUREMENT & TEST, 2024, 50(8): 101-108
- http://dx.doi.org/10.11857/j.issn.1674-5124.2023020114
-
文章历史
- 收稿日期: 2023-02-25
- 收到修改稿日期: 2023-06-05
2. 西南交通大学 轨道交通运载系统全国重点实验室 摩擦学研究所,四川 成都 610031;
3. 唐山百川智能机器股份有限公司,河北 唐山 063000;
4. 浙江师范大学 浙江省城市轨道交通智能运维技术与装备重点实验室,浙江 金华 321004
2. Tribology Research Institute, State Key Laboratory of Rail Transit Vehicle System, Southwest Jiaotong University, Chengdu 610031, China;
3. Thangshan Baichuan Intelligent Machine Co., Ltd., Tangshan 063000, China;
4. Key Laboratory of Urban Rail Transit Intelligent Operation and Maintenance Technology & Equipment of Zhejiang Province, Zhejiang Normal University, Jinhua 321004, China
铁路交通因其速度快、运能高、安全性高等特点,成为我国重要的运输方式。随着列车轴重、运营里程与列车速度的增加,车轮磨耗逐渐增加,车轮的型面参数会逐渐脱离正常值,甚至表面会出现擦伤、材料剥离等表面缺陷,这些问题不仅影响乘车舒适度,还会直接危害行车安全。因此需要对列车轮对及时进行检测,并在此基础上进行车轮维护对于保障列车安全运行具有重要意义。
国内外学者对车轮检测方法进行了深入研究。孙琦等[1]根据波长固定原理确定轮对多边形阶次,再对该阶次多边形对应的频率带宽范围进行带通滤波,联合时域和频域特征参数定量表征车轮多边形不圆度;阮成雄等[2]提出了一种基于LoG梯度加权的Haar-like特征方法可有效检测并定位列车车轮裂纹;戚潇月等[3]对带有多边形化的车辆轨道刚柔耦合动力学模型进行分析提出了一种车轮多边形在线诊断方法,通过轴箱垂向加速度频谱动态识别车轮多边形阶数,建立带有多边形的车轮轴箱垂向加速度系数检测多边形深度;ZHOU等[4]通过在轨腰上安装超声波阵列传感器来检测轮轨接触力,从而得到轮轨接触应力在轨道分布云图,为检测车轮踏面状态提供基础依据;Roveri等[5]通过在钢轨上安装FBG传感器收集车辆振动信号,通过对振动信号进行时频分析来检测车轮是否存在故障;Brizuela等[6]设计了利用超声波技术检测车轮扁疤的方法,这种测量方式更易于实现动态检测;Pedro等[7]通过在车轮上安装应变片获取轮轨垂向力,通过分析载荷与应变片输出之间的对应关系来判断车轮是否存在不圆度缺陷。
目前虽然有较多关于车轮动态检测方法的研究[8-10],但是这些检测方式存在一些缺点。如常用车轮检测方式有激光检测与振动加速度检测,激光检测方式会受到列车驶过检测区域造成钢轨变形使得激光光线方向发生改变的影响,并且车轮运动过程中会产生定位误差;对于振动加速度检测,当钢轨出现波磨或列车经过轨缝时产生的异常振动可能会造成系统误判,并且这种检测方式只能检测缺陷,不能检测车轮参数。双目相机与结构光相结合的检测方式具备检测精度高、实时性强、易安装等优点。因此,本文提出了一种基于结构光与双目相机相结合的列车轮对型面参数及擦伤缺陷动态检测方法。本测量方法对现场车轮型面参数与缺陷快速检测具有较强工程实用意义。
1 轮对表面缺陷及型面参数检测系统搭建 1.1 检测系统搭建结构光与双目立体视觉相结合的非接触式列车轮对型面检测系统由触发模块、控制模块、车轮数据采集模块、数据处理模块构成,轮对检测系统现场布置如图1所示。触发模块采用电感式传感器,负责判断列车是否到达数据采集区域。当电感式传感器内部振荡器产生的磁场感应到列车经过时就会给控制模块单片机传递电信号。单片机收到电信号之后控制数据采集模块启动。数据采集模块主要由双目相机与散斑点结构光组成。双目视觉生成点云可以分为四个步骤[11]:相机标定、立体校正、立体匹配、三维建模,其中传统立体匹配对于弱纹理或重复图案的匹配效果会大大降低,而结构光可以赋予被测物体表面特征,解决了传统双目相机检测物体表面特征不足时导致的误匹配问题,从而使列车轮对检测系统具有更高的检测精度[12]。由双目相机与结构光组成的系统另一个优点是仅需要标定两个相机之间的位置,投影仪不需要进行标定,相对于单相机加结构光的检测方式来说,系统更加灵活[13]。通过双目相机采集的数据会被传输到数据处理模块的视觉控制器进行处理。

|
| 图 1 轮对检测系统现场布置图 1.视觉控制器;2.单片机;3.电感式传感器;4.投影仪;5.双目相机。 |
1.2 轮对检测系统工作原理
本文所述轮对检测系统使用的双目相机为海康威视MV-CH089-10UM型号相机,根据相机的拍摄帧率与曝光时间的限制列车驶过检测区域的最大时速为20 m/s;由于列车驶过会引起强烈振动影响相机拍摄质量,所以相机镜头采用Kowa的LM12HC-V型号抗振镜头。列车轮对系统采用A-F六组双目相机对经过检测区域的列车车轮型面数据进行采集。每一组双目相机由一个电感式传感器控制开闭,当列车经过该分组时会触发电感式传感器向单片机传输电信号,如图2中蓝色虚线所示,单片机接收到电信号之后开启该分组所有双目相机采集数据,如图2中蓝色实线所示。除2-7号电感式传感器外,还配置1号与8号电感式传感器检测列车的到来与离去。采集完数据传输到数据处理模块,该模块主要进行滤波、将各帧数据拼接为整体车轮点云模型、缺陷检测等操作。轮对检测系统布置在轨道旁,列车以一定速度驶过检测区域,触发相机拍摄车轮踏面,最终获得轮对整体三维检测结果。

|
| 图 2 轮对检测系统原理图 |
2 点云数据处理
相机采集的车轮型面数据需要进行处理,包括滤波、特征点提取、特征点描述、粗配准、精配准,最终形成整体车轮点云模型用于后续车轮参数计算与缺陷检测。点云滤波主要是去除点云中各类噪声点;特征点提取是将数据中具有显著性与稳定性的点云集合提取出用于粗配准工作,通过少量特征点就可以识别物体并进行拼接操作;特征点描述是判断两片点云中特征点是否能匹配,从而寻找出两片点云中成对特征点;粗配准可以使两片点云获得良好初始位置;精配准是通过不断迭代使两片点云有更好拟合效果,提高配准精度。
2.1 数据预处理相机在数据采集过程中会引入噪声,本文通过统计滤波去除点云噪声。该方法基本原理是计算检测点到最近k个点的平均距离,假设结果符合均值为μ并且标准差为σ的高斯分布,当任意检测点与最近k(根据实验结果,在k=50下统计滤波对本点云数据滤波效果最佳,因此本研究中设置k=50)个点的平均距离超过标准范围
1)利用Kd-Tree搜索距离检测点pi的k个最近点,然后通过下式计算点
| $ {d_i} = \sqrt {{{({x_{i - 1}} - {x_i})}^2} + {{({y_{i - 1}} - {y_i})}^2} + {{({{\textit{z}}_{i - 1}} - {{\textit{z}}_i})}^2}} $ | (1) |
2)通过下式计算所有距离的平均值以及标准差:
| $ \left\{\begin{array}{l}\mu =\dfrac{1}{n}{\displaystyle \sum }_{i=1}^{n}{d}_{i}\\ \sigma =\sqrt{\dfrac{1}{n}{\displaystyle \sum }_{i=1}^{n}{\left({d}_{i}-\mu \right)}^{2}}\end{array}\text{ }i=1,2,3,\cdots ,n\right. $ | (2) |
式中:
μ——平均值;
σ——标准差。
3)剔除超过标准范围
图3显示了滤波前后的点云对比效果,可以看出在经过统计滤波之后车轮点云数据的噪声点明显被去除,使用去除噪声之后的点云数据更有利于后续整体车轮的拼接。

|
| 图 3 数据滤波后点云 |
2.2 特征点提取与特征点描述 2.2.1 特征点提取
由于车轮表面整体特征不明显,不利于特征点提取。所以进行车轮数据采集时在轮对踏面贴上标记物以辅助特征点提取,如图4所示。标记物只在设备初始化时使用,当设备正式上线之后直接利用通过标记物得到的转换矩阵对各相机拍摄的点云进行变换。

|
| 图 4 车轮标记物 |
本文采用内部形态描述算法(intrinsic shape signatures, ISS)对特征点进行提取,该算法利用点云协方差矩阵特征值之间的关系选取特征点。基于协方差分析对每个点构建局部坐标系(local reference frame, LRF),该坐标系独立于世界坐标系,不会受到传感器位姿变换的影响,算法流程如下:
1)通过下式计算查询点
| $ {w_{ij}} = \frac{1}{{||{{\boldsymbol p}_i} - {{\boldsymbol p}_j}||}}{\text{ }}(||{{\boldsymbol p}_i} - {{\boldsymbol p}_j}|| < r) $ | (3) |
2)通过下式计算所有点
| $ {\bf{cov}}({{{p}}_i}) = {\frac{{\displaystyle \sum\limits_{||{{\boldsymbol p}_i} - {{\boldsymbol p}_j}|| < r} {{w_{ij}}({{\boldsymbol p}_i} - {{\boldsymbol p}_j})({{\boldsymbol p}_i} - {{\boldsymbol p}_j})} }}{{\displaystyle \sum\limits_{||{{\boldsymbol p}_i} - {{\boldsymbol p}_j}|| < r} {{w_{ij}}} }}^{\rm T}} $ | (4) |
3)计算协方差矩阵的特征值
4)设置阈值
| $ \left\{ \begin{gathered} \frac{{\lambda _i^2}}{{\lambda _i^1}} \leqslant {\varepsilon _1} \\ \frac{{\lambda _i^3}}{{\lambda _i^2}} \leqslant {\varepsilon _2} \\ \end{gathered} \right. $ | (5) |
仅对部分车轮数据进行特征点提取将会大幅减少算法运行时间,并且可以减少非对应点对误匹配问题。因此本文只对针对标记物部分车轮点云数据进行特征点提取。图5显示了基于ISS算法的特征点提取效果,其中红色分布较为均匀的点即为特征点。

|
| 图 5 车轮点云特征点提取 |
2.2.2 特征点描述
特征点描述是通过计算特征点与半径邻域内的几何特征关系来描述该点的位置信息,当知道两片点云中特征点位置信息之后就可以判断该特征点是否匹配,本文使用快速点特征直方图(fast point feature histogram, FPFH)进行特征点描述。该算法流程如下:
1)计算查询点的r邻域内各点与其自身的简化点特征点直方图(simplified point feature histogram, SPFH)。
2)以r邻域内各点为中心,同样计算其r邻域内各点与其自身的SPFH。
3)应用邻近SPFH计算查询点FPFH,如下式所示:
| $ {\text{FPFH}}({p_q}) = {\text{SPFH}}({p_q}) + \frac{1}{k}\mathop \sum \limits_{i = 1}^k \frac{1}{{{m_i}}}{\text{SPFH}}({p_i}) $ | (6) |
式中:
点云配准是将各个相机采集的数据拼接为整体车轮点云模型,本文首先利用采样一致性算法 (sample consensus initial alignment, SAC-IA)进行粗配准,然后通过迭代最近点算法(iterative closest point, ICP)进行精配准不断迭代得到最优结果。
2.3.1 粗配准过程SAC-IA算法是一种基于特征的点云配准方法,经过配准之后的两点云可获得良好的初始位置。该算法流程如下:
1)选取采样点。在点云P中随机采样n个点(
2)对应点查询。在点云Q中寻找与点云P中采样点
3)计算变换矩阵。根据对应点对求得转换矩阵,并且通过Huber损失函数进行误差度量,如下式所示:
| $ L\mathrm{_h}(s_i)=\left\{\begin{gathered}\frac{1}{2}s_i^2,\text{ }||s_i||\leqslant t_{\text{e}} \\ \frac{1}{2}t_{\text{e}}(2||s_i||-t_{\text{e}}),\text{ }||s_i|| > t_{\text{e}} \\ \end{gathered}\right. $ | (7) |
式中:
4)重复以上3个步骤,选出最佳误差度量的转换。
首先使用SAC-IA算法对提取出的含有标记部分的车轮点云进行粗配准得到相应的转换矩阵。然后将该转换矩阵再应用到相机拍摄的整帧车轮数据,即可得到两帧数据粗配准之后的车轮点云模型。图6显示了经过SAC-IA算法配准之后的两帧点云数据,可以看出经过粗配准之后两帧点云之间有较大误差不能应用于后续计算,所以还需要再经过精配准不断迭代降低误差。
|
| 图 6 两帧数据间车轮粗配准后模型 |
2.3.2 精配准过程
通过SAC-IA粗配准之后,两片点云已经获得了较好初始位置,接下来再使用ICP算法对两点云进行不断迭代获取最优转换矩阵。ICP算法执行步骤如下:
1)利用Kd-Tree在目标点云Q与源点云P中搜索对应点对,距离
2)构建最小二乘问题,利用下式求解最优旋转矩阵R与平移矩阵t,使得误差函数最小:
| $ E\left( {{\boldsymbol R},{\boldsymbol t}} \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^n {\left| {\left| {{{{\boldsymbol q}}_i} - \left( {{\boldsymbol R}{{{\boldsymbol p}}_i} + {\boldsymbol t}} \right)} \right|} \right|^2} $ | (8) |
3)利用步骤2)求得的旋转矩阵R与平移矩阵t对点云
| $ e = \frac{1}{n}\mathop \sum \limits_{i = 1}^n {\left| {\left| {{{{\boldsymbol p}}_i}^\prime - {{{\boldsymbol q}}_i}} \right|} \right|^2} $ | (9) |
4)如果误差e小于设定阈值或者达到迭代次数,则停止迭代,否则继续迭代。
将各个相机采集的车轮数据均应用上述方法拼接为一个整体车轮点云模型,如图7所示。完成该拼接之后,将得到的各帧数据之间的转换矩阵应用到不打标记的车轮型面数据,即可得到正常车轮模型,如图7(f)所示,本文基于该正常车轮模型实现车轮型面参数及缺陷检测。

|
| 图 7 各帧数据拼接过程 |
3 车轮型面参数及缺陷检测
利用第2节搭建的轮对检测系统完成了车轮型面点云数据的采集,并且通过ICP算法将各双目相机采集的点云数据拼接形成一个整体车轮点云模型。本节基于整体车轮点云模型进行车轮参数与擦伤缺陷检测,包括滚动圆直径、轮缘厚度、轮缘高度、擦伤深度等数据。
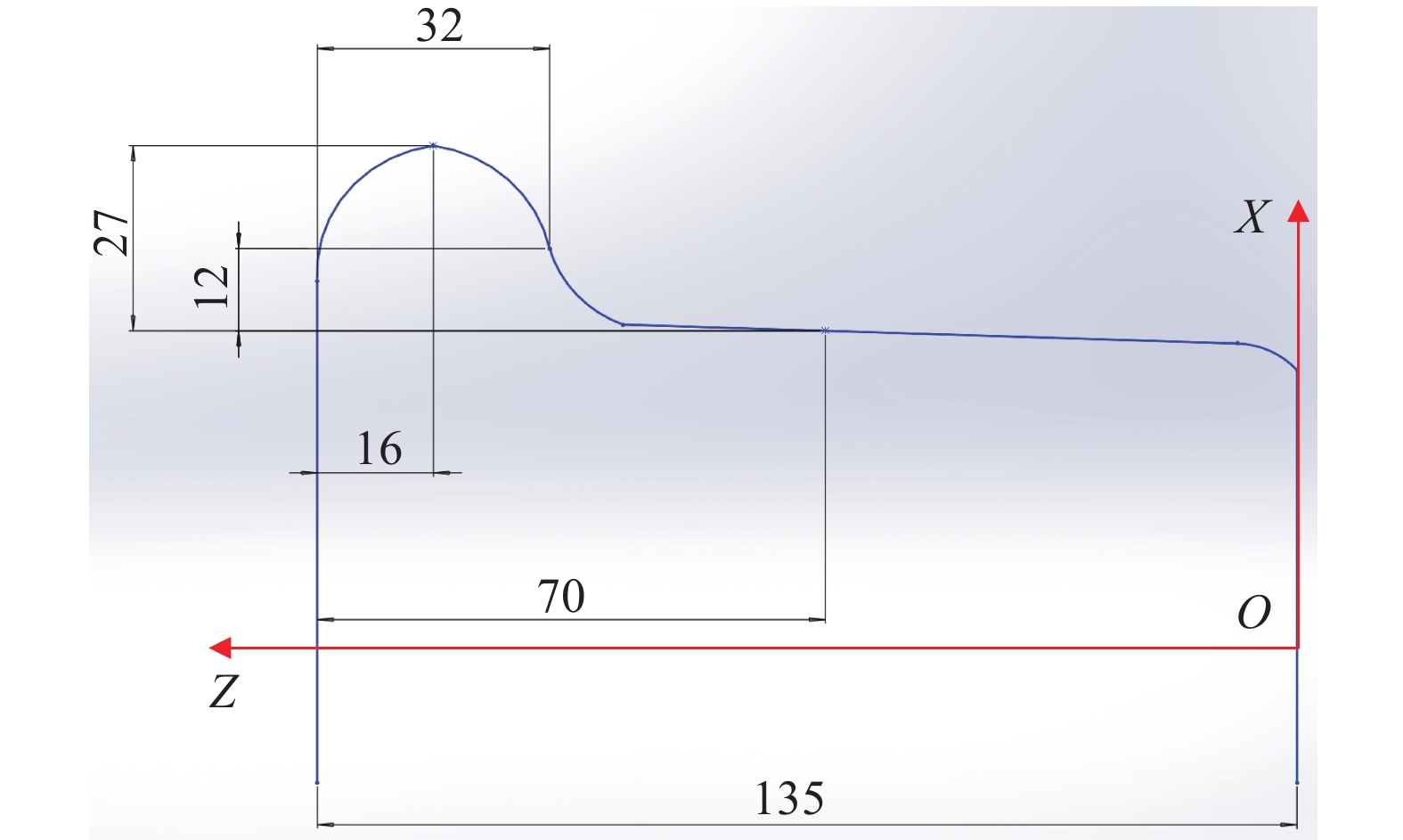
距离轮缘内侧70 mm处的圆称为滚动圆,随着列车服役时间的增加,车轮滚动圆磨耗也会逐渐增加,若滚动圆直径偏离过大会造成脱轨、断轴等事故。因此,测量分析车轮滚动圆直径对于避免列车事故有重要意义。列车轮缘主要作用是防止脱轨,评价列车轮缘是否达标的两大重要参数分别为轮缘高度与轮缘厚度,轮缘高度是指轮缘顶点到踏面基准线之间的距离,轮缘厚度是指以踏面基准线向上12 mm的轮缘厚度值。
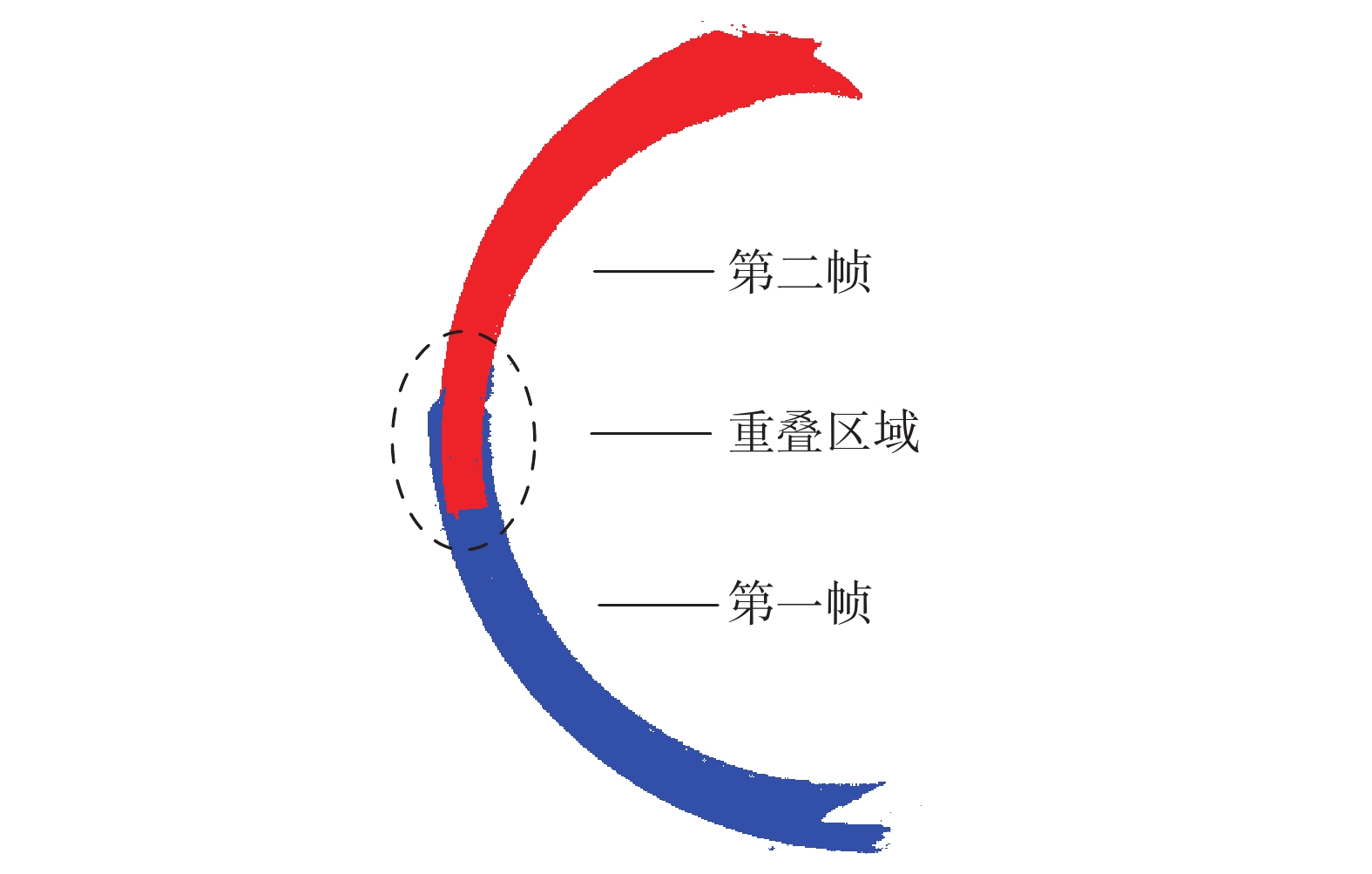
3.1 滚动圆直径检测根据图8所示车轮设计尺寸,只需要提取出Z轴正方向为65 mm处的点即为滚动圆。将滚动圆数据提取出之后,通过最小二乘法拟合轮廓圆得到圆心坐标与半径。表1显示了滚动圆拟合结果,对于多帧拼接滚动圆直径检测误差可以控制在0.22 mm内。对单帧滚动圆提取数据也分别进行拟合,可以发现对于单帧数据拟合误差普遍高于多帧拼接滚动圆的拟合误差,因此对于滚动圆的计算,应采用拟合多帧拼接滚动圆的计算方法。
|
| 图 8 车轮设计尺寸图(单位:mm) |
| mm | ||||
| 数据 | 圆心 | 半径 | 标准值 | 差值 |
| 多帧 | (0.00,0.00) | 419.89 | 420 | 0.11 |
| 单帧1 | (0.36,0.30) | 420.16 | 0.16 | |
| 单帧2 | (0.36,0.08) | 420.12 | 0.12 | |
| 单帧3 | (0.28,0.26) | 420.64 | 0.64 | |
| 单帧4 | (0.4,0.0) | 419.87 | 0.13 | |
| 单帧5 | (0.3,–0.32) | 419.04 | 0.96 | |
| 单帧6 | (–0.39,0.04) | 420.28 | 0.28 | |
3.2 轮缘高度检测
根据标准车轮设计尺寸图(图8),与提取滚动圆不同的是轮缘顶点圆需要提取出Z轴正方向为119 mm处的车轮表面轮廓圆,此圆称为轮缘顶点圆。然后同样利用最小二乘法分别拟合滚动圆与轮缘顶点圆,在得到两轮廓圆的半径之后,计算其半径差值即为轮缘高度,轮缘高度测量示意如图9所示。
|
| 图 9 轮缘高度测量示意图 |
本文所测量车轮轮缘高度理论值为27 mm,为了获得车轮轮缘高度的实际值,并对本文所提出的方法进行测量误差计算,因此使用轮缘尺(JLJ-4C机车车轮第四种检查器)测量车轮20个不同位置的轮缘高度数据,求得其平均值为27.03 mm。表2显示了使用本文列车轮对动态检测系统测量的轮缘高度与使用轮缘尺测量轮缘高度的对比,本文搭建的列车轮对动态检测系统测量值为27.11 mm,两者测量的差值为–0.08 mm。
3.3 轮缘厚度检测
列车在运行过程中轮缘与轨道之间产生摩擦,使得轮缘厚度变小。如果轮缘厚度过小,列车就会有脱轨的风险。所以需要及时检测轮缘厚度是否正常,保证列车安全运行。轮缘厚度计算具体流程如下:
1)因为滚动圆向外扩展12 mm是计算车轮轮缘厚度的地方。所以,应该以R=432 mm为半径,以车轮轮心为轴心生成一个与车轮点云相交的圆柱形轮廓,如图10(b)所示。

|
| 图 10 轮缘厚度计算过程 |
2)分别提取出圆柱形轮廓与车轮点云模型相交的两条轮廓线A和B,如图10(c)所示。
3)首先分别拟合两轮廓线所在的两个平面,然后在两个拟合平面中,利用最小二乘法拟合两条轮廓线的圆心,得到圆心坐标值。最后根据圆心坐标值获取拟合平面上Z轴方向坐标值,计算两条轮廓线Z轴坐标的差值即为轮缘厚度。
本文所测量车轮的轮缘厚度理论值为32 mm,使用轮缘尺测量车轮20个位置的轮缘厚度数据,其平均值为31.94 mm。表3显示了使用本文轮对动态检测系统测量的轮缘厚度值,与轮缘尺测量平均值的差值为0.07 mm。
3.4 车轮擦伤检测
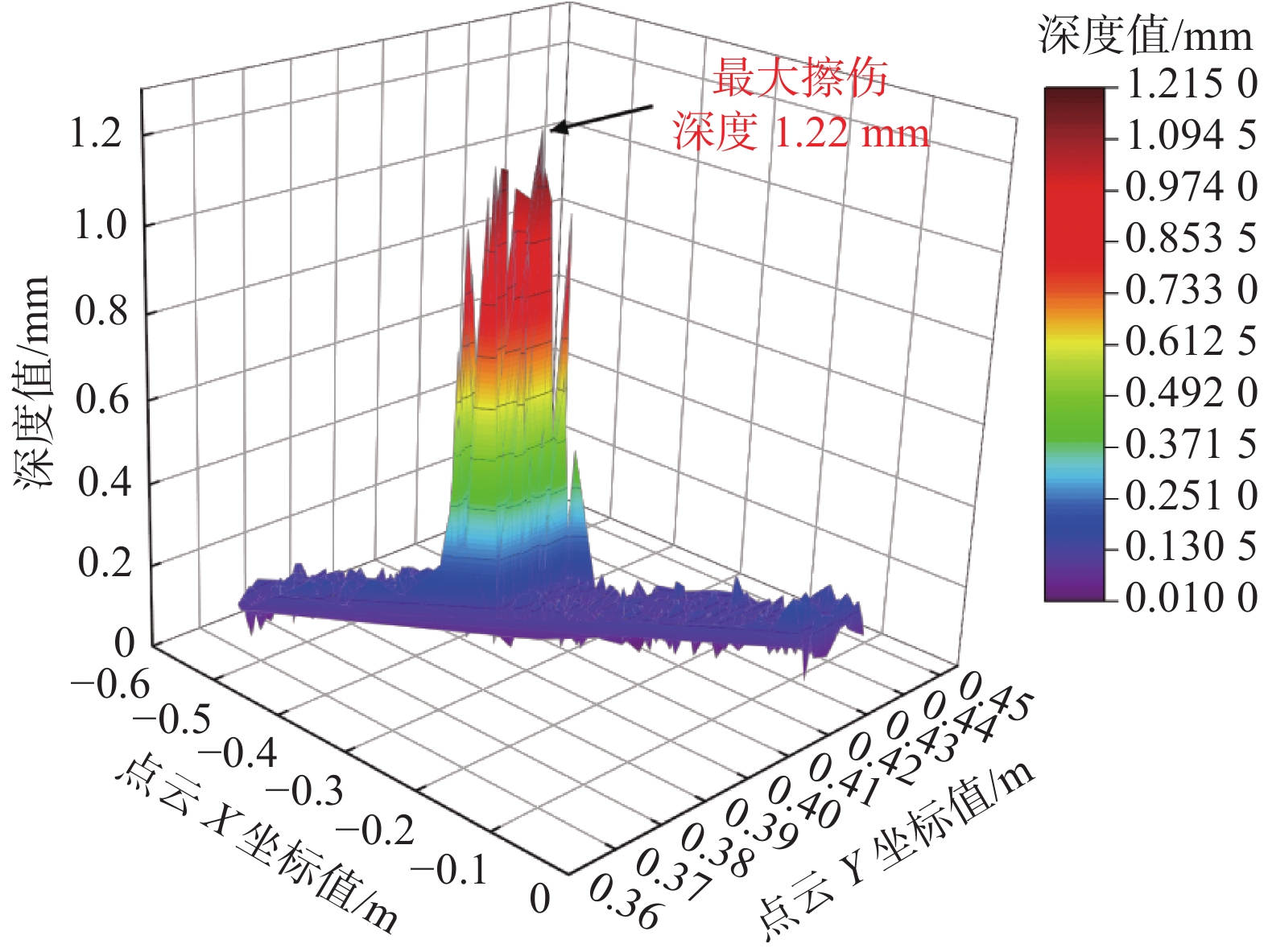
为了开展车轮擦伤检测方法研究,首先利用角磨机在列车车轮上模拟制造出一处擦伤,如图11(a)所示。本文采用模式匹配的方法检测车轮擦伤,利用带缺陷的车轮匹配正常车轮,计算最近点之间的距离检测表示车轮是否具有擦伤。图11(b)显示了正常车轮与带有擦伤的车轮匹配之后的效果,从图中可以看出车轮擦伤部分与正常车轮之间的匹配区域显示红色,说明该区域与正常车轮之间的距离差值较大,即车轮存在损伤。利用Kd-Tree在擦伤车轮数据与正常数据之间计算两个最近点的距离,即可检测出车轮擦伤深度。擦伤深度三维检测结果如图12所示,正常区域的车轮匹配距离差值普遍在0.1 mm左右,擦伤区域匹配距离差值明显增加,其中显示的最大擦伤深度为1.22 mm,实际最大擦伤深度测量值为1.4 mm,因此获得本方法最大擦伤深度测量误差为0.18 mm。

|
| 图 11 车轮擦伤检测流程 |
|
| 图 12 擦伤深度三维检测结果 |
本套检测设备与其他检测设备对比如下:有学者[14]使用CCD相机加线激光源的方式实现了轮缘高度与轮缘厚度检测,检测精度可以控制在±0.2 mm。在精度方面,本套检测装置对于上述检测装置具有一定优势。也有学者[15]使用两个线结构光与单目相机实现了100 km/h下的列车车轮滚动圆直径检测,并且精度可以控制在0.18 mm,本套检测装置在检测精度方面与其非常接近,在实时性方面处于劣势,但是本套检测装置可以形成一个整体车轮点云模型让用户更直观的观测车轮状态。
4 结束语车轮表面损伤以及型面尺寸快速精确检测一直是铁路行业亟需解决的难题,对于维护车辆的运行安全具有重要的意义。本文基于双目相机与结构光成像完成了列车车轮型面参数与擦伤缺陷的检测。主要结论如下:
1)搭建出结构光与双目立体视觉相结合的非接触式列车轮对型面检测系统,基于该设备可完整获取车轮踏面点云数据。
2)设计出多帧点云数据粗配准与精配准相结合的配准算法,即利用SAC-IA算法进行粗配准,然后通过ICP算法进行精配准,有效提高了配准精度,最终完成各相机多帧点云拼接得到整体车轮点云模型。
3)基于整体车轮点云模型并根据车轮实际尺寸特征设计相应测量方法计算出轮缘高度、轮缘厚度、滚动圆直径参数。滚动圆直径最大测量误差0.22 mm,轮缘高度测量误差–0.08 mm,轮缘厚度测量误差0.07 mm。
4)基于整体车轮点云模型,设计出模式匹配方法实现了车轮擦伤的检测,获得了擦伤深度的三维检测结果,最大擦伤深度为1.22 mm,测量误差为0.18 mm。
本套检测设备仍存在以下不足和值得深入研究的工作:投影仪发出的散斑点照射到车轮上会有反光的问题,当反光强烈时会影响相机的拍摄质量。同时由于长时间采集会引起相机温度升高,相机温度升高之后会引起像点偏移,本文通过在相机上安装散热片来缓解该问题。对于以上问题还需进一步研究改善。
| [1] |
孙琦, 张兵, 李艳萍, 等. 一种波长固定的车轮多边形在线故障检测方法[J].
铁道科学与工程学报, 2018, 15(9): 2343-2348.
SUN Q, ZHANG B, LI Y P, et al. Wavelength-fixing mechanisms for detecting the wheel polygon-shaped fault onsite[J].
Journal of Railway Science and Engineering, 2018, 15(9): 2343-2348.
|
| [2] |
阮成雄, 阮秋琦. 基于LoG梯度加权Haar-like特征的车轮裂纹检测[J].
铁道学报, 2013, 35(5): 62-68.
RUAN C X, RUAN Q Q. Wheel crack detection based on LoG gradient weighted Haar-like features[J].
Journal of the China Railway Society, 2013, 35(5): 62-68.
DOI:10.3969/j.issn.1001-8360.2013.05.010 |
| [3] |
戚潇月, 宋冬利, 张卫华. 车轮多边形对车辆动力学的影响分析及在线诊断方法研究[J].
铁道机车车辆, 2018, 38(4): 10-17.
QI X Y, SONG D L, ZHANG W H. Analysis influence of wheel polygonalization on vehicle dynamics and research on online diagnosis[J].
Railway Locomotive & Car, 2018, 38(4): 10-17.
DOI:10.3969/j.issn.1008-7842.2018.04.03 |
| [4] |
ZHOU L, BRUNSKILL H, PLETZ M, et al. Real-time measurement of dynamic wheel-rail contacts using ultrasonic reflectometry[J].
Journal of Tribology, 2019, 141(6): 061401.
DOI:10.1115/1.4043281 |
| [5] |
ROVERI N, CARCATERRRA C, SESTIERI A. Real-time monitoring of railway infrastructures using fibre bragg grating sensors[J].
Mechanical Systems and Signal Processing, 2015, 60: 14-28.
|
| [6] |
BRIZUELA J, FRITSCH C, IBANEZ A. Railway wheel-flat detection and measurement by ultrasound[J].
Transportation Research Part C, 2011, 19(6): 975-984.
DOI:10.1016/j.trc.2011.04.004 |
| [7] |
PEDRO U, SERGIO M, JAVIER F, et al. Wheel-rail contact force measurement using strain gauges and distance lasers on a scaled railway vehicle[J].
Mechanical Systems and Signal Processing, 2020, 138: 106555.
DOI:10.1016/j.ymssp.2019.106555 |
| [8] |
SONG Y, LIANG L, DU Y L, et al. Railway polygonized wheel detection based on numerical time-frequency analysis of axle-box acceleration[J].
Applied Sciences, 2020, 10(5): 309-321.
|
| [9] |
WANG Y W, NI Y Q, WANG X. Real-time defect detection of high-speed train wheels by using bayesian forecasting and dynamic model[J].
Mechanical Systems and Signal Processing, 2020, 139: 106654.
DOI:10.1016/j.ymssp.2020.106654 |
| [10] |
LIU X Z, XU C, NI Y Q. Wayside detection of wheel minor defects in high-speed trains by a bayesian blind source separation method[J].
Sensors, 2019, 19(18): 3981.
DOI:10.3390/s19183981 |
| [11] |
周茂, 胡立锦, 欧开鸿, 等. 改进稠密双目匹配算法在输电线路基础三维重建的应用研究[J].
电子测量术, 2022, 45(7): 1-7.
ZHOU M, HU L J, OU K H, et al. Application of 3D rebuild based on improved dense binocular matching algorithm in transmission line foundation positioning and measurement[J].
Electronic Measurement Technology, 2022, 45(7): 1-7.
|
| [12] |
伍川辉, 邓越, 于涛, 等. 受电弓滑板磨耗检测中多视觉传感器标定方法研究[J].
中国测试, 2023, 49(1): 7-13.
WU C H, DENG Y, YU T, et al. Research on the calibration method of multi-vision sensors in the wear detection of pantograph skateboard[J].
China Measurement & Test, 2023, 49(1): 7-13.
|
| [13] |
王永信, 卢秉恒, 梁晋, 等. 一种三维人体模型快速测量方法[J].
中国测试, 2023, 49(3): 114-119.
WANG Y X, LU B H, LIANG J, et al. A fast measuring method of three-dimensional human body model[J].
China Measurement & Test, 2023, 49(3): 114-119.
|
| [14] |
贾传宝, 吴开华, 陈强元. 倾斜位置成像的轮对几何参数计算方法[J].
传感器与微系统, 2017, 36(2): 150-153.
JIA C B, WU K H, CHEN Q Y. Calculation method of wheel set geometrical parameters by imaging at inclined position[J].
Transducer and Microsystem Technologies, 2017, 36(2): 150-153.
|
| [15] |
CHEN X, SUN J H, LIU Z. Dynamic tread wear measurement method for train wheels against vibrations[J].
Applied Optics, 2015, 54(17): 5270-5280.
DOI:10.1364/AO.54.005270 |
 2024, Vol. 50
2024, Vol. 50