0 引　言

在碳达峰、碳中和背景下，绿色智慧转型成为经济高质量发展的必由之路^[1-2]，开发可再生无污染能源已成为海洋能领域的研究重点。海洋能作为一种清洁、可再生的能源，资源丰富，可以满足不同地区的能源需求。而潮流能作为海洋能的一种，其资源丰富，能量集中，具有极大的开发价值和利用前景^[3]。而水轮机作为潮流能开发利用的关键水动力部件，直接关系到整个系统能量利用率^[4]。对于给定的水轮机，其输出功率与水流流速的立方成正比，因此提高水轮机输出功率的一个可行方法是局部提高水速，而导流罩作为一种合适的导流装置，可导致局部流速增加。因此，研究导流罩式潮流能水轮机水动力性能具有重要的学术意义和应用价值。

导流罩由三部分组成：喷嘴、扩散器和法兰，根据导流罩这三部分的配置，前人已经提出并评估了不同的几何形状^[5-7]。WU K T等^[8]设计一种可被动旋转的导流板，并用于利用潮汐流发电的水轮机。导流板能够随着水流的变化自动调整位置。通过 CFD 模拟，将导流板和导流尾翼的几何设计与不带导流板的涡轮机和带原始导流板的涡轮机在整个运行范围内进行了比较。结果表明，加装改进型导流板后，水轮机的获能系数是原来的 3.13 倍。陈存福等^[9]使用算法LBM（Lattice Boltzmann method）研究了导流罩水轮机的水动力特性。AYADI A等^[10]针对Savonius水轮机获能效率低的问题设计了一种导流板，通过数值研究发现加装改进型导流板后，水轮机的最大获能系数可提高34%。ElZAHABY A等^[11]基于Fluent软件研究导流罩的出口法兰角对水轮机的影响，结果表明，法兰角度为15°是最佳角度，可以加速扩散器入口处的流动。RAHMATIAN M等^[12]研究了微型 HAWT（horizontal axis wind turbine）在无导流罩、原始导流罩和优化后导流罩三种不同条件下的空气动力性能。结果表明，改进后的风道可将入口风速从5 m/s提高到10.5 m/s。SHAHSAVARIFARD M等^[13]评估了偏航条件下的导流罩式水轮机水动力特性。研究表明，在偏航角为 10° 时水轮机功率系数减小的幅度最初可以忽略不计，但随着偏航角的增大，水轮机功率系数减小的幅度随之增大。MADUKA M等^[14]基于水槽实验研究了双向潮流能中导流罩水轮机的性能。结果表明，导流罩水轮机每转子单位面积的发电量比裸机高40%，但在导流罩水轮机中尾流速度的下降范围和湍流强度的增加范围更大。BORG M G等^[15]研究了偏航角在0°~45°工况下导流罩水轮机的性能，得出当偏航角在23.2°时水轮机的性能最佳。

如上所述，一些研究者已经进行了不同的实验和数值研究。总的结论是，导流罩的存在会增加局部流速，然而，导流罩内的流场是三维的、高度湍动的，而且非常复杂，尤其是当水轮机在导流罩内运行时，情况更为复杂。因此，仍有必要进一步研究导流罩式水轮机的水动性能，并改进此类水力系统。本文设计了一种适用于水平轴水轮机的“M”型文丘里管式导流罩,基于HMB3（Helicopter Multi-Block 3）方法优化导流罩入口的开口角度，探讨HMB3所得最优导流罩对水轮机水动力特性的影响。

1 理论基础 1.1 控制方程

对于不可压缩流体，连续性和动量守恒方程可以表示为：

式中：$ \rho $——不可压缩流体密度；

$ {{p}} $——流体压力；

$ \mu $——不可压缩流体粘度。

水平轴水轮机的水动力性能由三个无量纲参数来描述：能量利用系数C_p、轴向载荷系数C_Z和尖端速度比TSR。C_p反映了潮流水轮机的能量吸收能力，C_Z代表了水轮机轴向载荷系数,速比$\lambda $是转子的角速度ω和水流速度U之间的比率：

式中：$ M $——扭矩，N·m；

$ \omega $——角速度，r/min；

$ \rho $——流体密度，kg/m³；

$ U $——流体速度，m/s。

1.2 导流罩设计

1.2.1 导流罩物理建模

轴向速度系数（$ {{C}}_{{U}}{}_{，{x}} $）被定义为导流罩的喉部速度$ {U_x} $与来流速度$ {U_{\infty} } $的比值。表示为：

静压系数（$ {{C}}_{{p}，{s}} $）被定义为导流罩的喉部的静压$ {P_S} $与来流动压$ \dfrac{{{1}}}{{{2}}}\rho U_{\infty }^2 $的比值。表示为：

雷诺数(Re)被定义为：

式中：$ \mu $——流体粘度；

$ D $——水轮机直径。

由导流罩进口处宽度$ {H_{{1}}} $与导流罩外径$ {H_{{\rm{ext}}}} $的关系，得出与质量流速有关的质量守恒方程。

式中：$ {H_{{\rm{in}}}} $——导流罩内径；

$ {H_{{\rm{ext}}}} $——导流罩外径。

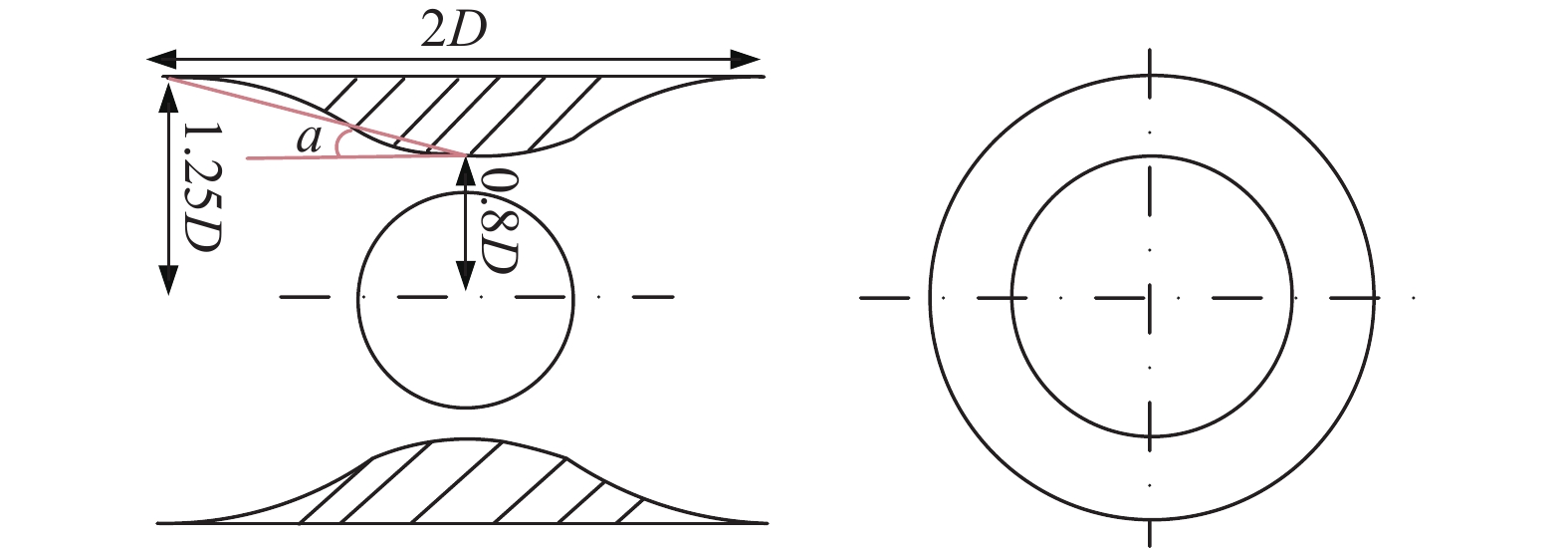
根据相关文献，导流罩设计遵循的以下原则^[16]：1）水轮机前的平均速度大于来流流速；2）水轮机前的入流均匀；3）流道阻力小；4）结构简单，易于制造；5）当这些原则发生冲突时，水动力性能优先。本文设计了一种文丘里型导流罩，如图1所示，并通过不断优化$ \alpha $的角度，$ \alpha $为导流罩喷嘴的角度，比较不同角度下导流罩水轮机的水动力性能。导流罩的内壁设置为轴对称模式，总长度为2D（D为水轮机直径），导流罩的入口和出口距离旋转轴均为1.25D，喉部距离旋转轴为0.8D。

2 优化程序 2.1 HMB3邻接法

采用了以高效处理大量设计变量和少量目标函数而著称的HMB3邻接法对导流罩进行优化研究^[17]。目前的优化研究涉及许多设计变量，这些变量控制着导流罩的形状，而目标/约束函数只有几个目标/约束函数，目标函数$I$定义为：

式中：$ \alpha $——设计变量，通常定义几何形状并包含3个参数；

$I$——空气动力载荷或其组合的集合，它依赖于$ W\left( \alpha \right) $，W不是独立变量，而是受制于设计变量$ \alpha $。

与方程（12）类似离散化的流动方程的稳态残差向量$R$可以定义为：

要评估$I$随设计变量$ \alpha $的变化而发生的变化，必须求解$I$相对于$ \alpha $的灵敏度方程。如果使用直接微分法或有限差分法，由于设计变量较多，计算要求较高。但通过引入一个与方程（12）和（13）相关联的邻接向量${\boldsymbol{ \lambda }}$，灵敏度方程可以在方程（12）和（13）中重构。

灵敏度方程可以用邻接形式重拟为：

2.2 优化过程

优化变量的一般形式可以写成：$ {\rm{min}}\left( {I\left( {\boldsymbol{\alpha}} \right)} \right) $；以式(16)为准。

式中：$ \left( {I\left( {\boldsymbol{\alpha }}\right)} \right) $是最小化的目标函数，受m个不等式约束条件$ {{g} _j}\left( {\boldsymbol{\alpha}} \right) $和p个等式约束条件$ {h_k}\left( {\boldsymbol{\alpha}} \right) $的限制。$ {\boldsymbol{\alpha}} = \left( {{\alpha _1}{,}\cdots {,}{\alpha _n}} \right) $是n个设计变量的向量。

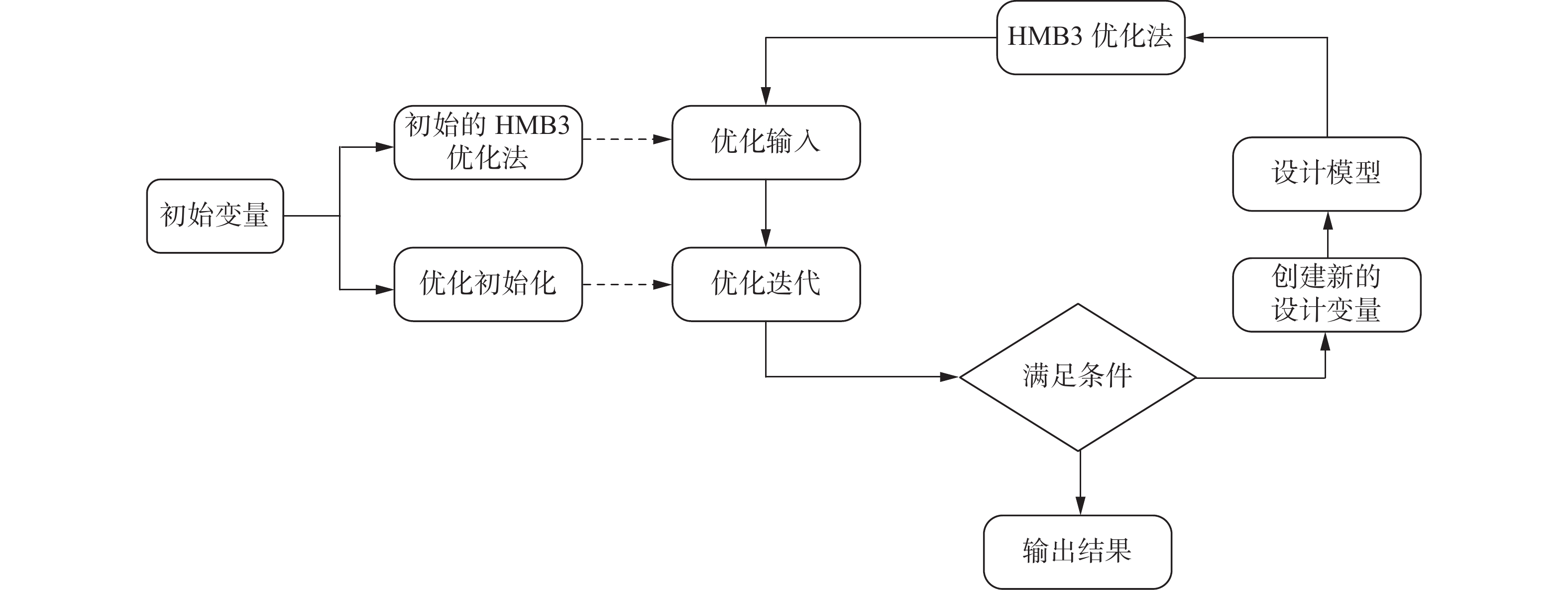
图2 流程图描述了优化框架。该框架由独立的工具组成，包括流程求解器、优化器以及文件输入/输出和系统操作的辅助工具。在目前的工作中，目标函数和约束函数，以及它们与设计变量都是通过 HMB3辅助求解器计算所得。导流罩动力学形状被参数化^[18]，并由一组设计变量表示，如图2 所示。检查基线设计的 HMB3 初始解后，优化器初始化并开始优化循环，在每次迭代中产生新的设计变量。设计变量如表1所示，导流罩厚度及长度设置为定值，优化不同导流罩入口开口角度。

3 物理模型 3.1 计算域创建和网格划分

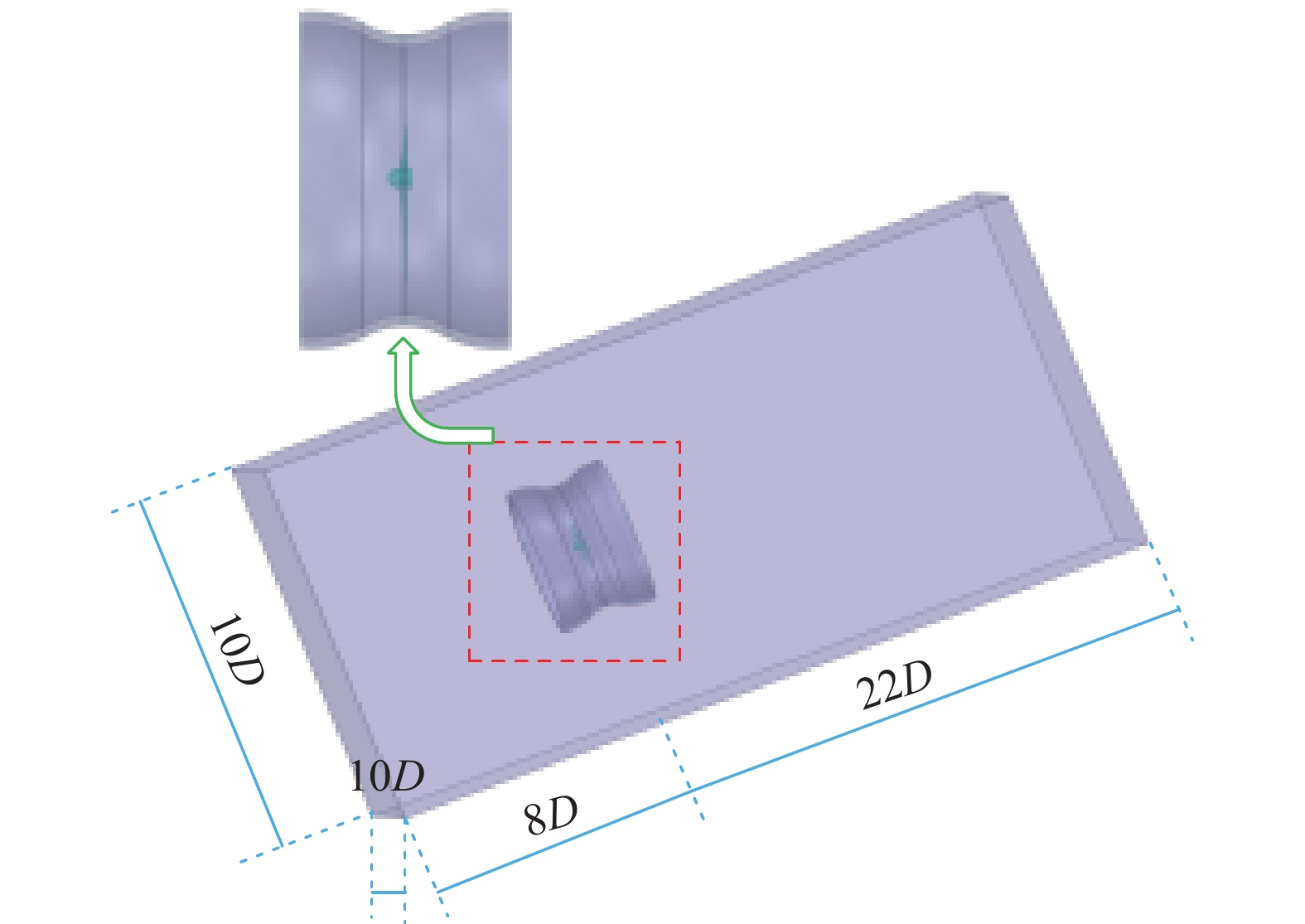
仿真采用三叶片水轮机，水轮机的直径为0.4 m，轮毂的直径为0.02 m。采用滑移网格来模拟HATT（horizontal axis tidal turbine）的旋转，使用两个独立的域：一个长方体域和一个旋转的圆柱域（包括叶片），如图3所示。为分析水平轴潮流能水轮机的流场特性，建立了一个长30D（D为水轮机直径）、宽和高10D的长方体计算域，旋转域设置为底面半径为0.5 m的圆柱形域，入口距水轮机旋转平面8D。

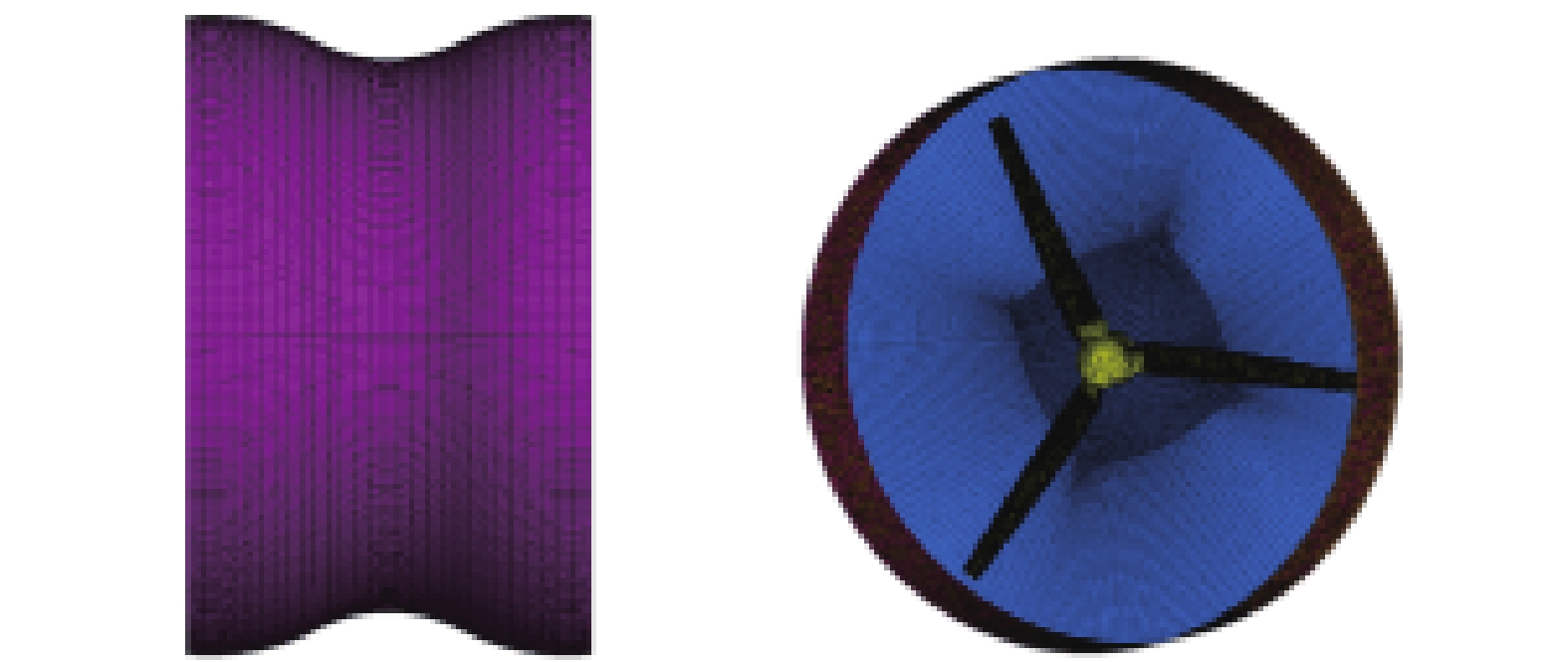
如图4所示，使用ICEM划分网格，网格类型为结构网格结合非结构网格。非结构化网格在处理复杂的几何形状和拓扑结构时更加灵活，将水轮机与旋转域一起划分为非结构化网格，而计算域和导流罩由于其形状规则和结构简单划分为结构化网格以提高计算效率。叶片表面的第一个网格层的高度为0.0005 m，边界层设置为10层，网格质量为0.34。

3.2 设置边界条件

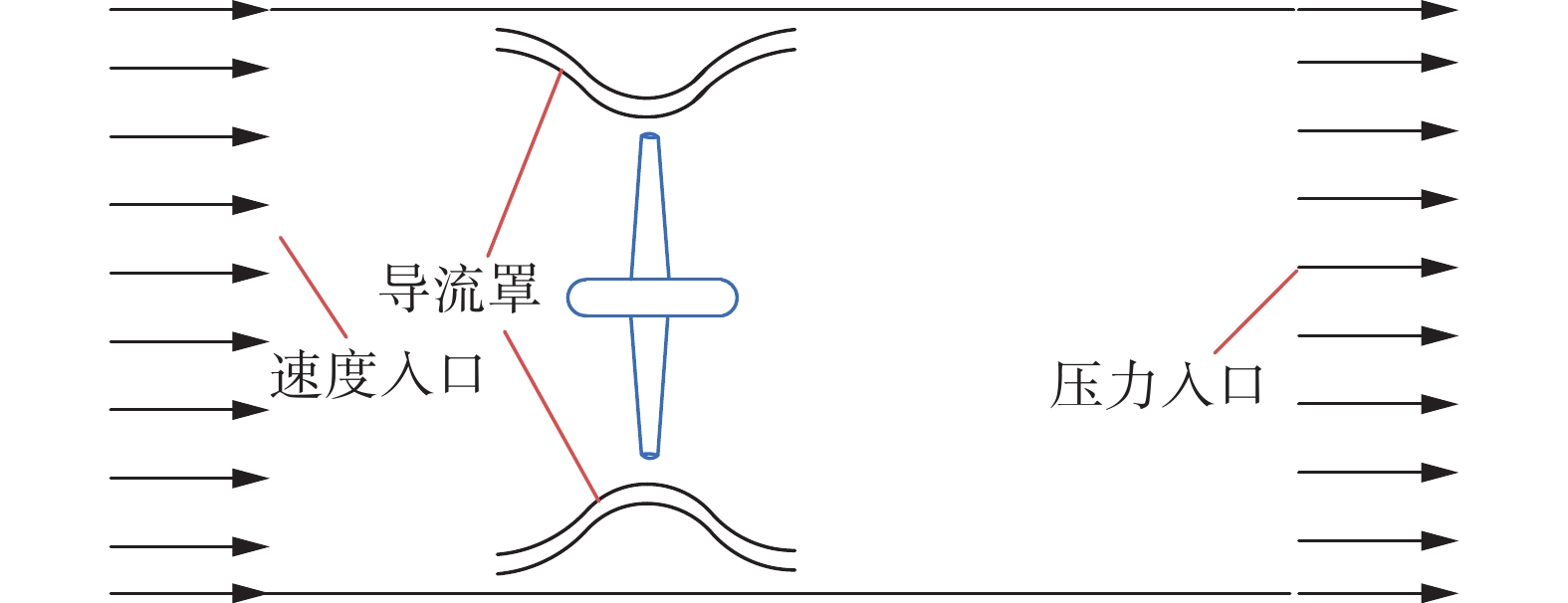
边界条件的设置如图5所示。入口设置为速度入口，给定均匀来流速度1 m/s和湍流强度5%。出口设置为压力出口，压力大小为默认值。壁面设置为自由滑移壁面，叶片和轮毂设置为无滑移壁面，重力加速度设置为负Z方向9.8 N/kg，湍流模型选择$ {\rm{SSTk }} - \omega $。水轮机的旋转是通过滑移网格技术实现，选用瞬态求解器求解，压力-速度耦合采用SIMPLEC算法，时间离散采用二阶隐式格式，动量离散采用一阶迎风格式，时间步长为水轮机旋转1°所用的时间（0.00196 s）。

3.3 网格无关性验证

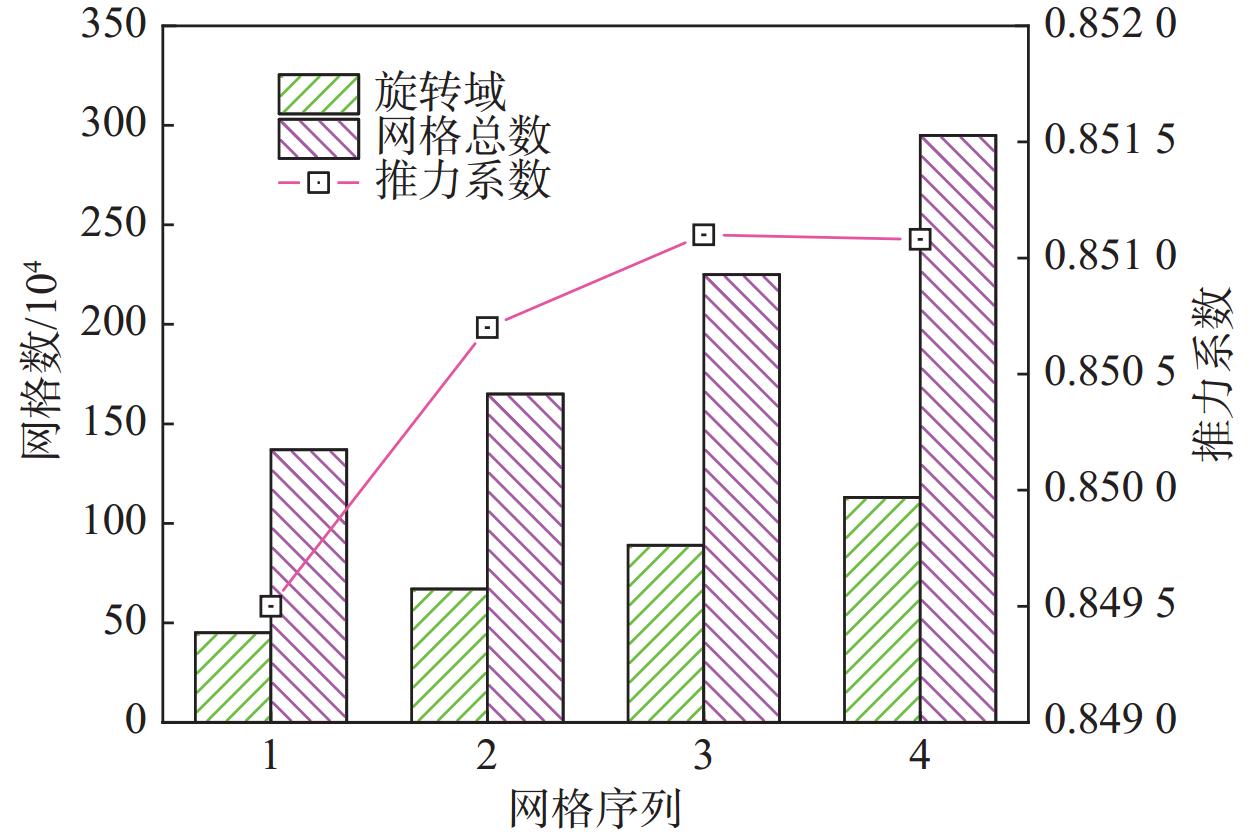
在数值模拟中，计算结果的精确性与网格数量密切相关，网格数量过少可能无法充分捕捉流场或物理现象的细节，从而导致较大的数值误差。网格数量较多可以减小数值误差，提高计算结果的准确性。但是增加网格数量会增加计算成本，包括计算资源和时间，更多的网格单元需要更多的内存和计算能力来存储和处理。因此，在实际应用中，需要在计算结果的准确性和计算成本之间进行权衡，选择适当的网格数量。本文在ICEM软件中对水轮机叶片部分进行局部加密。如图6所示，以水轮机推力系数为参考值，从图6可以看出，当网格总数为225 万时，水轮机推力系数与实际推力系数接近，继续增加网格数到295 万时，水轮机推力系数基本不变，说明网格对计算结果影响很小。鉴于计算资源及计算效率，后续各项计算使用网格3计算。

4 CFD数值模拟 4.1 水轮机载荷分析

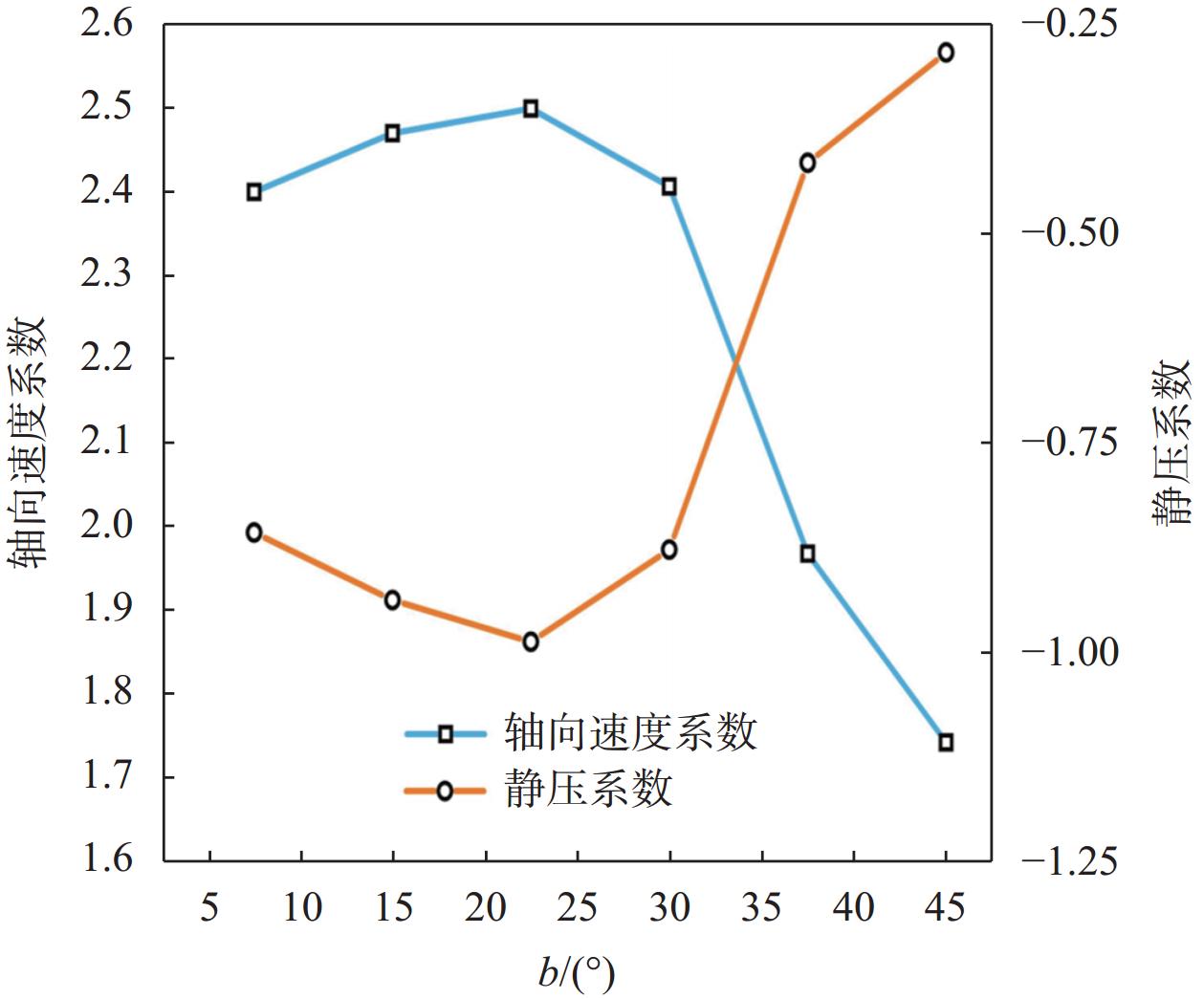
如图7所示，优化后的导流罩根据阻力与升力的关系，确定了导流罩喉部轴向速度和静压的变化。当导流罩入口开口角度为22.5°时轴向速度系数最大，静压系数最小，即此时导流罩达到了最佳的聚能效果和流动稳定性。后续分析导流罩入口开口角度为22.5°时水轮机水动力性能。

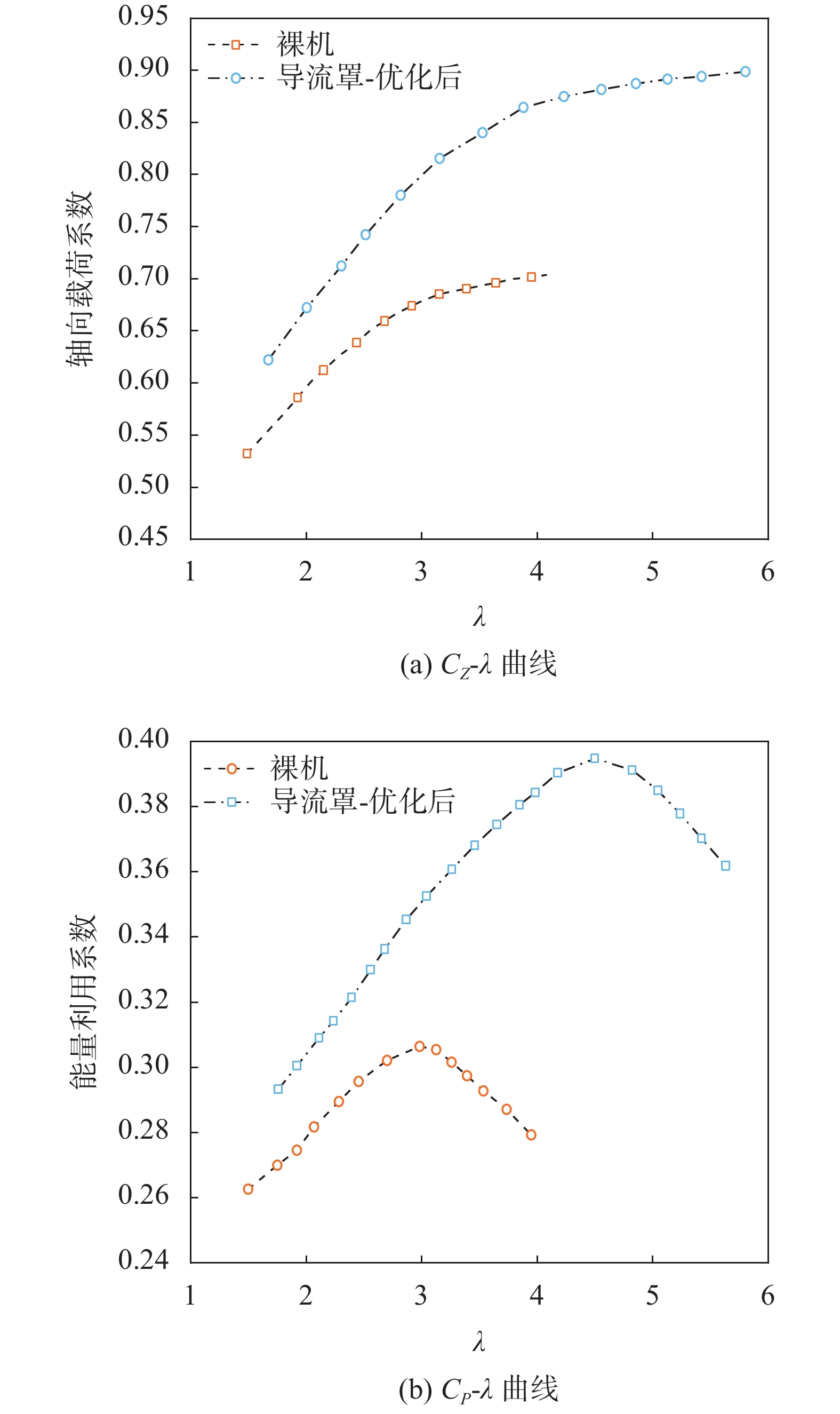
图8（a）对比了裸机与优化后导流罩水轮机的轴向载荷系数-叶尖速比（$ {C_Z} - \lambda $）的变化曲线。图中呈现出水轮机在有无导流罩得工况下轴向载荷系数均随着$ \lambda $的增加而逐渐增大，但有导流罩时水轮机轴向载荷系数均大于裸机值。图8（b）所示为裸机与优化后导流罩水轮机的能量利用系数-叶尖速比（$ {C_P} - \lambda $）的变化曲线，裸机在最优速比$ \lambda = {{3}} $的能量利用系数最大，改进后的导流罩水轮机在最优速比$ \lambda = 4.5 $时能量利用系数达到最大值。很明显，增加导流罩可以提高水轮机的水动力特性。

4.2 水轮机流场分析

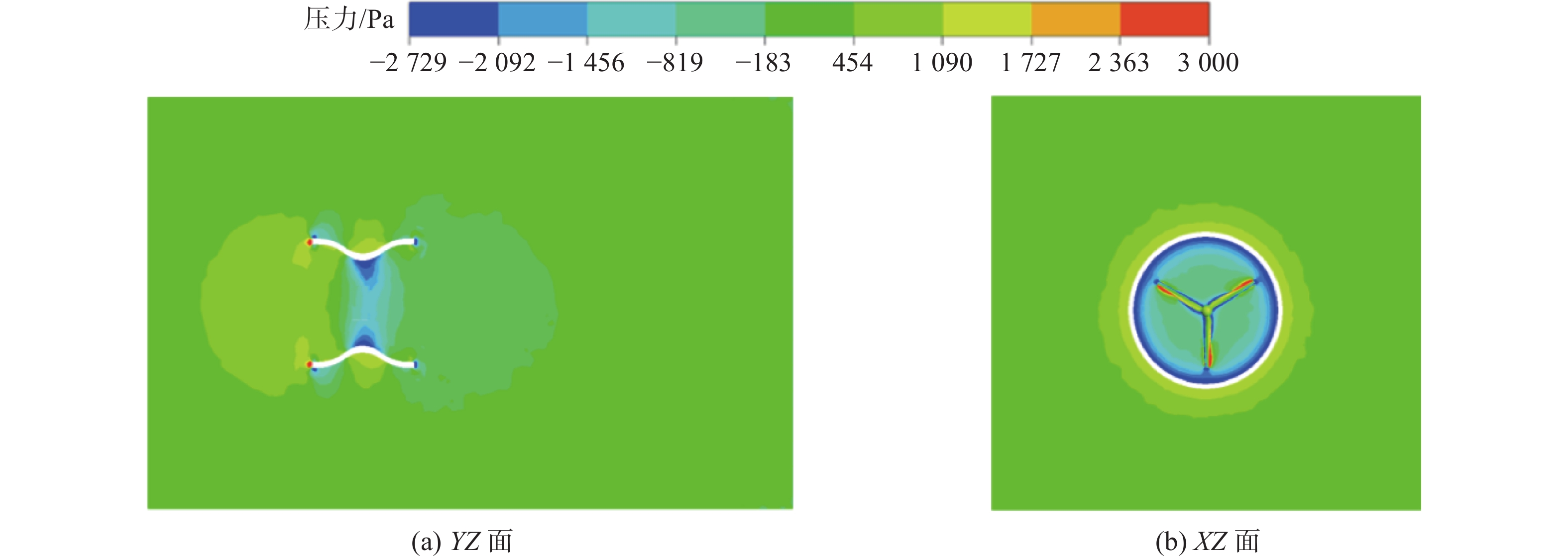
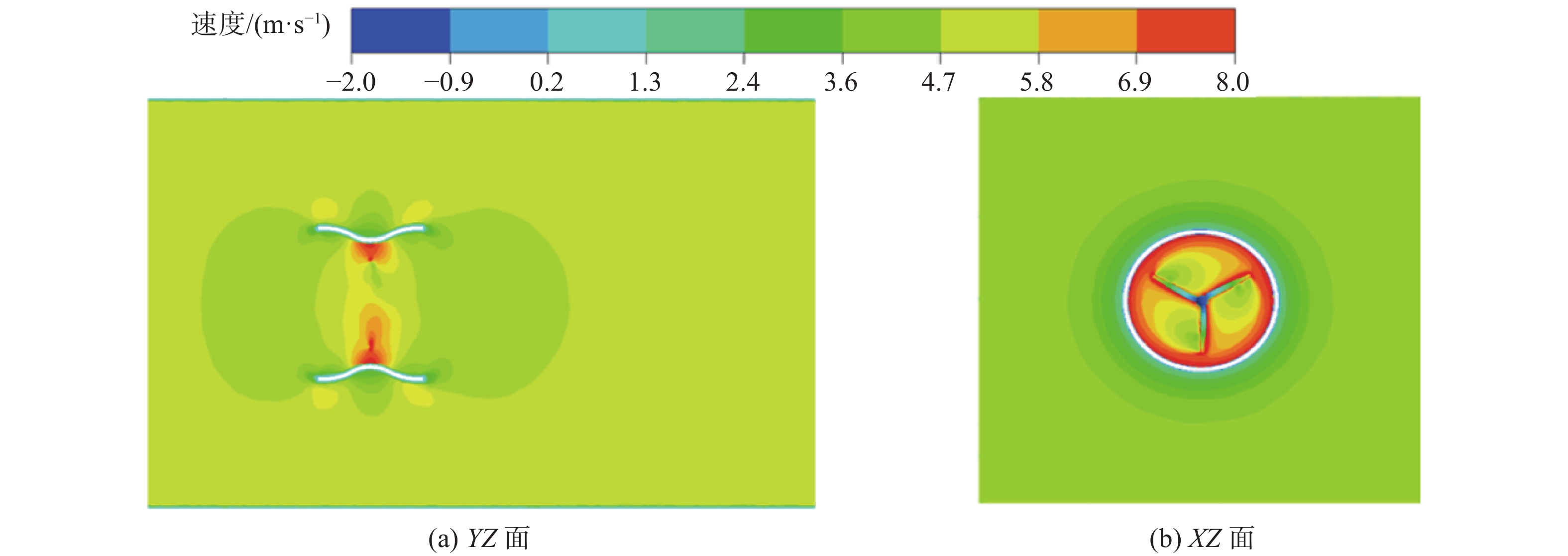
图9显示了最优入口开口角（即22.5°）的导流罩周围和内部的压力分布图。由图可知在导流罩内部和导流罩后面出现分离区，从而形成低压区，造成压力差，这将使更多水流流入导流罩并使其加速。图10显示了最优入口开口角的导流罩周围和内部速度分布图。在导流罩的进口处，轴向速度显示出一个加速区域，可以通过引导和加速水流。在导流罩内由于导流罩的形状和设计使水流在导流罩的中心区域内形成高速流动。从而在导流罩的中心区域显示出一个峰值区域。这个峰值区域代表了水轮机叶轮受到最大速度的冲击，从而提供最大的动力输出。原来流入口水速为1 m/s，而在优化后的导流罩入口速度则达到了3.7 m/s（比原来增加约27%）。从理论上讲，水轮机的转换功率将增加大约10%。

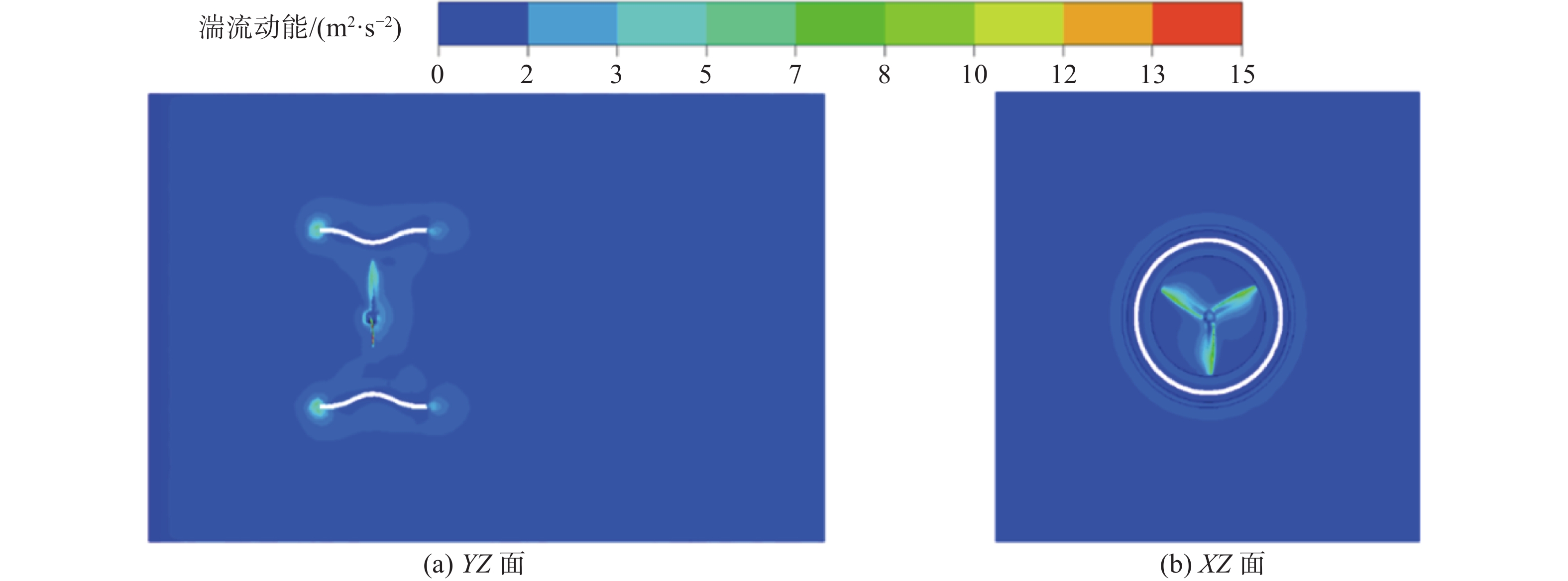
如图11显示了在导流罩内不同横剖面和纵剖面湍流的强度分布。图中的湍流动能分布显示出湍流强度在不同位置的变化情况，由于湍流在流动过程中受到导流罩壁面的阻碍和衰减，导流罩壁面的摩擦和阻力作用会减弱湍流的能量，使湍流强度降低。也正是由于水流在导流罩内部受到约束和引导，湍流得以发展和积聚。在导流罩的中心区域，水流的速度和压力变化较大，形成湍流涡旋并相互作用，导致湍流强度增加。

5 结束语

本文基于HMB3方法优化导流罩入口角度，优化结果集成于Fluent软件模拟了导流罩水轮机水动力特性，并分析了增加导流罩对水轮机能量利用系数和轴向载荷系数的影响。得出了以下结论：

1）随着速比的增加，裸露的水轮机的能量利用系数逐渐增加。当速比增加到3时，水轮机能量利用系数达到最大值，裸机加装导流罩后，水轮机能量利用系数增大，经过不断优化导流罩，当导流罩入口角度为22.5°时，水轮机能量利用系数较裸机增加了约10%。

2）优化后的导流罩实现了良好的聚能效果，这是由于导流罩在速度入口处收缩，在压力出口处拉伸的设计造成的。这种设计可以使能量在水流进入导流罩入口处时汇聚，在出口处释放压力，从而提高水轮机的水动力特性。