0 引　言

海洋是高质量发展的战略要地，海洋科技是推动高质量发展的关键。近年来，我国海洋科技发展日新月异，各种海上平台应运而生。除了传统的海上石油平台外，海上平台在海洋牧场^[1]、海洋能发电^[2-5]、海洋仪器测试^[6]、深海养殖^[7]等领域也取得了新进展，这些新型海上平台大多采用浮式结构，平台通过系泊系统稳定在海面上。与传统海上浮式平台相比，新型浮式海上平台具有更高的灵活性和多功能性，工程成本相对较低，建设周期短，且能够更好地适应不同海洋环境条件，是未来海洋工程发展的重要方向之一。海上平台长期在海上生产作业，会受到大小变化不同的风、浪、流等海洋环境条件影响。近年来，台风等恶劣天气频发，为了保障平台结构及各种设施能经受住风浪的侵袭而不致损坏，必须要对平台进行极端海况下的生存性试验。保障海上平台的安全性是实现海上平台高质量发展的关键，而海上平台的安全性离不开相关海洋标准的助力，正是缺乏极端海况下浮式海上平台生存性试验方法的相关标准，使得这些新型海洋平台在实际应用中难以得到更好的利用。

对于浮式海上平台而言，平台与系泊系统之间存在相互影响，很难直接选择某一特定的海况作为极端海况^[8]。因此研究极端海况下新型浮式海上平台的生存性试验方法，关键在于选取何种海洋环境条件组合作为极端海况。范亚丽等^[9]取南海100年一遇的波浪条件作为半潜式支持平台试验研究的恶劣海况；李蜀军等^[10]取50年一遇的波浪条件作为漂浮式风力机响应分析的极端海况；但考虑到浮式系统所受到的载荷和响应并非完全由波浪所主宰，有些学者也取某些实测的台风数据^{[11- 12]}作为平台承受的极端海况。

对于极端海况的选取，本文参考国际电工技术委员会（international electrotechnical commission，IEC）编制的生存条件下波浪能转换装置的试验标准^[13]，提出了针对新型浮式海上平台的极端海况下的生存性试验方法，并以布放于国家海洋综合试验场的“国海试Ⅰ”海上试验平台为例，应用威海海域实测与重现期推算数据，通过数值模拟的方法，来验证该试验方法的可行性。研究结果可为将来相关标准的制定提供理论依据，从而推动海洋平台的高质量发展。也可为浮式海上平台在设计与优化阶段提供极端海况下的生存性试验参考，从而进一步保证平台的安全性与可靠性。

1 生存性试验方法 1.1 海上装置生存性试验方法

对于海上装置生存性试验方法的研究，IEC出版的波浪能转换装置初期开发指南IEC TS 62600-103指出了对波浪能转换装置在生存环境下的试验目标，即引入极端海况条件以观察设备在生存条件下的响应，获得装置特有的故障模式。并对测试所需的波浪参数进行了说明。

由于不能完全明确何种海况或波浪组合会产生极限状态，因此需要大量的环境参数组合作为对照条件。可以改变的参数有：波浪的能量、谱形、方向、扩散以及海流和风。首先依据IEC TS 62600-2^[14]确定50年一遇的波浪条件作为基准条件，之后按如下步骤获得其他海况条件：

以基准波浪条件为中心值，分别生成2组波浪方向不同、2组波浪扩散不同、2组波浪谱形不同、2组波浪能量不同的对照海况条件；

1）生成的对照波浪方向应尽可能接近90°；

2）生成的对照波浪扩散方向应从长峰波到$ {\rm cos}^{2n}\theta $型（n=3）短峰波；

3）生成的对照波浪谱形应从宽频谱到用等效单峰谱描述的双峰谱；

4）生成的对照波浪能量范围应由海况轮廓线的峰值点（最大有效波高）偏移±30%。

通过上述步骤最终形成12组独立的环境条件，用于测试装置针对某一海况的响应敏感性。分析装置对上述12种海况的响应后，可确定装置达到极限状态时的海洋环境条件。确定该条件后，还需在最后一组试验中引入风和流的影响，风与海流的极限条件依据 IEC TS 62600-2中的要求均取5年一遇。为明确风、海流、波浪对装置的共同影响，应至少补充3组测试：1）风、海流与波浪共向；2）风与海流共向且与波浪不共向；3）风、海流、波浪均不共向。

1.2 浮式海上平台生存性试验方法

波浪能转换装置对波浪要素更敏感，因此IEC编制的极端海况下波浪能转换装置的生存性测试标准更加关注波浪参数，需要设置不同的波浪能量、谱形、方向、扩散作为对照组，这些条件在试验中的可操作性不强，使得该方法的可行性不高。

与波浪能转换装置相比，新型浮式海上平台的建设成本更高，且在经历极端海况后，也要确保工作人员能够返回平台继续进行生产作业。为了保障平台与工作人员的安全，50年一遇的波浪条件和5年一遇的风、流条件难以满足实际工程应用。

针对以上不足，本文适当放宽了对波浪条件的要求，使其在试验中可操作性更强；此外根据挪威船级社的相关要求，对于极端海况下的环境组合应不少于百年一遇的环境条件^[15]。在IEC制定的极端海况下波浪能转换装置的生存性试验标准基础上，本文做出了如下改进：

1）选取100年一遇的波浪条件作为基准条件，并以基准波浪条件为中心值，分别选取两组波浪朝向不同、谱形不同、能量不同的对照海况条件，最终形成9组独立的环境条件，用于测试平台针对某一确定海况下的最大响应。

2）由于平台和系泊系统受到的最大响应和载荷并非在百年一遇风、浪、流的方向一致时发生，确定该波浪条件后，选取100年一遇的风、流条件，至少补充3组测试：风、海流与波浪共向；风与波浪共向且与海流不共向；风、海流、波浪均不共向。

3）风浪流联合试验作为生存性测试重要部分，若有该海域实测现场数据，风、流条件应以海域实测数据为准；若无实测数据，应采用不同的风向、流向组合来确定使平台产生最不利影响的风和流条件。

进行极端海况下新型浮式海上平台生存性试验的目的是希望获得平台受到的最大环境载荷，以此来判断平台结构、系泊系统是否能经受住风浪的侵袭而不致损坏。除了关注平台所受的环境载荷之外，平台的漂移量、六自由度响应和锚泊定位能力也是重要指标。在试验数据分析时，不仅要得出平台漂移量变化值、六自由度运动响应幅值以及锚链张力变化值的时历曲线，还应对其进行统计分析。

本文以国家海洋综合试验场威海场区中的“国海试Ⅰ”海上试验平台为研究对象，应用数值模拟的方式，来验证新型浮式海上平台生存性试验方法的可行性。

2 应用实例

“国海试Ⅰ”海上试验平台为钢制漂浮式结构体，总吨位432 t，采用双浮体船型，船体长30 m，宽21 m，型深4.5 m，设计吃水2.2 m。平台布设点位于山东省威海市褚岛北部海域，该海域最大水深70 m。平台结构如图1所示。

2.1 威海海域情况

国家海洋技术中心通过多参数综合浮标搭载的波浪传感器对威海海域进行了全年的波浪观测，并使用ADCP对平台布放点附近进行了大小潮的观测。根据现场观测数据以及历史资料，推算了该海域不同重现期的风、浪、流要素，推算结果如表1所示。

2.2 系泊系统

系泊系统是浮式海上平台的重要组成部分，学者们在系泊配置^{[16- 17]}与锚系方式^[18-20]以及锚链安全性^[21]等方面，作了细致研究。海上平台会受到来自任意方向的风、浪、流作用，为了给平台各个方向提供回复力，锚泊定位系统中的各根锚链通常采用辐射对称式布置。本文选用4根直径为32 mm的AM2龙须链，并采用松弛式的锚系形式，锚链主要参数如表2所示。

2.3 环境载荷分析

“国海试Ⅰ”海上试验平台在海洋环境中主要受到海风、海流以及波浪3种外部环境载荷的作用。

2.3.1 风载荷

海洋结构物设计过程中，风载荷对稳性、定位系统和局部结构强度等是必须考虑的因素。对于海洋结构物来说，水上部分所受风载荷与结构物形状、高度以及受风投影面积等因素的影响，风压P计算公式如下：

式中：$ v $——设计风速，m/s；

$ \rho $——空气密度，取1.29 kg/m³。

结构物上的风载荷计算公式如下：

式中：$ {C}_{h} $——受风构件高度系数；

$ {{C}}_{{s}} $——受风构件形状系数；

$ S $——受风构件的正投影面积。

2.3.2 流载荷

对于平台的水下结构，除受到波浪作用外，还会受到流载荷作用，海流的变化比较缓慢，在对海洋平台的数值分析中常将海流视作稳定的流动。当仅仅考虑海流对于结构物的载荷作用时，可按照下式计算：

式中：ρ——海水密度；

C_d——曳力系数；

V——设计流速，m/s；

A——受力构件在与流速垂直平面上的投影面积。

2.3.3 波浪载荷

浮式平台受到的波浪力主要包括一阶波浪力和二阶波浪力，一阶波浪力的频率与波浪的频率相等，并且大小与波幅成线性关系，二阶波浪力使得平台做长周期的慢漂运动，其中二阶波浪平均漂移力与波幅的平方成正比关系。

在频域分析理论中，应用三维势流理论求解流场中的速度势后，应用线性化的伯努利方程（4）求解线性化的波浪载荷，

将入射势$ {{\phi }}_{{I}} $和绕射势$ {\phi }_{d} $代入伯努利方程，可得到一阶波浪力的表达式：

式中：$ {F}_{\rm j} $——单位波幅作用j方向的一阶波浪力；

$ {n}_{\rm j} $——平台表面法向量在j方向的分量；

$ S $——平台在平衡位置的湿表面积。

二阶波浪力包括平均波浪漂移力、低频波浪漂移力（又称差频力）以及和频波浪漂移力。在系泊计算中，一般忽略和频项，二阶波浪力由传递函数表示为：

式中：$ {P}_{jk} $、$ {Q}_{jk} $——与时间无关的传递函数；

$ {\omega }_{i} $、$ {\omega }_{j} $——一对波浪频率；

$ {\varepsilon }_{i} $、$ {\varepsilon }_{j} $——一对随机的相位角。

在实际海洋环境中，浮式平台受到风、浪、流的耦合作用，浮式平台与系泊系统组成的整体不再满足频域分析中做的线性假设，因此需要采用时域分析方法。

将频域分析结果中的一阶波浪力与二阶波浪力通过傅里叶逆变换后可得到时域分析下的结果。

时域分析下的一阶波浪力表达式为：

式中：$ \mathrm{\eta }\left(\mathrm{\tau }\right) $——$ \mathrm{\tau } $时刻的波形坐标；

$ {h}_{i}\left(t\right) $——与频域下一阶波浪力$ {F}_{j} $互为傅里叶变换。

时域分析下的二阶波浪力表达式为：

式中：$ \varsigma \left( t \right) $——波浪时历；

$ {\tau }_{1} $、$ {\tau }_{2} $——时间间隔；

$ g\left( {{\tau _1},{\tau _2}} \right) $——频域下二阶传递函数经傅里叶变换后的二次脉冲响应函数。

2.4 数值计算模型

2.4.1 平台-系泊耦合动力模型

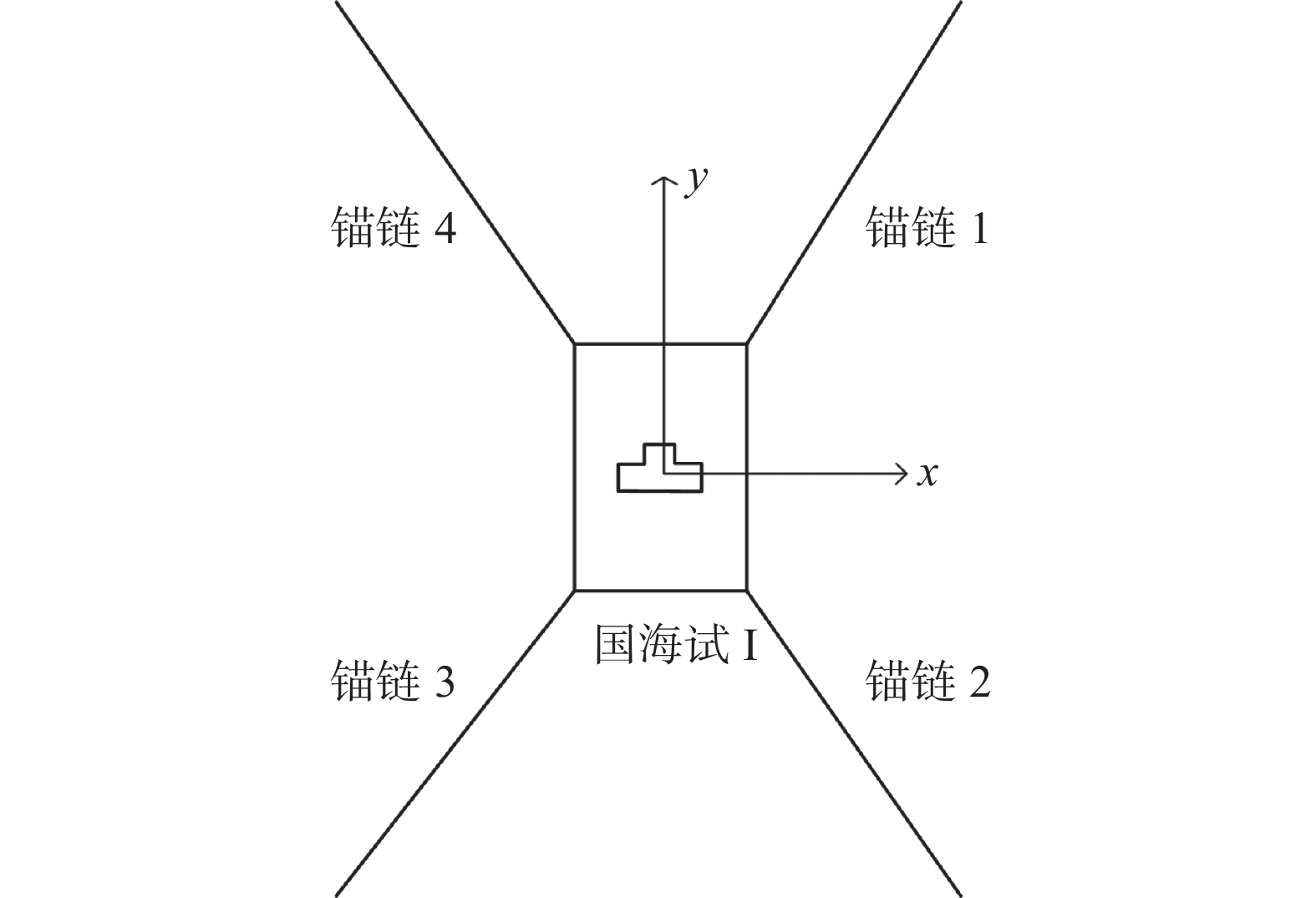
利用ANSYS AQWA构建平台的数值模型，简化后的“国海试Ⅰ”海上试验平台的有限元模型如图2所示，为双体船形式。平台的锚系布置如图3所示。平台的主要尺寸参数和静水力参数如表3所示。

2.4.2 设计工况组合

为了确定何种波浪组合会对平台运动产生最不利影响，首先考虑波浪作用下平台的运动响应。不规则波重现期取100年一遇，有效波高6.3 m，有效周期12.72 s。锚系形式为松弛式。应用ANSYS-AQWA进行平台不规则波数值模拟时的设计工况组合如表4所示。

确认使平台产生最不利影响的波浪条件后，引入100年一遇的风、流条件至少进行三组补充测试：1）风、浪、流共向；2）风、浪共向且与流不共向；3）风、浪、流均不共向。

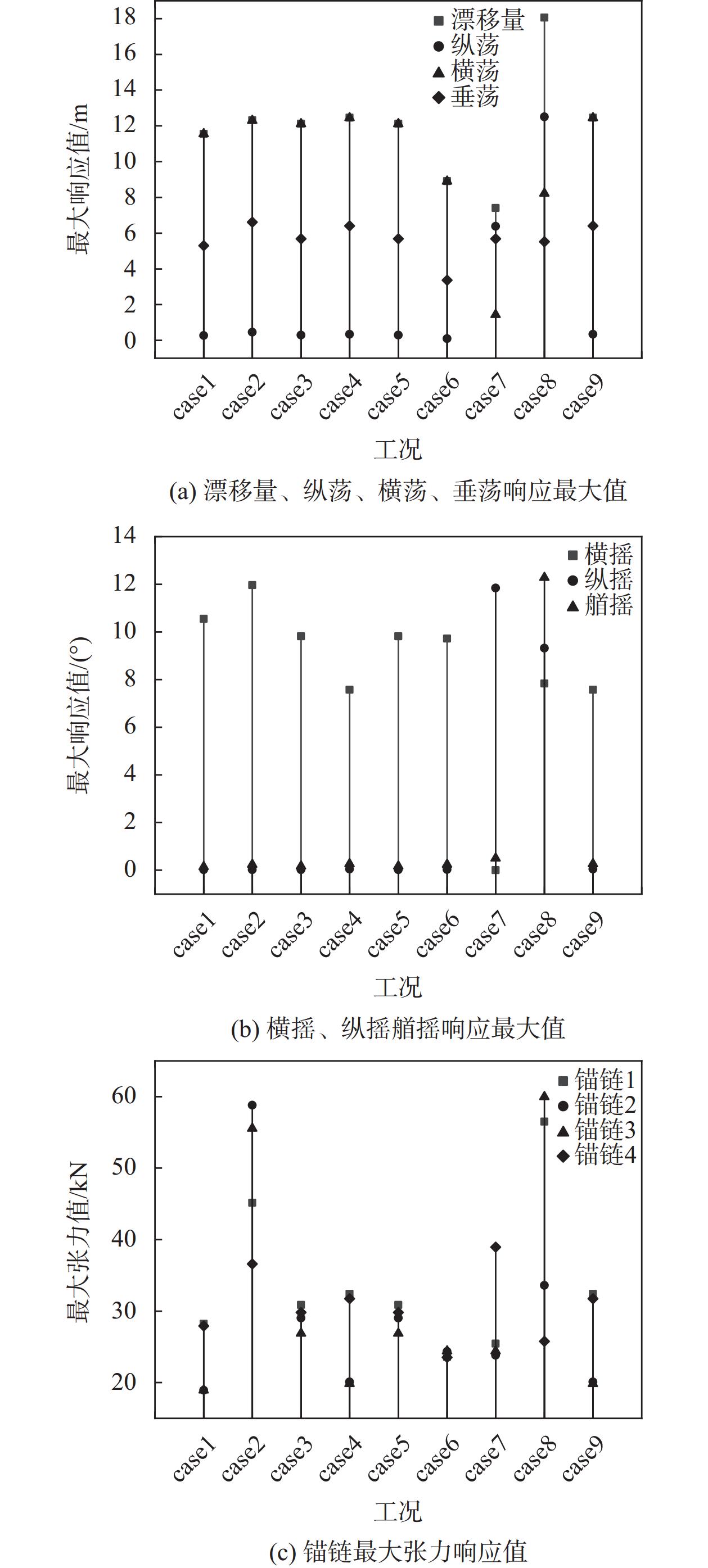
2.5 计算结果分析

2.5.1 不规则波分析

忽略风和流的影响，仅考虑不规则波作用下平台的运动响应，分别采取不同浪向、不同波浪谱、同一波浪谱不同谱峰因子的波浪条件组合，分析结果如图4所示。

针对这9组工况，通过改变谱峰因子来改变谱峰频率处的能量密度，对系泊系统影响更大，波浪能量对平台的漂移量和六自由度响应影响不大；采用Jonswap谱和P-M谱对平台的运动响应和系泊系统张力的影响不大，但采用Gaussian Swell谱后平台的运动响应和系泊系统张力有明显变化；采用不同的浪向角，平台最大漂移量有明显区别，在六自由度响应上，除垂荡方向的变化不明显外，其他自由度对波浪来向比较敏感，锚链张力随来浪方向不同而变化不同。

不规则波分析中，case8，即采用P-M谱且波浪方向为45°时，平台运动响应最明显。因此选择此工况作为基本的波浪要素组合。

2.5.2 风、浪、流同向

通过分析仅在波浪作用下平台和系泊系统的运动响应，确定了使其产生最不利影响的波浪条件：波浪方向取45°，波浪谱取P-M谱；接下来引入100年一遇的风和流条件，风向、流向分别与波浪方向相同，进行第一组补充测试。

该测试工况下，平台平均漂移量为16 m，最大漂移量达到了29 m；与平台的垂荡运动相比，其横荡与纵荡运动范围更大，横荡平均值为12 m，最大值为24 m。纵荡平均值为4 m，最大值为28 m；平台艏摇运动更显著，平均艏摇角为−0.4°，最大艏摇角为37°；与其他三根锚链相比，锚链3平均张力值更大，为85 kN，考虑到锚链破断载荷为583 kN，锚链2、锚链3和锚链4的最大瞬时张力均超过了锚链的破断载荷，其中锚链3的瞬时最大张力更是达到了2343 kN，说明在风、浪、流方向均为45°的情况下，锚链2、锚链3和锚链4有断裂的风险。平台漂移量、横荡、纵荡、艏摇响应值以及锚链3张力值如图5所示。

2.5.3 风、浪共向且与流不共向

在本组测试中，测试工况为风与波浪同向均为45°，流方向为90°。

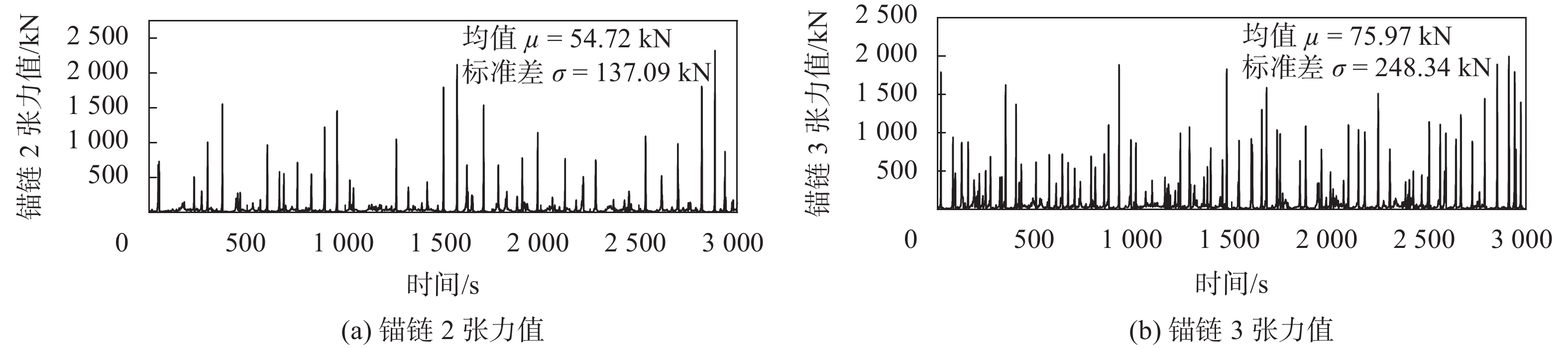
在该组测试工况下，平台的漂移量、横荡、纵荡和艏摇运动响应幅值与风、浪、流同向时大致相同；锚链2与锚链3承受的张力值要更大，锚链2承受的张力平均值为55 kN，最大值为2328 kN；锚链3承受的张力平均值为76 kN，最大值为2256 kN；四根锚链的最大瞬时张力均超过了锚链的破断载荷，锚链的断裂风险较风浪流同向时更大。锚链2和锚链3的张力值分析结果如图6所示。

2.5.4 风、浪、流均不共向

本组测试中取波浪方向45°、风向0°、流向90°。

该组测试工况下，平台平均漂移量为14 m，最大漂移量为27 m；纵荡运动最大值为27 m，平均值为14 m；横荡运动平均值为4 m，最大值为12 m；纵摇与横摇响应幅值大致相同，相比之下，艏摇响应更明显，艏摇平均值为-2°，艏摇最大值为2°；与其他三根锚链相比，锚链3张力值更大，平均值为26 kN，瞬时最大张力值为159 kN。四根锚链的瞬时最大张力值均未超过锚链的破断载荷。平台漂移量、横荡、纵荡、艏摇响应值以及锚链3张力值如图7所示。

2.5.5 小结

确定了使平台产生最不利影响的波浪条件后，继续添加风和流条件，平台漂移量、六自由度响应和系泊系统受力有了明显变化：

1）流向发生改变，平台的漂移量和六自由度响应基本没有变化，但系泊系统受力有明显改变：与风向、浪向、流向均为45°时相比，流向为90°时四根锚链的瞬时最大张力值均超过了锚链的破断载荷，此时的锚链断裂风险更大。

2）与风向为45°时相比，平台的漂移量和六自由度响应在0°风向时均有所降低。四根锚链的张力值也有明显降低，并且均未超过锚链的破断载荷。

对“国海试Ⅰ”海上试验平台应用本文提出的极端海况下新型浮式海上平台的生存性试验方法进行试验并且经过分析后发现：改变流向后，平台的系泊系统影响更大；改变风向后，平台的漂移量、六自由度运动响应和系泊系统受力均有改变。无论怎样改变风浪流参数，平台的水平面运动（纵荡、横荡、艏摇）都更明显，这与系泊系统所提供的回复力大小有关。在平台后期的维护中需要更加关注系泊系统受力和流向与风向这两个环境参数。

3 结束语

本文参考了IEC颁布的极端海况下波浪能转换装置的生存性测试标准，在其极端环境组合和可操作性等方面做出了改进，提出了针对新型浮式海上平台的生存性试验方法，并以布放于国家海洋综合试验场威海场区的“国海试Ⅰ”海上试验平台为例，采用威海海域实测数据，应用数值模拟的方法，对其在极端海况下的生存性能展开研究，研究过程验证了该方法的可行性。本文提出的极端海况下的生存性试验方法，可为新型浮式海上平台的设计、建造以及后期维护提供测试参考，也可为将来相关标准的制定提供理论依据。

本文提出的极端海况下新型浮式海上平台的生存性试验方法具体为：1）选取100年一遇的波浪条件作为基准波浪条件，并以基准波浪条件为中心值，分别选取两组波浪朝向不同、谱形不同、能量不同的对照海况条件，最终形成9组独立的环境条件，用于测试平台针对某一确定海况下的最大响应；2）引入100年一遇的风和流条件，对比分析风浪流同向、风与浪同向且与流不同向、风浪流均不共向三组测试工况对平台运动响应的影响。