文章信息
- 吴伟宁, 李春梅, 韦莹莹, 孙亚峰, 卢青针, 岳前进, 尹原超
- WU Weining, LI Chunmei, WEI Yingying, SUN Yafeng, LU Qingzhen, YUE Qianjin, YIN Yuanchao
- 动态缆上弯段曲率分布特征研究
- Study on the curvature distribution characteristics of bend sections on dynamic cables
- 中国测试, 2024, 50(8): 34-40
- CHINA MEASUREMENT & TEST, 2024, 50(8): 34-40
- http://dx.doi.org/10.11857/j.issn.1674-5124.2024050110
-
文章历史
- 收稿日期: 2024-05-27
- 收到修改稿日期: 2024-07-13
2. 江苏亨通高压海缆有限公司,江苏 苏州 215537
2. Hengtong Submarine Power Cable Co., Ltd., Suzhou 215537, China
动态缆作为海上浮式风电系统的关键装备,以一定线型悬挂于浮式平台下方,并连接海底设备,为海底设备提供电力、数据及信号[1]。动态缆在周期性海洋环境荷载作用下极易发生疲劳失效,因此需进行疲劳寿命分析。动态缆与浮式平台连接处的顶部位置同时受到较大的自重引起的拉伸荷载和恶劣工况、浮体运动引起的反复弯曲荷载,是疲劳失效的最危险部位[2],在疲劳寿命分析的过程中需要获得动态缆上弯段疲劳热点位置的准确响应。
对此,许多学者采用理论、数值的方法针对与动态缆具有相似结构特点的柔性立管、脐带缆的上弯段曲率分布以及疲劳热点位置分析展开研究。Kim等[3]提出了考虑剪切变形与变拉力影响下的柔性立管的动态响应改进分析方法,建立了更加精确的弯曲行为预测模型。Hoffman等[4]和Jose等[5]分别基于Miner线性累积损伤理论提出了柔性管缆的疲劳寿命分析流程。庞国良[6]采用数值方法建立了海洋管道的整体耦合分析模型,探究了管道线型、张力及曲率分布的影响。刘军鹏等[7]采用数值方法对海洋柔性管道和防弯器进行整体建模分析,加入接触非线性的假设。Caire等[8]对线弹性梁模型提出扩展,研究了柔性管道的弯曲行为及曲率响应对疲劳寿命的影响。Demanze等[9]根据有效应变强度因子理论,对防弯器与柔性立管的接触部位进行疲劳寿命分析。Dos Santos[10]采用解析方法,将防弯器滑动磨损率当作其摩擦函数,得到了新的防弯器失效依据,来预测其疲劳寿命。宋磊建等[11]基于悬链线和缓波形理论公式对不同线型的柔性海缆进行选型设计,得到了其张力和曲率的分布特性,并获取了曲率最大值点。许金锦[12]使用代理模型法,对柔性管缆设计方法进行完善,提出了抗疲劳线型的优化设计。
然而理论与数值方法均基于一定的假设,因此采用试验进行验证是十分必要的,部分学者在疲劳试验测量方法方面展开了相关研究。Connaire等[13-14]使用美国TMT公司的疲劳试验机,采用应变片粘贴法,获取脐带缆内部钢管的应变信息。Doynov和Belson等[15]将动态脐带缆与防弯器组合进行拉弯疲劳实验,并考虑温度带来的影响,采用温度传感器进行测量,得到了更为准确的应变结果。Saevik[16-17]利用SINTEF的拉弯组合疲劳试验机进行了大量海洋脐带缆结构的疲劳试验,开展了弯曲应力与结构疲劳寿命的研究。Tanaka等[18]将光学测试系统应用到柔性管缆的疲劳实验中,获取缆体表面的轴向位移。
目前原型测试所采用的方法有应变片粘贴法、光学测量法、压电片法。应变片法和光学测量法均为采点式测量,由于测试数据不连续,因此存在一定的局限性,而压电片法会导致柔性管缆与防弯器间接触形式和接触应力发生改变,导致结果不准确,因此需要提出新的测试方法来提高测量结果的准确性。光纤传感器体积小,许多学者将其用于柔性管缆的应变监测中。Andersen等[19]将光纤传感器嵌入柔性管缆内部抗拉铠装层中的环氧树脂槽中,证明了光纤光栅传感技术用于柔性管缆应变监测中的可行性。Weppenaar和Kristiansen[20]建立了一种集成在抗拉铠装线层的光纤光栅测试系统,该系统可以沿着管道的长度方向任意选点,并监测关键位置(如顶部连接处)的应变数据。Morikawa等[21]建立了在位有线光学监测系统,将管缆内部抗拉铠装层中的所有钢丝均安装光纤传感器,以达到实时监测的效果。Gasparetto[22]提取了安装顶柔性管缆部与接头连接处附近的光学监测系统的应变监测结果,用于计算柔性管缆接头的疲劳寿命。
综上所述,针对当前常规曲率测量方法难以直接获得动态缆缆体曲率分布情况的问题,本文建立了含空隙情况下的动态缆-防弯器系统疲劳荷载有限元数值模型,提出了基于分布式光纤测量技术的动态缆曲率测量方法,并设计了动态缆-防弯器系统原型拉弯试验,采用所提出的测量方法进行动态缆曲率分布测量,验证所提出测量方法的可行性。本文提出的基于分布式光纤测量技术的动态缆曲率测量方法可为浮式风电动态缆的原型试验提供参考。
1 有限元分析模型由于动态缆与防弯器中存在一定的几何空隙,导致测量位置不同引起的曲率测量结果的不同。为了对动态缆的曲率测量位置进行确定,本文通过ABAQUS软件建立了动态缆上弯段系统的数值模型,如图1所示。

|
| 图 1 动态缆上弯段系统有限元模型 |
为了模拟实际情况,建立了动态缆与防弯器两个实体装配的模型。考虑动态缆结构形式的复杂性,为了提高计算效率,将其等效为均质圆筒结构。动态缆结构的弯曲刚度与拉伸刚度难以统一于同一等效模型中,而动态缆弯曲刚度对曲率分析结果具有较大影响,因此在对模型属性的确定中忽略了动态缆的拉伸刚度。通过在动态缆与防弯器接触表面设置不可穿透接触的方法模拟动态缆与防弯器间的几何空隙与接触,并忽略表面间摩擦的影响。防弯器的几何参数如图2与表1所示。

|
| 图 2 动态缆与防弯器间的几何空隙 |
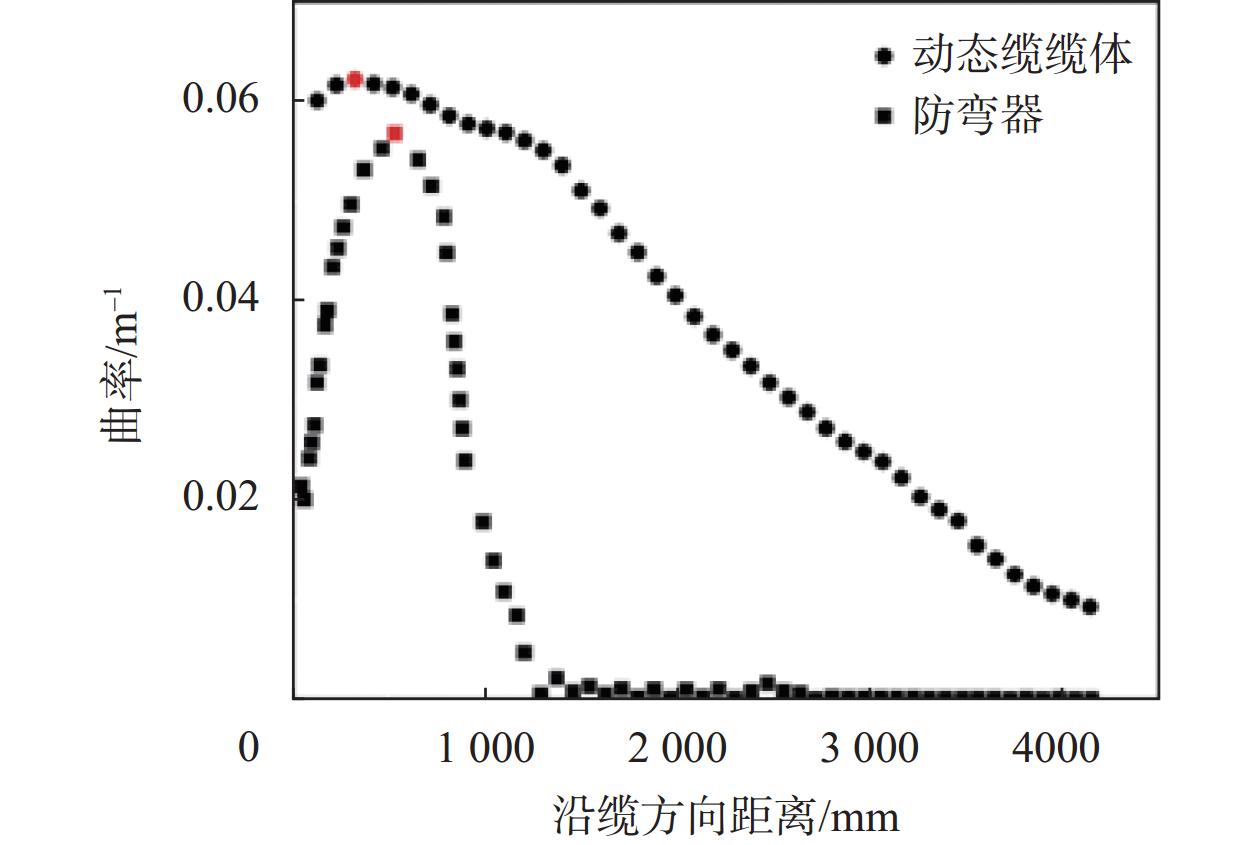
通过所建立有限元模型可计算动态缆上弯段系统中各部件的变形与曲率分布情况,如图3所示。以防弯器端部作为坐标原点,沿动态缆轴向分别提取动态缆缆体与防弯器结构的曲率值如图4所示。根据有限元分析结果可发现,由于几何空隙的影响,动态缆缆体与防弯器结构的曲率分布情况明显不同,动态缆缆体的曲率大于防弯器曲率。动态缆缆体上最大曲率为0.0631 m–1,出现于沿缆轴向330 mm处,防弯器最大曲率为0.0568 m–1,出现于沿缆轴向537 mm处。动态缆缆体处的最大曲率较防弯器最大曲率值大9.9%。

|
| 图 3 动态缆上弯段曲率分布图 |
|
| 图 4 动态缆缆体与防弯器结构曲率分布图 |
2 分布式光纤曲率测量整体方案设计 2.1 光纤传感器布置方案
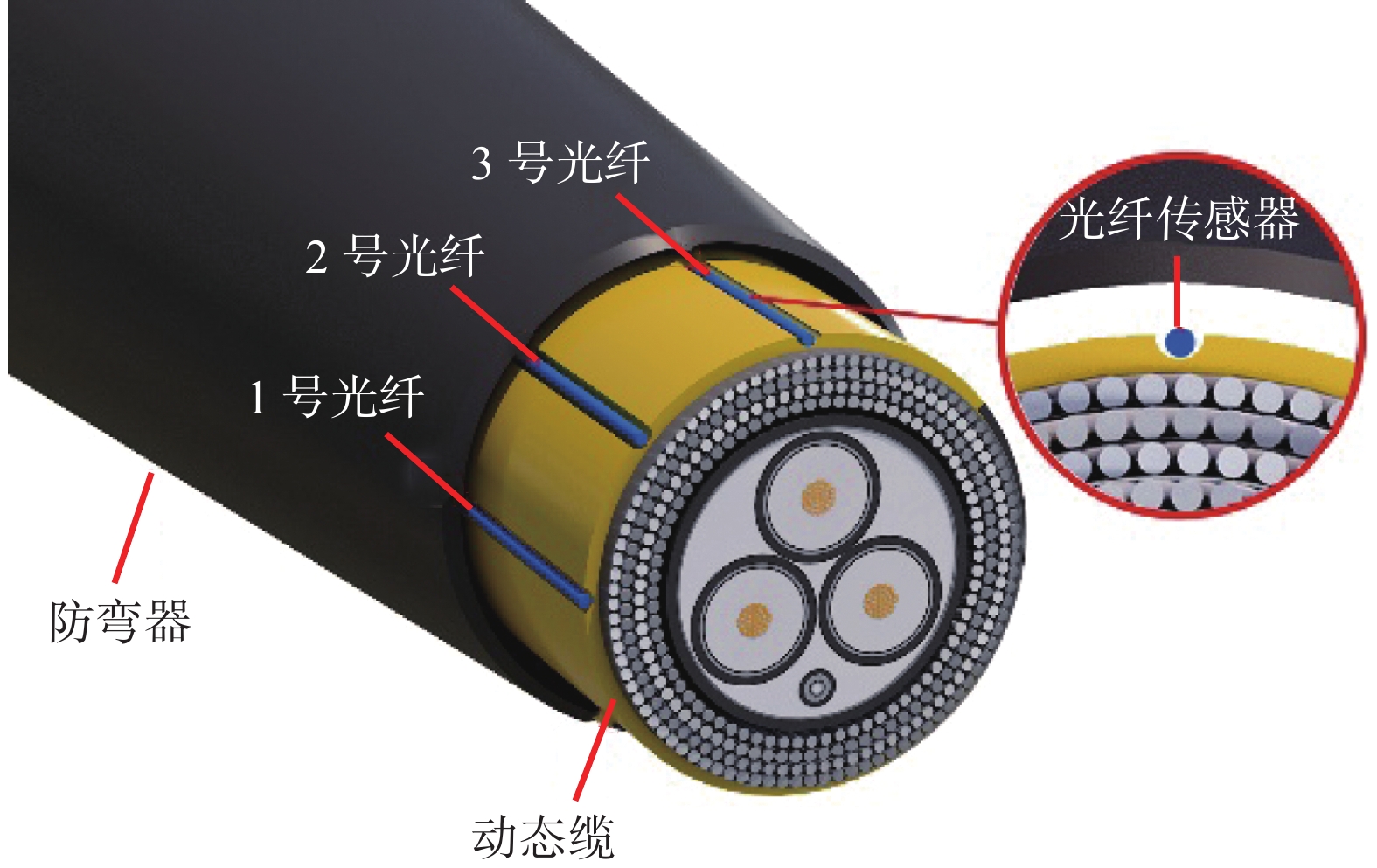
为了保证动态缆曲率测量的准确性,在防弯器内部处动态缆外表面布置三根沿轴向分布的光纤传感器进行测量,如图5所示。其中1号光纤传感器位于弯曲中性轴上,2号光纤传感器与中性轴夹角45º,3号光纤传感器与中性轴夹角90º。三根光纤传感器分别由防弯器的两个端部伸出,在光纤传感器的一端使用光纤匹配膏来隔截空气反射,另一端连接光纤测量与采集设备。
|
| 图 5 光纤传感器截面布置 |
经过多次光纤传感器布置方案的比较,通过在动态缆表面进行开槽并埋入测量光纤的方法能够最大程度保障测试光纤的存活率。首先退去防弯器,在动态缆测试位置进行标记,根据标记沿缆轴向切割一个2~3 mm的U形槽并进行清理,保证测试光纤能够完全埋入开槽中,如图6所示。其次将测试光纤置于U形槽中,保证光纤两侧具有足够的长度用于与测量设备连接。选取位于U形槽端部附近的某一位置,利用胶水将光纤粘贴于缆体上,待光纤传感器与缆体在连接点处完全粘合后,在光纤另一端施加较小的拉力,沿光纤方向点涂胶水保证光纤与缆体的完全粘合。最后在U形槽内注入环氧树脂胶对光纤进行保护,保证测试光纤不会与防弯器内壁发生接触,待环氧树脂胶完全凝固后安装防弯器,将两端光纤分别由开孔处伸出并连接测量装置,如图6所示。

|
| 图 6 动态缆表面光纤布置情况 |
2.2 基于应变的平面曲率算法
在进行动态缆的曲率计算时,需要消除拉伸应变的影响。布置于缆体上的光纤传感器所测应变包含了拉伸产生的应变与弯曲产生的应变:
| $ \varepsilon=\varepsilon_{\mathrm{tension}}+\varepsilon\mathrm{_{bending}} $ | (1) |
式中:ε——光纤传感器测得的总应变;
εtension与εbending——总应变中拉伸与弯曲所贡献的应变值。
动态缆护套表面光纤传感器的曲率可表示为:
| $ \kappa=\frac{\varepsilon\mathrm{_{bending}}}{y}=\frac{2\left(\varepsilon-\varepsilon_{\mathrm{tension}}\right)}{d\sin\theta} $ | (2) |
式中:y——所布置的光纤传感器与弯曲中性轴的距离;
θ——所布置的光纤传感器与弯曲中性轴的夹角;
d——光纤传感器距离动态缆中心距离的2倍,由于光纤传感器布置于外护套边缘,可近似地认为d为动态缆的外径。
按照图5中的方式布置光纤传感器,1号光纤传感器位于动态缆的中性轴上,由弯曲引起的应变值为0,测得的应变均为拉伸引起的应变,可认为:
| $ \varepsilon\mathrm{_{tension}}=\varepsilon_1 $ | (3) |
2号、3号光纤传感器所测应变为拉伸与弯曲荷载共同导致的应变。根据三根传感器的布置位置可计算得到被测动态缆在拉弯组合试验中的曲率为:
| $ \kappa = \frac{{{\varepsilon _3} - {\varepsilon _1}}}{d} + \sqrt 2 \frac{{{\varepsilon _2} - {\varepsilon _1}}}{d} $ | (4) |
其中ε1,ε2,ε3分别为1-3号光纤传感器测量所得到的应变值。
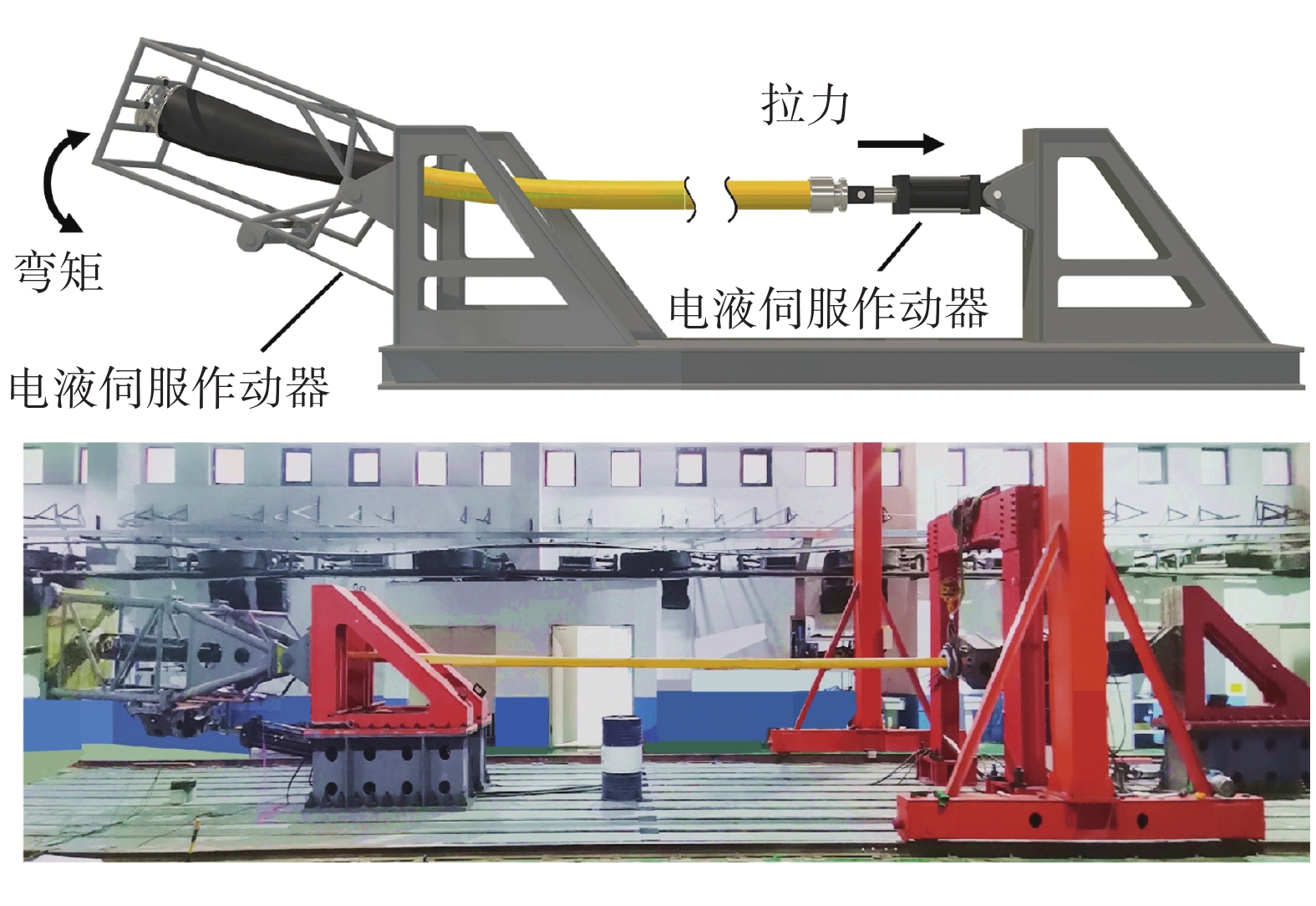
3 试验结果及分析本节通过原型动态缆拉弯组合试验,验证所提出的动态缆曲率测量方法的可行性,并对动态缆在防弯器处的曲率分布情况进行分析研究,试验布置如图7所示。
|
| 图 7 动态缆上弯段拉弯组合试验 |
在进行动态缆拉弯组合试验过程中,由于光纤传感器的粘贴与布置存在一定的缺陷,需要先进行一次预拉伸试验,验证光纤粘贴的紧密程度,同时测量在给定张力下的缆体应变情况。首先令试验设备的摆头摆动至水平,使被测动态缆保持平直,随后通过位移控制以5 mm/min的加载速率缓慢为测试动态缆加载,直至最终拉力达到60 kN。在试验加载过程中采集并记录试验中的力值与光纤测得的应变值。为保证试验结果的准确,需重复进行三次相同参数的测试,对试验结果取平均值进行分析。
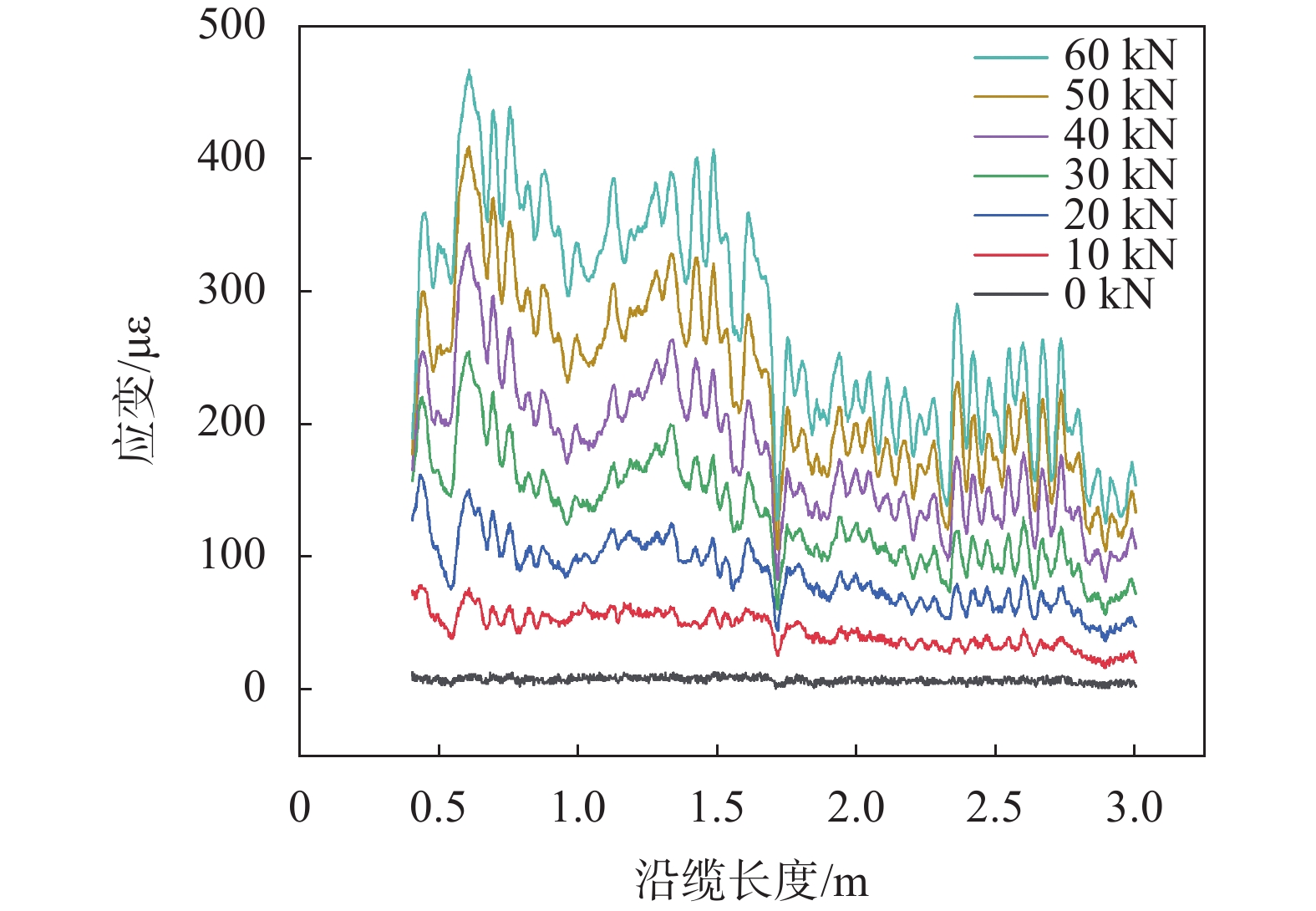
作不同拉力情况下3号光纤传感器沿坐标轴x方向的应变曲线,如图8所示。通过曲线可发现,随着拉力值的增加,传感器在各点所测应变值成比例增大,这符合护套层在拉伸荷载下的变形规律。观察在固定拉力值下测得的应变趋势,虽然应变值存在一定的波动,但整缆应变情况基本维持稳定。在沿缆长度1.7 m测点处应变值发生急速下降,但其他测点处应变变化趋势相同,可认为在该测点处光纤未与缆体粘接或粘接力较小,导致该点测得应变值偏小。
|
| 图 8 不同拉力下的拉伸应变 |
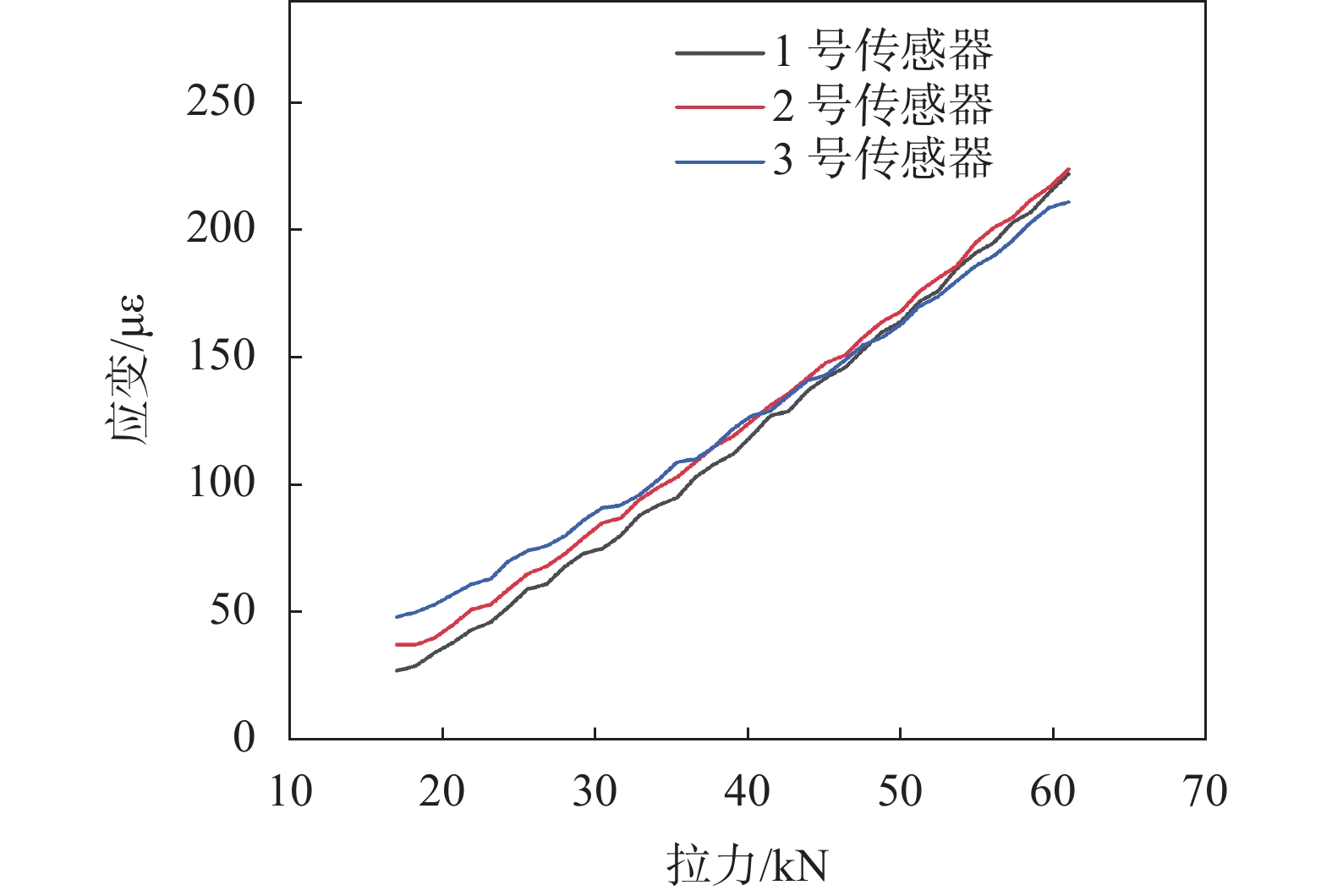
为验证三根传感器测量数据的一致性,绘制拉伸试验中相同截面处三根传感器测得的应变-拉力曲线如图9所示。根据图像可发现,所测应变随拉力增大线性增大,符合拉伸荷载下的应变变化规律。不同传感器测量的应变值间存在一定的差别,当拉力值为18 kN时,三根传感器的应变测试差值最大可达14 με,相对误差为12%。但随着拉力值的逐渐增大,各传感器间的测量误差逐渐减小,在拉力值达到40 kN后,不同传感器间的测量误差小于5%。在拉弯组合试验中,当恒拉力大于40 kN时,可忽略不同传感器间的测量误差。
|
| 图 9 相同截面处不同传感器的测量结果 |
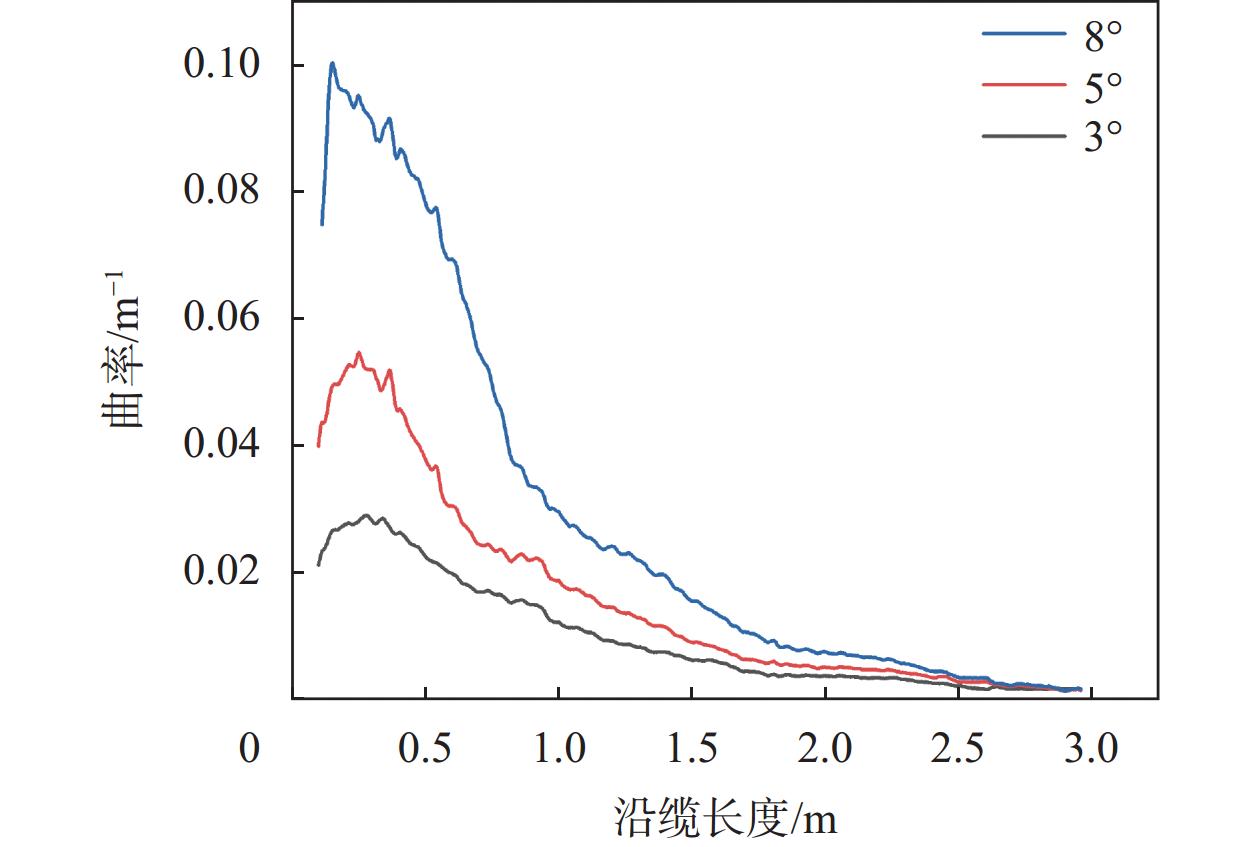
在进行过预拉伸试验后开展动态缆的静态拉弯组合试验,获得动态缆在防弯器处的曲率分布情况,验证提出的测量方法的可行性,同时确定不同加载参数对动态缆曲率分布的影响规律。根据预拉伸试验中提出的建议,给定动态缆拉伸荷载为100 kN,摆动角度分别为3°、5°、8°。绘制相同拉力值不同摆动角度情况下的动态缆曲率分布曲线、最大曲率及其发生位置与摆动角度关系图分别如图10、11所示。
|
| 图 10 不同摆动角度下的曲率分布 |
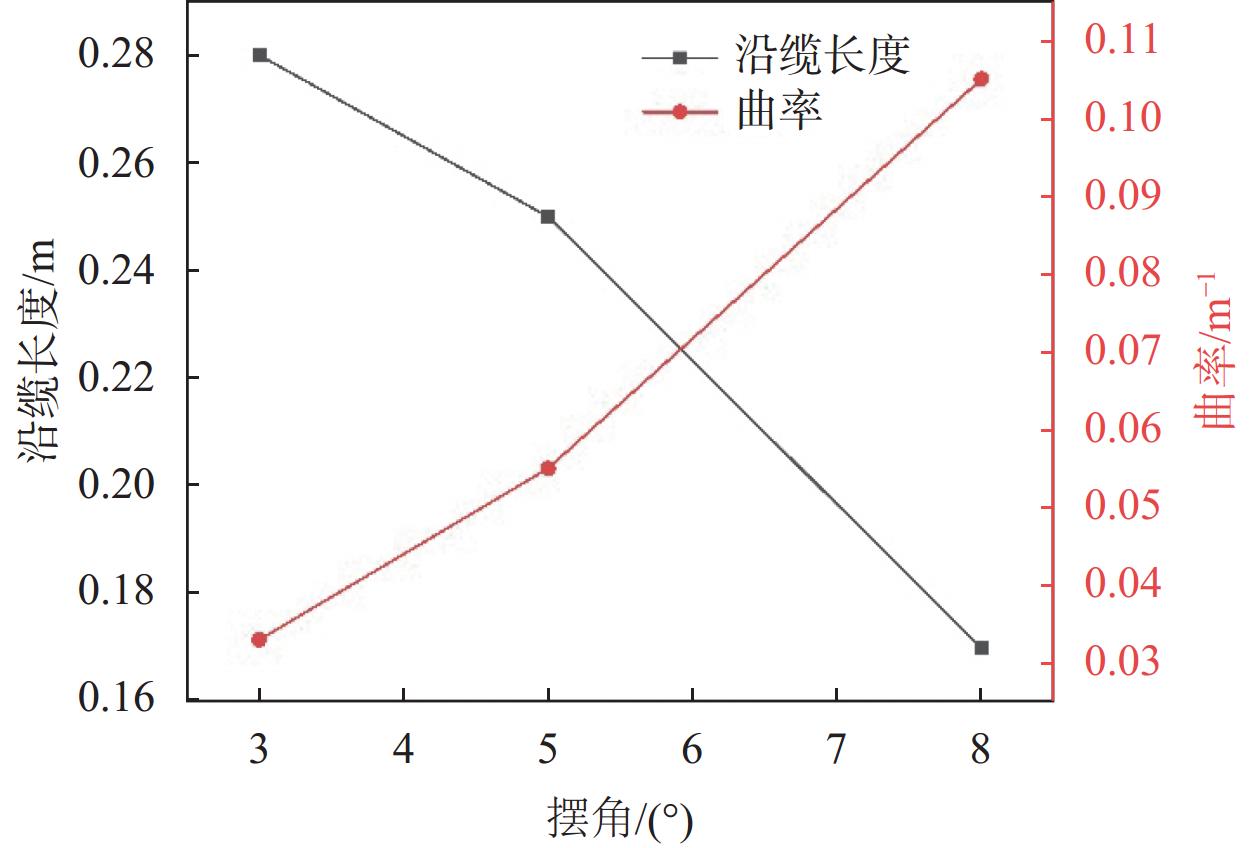
|
| 图 11 最大曲率及其位置与摆动角度关系 |
根据图像分析可发现,动态缆在坐标原点的初始位置处已经存在一定的初始曲率,曲率分布沿缆长方向首先呈上升趋势。在沿缆方向0.16 m至0.27 m处曲率达到最大值,随后曲率沿缆方向逐渐减小直至趋近于0。对比曲率减小阶段的曲率变化速率可发现,在曲率最大值与0.45 m区间段曲率变化速率相对较小,在0.45 m后曲率变化速率迅速增加。对比表1中防弯器形状参数可发现,在0.42 m前防弯器外径不变化,在0.42 m后防弯器外径逐渐减小,曲率变化率随之升高,测试所得的曲率变化与图4中的分析的曲率分布趋势一致。这些结果证明了OFDR分布式光纤曲率测量方法的可行性。
对不同摆动角度下的曲率分布情况进行分析。通过图像分析可发现,动态缆在坐标原点处的初始曲率随摆动角度的增大而增大。通过图11可发现,最大曲率随着摆动角度的增加而线性增大,最大曲率的发生位置随着摆动角度增大逐渐向防弯器直径较大的一端移动。试验结果表明最大曲率发生位置是根据摆动角度的不同而变化的。为了进行更准确的动态缆疲劳分析,需要对其拉弯组合荷载情况下的曲率分布进行更加精确的测量与监测。
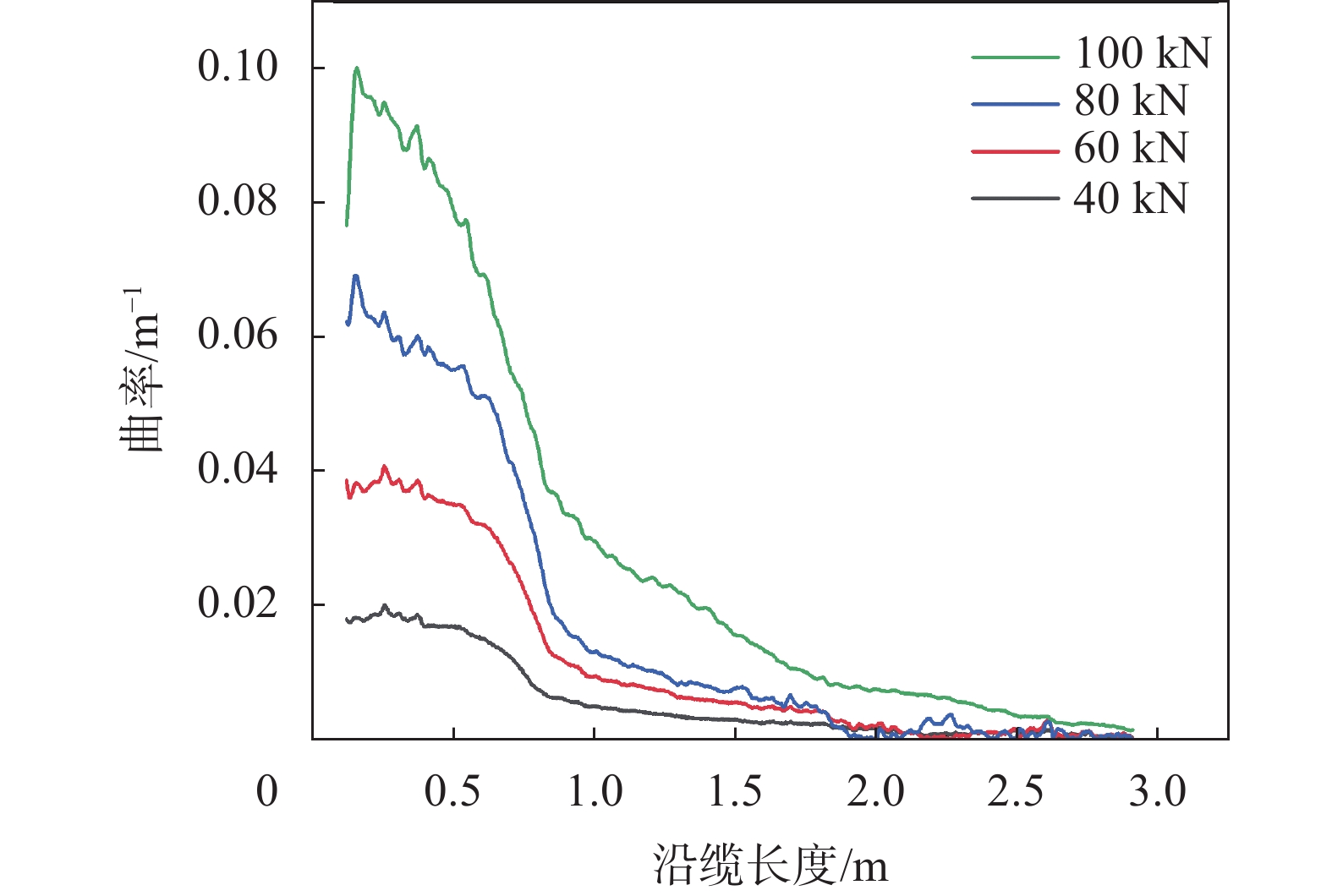
动态缆在拉弯组合情况下所受的拉力值同样会影响缆体曲率的分布情况。为了对这一参数进行试验研究与验证,在试验中设定恒定的摆动角度为8°,改变施加在动态缆上的拉力值分别为40、60、80、100 kN,对曲率分布规律进行分析。试验测得的不同拉力下动态缆曲率分布情况如图12所示。通过观察可发现,在相同摆动角度下,随着动态缆轴向拉力的增大,其曲率呈增大趋势。汇总不同拉力情况下的动态最大曲率及其发生位置如图13所示。试验结果表明最大曲率随拉力的增加呈线性增大,同时最大曲率的发生位置也向防弯器直径较大端移动。当最大曲率位置达到沿缆长0.16 m后,其位置不再随拉力增加而继续变化。上述分析表明拉力值的波动会对动态缆的极值曲率产生影响,进而影响疲劳寿命,因此有必要在进行疲劳分析时考虑拉力变化的影响。
|
| 图 12 不同拉力下的曲率分布 |

|
| 图 13 最大曲率及其位置与拉力关系 |
4 结束语
本文针对动态缆上弯段的曲率分布特征与测量方法进行研究,通过对动态缆上弯段疲劳热点位置附近处非线性因素导致的复杂曲率分布分析,得到如下结论:
1)在仅考虑动态缆与防弯器几何空隙影响的情况下,动态缆缆体处最大曲率较防弯器处最大曲率偏大9.9%;
2)本文提出的基于OFDR分布式光纤技术的动态缆曲率测量方法可对动态缆缆体曲率分布进行直接测量,实现了2.6 mm测点间隔的高空间分辨率连续应变与曲率测量,测量结果与有限元分析趋势一致;
3)利用静态拉弯组合试验验证了所提测量方法的可行性,结果表明通过增大拉力值与摆动角度将增大动态缆最大曲率并使最大曲率发生位置前移。
本文提出的曲率分布测量方法可为动态缆整体疲劳响应与局部应力分析的荷载输入提供支持。
| [1] |
蒲定, 杨婉秋, 丰如男, 等. 浅水浮式风机动态电缆线型设计[J].
海洋工程装备与技术, 2020, 7(6): 412-418.
PU D, YANG W Q, FENG R N, et al. Configuration design of a dynamic cable in floating wind turbine[J].
Ocean Engineering Equipment and Technology, 2020, 7(6): 412-418.
|
| [2] |
阎军, 胡海涛, 苏琦, 等. 海洋电缆中关键力学问题的研究进展与展望[J].
力学学报, 2022, 54(4): 846-861.
YAN J, HU H T, SU Q, et al. Prospect and progression of key mechanical problems in marine cables[J].
Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(4): 846-861.
DOI:10.6052/0459-1879-22-113 |
| [3] |
KIM J D, JANG B S, YUN R H. Application of analytical model in the prediction of dynamic responses and fatigue damage of flexible risers: part I - Improvement of analytical model considering shear deformation and varying tension effects[J].
Marine Structures, 2021, 79: 103044.
DOI:10.1016/j.marstruc.2021.103044 |
| [4] |
HOFFMAN J, DUPONT W, REYNOLDS B. A fatigue-life prediction model for metallic tube umbilicals[C]//All Days. OTC, 2001. https://doi.org/10.4043/13203-ms.
|
| [5] |
JOSE J, CHOI S J, GUDMESTAD O T. Sensitivity study on a 3D numerical model for estimating breaking wave forces on a jacket structure[C]//The 27th International Ocean and Polar Engineering Conference. OnePetro, 2017.
|
| [6] |
庞国良. 海洋非粘结柔性管截面力学特性及典型失效分析研究[D]. 广州: 华南理工大学, 2020.
PANG G L. Research on cross sectional mechanical characteristics and typical failures analyses of marine unbonded flexible pipe[D]. Guangzhou: South China University of Technology, 2020.
|
| [7] |
刘军鹏, 齐华林, 罗晓兰, 等. 基于有限元方法的柔性立管防弯器疲劳寿命分析[J].
海洋工程, 2021, 39(3): 141-147.
LIU J P, QI H L, LUO X L, et al. Fatigue life of flexible riser bend stiffener based on finite element method[J].
The Ocean Engineering, 2021, 39(3): 141-147.
|
| [8] |
CAIRE M , VAZ M A . Theeffect of flexible pipe non-linear bending stiffness behavior on bend stiffener analysis[C]// Asme International Conference on Offshore Mechanics & Arctic Engineering, 2007.
|
| [9] |
DEMANZE F, HANONGE D, CHALUMEAU A, et al. Fatigue life analysis of polyurethane bending stiffeners[C]//Proceedings of the 24th International Conference on Offshore Mechanics and Arctic Engineering. ASME, 2005: 261-267.
|
| [10] |
DOS SANTOS L V, GON ALVES E. Proposed new failure criterion for bending stiffeners[C]// Proceedings of the Twenty-fifth International Ocean and Polar Engineering Conference. International Society of Offshore and Polar Engineers, 2015: 328-335. https://kns.cnki.net/KCMS/detail/detail.aspx?filename=HYGC202103015&dbname=CJFD&dbcode=CJFQ.
|
| [11] |
宋磊建, 付世晓, 陈希恰, 等. 深海脐带缆总体响应特性比较研究[J].
振动与冲击, 2014, 33(1): 119-124.
SONG L J, FU S X, CHEN X Q, et al. Comparative study on deepwater umbilical overall response characteristics[J].
Journal of Vibration and Shock, 2014, 33(1): 119-124.
DOI:10.3969/j.issn.1000-3835.2014.01.020 |
| [12] |
许金锦. 水下生产系统动态脐带缆抗疲劳优化设计及疲劳可靠性分析[D]. 大连: 大连理工大学, 2020.
XU J J. The fatigue optimization design and reliability analysis of umbilical in subsea production system[D]. Dalian: Dalian University of Technology, 2020.
|
| [13] |
CONNAIRE A, DOYNOV K, NESTOR R, et al. Validated methodology for calculating fatigue capacity of deepwater umbilicals[C]//International Conference on Offshore Mechanics and Arctic Engineering. Madrid, Spain. 2018, 51241.
|
| [14] |
DOBSON A, FOGG D. Fatigue testing and analysis of a deep water steel tube umbilical[C]//International Conference on Offshore Mechanics and Arctic Engineering. Estoril, Portugal. 2008, 48203: 133-140.
|
| [15] |
DOYNOV K, BELSON E, YUAN H, et al. Root cause analysis of bend stiffener failure during umbilical full-scale fatigue testing[C]//International Conference on Offshore Mechanics and Arctic Engineering. Busan, South Korea. 2016, 49965.
|
| [16] |
SAEVIK S. Comparison between theoretical and experimental flexible pipe bending stresses[C]//International Conference on Offshore Mechanics and Arctic Engineering. Shanghai, 2010, 49132: 395-402.
|
| [17] |
SAEVIK S, BERGE S. Fatigue testing and theoretical studies of two 4 in flexible pipes[J].
Engineering Structures, 1995, 17(4): 276-292.
DOI:10.1016/0141-0296(95)00026-4 |
| [18] |
TANAKA R L, GONALVES R T, FERREIRA T B, et al. Minimum bending radius (MBR) tests of flexible pipes: an experimental approach via optical motion capture and image processing[C]//Offshore Technology Conference Brazil. Rio de Janeiro, Brazil, 2011.
|
| [19] |
ANDERSEN M, BERG A, SAEVIK S. Development of an optical monitoring system for flexible risers[C]//Offshore Technology Conference, Houston, Texas, 2001 OTC13201-MS.
|
| [20] |
WEPPENAAR N, KRISTIANSEN M. Present and future possibilities in optical condition monitoring of flexible pipes[C]//Offshore Technology Conference, Houston, Texas, 2008 OTC-19427-MS.
|
| [21] |
MORIKAWA S R K, CAMERINI C S, BRAGA A M, et al. Real time continuous structural integrity monitoring of flexible risers with optical fiber sensors[C]//Offshore Technology Conference, Houston, Texas, 2010 OTC-20863-MS.
|
| [22] |
GASPARETTO V. Method of evaluating the fatigue life of flexible risers by monitoring the tensile armor wires strain[D]. Rio de Janeiro: Federal University of Rio de Janeiro,2017.
|
 2024, Vol. 50
2024, Vol. 50