文章信息
- 梁瑞庆, 邓燕飞, 冯玮
- LIANG Ruiqing, DENG Yanfei, FENG Wei
- 基于LSTM模型的浮式风机系泊监测数据解算方法
- Calculation method for mooring monitoring data of floating wind turbines using LSTM model
- 中国测试, 2024, 50(8): 28-33
- CHINA MEASUREMENT & TEST, 2024, 50(8): 28-33
- http://dx.doi.org/10.11857/j.issn.1674-5124.2024050008
-
文章历史
- 收稿日期: 2024-05-07
- 收到修改稿日期: 2024-05-27
2. 哈尔滨工业大学(深圳),广东 深圳 518000;
3. 电子科技大学(深圳)高等研究院,广东 深圳 518000
2. Harbin Institute of Technology (Shenzhen), Shenzhen 518000, China;
3. Shenzhen Institute for Advanced Study, UESTC, Shenzhen 518000, China
浮式风机作为深远海风电开发的关键装备,其系泊系统可靠性受到了广泛关注。针对系泊系统姿态进行监测,能够判断锚链状态是否正常,也可用于系泊张力的计算[1]。国内外普遍开发专用的倾角传感器对锚链姿态进行监测[2-3]。
基于系泊倾角监测数据准确计算系泊张力响应,是系泊安全监测的关键问题之一。传统系泊张力预测主要基于悬链线方程,该方法在准静态条件下具有一定的适用性,但在面对复杂海洋环境激励时,其预测精度往往受限[4]。近年来,基于数据驱动的机器学习方法在各个领域的应用逐渐增多[5-7],尤其是长短时记忆(LSTM)网络因其在处理时间序列数据方面的优势而被广泛研究[8-10]。LSTM网络能够捕捉长期依赖关系,对于非线性和动态系统建模具有独特优势,这为浮式风机系泊张力的准确预测提供了新的思路。比如,靳丛林[11]采用基于注意力机制的LSTM网络实现了通过浮体运动响应对水下软钢臂系泊受力的估算。杨洁[12]基于神经网络模型对船体运动响应和系泊动态张力之间的关系进行了研究,并且对短期系泊张力进行实时预测。QIAO等[13]基于LSTM模型建立了实时监测作业状态下船舶系缆响应的计算模型。SAAD等[14]对比分析了MLP模型与LSTM模型在运动响应预测上的优劣,并基于预测运动与测量运动的差异识别系泊故障问题。
现有研究局限于采用悬链线方程获得系泊倾角与张力之间的关系,而神经网络模型在系泊张力预测上的研究大多以船舶运动数据作为输入。为此,本文提出了一种基于LSTM网络与全连接网络(FCN)相结合的系泊张力计算分析模型,旨在基于系泊倾角监测信息准确计算浮式风机系泊张力响应,并阐明神经网络模型相比传统悬链线方法的优势及其原因。研究表明,所提出的神经网络模型能够有效考虑系泊运动的动态过程,相比传统悬链线方程,在系泊张力时程曲线、均值、标准差及最大值等方面均显示出更好的预测效果。
1 人工神经网络模型 1.1 FCN网络FCN网络是一种前馈神经网络,其中相邻层的节点通过权重和偏置相互连接。激活函数通常被引入以在设计网络中引入非线性。节点之间的连接可以简单表示为:
| $ Y = f(W \cdot X + b) $ | (1) |
式中:X和Y——前一层和后一层节点的值;
W和b——权重和偏置;
f——激活函数。
一些流行的激活函数包括sigmoid函数、双曲正切函数(Tanh)和修正线性单元(ReLU)。对于回归问题,通常在最后一层不使用激活函数。
1.2 LSTM网络LSTM网络是一种改进的循环神经网络(RNN),能够避免梯度消失问题。因此,LSTM可以处理长时间延迟和具有低频和高频分量混合的信号。所有RNN,包括LSTM网络,都具有重复神经网络单元链的形式。与只有一个Tanh层不同,LSTM网络中的重复单元更为复杂。LSTM网络引入了三种类型的门:遗忘门ft、输入门it和输出ot,以确定从当前单元状态C中丢弃、添加或导出多少信息。内部交互可以表示为:
| $ \left\{ \begin{aligned} {f_t} =& \sigma ({W_f} \cdot [{h_{t - 1}},{x_t}] + {b_f}) \\ {i_t} =& \sigma ({W_i} \cdot [{h_{t - 1}},{x_t}] + {b_i}) \\ {c_t} =& \tanh ({W_c} \cdot [{h_{t - 1}},{x_t}] + {b_c}) \\ {C_t} =& {f_t} \times {C_{t - 1}} + {i_t} \times {c_t} \\ {o_t} =& \sigma ({W_o} \cdot [{h_{t - 1}},{x_t}] + {b_o}) \end{aligned}\right.$ | (2) |
式中:σ——sigmoid函数;
ht——在时间步t的隐藏状态;
Ct——在时间步t的单元状态。
1.3 FCN与LSTM组合网络本文构建了一个基于LSTM网络和FCN网络的混合神经网络模型,在模型设计上考虑了时序数据的特点,并充分利用时序数据之间的记忆效应。预测模型是在Keras框架内实现的,并采用了TensorFlow作为后端引擎。
如图1所示,神经网络的输入是一个指定时间步m的系泊缆某位置处的倾角,即
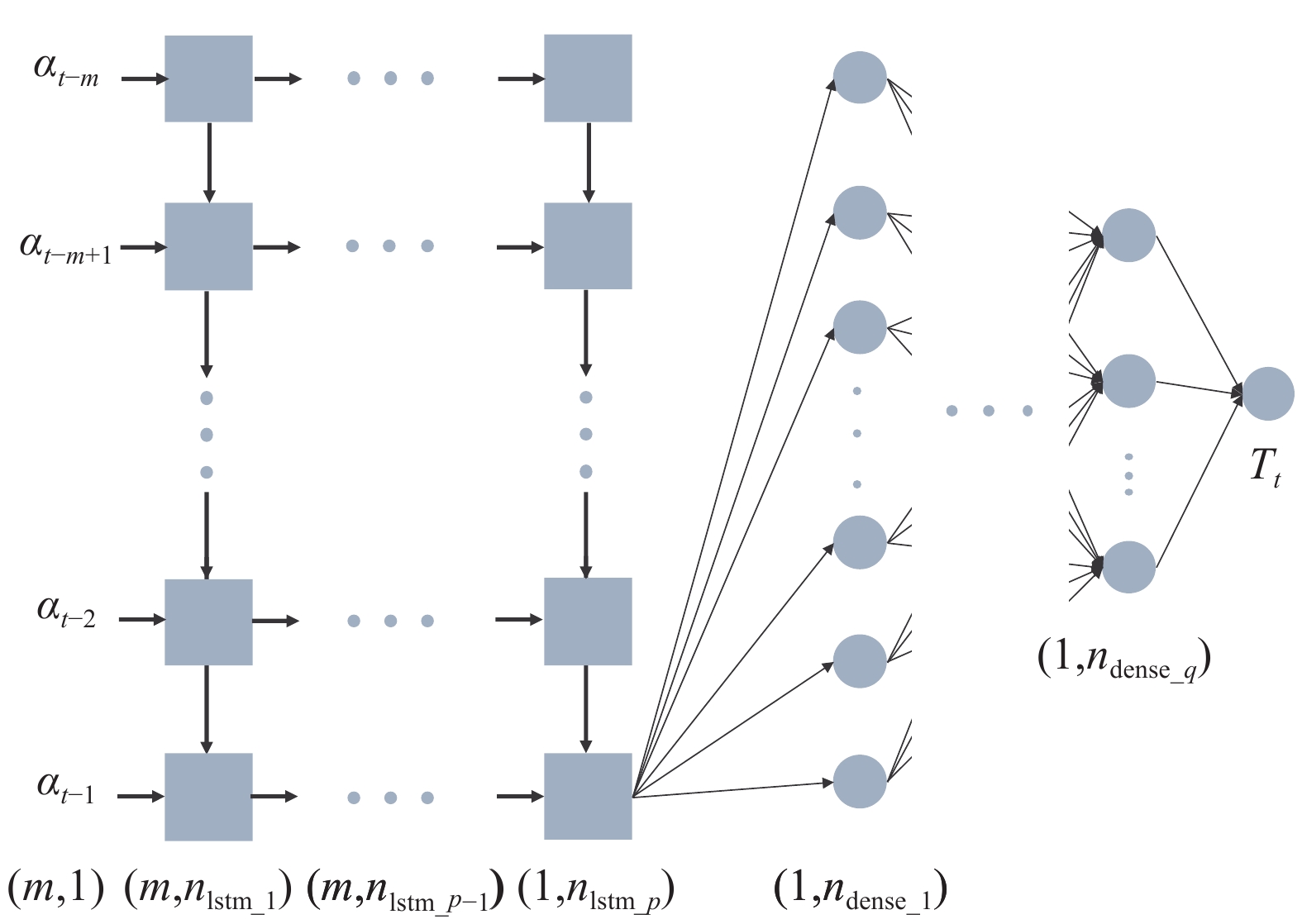
|
| 图 1 FCN与LSTM组合网络结构 |
1.4 神经网络超参数选取
LSTM层的输出反映不同时间点上历史系泊倾角对当前输出的贡献。为了避免过拟合和收敛问题,LSTM层的数量p 不超过三层。当验证损失值接近时,选取了具有较少训练参数(权重+偏置)的模型,即:采用了1层LSTM层和1层Dense层构建神经网络,LSTM层及Dense层的节点数均为128节点。
2 数据集构建与模型训练在系泊系统状态监测中,需要通过系泊缆上某一位置的倾角测量信息解算获得系泊缆导缆孔端最大张力信息。为了获得系泊倾角与系泊张力之间的输入-输出模型,本文针对部署在广东徐闻海域的“扶摇号”浮式风机建立了风-浪-流联合耦合时域仿真模型,获得了不同工况下浮式风机系泊运动及张力数据,并作为浮式风机系泊监测数据解算神经网络模型的数据集。
2.1 “扶摇号”数值模型“扶摇号”浮式风机是一座半潜式结构的浮体基础,装配了中船海装6.2 MW风机机组,额定风速11.8 m/s。“扶摇号” 平台主要参数如表1所示。
如图2所示,“扶摇号”采用了3×3的悬链线系泊系统,锚固结构为固定桩锚。同组的3根锚链近乎平行分布,并固定在同一个桩锚上。每根锚链分为3段,由不同等级不同直径的锚链构成。单根锚链长度约为470 m。
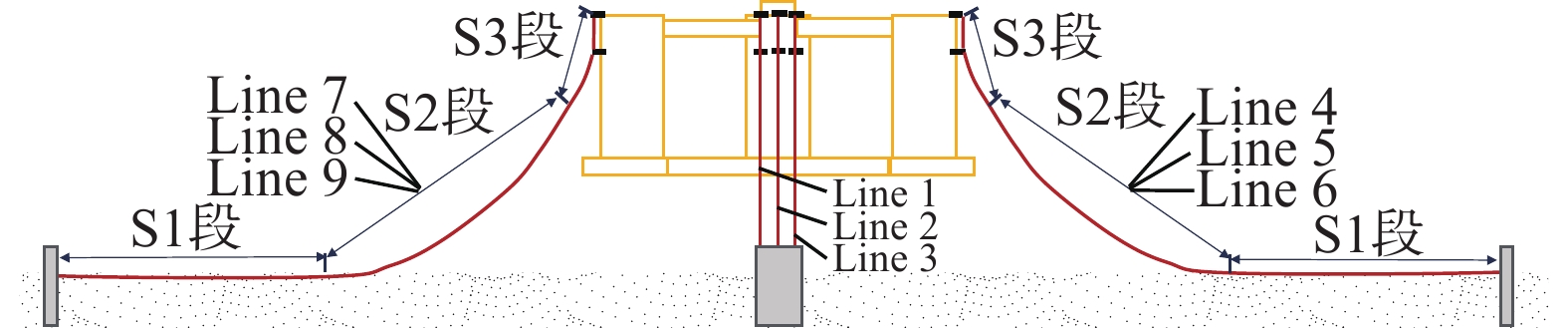
|
| 图 2 扶摇号系泊布置方案 |
数值仿真采用Orcaflex软件开展,模拟了风轮、塔筒、平台及系泊系统各部分的运动及动力响应。风轮气动载荷计算采用了通用的叶素-动量理论,并考虑了Øye动态入流模型、Prandtl叶尖-叶根损失模型及尾流修正模型。入流风场采用IEC规范中的正常湍流风模型以及Kaimal风谱,并采用Trubsim生成风场数据。浮体平台水动力模型由势流面元模型与Morison模型构成,水动力系数则由HydroD软件计算得到。采用了集中质量法模拟系泊系统,系泊水动力载荷同样由Morison方程计算获得。随机波浪采用了JONSWAP谱生成,流场采用均匀流剖面。数值模型模拟海况条件如表2所示,由于罗斗沙海域地处外罗水道,水深流急,流速相对较大。
| 海况 编号 | 风速/ (m·s–1) | 湍流 强度 | 有义波 高/m | 谱峰周 期/s | 谱峰 因子 | 流速/ (m·s–1) |
| 1 | 4.0 | 0.25 | 2.0 | 8.0 | 2.7 | 1.5 |
| 2 | 11.8 | 0.15 | 4.3 | 9.0 | 2.7 | 2.5 |
| 3 | 23 | 0.10 | 7.0 | 10.0 | 2.7 | 4.0 |
2.2 数据集描述
基于上述耦合时域分析模型对“扶摇号”在不同海况下的系泊动力响应进行数值模拟,得到锚链某一位置的倾角与导缆孔端张力等时序数据作为训练数据。为了与实测数据保持一致,训练数据采样频率设置为1 Hz,并选取距离导缆孔20.5 m位置作为倾角仪安装位置。
在训练之前,需要将数值仿真数据转换为监督学习数据集。LSTM网络在进行时间序列预测时,当天时间t的预测值依赖一定步数m范围内的历史观测值。本文采用从t–m到t–1范围内的倾角数据作为神经网络模型的输入序列,并将t时刻的响应值作为输出。所有的输入和输出数据均基于原始数据的均值和标准差进行缩放,以提升神经网络训练效率及精度。本研究每个工况仿真时长为3 h,同时输出9根锚链的仿真结果,数据样本接近
为了验证模型的准确性,将数据集划分为训练集、验证集和测试集,三者分别占比50%、30%和20%。
2.3 模型训练过程选择Adam优化算法作为模型的优化器,该算法结合了AdaGrad和RMSProp算法的优点,能够在多数情况下取得快速且良好的结果。Adam优化器的参数配置如下:learning rate=0.001,β1=0.9,β2=0.999,ε=1×10−8,decay=0。
由于系泊张力响应极值对于预测至关重要,选择均方误差(MSE)作为损失函数,以优化并评估神经网络的性能。同时,为了避免过拟合现象,采用了Early Stopping回调函数,并设置了Batch size为100,最大epoch数为200,以及Early Stopping的patience参数为5。最后,设置了检查点来保存表现最佳的模型。
神经网络模型训练过程训练集与验证集损失函数值的变化历史如图3所示。图中可见,训练过程中训练集及验证集的损失值均迅速大幅下降,在经过3个迭代周期后达到了较低的损失值水平。此后的5个迭代周期内,验证损失值结果并没有进一步下降,神经网络模型训练过程自动结束,并保留第3个迭代周期的训练参数为后续神经网络预测模型。
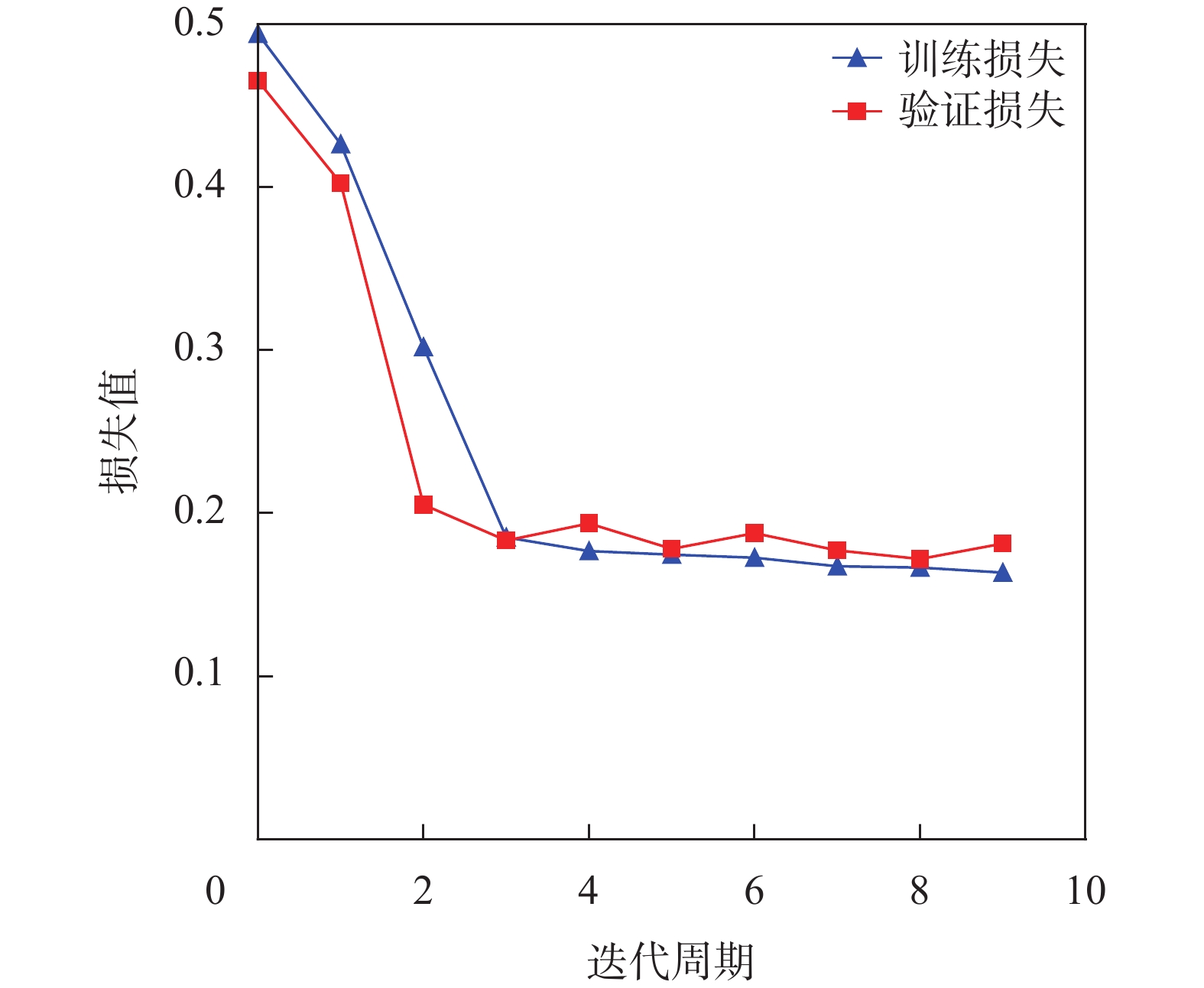
|
| 图 3 模型训练过程损失值变化 |
上述训练过程耗时约181 s。所获得的神经网络模型对训练集、验证集的均方根误差(RMSE)分别为46.7 kN和48.6 kN, 而系泊张力水平整体处于
在不考虑惯性力和流体动力情况下,准静态悬链线方程常用于表达系泊张力与系泊运动之间的关系。如图4所示,基于悬链线方程,能够推导如下系泊水平跨距X、竖向高度Z与系泊张力T和水平张力TH之间的关系。
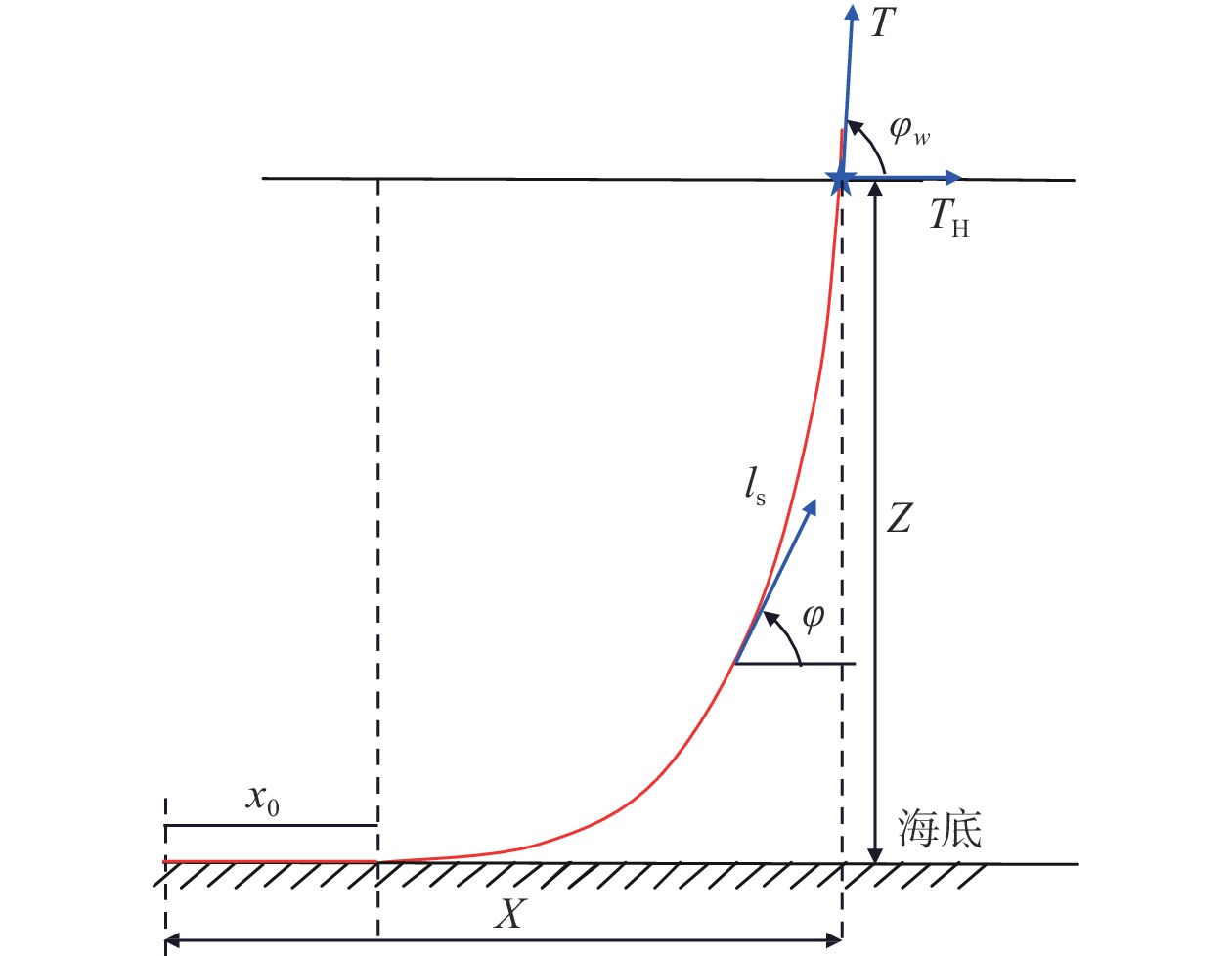
|
| 图 4 悬链线系泊模型 |
| $ X = l - Z\sqrt {1 + \frac{{2{T_{\rm H}}}}{{wZ}}} + \frac{{{T_{\rm H}}}}{w}{\cosh ^{ - 1}}\left( {1 + \frac{{wZ}}{{{T_{\rm H}}}}} \right) $ | (3) |
| $ T = {T_{\rm H}} + wZ $ | (4) |
式中:w——单位长度锚链的水中重量;
l——系泊缆长度。
上述方程组具有2个方程,4个未知量,需要2个定解条件。假定平台仅在水平面运动,则水平跨距与系泊张力将一一对应。在此情况下,系泊缆特定悬空位置处的倾角
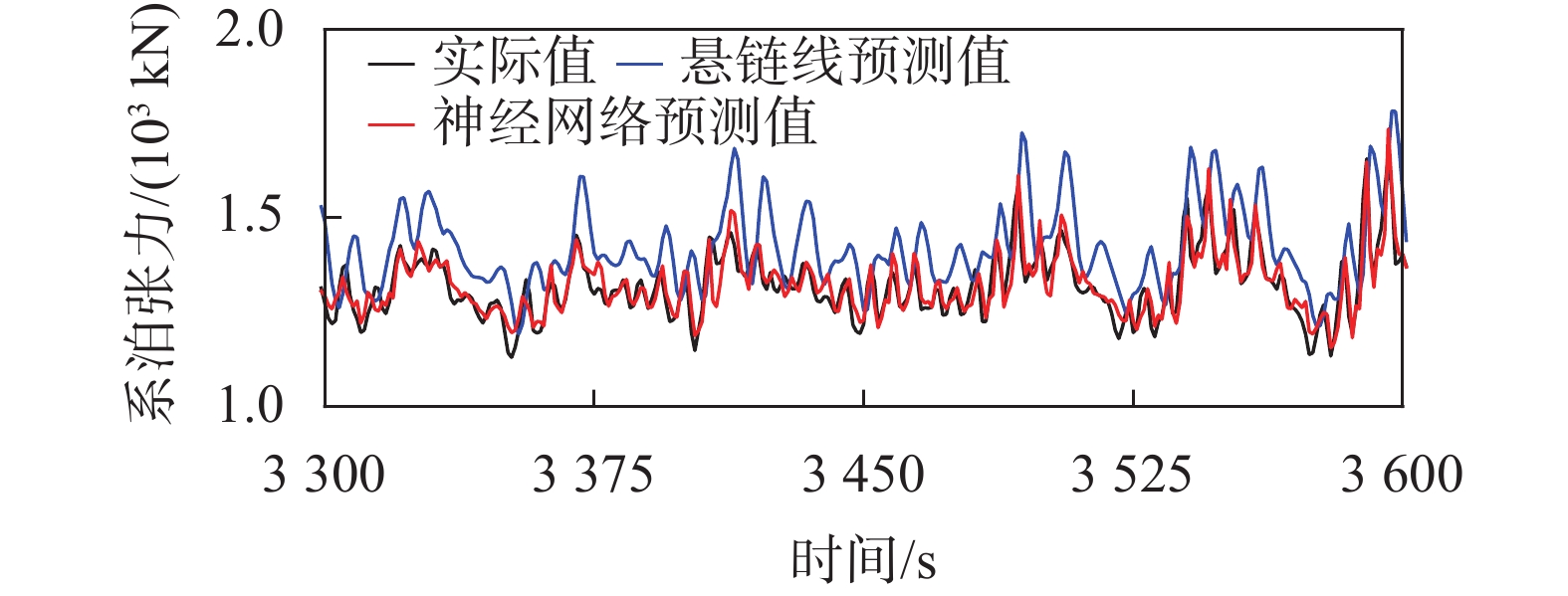
图5给出了分别采用悬链线方程及神经网络模型对系泊张力的预测结果与实际值的对比。为了评估两种数据解算方法的精度,此处采用了耦合数值分析结构中的测试集数据进行分析。表3给出了两种解算方法获得的系泊张力统计值与实际值的对比情况。可见,采用神经网络模型获得的时序曲线与实际值高度吻合,而基于悬链线方程的预测结果在均值及波动范围相比实际值偏大。最大值上,两者与实际值之间的误差分别为17.1%和6.4%。
|
| 图 5 系泊张力时域预测结果 |
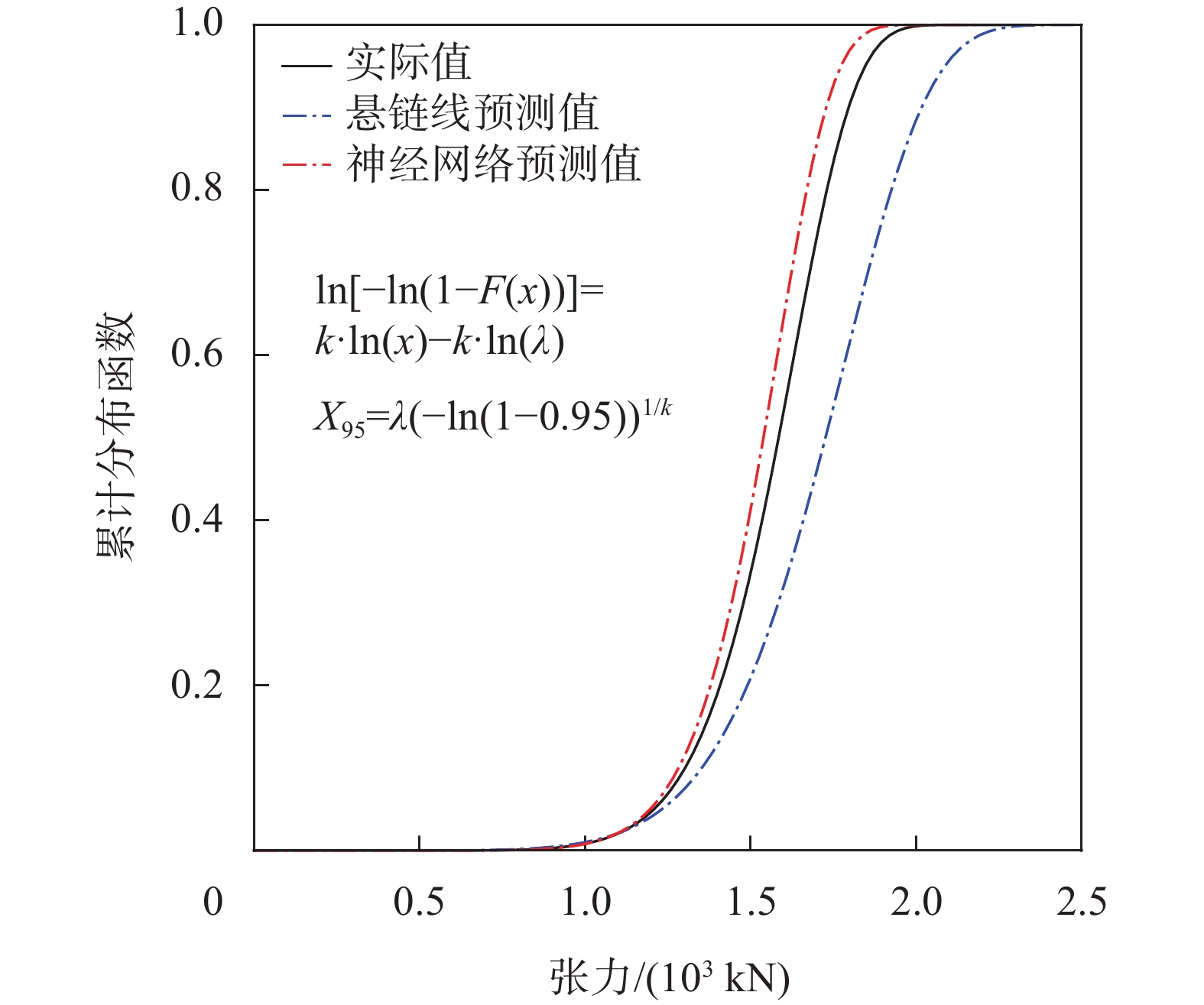
图6给出了不同系泊张力时序结果极值拟合获得的Weibull分布图及相应的95th百分位数。基于神经网络模型的预测结果,其Weibull分布曲线尽管比实际值偏小,但其与实际值对应的Weibull分布曲线明显更加接近。两者的95th百分位数预测值与实际值之间的误差分别为13.0%和4.0%。
|
| 图 6 系泊张力Weibull分布拟合曲线图 |
从表3中可见,悬链线方程预测结果的标准差显著高于实际值,而神经网络预测标准差偏小。在强流条件下,浮式风机水平运动固有周期出现大幅下降,而垂向运动固有周期基本不变。“扶摇号”风机在强流强风环境下,纵荡周期能够从静水条件下的116 s下降至45 s附近,而纵摇、垂荡周期均在25 s附近。
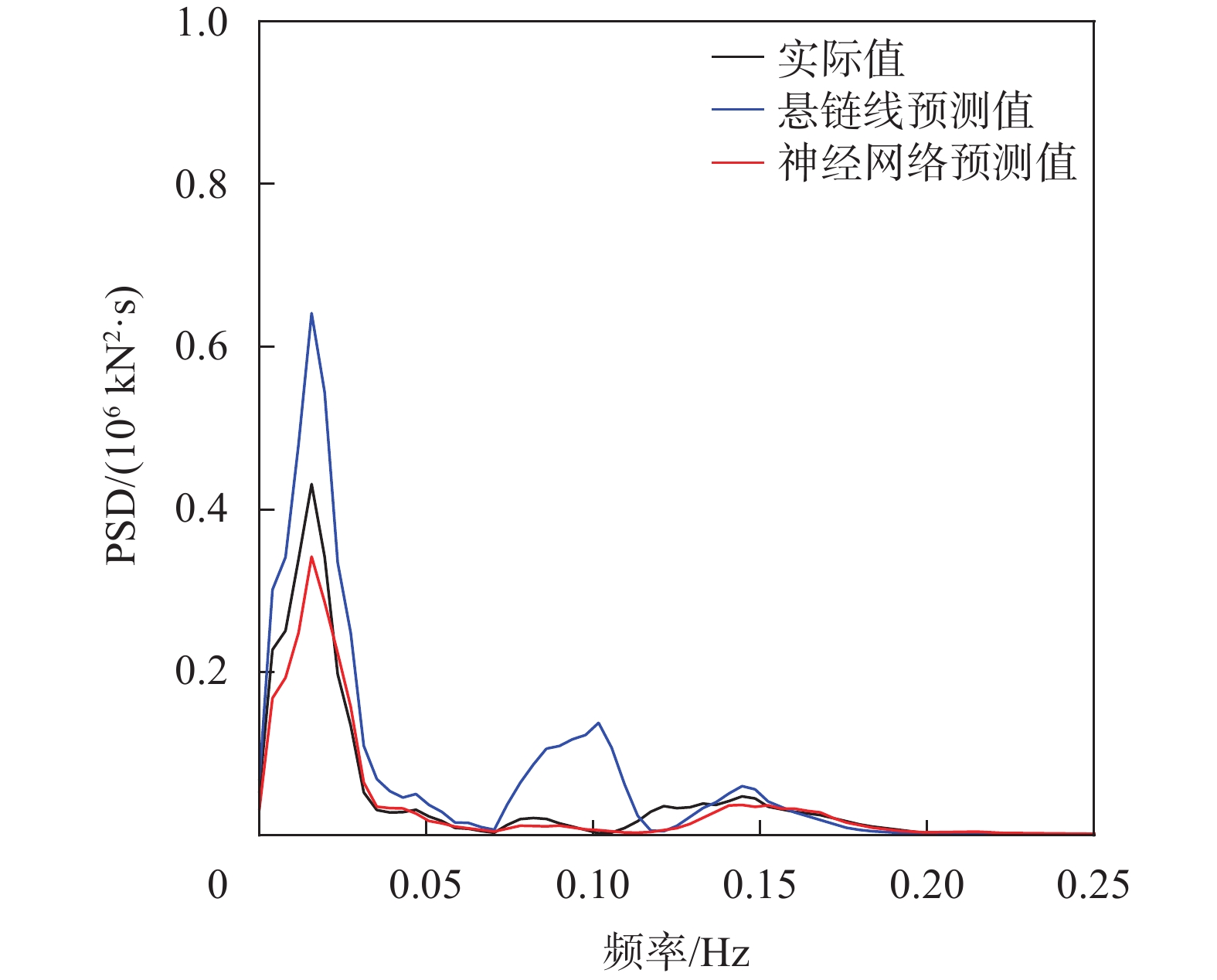
图7给出了系泊张力结果的功率谱密度分布图。可见,系泊张力由低频纵荡运动主导,在0~0.05 Hz范围内,悬链线预测结果谱密度显著高于实际值,与统计值结果一致,神经网络在此频率范围内谱密度偏低。原因在于神经网络的输入信息对于系泊张力预报仍不充分,预报结果存在微小的误差。在0.1 Hz附近,悬链线预测结果出现了次峰现象,这在实际系泊张力结果中是不存在的。这一现象可能与垂荡、纵摇耦合形成的倍频现象有关,而垂荡、纵摇在垂直方向上运动引起的倾角变化对于系泊张力的影响较小。
|
| 图 7 系泊张力功率谱密度分布 |
基于悬链线方程进行系泊张力结算时,默认浮式平台保持在水平面运动,无法避免夸大部分倾角变化对系泊张力的贡献。此外,在强流及风轮推力的作用下,浮式平台出现的平均倾角会引起导缆孔高度出现偏差。导缆孔高度偏差和系泊倾角类似,跟风浪流的环境相关。基于神经网络模型的预测方法,能够在训练过程中自动考虑到相关因素,因此,基于神经网络模型的预测均值与实际值十分接近。最后,基于LSTM网络的预测模型,能够充分利用历史数据信息,在一定程度上考虑了系泊动态运动过程,相比准静态悬链线方程在系泊动态效应的描述上能力更强。
4 结束语针对深远海浮式风机系泊倾角监测数据的解算问题,提出了一种基于LSTM网络的系泊张力解算方法,并与传统的悬链线模型进行了对比分析。
1)基于Keras框架建立了FCN网络与LSTM网络的组合模型,以当前时间往前数十秒倾角数据作为输入,当前系泊张力值作为输出,并采用耦合数值仿真结果作为数据集实现了神经网络模型的训练、验证和测试。
2)神经网络模型预测结果与实际值在时程曲线上高度吻合,在均值、标准差及最大值上比基于悬链线方程的预测结果更接近实际值。
3)神经网络模型预测一定程度上能够考虑到不同系泊倾角对应的导缆孔平均高度变化,且利用历史倾角信息能够更好地考虑系泊运动的动态过程,实现了基于有限倾角监测数据准确预测系泊张力的功能。
| [1] |
李达, 吕柏呈, 武文华, 等. 海洋平台现场监测技术现状及展望[J].
中国海上油气, 2022, 34(2): 165-179.
LI D, LYU B C, WU W H, et al. Status and prospect of offshore platform on-site monitoring technology[J].
China Offshore Oil and Gas, 2022, 34(2): 165-179.
DOI:10.11935/j.issn.1673-1506.2022.02.019 |
| [2] |
锁刘佳, 唐达, 马书义. 深水半潜式平台锚链倾角监测的自容式传感器的设计[J].
海洋技术, 2012, 31(2): 77-80.
SUO L J, TANG D, MA S Y. Design of self-contained sensors used in monitoring the deep water semi-submersible platform mooring anchor inclination[J].
Ocean Technology, 2012, 31(2): 77-80.
DOI:10.3969/j.issn.1003-2029.2012.02.018 |
| [3] |
杜宇, 武文华, 王延林, 等. 基于自容式技术的系泊缆水下监测方法[J].
哈尔滨工程大学学报, 2016, 37(8): 1003-1008.
DU Y, WU W H, WANG Y L, et al. An underwater monitoring method for mooring lines based on self-contained technique[J].
Journal of Harbin Engineering University, 2016, 37(8): 1003-1008.
DOI:10.11990/jheu.201506004 |
| [4] |
包建平. 悬链线式系泊系统测量技术研究与实测分析[D]. 大连: 大连理工大学, 2014.
BAO J P. Research on measurement technique for catenary mooring system and analysis for measurement result[D]. Dalian: Dalian University of Technology, 2014.
|
| [5] |
杨健, 廖晨茜, 蔡晋辉, 等. 基于改进对抗迁移学习的滚动轴承故障诊断研究[J].
中国测试, 2022, 48(5): 96-101.
YANG J, LIAO C X, CAI J H, et al. Rolling bearing fault diagnosis based on improved adversarial transfer learning[J].
China Measurement & Test, 2022, 48(5): 96-101.
DOI:10.11857/j.issn.1674-5124.2021030113 |
| [6] |
史业照, 郭斌, 郑永军. 基于 LSTM 网络的 IGBT 寿命预测方法研究[J].
中国测试, 2024, 50(2): 54-58.
SHI Y Z, GUO B, ZHENG Y J. Research on IGBT life prediction based on LSTM network[J].
China Measurement & Test, 2024, 50(2): 54-58.
DOI:10.11857/j.issn.1674-5124.2020040009 |
| [7] |
范玉莹, 何赟泽, 孙高森, 等. 无人机图像风力发电机轮毂中心检测与跟踪[J].
中国测试, 2022, 48(7): 90-96.
FAN Y Y, HE Y Z, SUN G S, et al. Wind turbine hub center detection and tracking based on UAV images[J].
China Measurement & Test, 2022, 48(7): 90-96.
DOI:10.11857/j.issn.1674-5124.2021120110 |
| [8] |
李琰, 肖龙飞, 魏汉迪, 等. 半潜式平台波浪爬升在线预报神经网络模型对比研究[J].
中国造船, 2023, 64(4): 28-40.
LI Y, XIAO L F, WEI H D, et al. Comparative study of two neural network models for online prediction of wave run-up on semi-submersible[J].
Shipbuilding of China, 2023, 64(4): 28-40.
DOI:10.3969/j.issn.1000-4882.2023.04.003 |
| [9] |
肖裕程, 李亮, 徐铭泽. 基于长短期记忆神经网络的涡激振动快速预报[J].
中国造船, 2023, 64(5): 130-145.
XIAO Y C, LI L, XU M Z. Efficient prediction for vortex induced vibration based on long short-term memory neural network[J].
Shipbuilding of China, 2023, 64(5): 130-145.
DOI:10.3969/j.issn.1000-4882.2023.05.012 |
| [10] |
范高杰. 基于深度学习的半潜平台极短期运动和系泊张力预报研究[D]. 大连: 大连海事大学, 2023.
FAN G J. Prediction of short-term motion and mooring tension of semi-submersible based on depth learning[D]. Dalian: Dalian Maritime University, 2023.
|
| [11] |
靳丛林. 基于LSTM-AM神经网络的水下软钢臂动态系泊力估算[D]. 哈尔滨: 哈尔滨工程大学, 2024.
JIN C L. Study on dynamic tension estimation for the underwater soft yoke mooring system with LSTM-AM neural network[D]. Harbin: Harbin Engineering University, 2024.
|
| [12] |
杨洁. 基于深度学习的单点系泊系统动态张力预测方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2022.
YANG J. Research on the dynamic tension prediction method of single mooring system based on deep learning[D]. Harbin: Harbin Engineering University, 2022.
|
| [13] |
QIAO D, LI P, MA G, et al. Realtime prediction of dynamic mooring lines responses with LSTM neural network model[J].
Ocean Engineering, 2020, 219(4): 108368.
DOI:10.1016/j.oceaneng.2020.108368 |
| [14] |
SAAD A M, SCHOPP F, BARREIRA R A, et al. Using neural network approaches to detect mooring line failure[J].
IEEE Access, 2021, 9: 27678-27695.
DOI:10.1109/ACCESS.2021.3058592 |
 2024, Vol. 50
2024, Vol. 50


 ,
,