文章信息
- 刘葳兴, 杜运男, 段昌朋, 胡婉婷, 张之阳, 孙成娇
- LIU Weixing, DU Yunnan, DUAN Changpeng, HU Wanting, ZHANG Zhiyang, SUN Chengjiao
- 胸尾鳍协同推进的仿生机器鱼设计
- Design of a biomimetic robotic fish with coordinated propulsion of pectoral and caudal fins
- 中国测试, 2024, 50(8): 11-19
- CHINA MEASUREMENT & TEST, 2024, 50(8): 11-19
- http://dx.doi.org/10.11857/j.issn.1674-5124.2024050042
-
文章历史
- 收稿日期: 2024-05-14
- 收到修改稿日期: 2024-05-29
2. 江苏海洋大学马卡洛夫海洋工程学院,江苏 连云港 222005;
3. 湖北文理学院计算机工程学院,湖北 襄阳 441053
2. School of Makarov Marine Engineering, Jiangsu Ocean University , Lianyungang 222005, China;
3. College of Compute Engineering, Hubei University of Arts and Science , Xiangyang 441053, China
在追求水下资源的探索愈发急迫的当下,水下机器人技术[1]已经跃升至机器人研究领域中最受追捧的前沿课题之一。仿生鱼类机器人,作为水下机器人的创新形态,正以其独特的优势在多个领域显现出巨大的应用潜力,包括海洋资源勘探、生物监测、水环境监测以及军事侦察等方面[2-3]。
作为设计机器鱼的基础问题,鱼类的动力学建模[4]引起了人们的广泛关注。Lighthill的细长体理论[5]和大幅度细长体理论[6]是被广泛接受的机器鱼建模方法,因为它们在保真度和简单性之间保持了良好的平衡。YU Z [7] 开发了一种仿生射线机器鱼,它的两对胸鳍以单自由度串联排列,通过适当的相位差提高了前进速度,利用胸鳍和尾鳍的协同推进,前进速度可达 0.37 m/s。BIANCHI G [8]提出了一种仿生水下机器人,其灵感来自蝠鲼,可通过鳍的被动变形产生推力,但由于材料限制,原型机速度较低,无法承载负荷。CASTANO M [9]针对胸鳍划动的机器鱼,提出了一种基于双回路反推的轨迹跟踪控制方法。但并未对2自由度胸鳍的动力学进行分析。ZHONG Y [10]设计出来新型的机器鱼能主动将线驱动的身体与柔软的顺应性尾巴相结合,以实现波动游泳。
鉴于仿生机器鱼的诸多优点,以热带观赏鱼暗绿鲀为仿生对象,设计一款二自由度胸鳍和双关节尾鳍协调驱动的暗绿鲀机器鱼,侧重于实验分析验证的方法,研究仿生鱼胸尾鳍协同推进的不同模式下其运动的机理及姿态。另外,设计出外观和运动姿态更好的观赏性机器鱼,使仿生机器鱼代替珍稀野生鱼类用于水族馆科普,具有重要的理论意义和广泛的实用价值。
1 研究方法如图1所示,建模和控制是开发和利用仿生机器鱼的两个关键问题。在许多基于机器鱼的应用中,深入了解鱼类游动的流体力学和运动学原理也至关重要。流体力学和运动学模型不仅是量化游动生物与周围流体之间关键物理过程的工具,还能指导工程设计和评估外在效应。本节简要介绍了鱼类游泳的水动力模型和测试方法。
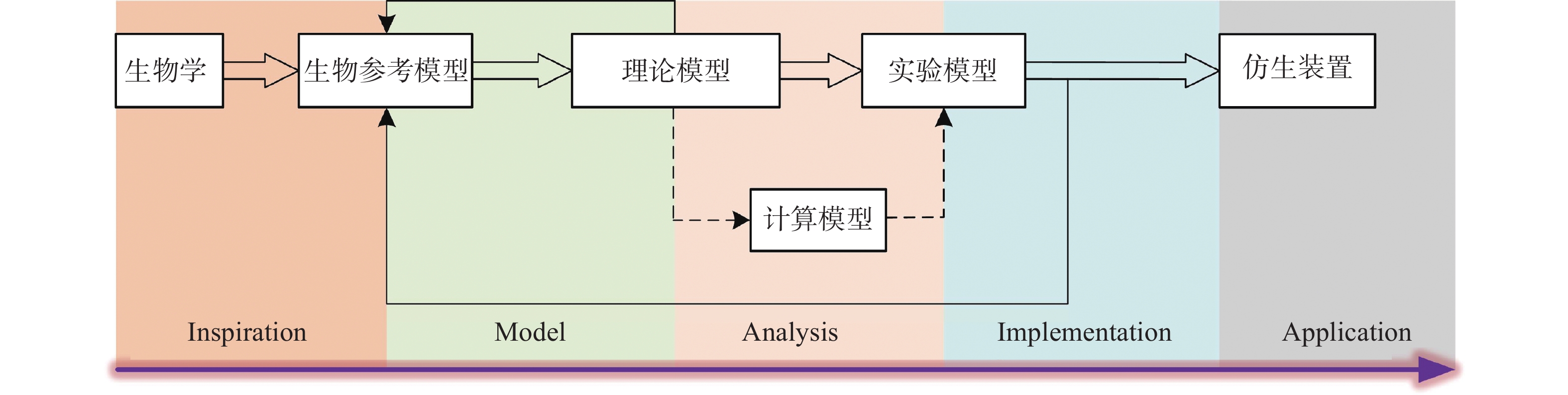
|
| 图 1 仿生装置生产流程示意图 |
鱼类运动已经研究了很多年。已经开发了许多模型和方法,包括细长体理论 [11],阻力理论 [12],3D波浪板理论 [13]和大幅度细长体理论 [14],采用细长体理论方法,因为该方法计算量较少,且能较好地预测鱼类运动。
2 设计方法 2.1 仿生机器鱼结构暗绿鲀,又名潜水艇鱼,如图2,是四齿鲀科鲀属的一种鱼类,其身体在长度的前三分之二到四分之三处是刚性的,其机动性和稳定性由胸鳍、臀鳍、背鳍和尾鳍调节。由于现阶段主要考虑的是在胸鳍和尾鳍的耦合运动影响下身体航向的稳定性,因此省略了其他鳍的作用。因此,胸鳍原型被简化为两侧正交的两个伺服电机结构,分别模拟胸鳍的旋转和拍动。

|
| 图 2 暗绿鲀的形状及其鳍的形状 |
图3展示了仿生鱼的胸鳍推进机构。该机构可实现机器鱼以舵机1为中心的摇翼运动和以舵机2为中心的拍翼运动,或两者的组合。舵机1的输出轴带动传动轴、舵机2、舵机支架和胸鳍旋转。舵机2连接到舵机支架上,传动轴连接到舵机摇臂上,使舵机2与舵机1的输出分离。
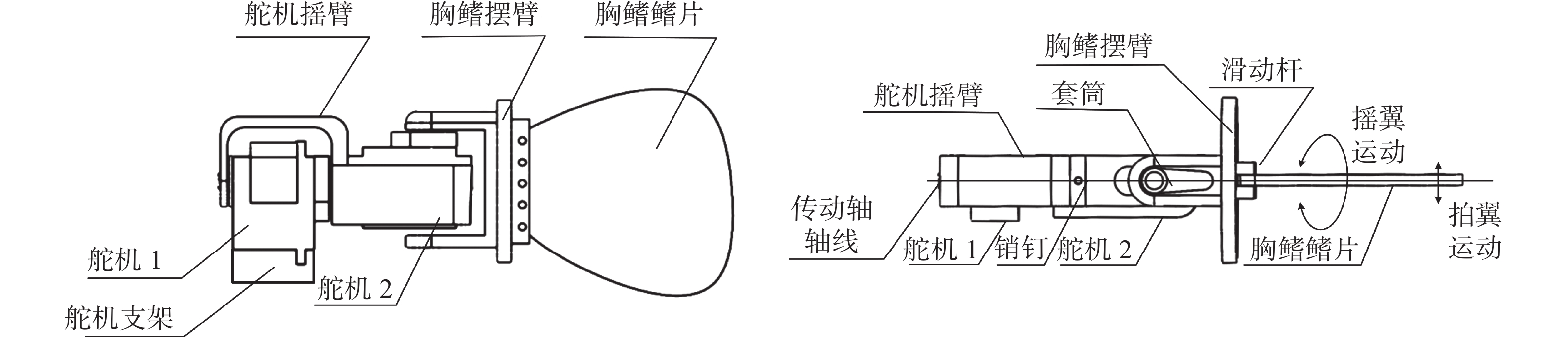
|
| 图 3 机器鱼的胸鳍推进机制 |
机器鱼样机整体模型如图4所示。图5为仿生鱼整体推进机械结构,原型机的主体是一个通过3D打印技术用硬质树脂制成的密封腔体,由头部和腹部组成。这两部分是密闭的,鱼体内装有伺服电机、控制系统、锂离子电池、惯性测量单元等电子设备。两个圆形连接器用于给电池充电和向电路板下载程序,样机的规格见表1。
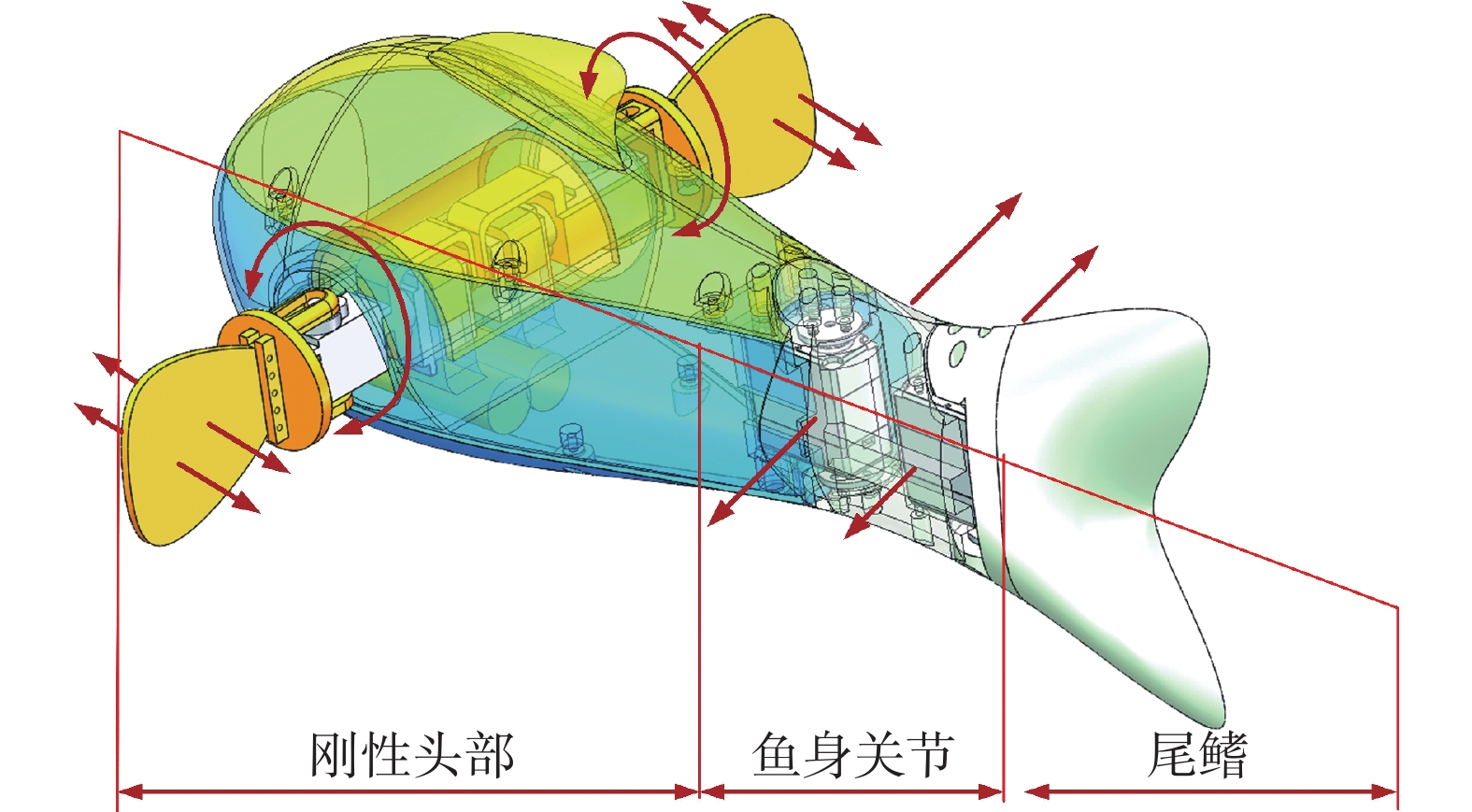
|
| 图 4 拟定的机器鱼原型。 |
|
| 图 5 仿生鱼的整体推进结构 |
原型的整体密度可以通过在密封舱内放置钢制重物来调整,因此经过多次调整后,原型可以悬浮在水中。配重后,样机的总重量约为3.6 kg。
| 参数 | 特征 |
| 尺寸 (L×W×H) | 400 mm×140 mm×142 mm |
| 重量 | 3.6 kg |
| CPU | Esp32 |
| 工作电压 | DC 6 V |
| 外壳材料 | 聚乳酸 |
| 驱动方式 | 直流伺服电机(2.3 kg·cm) |
2.2 仿生机器鱼的控制系统
仿生机器鱼的控制系统由上位计算机系统、串行通信单元、下位机控制单元、传感器和其他装置组成,其结构如图6 所示。

|
| 图 6 仿生机器鱼控制系统 |
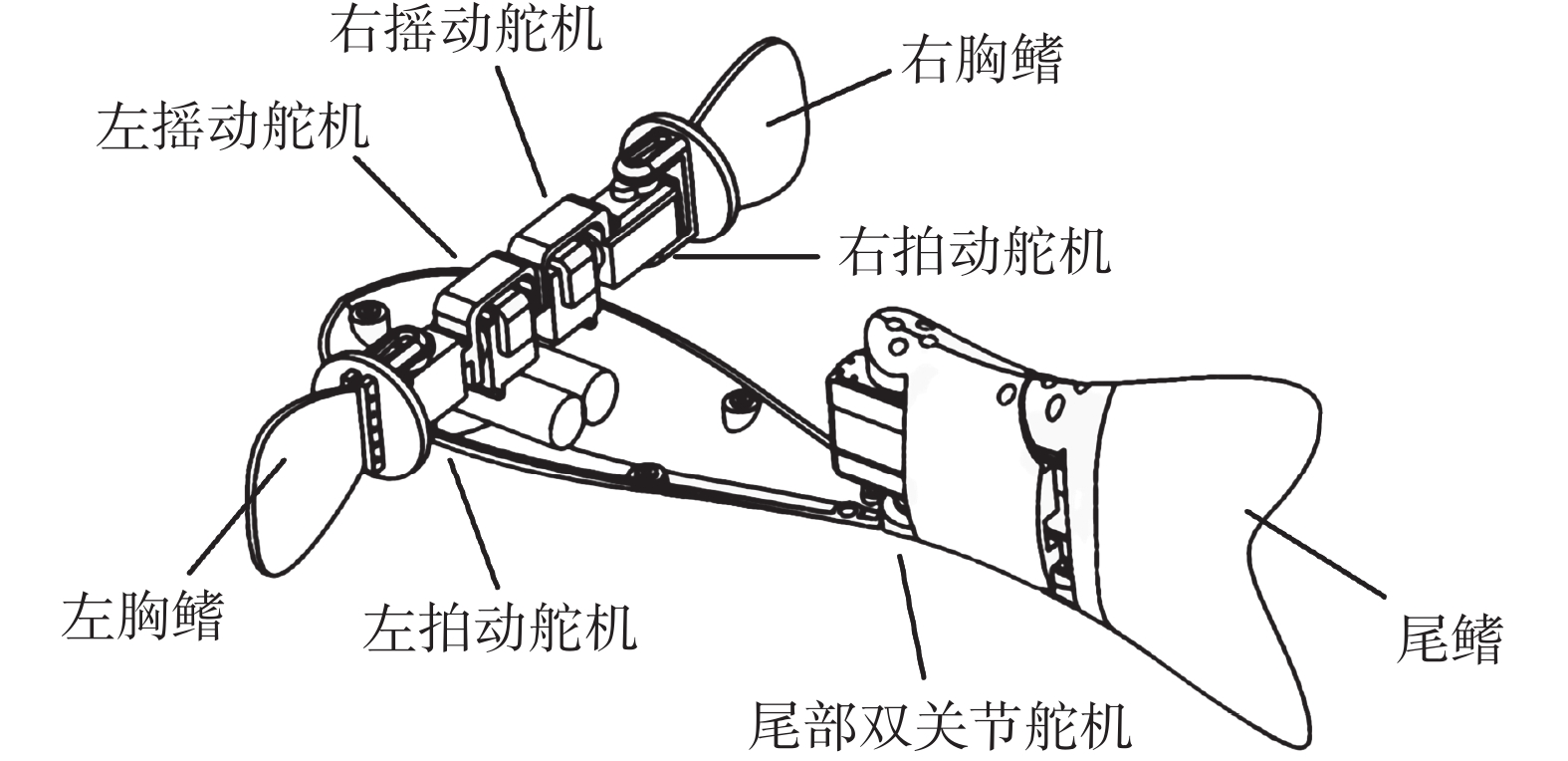
电压转换模块可以检测整个样机的瞬时电压和功耗,工作时,电源输出经电压转换模块将电池电压转换为5 V和3.3 V,供外围设备和单片机Esp32使用。上位机与样机之间采用串口通信,单片机Esp32输出脉宽调制信号给胸尾鳍模块的伺服电机,以控制其转动的角度、频率和相位差。最后再由单片机接收指令,将电压、负载和俯仰角等信息反馈给上位机。图7为仿生机器鱼样机。

|
| 图 7 仿生机器鱼样机 |
3 机器鱼的运动学建模 3.1 二自由度胸鳍运动的运动学分析
仿生机器鱼胸鳍的运动是由三个运动分量组成[15]:1)前后拍翼运动;2)摇翼运动;3)上下拍翼运动,如图8所示。

|
| 图 8 胸鳍运动的不同类型 |
为了方便描述胸鳍运动,建立固定在鱼体上的坐标系,其原点

|
| 图 9 定义随体坐标 |
三自由度运动模型方程:
| $ \left\{ \begin{aligned} &{\phi }_{L}={\phi }_{LC}-{\phi }_{LA}{\rm cos}({\omega }_{\rm fin}\cdot t)\\ &{\phi }_{FE}=-{\phi }_{FEC}-{\phi }_{FEA}{\rm cos}({\omega }_{\rm fin}\cdot t+\Delta {\phi }_{FE})\\ &{\phi }_{FL}={\phi }_{FLC}+{\phi }_{FLA}{\rm cos}({\omega }_{\rm fin}\cdot t+\Delta {\phi }_{FL}) \end{aligned}\right.$ | (1) |
式中:
2自由度复合运动由摇翼运动和前后拍翼运动复合而成,仿生机器鱼胸鳍的摆动由摇翼运动和拍翼运动复合而成,如公式(2)所示。
| $ \left\{ \begin{aligned} {\theta _{{f}}} =& {\theta _{{{f0}}}} + \frac{{{B_{{f}}}}}{2}{\rm{sin}}\left( {2{\rm{\pi }}{f_{{f}}}t + {\varphi _{{f}}}} \right){\rm{,}}t \in \left[ {0{{,T}}} \right] \\ {\theta _{{l}}} =& {\theta _{{{l0}}}} + \frac{{{B_{{l}}}}}{2}{\rm{sin}}\left( {2{\rm{\pi }}{f_{{l}}}t + {\varphi _{{l}}}} \right){\rm{,}}t \in \left[ {0{{,T}}} \right] \end{aligned}\right. $ | (2) |
式中:
实验中可通过改变不同的运动参数实现胸鳍不同的运动姿态。
对式(2)求导,可以得到胸鳍二自由度摆动的速率表达式:
| $ \left\{ \begin{aligned} {\omega _{{f}}} =& 2{\rm{\pi }}{f_{{f}}}\frac{{{B_{{f}}}}}{2}{\rm{cos}}\left( {2{\rm{\pi }}{f_{{f}}}t} \right){\rm{,}}t \in \left[ {0{{,T}}} \right] \\ {\omega _{{l}}} =& 2{\rm{\pi }}{f_{{l}}}\frac{{{B_{\rm{l}}}}}{2}{\rm{cos}}\left( {2{\rm{\pi }}{f_{{l}}}t} \right){\rm{,}}t \in \left[ {0{{,T}}} \right] \end{aligned}\right. $ | (3) |
根据飞机机翼纵横比的定义,对尾鳍进行了数字化描述:
| $ R = \frac{{{b^2}}}{{{S_C}}} $ | (4) |
式中:
本设计中尾鳍的面积为
|
| 图 10 Lighthill标准曲线 |
| $\left\{ \begin{aligned} &{y_{\rm body}}\left( {x,t} \right) = \left( {{c_1}x + {c_2}{x^2}} \right){\rm{sin}}\left( {kx + \omega t} \right) \\ &k = \dfrac{{2{\rm{\pi }}}}{\lambda },\omega = 2{\rm{\pi }}{f} = \dfrac{{2{\rm{\pi }}}}{{{T}}} \end{aligned}\right.$ | (5) |
式中:
机械鱼的尾部位置满足鱼体波曲线方程式,对机械鱼两个关节的末端进行分析,假设尾部第一个关节转动
| $ \frac{{{y_1}}}{{{l_1}}} = {\theta _1} $ | (6) |
根据 (5) 和 (6) 可以推导出第一个关节旋转的角度时间关系:
| $ {\theta _1} = \left( {{c_1} + {c_2}{l_1}} \right){\rm{sin}}\left( {k{l_1} + wt} \right) $ | (7) |
根据(7)推导出的关系式,可以推出第一个关节的角度符合普通正弦规律,根据上述方法,可以推导出第二个关节也符合正弦关系。每个关节的频率相同,但振幅不同,关节之间存在相位差,产生的鱼体波从机械鱼的头部传到尾部,完成仿生游泳,关节的振荡方程如下:
| $ \left\{ \begin{aligned} {A_1}\left( t \right) =& {K_a}{A_1}_{{\rm{max}}}{\rm{sin}}\left( {2{\rm{\pi }}ft - {\varphi _1}} \right) + {K_i}\left( {1 - {K_a}} \right){A_{2{\rm{max}}}} \\ {A_2}\left( t \right) =& {K_2}{A_2}_{{\rm{max}}}{\rm{sin}}\left( {2{\rm{\pi }}ft} \right) + {K_i}\left( {1 - {K_a}} \right){A_{1{\rm{max}}}} \end{aligned}\right.$ | (8) |
式中:
当
实验的目的是通过不同的游动模式实验,验证生物机器鱼的密封性和可靠性,以及控制方法的可行性,为后续复杂游动模式的数据采集和改进方法提供启示和数据。仿生机器鱼实验系统主要由生物机器鱼原型、水池、上位机、摄像头等模块组成。实验地点选择在实验室水池,如图11所示。在整个实验过程中,机器鱼原型将被限制在摄像机的可视范围内。摄像头位于实验水池上方约3 m处,可实时采集水池中的图像信息,包括水池环境信息和鱼的位置信息等。同时,通过与上位机连接的串行通信模块,可以发送控制命令来控制鱼的运动,并可接收鱼的反馈信号。摄像机通过网络交换机与计算机相连接,实现了对附着在机器鱼上的标志点的捕获,并对其进行了计算,得到了其在运动状态下的运动参数及运动姿态。

|
| 图 11 仿生鱼实验环境设备 |
实验分为三个部分,第一部分是由胸鳍推动的直游实验,第二部分是由尾鳍推动的直游实验,第三部分是由胸鳍和尾鳍共同推动的直游和转弯实验。
在实验中,机器鱼漂浮在水面上,约90%的表面积和约95%的尾鳍浸没在水中。在模拟中,尾鳍尖端处的模拟表面积和附加质量均基于该实验情况,即
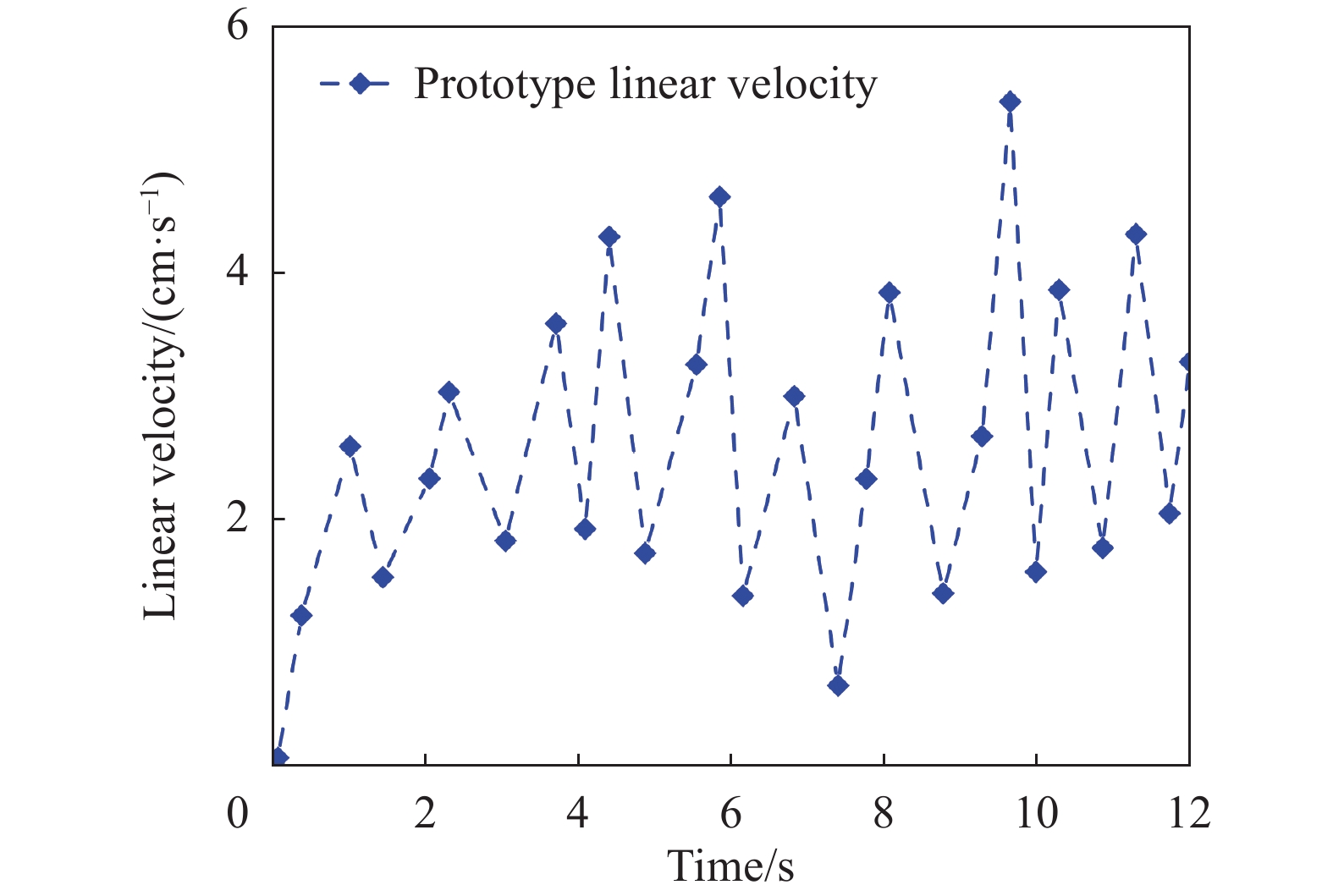
仿生机器鱼直游实验如图12,该图显示了机器鱼在双胸鳍推进下使用MPF模式进行直游的实验,胸鳍摆动周期T=2 s,摆动幅度B=70°。机器鱼在此频率下的速度如图13所示,其平均游速为0.04 m/s。在这种模式下,机器鱼直游时头部没有明显的侧向振荡,这反映了自然界中真鱼MPF游泳模式的平滑性。

|
| 图 12 胸鳍直泳实验 |
|
| 图 13 机器鱼在 MPF 模式下的巡航速度 |
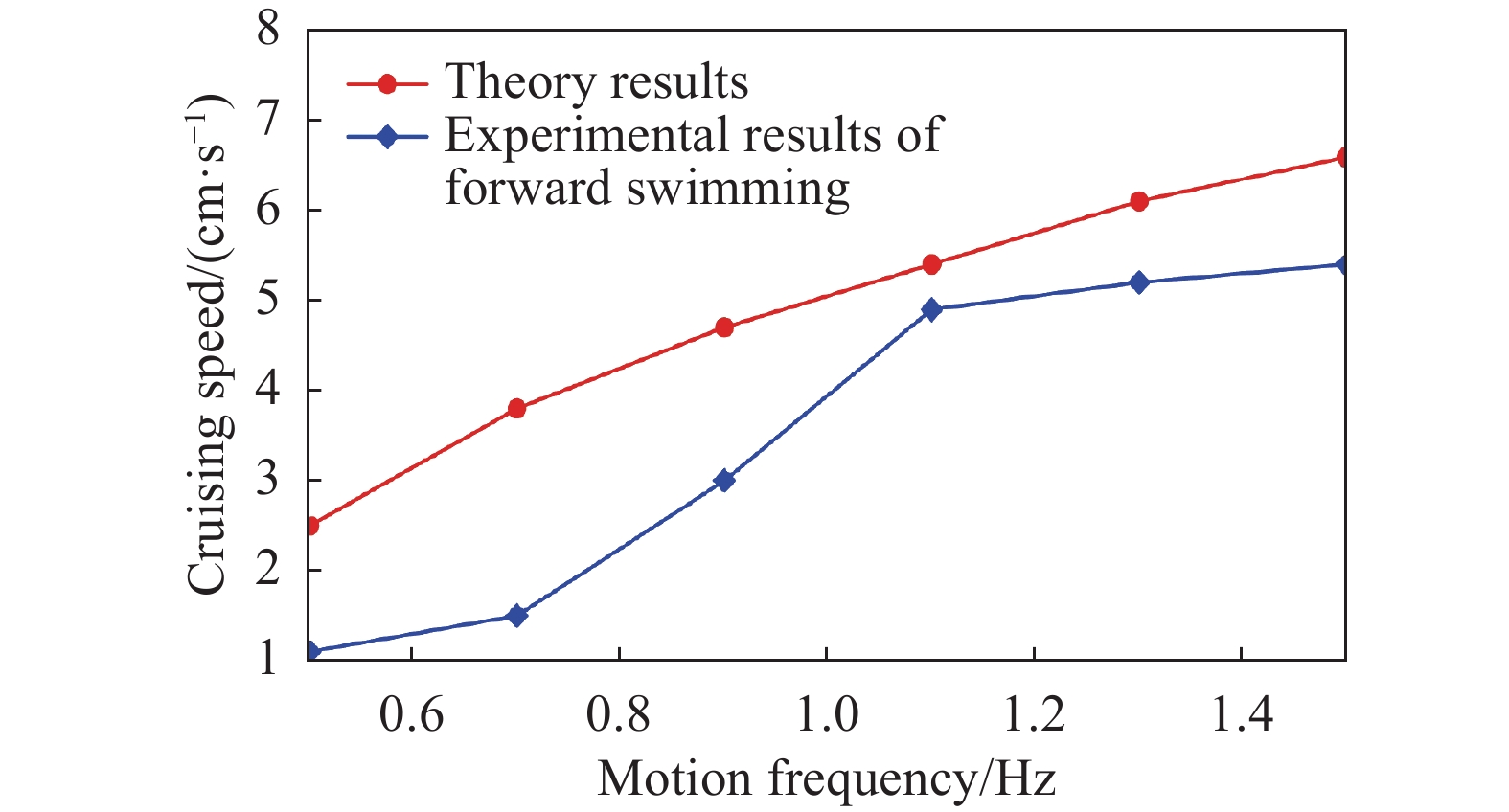
测试中,尾鳍保持静止不动。在一个运动周期内,胸鳍由舵的两个参数控制。设定垂直于水平面为鳍的初始位置,因此初始值
|
| 图 14 摆动频率与巡航速度的关系 |
|
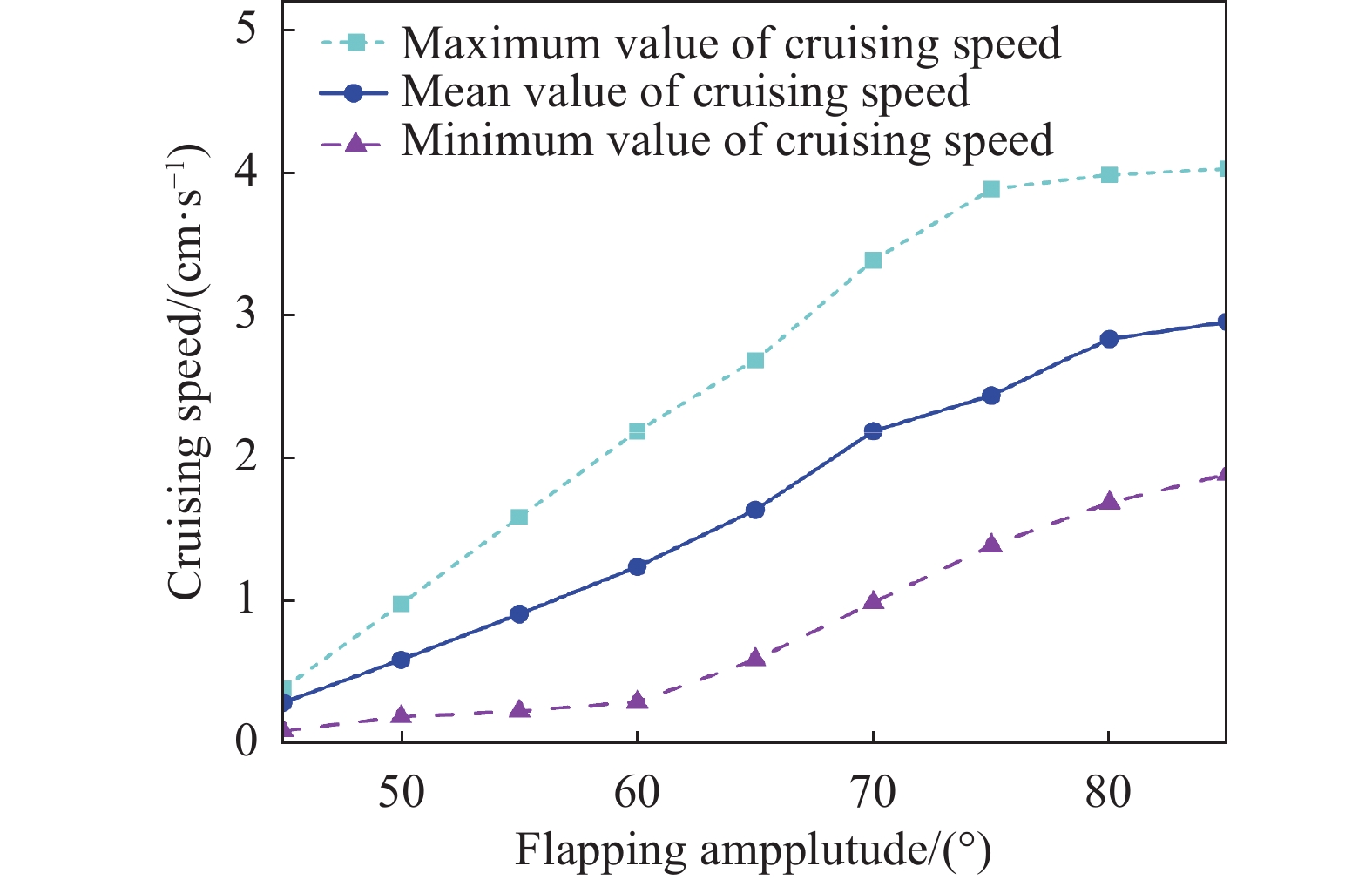
| 图 15 摆动幅度与巡航速度的关系 |
4.2 尾鳍推进巡航实验
图16所示为利用 BCF 模式使机器鱼在柔性身体/尾鳍推动下直游的实验,其中胸鳍在水平面上保持静止。在实验中,仿生机器鱼的尾鳍摆动周期为1 s,振幅为60°。观察到机器鱼在此频率下的平均游速约为0.14 m/s。

|
| 图 16 摆动幅度与巡航速度实验 |
BCF模式下机器鱼的直线巡游速度如图17所示。
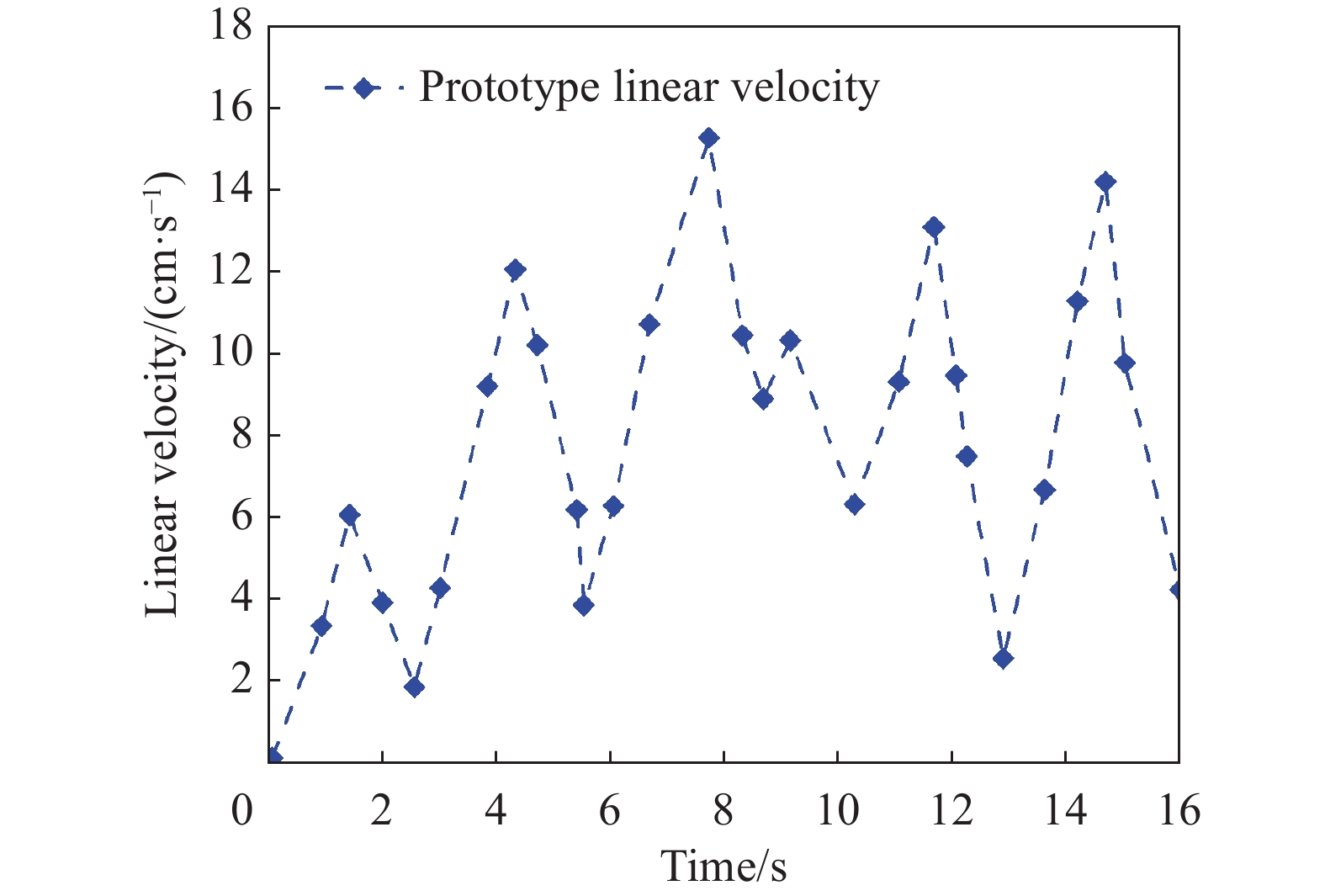
|
| 图 17 机器鱼在 MPF 模式下的巡航速度 |
机器鱼在第4个周期达到稳定状态,随着振荡频率的增加,速度逐渐增加。结合图18可以看出,当仿生机器鱼尾鳍摆动频率在0.5 Hz 以下,摆动幅度不超过25°时,速度增加幅度不大,当频率达到0.8 Hz 以上,摆动幅度达到30°以上时,机器鱼的巡游速度增长较快,当频率达到1.6 Hz,摆动幅度达到65°时,速度又呈下降趋势。因此,对于特定的机器鱼模型,存在一个使推力最大化的最佳振幅与频率,适当的摆动幅值与频率可在鱼的流场后方形成稳定的涡流,这种涡流在推进方向上的力分量较大,而在横向方向上的力分量较小,因此适合以较高的速度游动。尾鳍摆动频率和振荡幅度对游速的影响如图19所示。
|
| 图 18 摆动频率与巡航速度的关系 |
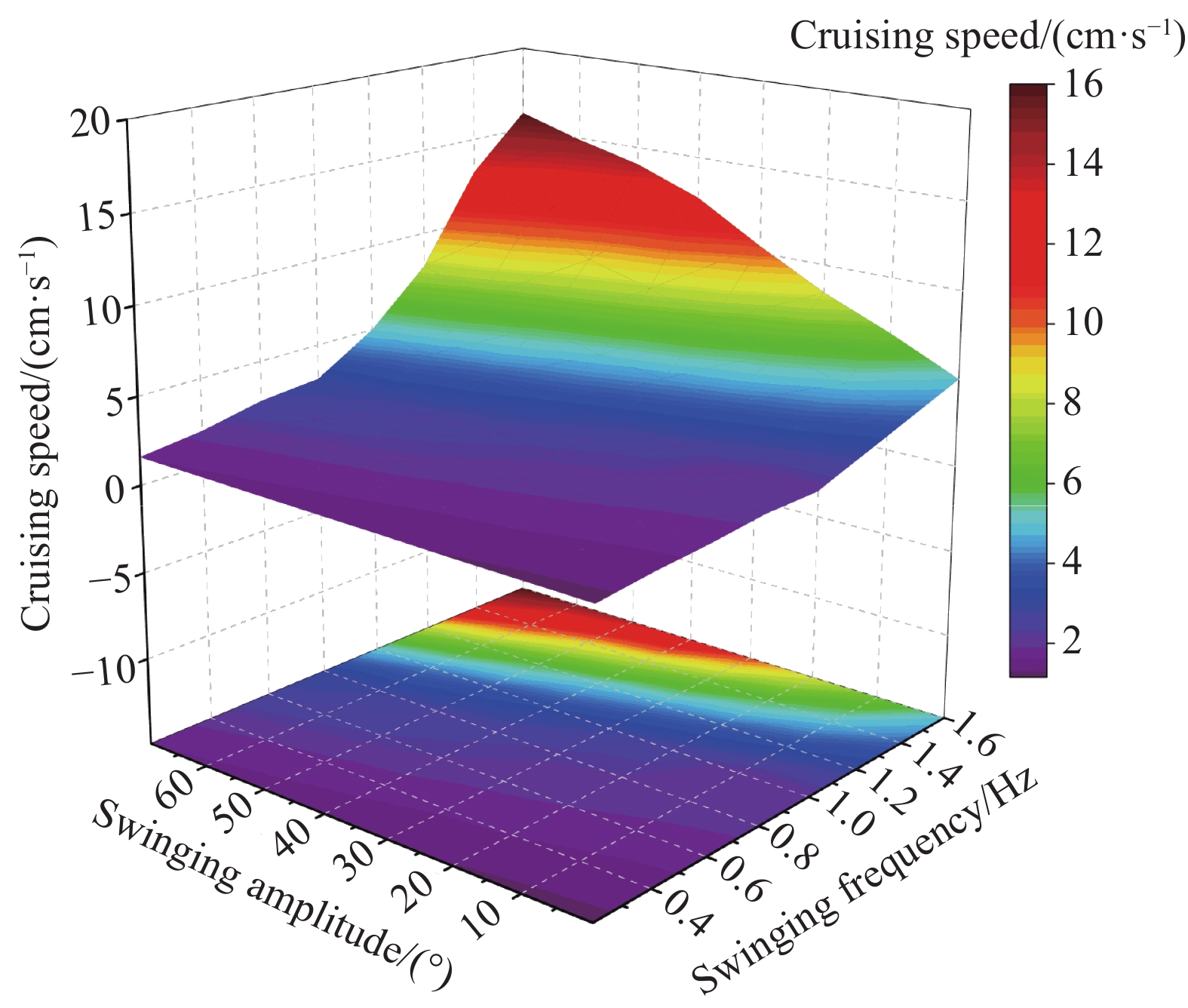
|
| 图 19 尾鳍摆动频率和振幅对巡游速度的影响 |
4.3 胸尾鳍协同推进巡航和转弯实验 4.3.1 转向分析
图20显示了机器鱼在胸鳍下使用MPF/BCF 模式以及在胸鳍摆动幅值为70°、周期为 2 s的情况下使用柔性身体/尾鳍协同推进的直泳和转向实验。对胸鳍外圈的转向进行了改动,使其摆动的幅度和频率更大。尾鳍振幅为60°,并以一定的偏转系数向一侧摆动。

|
| 图 20 胸尾鳍协同推进 |
图21显示了机器鱼的速度变化,该频率下机器鱼的平均游速为0.16 m/s,说明在MPF/BCF模式下,胸鳍的叠加以及柔性体/尾鳍的摆动可以产生较大的推力,从而使游速也随之提高,该频率下机器鱼在转弯方向的平均角速度为0.4 rad/s。
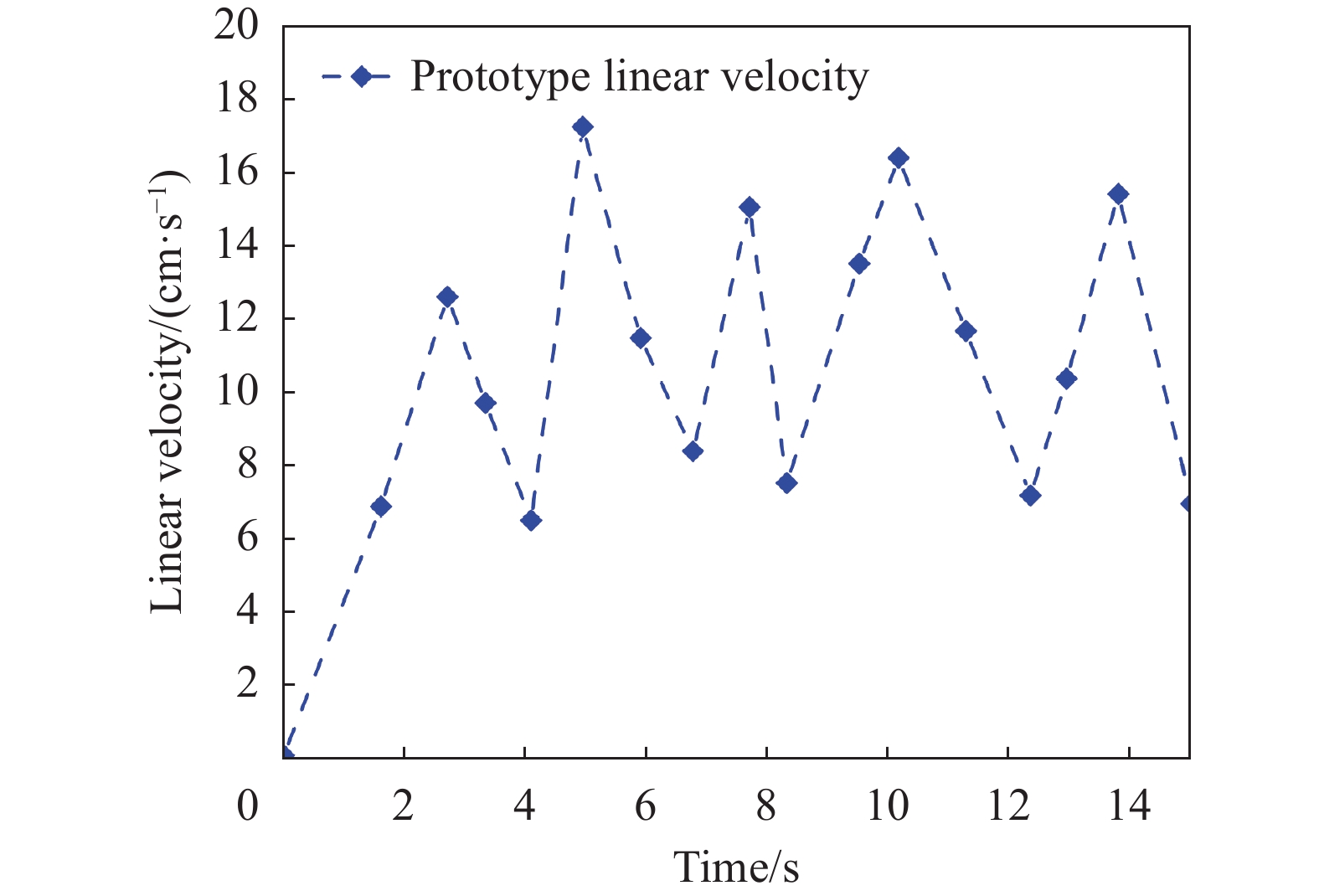
|
| 图 21 机器鱼在BCF/MPF模式下的巡航速度 |
在自然界中,鱼类的所有鳍在游泳时都会相互配合,尤其是在机动时。在本次测试中,对鱼鳍的协调性进行了初步研究,特别是在转弯时。图20(b)所示的视频帧显示了一个典型的回转运动,在每个回转周期中,机器鱼首先快速拍打尾鳍至极限位置,该位置被定义为跳跃阶段(由机械结构和程序设置决定),然后缓慢恢复至初始位置,该位置被定义为恢复阶段。
平均转弯角度和平均转弯半径是衡量机器人转弯性能的常用指标。以左转弯为例,不同运动频率和不同摆动幅度下的平均转弯角度和平均转弯半径如图20(b),图22(摆动幅度保持40°)和图23(运动频率保持1 Hz)所示。在1.5 Hz的运动频率和 40°的摆动幅度下,转向性能达到最佳。最小平均转弯角度可达36°,最小平均转弯半径可达0.13 m。
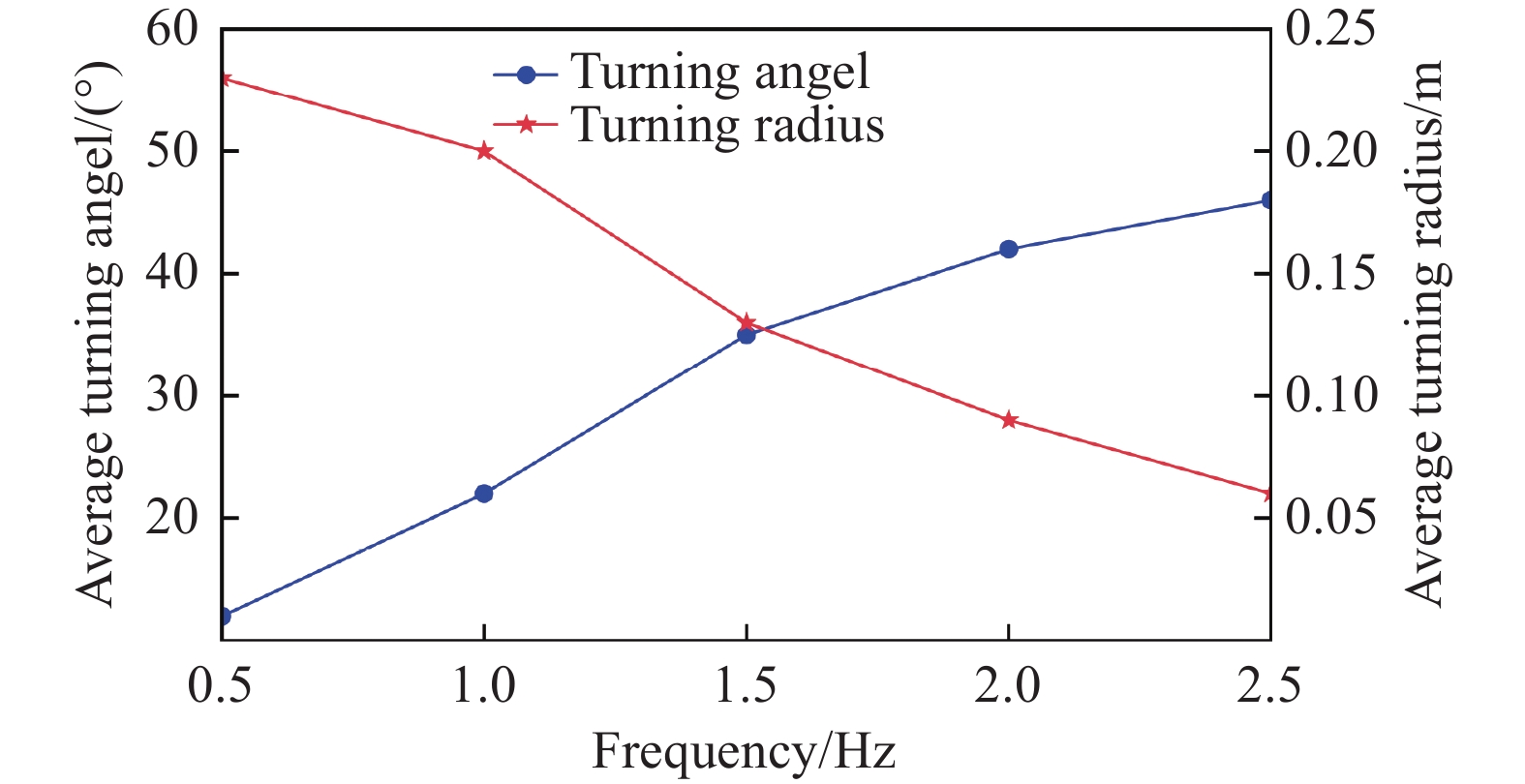
|
| 图 22 不同频率下的平均转弯角度和平均转弯半径 |

|
| 图 23 不同振幅下的平均转弯角度和平均转弯半径 |
4.3.2 巡游分析
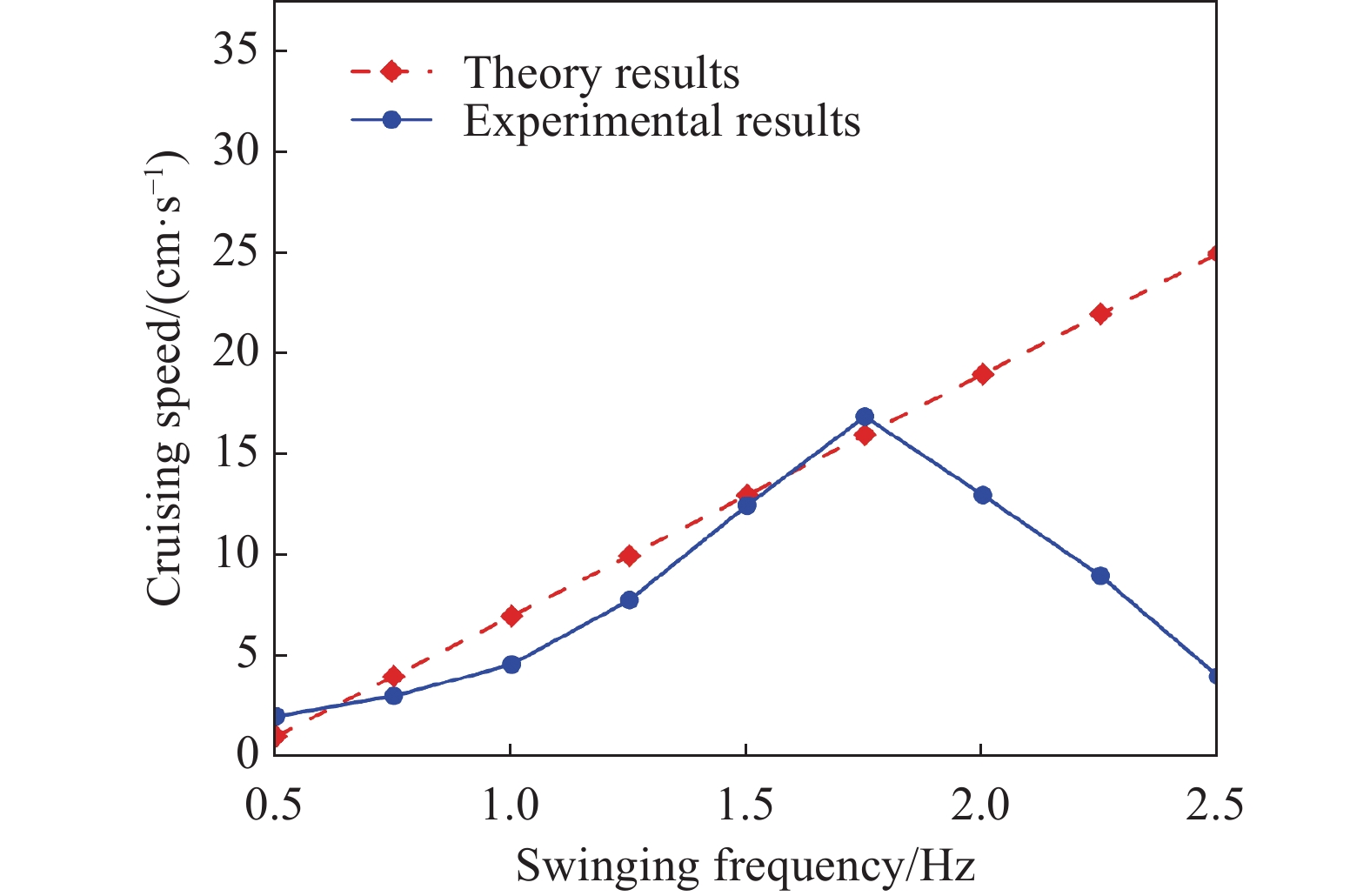
比较图24,随着机器鱼尾鳍振荡频率的升高,巡航速度也在增加,当频率为1 Hz时,巡航速度迅速变快。当频率接近1.6 Hz时,巡航速度达到最大值;当频率高于1.6 Hz时,巡航速度急剧下降。这可能有几个具体原因:首先,水箱尺寸不够大,无法达到室外真实水池的条件,当拍打速度较快时,水流会变得湍急,从而影响巡航性能。其次,方向舵响应频率较慢,机器鱼的实际摆动幅度会变小,从而降低巡航速度。例如,当摆动频率为2 Hz时,尾鳍的实际摆幅约为60°。当摆动频率为2.5 Hz时,尾鳍的实际振幅约为40°。仅为输出指令的57%。在所有测试中,最大巡航速度约为17 cm/s,最大转弯速度为0.6 rad/s。
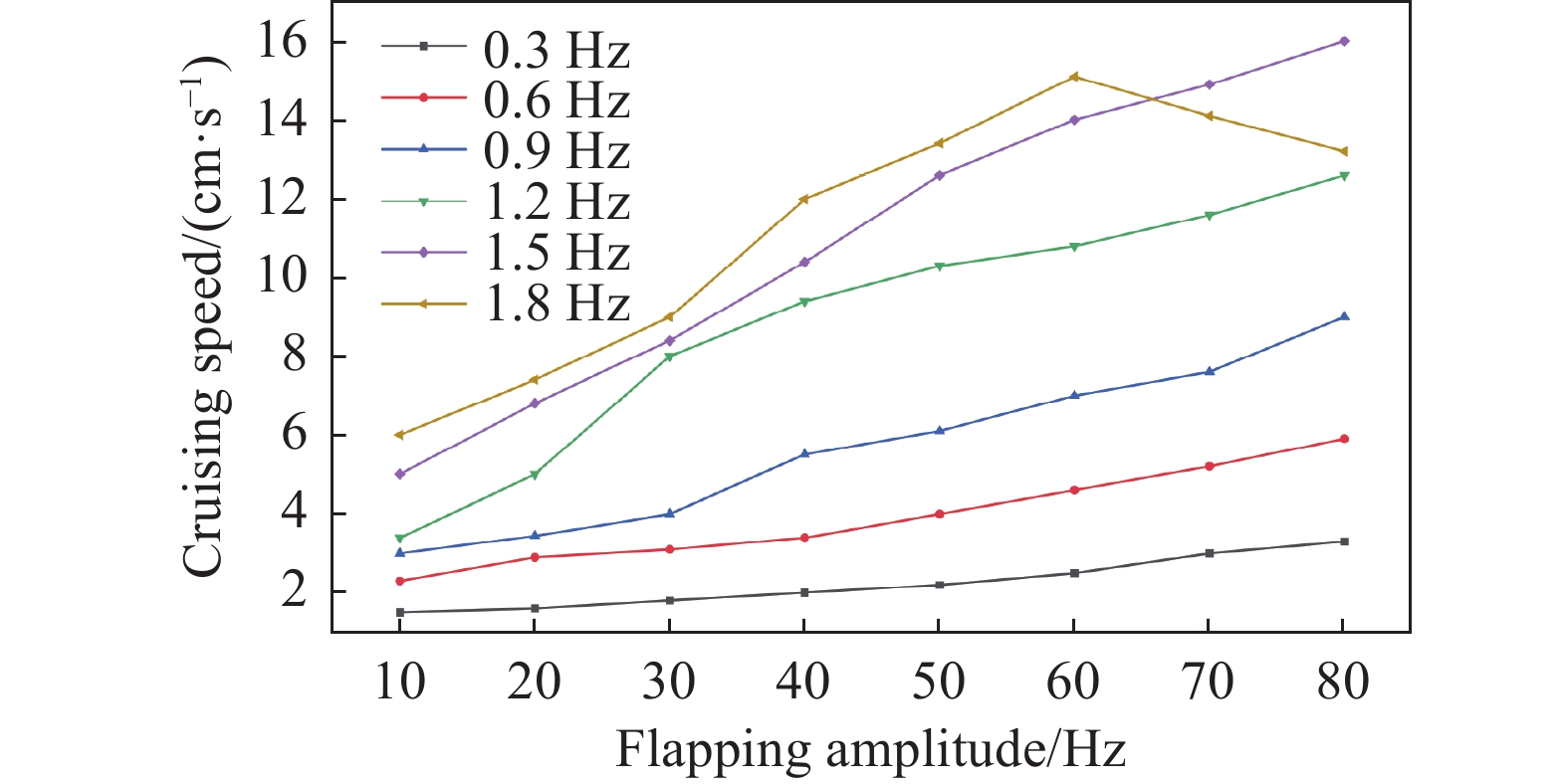
|
| 图 24 巡航速度与拍动频率与振幅的关系 |
从胸鳍和尾鳍协同推进速度变化图可以分析出,在协同推进模式下,机器鱼的巡航速度比单独的BCF或MPF推进模式更快,达到峰值的速度也更快,比较图24和图25,可以看出,胸尾鳍协同推进运动的平均游速有时还不及BCF模式的游速,并且最高游动速度与BCF模式相比几乎相同。这一结果的原因可能是,胸鳍与尾鳍协同推进时,胸鳍摆动产生的推理波与尾鳍的推动波之间存在耦合关系,阻碍整体推进。图25显示了三种推进模式下的理论游速和实际平均游速,其中胸鳍和尾鳍协同推进模式下的平均误差约为16.4%。
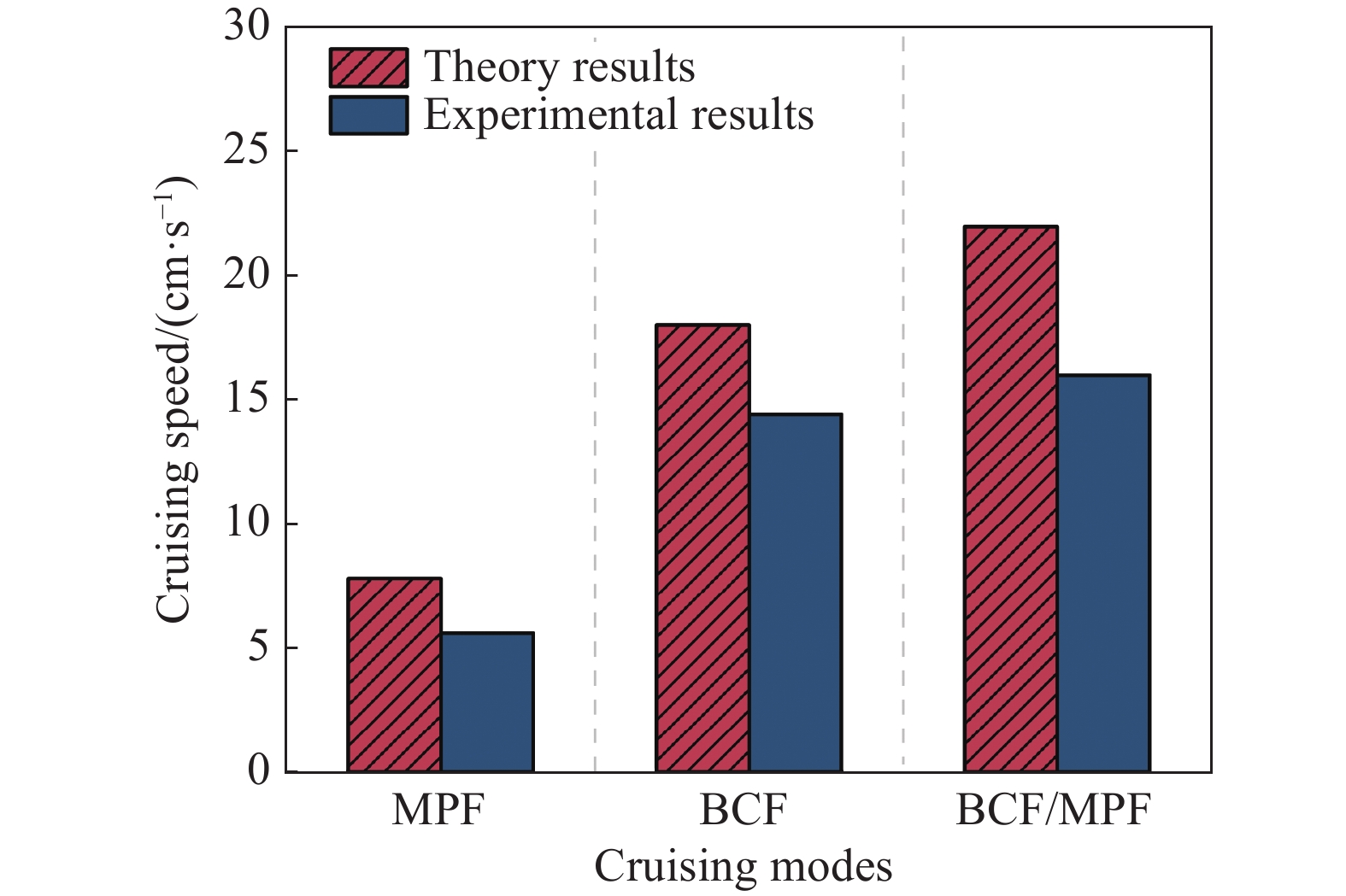
|
| 图 25 不同模式下巡航速度之间的关系 |
5 结束语
以暗绿鲀为灵感,研发了一种仿生机器鱼,实现了胸鳍和尾鳍的协同推进。重点研究了其在直线和转弯时的游泳性能,分别探讨了胸鳍推进、尾鳍推进以及两者复合联动推进的效果。
根据实验结果显示,当仿生机器鱼采用胸鳍和尾鳍协同推进时,其游速可达0.19 m/s,比仅使用尾鳍推进时提高了35%。胸鳍起到了平衡身体和辅助转弯的作用,最大转弯速度为0.4 rad/s,最小转弯半径为0.13 m。在MPF模式下,仿生机器鱼的游速约为0.04 m/s,并且能够稳定游动。由此可见,所设计的仿生机器鱼能够以多种模式直线游动,并且在保持稳定游动的同时,其游速范围较为广泛。此外,实验也存在不足:机器鱼的胸鳍没达到最优位置,胸鳍的游动速度不仅受摆动频率的影响,还受到摆动幅值和初始角度的影响。当初始角增加到60°以后,继续增大会减小胸鳍的摆动幅值,游速会有所下降。改变胸鳍初始角度可进一步提升机器鱼在三种推进模式下的游动速率。
随着水下机器人研究的不断深入,目前仿生机器鱼技术已更偏向于工程应用,面对不同的工况环境,未来可进一步研究以下几个方面:
1) 优化机器鱼游动速度与效率;
2) 改善胸尾鳍协同推进的机动性;
3) 多功能模块组;
4) 人工智能机器鱼。
在后续工作中,将继续从两个方向进行深入研究。一方面,将利用CFD技术进行水动力分析,进一步研究胸鳍和尾鳍叠加的精确控制和机理;另一方面,将从机器鱼的自由潜浮、水下无线通信优化、水下避障等方面提高机器鱼的性能与多样性。
| [1] |
郭海艳, 程亮, 杨春利, 等. 面向水面无人艇的目标检测与船舶分类系统研究[J].
中国测试, 2023, 49(6): 114-121.
GUO H Y, CHENG L, YANG C L, et al. Research on target detection and ship classification system for surface unmanned vessels[J].
China Measurement & Test, 2023, 49(6): 114-121.
DOI:10.11857/j.issn.1674-5124.2022010076 |
| [2] |
李国洪, 周琪钧. 5R串联机器人运动学分析及其控制系统研究[J].
中国测试, 2021, 47(11): 21-27.
LI G H, ZHOU Q J. Research on kinematics analysis and control system of 5R series robot[J].
China Measurement & Test, 2021, 47(11): 21-27.
DOI:10.11857/j.issn.1674-5124.2021050022 |
| [3] |
KATIJA K. Autonomous agents for observing marine life[J].
Science Robotics, 2023, 8(80): eadi6428.
DOI:10.1126/scirobotics.adi6428 |
| [4] |
ZHANG P, WU Z, MENG Y, et al. Nonlinear model predictive position control for a tail-actuated robotic fish[J].
Nonlinear Dynamics, 2020, 101(4): 2235-2247.
DOI:10.1007/s11071-020-05963-2 |
| [5] |
LIGHTHILL M. Note on the swimming of slender fish[J].
Journal of fluid Mechanics, 1960, 9(2): 305-317.
DOI:10.1017/S0022112060001110 |
| [6] |
LIGHTHILL M. Large-amplitude elongated-body theory of fish locomotion[J].
Proceedings of the Royal Society of London. Series B. Biological Sciences, 1971, 179(1055): 125-138.
|
| [7] |
YU Z, LI K, JI Y, et al. Fast motion performance of a bionic ray robot with serial pectoral fins[J]. IEEE Robotics and Automation Letters, 2023.
|
| [8] |
BIANCHI G, TEALDI M, CINQUEMANI S. Design of a bioinspired ray robot with flexible fins[C]//Bioinspiration, Biomimetics, and Bioreplication XII. SPIE, 2022, 12041: 151-157.
|
| [9] |
CASTANO M, TAN X. Trajectory tracking control of rowing pectoral fin-actuated robotic fish[J].
IEEE/ASME Transactions on Mechatronics, 2022, 27(4): 2007-2015.
DOI:10.1109/TMECH.2022.3175765 |
| [10] |
ZHONG Y, DU R, GUO P, et al. Investigation on a new approach for designing articulated soft robots with discrete variable stiffness[J].
IEEE/ASME Transactions on Mechatronics, 2021, 26(6): 2998-3009.
DOI:10.1109/TMECH.2021.3049592 |
| [11] |
WALKER B, ISHIMOTO K, GAFFNEY E A. Hydrodynamic slender-body theory for local rotation at zero Reynolds number[J].
Physical Review Fluids, 2023, 8(3): 034101.
DOI:10.1103/PhysRevFluids.8.034101 |
| [12] |
LIU J, FU Y, LIU X, et al. A bar-joint model based on the corrected resistive force theory for artificial flagellated micro-swimmers propelled by acoustic waves[J].
Bioinspiration & Biomimetics, 2023, 18(3): 035003.
|
| [13] |
ELOY C, MICHELIN S. On Lighthill's elongated-body theory[J]. Bulletin of the American Physical Society, 2023.
|
| [14] |
XU M, YU Y. Effects of body stiffness on propulsion during fish self-propelled swimming[J]. Physics of Fluids, 2023, 35(7).
|
| [15] |
LI Z, XIA D, YANG G, et al. Hydrodynamics of the self-diving function of thunniform swimmer relying on switching the caudal fin shape[J].
Journal of Marine Science and Technology, 2023, 28(1): 326-340.
DOI:10.1007/s00773-023-00927-8 |
 2024, Vol. 50
2024, Vol. 50


 ,
,