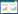中国测试  2024, Vol. 50 Issue (8): 1-10

文章信息

宋大雷, 孙兆阳, 孙康康, 张家乐, 贺同福
SONG Dalei, SUN Zhaoyang, SUN Kangkang, ZHANG Jiale, HE Tongfu
基于改进WOA-MP算法的多普勒海流计回波信号频率估计研究
Research on frequency estimation of Doppler current meter echo signal based on optimization WOA-MP algorithm
中国测试, 2024, 50(8): 1-10
CHINA MEASUREMENT & TEST, 2024, 50(8): 1-10
http://dx.doi.org/10.11857/j.issn.1674-5124.2024030129

文章历史

收稿日期: 2024-03-28
收到修改稿日期: 2024-05-20
 Abstract              PDF               Figures               Tables
引用本文 0
宋大雷, 孙兆阳, 孙康康, 张家乐, 贺同福. 基于改进WOA-MP算法的多普勒海流计回波信号频率估计研究[J]. 中国测试, 2024, 50(8): 1-10.
SONG Dalei, SUN Zhaoyang, SUN Kangkang, ZHANG Jiale, HE Tongfu. Research on frequency estimation of Doppler current meter echo signal based on optimization WOA-MP algorithm[J]. CHINA MEASUREMENT & TEST, 2024, 50(8): 1-10.
基于改进WOA-MP算法的多普勒海流计回波信号频率估计研究
宋大雷1 , 孙兆阳1 , 孙康康2 , 张家乐1 , 贺同福1     
1. 中国海洋大学工程学院，山东 青岛 266000;
2. 中石化胜利石油工程有限公司钻井工艺研究院，山东 东营 257017
收稿日期：2024-03-28; 收到修改稿日期：2024-05-20
基金项目：国家自然科学基金(52301390)；山东省自然科学基金(ZR2022QE072）；中央高校基本科研业务费专项资金(202213029)
作者简介：宋大雷（1972-），男，黑龙江哈尔滨市人，教授，博士，研究方向为智能感知与控制、检测技术与自动化装置。
通信作者：贺同福（1989-），男，山东淄博市人，讲师，博士，研究方向为智能感知与先进控制技术。
摘要：受海洋环境复杂干扰影响，多普勒式海流计的超声波回波信号易受干扰影响，包含多种频率成分，这给海流流速信息的解算带来困难。为解决多普勒海流计回波信号频率估计精度较差的问题，提出一种基于信号匹配追踪（MP）的频率估计方法，并融合改进型鲸鱼优化算法（MWOA）提高估计过程的效率。该方法利用混沌映射提升初始种群多样性，并引入自适应权重和非线性收敛因子提高算法局部寻优能力、搜索速度和求解精度。而后，对改进算法与其他优化算法进行对比测试，结果显示所设计改进算法在收敛速度和寻优能力上具有有效性和优越性。此外，通过对多普勒回波信号进行特征重构，开展MWOA-MP算法在噪声环境下的频率估计精度性能测试。在回波信号信噪比为–10 dB条件下，MWOA-MP算法相对传统方法抗噪声能力提高30%。与其他智能方法融合MP后的频率估计算法相比，MWOA-MP算法的估计误差在10 Hz以内，可满足多普勒海流计频率测量精度要求。
关键词：多普勒海流计    频率信号估计    鲸鱼优化算法    匹配追踪    
Research on frequency estimation of Doppler current meter echo signal based on optimization WOA-MP algorithm
SONG Dalei1 , SUN Zhaoyang1 , SUN Kangkang2 , ZHANG Jiale1 , HE Tongfu1     
1. School of Engineering, Ocean University of China, Qingdao 266000, China;
2. Drilling Technology Research Institute, Sinopec Shengli Petroleum Engineering Co., Ltd., Dongying 257017, China
Abstract: Due to the complex interference of the marine environment, the ultrasonic echo signal of the Doppler current meter is easily affected by interference and contains multiple frequency components, which makes it difficult to calculate the current velocity information. To tackle the issue of reducing frequency estimation accuracy of the echo signal, a frequency estimation method based on signal matching pursuit is proposed, improving the estimation process’s efficiency with a modified whale optimization algorithm. The modified method uses chaotic mapping to enhance the diversity of the initial population, and introduces adaptive weights and nonlinear convergence factors to improve the algorithm's local optimization capability, search speed, and solution accuracy. Subsequently, the improved algorithm was compared with other optimization algorithms in a test, and the results showed that the designed improved algorithm was effective and superior in terms of convergence speed and optimization ability. In addition, by reconstructing the characteristics of Doppler echo signals, the frequency estimation accuracy performance of the MWOA-MP algorithm in noisy environments was tested. Under the condition of an echo signal-to-noise ratio of -10 dB, the MWOA-MP algorithm has a 30% improvement in noise immunity compared to traditional methods. Compared with other intelligent methods that fuse MP with frequency estimation algorithms, the MWOA-MP algorithm has an estimation error within 10 Hz, which meets the frequency measurement accuracy requirements of Doppler current meters.
Key words: Doppler current meter     frequency signal estimation     whale optimization algorithm     matching pursuit    
0 引　言

声学多普勒海流计作为一种先进的海洋观测技术，其独特的非侵入性测量方式以及高时空分辨率的特性，为深入理解海洋动力学和气候变化提供了有力工具。本文中所设计的多普勒海流计的硬件整体结构由主控单元、发射模块和接收模块组成，如图1所示。

图 1 多普勒海流计电路功能示意图
图选项

发射端发出的超声波信号经水体发射后，通过测量接收频率与发射频率之间的频率差，可以获取移动水团包含的流速流向信息。而针对频率成分复杂的超声波回波信号，传统频率估计方法如快速傅里叶变换（FFT）、自相关函数法（AF）等方法受限于采样数据个数和较低的频率分辨率，无法对复杂频率成分进行精确估计，因此亟需一种新的频率估计方法解决上述问题。

近年来，国内外学者通过改进多种智能优化算法结合匹配追踪算法，对频率信号进行估计和重构的研究越来越丰富。例如，LI X等人利用帝国竞争算法（ICA）结合WOA对管道内的污垢厚度进行监测，将接收到的超声波回波信号进行稀疏分解，并使用Chirp原子的参数对原信号进行重构，有较好的信号拟合效果[1]。ZHANG X等人使用鲸鱼优化算法和正交匹配追踪（OMP）方法对轴承故障进行诊断，通过WOA-OMP与构建的Gabor原子OMP比较，对模拟故障信号进行拟合实验验证，结果表示，融合WOA算法后提高了信号稀疏表示的效率和准确性[2]。CHANG M等人在超声无损检测中利用联合稀疏表示和花授粉算法（FRA）对超声信号进行参数估计和重构，提出改进的匹配追踪方法，降低了噪声，减少了信号叠加并提高了重构精度[3]。陈果等人提出一种非局部均值的鲸鱼优化去噪算法，准确检测套管内部引线变形情况，有效降低由振动引入超声波回波信号中的噪声影响[4]。林涛等人提出一种改进鲸鱼优化轻梯度提升机的算法，用于对风机主轴轴承的早期故障进行预警，达到了快速准确的预警效果[5]。

综上，本文针对多普勒海流计回波频率成分复杂，难以有效提取的问题，提出了一种改进鲸鱼优化结合匹配追踪的频率估计算法。针对相关改进步骤进行设计，并通过仿真实验验证频率估计算法的有效性和可靠性。

1 鲸鱼优化算法

鲸鱼优化算法借鉴鲸鱼群体行为，模拟集体智慧，主要的步骤有：初始化种群、寻找猎物、包围猎物、捕食猎物、更新种群。WOA包含两个关键阶段：探索阶段和开发阶段[6]。假设种群中有$ {{N}}_{{\rm pop}} $头鲸鱼，觅食空间为$ {{d}}_{{s}} $维，第i头鲸鱼位置为$ {{{\boldsymbol{X}}}}_{{i}}{=}{(}{{x}}_{{i}}^{{1}}{,}{{x}}_{{i}}^{{2}}{,\cdots ,} {{x}}_{{i}}^{{{d}}_{{s}}}{)} $。

1.1 包围猎物和气泡驱赶攻击机制

鲸鱼在狩猎前，必须先找到猎物，鲸鱼进行位置更新以包围猎物，式(1)和(2)是鲸鱼的位置更新表达式。

$ {\boldsymbol{X}}(t + 1) = {{\boldsymbol{X}}^ * }(t) - {\boldsymbol{A}} \cdot {{D}} $ (1)
$ {{D}} = \left| {{\boldsymbol{C}} \cdot {{\boldsymbol{X}}^ * }(t) - {\boldsymbol{X}}(t)} \right| $ (2)

式中：$ {{\boldsymbol X}}^{\text{*}}\text{(}{t}\text{)} $——第t次迭代后当前鲸鱼种群中的最佳位置，当前鲸鱼的位置表示为$ {X}\text{(}{t}\text{+1)} $；

D——鲸鱼和猎物之间的距离；

A和C——稀疏向量，其表达式如下：

$ {\boldsymbol{A}} = 2 \cdot {\boldsymbol{a}} \cdot {\boldsymbol r}_{1} + {\boldsymbol{a}} $ (3)
$ {\boldsymbol{C}} = 2 \cdot {\boldsymbol r}_{2} $ (4)

其中，a从2开始逐渐减小，直至迭代结束时降至0；$ {{\boldsymbol r}}_{\text{1}} $和$ {{\boldsymbol r}}_{\text{2}} $为取值范围在0和1之间不相关的两个随机数。鲸鱼靠近猎物的区域可以通过A和C的值来控制，模拟鲸鱼群体中的两种不同行为，即“躲避”和“聚集”。此外，鲸鱼优化算法可采取螺旋气泡围捕策略，靠近猎物：

$ {\boldsymbol{X}}(t + 1) = {{\rm e}^{bl}} \cdot \cos (2\pi l) \cdot {{{D}}^ * } + {{\boldsymbol{X}}^ * }(t) $ (5)
$ {{{D}}^ * } = \left| {{{\boldsymbol{X}}^ * }(t) - {\boldsymbol{X}}(t)} \right| $ (6)

其中，D*表示使用螺旋气泡围捕策略后鲸鱼与猎物之间的距离；b取常数1，表示对数螺线形状；l为范围在[–1,1]的随机数，每次迭代过程中使用式(7)，等概率的选择收缩和螺旋包围机制：

$ \boldsymbol{X}(t+1)=\left\{\begin{array}{*{20}{l}}\boldsymbol{X}^*(t)-\boldsymbol{A}\cdot{D}& \mathrm{if}\; p < 0.5 \\{\rm{e}}^{bl}\cdot\cos(2\pi l)\cdot{ D}^*+{\boldsymbol X}^*(t)& \mathrm{ if}\; p\geqslant0.5\end{array}\right. $ (7)

其中，p为[0,1]中任意的值。

1.2 搜索猎物

在开发阶段，算法采用随机搜索方法而非依赖已找到的最佳位置进行位置更新，使用矢量A来控制当前鲸鱼与现有鲸鱼的相对距离。当|A|>1时，远离现有鲸鱼，当|A|≤1时，靠近现有鲸鱼。

$ {\boldsymbol{X}}(t + 1) = {{\boldsymbol{X}}_{\rm rand}}(t) - {\boldsymbol{A}} \cdot {{D}} $ (8)
$ {{D}} = \left| {{\boldsymbol{C}} \cdot {{\boldsymbol{X}}_{\rm rand}}(t) - {\boldsymbol{X}}(t)} \right| $ (9)

其中，$ {\boldsymbol{X}}_{{\rm rand}}\left({t}\right) $为第t次迭代中从整个鲸鱼种群中随机选择的某鲸鱼位置。在确定合适的寻优算法后，可提升匹配追踪算法的运算效率和搜索速度。

2 匹配追踪算法

匹配追踪是一种贪婪算法，它在每次迭代时筛选出与待测信号近似的频率成分[7]。MP算法的一个显著特点是使用过完备频率原子字典来表示信号。因此，实现MP算法的关键问题是：选择与待测信号匹配度更高的原子字典和设计快速准确的稀疏分解算法[8]。

2.1 频率原子库构建

建立频率原子字典主要分为两个步骤：第一步，利用基函数，生成与待测信号采样频率相同的频率原子；第二步，对基函数生成的频率原子进行归一化，每个原子的范数都为1，可以更好的控制和维护数值的稳定性，减小数值误差的影响[9]。根据待测信号的频率特征，设计如下频率原子字典基函数[10]：

$ {g_\gamma }(n) = \cos (2\pi {f_m}n) $ (10)

式中：$ {n}{=0,1,}{}{\cdots ,}{{N}}_{{s}}{-1} $；$ {m}{=0,1,}{}{\cdots ,}{{M}}_{{s}}{-1} $；

$ {{f}}_{{m}} $——按照频率搜索精度和频率范围取值的频率参量；

$ {{N}}_{{s}} $——频率原子按采样频率所得到的采样个数，即信号的维度；

$ {{M}}_{{s}} $——频率搜索个数，即整个频率原子字典的原子数量；

$ \gamma $——原子参数，仅与m相关。

将生成的原子放入原子字典$ {{{\boldsymbol{G}}}}_{{ \Gamma }} $中，得到$ {{{\boldsymbol{G}}}}_{{ \Gamma }}{=}{[}{{g}}_{{1}}{,}{{g}}_{{2}}{,\cdots ,}{{g}}_{\gamma}{]} $，$ { \Gamma } $为参数组$\gamma $的集合。接着对原子字典按列归一化：

$ {{\boldsymbol{\varPhi}} _N} = {\rm Norm}({{\boldsymbol{G}}_\Gamma }) $ (11)

归一化后的频率原子字典$ {{\boldsymbol{\varPhi}}}_{{N}}\text{=}\left[{\phi}_{\text{1}}\text{,}{\phi}_{\text{2}}\text{,…,}{\phi}_{\gamma}\right] $，且$ {\phi}_{\gamma}\text{=}||{{g}}_{\gamma}|| $，也称为单位频率原子字典。

2.2 模拟信号构建

多普勒海流计接收的回波信号可以被视为由P个余弦信号组合而成，第i次取样的回波信号其模型可以表示为：

$ x(i) = \sum {_{p = 1}^P{A_p}\cos [2\pi {f_p}(n - {u_p}) + {\theta _p}]} + \sigma (n) $ (12)

式中：$ {{A}}_{{p}} $——该频率成分的幅度；

$ {{f}}_{{p}} $——回波信号中的某一个频率成分；

$ {{u}}_{{p}} $——信号在时间轴上的延迟；

$ {\theta }_{{p}} $——相位角；

$ \sigma{(}{n}{)} $——引入噪声。

进行MP运算的目的是在待测信号$ {x}{(}{i}{)} $中估计P个余弦信号的频率。因此，在建立模型时，信号表示为存在时间延迟和角度偏移的几种不同频率信号的叠加。

2.3 MP算法步骤

构建好过完备频率原子字典并确立好模拟信号后，就可以确定运算的输入输出参量。输入量为单位频率原子字典$ {\boldsymbol{\varPhi}}_{{N}} $，待分解信号x，稀疏度K；输出量为重构稀疏向量$ \hat{{x}} $。MP方法分解信号的过程如下：

1) 从过完备频率原子字典中选出与待分解信号x内积运算最大的原子，即最匹配的原子$ \phi_{\gamma\text{0}} $，如下所示：

$ \left| {\left\langle {x,{\phi _{{\gamma _0}}}} \right\rangle } \right| = \mathop {\sup }\limits_{\gamma \in \Gamma } \left| {\left\langle {x,{\phi _\gamma }} \right\rangle } \right| $ (13)

2) 信号x可以分解成投影在最佳原子$ \phi_{\gamma\text{0}} $上的分量和残差，如下所示：

$ x = \left\langle {x,\phi {}_{{\gamma _0}}} \right\rangle {\phi _{{\gamma _0}}} + {R^1}x $ (14)

其中，$ {{R}}^{\text{1}}{x} $为残差，对最佳匹配后的残差重复上述分解操作：

$ {R^j}x = \left\langle {{R^j}x,{\phi _{{\gamma _j}}}} \right\rangle {\phi _{{\gamma _j}}} + {R^{j + 1}}x $ (15)

其中，j∈[1,k]，$ {{R}}^{{j}}{x} $表示第j次分解的残差，分解次数与稀疏度K有关。

$ \left| {\left\langle {{R^j}x,{\phi _{{\gamma _j}}}} \right\rangle } \right| = \mathop {\sup }\limits_{\gamma \in \Gamma } \left| {\left\langle {{R^j}x,{\phi _\gamma }} \right\rangle } \right| $ (16)

3) 经过K次分解后，信号被分解为：

$ x = \sum {_{j = 0}^{K - 1}\left\langle {{R^j}x,{\phi _{{\gamma _j}}}} \right\rangle } {\phi _{{\gamma _j}}} + {R^K}x $ (17)

在信号长度有限的情况下，每次分解时都有与剩余残差最匹配的原子被筛选出来，当稀疏度不太大时，$ {{R}}^{{K}}{x} $已按指数减小至靠近0。舍去该残差后重构信号表示为：

$ \hat x = \sum {_{j = 0}^{K - 1}\left\langle {{R^j}x,{\phi _{{\gamma _j}}}} \right\rangle } {\phi _{{\gamma _j}}} $ (18)

其中，$ {K}\ll {{M}}_{{s}} $，公式(17)和(18)体现了信号稀疏分解的思想，待测信号频率特征被稀疏表示。然而，使用 MP方法对信号进行重构时，存在特征匹配精度不足，原子搜索速度慢等缺点。为了在原子库中快速搜索与待测信号最相似的频率原子，下文将融合改进后的鲸鱼优化算法解决上述问题。

3 融合与改进方法

由于WOA存在全局搜索和局部开发能力不平衡，容易陷入局部最优的问题，本文采用改进后的WOA算法，通过在连续空间中的优化更新步骤来替代MP运算的逐次比较和遍历优化过程，从而提高了算法的效率和性能。

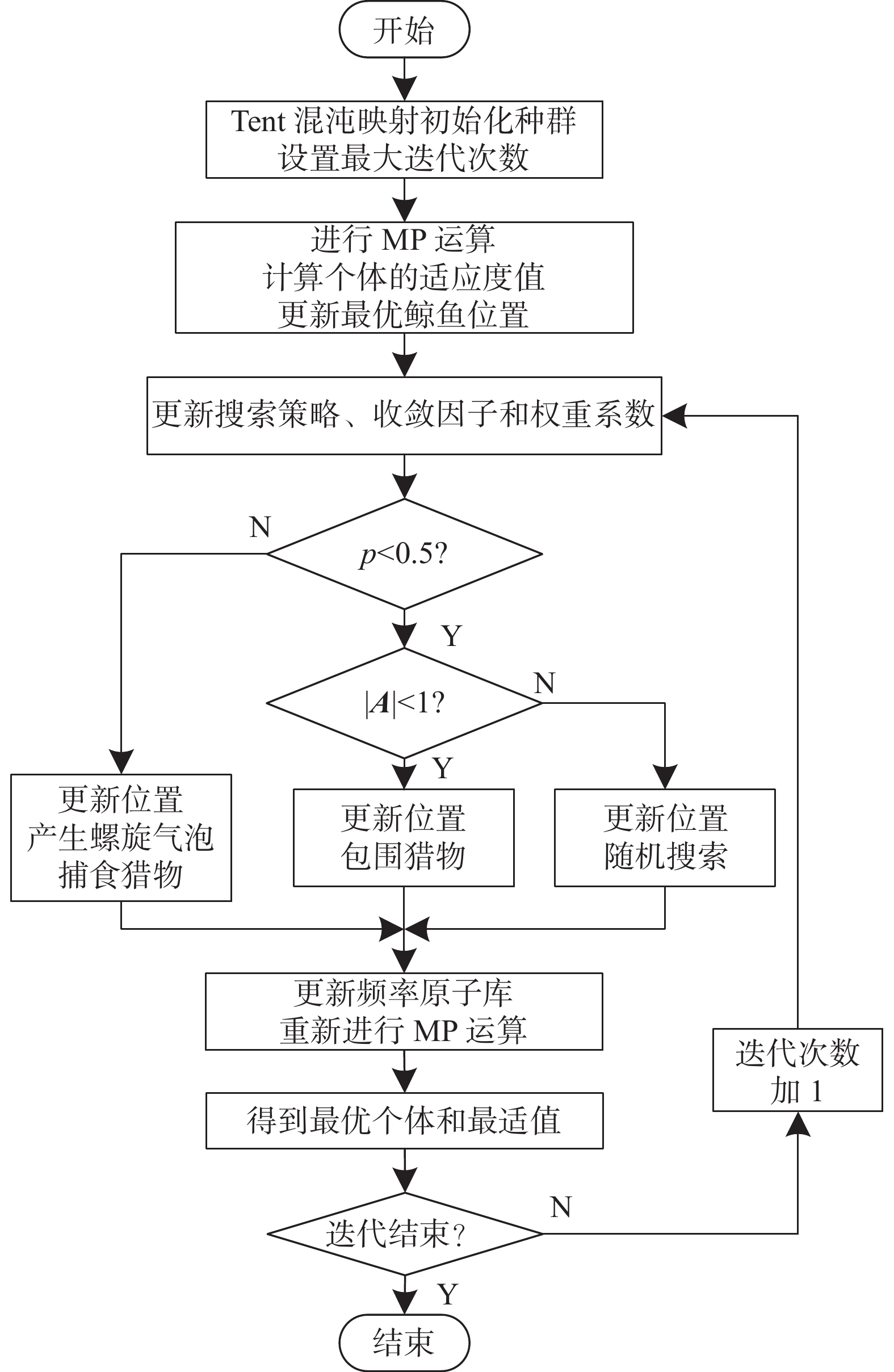
3.1 融合方法

针对MP计算中的问题，构造WOA-MP的融合算法，其设计步骤如下：

1) 建立初始鲸鱼种群，设置种群的数量、维度。使用式(10)生成频率原子字典中的原子，设置相应采样个数和频率原子数目，并将生成的频率原子进行归一化处理。

2) 进行MP运算，计算待测信号与原子字典频率原子的内积，获得内积最大值，更新适应值，含义为种群中最佳鲸鱼与猎物的距离。

3) 利用式(3)和(4)，设置影响鲸鱼种群在位置更新、收缩包围和捕食过程中各随机变量的值，利用式(1)、(5)和(8)，在迭代过程中选择不同的收缩包围策略。

4) 更新最佳鲸鱼个体的位置信息，即频率原子字典中的最优原子。保留经MP运算后最优鲸鱼个体对应的最适值。

5) 计算得到信号残差R，继续进行MP运算，直到提取出信号的主要特征，使重构的稀疏矩阵满足稀疏度K，停止WOA-MP迭代计算。

使用融合算法对待测信号进行分解后，待测信号所包含的频率特征被原子库稀疏表示，从而用较少的符合信号本身特点的原子线性组合来表示待测信号。

3.2 改进方法

由于WOA自身存在局限性，易陷入局部最优且求解精度受限。为了提升融合算法在频率信号估计中的性能，深入改进和优化至关重要。

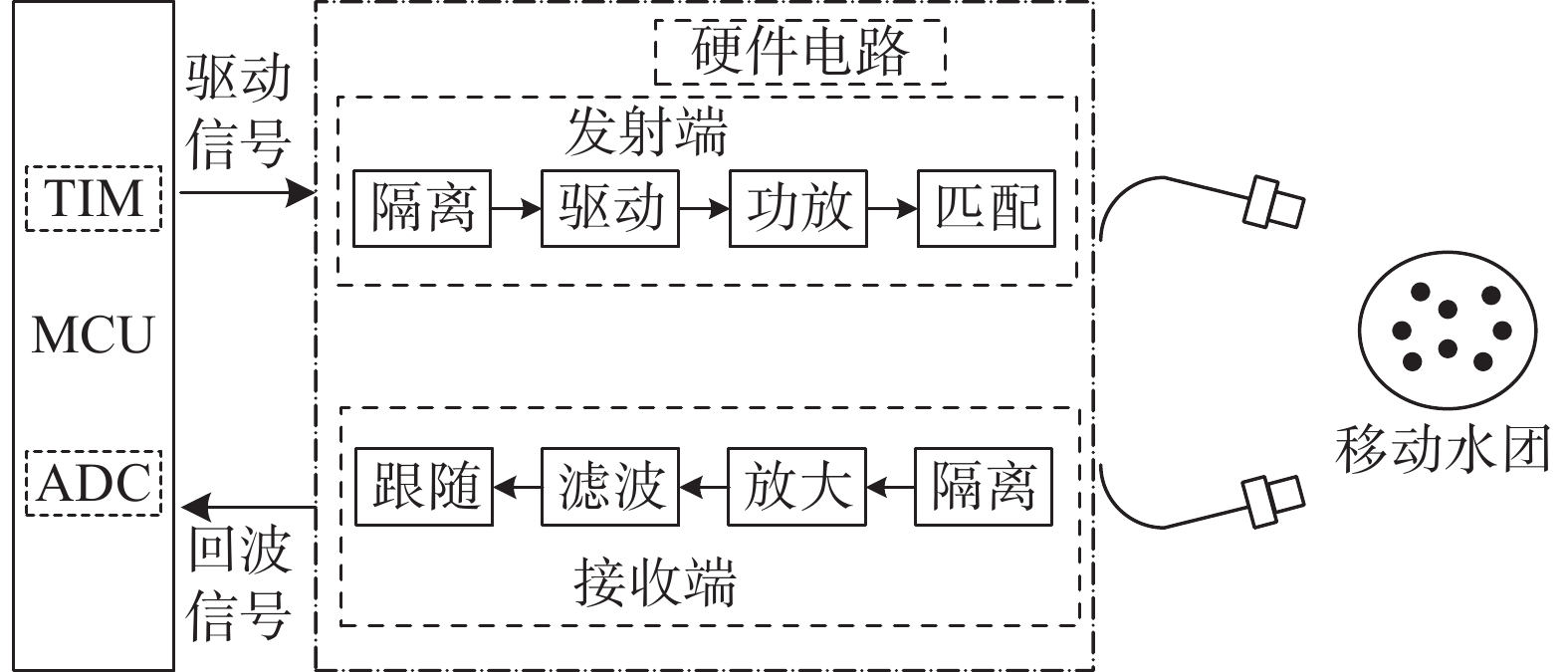
3.2.1 混沌映射初始化种群

混沌映射是一种结合确定性和随机性的方法。在初始化位置更新过程中，混沌变量替代了随机变量，因此混沌映射策略相较于随机搜索策略，在解空间的搜索范围更为广泛。对于随机初始化过程而言，混沌初始化有助于提升优化算法的搜索广度[11]。为了提高种群初始解的多样性，本设计采用改进型Tent混沌映射来生成高度多样化的初始鲸鱼种群[12]。

$ {{\textit{z}}}_{k+1}=\left\{\begin{array}{c}\begin{array}{l}2\cdot ({{\textit{z}}}_{k}+0.1\cdot {\rm rand}(0\text{，}1))\\ {\rm if}\;0\leqslant {{\textit{z}}}_{k} < {a}_{c}\\ 2-2\cdot \left({{\textit{z}}}_{k}+0.1\cdot {\rm rand}(0\text{，}1)\right)\\ {\rm if}\;{a}_{c}\leqslant {{\textit{z}}}_{k}\le 1\end{array}\end{array}\right. $ (19)

其中，ac是映射参数，取值范围在0到1之间，初始映射值 $ {\textit{z}}_{\text{0}} $设置为0.342。图2是未进行混沌映射的随机初始种群，与根据式(19)定义的Tent混沌映射生成随机初始种群进行比较。ac取0.5，初始种群数量为900，随机在[–10,10]间，生成初始种群。经过混沌映射的初始种群，在[–10,10]之间的种群特征较为平衡，在各个取值点上呈现均匀分布。

图 2 初始鲸鱼种群分布
图选项

3.2.2 引入非线性收敛因子

在传统的鲸鱼位置更新中，由式(1)中的$ \boldsymbol{A}\cdot {D} $决定每次的收缩步长，A决定着鲸鱼优化算法的全局探索和局部开发能力。其中，a为线性收敛因子，其随着迭代次数增加而线性减小，使收敛速度变慢。通过引入非线性收敛因子，调整算法的收敛速度[13]。另外对$ {{r}}_{\text{1}} $引入三角函数惯性因子，以匹配a值的收敛趋势，具体公式如下：

$ {{a}} = 2 \cdot \left(1 - \frac{t}{{{T_{\max }}}}\right) \cdot \left(1 - \frac{{{t^2}}}{{T_{\max }^2}}\right) $ (20)
$ {{\boldsymbol{r}}}_{1}^{\ast }=\mathrm{sin}\left[\frac{\pi }{2}\cdot \left(1-\frac{t}{{T}_{\mathrm{max}}}\right)\right]\cdot {\rm rand}(0\text{，}1) $ (21)

在进行鲸群位置更新时引入自适应权重系数，进一步提高算法收敛速度。定义如下：

$ {\boldsymbol{X}}(t + 1) = \left(\frac{{{t^2}}}{{T_{\max }^2}}\right) \cdot {{\boldsymbol{X}}^ * }(t) - {\boldsymbol{A}} \cdot {{D}} , \left| {\boldsymbol{A}} \right| < 1,p < 0.5 $ (22)
$ \boldsymbol{X}(t+1)= \left(\frac{t^2}{T_{\max}^2}\right)\cdot\boldsymbol{X}\mathrm{_{rand}}(t)-\boldsymbol{A}\cdot{D}, \left|\boldsymbol{A}\right|\geqslant1,p < 0.5$ (23)
$ \begin{split} {\boldsymbol{X}}(t + 1) =& {{D}}^* \cdot {{\rm e}^{bl}} \cdot {\mathrm{cos}}(2\pi l) + (1 - {t^2}/({T_{\max }}^2) \cdot {{\boldsymbol{X}}^ * }(t) \\ &p \geqslant 0.5 \end{split}$ (24)

$ {{t}}^{\text{}\text{2}}\text{/}{{T}}_{\text{max}}^{\text{}\text{2}} $为猎物位置的自适应权重，随着迭代次数的增加，使鲸鱼朝向猎物收缩的速率越快。当p<0.5时，引入$ {{t}}^{\text{}\text{2}}\text{/}{{T}}_{\text{max}}^{\text{}\text{2}} $权重，以便寻优问题中的最优解被充分利用；当p≥0.5时，引入$ {1-}{{t}}^{\text{}\text{2}}\text{/}{{T}}_{\text{max}}^{\text{}\text{2}} $权重，使用螺旋收缩的方法更新鲸鱼位置，当迭代次数累积后，权重减小，进一步提高鲸鱼种群的局部搜索能力[14]。改进后的MWOA-MP的融合算法流程图如图3所示。

图 3 融合算法流程图
图选项

4 仿真结果与分析

首先，为了测试改进型鲸鱼优化算法的效果，用国际进化会议（CEC）测试函数中10个基准函数对粒子群优化算法（PSO）、帝国竞争算法（ICA）、灰狼优化算法（GWO）、鲸鱼优化方法（WOA）和改进鲸鱼优化方法（MWOA）进行算法性能对比实验[15]。其次，通过引入带高斯噪声的模拟信号，将MWOA-MP与FFT和AF进行对比，突出改进后频率估计算法抗噪能力强与频率分辨率高的优势。最后，比较在处理标准信号过程中，ICA-MP、GWO-MP、WOA-MP和MWOA-MP各自的运算时间、最优值和频率估计精度，综合对比下突出MWOA-MP算法的优越性。

4.1 基准函数测试

CEC基准函数集中包括单峰函数（f1~f4）、多模态函数（f5~f7）、混合函数（f8~f10），使用智能优化算法对基准函数的峰值进行寻优，寻优结果用于评价算法的开发与勘探能力。表1是各智能优化算法的参数，表2是在CEC中使用到的基准函数，表3是各优化算法在搜索最优值的均值与标准差。

表 1 智能优化算法参数
算法名称参数设定
PSOSA=30; It=200; Max=0.9; Min=0.2; c1=2; c2=2
ICASA=30; It=200; Imp=5; a1=2; RR=0.4; Zeta=0.02
WOASA=30; It=200; e=2.717; b2=1; P2=0.5
GWOSA=30; It=200; A1=0.2; A2=0.3; A3=0.4
MWOASA=30; It=200; e=2.717; b3=1; P3=0.5; a0=0.99; r0=0.99; E=0.5
表选项

表 2 标准测试函数集
基准函数维度范围理论最小值
${f_1}(x) = \displaystyle \sum\limits_{i = 1}^n {x_i^2} $30[–100,100]0
${f_2}(x) = \displaystyle \sum\limits_{i = 1}^n {\left| {{x_i}} \right|} + \displaystyle \prod\limits_{i = 1}^n {\left| {{x_i}} \right|} $30[–10,10]0
${f_3}(x) = {\displaystyle \sum\limits_{i = 1}^n {\left(\displaystyle \sum\limits_{j - 1}^i {{x_j}} \right)} ^2}$30[–100,100]0
${f_4}(x) = \displaystyle \sum\limits_{i = 1}^{n - 1} {\left[ {100{{\left( {{x_{i + 1}} - x_i^2} \right)}^2} + {{({x_i} - 1)}^2}} \right]} $30[–30,30]0
${f_5}(x) = \displaystyle \sum\limits_{i = 1}^n {[x_i^2 - 10\cos (2\pi {x_i}) + 10]} $30[–5.12,5.12]0
${f_6}(x) = - 20\exp \left( { - 0.2\sqrt {\dfrac{1}{n}\displaystyle \sum\limits_{i = 1}^n {x_i^2} } } \right) - \exp \left( {\dfrac{1}{n}\displaystyle \sum\limits_{i = 1}^n {\cos (2\pi {x_i})} } \right) + 20 + e$30[–32,32]0
${f_7}(x) = \dfrac{1}{{4000}}\displaystyle \sum\limits_{i = 1}^n {x_i^2} - \displaystyle \prod\limits_{i = 1}^n {\cos \left( {\dfrac{{{x_i}}}{{\sqrt i }}} \right)} + 1$30[–600,600]0
${f_8}(x) = {\left( {0.002 + \displaystyle \sum\limits_{j = 1}^{25} {[j + \displaystyle \sum\limits_{i = 1}^2 {({x_i} - {a_{ij}}){]^{ - 6}}} } } \right)^{ - 1}}$2[–65,65]1
${f_9}(x) = 4x_1^2 - 2.1x_1^4 + \dfrac{1}{3}x_1^6 + {x_1}{x_2} - 4x_2^2 + 4x_2^4$2[–5,5]–1
${f_{10}}(x) = {\left( {{x_2} - \dfrac{{5.1}}{{4{\pi ^2}}}x_1^2 + \dfrac{5}{\pi }{x_1} - 6} \right)^2} + 10\left( {1 - \dfrac{1}{{8\pi }}} \right)\cos {x_1} + 10$2[–5,5]0.3
表选项

表 3 CEC函数测试均值与标准差比较
测试函数 PSO ICA WOA GWO MWOA
Avg SD Avg SD Avg SD Avg SD Avg SD
1 1.004$ \times $10–26 3.441$ \times $10–26 1.780 7.698$ \times $10–1 8.598$ \times $10–9 7.674$ \times $10–9 2.728$ \times $10–1 1.975$ \times $10–1 1.126$ \times $10–157 5.715$ \times $10–157
2 9.484$ \times $10–19 6.019$ \times $10–18 6.839$ \times $101 4.674$ \times $101 5.782$ \times $10–6 2.070$ \times $10–6 1.386 5.351$ \times $10–1 1.356$ \times $10–80 5.375$ \times $10–80
3 7.824$ \times $104 1.766$ \times $104 1.142$ \times $104 4.621$ \times $103 4.248 5.237 4.629$ \times $102 1.797$ \times $102 5.892$ \times $10–143 3.714$ \times $10–142
4 5.169$ \times $101 2.738$ \times $101 3.069$ \times $101 6.810 3.666$ \times $10–2 2.733$ \times $10–2 2.531 5.192$ \times $10–1 1.950$ \times $10–77 1.068$ \times $10–76
5 2.258 1.581$ \times $101 1.752$ \times $102 2.919$ \times $101 1.489$ \times $101 1.571$ \times $101 1.086$ \times $101 3.085$ \times $101 0 0
6 2.050$ \times $10–14 1.734$ \times $10–14 9.007 6.474 1.836$ \times $10–5 8.047$ \times $10–6 1.376 6.665$ \times $10–1 8.882$ \times $10–16 0
7 1.444$ \times $10–2 7.081$ \times $10–2 8.761$ \times $10–1 1.632$ \times $10–1 9.991$ \times $10–3 1.509$ \times $10–2 5.831 2.795 0 0
8 4.660 4.169 9.980$ \times $10–1 0 4.531 3.615 2.950 2.492 4.516 4.573
9 –1.031 5.566$ \times $10–8 –1.031 0 –1.031 1.250$ \times $10–7 –1.031 0 –1.026 8.494$ \times $10–3
10 3.981$ \times $10–1 3.380$ \times $10–4 3.979$ \times $10–1 1.940$ \times $10–9 3.979$ \times $10–1 1.344$ \times $10–5 3.979$ \times $10–1 0 3.996$ \times $10–1 6.543$ \times $10–3
表选项

在Matlab中设置好各算法的参数后，对上述的五种智能优化算法进行测试，表3显示了这五种算法在100次独立运行后的平均值和标准差。图4表示各算法随迭代数增加的寻优效果。通过分析上述图表，可知MWOA算法在求解f1~f7基准函数时寻优效果最好，这表明MWOA在单峰测试函数和多峰测试函数中具有良好的探索和寻优能力，而在混合模态函数中的效果跟其他经典算法效果相差不大。该实验表明在WOA中添加非线性因子和自适应权重对提高WOA的寻优速度和搜索能力是行之有效的。

图 4 各优化算法收敛曲线
图选项

4.2 传统频率估计算法的比较

传统的FFT算法和AF算法都是频率估计常用方法，以下实验将从频率估计误差和抗噪能力两个方面把传统方法与MWOA-MP算法进行对比。标准测试信号是由Matlab生成的离散余弦函数，含多个频率成分，同时严格确保其采样频率和数据长度与原子库中的原子相匹配。

标准测试信号为三种余弦频率成分叠加的信号，$ {{A}}_{{0}} $为信号幅值，$ {{A}}_{{0}}{=1} $；初相位θ为随机位置；n为采样数据点，其个数为2048；纯净信号下的σ(n)=0。信号表示如下：

$ \begin{split} x(n) =& {A_0}\cos (2\pi {f_{{\text{p}}1}}n + {\theta _1}) + {A_0}\cos (2\pi {f_{{\text{p}}2}}n + {\theta _2})+\\ & {A_0}\cos (2\pi {f_{{\text{p}}3}}n + {\theta _3}) \end{split}$ (25)

其中，fp1，fp2，fp3分别设置为4800、5000、5200 Hz，图5显示了标准信号与三种方法的估计效果图。

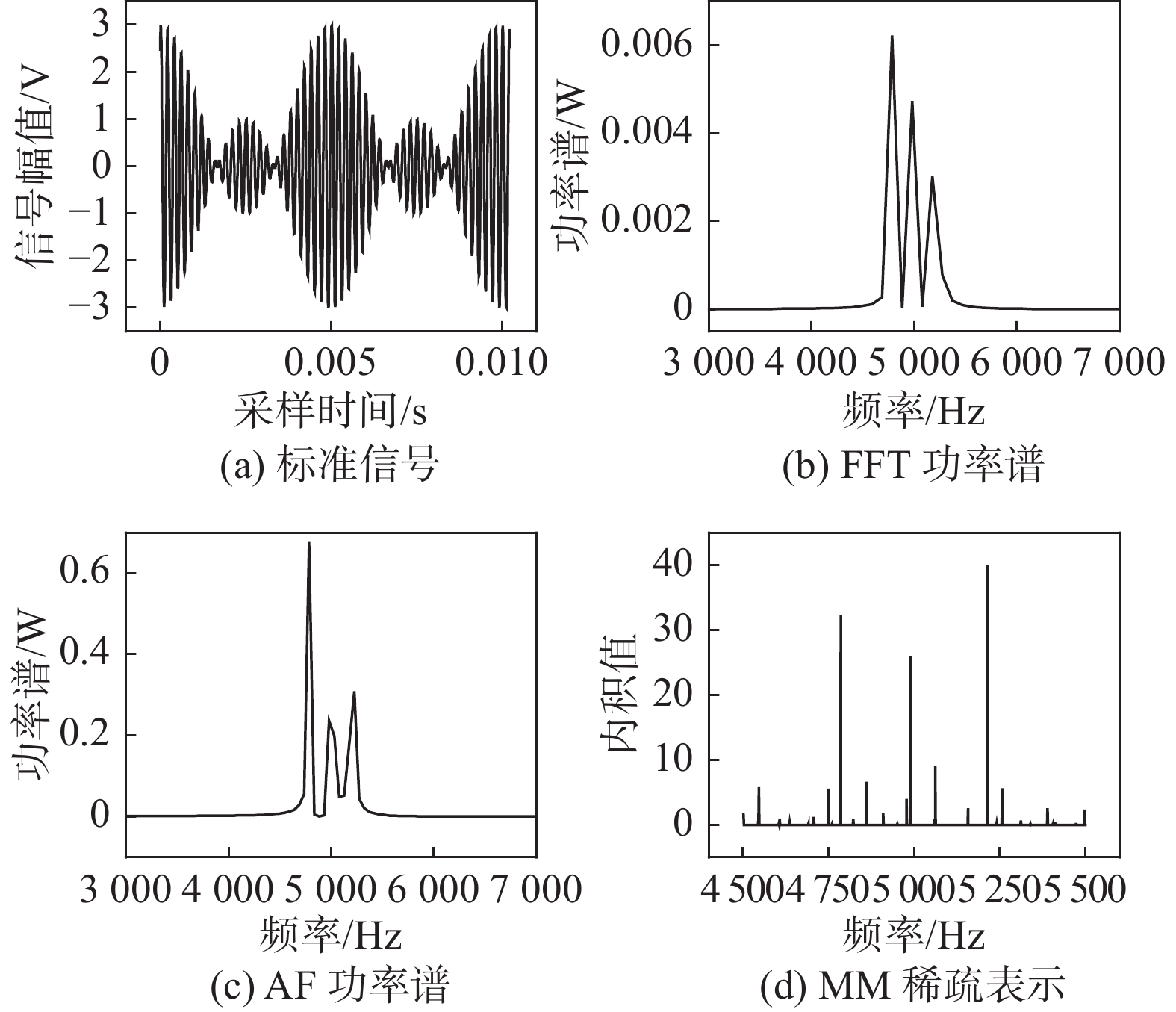
图 5 各算法频率估计效果对比
图选项

图5（a）是标准待测信号共2048个采样点；图5（b）是FFT运算后的频谱图；图5（c）是AF的功率谱图；图5（d）是迭代后的MWOA-MP算法的信号稀疏分解表示。可以看到，改进后的MWOA-MP算法降低了频谱的泄露，同时，考虑到FFT算法和自适应函数算法的频率分辨率都取决于信号的采样点个数，而MP算法的频率分辨率则与原子字典的精度相关。根据分辨率要求，设计原子字典保证算法的频率分辨率，MWOA-MP的频率分辨率较前两者更高。表4展示了20次独立运行后，三种算法的频率测量平均值与三个标准信号频率理论值（fp1、fp2、fp3）的对比结果，并列出了这些测量值与理论值之间的相对误差。

表 4 模拟回波信号下的频率估计相对误差分析
估计算法 fp1 fp2 fp3
AVG/Hz RE/% AVG/Hz RE/% AVG/Hz RE/%
FFT 4786 0.29 4980 0.30 5226 0.50
AF 4785 0.31 4980 0.40 5176 0.46
MM 4790 0.20 4999 0.02 5210 0.19
表选项

其中，AVG代表频率估计均值，以频率单位Hz表示；RE代表估计值相对理论值的相对估计误差，以百分比%表示；MM表示MWOA-MP算法。

此外，在不同噪声环境下评估算法抗噪性能。实验选取四个信噪比等级：–10 、–5 、1 、5 dB，对FFT算法、AF算法和MWOA-MP算法进行测试，并使用均方根误差（RMSE）评价以上方法[16]：

$ {\mathrm{RMSE}} = \sqrt {\frac{1}{Q}\sum\nolimits_{i = 1}^Q {{{\left( {{f_i} - {f_{{\text{p}}1}}} \right)}^2}} } $ (26)

式中：fp1——理论值4800 Hz；

$ {{f}}_{{i}} $——使用算法运算的计算值；

Q——要处理的运算次数。

评价结果如表5所示。

表 5 各频率估计算法RMSE对比
Hz
信噪比/dB FFT AF MM
–10 24.06 19.48 14.97
–5 22.07 20.09 9.83
1 21.25 19.62 8.95
5 19.69 19.21 7.67
表选项

由表5，MWOA-MP算法的RMSE在信噪比较低时稍大，但仍优于传统方法。FFT和AF固有的最小频率分辨率为：

$ \Delta f = \frac{{{f_{\text{s}}}}}{{{N_0}}} $ (27)

式中：fs——采样频率；

N0——信号的数据点个数。

当选取较少的信号数据点进行运算时，可知上述两种方法频率分辨率较差。MWOA-MP算法在–10 dB下对待测信号进行频率估计，其抗噪性能相较另外两种频率估计方法提升30%。

4.3 融合算法的比较

本实验将比较MP与智能优化算法融合后的频率估计效果，将从各算法的运算时间、最优值、频率估计精度这几个方面对算法性能进行测试，使用前文中的标准测试信号开展仿真对比实验。首先，设置算法的迭代次数为200，记录各算法在进行MP运算全部迭代次数之后的总时间，每个算法重复进行100次蒙特卡洛实验[17]，实验结果如图6所示。

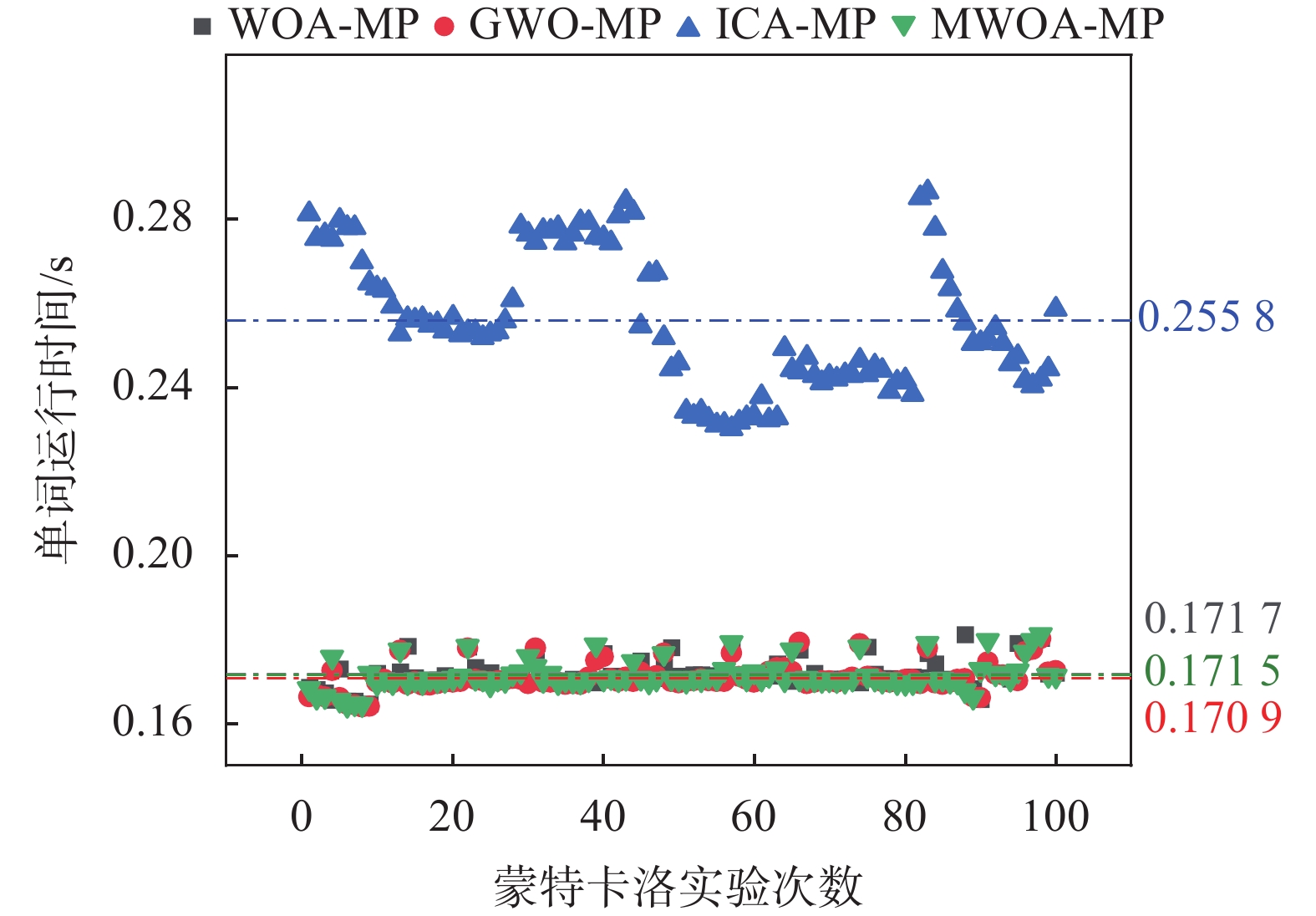
图 6 各算法的运行时间对比图
图选项

经计算，WOA-MP算法、GWO-MP算法和MWOA-MP算法的运算时间相近，而ICA-MP算法的运算时间最长，整个迭代过程中运算时间的跳变幅度也较大。下面开展各算法探索内积最优值的比较，用于比较各算法的全局搜索能力。同样进行100次蒙特卡洛实验，找出每次实验的最优值，即过完备原子字典中最匹配原子与待测信号进行MP运算的内积值。实验结果如图7所示。

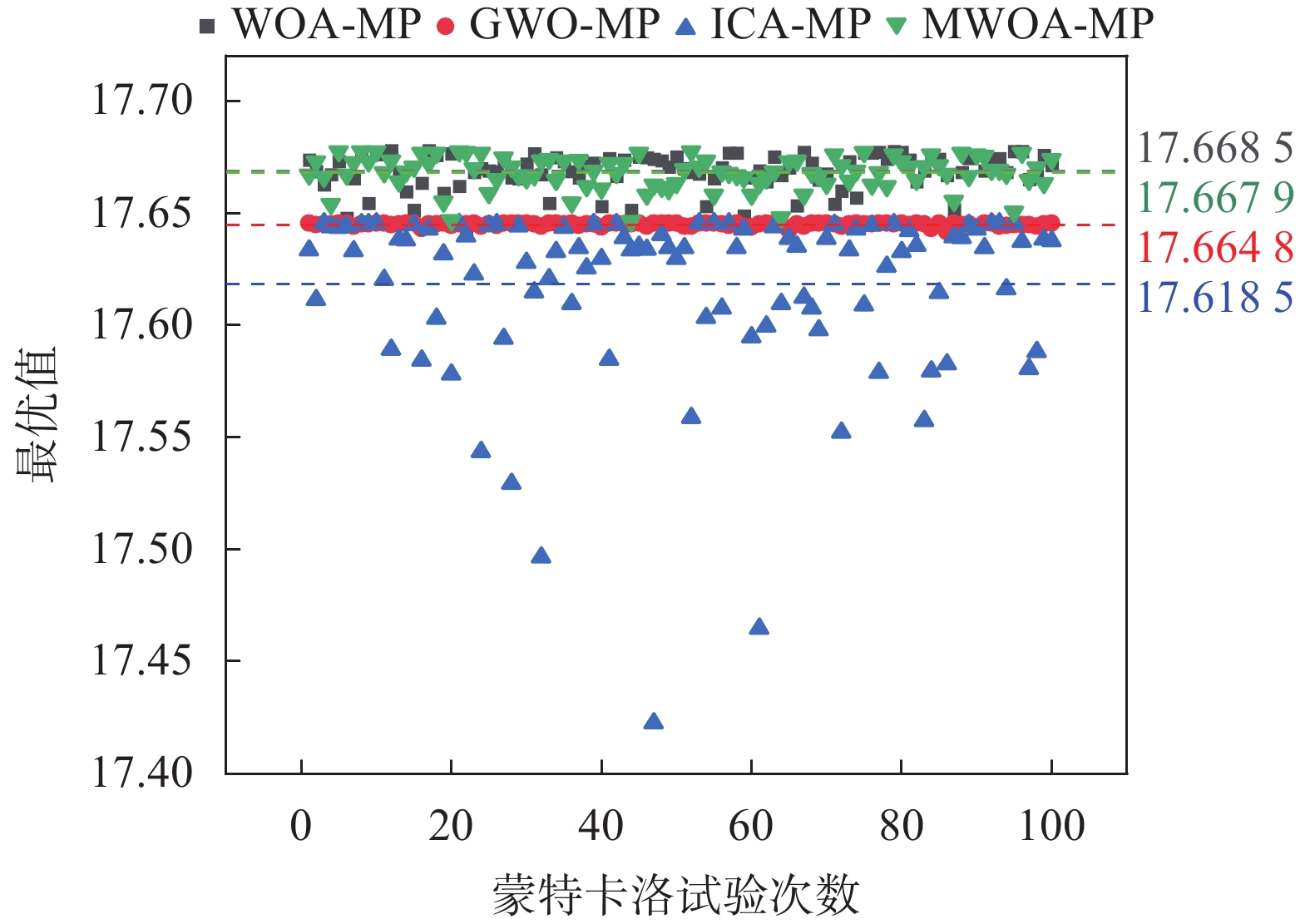
图 7 各优化算法搜索MP运算内积最大值
图选项

由上图的仿真结果，WOA-MP算法和MWOA-MP算法的全局搜索性能较好，GWO-MP算法易陷入局部最优解，而ICA-MP算法的寻优能力和稳定性均较差。

标准信号的频率成分为：4800 Hz（fp1）、5000 Hz（fp2）、5200 Hz（fp3），计算各算法对标准信号的频率估计值，并进行分析。各算法在结束迭代后，从稀疏矩阵中，提取出3个最匹配的频率成分，如图8所示。

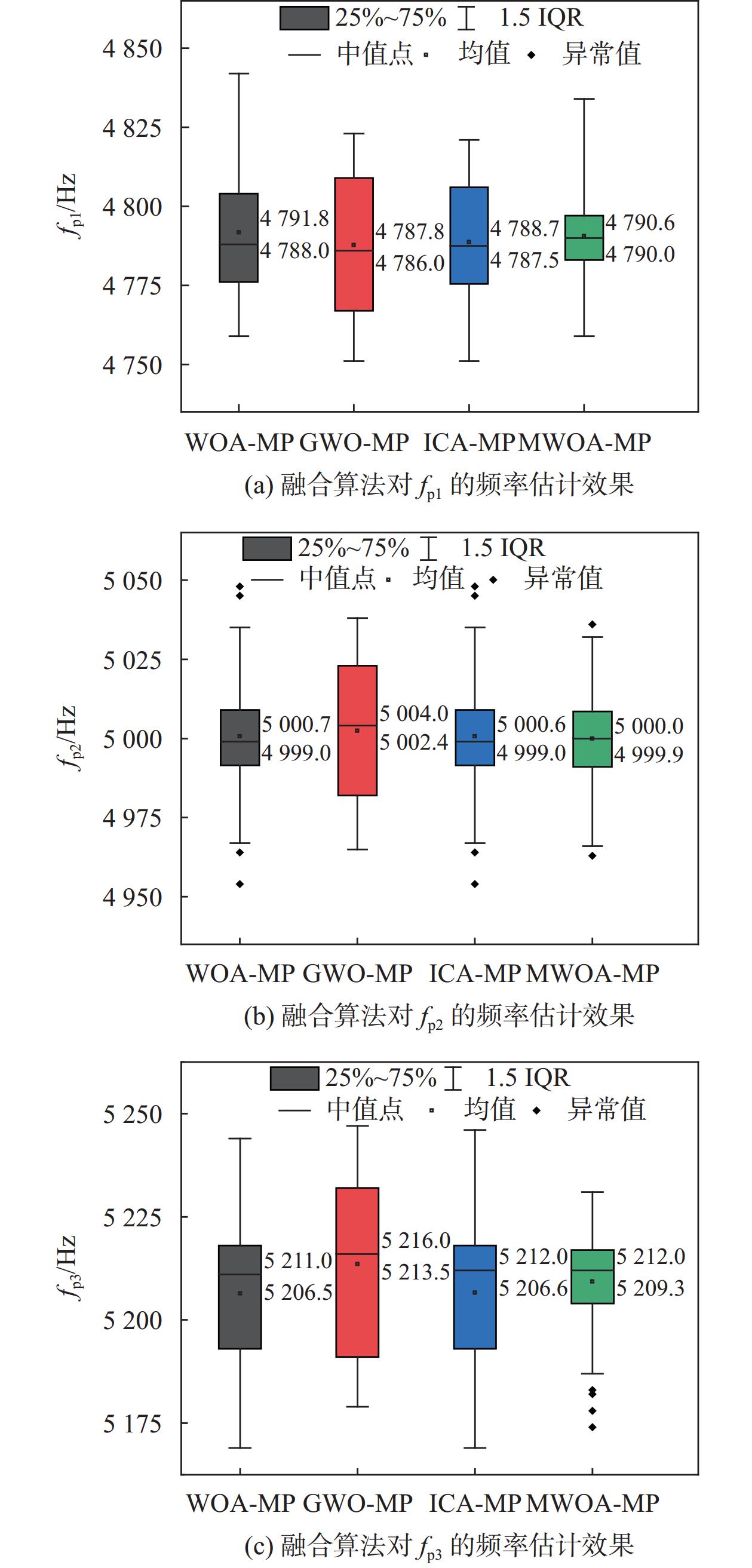
图 8 各融合算法对目标信号的频率估计效果
图选项

实验结果表明，在fp1、fp2、fp3频率下，MWOA-MP的频率估计一致性较好，在各频率成分的统计值较为收敛，其均值与参考频率之间的差值小于10 Hz，有较好的频率估计精度。其他三种算法在fp1、fp2、fp3下的频率统计值的收敛度一般，其估计精度误差值也较大。

5 结束语

本文提出了一种基于改进WOA-MP算法的超声波频率估计方法。改进后的鲸鱼优化算法加快了对目标空间的搜索速度，提高了搜索能力。实验情况表明，MWOA算法在引入MP运算之后，与传统的频率估计算法相比，其抗噪声能力提高30%以上。本文提出的MWOA-MP与其他智能优化结合MP算法对比，MWOA-MP算法的在运算时间相差不大的情况下，寻优能力更强，经MWOA-MP算法估计后的信号频率值与标准信号频率值相比，频率估计误差在10 Hz以内，满足多普勒式海流计的频率测量精度要求。该方法也为多普勒式海流计的回波信号频率成分的估计和提取提供了有力的帮助。

参考文献
[1]
LI X, CHEN J, LI J, et al. Research on sparse decomposition processing of ultrasonic signals of heat exchanger fouling[J]. IEEE Sensors Journal, 2023, 14(23): 15795-15802.
[2]
ZHANG X, LIU Z, MIAO Q, et al. Bearing fault diagnosis using a whale optimization algorithm-optimized orthogonal matching pursuit with a combined time–frequency atom dictionary[J]. Mechanical Systems and Signal Processing, 2018, 107: 29-42. DOI:10.1016/j.ymssp.2018.01.027
[3]
CHANG M, LU Z, HUANG Q, et al. Parameter estimation for ultrasonic echo signals through improved matching pursuit and flower pollination algorithms[J]. Measurement, 2022, 194: 101-110.
[4]
陈果, 何海峰, 吴肖锋, 等. 基于非局部均值-鲸鱼优化算法的套管引线超声波检测方法研究[J]. 中国测试, 2020, 46(4): 102-108. CHEN G, HE H F, WU X F, et al. Research on ultrasonic testing method for casing leads based on non local mean whale optimization algorithm[J]. China Measurement ＆ Test, 2020, 46(4): 102-108. DOI:10.11857/j.issn.1674-5124.2019110057
[5]
林涛, 严寒, 赵丹阳. 基于IWOA-LightGBM的主轴轴承故障预警研究[J]. 中国测试, 2023, 49(5): 82-88. LIN T, YAN H, ZHAO D Y. Research on spindle bearing fault warning based on IWOA LightGBM[J]. China Measurement & Test, 2023, 49(5): 82-88. DOI:10.11857/j.issn.1674-5124.2021080134
[6]
秋兴国, 王瑞知, 张卫国, 等. 基于混合策略改进的鲸鱼优化算法[J]. 计算机工程与应用, 2022, 58(1): 70-78. QIU X G, WANG R Z, ZHANG W G, et al. Whale optimization algorithm based on hybrid strategy improvement[J]. Computer Engineering and Applications, 2022, 58(1): 70-78. DOI:10.3778/j.issn.1002-8331.2012-0316
[7]
QI R, YANG D, ZHANG Y, et al. On recovery of block sparse signals via block generalized orthogonal matching pursuit[J]. Signal Processing, 2018, 153: 34-46. DOI:10.1016/j.sigpro.2018.06.023
[8]
LI X, CHEN J, SUN L, et al. Research on extraction of ultrasonic signal features of heat transfer fouling[C]//Proceedings of the 2022 4th International Conference on Intelligent Control, Measurement and Signal Processing (ICMSP), 2022, 765-769.
[9]
SADEGHIPOOR Z, BABAIE-ZADEH M, JUTTEN C. Dictionary learning for sparse decomposition: A new criterion and algorithm [C]//Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, 2013, 26-31.
[10]
王建英, 尹忠科, 陈磊. 基于非正交分解的频率估计算法[J]. 电波科学学报, 2007, 1: 64-68. WANG J Y, YIN Z K, CHEN L. Frequency estimation algorithm based on non orthogonal decomposition[J]. Journal of Radio Science, 2007, 1: 64-68. DOI:10.3969/j.issn.1005-0388.2007.01.013
[11]
范九伦, 张雪锋. 分段Logistic混沌映射及其性能分析[J]. 电子学报, 2009, 37(4): 720-725. FAN J L, ZHANG X F. Segmented logistic chaotic mapping and its performance analysis[J]. Acta Sinica, 2009, 37(4): 720-725. DOI:10.3321/j.issn:0372-2112.2009.04.009
[12]
潘劲成, 李少波, 周鹏, 等. 改进正弦算法引导的蜣螂优化算法[J]. 计算机工程与应用, 2023, 59(22): 92-110. PAN J C, LI S B, ZHOU P, et al. Improved sine algorithm guided beetle optimization algorithm[J]. Computer Engineering and Applications, 2023, 59(22): 92-110. DOI:10.3778/j.issn.1002-8331.2305-0021
[13]
周欣荣, 王芳, 阴良魁, 等. 基于改进动态因子的鲸鱼优化算法[J]. 科学技术与工程, 2023, 23(28): 12145-12151. ZHOU X R, WANG F, YIN L K, et al. Whale optimization algorithm based on improved dynamic factors[J]. Science, Technology and Engineering, 2023, 23(28): 12145-12151. DOI:10.12404/j.issn.1671-1815.2023.23.28.12145
[14]
MOHAMMED H M, UMAR S U, RASHID T A. A systematic and Meta-Analysis survey of whale optimization algorithm[J]. Computational Intelligence and Neuroscience, 2019, 1: 1-25.
[15]
MOHAMMED H, RASHID T. A novel hybrid GWO with WOA for global numerical optimization and solving pressure vessel design[J]. Neural computing applications. 2020, 32(18). 14701-14718.
[16]
滕永兴, 翟术然, 卢静雅, 等. 基于自适应权重MOEAD的台区电能表误差在线预测[J]. 中国测试, 2023, 49(S1): 225-230. TENG Y X, ZHAI S R, LU J Y, et al. Online prediction of errors in substation electric energy meters based on adaptive weight MOEAD[J]. China Measurement ＆ Test, 2023, 49(S1): 225-230.
[17]
吴泽南, 陈贤雷, 郝华东, 等. 基于蒙特卡洛法的立式金属罐容量测量不确定度评定[J]. 中国测试, 2022, 48(S2): 63-68. WU Z N, CHEN X L, HAO H D, et al. Uncertainty evaluation of vertical metal tank capacity measurement based on Monte Carlo method[J]. China Measurement ＆ Test, 2022, 48(S2): 63-68.