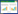文章信息
- 陈超云, 王灿, 文慧卿
- CHEN Chaoyun, WANG Can, WEN Huiqing
- 一种抗磁性材料密度高分辨率测量方法
- A high-resolution measurement method for the density of diamagnetic materials
- 中国测试, 2024, 50(7): 186-190
- CHINA MEASUREMENT & TEST, 2024, 50(7): 186-190
- http://dx.doi.org/10.11857/j.issn.1674-5124.2023050145
-
文章历史
- 收稿日期: 2023-05-31
- 收到修改稿日期: 2023-07-19
密度是材料的重要特性[1],其量值测量装置包括比重计、密度梯度柱、真密度计和密度天平等[2]。这些装置大多价格昂贵,且无法测量蜡、凝胶等低质量(<5 mg)、小尺寸(直径<5 mm)、不均匀、不规则材料的密度,难以普及和推广[3]。
多年来,磁力悬浮技术因其成本低、方法灵活、易于操作等优点,在生命科学、医疗卫生、智能制备、新材料等领域有着独特的应用优势[4]。在抗磁材料密度的精密测量中,应用最广泛的是以N极正对的方形磁铁构造出近线性磁场,并将抗磁性材料在顺磁性介质中稳定悬浮,通过测量悬浮高度实现密度的测量[5]。但这种方法的测量范围与灵敏度均有限,因此国内外学者通过调节磁浮力与重力的平衡关系,研究了一系列高灵敏度、适用于大密度材料的测量方法[6-7]。通过倾斜测量装置的方式使得密度测量范围扩展至800~3000 kg/m3;引入离心力的作用,通过调节水平方向可控的向心力与磁浮力的平衡关系,实现测量灵敏度的可调性;利用圆环状磁铁替代方形磁铁,使得该测量方法具有更灵活的可操控空间,方便检测过程中抗磁材料的添加与提取。但现有磁力装置缺乏足够的灵敏度来克服样品之间的接触、排斥作用,容易发生聚集,导致分辨率较低[8]。对于检测材料微小密度差异,如杂质分析、无损检测、质量控制和分离技术等,还需要进一步提高装置的分辨率。
综上所述,针对当前磁力悬浮法存在的问题,本文根据不同磁化方向上磁感应强度的不同,将原本两个N极正对的磁体旋转90°,使磁化方向与重力方向垂直,并设计了沿着弱磁化方向的测量装置。该装置将抗磁性样品置于顺磁性介质中,在外部磁场中,样品受到磁斥力以及由介质磁引力传递到样品上的附加浮力作用,增大斥力的作用效果,使样品稳定悬浮于介质某一高度,根据悬浮高度来测量密度。与N极正对的磁场不同,本装置的磁场梯度减小,测量范围减小,但分辨率显著提高,能有效克服密度相近样品间体积相互排斥的影响,识别出微小的密度差异,且不需要改变磁场梯度大小,不增加装置的复杂性。通过标准玻璃浮子(浮子)的测量实验,验证了该方法的准确性和可靠性。
1 磁力悬浮理论 1.1 测量原理自然界中的材料一般可以分为铁磁性、顺磁性和抗磁性。顺磁性材料的磁化方向与外部磁场相同,在外部磁场中受到引力作用;抗磁性材料则相反,在外部磁场中受到斥力作用,斥力的大小与材料的磁化率、体积以及磁场梯度有关[9]。顺磁性介质的引入,使磁力悬浮装置不需要施加强磁场,永磁铁也能使抗磁性样品稳定悬浮[10]。
介质采用MnCl2溶液,磁化率通常为10–4。磁体采用钕铁硼永磁铁,L×W×H(长×宽×高)为60 mm×20 mm×10 mm,中心表面磁感应强度为(0.375±0.002)T。将被测样品沉浸于介质中,在介质两端施加N极正对的磁体。样品受到重力、浮力和磁力的作用悬浮于某一高度。为了提高密度分辨率将磁体旋转90°,得到样品受力情况如图1所示,图中定义了x、y、z的参考坐标系。
|
| 图 1 样品受力分析 |
设样品的体积为V、密度为ρs、磁化率为χs,介质的密度为ρm、磁化率为χm。作用在样品上的磁力Fmag由下式表示[11]:
| $ {{{F}}_{{\rm{mag}}}}{\text{ = }}\frac{{{\chi _{\text{s}}} - {\chi _{\text{m}}}}}{{{\mu _0}}}V\left( {{{B}} \cdot \nabla } \right){{B}} $ | (1) |
式中:μ0——真空磁导率,4π×10−7 N/A2;
B——磁感应强度,T;
样品重力和浮力的合力Fgrav由下式表示:
| $ {{{F}}_{{\rm{grav}}}}{\text{ = }}\left( {{\rho _{\text{s}}} - {\rho _{\text{m}}}} \right)V{{g}} $ | (2) |
其中g是重力加速度,9.810 m/s2;当Fmag+Fgrav=0时,通过式(1)和式(2)可以计算出样品密度ρs:
| $ {\rho _{\text{s}}}{\text{ = }}\frac{{{\chi _{\text{s}}} - {\chi _{\text{m}}}}}{{{\mu _0}\ {{g}} }}\left( {{{B}} \cdot \nabla } \right){{B}} + {\rho _{\text{m}}} $ | (3) |
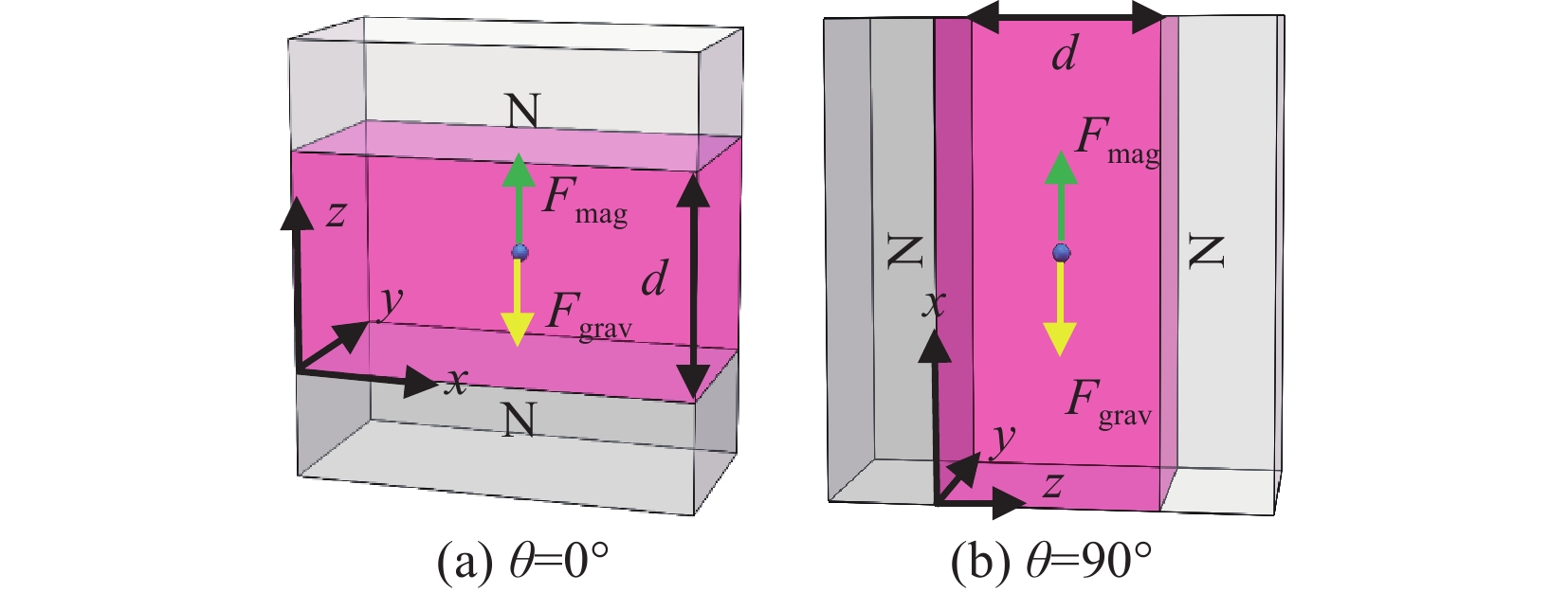
为了研究磁力悬浮机理,对装置悬浮区域磁场进行仿真[12]。使用有限元仿真软件对磁体间距半宽d/2进行参数化扫描(起始0.002 m,步长0.003 m,终止0.035 m),得到θ=0°和90°的磁感应强度B(x,z)的分布如图2所示,箭头表示大小和方向。
|
| 图 2 磁场仿真 |
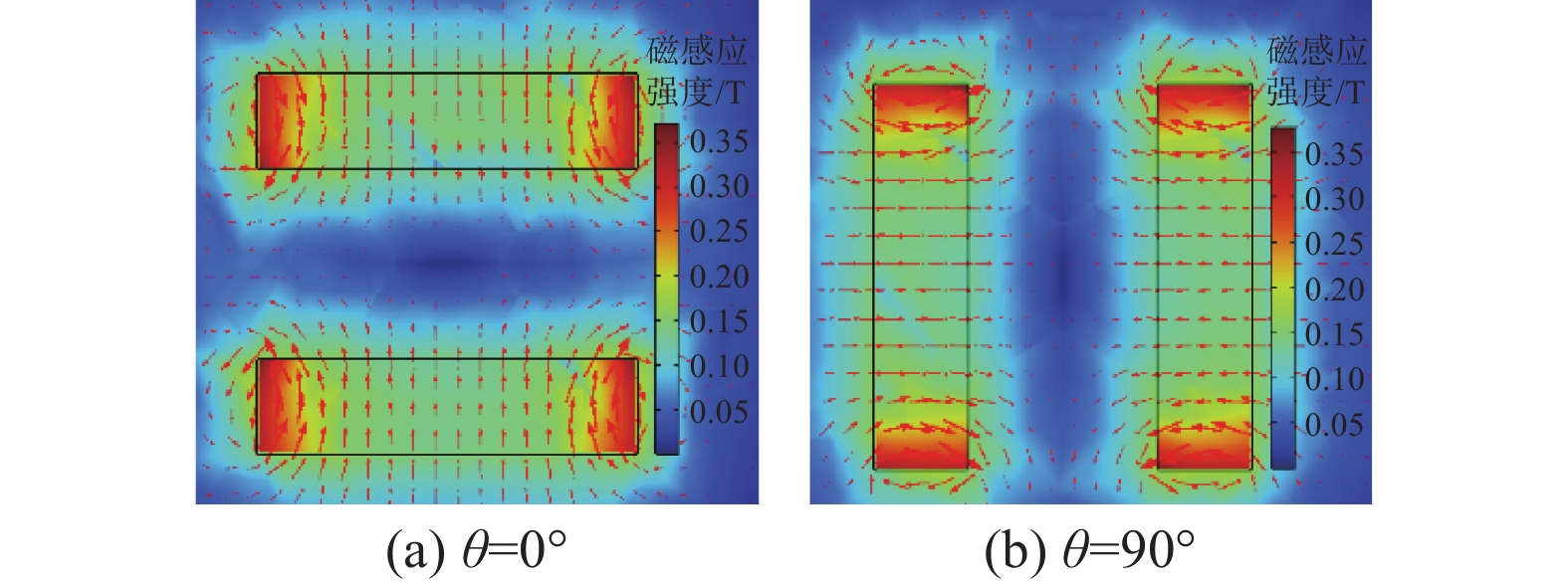
结果表明,磁场梯度由磁体两端向中间递减,在中间出现磁感应强度为0的区间。由于磁场的对称性,样品仅受到水平或垂直方向的磁力作用,使样品趋向于局部磁场最弱的区域,从而简化了磁合力。在θ=0°时,样品受到底部磁体斥力而上浮,受到顶部磁体斥力而下沉,最终悬浮在合力平衡的位置。在θ=90°时,磁场在x轴方向比z轴方向弱,样品受到的磁力大小也较弱,进一步绘制B与间距d的线图如图3所示。
|
| 图 3 磁感应强度线图 |
结果表明,θ=0°时,磁场始终沿z轴对称;d≤1.5W时,磁场呈现出较高线性度,但线性区间短,难以观察样品的运动变化;1.5W≤d≤L时,磁场出现波动,并可以恢复到线性状态;d≥L时,磁场出现突变,并无法恢复到线性状态。θ=90°时,磁场沿x轴对称;d≤1.5W时,磁感应强度较强,测量范围相对较大;1.5W≤d≤L时,磁感线迅速下降并趋于平滑;d≥L时,磁感应强度B趋于0,此时具有最高的分辨率,但同时测量范围也最小,此时式(3)可变换为样品表观密度与悬浮高度Δz的函数:
| $ \Delta \rho {\text{ = }}\frac{{\Delta \chi {B^2}}}{{{\mu _0}g}}{\textit{z}}= \frac{1}{S}\Delta {\textit{z}} $ | (4) |
| $ \Delta {\rho _{{\text{min}}}}{\text{ = }}\frac{1}{S} $ | (5) |
其中S为灵敏度系数,mm /(kg/m3),其倒数即为磁力悬浮装置的分辨率。在磁力悬浮装置中,灵敏度和测量范围耦合,处于低灵敏度,可以测量密度相差较大的样品,但失去分辨微小密度差异的能力;在高灵敏度下,磁场梯度减小,能够在较长的悬浮位移上察觉微小的密度差异。因此,提高分辨率可以通过旋转装置,增大磁体间距,沿着较弱磁场梯度测量。进一步对不同尺寸比例的磁体仿真得出,分辨率还与磁体的长宽比以及磁感应强度密切相关。本装置采用L×W×H(长×宽×高)为60 mm×20 mm×10 mm的钕铁硼永磁铁来获得最佳线性拟合关系。
2 磁力悬浮实验 2.1 浮子悬浮实验要求环境温度(23±0.2)℃,相对湿度55%~60%。采用TD8620数字式特斯拉计测量磁感应强度,准确度1%;液体密度采用DM45密度计,U=0.05 kg/m3(k=2);介质温度采用TFX430温度计,MPE:±0.05℃;样品悬浮高度采用CCD工业相机和刻度尺来测量。磁力悬浮实验的参数如表1所示。
| 参数 | 描述 | 数值 |
| B0 | 磁感应强度 | (0.375±0.002)T |
| d | 磁体间距 | 20~60 mm |
| D | 浮子直径 | 3~5 mm |
| χs | 样品磁化率 | –2×10–5 |
| ρm | 介质密度 | 960.0 kg/m3 |
| χm | 介质磁化率 | 5×10–5 |
| μ0 | 真空磁导率 | 4π×10−7 N/A2 |
| g | 重力加速度 | 9.810 m/s2 |
实验所用样品来自英国H&D公司的浮子,U= 0.1 kg/m3(k=2)。介质采用MnCl2乙醇水溶液。在水平和垂直方向分别施加N极正对的磁体,图4显示了浮子在两种磁化方向的悬浮状态。

|
| 图 4 样品悬浮状态 |
图4(a)显示了在θ=0°,d=25 mm条件下,5颗密度范围为940~980 kg/m3的浮子悬浮情况。开始时浮子沿着磁场梯度向中间区域运动,随着合力平衡保持相对稳定。但浮子体积间的接触、排斥,阻碍了其继续运动。此时装置的灵敏度系数Sz=0.41 mm/(kg/m3),分辨率Δρmin=2.4 kg/m3,测量范围的极差Δρ=40 kg/m3。装置具有测量范围大、悬浮间距短、分辨率低的特点。更换5颗浮子,对标称值为960.0 kg/m3的3颗浮子进行悬浮实验。由于密度的微小差异,装置缺乏足够的灵敏度来克服体积间的相互排斥,浮子始终聚集在一起。对介质进行搅拌,其分布状态不断发生变化,但始终聚集在一起,无法拟合密度与高度的函数关系。
图4(b)显示了沿着弱磁化方向,标称值为960.0 kg/m3的3颗浮子的悬浮情况。在初始状态下(d=25 mm),装置灵敏度略微提高,浮子由聚集状态逐渐向上下两端分离,呈现出线性有序排列,但密度相近的浮子间仍然保持硬接触。随着磁体逐渐分离至40 mm时,灵敏度显著提高,密度差异变得更容易察觉,顶部与底部两颗密度差异较大的浮子发生分离。当磁体间距达到60 mm时,3颗浮子完全分离,此时装置灵敏度系数Sx=45.5 mm/(kg/m3),分辨率提高到Δρmin=0.02 kg/m3,测量范围的极差降低至Δρ=1 kg/m3。实验结果表明,即使是同一制造商、同一批次、标称值相同的浮子依然存在密度差异。
2.2 曲线拟合在θ=90°时,对不同磁体间距d(25 mm,40 mm,60 mm)进行拟合,得到表观密度与悬浮高度曲线,如图5所示。其中密度差异最小的是底部黄色和白色浮子,两颗浮子间距为95 pixels(24 pixels/mm),密度差为0.08 kg/m3。传统密度测量方法是难以区分的。
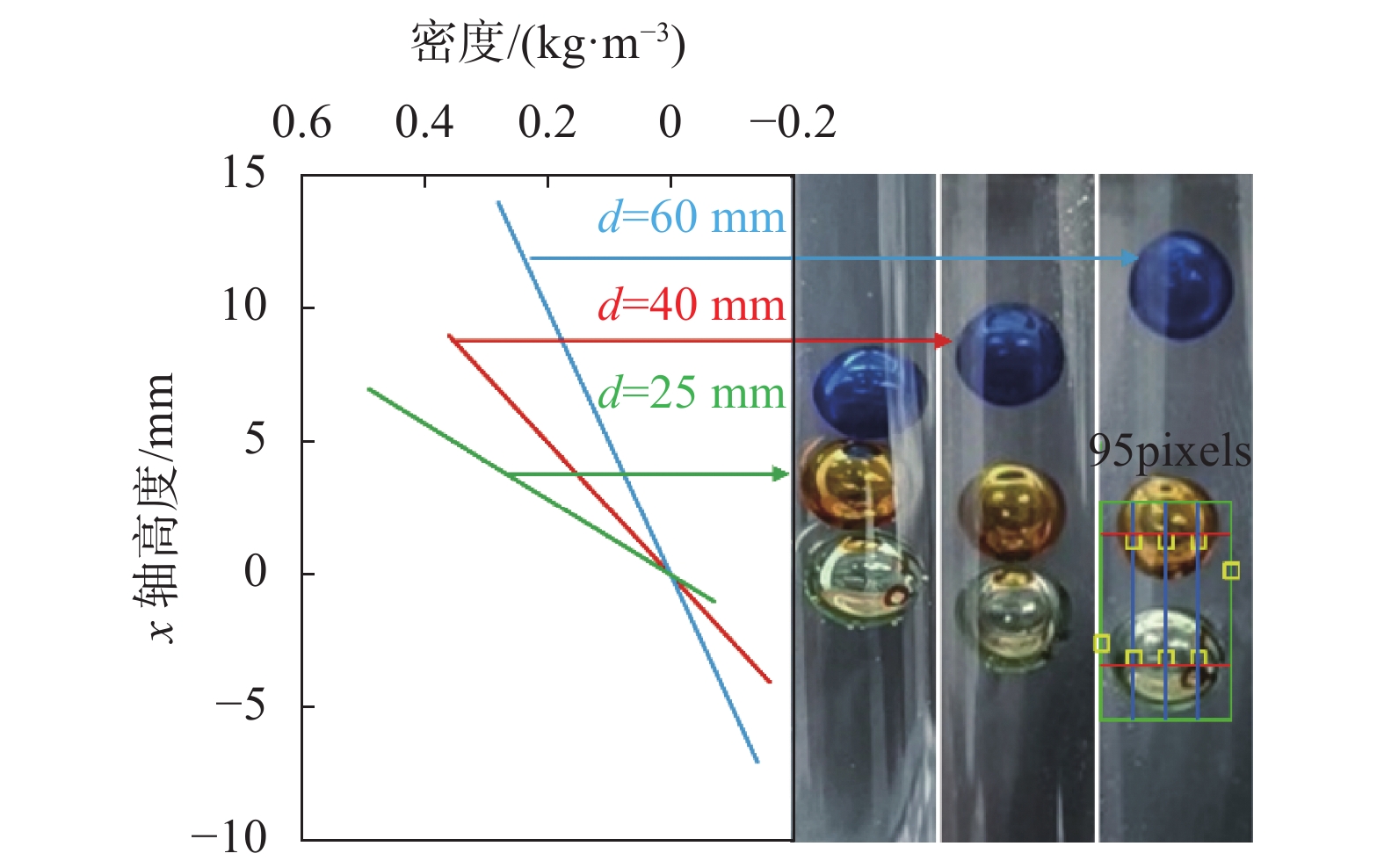
|
| 图 5 不同间距的拟合曲线 |
进一步研究发现,提高灵敏度除了旋转装置改变磁化方向的测量方式外,还可以通过降低磁感应强度、延长磁体或者增大磁体间距3种方式。然而,这些方式也有限制条件:1)随着灵敏度的提高,被测样品容易向两端运行,测量范围减小,能检测的样品数量少,甚至难以配置合适的溶液来匹配样品密度,使样品满足线性拟合条件;2)极高的灵敏度配置会导致密度和悬浮高度具有非线性关系。虽然这种特性不会妨碍密度的精确测量,但此时密度与悬浮高度的函数关系比线性情况更为复杂。
3 结束语根据磁阿基米德浮力定律,提出了一种抗磁性材料密度高分辨率测量方法,并设计了实验装置。浮子实验表明,旋转磁体(θ=90°)后沿着弱磁化方向的测量方式,使装置的分辨率提高到0.02 kg/m3,,能够区分出标称值相同的浮子之间的微小密度差异。磁体旋转后的另一个优点是试管顶部没有被磁铁遮挡,方便向试管容器中添加或移除样品,或调整介质的密度(如添加MnCl2粉末),而不会干扰磁场。磁力悬浮装置适用于低质量(<5 mg)、小尺寸(直径<5 mm)样品的密度测量。
装置也存在不足之处:装置只适用于抗磁性材料密度测量,对其他固体材料来说不具有普遍适用性;增大悬浮间距则会减弱磁场梯度,降低密度和高度的线性关系;装置的参数由仪器结合仿真软件得到,拟合曲线可能存在偏差,还需要固体标准密度对装置进行校准。总体而言,本装置拓宽了磁力悬浮法的应用范围,为密度计量技术提供一条新的研究思路。
| [1] |
徐秀华. 密度测量技术[M]. 北京: 中国计量出版社, 2021.
|
| [2] |
魏传喆, 潘江, 王功明. 一种直接驱动式振动管密度计研究[J].
中国测试, 2020, 46(6): 83-88.
WEI C Z, PAN J, WANG G M. Research on a direct drive vibration tube density meter[J].
China Measurement & Test, 2020, 46(6): 83-88.
|
| [3] |
DAVID K B, MARTIN M T, MANZA B J A, et al. Paramagnetic ionic liquids for measurements of density using magnetic levitation[J].
Analytical Chemistry, 2013, 85(17): 8442-8447.
DOI:10.1021/ac401899u |
| [4] |
刘春程, 方肖勇, 李修远, 等. 电磁MEMS微镜贴片封装残余应力测试与特性研究[J].
仪表技术与传感器, 2023(6): 18-25.
LIU C C, FANG X Y, LI X Y, et al. Die bonding residual stress measurement and characteristics of electromagnetic mems micromirror[J].
Instrument Technique and Sensor, 2023(6): 18-25.
|
| [5] |
赵帅杰, 张吉堂, 周俊峰, 等. 基于高温EMAT铁磁性材料的声速变化规律研究[J].
中国测试, 2022, 48(9): 1-6.
ZHAO S J, ZHANG J T, ZHOU J F, et al. Study on the variation of sound velocity based on high temperature EMAT ferromagnetic materials[J].
China Measurement & Test, 2022, 48(9): 1-6.
|
| [6] |
张承谦, 赵朋, 颉俊, 等. 抗磁性高密度物质的磁悬浮密度测量方法[J].
浙江大学学报(工学版), 2018, 52(4): 613-618.
ZHANG C Q, ZHAO P, XIE J, et al. Density measurement by magnetic levitation for diamagnetic high-density materials[J].
Journal of Zhejiang University(Engineering Science), 2018, 52(4): 613-618.
|
| [7] |
NEMIROSKI, ALEX, KUMAR, A. A. , SOH, SIOWLING, et al. High-sensitivity measurement of density by magnetic levitation[J]. Analytical chemistry, 2016, 88(5): 2666-2674.
|
| [8] |
刘丽辉, 谢瑞芳, 陈棣湘, 等. 基于ARM和FPGA的双核电磁无损检测系统[J].
中国测试, 2016, 42(1): 65-68.
LIU L H, XIE R F, CHEN D X, et al. Double-core electromagnetic nondestructive testing system based on ARM and FPGA[J].
China Measurement & Test, 2016, 42(1): 65-68.
|
| [9] |
任飞安, 许金鑫, 由强, 等. 能量天平永磁体系统的温度场分析[J].
计量学报, 2019, 40(3): 353-360.
REN F A, XU J X, YOU Q, et al. Thermal analysis of permanent-magnet system in the joule balance[J].
Acta Metrologica Sinica, 2019, 40(3): 353-360.
|
| [10] |
丁安梓. 基于负磁泳的双磁环式磁悬浮技术及应用研究[D]. 武汉: 华中科技大学, 2021.
DING A Z. Research on the negative magnetophoresis-based magnetic levitation technology and its performances[D]. Wuhan: Huazhong University of Science and Technology, 2021.
|
| [11] |
MIRICA K A, PHILLIPS S T, MACE C R. Magnetic levitation in the analysis of foods and water[J]. Journal of Agricultural & Food Chemistry. 2010, 58(11): 6565–6569.
|
| [12] |
陈超云, 王灿, 文慧卿. 基于COMSOL的铁磁性材料密度数值模拟[J].
计量技术, 2019(1): 14-17.
|
 2024, Vol. 50
2024, Vol. 50