文章信息
- 徐佳宝, 张国良, 汪坤
- XU Jiabao, ZHANG Guoliang, WANG Kun
- 基于增量MPC和转向角优化的泊车轨迹跟踪研究
- Research on parking trajectory tracking based on incremental MPC and steering angle optimization
- 中国测试, 2024, 50(7): 170-177
- CHINA MEASUREMENT & TEST, 2024, 50(7): 170-177
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022090037
-
文章历史
- 收稿日期: 2022-09-07
- 收到修改稿日期: 2022-12-05
2. 人工智能四川省重点实验室,四川 宜宾 644000
2. Artificial Intelligence Key Laboratory of Sichuan Province, Yibin 644000, China
作为无人驾驶系统的一部分,泊车系统的出现能够有效地解决城市道路停车难的问题。目前,在泊车过程中,主要包括车位探测、路径规划与轨迹跟踪[1-2]。轨迹跟踪是自动泊车的最后一个环节,也是研究重点之一。轨迹跟踪根据控制器规划和实时反馈车辆状态,能够使车辆稳定、准确地跟踪参考轨迹。由于车辆具有欠驱动的非完整约束系统,所以设计合适的控制器完成车辆泊车轨迹跟踪是一个值得研究的问题。
模型预测控制(model predictive control, MPC)具有前馈-反馈的结构,可以处理带有约束的非完整系统[3]。杨博等人[4]通过多项式进行路径规划,加入了防碰撞和防侧翻约束条件,利用传统MPC设计出避障路径跟踪控制器,提高了避障换道过程中的安全性。PAOLO F等人[5-6]通过建立三自由度的车辆非线性模型,再使用MPC方案,控制效果较好。胡远志等人[7]针对泊车场景使用了MPC方法,同时加入动态障碍物,对车辆停车避障进行研究,增加了泊车安全性。顾青等人[8]对自动泊车路径跟踪采用非线性MPC方法,比起MPC跟踪精度和稳定性都将能有所保证,在实时性方面性能有所降低,但在可接受范围内。
传统MPC控制方案应用到车辆泊车轨迹跟踪时,第一,没有考虑增量约束,这会影响轨迹跟踪的稳定性和实时性。第二,在泊车转向过程中存在转向角突变的情况,这会导致轨迹跟踪精度降低。
针对传统MPC控制方案存在的问题,本文设计了一种基于增量MPC轨迹跟踪控制方案。首先建立车辆二自由度运动学模型及约束,将状态量和控制量改写为状态增量和控制增量形式,设计增量MPC控制器,提高了轨迹跟踪实时性和稳定性;其次,利用卡尔曼滤波算法对前轮转角进行优化处理,提高了轨迹跟踪的精度。最后通过搭建Matlab和Carsim联合仿真环境验证了在平行泊车和垂直泊车两种工况下所设计控制器和转向角优化策略的有效性。
1 车辆运动学模型及约束车辆运动学模型如图1所示,在泊车过程中车辆属于低速运动,可以忽略轮胎侧滑对轨迹跟踪控制的影响[9]。因此选择车辆运动学模型设计轨迹跟踪控制器。
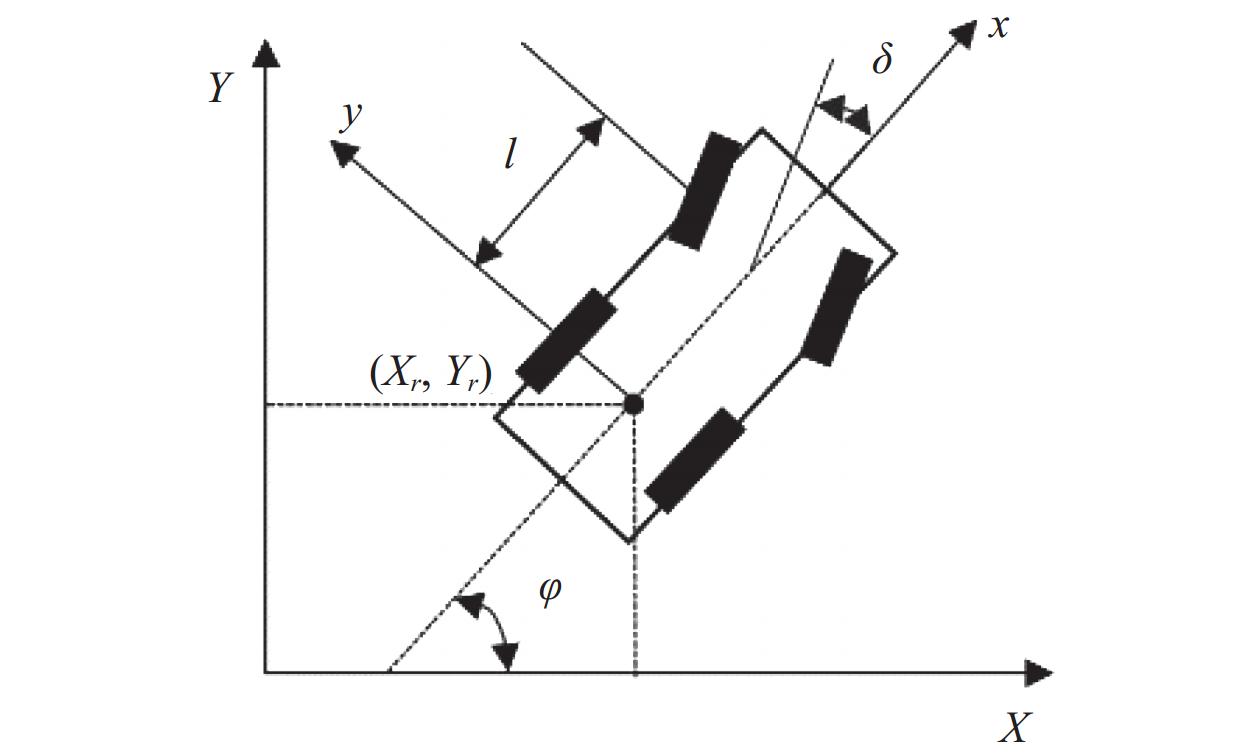
|
| 图 1 车辆运动学模型 |
由于车速较低时车辆后轴横向速度可以近似为零,将车辆后轴中心设置为车辆轨迹点,车辆运动学模型表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot x = v{\rm cos}\varphi } \\ {\dot y = v{\rm sin}\varphi } \\ {\dot \varphi = \left( {v{\rm tan}\delta } \right)/l} \end{array}} \right. $ | (1) |
式中:x、y——以后轮车轴为基点的横、纵坐标;
v——当前车辆速度;
l——前后车轮轴距;
本文以车辆参数以D级车Sendan为原型,整车参数如表1所示。
| 车辆参数 | 数值 |
| 车辆轴距 |
2.776 m |
| 车辆前悬 |
0.713 m |
| 车辆后悬 |
1.073 m |
| 质心到前轴距离 |
1.110 m |
| 质心到后轴距离 |
1.666 m |
| 最大前轮转向角 |
39° |
| 车宽 |
1.773 m |
泊车过程中,约束条件主要考虑的是车辆前轮偏转角及其增量约束和横向速度及其增量约束[10]。前轮转向角约束
| $ \left\{ {\begin{array}{*{20}{l}} { - 5\;{\text{m}}/{\text{s}} \leqslant v \leqslant 5\;{\text{m}}/{\text{s}}} \\ { - 0.1\;{\text{m}}/{\text{s}} \leqslant \Delta v \leqslant 0.1\;{\text{m}}/{\text{s}}} \\ { - {{39}^{\circ} } \leqslant \delta \leqslant {{39}^{\circ} }} \\ { - {{1.35}^{\circ} } \leqslant \Delta \delta \leqslant {{1.35}^{\circ} }} \end{array}} \right. $ | (2) |
在泊车轨迹跟踪控制器框图如图2所示,增量MPC控制器根据参考轨迹和车辆当前状态计算出前轮转角和车速,再经过卡尔曼滤波算法对车辆前轮转角进行优化处理,最后将优化后的转向角输入到Carsim车辆模型中进行控制。Carsim车辆模型再将计算后的车辆状态反馈到增量MPC控制器中进行处理,如此往复循环,从而完成车辆的泊车轨迹跟踪控制。

|
| 图 2 轨迹跟踪控制框图 |
2.2 增量模型预测控制器设计
式(1)中所建立的车辆运动学模型是非线性的,为设计合适的增量模型预测控制器,将非线性车辆运动学模型线性化再转化成二次规划问题求解。
首先将式(1)看作一个控制量为
| $ {\dot {\boldsymbol{\chi}} _r}(t + 1) = {\boldsymbol{f}}\left( {{{\boldsymbol{\chi}} _r}(t),{{\boldsymbol{u}}_r}(t)} \right) $ | (3) |
其中
当对车辆施加控制时
| $ \dot {\boldsymbol{\chi}} (t + 1) = {\boldsymbol{f}}\left( {{\boldsymbol{\chi}} (t),{{\boldsymbol{u}}}(t)} \right) $ | (4) |
对式(3)在轨迹点
| $ \begin{split} {{\dot {\boldsymbol{\chi}} }_r}(t + 1) = \;& {\boldsymbol{f}}\left( {{{\boldsymbol{\chi}} _r}(t),{{\boldsymbol{u}}_r}(t)} \right) + \frac{{\partial {\boldsymbol{f}}\left( {{\boldsymbol{\chi}} ,{\boldsymbol{u}}} \right)}}{{\partial {\boldsymbol{\chi}} }} \\ \;& \left| {\left( {\dot {\boldsymbol{\chi}} (t) - {{\boldsymbol{\chi}} _r}(t)} \right) + \frac{{\partial {\boldsymbol{f}}\left( {{\boldsymbol{\chi}} ,{\boldsymbol{u}}} \right)}}{{\partial {\boldsymbol{\chi}} }}} \right|\left( {{\boldsymbol{u}}(t) - {{\boldsymbol{u}}_r}(t)} \right) \end{split} $ | (5) |
将式(5)与式(4)相减,同时,得到新方程:
| $ \tilde {\boldsymbol{\chi}} \left( {t + 1} \right) = {\boldsymbol{A}}(t)\tilde {\boldsymbol{\chi}} \left( t \right) + {\boldsymbol{B}}(t)\tilde {\boldsymbol{u}}\left( t \right) $ | (6) |
采用前向欧拉法对式(6)进行离散化处理,故离散的状态空间方程为:
| $ \left\{ \begin{split} &\tilde {\boldsymbol{\chi}} \left( {k + 1} \right) = {\boldsymbol{A}}(k)\tilde {\boldsymbol{\chi}} \left( k \right) + {\boldsymbol{B}}(k)\tilde {\boldsymbol{u}}\left( k \right) \\ & {\boldsymbol{y}}(k) = C\tilde {\boldsymbol{\chi}} (k) \end{split} \right. $ | (7) |
式(7)中:
| $\begin{split} {\boldsymbol{A}}(k) =& \left[ {\begin{array}{*{20}{c}} 1&0&{ - {v_r}\cos {\varphi _r}T} \\ 0&1&{{v_r}\cos {\varphi _r}T} \\ 0&0&1 \end{array}} \right],\\ {\boldsymbol{B}}(k) =& \left[ {\begin{array}{*{20}{c}} {\cos {\varphi _r}T}&0 \\ {\begin{array}{*{20}{c}} {\sin {\varphi _r}T} \\ {\frac{{\tan {\delta _r}}}{l}T} \end{array}}&{\begin{array}{*{20}{c}} 0 \\ {\frac{{{v_r}}}{{l{{\cos }^2}{\delta _r}}}T} \end{array}} \end{array}} \right],\\ {\boldsymbol{C}} =& \left[ \begin{gathered} \begin{array}{*{20}{c}} 0&1&0 \end{array} \\ \begin{array}{*{20}{c}} 0&0&1 \end{array} \\ \end{gathered} \right] \end{split} $ |
T为采样时间。由式(7)可知,输出
| $ {\boldsymbol{y}}(k + 1) = {\boldsymbol{CA}}(k)\tilde {\boldsymbol{\chi}} \left( k \right) + {\boldsymbol{CB}}(k)\tilde {\boldsymbol{u}}\left( k \right) $ | (8) |
为了将该数学模型用于增量MPC控制器[10]。定义控制增量
| $ \left\{\begin{aligned} & \left[ \begin{gathered} \Delta {\boldsymbol{\chi}} (k + 1) \\ {\boldsymbol{y}}(k + 1) \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{A}}(k)}&0 \\ {{\boldsymbol{CA}}(k)}&{\boldsymbol{I}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {\boldsymbol{\chi}} (k)} \\ {{\boldsymbol{y}}(k)} \end{array}} \right] + \\ &\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{B}}(k)} \\ {{\boldsymbol{CB}}(k)} \end{array}} \right]\Delta {\boldsymbol{u}}(k) \\ & {\boldsymbol{y}}(k) = \left[ {\begin{array}{*{20}{c}} 0&{\boldsymbol{I}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {\boldsymbol{\chi}} (k)} \\ {{\boldsymbol{y}}(k)} \end{array}} \right] \end{aligned} \right. $ | (9) |
简写为:
| $ \left\{ \begin{aligned} & \xi \left( {k + 1} \right) = \tilde {\boldsymbol{A}}(k)\xi \left( k \right) + \tilde {\boldsymbol{B}}(k)\Delta {\boldsymbol{u}}\left( k \right) \\ &{\boldsymbol{y}}(k) = \tilde C\xi (k) \end{aligned} \right. $ | (10) |
将最新的测量值作为初始条件,设定预测时域为
| $ \boldsymbol{Y}(k)=[\boldsymbol{y}(k+1),\boldsymbol{y}(k+2),\cdots,\boldsymbol{y}(k+N_p)]^{\text{T}} $ | (11) |
同时预测时刻内的控制增量也写成如下形式:
| $ \Delta\boldsymbol{U}(k)=[\Delta\boldsymbol{u}(k),\Delta\boldsymbol{u}(k+1),\cdots,\Delta\boldsymbol{u}(k+N_c-1)]^{\text{T}} $ | (12) |
根据模型预测控制原理[12]。通过推导得到系统在第k时刻的预测输出方程:
| $ {\boldsymbol{Y}}(k) = {{\boldsymbol{\psi}} _k}\xi (k) + {{\boldsymbol{\varTheta}} _k}\Delta {\boldsymbol{U}}(k) $ | (13) |
式(13)中,
| ${{\boldsymbol{\varTheta}} _k} = \left[ {\begin{array}{*{20}{c}} {\tilde {\boldsymbol{C}}\tilde {\boldsymbol{B}}(k)}&0& \cdots &0 \\ {\tilde {\boldsymbol{C}}\tilde {\boldsymbol{A}}(k)\tilde {\boldsymbol{B}}(k)}&{\tilde {\boldsymbol{C}}\tilde {\boldsymbol{B}}(k)}& \cdots &0 \\ \vdots & \vdots &{}& \vdots \\ {\tilde {\boldsymbol{C}}\tilde {\boldsymbol{A}}{{(k)}^{{N_p} - 1}}\tilde {\boldsymbol{B}}(k)}&{\tilde {\boldsymbol{C}}\tilde {\boldsymbol{A}}{{(k)}^{{N_p} - 2}}\tilde {\boldsymbol{B}}(k)}& \cdots &{\tilde {\boldsymbol{C}}\tilde {\boldsymbol{A}}{{(k)}^{{N_p} - {N_c}}}\tilde {\boldsymbol{B}}(k)} \end{array}} \right] \text{} $ |
控制器要保证车辆能快速平稳地跟踪上参考轨迹,在设计轨迹跟踪控制器时,采用如下的目标函数进行求解:
| $ \begin{split} & {\boldsymbol{J}}(\xi (k),{\boldsymbol{u}}(k - 1),\Delta {\boldsymbol{U}}(k)) = \sum\nolimits_{i = 1}^{{N_p}} {\left\| {{\boldsymbol{y}}(k + i)} \right\|} _Q^2 + \\ & \sum\nolimits_{i = 0}^{Nc - 1} {\left\| {\Delta {\boldsymbol{U}}(k + i)} \right\|} _R^2 + \rho {\varepsilon ^2} \end{split} $ | (14) |
式中:
将式(14)改写为矩阵向量的形式为:
| $ \begin{split} & {\boldsymbol{J}}(\xi (k),{\boldsymbol{u}}(k - 1),\Delta {\boldsymbol{U}}(k)) = {{\boldsymbol{Y}}^{\text{T}}}(k){\boldsymbol{QY}}(k) + \\ & \Delta {{\boldsymbol{U}}^{\text{T}}}(k){\boldsymbol{R}}\Delta {\boldsymbol{U}}(k) + {\varepsilon ^{\text{}}}\rho \varepsilon \end{split}$ | (15) |
将式(12)带入式(15)得到:
| $ \begin{split} & {\boldsymbol{J}}(\xi (k),{\boldsymbol{u}}(k - 1),\Delta {\boldsymbol{U}}(k)) = \Delta {{\boldsymbol{U}}^{\text{T}}}(k)[{{\boldsymbol{\varTheta}} ^{\rm T}}\tilde {\boldsymbol{Q}}{\boldsymbol{\varTheta}} + \tilde {\boldsymbol{R}}]\Delta {\boldsymbol{U}}(k)+ \\ & 2{\boldsymbol{E}}{(k)^{\rm T}}\tilde {\boldsymbol{Q}}{\boldsymbol{\varTheta}} \Delta {\boldsymbol{U}}(k) + {\boldsymbol{E}}{(k)^{\text{T}}}\tilde {\boldsymbol{Q}}{\boldsymbol{E}}(k) + {\varepsilon ^{\text{}}}\rho \varepsilon \\[-1pt] \end{split}$ | (16) |
式(16)中,预测时域内的跟踪误差为
将目标函数转为为标准二次型为:
| $ \begin{split} {\boldsymbol{J}}(\xi (k),{\boldsymbol{u}}(k - 1),\Delta {\boldsymbol{U}}(k)) = &\frac{1}{2}{\left[ {\begin{array}{*{20}{c}} {\Delta {\boldsymbol{U}}} \\ \varepsilon \end{array}} \right]^{\text{T}}}{\boldsymbol{H}}\left[ {\begin{array}{*{20}{c}} {\Delta {\boldsymbol{U}}} \\ \varepsilon \end{array}} \right] + \\ &{{\boldsymbol{f}}^{\text{T}}}\left[ {\begin{array}{*{20}{c}} {\Delta {\boldsymbol{U}}} \\ \varepsilon \end{array}} \right] \end{split} $ | (17) |
其中
| $ {\boldsymbol{H}}=\left[\begin{array}{cc}2({{\boldsymbol{\varTheta}} }_{k}^{\text{T}}\tilde{{\boldsymbol{Q}}}+\tilde{{\boldsymbol{R}}})& 0\\ 0& 2\rho \end{array}\right];{{\boldsymbol{f}}}^{\text{T}}=\left[\begin{array}{cc}2{{\boldsymbol{E}}}^{\text{T}}(k)\tilde{{\boldsymbol{Q}}}{{\boldsymbol{\varTheta}} }_{k}& 0\end{array}\right];$ |
那么增量MPC的每一步求解就可以转换成带约束的二次规划问题:
| $ \begin{split} &\min {\boldsymbol{J}}(\xi (k),{\boldsymbol{u}}(k - 1),\Delta {\boldsymbol{U}}(k)), \\ &{\rm s.t.}\left\{ \begin{gathered} {{\boldsymbol{U}}_{\min }} \leqslant {{\boldsymbol{A}}_I}\Delta {{\boldsymbol{U}}_t} + {{\boldsymbol{U}}_t} \leqslant {{\boldsymbol{U}}_{\max }} \\ {{\boldsymbol{U}}_{\min }} \leqslant \Delta {{\boldsymbol{U}}_t} \leqslant {{\boldsymbol{U}}_{\max }} \\ {{\boldsymbol{Y}}_{n,\min }} - \varepsilon \leqslant {{\boldsymbol{Y}}_n} \leqslant {{\boldsymbol{Y}}_{n,\max }} + \varepsilon \\ \end{gathered} \right. \end{split} $ | (18) |
在式(18)中,
| $ \Delta {\boldsymbol{U}}_t^*(k) = {\left[ {\begin{array}{*{20}{c}} {\Delta {{\boldsymbol{u}}^*}(t)}& \cdots &{\Delta {{\boldsymbol{u}}^*}(t + {N_c} - 1)} \end{array}} \right]^{\text{T}}} $ | (19) |
将该序列中的首个元素作为实际控制输入增量作用于车辆模型,同时重新计算车辆状态,重述上述过程,实现对车辆的轨迹跟踪控制。
2.3 转向角优化策略在将车辆运动学模型线性化过程中,由于忽略了泰勒公式的高阶部分,这使得增量MPC的跟踪精度有所下降。同时为了解决车辆角速度存在突变的情况,需要计算合适的转向角。因此通过设计卡尔曼滤波算法对转向角进行优化校正,以提高控制器稳定性[13-14]。
设计离散的状态观测方程分别如下:
| $ {\boldsymbol{x}}(k + 1) = {\boldsymbol{f}}({\boldsymbol{x}}(k),{\boldsymbol{u}}(k)) + {\boldsymbol{w}}(k) = {{\boldsymbol{A}}_k}{\boldsymbol{x}}(k) + {{\boldsymbol{B}}_k}{\boldsymbol{u}}(k) + {\boldsymbol{w}}(k) $ | (20) |
| $ {\boldsymbol{y}}(k) = {\boldsymbol{g}}({\boldsymbol{x}}(k),{\boldsymbol{u}}(k)) + {\boldsymbol{v}}(k) = {{\boldsymbol{H}}_k}{\boldsymbol{x}}(k) + {\boldsymbol{v}}(k) $ | (21) |
式中:
二者协方差矩阵分别为
卡尔曼滤波算法分为预测转向角部分和测量更新转向角部分:
预测部分是通过
| $ {\boldsymbol{x}}(k + 1|k) = {{\boldsymbol{f}}_k}({\boldsymbol{x}}(k|k - 1),{\boldsymbol{u}}(k - 1)) $ | (22) |
通过式(21)可知,由于系统噪声存在,求解出预测误差协方差矩阵:
| $ {{\boldsymbol{P}}_{k + 1|k}} = {{\boldsymbol{A}}_{k + 1|k}}{{\boldsymbol{P}}_k}{\boldsymbol{A}}_{k + 1|k}^{\text{T}} + {\boldsymbol{Q}} $ | (23) |
测量更新部分通过卡尔曼增益矩阵
| $ {{\boldsymbol{K}}_{k + 1|k}} = {{\boldsymbol{P}}_{k + 1|k}}{\boldsymbol{H}}_{k + 1|k}^{\text{T}}[{{\boldsymbol{H}}_{k + 1|k}}{{\boldsymbol{P}}_{k + 1|k}}{\boldsymbol{H}}_{k + 1|k}^{\text{T}} + {\boldsymbol{R}}] $ | (24) |
| $ {\boldsymbol{x}}(k + 1) = {\boldsymbol{x}}(k + 1|k) + {{\boldsymbol{K}}_{k + 1|k}}{({\boldsymbol{y}}(k) - {{\boldsymbol{H}}_{_{k + 1|k}}}{\boldsymbol{x}}(k))^{ - 1}} $ | (25) |
最后通过更新下一时刻协方差矩阵表示估计误差以用于下一次计算:
| $ {{\boldsymbol{P}}_{k + 1}} = ({\boldsymbol{I}} - {{\boldsymbol{K}}_{k + 1|k}}{{\boldsymbol{H}}_{k + 1|k}}){{\boldsymbol{P}}_k} $ | (26) |
通过式(22)~(26)在每个时刻进行计算,对转向角进行了优化处理。定义车辆输出结果的横向误差和航向误差如图3所示,作为评判跟踪控制效果的标准[8]。
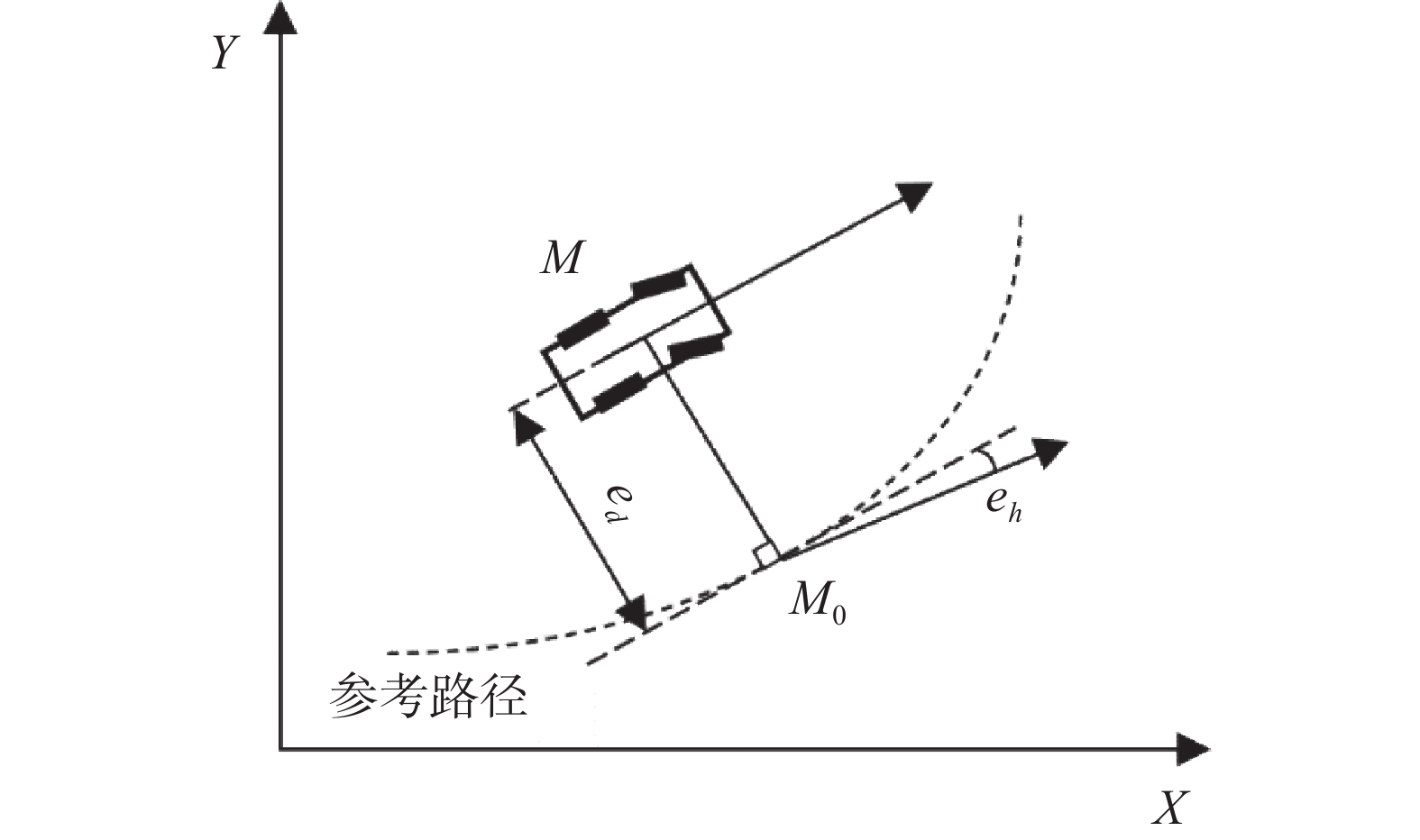
|
| 图 3 航向误差和横向误差 |
横向误差
通过Simuilink和Carsim进行联合仿真,在Simulink中搭建增量MPC控制器和加入卡尔曼滤波算法,在Carsim中搭建仿真车辆模型。仿真软件为Matlab2018a,搭载仿真环境的处理器为AMD Ryzen74800U,内存为16GB。
分别设计A、B两种控制器对泊车轨迹进行仿真分析。控制器A用增量MPC控制器进行轨迹跟踪,控制器B则采用MPC控制器,两个控制器参数如表2所示:
| 参数 | 增量MPC | MPC |
| 控制时域 | 30 | 30 |
| 预测时域 | 30 | 30 |
| 状态量 | 3 | 3 |
| 控制量个数 | 2 | 2 |
| 松弛因子权重 | 10 | 10 |
| 控制量约束 | –39~39 | – |
| 控制增量约束 | –1.35~1.35 | – |
3.2 平行泊车工况
设置车位参数,车库长6.4 m,车位宽2 m,在Carsim中搭建泊车环境,仿真模型如图4所示。

|
| 图 4 Carsim平行泊车 |
图4中可以看出,在Carsim仿真中车辆模型能够完成平行泊车。Simulink输出轨迹对比,如图5所示。
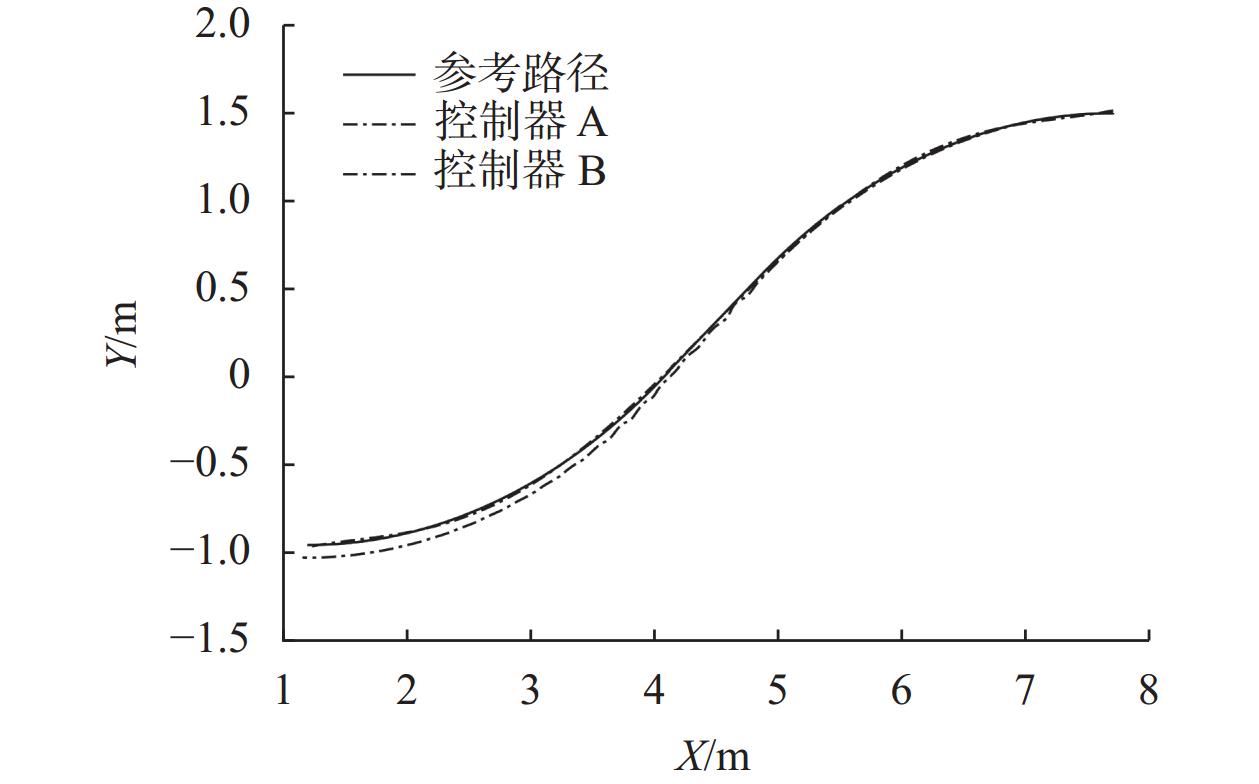
|
| 图 5 平行泊车轨迹对比 |
对图5结果分析,控制器A下的轨迹与参考轨迹大致相同,说明控制器A能够使车辆按照规划的轨迹行驶。而在控制器B下的轨迹跟踪,由于将非线性模型线性化,省略了泰勒公式的高阶部分,随着误差的累积,会出现控制偏差。
图6展示了两个控制器的横向误差和航向误差,在图6(a)中,控制器A下的轨迹跟踪最大横向误差为0.016 m,控制器B最大横向误差为0.079 m。在图6(b)中,控制器A最大航向误差为0.15°,而控制器B最大航向误差为1.83°。控制器A整体航向误差波动小,比控制器B效果更好。
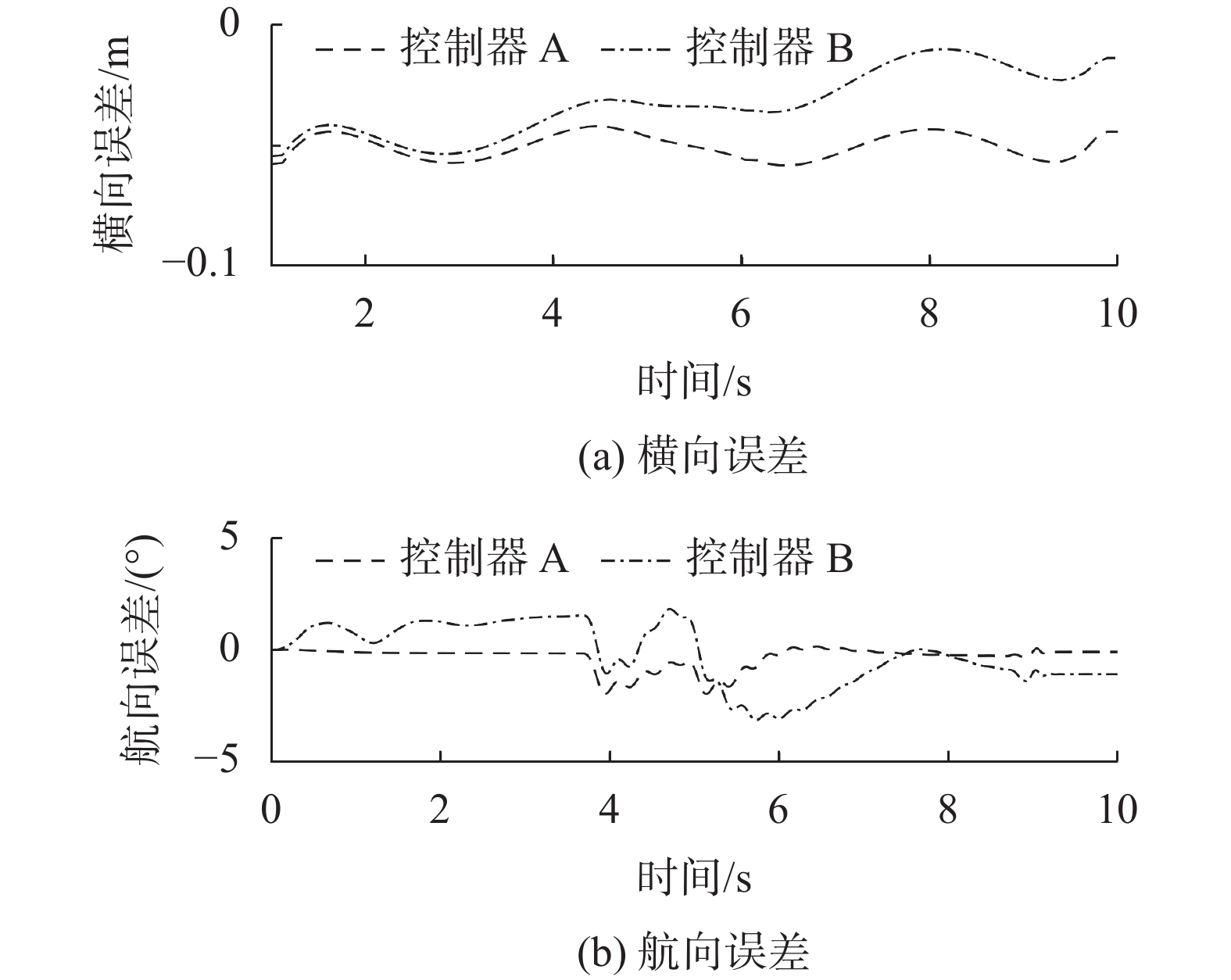
|
| 图 6 横向误差和航向误差 |
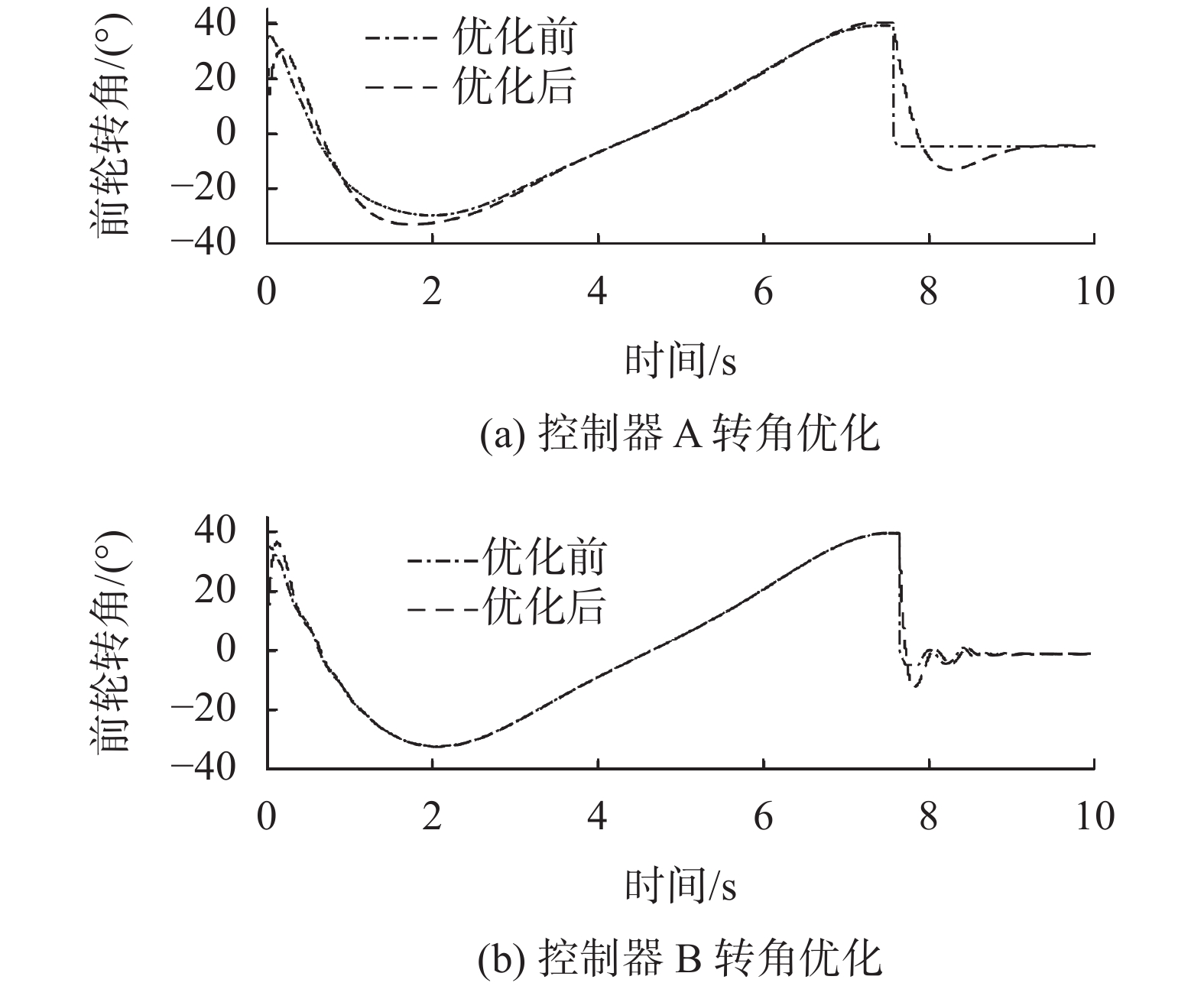
图7展示了两种控制器的在平行泊车工况下经过卡尔曼滤波后转向角输出结果。由图6得出,车辆转向角经卡尔曼滤波之后有明显的优化,更符合真实物理情况。通过对比图7(a),控制器A转向角优化前缓冲时间为0.57 s,优化后为1.521 s,适当延长的缓冲时间,能够提高车辆在轨迹跟踪过程的稳定性,安全性和舒适性。
|
| 图 7 转向角优化及对比 |
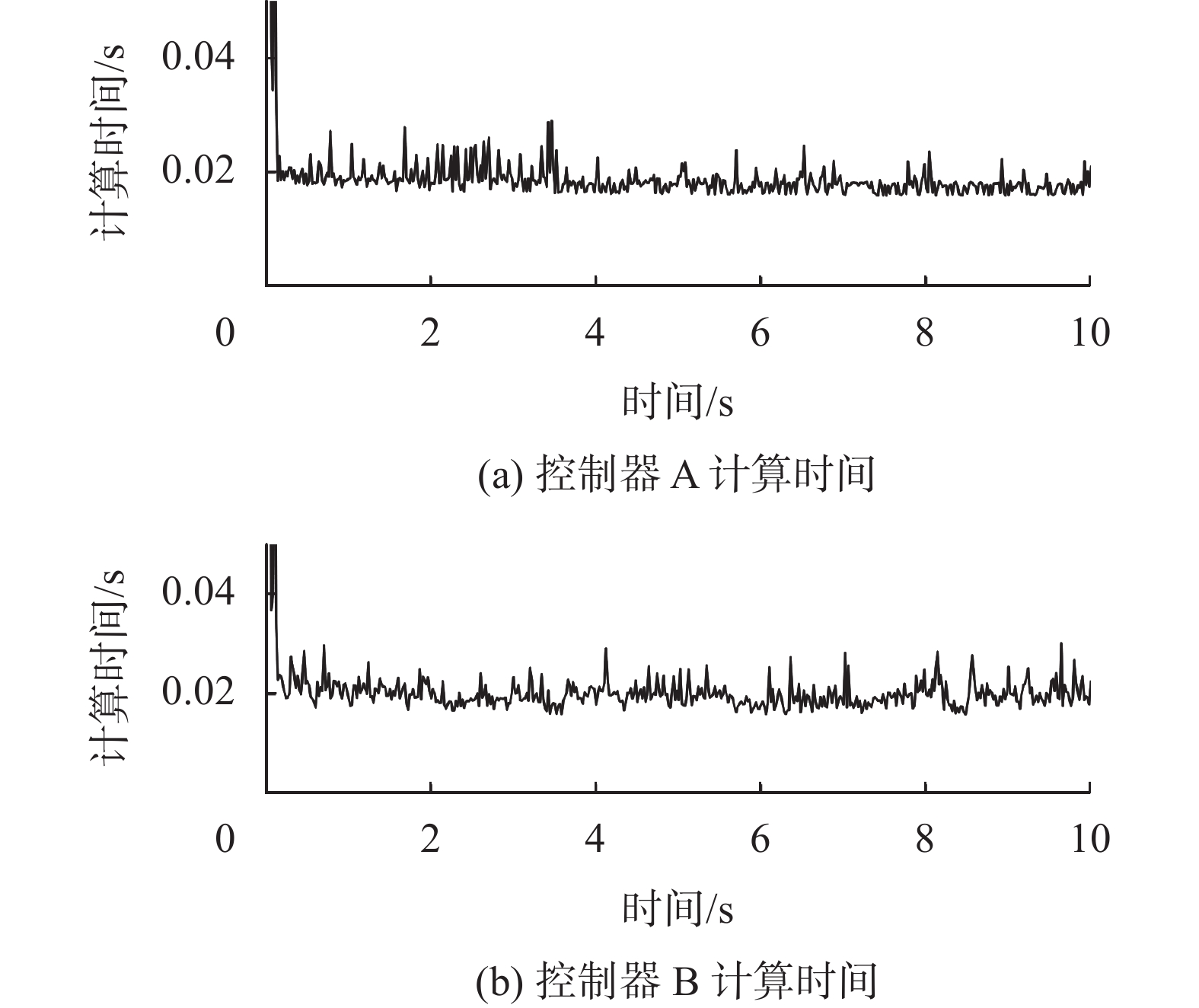
图8展示位两个控制器的在泊车过程中每个控制周期的计算时间,控制器A的平均运算时间为0.019 s,而控制器B的平均运算时间为0.021 s。
|
| 图 8 计算时间对比 |
表3为平行泊车轨迹跟踪性能对比表,能够看出,在平行泊车工况下,控制器A的性能指标比控制器B的更加稳定,改善效果明显。
| 轨迹跟踪性能参数值 | 增量MPC | MPC | |
| 横向误差/m | 最大值 | 0.016 | 0.079 |
| 航向误差/(°) | 最大值 | 0.15 | 1.83 |
| 转角优化前/s | 缓冲时间 | 0.57 | 1.394 |
| 转角优化后/s | 缓冲时间 | 1.521 | 1.736 |
| 计算时间/s | 平均值 | 0.019 | 0.021 |
3.3 垂直泊车工况
在垂直泊车中,通过设置车位长为5 m,车位宽为2.6 m。在Carsim中搭建仿真泊车环境如图9所示。

|
| 图 9 垂直泊车 |
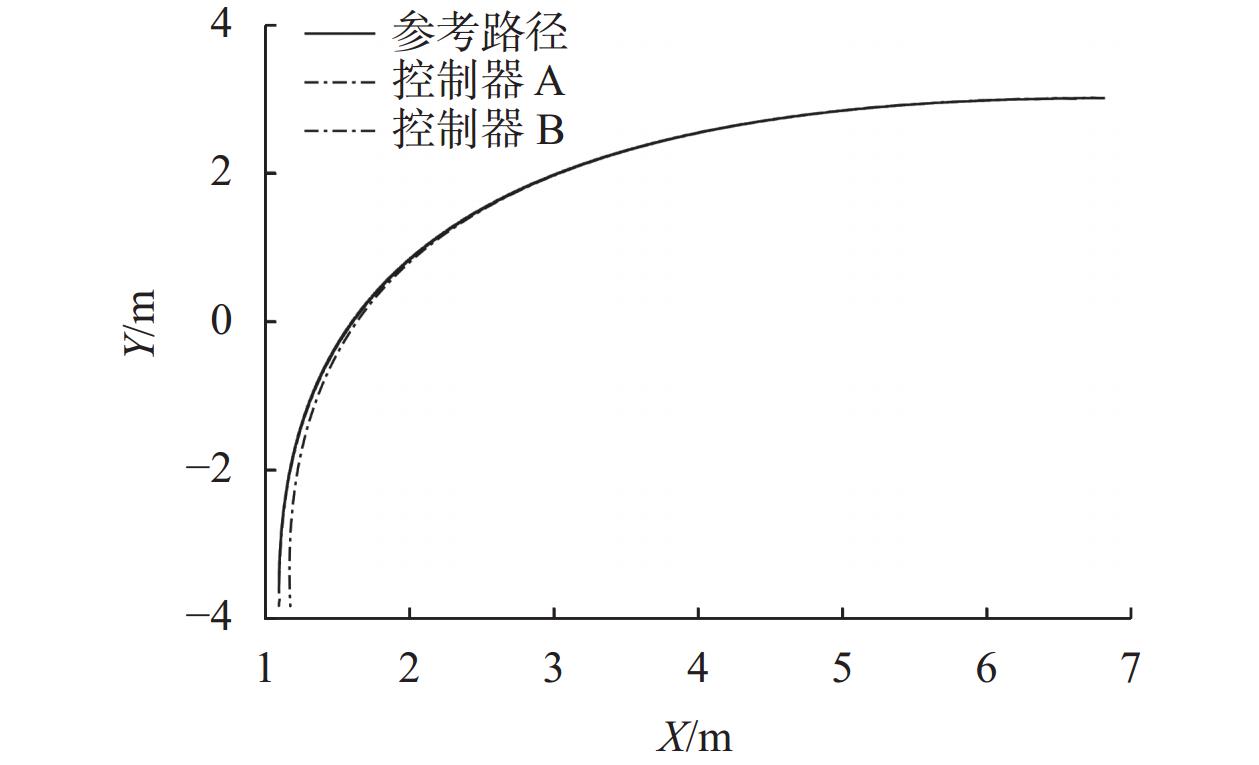
图9中可以看出,在Carsim仿真中车辆模型能够完成垂直泊车,Matlab/Simulink输出轨迹如图10所示。
|
| 图 10 垂直泊车轨迹对比 |
对图10输出结果分析,当车辆进行垂直泊车时,两种控制器的跟踪精度相近,都能够按照期望的参考轨迹行驶。在控制器A基本上可以准确完成轨迹的跟踪,同时精度较高。而控制器B的控制精度则略有下降。
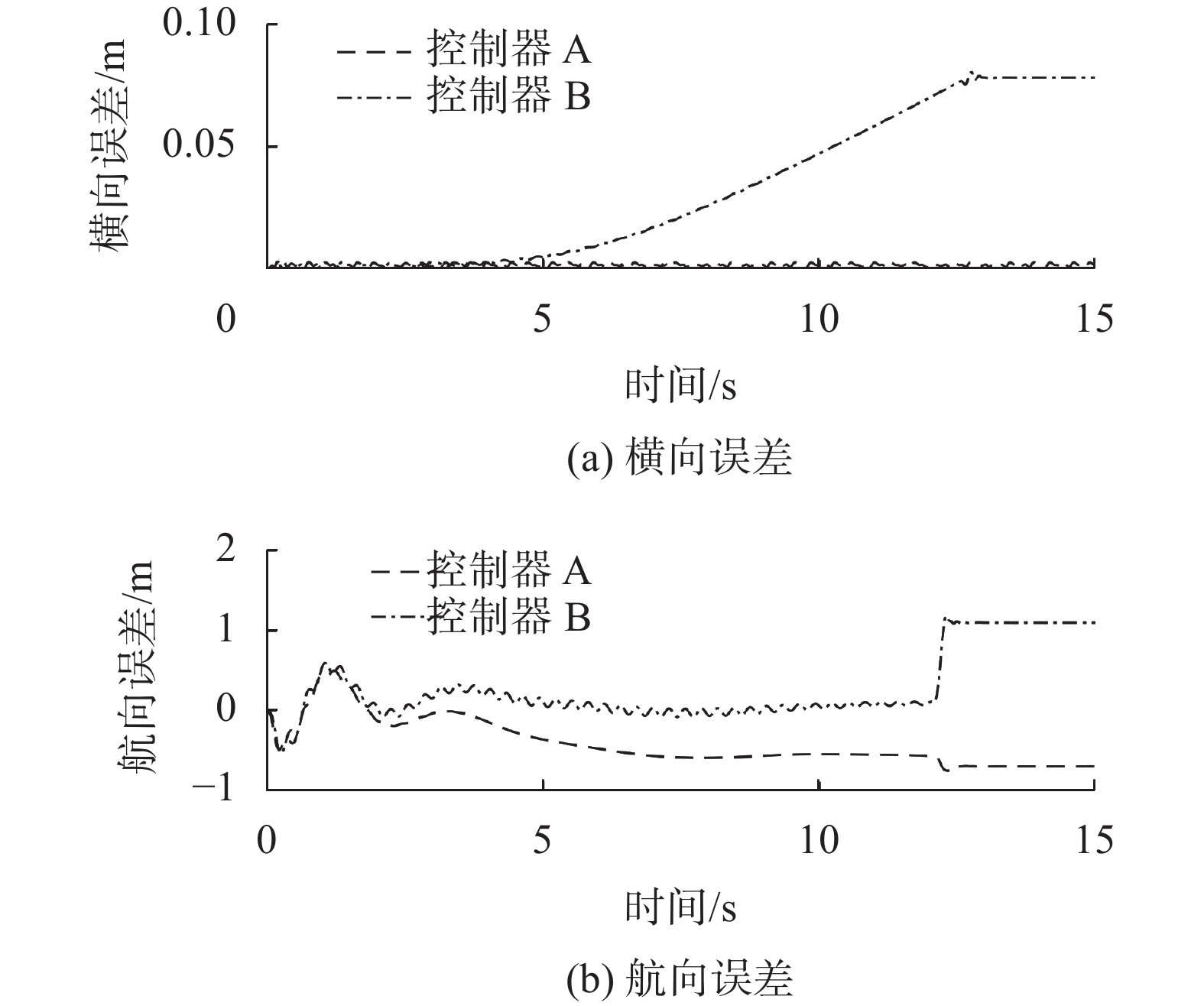
图11展示为垂直泊车工况下的两种误差结果。在图11(a)中,控制器A的最大横向误差为0.01 m,最大航向误差为0.742°,在图11(b)中,控制器B的最大横向误差为0.08 m,最大航向误差为1.194°。
|
| 图 11 横向误差和航向误差 |
图12显示的车辆前轮转角在两个控制器作用下的对比输出,和平行泊车工况相似,控制器A比控制器B更加平稳,同时前轮转角突变的情况也得到良好的改善。控制器A优化后的缓冲时间为1.04 s,控制器B优化后的缓存时间为3.05 s,控制器A相比与控制器B在转向过程中响应更快。
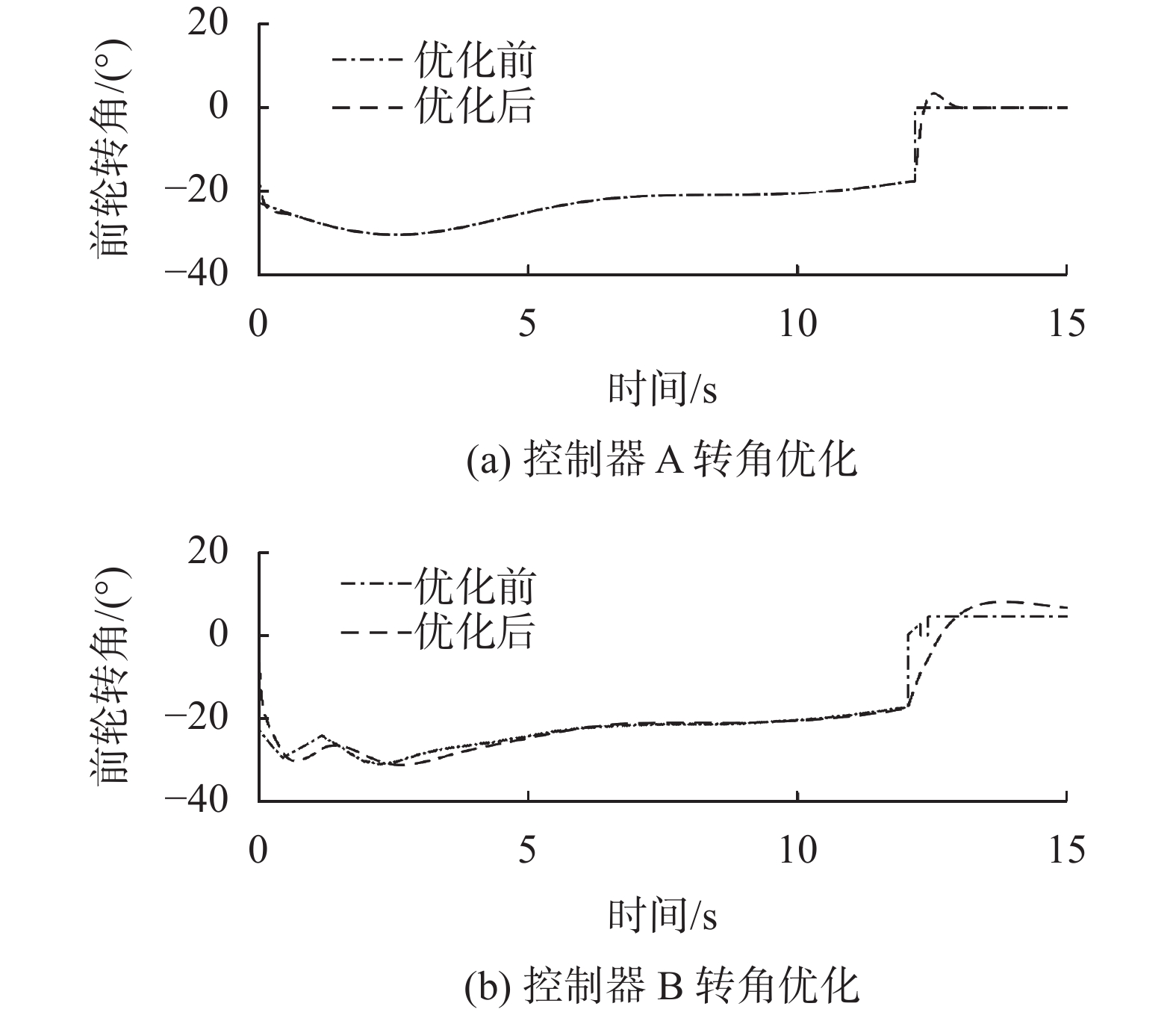
|
| 图 12 转角优化及对比 |
图13展示了两个控制器的每个控制周期的计算时间,控制器A平均运算时间为0.009 s,而控制器B的平均运算时间为0.012 s,可以看出垂直泊车工况下控制器A相对于控制器B能减少部分运算时间,同时稳定性也得到良好的控制。
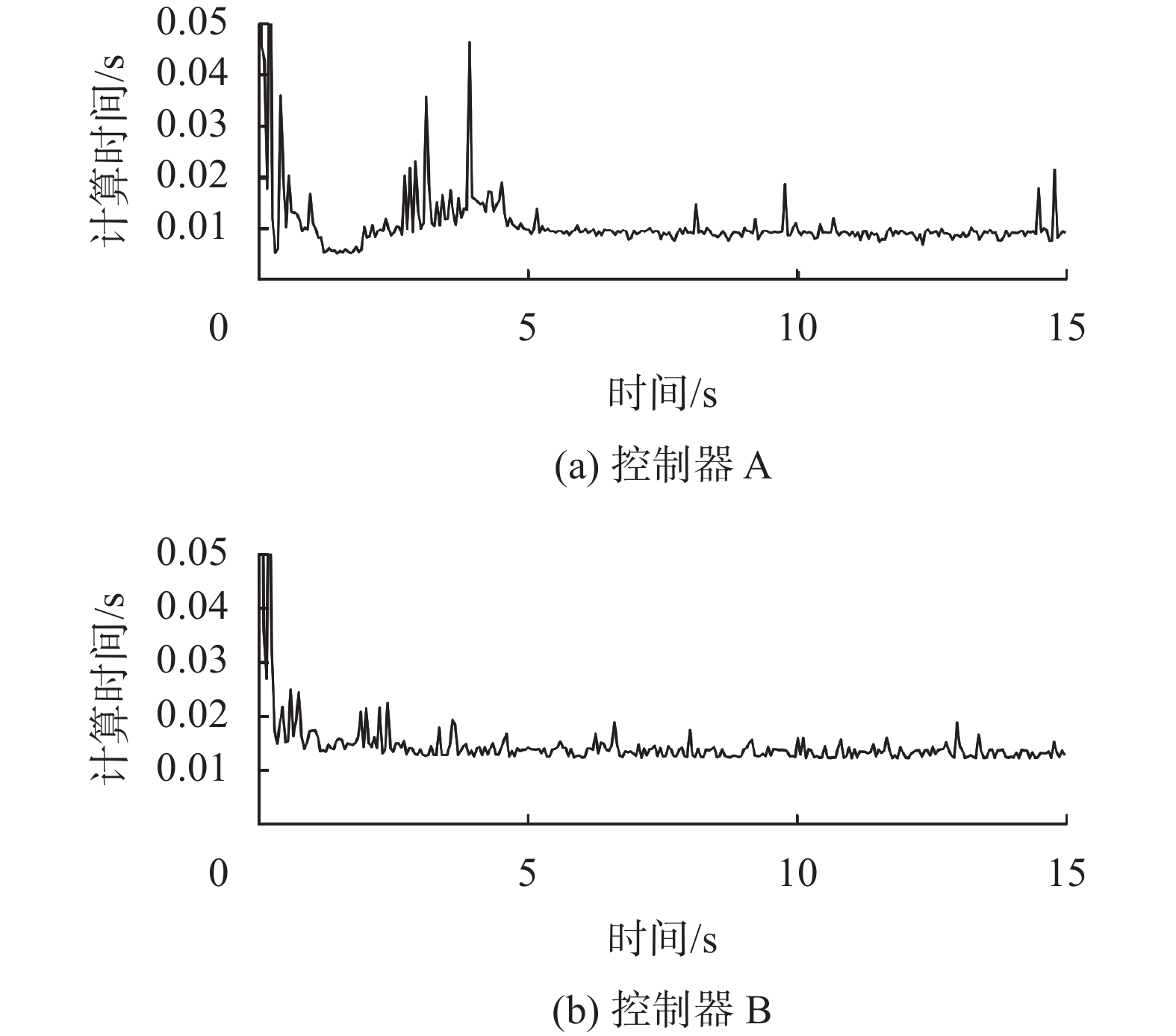
|
| 图 13 仿真时间 |
表4为垂直泊车轨迹跟踪性能对比表,可以看出,在控制器A在垂直泊车工况下的各方面性能都比控制器B的跟踪精度更高。结合表3,说明控制器A在两种泊车工况下,控制效果相比与控制器B更好,验证了增量MPC控制方案的可靠性。
| 轨迹跟踪性能参数值 | 增量MPC | MPC | |
| 横向误差/m | 最大值 | 0.01 | 0.08 |
| 航向误差/(°) | 最大值 | 0.742 | 1.194 |
| 转角优化前/s | 缓冲时间 | 0.18 | 0.52 |
| 转角优化后/s | 缓冲时间 | 1.04 | 3.05 |
| 计算时间/s | 平均值 | 0.009 | 0.012 |
4 结束语
本文针对传统MPC控制方案在泊车轨迹跟踪中出现的问题,设计了一种基于增量MPC的控制方案。首先,建立车辆二自由度运动学模型并将其线性化得到车辆轨迹跟踪的线性误差模型,再根据MPC原理设计增量MPC控制器;其次,在此基础之上,增设转向角优化策略。最后通过仿真实验表明,增量MPC控制方案相比传统MPC控制方案,降低了横向误差和航向误差,提高了实时性。同时转向角优化策略在转向过程中优化了前轮转角曲线突变的情况,提高轨迹跟踪精度和鲁棒性。
文中所设计的增量MPC控制方案适用于跟踪精度较低、实时性较差的泊车场景。在之后的研究中,将考虑车辆外部扰动等问题所带来的影响,在此基础上进一步完善本文所提出的控制方案,以提高轨迹跟踪控制性能。
| [1] |
李红. 自动泊车系统路径规划与跟踪控制研究[D]. 长沙:湖南大学, 2014.
LI H. Research on path planning and tracking control of automatic parking systems [D]. Changsha :Hunan University, 2014.
|
| [2] |
李永丹, 马天力, 陈超波, 等. 无人驾驶车辆路径规划算法综述[J].
国外电子测量技术, 2019, 38(6): 72-79.
LI Y D, MA T L, CHEN C B, et al. Overview of path planning algorithms for autonomous vehicles[J].
Foreign Electronic Measurement Technology, 2019, 38(6): 72-79.
|
| [3] |
唐圣学, 孙志国, 宋晓. 基于Lyapunov控制的多约束模型预测控制方法[J].
电子测量技术, 2022, 45(1): 172-176.
TANG S X, SUN Z G, SONG X. A multi constraint model predictive control method based on lyapunov control[J].
Electronic Measurement Technology, 2022, 45(1): 172-176.
|
| [4] |
杨博, 张缓缓, 江忠顺. 智能车辆的避障路径规划与跟踪控制仿真分析[J].
中国测试, 2021, 47(7): 71-78.
YANG B, ZHANG Q H, JIANG Z S. Simulation analysis of obstacle avoidance path planning and tracking control for intelligent vehicles[J].
China Measurement & Test, 2021, 47(7): 71-78.
DOI:10.11857/j.issn.1674-5124.2020080001 |
| [5] |
PAOLO F, FRANCESCO B, et al. Predictive active steering control for autonomous vehicle systems[J].
IEEE Transaction on Control Systems Technology, 2007, 15(3): 566-580.
DOI:10.1109/TCST.2007.894653 |
| [6] |
FRANCESCO B, PAOLO F. MPC-based approach to active steering for autonomous vehicle systems[J].
International Journal on Vehicle Autonomous Systems, 2005, 3(2-4): 265-291.
|
| [7] |
胡远志, 何朋声, 刘西. 基于模型预测控制的平行泊车控制方法[J].
重庆理工大学学报(自然科学), 2020, 34(10): 1-8.
HU Y Z, HE P S, LIU X. Parallel parking control method based on model predictive control[J].
Journal of Chongqing University of Technology (Natural Science), 2020, 34(10): 1-8.
|
| [8] |
顾青, 白国星, 孟宇, 等. 基于非线性模型预测控制的自动泊车路径跟踪[J].
工程科学学报, 2019, 41(7): 947-954.
GU Q, BAI G X, MENG Y, et al. Automatic parking path tracking based on nonlinear model predictive control[J].
Chinese Journal of Engineering, 2019, 41(7): 947-954.
|
| [9] |
龚建伟, 姜岩, 徐威. 无人驾驶车辆模型预测控制[M]. 北京: 北京理工大学出版社, 2014.
GONG J W, JIANG Y, XU W. Model predictive control for autonomous vehicles [M]. Beijing: Beijing Institute of Technology Press, 2014.
|
| [10] |
吕沛龙, 丁宝苍, 王丽, 等. 基于增量状态空间模型的双层预测控制[J].
控制工程, 2021, 28(10): 1923-1930.
LV P L, DING B C, WANG L, et al. Double layer predictive control based on incremental state space model[J].
Control Engineering, 2021, 28(10): 1923-1930.
|
| [11] |
FALCONE P. Nonlinear model predictive control for autonomous vehicles[D]. Benevento: University of Sannio, 2007.
|
| [12] |
陈虹. 模型预测控制[M]. 北京:科学出版社, 2013.
CHEN H. Model predictive control [M]. Beijing:Science Press, 2013.
|
| [13] |
郭孔辉, 付皓, 丁海涛. 基于扩展卡尔曼滤波的汽车质心侧偏角估计[J].
汽车技术, 2009(4): 1-3.
GUO K H, FU H, DING H T. Estimation of automobile center of mass lateral angle based on extended Kalman filter[J].
Automobile Technology, 2009(4): 1-3.
DOI:10.3969/j.issn.1000-3703.2009.04.001 |
| [14] |
章仁燮, 熊璐, 余卓平. 智能汽车转向轮转角主动控制[J].
机械工程学报, 2017, 53(14): 106-113.
ZHANG R X, XIONG L, YU Z P. Active control of steering wheel angle in intelligent vehicles[J].
Journal of Mechanical Engineering, 2017, 53(14): 106-113.
|
 2024, Vol. 50
2024, Vol. 50


 ,
,