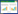文章信息
- 顾爱军, 关庆圆, 徐波, 苏铭, 李非凡
- GU Aijun, GUAN Qingyuan, XU Bo, SU Ming, LI Feifan
- 基于声发射断层总面积和b值的钢筋混凝土梁损伤表征
- Damage characterization of reinforced concrete beams based on total acoustic emission fault area and b-value
- 中国测试, 2024, 50(7): 147-154, 198
- CHINA MEASUREMENT & TEST, 2024, 50(7): 147-154, 198
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022050206
-
文章历史
- 收稿日期: 2022-05-28
- 收到修改稿日期: 2022-08-04
2. 淮安市水利勘测设计研究院有限公司,江苏 淮安 223005
2. Huai’an Water Conservancy Survey and Design Institute Co., Ltd., Huai’an 223005, China
混凝土作为现代工程建设中最主要的材料在建筑、公路、桥梁、隧道、水利等建设领域中发挥着不可替代的作用。由于混凝土材料复杂,结构受人为、环境等多种影响因素,受力特征呈现非线性和随机性,关于混凝土损伤演化表征的研究一直受到国内外学者的广泛关注[1-2]。
声发射技术(AE)作为一种无损检测技术,可以很好地反映混凝土受载过程中损伤的产生和发展特征,识别混凝土结构的损伤演化规律和破坏机理,做到实时监测,并给出可靠的预警信息,近年来在国内外混凝土损伤检测领域的研究和应用越来越多。Nguyen-Tat T等[3]认为混凝土梁损伤演化与声发射活动之间有强烈相关性,提出了描述损伤演化与声发射活动之间关系的经验定律。Rami Eid等[4]对轴向压缩载荷下的HSC色谱柱进行了AE监测研究,表明AE监测可以为受轴向载荷施压的高强度混凝土柱提供损坏和负载水平的指示。刘思孟等[5]揭示了声发射现象和混凝土梁剪应力分布的内在关联。通过对12根钢筋混凝土梁的测试表明,当梁处于工作阶段和破坏阶段时,声发射源强度分布与梁段剪应力分布密切相关。龙小江等[6]采用广义S变换对钢材声发射检测信号进行时频分析用于评价钢材损伤各个阶段。
对声发射信号的分析方法目前以参数分析法应用最为广泛,即通过对采集信号同步提取的特征参数进行分析,以获取实时的材料损伤信息。但是对声发射参数与力学指标(断裂能、损伤度等)相互关系的研究相对较少,较为成熟的方法主要有b值分析、RA-AF关联分析、Kaiser效应分析等,这些方法虽然能表征混凝土损伤,但在精准性和实用性方面仍有很多不足。
b值分析法由Gutenberg和Richter提出,结合频度和震级用于对地震活动性进行评估。由于混凝土破坏与地震相似,在声发射领域,b值可反映事件数和幅度的关系,用于混凝土损伤评估,近年来一直有很多研究。Burud N B等[7]将最近提出的马斯洛夫广义逻辑方程(GLE)用于b值分析,发现GLE的b值与普通混凝土损坏过程中的有效裂缝长度相关性良好。董胧军等[8]进行了花岗岩三轴压缩实验,以实验中AE有效数据的占比对b值的计算方法的误差进行分析表明最大似然法所受影响因素较小。Li等[9]分析在三点弯曲加载下的混凝土断裂过程的AE数据,并通过b值把水工混凝土的断裂分为微裂纹成核、大裂纹成核和宏观裂纹传播三个阶段。
断层总面积是地震学领域用于评估地震活动性高低的标志,同时考虑了地震频度和地震能量,目前主要应用于地震领域的预测评估方面[10]。宋德熹等[11]对华北地区16例中强地震进行了研究,对断层总面积值随时间变化的特征进行分析表明其有较好的预测效果。肖淑娟等[12]对祁连山中西段中强地震前的变化特征进行研究,发现断层总面积在震前有明显的峰值异常,对强震有较好的预测效果,在采矿工程中对冲击矿压的有效监测预警也有应用。窦林名等[13]将断层总面积值的峰值异常作为煤岩灾变破坏的前兆进行了研究。断层总面积是一种对信号活动性评估的方法,由于混凝土开裂和地震破坏相似,可考虑将断层总面积理论应用于通过声发射信号对混凝土开裂破坏评估中去。
为探究混凝土损伤规律,利用声发射技术对钢筋混凝土的破坏进行识别和预警,声发射信号的事件数、幅度、能量都是重要的基本参数。以往的参数分析多以声发射基本参数的变化进行规律性分析,本文利用断层总面积理论,同时结合事件数和能量,得到声发射断层总面积,并结合声发射b值对钢筋混凝土损伤进行表征,综合考虑了信号的事件数、幅度和能量,提升了对混凝土结构损伤预警识别的精准性,从而为运用声发射技术进行损伤识别和预警提出合理的声发射信号监测方法,为实际工程中的钢筋混凝土损伤的判别提供合理的依据。
1 声发射断层总面积在地震领域,根据Gutenberg公式,能量和震级存在以下关系:
| $ {\lg}E = a + bM $ | (1) |
式中:E——地震能量,J;
M——里氏震级;
a,b——常数,由线性拟合求得。
可认为震级差1级,释放能量差
| $ K = {{\mathrm{lg}} }E $ | (2) |
其中,E为声发射绝对能量,aJ(1 aJ=10–18 J)。
声发射的绝对能量是声发射撞击信号能量的真实反映,不受前置增益的影响,可以等效反映声源的物理能量。因此可采用声发射绝对能量去定义声发射能级。声发射传感器后端往往需要连接前置放大器,绝对能量要求消除该增益,只计算传感器输出端的电压。传感器输出端的电压的平方在时间上进行积分并除以相应阻抗(本系统为10 kΩ),得到绝对能量。可由下面公式求得:
| $ E = \int_{{t_1}}^{{t_2}} {\frac{{V_{{\text{rms}}}^2}}{R}} {\mathrm{d}}t $ | (3) |
式中:E——绝对能量,aJ;
R——10 kΩ的阻抗。
结合公式(2)和公式(3)可求得声发射能级。
断层总面积早期称为“加权和”方法,定义一个介于地震频度和地震能量之间的断层总面积A(t),本质上为了兼顾低能量事件占比较大的问题,通过频次和能量评价活动性的过程中,低能量事件的数量通常远超高能量事件数,事件数实际由低能量事件决定,而总能量通常由占少数的高能事件决定。类似地,在声发射系统中,为了克服这一矛盾可同样引用断层总面积A(t),既考虑了事件数,又考虑了能量。
断层总面积理论首先结合频度和能级的关系定义函数A(t):
| $ A(t) = \sum\nolimits_K {N(K)} {L^K} $ | (4) |
式中:K——能级,定义为
N(K)——能级等于K的次数;
L——常数。
结合公式(4)可以看出L的取值标准为,当L=1时,A(t)代表全部能级的事件总和,当L=10时,A(t)代表全部事件的总能量。可见L的取值(1~10)决定了函数A(t)的物理意义更倾向于AE事件数还是AE总能量。
在断层总面积理论中,假定一个破裂发生前其构件内均达到破裂前的临界应变状态,而这种临界应变又大体是一个常值,因能量正比于破裂源体积,即正比于破裂源断层面积的3/2次方,即
| $ {\left[ {A(t)} \right]^{3/2}} \propto \sum\nolimits_K {N(K)} {10^K} $ | (5) |
故此可将L取为10的2/3次方,有:
| $ A(t) \approx \sum\nolimits_K {N(K)} {10^{\frac{2}{3}K}} $ | (6) |
此时A(t)与断裂总面积成正比。
为方便计算,实际应用中取
| $ A(t) = \sum\nolimits_{{K_0}}^{K - 1} {N(K)} {10^{\frac{{2(K - {K_0})}}{3}}} $ | (7) |
其中
在地震领域,1941年Gutenberg和Richter建立了震级和频度关系的G-R准则:
| $ {\lg}N = a - bM $ | (8) |
式中:N——震级大于M的地震次数;
M——地震震级;
a,b——常数。
其中b值的大小随空间和时间而变化,可作为地震预报中可利用的指标。
由于材料轻微开裂释放的声发射事件数多于严重开裂的事件数,同地震相似,可将G-R准则应用于声发射领域。一般使用声发射幅度来反映声发射事件的大小,通常以AdB作为声发射幅值,定义声发射传感器输出1 μV时为0 dB,AdB可由下式算出:
| $ A_{\text{dB}}=20{\mathrm{lg}}\frac{V_{\text{AE}}}{1\ \text{μV}} $ | (9) |
其中
| $ {{\mathrm{lg}} }N = a - b\frac{{{A_{{\text{dB}}}}}}{{20}} $ | (10) |
式中:N——幅度超过
AdB——声发射幅值;
a和b——线性拟合参数,参数b代表曲线斜率即为所求b值。
b值的计算方法目前有最小二乘法和最大似然法,最小二乘法可能因孤立点的偏离导致结果不精确,当事件总数足够多时采用最大似然法会有较大的可信度,即假设随机量N服从泊松分布,若考虑到对数概率分布和最大真值的原理,可得出b值计算公式为
| $ b = \frac{{20\lg {\mathrm{e}}}}{{\overline {{A_{{\text{dB}}}}} - ({A_{{\text{dBmin}}}} - \dfrac{\Delta }{2})}} $ | (11) |
式中:
通过公式(11)可求得混凝土破坏过程中的声发射b值。
3 实 验为探究混凝土损伤破坏过程,对钢筋混凝土梁进行了四点弯曲加载破坏实验,在钢筋混凝土梁试件一面两侧分别设置一个声发射传感器,采用四点弯曲分级加载方式进行加载,并在加载过程中持续记录声发射各个基本参数。
3.1 试件准备试验中钢筋混凝土梁试件采用的混凝土强度为C20,试验采用100 mm×150 mm×1200 mm的梁,并配必要的钢筋,钢筋保护层厚度为20 mm。配筋图及主要尺寸见图1。28天抗压实测值为22 MPa。
|
| 图 1 钢筋混凝土梁配筋图(单位:mm) |
3.2 实验过程
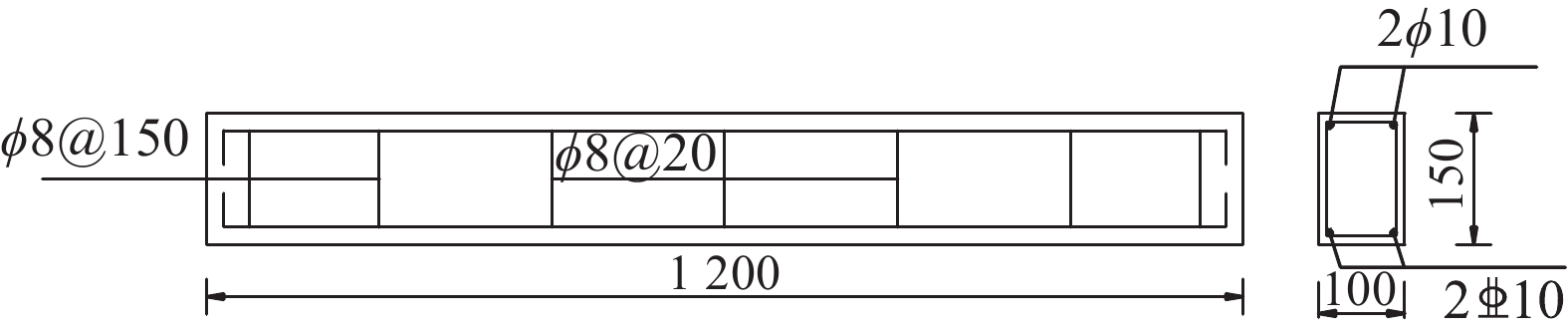
加载系统由自平衡反力架、手动油压千斤顶、压力传感器和计量挠度的百分表组成,利用反力架进行竖向加载,采用四点弯曲加载使梁的中部处于纯弯曲受力状态,并采用分级加载使混凝土的变形得以及时释放。按估算的最大荷载确定每级加载量为5 kN,到达每一加载等级后维持一定时间,再进行下一级加载,直至梁破坏失去承载能力。采用宽频AE传感器(PAC WDI-AST)进行数据采集,通过梁下方的百分表计量梁跨中的挠度。传感器粘贴在梁表面,布置图如图2所示。
|
| 图 2 传感器布置及加载示意图(单位:mm) |
4 实验结果与分析 4.1 实验结果
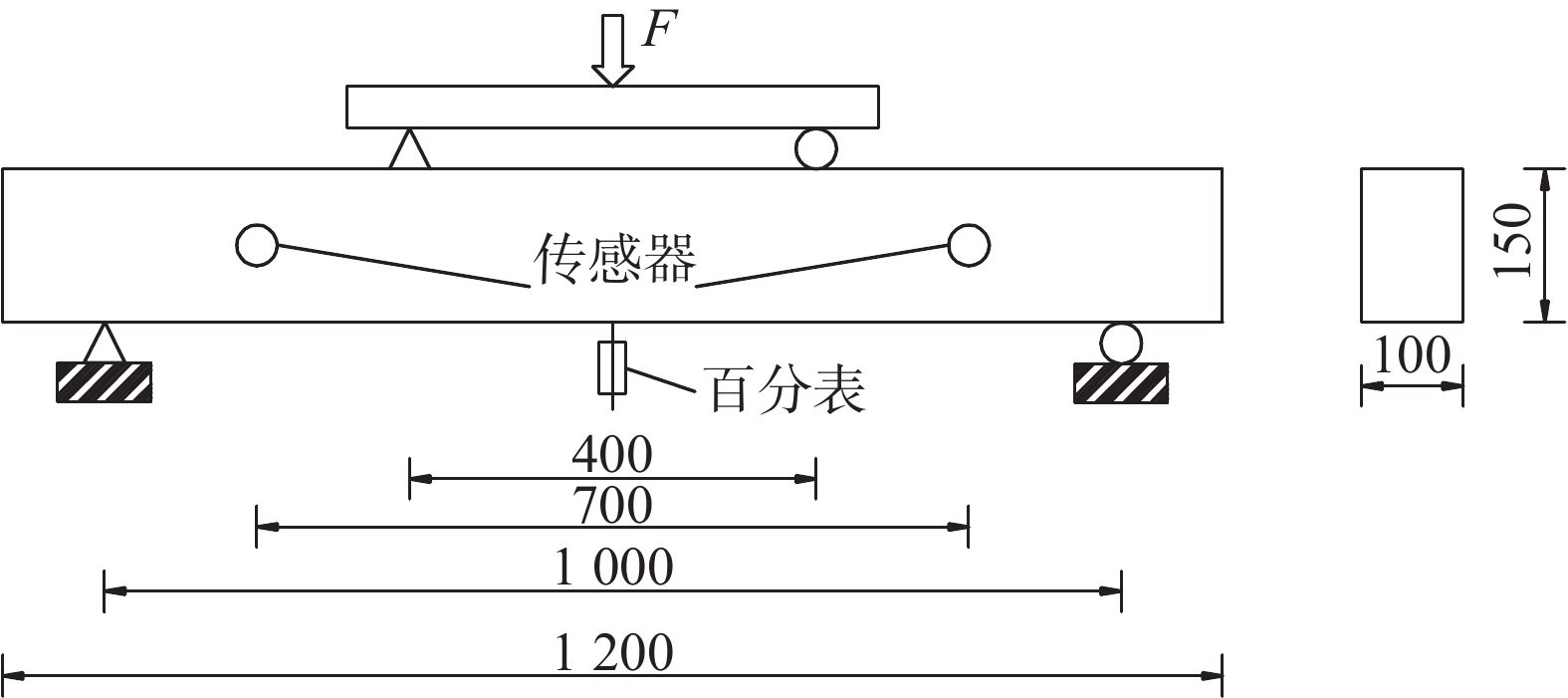
四点弯曲条件下钢筋混凝土梁的破坏过程,主要是混凝土裂纹的萌发、扩展、贯通的过程。跨中挠度变化曲线如图3所示,为便于观察,对实验过程中产生的表面裂纹用黑色记号笔做了标记,如图4所示。声发射基本参数随时间的变化如图5所示。在试验过程中大部分时间内,事件数、能量释放和振铃计数比较稳定且数值处于较低水平,但也存在一些能量和振铃计数集中增长的时间段,如图5中的时间点A左右,时间点B左右,时间段C到D,时间段E到F,通常象征着材料内部裂纹发生剧烈变化。
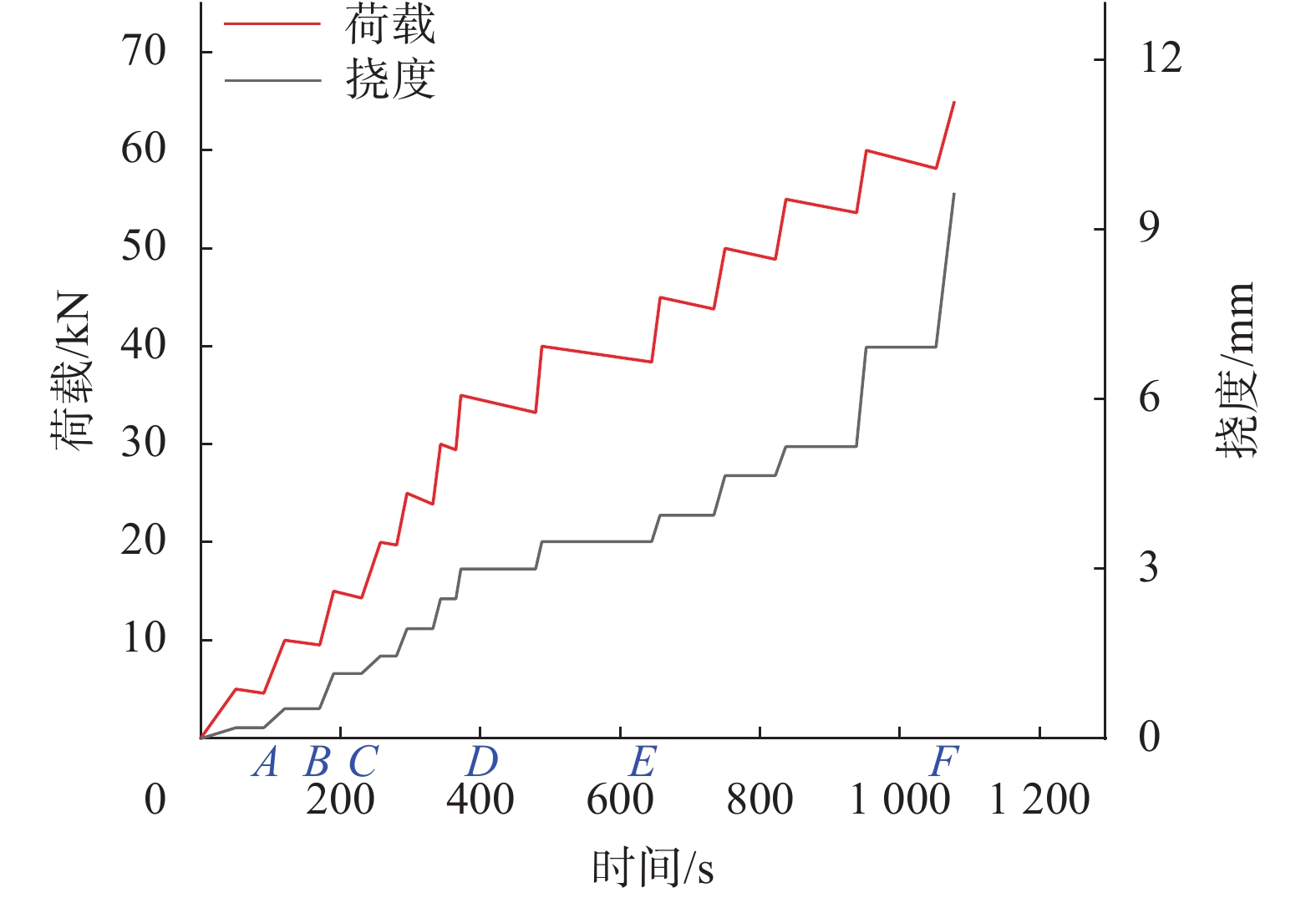
|
| 图 3 跨中挠度曲线 |

|
| 图 4 混凝土梁实验过程图 |

|
| 图 5 声发射参数变化历程图 |
在0到110 s内,幅度、事件数、能量和振铃计数比较稳定且数值处于较低水平,混凝土梁应处于孔隙压实状态。在110 s图中时间点A左右,声发射幅度、能量和振铃计数开始出现小幅度的集中变化,声发射振铃计数在113 s出现第一个峰值98,声发射能量在113 s出现第一个峰值263.45 mV·ms,说明梁内部开始出现微裂纹,但试件表面未见宏观裂纹如图4(a)所示。在182 s图中时间点B左右,荷载约10.4 kN,梁跨中底部出现第一条细微的裂纹如图4(b)所示,声发射幅度、能量和振铃计数开始出现密集性增长,声发射振铃计数在182.5 s出现峰值376,声发射能量在182.5 s出现峰值1078.56 mV·ms。在245 s到414 s图中C到D时间段内,荷载约从20 kN加至30 kN的过程中,原有裂纹向上扩展,宽度增大,同时多条裂纹萌发如图4(c)所示。高幅度事件数大量出现,能量和振铃计数也出现多个高峰值,声发射振铃计数在365 s时高达10545,声发射能量在365 s高达16868.88 mV·ms。当试验进行到648 s图中时间点E之后,多条细微裂纹逐渐贯通朝向跨中顶部迅速扩展如图4(d)所示,高幅度事件数大量出现,能量和振铃计数也持续出现多个高峰值。当加载至65 kN时及1078 s图中时间点F时,跨中裂纹贯通,一条较宽的裂纹从梁跨中底部右侧延伸至梁跨中顶部,试验过程中可以听到崩裂声,钢筋混凝土梁失去承载能力,能量和振铃计数也达极大值17108.4 mV·ms和13627。
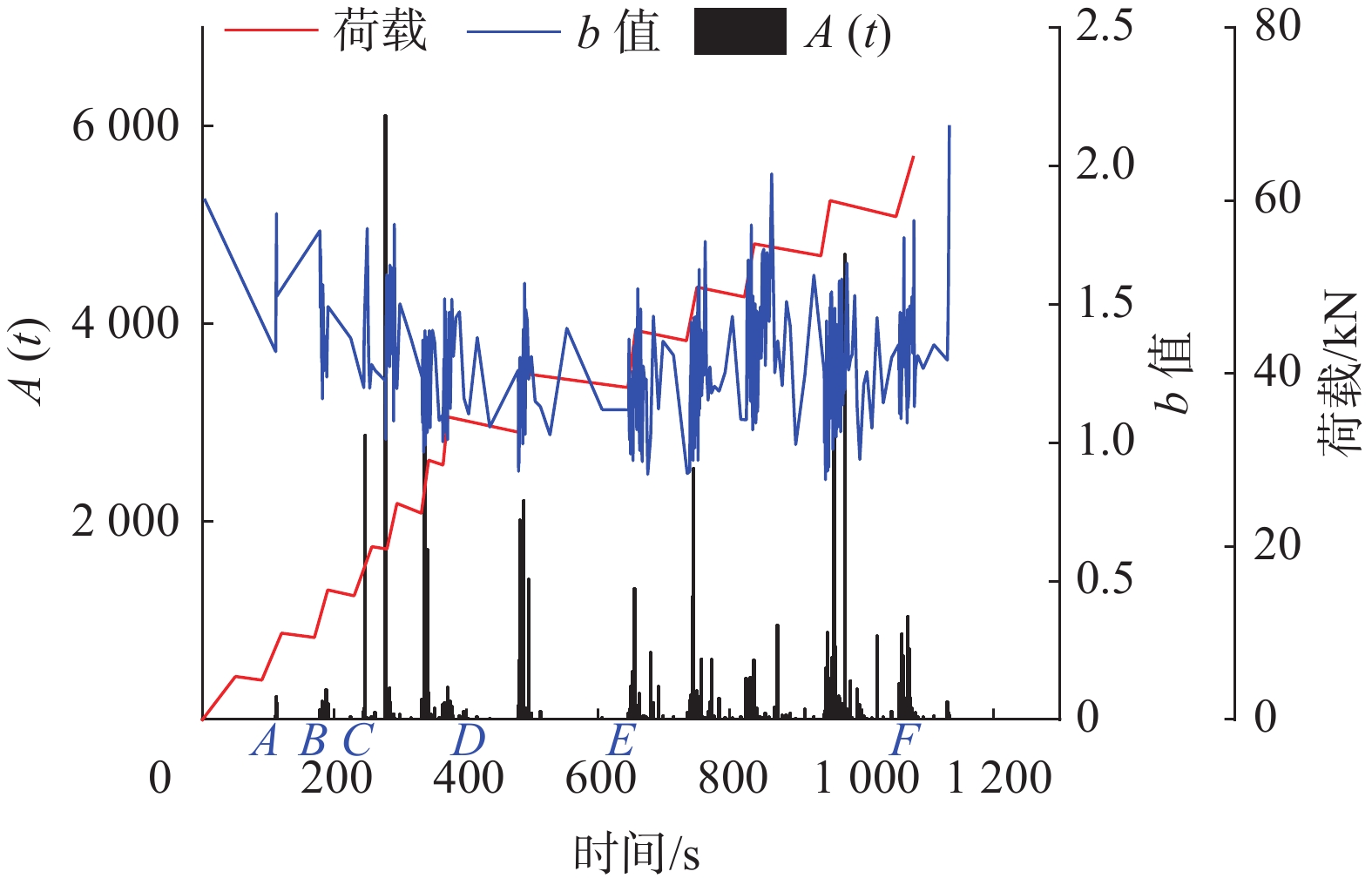
4.2 结果分析 4.2.1 断层总面积A(t)和b值的计算结果断层总面积A(t)和b值的计算均需要对声发射信号的数据进行分组处理,一般有按次数滑动和时间滑动两种方法,按次数滑动优点是误差变化不大,缺点是时间间隔可能随事件活动频次的减少而增大,按时间滑动,优点是时间分段相同,便于时间变化空间分布同时性比较,缺点是误差起伏大,有时出现错误结果。由于本次实验中持续有声发射事件产生,故采用按次数滑动,对实验数据进行分组,以每50点为一组,引用公式(7)和(11),计算混凝土梁破坏过程的断层总面积A(t)和b值如图6所示。
|
| 图 6 断层总面积A(t)和b值随时间变化的历程图 |
4.2.2 断层总面积A(t)和b值之间的关系
A(t)综合了事件数和能量,物理意义上可评估断裂总面积,在大断裂破坏前即高能量释放前,能量会通过微裂纹进行释放,A(t)会出现峰值异常可说明内部微裂纹的增多。b值反映不同幅度声发射事件的组合情况,小幅度事件数占比变多时b值上升,大幅度事件数占比变多时b值下降可说明内部损伤的加重。如图6所示,在混凝土试件发生破坏的关键时期即图中A、B时间点,C到D时间段,E到F 时间段,断层总面积A(t)的值会出现多个高峰值,而b值也会出现多次连续下降的趋势。
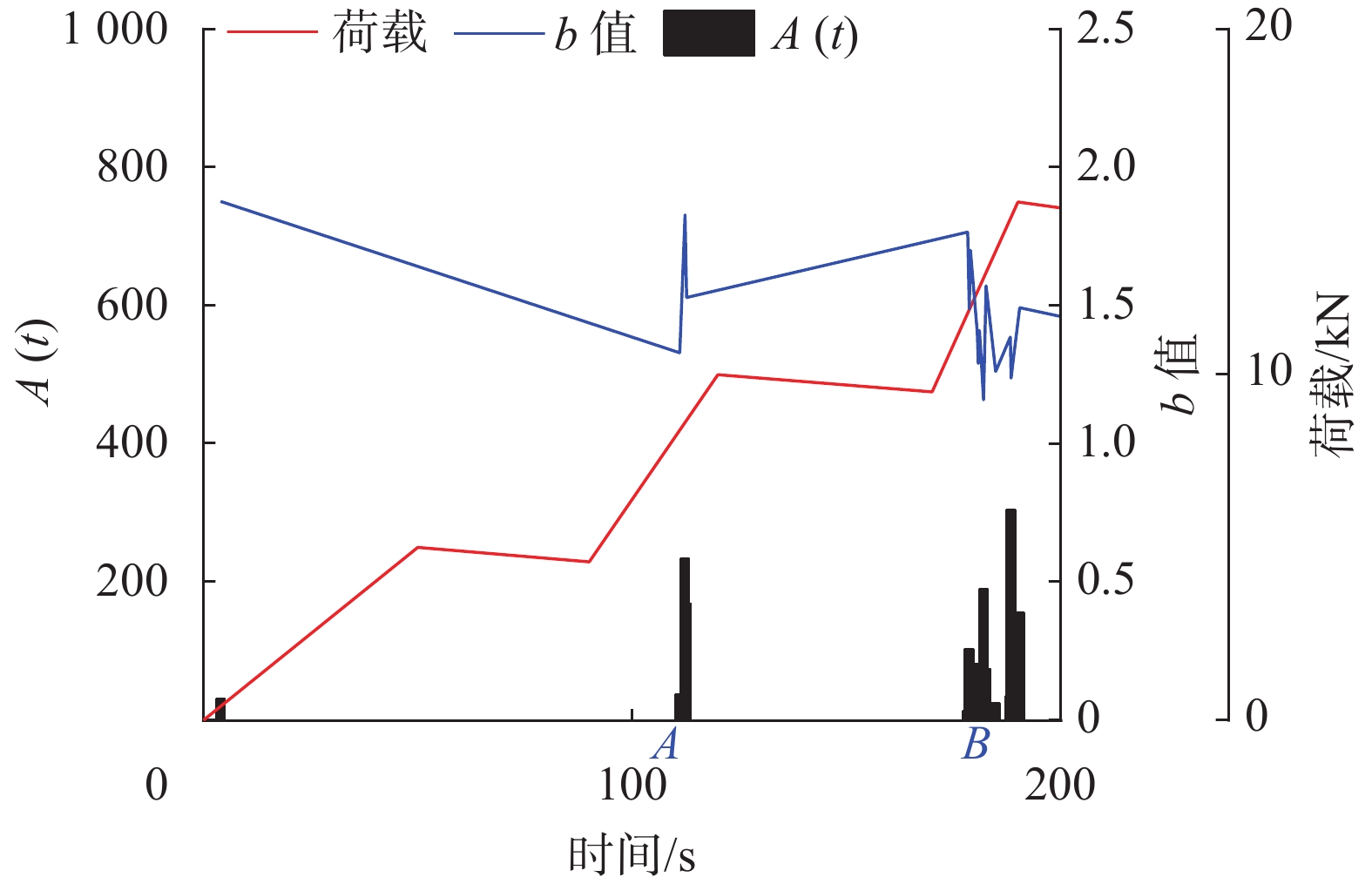
如图7所示,图中时间点A即110 s左右,梁虽表面不见裂纹,A(t)在高能量释放前会出现峰值异常,A(t)此时出现多个高峰值点,在112.3 s时达232.37,说明梁内部随着荷载的增加开始产生微裂纹破坏并释放能量,b值在111.1 s降至1.33,b值的下降表明高幅度事件数占比增加,内部开始出现损伤,而后随着能量的释放和高幅度事件数的减少,A(t)不出现高峰值,b值回弹上升。至图中B点182 s左右梁产生第一条裂纹时,A(t)出现多个高峰值点,最高达303.45,此时的异常峰值对应大裂纹的产生和高能量的释放,b值出现多次下降,在181.9 s时降至1.16,表明随着第一条裂纹的产生,高幅度事件数占比增加。
|
| 图 7 试件加载至第一条裂纹产生时间段 |
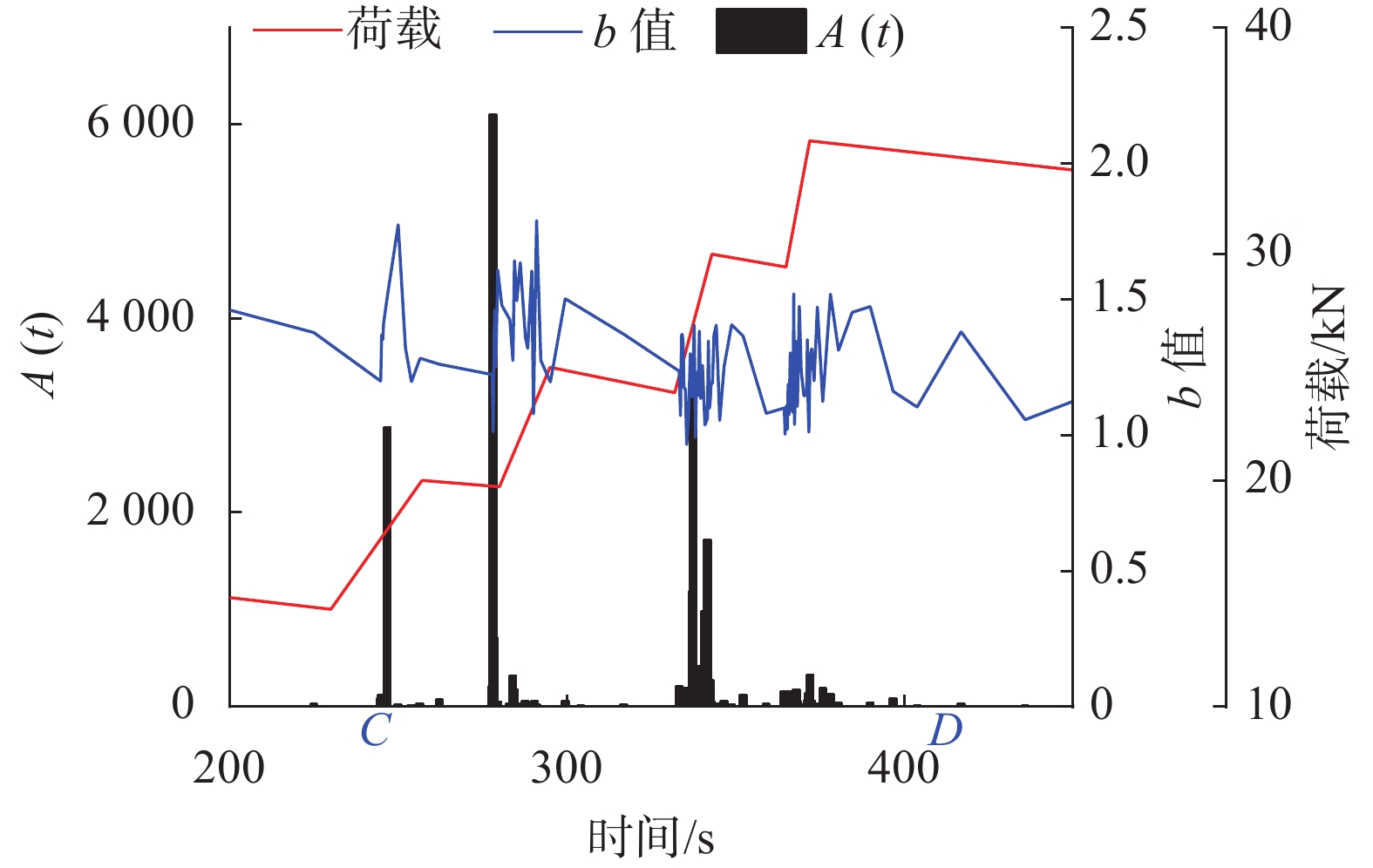
如图8所示,图中C到D时间段即245 s到414 s内,随着荷载的增加,混凝土梁的原有裂纹拓展,多条裂纹萌发,A(t)出现多个高峰值,最高达6105.6,这些高峰值的出现说明内部微裂纹的不断产生和发展伴随着能量的多次释放,并最终形成表面裂纹。b值在这段时间内也出现多次连续下降,在338.1 s时降至0.99,说明在这段时间内高幅度事件数占比增大的现象不断出现,这些时间段可对应梁内部出现多次严重损伤。
|
| 图 8 试件多条裂纹萌发时间段 |
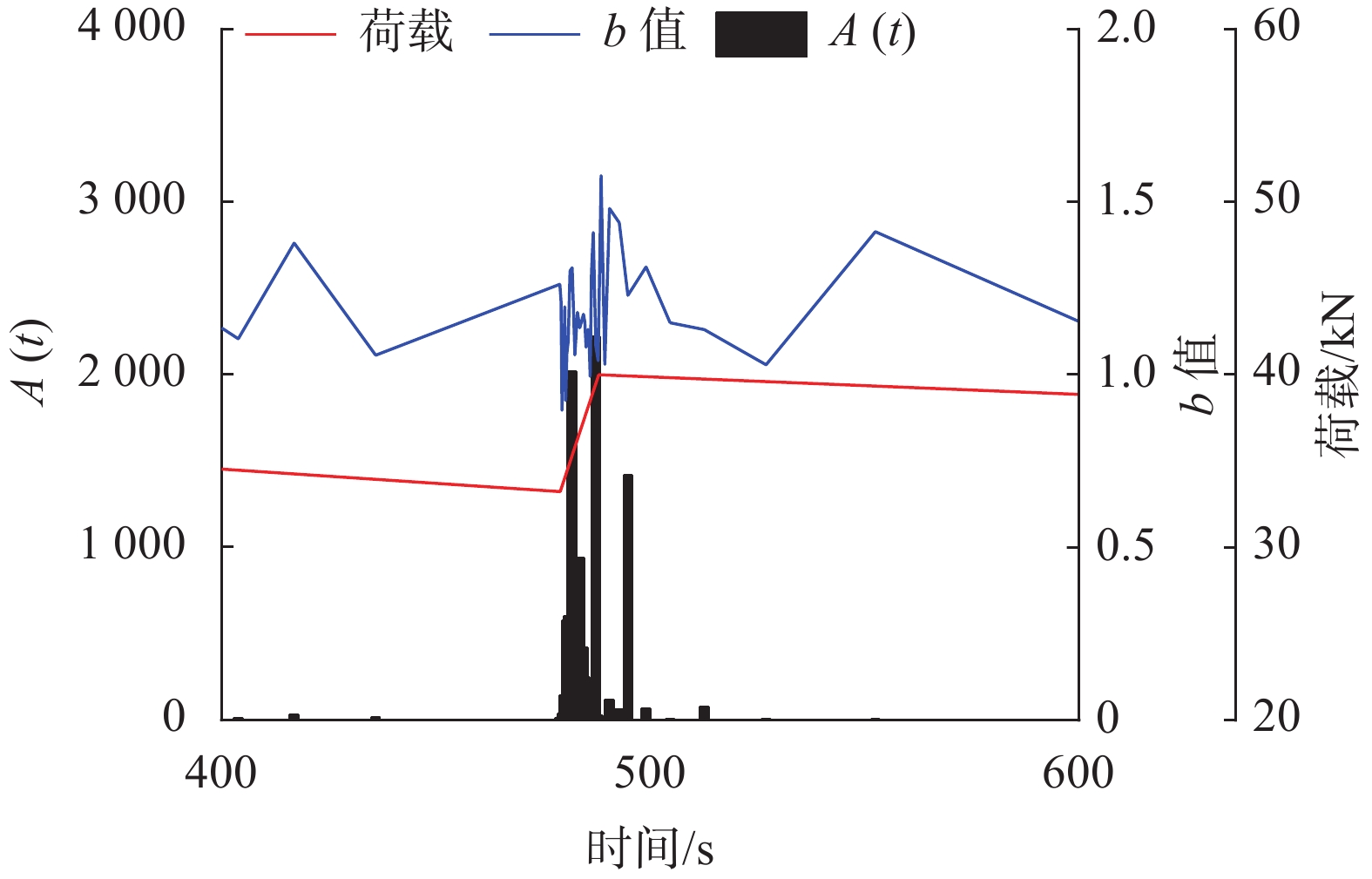
如图9所示,在400 s到600 s时间段内,表面无明显的裂纹产生,荷载从35 kN加到40 kN以外的时间A(t)值无高峰值出现,b值也无明显的多次连续下降,推测是因为由于骨料的阻裂作用和钢筋的抗拉作用阻止了裂纹的发展,由于裂纹的发展受到限制,无明显的能量释放,事件数也很少,因此A(t)值和b值均较为稳定。而在荷载从35 kN加到40 kN的时期,A(t)值出现多个高峰值,最高在487.3 s时达2216.68,说明虽然表面未见裂纹,但随着荷载的施加,试件内部有明显的能量释放即微裂纹的产生和发展,而这段时间b值也出现多次连续下降,在479.4 s降至0.89,说明在荷载增加的这段时间高幅值事件数的占比有多次明显的提升,这也说明试件内部受荷载增加的影响损伤在加重。
|
| 图 9 试件无表面裂纹产生时间段 |
如图10所示,图中E到F时间段内梁表面多条微裂纹逐渐朝向跨中顶部迅速扩展至最终一条宽裂纹彻底贯通,梁失去承载力。这一期间,A(t)出现多个高峰值点,最高在974.4 s时达4703.36,说明在这段时间,裂纹的迅速发展导致大量能量释放,且在最终破坏高能量事件产生即时间点F之前A(t)出现明显的峰值异常现象。b值在这一时期也出现多次连续下降,在944.8 s时降至0.86,说明随着裂纹的迅速发展,在最终破坏来临前,高幅值事件数的占比多次提高,试件内部的损伤多次加重。在最终破坏之后,A(t)值依然有多个高峰值出现,这是由于未卸载前裂纹延伸发展并未停止,仍有能量产生。b值的回升现象是由于随着最终破坏的生成,事件数减少,高幅度事件数的占比也在迅速下降。

|
| 图 10 试件多条裂纹扩展贯通至最终破坏时间段 |
通过上述实验结果可以看出,A(t)出现多个高峰值点的时间段和b值出现整体多次持续性下降的趋势的时间段相对应,但发生变化的时间仍有细微差别,这是由于b值受幅度因素影响,A(t)受能量因素影响,高幅度事件和高能量事件并不完全对等,低幅度长时间的事件也可以是高能量事件,但高幅度事件和高能量事件均对应材料内部的高强度破坏。在大裂纹破坏即高能量事件出现前会有大量微裂纹的产生和能量释放,因此断层总面积A(t)值会出现明显的峰值异常,这是断层总面积A(t)对混凝土梁破坏预判和评估的原理。在混凝土梁破坏过程中声发射事件大多为低幅值事件,在大裂纹破坏出现前出现的声发射事件的幅值会有明显的提升,而b值会出现多次下降,这是b值对混凝土梁破坏预判和评估的原理。两者评价原理不同,A(t)依据大破坏前能量的趋势,b值依据大破坏前幅度的趋势,为更有效地预测和识别钢筋混凝土梁内部的破坏。在实际应用中可同时计算A(t)值和b值,综合考虑A(t)值和b值,即将A(t)集中出现多个高峰值点和b值出现多次连续下降作为钢筋混凝土构件发生破坏的预兆,这样可加强对混凝土结构损伤预警和识别。
从时间点B的第一条裂纹出现,到时间段C-D多条裂纹开始萌发,再到时间段E-F多裂纹迅速扩展贯通至最终破坏,对比A(t)出现高峰值点次数和b值出现极小值点次数可以发现,随着钢筋混凝土梁损伤程度的加重,A(t)出现高峰值点次数和b值出现极小值点次数均在增加,这是由于随着荷载的增加,破坏的剧烈程度也在增加,试件内部微裂纹产生和发展的速度也在增加,导致能量的迅速释放和高幅值事件的出现增多。可将A(t)值出现高峰值点次数和b值出现极小值点次数的增加作为判断钢筋混凝土构件破坏程度在加重的依据。
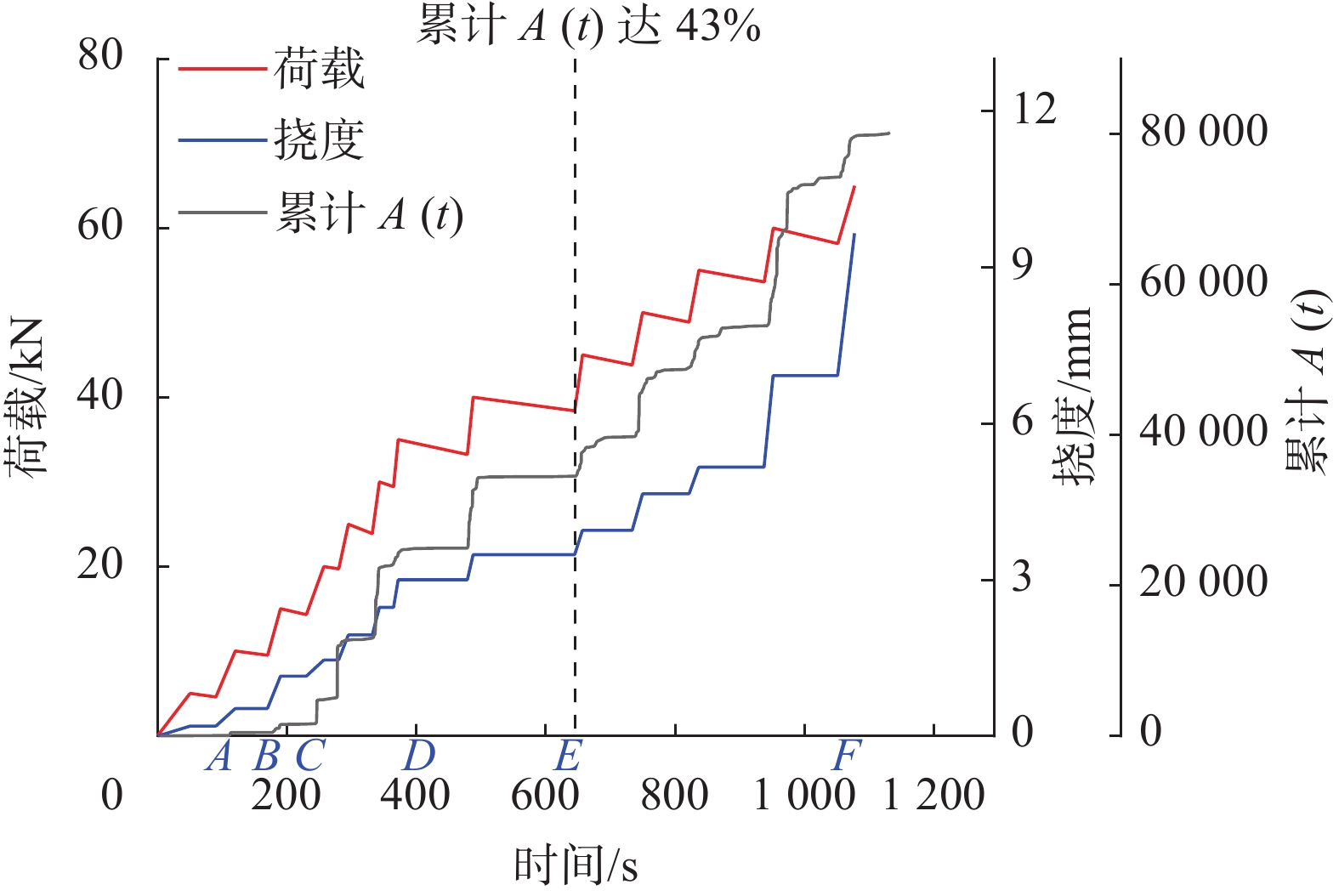
4.2.3 累计断层总面积A(t)从图11可以看出,随着荷载的施加,在0到182 s期间,梁无裂纹产生,挠度上升十分缓慢,此时累计A(t)上升也十分缓慢。从混凝土182 s出现裂纹后,不断有新的裂纹产生,构件抗弯刚矩减小,挠度每次上升的量基本稳定,这段时期的累计A(t)也在每次挠度上升时稳定增加。最后952 s到1078 s最终破坏时挠度产生激增,说明此时梁已丧失对继续破坏的抵抗能力,这段时期的累计A(t)的上升速度也明显加快。综上所述,累计断层总面积A(t)和挠度的变化规律基本对应,说明以断层总面积A(t)表征混凝土梁的损伤较为准确。
|
| 图 11 累计断层总面积A(t)随时间变化的历程图 |
从图11可以看出,整个实验过程中累计的断层总面积A(t)为80617,从开始加载到累计断层总面积A(t)达到34500左右过程中,即从开始到646 s左右,虽然钢筋混凝土梁不断有裂纹产生,但裂纹向上发展也极其缓慢,整体相对稳定。但在加载的后半阶段中,即646 s之后,累计断层总面积A(t)超过34500后,裂纹向上迅速发展,钢筋混凝土梁破坏严重,最终裂纹贯穿整个梁,钢筋混凝土梁彻底失稳破坏。综上所述,可通过累计断层总面积A(t)的占比对钢筋混凝土梁的破坏进行阶段划分,累计A(t)低于43%的时期为钢筋混凝土梁的初始损伤阶段,梁整体相对稳定,累计A(t)高于43%的时期为钢筋混凝土梁严重破坏阶段,梁上的裂纹扩展贯通并最终失稳破坏。可将累计断层总面积A(t)超过总数43%作为钢筋混凝土梁将发生严重破坏的特征。
5 结束语本文基于对钢筋混凝土梁所做的四点弯曲加载破坏实验,利用声发射技术对破坏过程进行了监测,对钢筋混凝土梁损伤过程中的声发射信号以断层总面积A(t)和b值为主要依据进行了处理和分析,主要结论如下:
1)本文根据断层总面积理论,在前人基础上,提出计算钢筋混凝土梁破坏过程中声发射断层总面积A(t)的新方法,即通过声发射信号的绝对能量求取能级K,将L取值10的2/3次方,使之与破坏源有更加良好的对应关系。
2)结合断层总面积A(t)和b值对混凝土构件进行分析,发现在混凝土构件发生明显破坏的时期,A(t)集中出现多个高峰值点和b值出现多次连续下降,A(t)出现高峰值点次数和b值出现极小值点次数也在增加,可将A(t)值出现高峰值点次数和b值出现极小值点次数的增加作为判断钢筋混凝土构件破坏程度加重的依据。由于两者评价原理不同,A(t)依据大破坏前能量的趋势,b值依据大破坏前幅度的趋势,可起到互补作用,在实际应用中,综合考虑A(t)值和b值可加强对混凝土结构损伤预警和识别。
3)累计断层总面积A(t)和挠度的变化规律基本对应,以断层总面积A(t)表征混凝土梁的损伤较为准确,可通过累计断层总面积A(t)的占比对钢筋混凝土梁的破坏进行阶段划分,累计A(t)低于43%的时期为钢筋混凝土梁的稳定阶段,高于43%的时期为钢筋混凝土梁失稳破坏阶段,作为钢筋混凝土梁将发生严重破坏的特征。
| [1] |
WILLIAMS B, HEARD W, GRAHAM S, et al. Mechanical response and damage evolution of high-strength concrete under triaxial loading[J].
Dynamic Behavior of Materials, 2019(1): 69-71.
|
| [2] |
余志武, 单智. 混凝土随机损伤本构模型研究新进展[J]. 工程力学, 2018(8): 1-8.
YU Z W, SHAN Z. Advances in researches on stochastic damage models of concrete[J]. Engineering Mechanics, 2018(8): 1-8.
|
| [3] |
NGUYEN-TAT T, RANAIVOMANANA N, BALAYSSAC J P. Characterization of damage in concrete beams under bending with acoustic emission technique (AET)[J].
Construction and Building Materials, 2018, 187: 487-500.
DOI:10.1016/j.conbuildmat.2018.07.217 |
| [4] |
EID R, MURAVIN B, KOVLER K. Acoustic emission monitoring of high-strength concrete columns subjected to compressive axial loading[J]. Materials, 2020, 13(14): 3114.
|
| [5] |
LIU S M, WU C X, ZHOU J T, et al. Relation between the shear stress distribution and the resulting acoustic emission variation in concrete beams[J]. Structural Control and Health Monitoring, 2020, 27(6): e2528.
|
| [6] |
龙小江, 黄丽霞, 何才厚, 等. 广义S变换钢材拉伸损伤声发射评价方法[J].
中国测试, 2018, 44(1): 129-135.
LONG X J, HUANG L X, HE C H, et al. Acoustic emission evaluation method of steel tensile damage based on generalized S transform[J].
China Measurement & Test, 2018, 44(1): 129-135.
DOI:10.11857/j.issn.1674-5124.2018.01.024 |
| [7] |
BURUD N B, KISHEN J M C. Application of generalized logistic equation for b-value analysis in fracture of plain concrete beams under flexure[J].
Engineering Fracture Mechanics, 2019, 210: 228-246.
DOI:10.1016/j.engfracmech.2018.09.011 |
| [8] |
董陇军, 张凌云. 岩石破坏声发射b值的误差分析[J].
长江科学院院报, 2020, 37(8): 75-81.
DONG L J, ZHANG L Y. Error analysis of b-value of acoustic emission for rock fracture[J].
Journal of Yangtze River Scientific Research Institute, 2020, 37(8): 75-81.
DOI:10.11988/ckyyb.20190430 |
| [9] |
LI X, CHEN X D, JIVKOV A P, et al. Assessment of damage in hydraulic concrete by gray wolf optimization-support vector machine model and hierarchical clustering analysis of acoustic emission[J]. Structural Control and Health Monitoring, 2022, 29(4): e2909.1-e2909.22.
|
| [10] |
陆远忠, 陈章立, 王碧泉. 地震预报的地震学方法[M]. 北京: 地震出版社, 1985.
|
| [11] |
宋德熹, 时文勇. 断层总面积理论在中强地震预测中的应用[J].
河南理工大学学报(自然科学版), 2005(3): 200-204.
SONG D X, SHI W Y. Theory of fault total area applied to predict medium and strong earthquakes[J].
Journal of Henan Polytechnic University(Natural Science), 2005(3): 200-204.
|
| [12] |
肖淑娟, 苏宏伟. 断层总面积在祁连山中西段中强地震前的变化特征[J].
科技资讯, 2018, 16(24): 219-220.
|
| [13] |
窦林名, 冯龙飞, 蔡武, 等. 煤岩灾变破坏过程的声震前兆识别与综合预警模型研究[J].
采矿与安全工程学报, 2020, 37(5): 960-968+976.
DOU L M, FENG L F, CAI W, et al. Seismo-acoustic precursor identification and comprehensive warning model for the catastrophic failure process of coal and rock[J].
Journal of Mining & Safety Engineering, 2020, 37(5): 960-968+976.
|
 2024, Vol. 50
2024, Vol. 50