0 引　言

导热系数是材料重要的热物性参数，在深海探索、航空航天、工业生产等领域都对材料导热系数有严苛的限制，要求准确测量材料在各种条件下的热导率。为此，如何在提高测试效率的同时保证测量精度成为最近几年来热物理性能测试技术领域的重要研究方向，而瞬态平面热源技术则是众多热物性测量方法中的佼佼者，受到广泛应用。瞬态平面热源（transient plane source，TPS）技术最早为瑞典Gustafsson 教授在瞬态热线法、瞬态热带法的基础上开发出的一项专利技术^[1-6]，也被称为“Hot Disk”法，其优点主要包括：测量材料种类多样、测量热导率范围广、测试时间短、测试精度高以及试样制备简单等。

自TPS法发明以来，许多学者都对其表现出强烈的兴趣，做了大量工作进一步修正其理论模型和分析误差。Bohac^[7]等基于灵敏度理论提出了参数估计的方法，该方法对 TPS 法准确测量样品热物性参数提供了时间约束条件，结果表明，当总测量时间与特征时间的比值在 0.3~1.1 之间时，能够得到可靠的导热系数和热扩散率的测量结果，是现阶段TPS测量方法的时间标准。He^[8-9]进一步研究了 TPS 法的原理，详细推导了测量块状材料和平板材料时温度与时间的关系公式。张国靖^[10]考察了TPS平板法中背景材料上的边界热损失问题，提供热补偿的前提下，使采用不同的探头尺寸和背景材料测量样品导热系数相对误差降低2%左右。Malinaric^[11]指出理论模型存在的“奇点”缺陷，随后列举不同的探头模型，结果表明同心圆环探头结构会对测量结果引入2%的理论误差。Huang^[12]等在使用方形探头测量食品导热系数时将求解困难的无量纲时间函数等效为一个幂函数多项式，大大降低了计算难度。国内王强^[13-14]、何小瓦 ^[15-17]分别研究了TPS法的误差因素和不同条件下的测量精度。

TPS法发展自瞬态热线法、瞬态热带法^[18]，基于点热源在半无限大物质中的传热过程这一理论假设，要求作为热源的镍丝厚度要尽可能小，因而对镍丝的加工技术与精度要求较高，导致价格昂贵。同时，厚度最小仅为4 μm的镍丝，有绝缘层保护的前提下也存在机械强度不足的情况，仅能在实验室中使用，一旦发生损坏难以修复，只能重新购买；且需要对样品提前处理，步骤繁琐，难以适应现场测量的要求。为了实现较低的使用成本和更广泛的适用性这两点需求，综合考虑各方面因素认为适当增加探头厚度具有理论可行性且易于实现。同时，现阶段的数值研究大多基于二维模型^[19-21]，该模型忽略了热源体积和形状上的差异，给测量带来一定误差。故本文从数值模拟角度出发，探究TPS三维加厚模型的理论正确性与实际可行性，为后续的实际应用提供理论指导。

1 TPS法测量原理

探头作为TPS法测量导热系数的核心元件，既是向外输送热量的热源，也是监测温度变化的测温传感器，它由双螺旋结构的条带状镍箔和完全包覆住镍丝的Kapton绝缘层组成。在测量时将探头紧紧地夹于在两块相同的待测样品中间，这样就形成TPS理论中关于同心圆环热源在半无限大介质中传热的假设，如图1所示。将探头接入测量电路并在探头上施加恒定的加热功率，电流通过镍丝产生焦耳热对样品进行加热，由于待测物体的热物性导致了不同的热量传递速度，作为热源的镍丝温度也随之改变，所以镍丝温度随时间的变化关系中隐含着材料导热系数这一因素，通过特定公式便可得出这一关系。

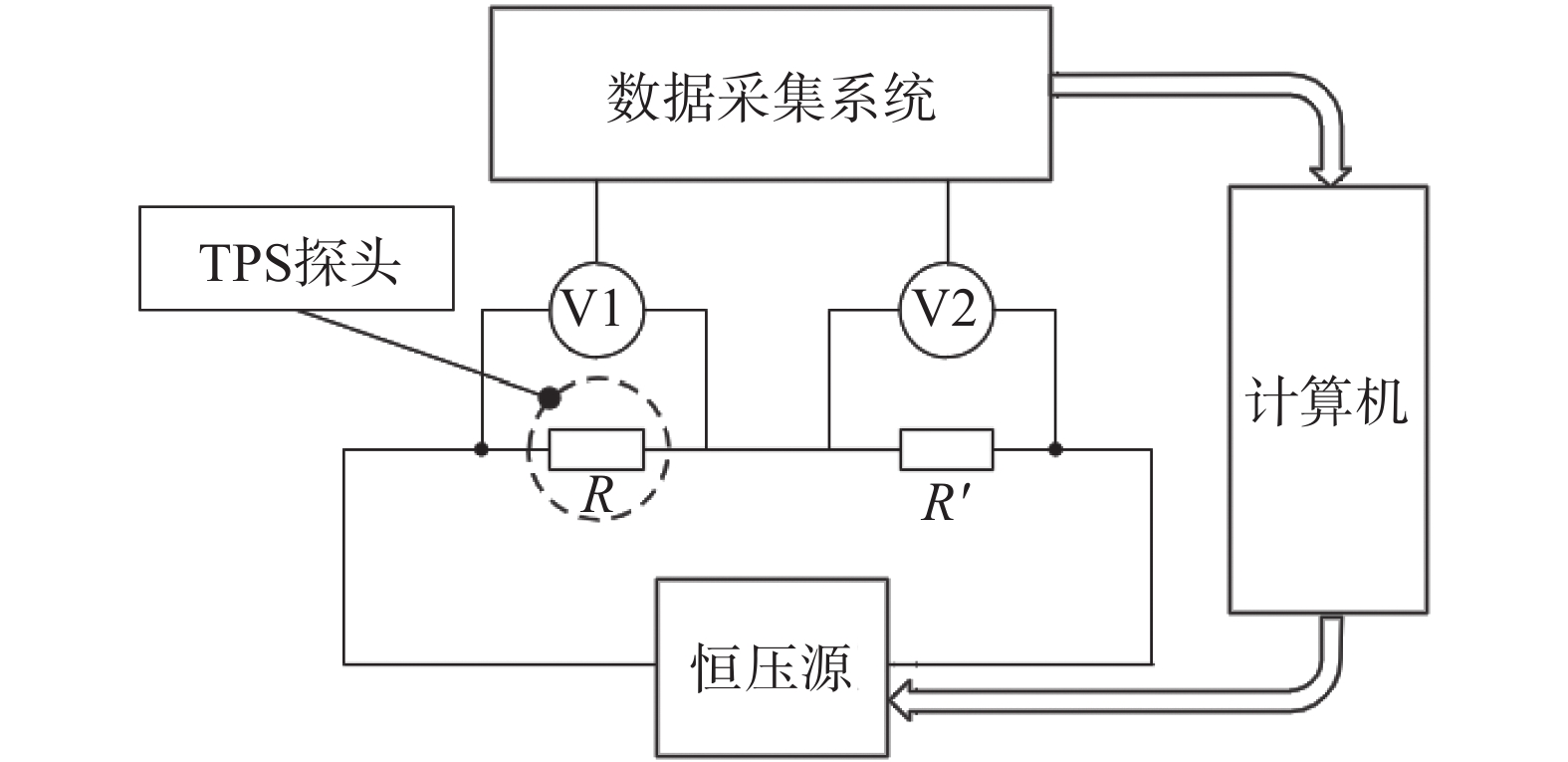
在测量过程中，探头的温度变化是通过测量镍丝的电阻变化实现的，测量电路如图2所示。

金属镍丝阻值与温度变化的关系用下式计算：

式中：$ R\left(t\right) $——$ t $时刻探头的阻值，$ \mathrm{\Omega } $；

$ t $——测量时间，s；

$ {R}_{0} $——探头的电阻初始值，$ \mathrm{\Omega } $；

$ \alpha $——镍的电阻温度系数（TCR），$ {{\mathrm{K}}}^{-1} $；

$ \Delta \bar{T}\left(t\right) $——探头的平均温升，${\mathrm{ K}} $。

无量纲时间$ \tau $与探头半径$ r $和样品的热扩散系数κ 有关，可由下式表示：

通过记录探头电阻的变化，可以得到探头温度随时间的变化曲线，从而根据下式计算样品导热系数：

式中：$ {P}_{0} $——探头的输入功率，${\mathrm{ W }}$；

$ \lambda $——待测样品的导热系数，$ {\mathrm{W}}/({{\mathrm{m}}}\cdot {{\mathrm{K}}})$；

$ D\left(\tau \right) $——无量纲时间函数；

$ k $ 和 $ l $——求和变量；

$ {I}_{0} $——第一类零阶修正贝塞尔函数。

由此可知，在加热功率不变的前提下，探头的平均温升$ \mathrm{\Delta }\bar{T}\left(t\right) $和无量纲时间函数$ D\left(\tau \right) $呈线性关系，然而无量纲时间常数$ \tau $中热扩散率κ是未知的，所以需要利用最小二乘法等方法对$ \mathrm{\Delta }\bar{T}\left(t \right) $曲线和$ D\left(\tau \right) $曲线进行线性拟合，在不断改变$ \kappa $值的过程中，存在一个$ \kappa $值，使得$ \mathrm{\Delta }\bar{T}\left(t \right) $曲线和$ D\left(\tau \right) $曲线拟合残差最小，服从最佳线性关系，此时被测材料的导热系数就可从直线的斜率中求出。

根据文献[5]可知，若要获得准确可靠的导热系数及热扩散系数测量结果，应限制特征时间与瞬态测量总时间的比值在0.3~1.1之间，即$ 0.3\leqslant {t}_{{\mathrm{max}}}/\theta \leqslant 1.1 $。同时TPS理论的关键假设之一是将传感器放置在无限介质中，这意味着在实验过程中产生的热量不应传播到样品的外部边界。因此，为满足从传感器的任意一点到样品表面任意一点的距离均大于探测深度$\Delta P $这一理论假设，则通常满足：$ \Delta P\geqslant 2\sqrt{\alpha t} $，即样品厚度应大于$\Delta P $，宽度应大于2$\Delta P $与探头半径之和。

2 实验研究与数值模拟 2.1 实验

实验部分采用的热常数分析仪为瑞典凯戈纳斯有限公司生产的 HOT DISK TPS-2500S，所用探头型号为Kapton 5501；双螺旋镍丝半径6.403 mm，外层包裹厚度25 μm、半径10 mm的聚酰亚胺绝缘层。实验采用的测量功率及测量时间均按国际标准中的推荐值选定。

选用三种待测材料分别为奥氏体不锈钢、美国康宁公司的Pyroceram 9606和标准材料Polymethyl methacrylate（PMMA），因为Pyroceram 9606和PMMA等材料是国际上公认的热物理性能标准材料之一，并且有很多文献通过不同的方法对这三种材料的导热系数进行过测量，可以保证实验与模拟过程的准确性。实验中涉及的相关材料的热物性参数如表1所示。

2.2 数值模拟

根据TPS理论的推导过程可知，在理想条件下，导热系数测量过程被认为是一系列圆环状平面热源在半无限大物体中的瞬态导热问题，故在本文中，柱坐标系下的各向同性材料中，具有一内热源的非稳态热传导的导热微分方程，可以表示为：

式中：$ \rho $——样品密度，$ {\mathrm{kg}}/{{\mathrm{m}}}^{3} $；

$ {C}_{{\mathrm{P}}} $——试样比热容，$ {\mathrm{J}}/({{\mathrm{kg}}}\cdot {{\mathrm{K}}}) $；

T ——过余温度，即传热过程某一时刻试样真实温度与初始温度之差，℃；

$ r,{\textit{z}},\varphi $——热传导方向的空间柱坐标；

t ——时间，$ {\mathrm{s}} $；

$ \lambda $——试样导热系数，$ {\mathrm{W}}/({{\mathrm{m}}}\cdot {{\mathrm{K}}}) $；

$ \dot{\varPhi } $——源项。

初始条件假设样品及探头内部温度均匀一致，皆为300 K；除与探头接触部分之外，样品其余边界和探头绝缘层侧面均设为绝热条件，温度与初始温度保持一致。

利用COMSOL Multiphysics 5.6 仿真软件进行数值计算。该软件采用有限元法，其特点在于能够自主划分保证网格独立结构的网格类型，模拟中所用的待测样品及探头结构如图3所示。探头与待测样品之间的接触热阻则根据传统Copper-Mikic-Yovanovich (CMY) 模型，粗糙平均高度设为1 μm，粗糙平均斜率设为0.5，接触压力设为100 kPa，显微硬度则根据材料属性设置。

模拟中选用的待测材料相关热物性参数与实验一致，探头及样品尺寸如表2所示。

为了确保模型准确性的同时尽可能减少计算时间，使物理模型具有最小的误差，进行了网格独立性验证，同时方程残差以 10^–6 作为收敛标准。通过体积平均温度来监控镍丝的温度变化情况。根据软件内置的不同物理场模型，选择较细化、超细化和极细化三种模式进行网格划分，时间步长设为0.1 s。在所有情况下都保持相同的输入参数并选择测量终点时刻的镍丝平均温度作为检查参数。表3显示了镍丝平均温度对网格数量的敏感性。

从表中可以看出，较细化相比超细化与极细化两个模式，其镍丝平均温度最大仅相差0.0027 ℃，相对于6.25 ℃的总体温升相差极小，因此选择较细化模式下的网格划分类型进行计算，并对传感器与样品接触面进行局部网格细化。最终形成1159085个四面体网格，其中细化区域四面体网格数为239653，网格划分情况如图4所示。

3 结果与分析 3.1 标准模型验证

虽然按照“Hot Disk”探头的真实尺寸与形状在软件中建立三维模型，但软件能否以此模型复现镍丝加热时热量的传播过程还不能确定，与TPS理论模型之间的误差也属于未知数，下面就对标准模型的准确性进行验证。

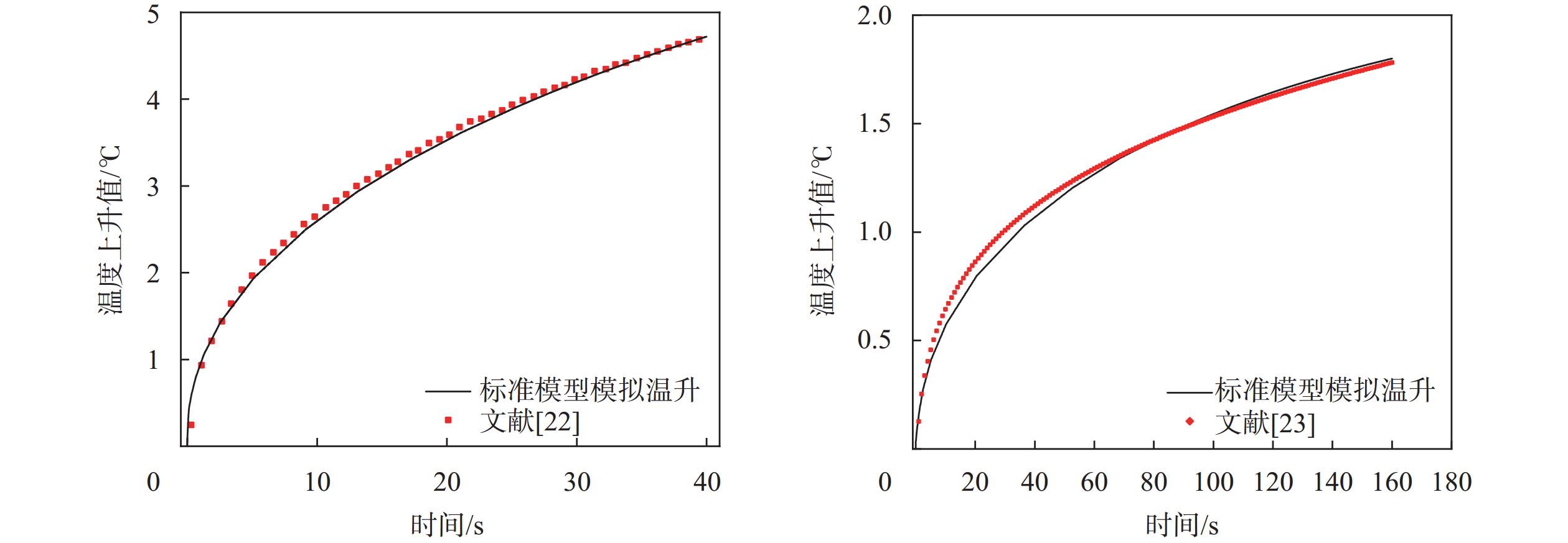
通过采用文献[22-23]中的测量参数，在软件中复现其测量过程与相关温度变化，探头平均温度上升值与文献中的实测值对比如图5所示。

从图5中可以看出，在相同的测量条件下，该三维模型的温升曲线较好的吻合了文献中读取自“Hot Disk”热常数分析仪中的温度数据，最大温差仅为0.2 K，说明了数值模拟中采用的模型有良好的正确性与精准度，能够用来模拟TPS探头在实际测量中的表现。

若$ \lambda $为待测样品导热系数的测量值或计算值，$ {\lambda }_{{\mathrm{s}}} $为导热系数标准值，则导热系数相对误差$ p $由下式计算：

利用型号为TPS-2500S的热常数分析仪测量三种热物理性能标准材料，环境温度为25 ℃，加热功率与时间的选用均参考国际标准中的参考值。此外由于温度的变化对测量有很大的影响，因此在测量前后，将样品与相关测量装置放入设定温度为25 ℃ 的恒温箱中等待10 min，高导热系数材料可适当缩短保温时间，以此确保实验前待测样品的温度变化小于±0.2 ℃；在测量结束后直接从设备自带的软件中读取测得的材料热导率。待测样品的导热系数测量值是在相同条件下重复5次测量的平均值。

在同等实验条件下，由“Hot Disk”热常数分析仪和数值模拟两种方式测量三种待测材料导热系数，测量结果如表4所示。

从结果来看，该仿真模型在测量三种不同待测材料导热系数时，其精度是令人满意的，相对误差在 1%~3% 之间浮动，这与文献中的结论相吻合，也满足国际标准中对于测量结果误差的要求，证明了该模型的正确性与有效性。

值得注意的是，随着待测物体导热系数的提高，实验测量和数值模拟所得的导热系数的相对误差呈现出相反的变化趋势。出现此现象的原因主要是未对数值模型进行修正。在实际测量过程中，TPS测试软件会将理想模型中忽略的误差因素考虑在内，例如探头与样品间的接触热阻、加热元件温度上升引起的功率变化等因素，随后在计算时予以修正，从而提高“Hot Disk”热常数分析仪的精确性。

3.2 加厚模型

在TPS的理论模型中，等效的同心圆环热源与实际上双螺旋在体积与热量传输等条件下存在一定误差，并且当加热元件厚度增加时，热量径向的传输所造成的误差将更加明显，所以有必要从理论上探究加厚模型的准确性与有效性。在模型中将标准模型的镍丝厚度更改为100 μm，Kapton绝缘层厚度仍为25 μm，以此加厚探头模型探究其在测量不同材料时的表现。

测量时间根据国际标准中对不同材料的推荐值选择，即不锈钢、Pyroceram 9606和PMMA的测量时间分别为10 s、40 s、120 s；同时根据材料的不同，选择加热功率变化范围，材料及探头初始温度设为300 K。去除最初的0 ~ 0.2 s内的温度数据之后，由数值模拟计算出的探头温度变化如图6所示。

在测量不同材料的过程中，探头的温升曲线有着类似的变化趋势，即无论何种加热功率，温度先以一个较快的速率增加，随后趋于平缓。但是加热功率会决定终点时刻温度的大小。

在测量过程中需要保证在半无限大物体中传热这一理论假设，确保热量没有传输到径向边界中，下面对这一点进行考察。当被测材料为PMMA材料，加热功率为0.4 W的测量情景下，模型的轴向切面在不同时刻的温度分布情况如图7所示。

总体来看，在事先设定好的加热功率和测量时间的控制下，温度变化被控制在加热元件附近的区域，确保热量不会传播至边界，从而保证了样品边界的绝热条件。

传感器径向温度分布如图8所示，镍丝宽度范围内的温度高于两侧绝缘层的温度，且传感器的平均温度随时间增加而增加，相较于与外圈，内圈表现出更高的温度；随着时间的推移，温度差异变得更加明显。由于在双螺旋结构的内圈范围内，镍丝同时发热，沿径向方向温差较小，热量主要沿轴向方向传播。而探头边缘处则因为没有相邻镍丝而存在温度差，有利于热量沿径向传递，导致边缘镍丝温度较内圈偏低。

数值模拟中探头的温度扩散过程与文献[24]中报道的实验观察结果一致，该文献中使用红外摄像机记录传感器测量时的热量传播过程。此外，数值模拟相比红外实验提供了更好的空间分辨率，能够更直观地了解测量过程中的温度分布与变化。

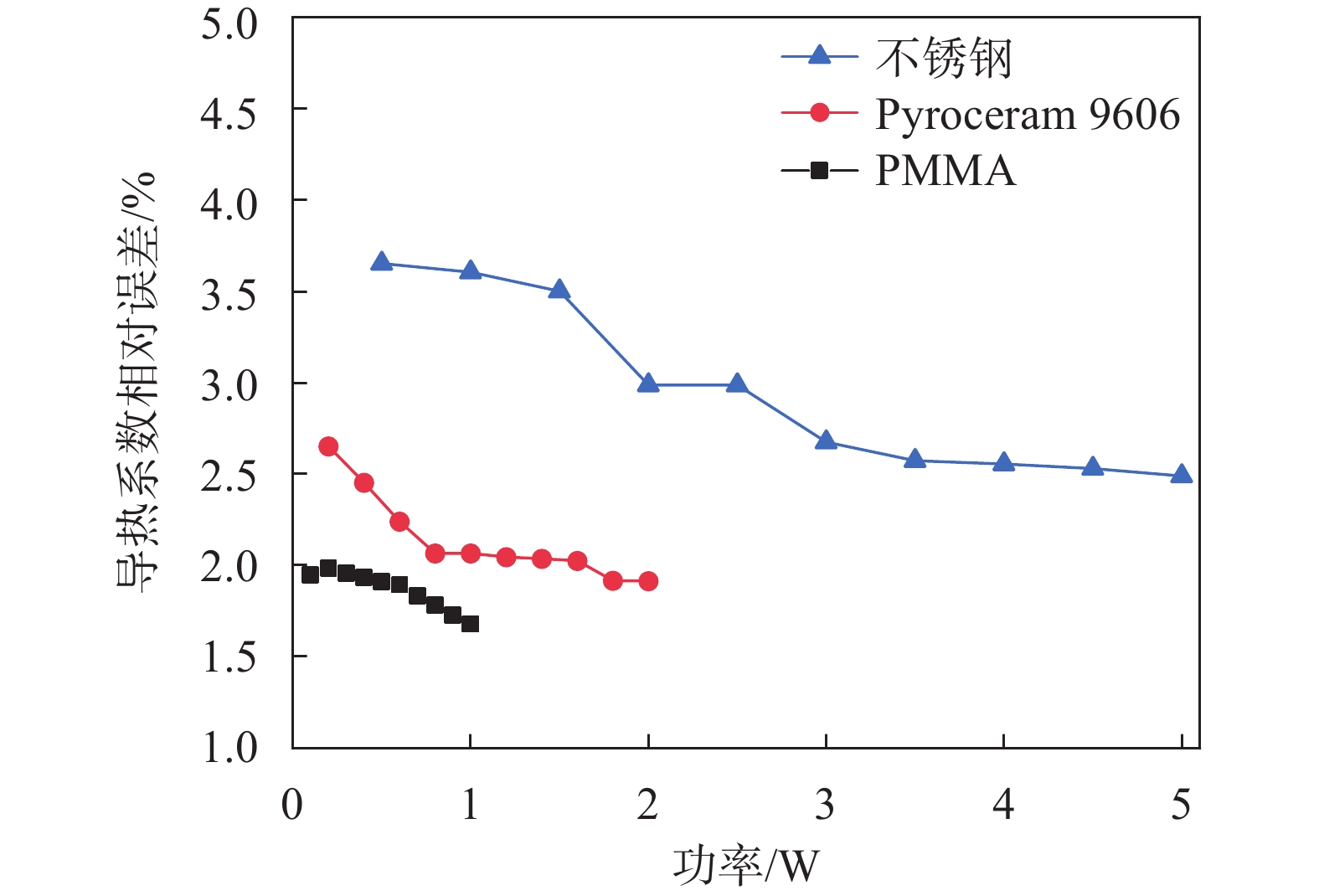
根据温度随时间的变化曲线可以计算出不同条件下的待测物体导热系数相对误差，结果如图9所示。

对比标准模型和加厚模型的测量结果可知，加厚模型明显增大了各材料导热系数的测量误差，该模型计算出的PMMA、Pyroceram 9606和不锈钢在不同条件下的导热系数相对误差平均值分别为1.87%、2.14%、2.96%，相比标准模型分别增大了0.82百分点、0.62百分点、0.40百分点左右，且随着功率的增加，相对误差都呈现出缓慢下降的趋势，这与文献[13]中的数据相符。值得注意的是，这三种待测材料较低的加热功率使得测量误差明显偏大，这主要是因为在功率较低时，绝缘层吸收的热量在镍丝发热总量中占比偏大。

加厚模型要比标准模型测得的导热系数相对误差更大，这表明镍丝厚度的增加的确对导热系数测量精度造成了较大影响，需要对加厚模型进行热容修正。

3.3 热容修正

TPS 探头理想温升模型的推导过程中，假设探头的厚度和热容是可以忽略不计的^[25-26]，即输入功率$ {P}_{0} $在 $ t $时间内产生的热量全部被传递给待测材料，然而在现实中，只能尽量减少而不能消除探头自身的热容，导致样品的实际加热能量偏小，实际输入功率小于额定输出功率$ {P}_{0} $。

设探头的热容为$ C $，则$ t $时刻探头待测样品的实际输出功率为：

将$ P\left(t\right) $带入式(3)，可得修正后的探头表面平均温升为：

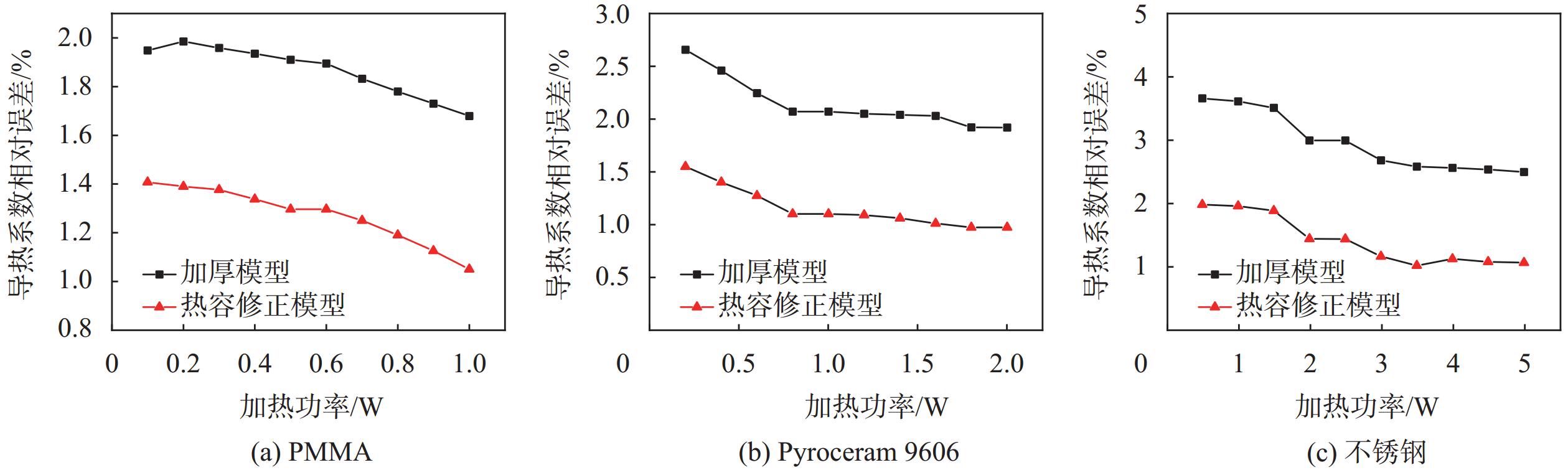
将修正后的计算公式即式（8）写入导热系数计算程序中，并结合数值模拟中三种待测材料的温升曲线，重新计算各材料的导热系数相对误差。经热容修正后的导热系数相对误差如图10所示。

从图中可以明显看出经过热容修正后的计算模型明显降低了各个材料的导热系数计算误差，测量PMMA、Pyroceram 9606和不锈钢的导热系数相对误差对比修正前分别降低了0.6百分点，1.0百分点、1.5百分点左右，即修正后的三种标准材料导热热系数相对误差平均值分别为1.27%、1.13%和1.4%，该精度满足TPS理论要求，这证明了热容修正模型的正确性与有效性，同时也表明修正后的探头加厚模型能够应用于实际测量中并且测量精度有一定保证。

综合模拟过程中的误差因素，发现热容修正模型对不同材料的修正幅度与探头比热容相对试样比热容有关，PMMA材料的比热容与探头比热容最为接近，而不锈钢材料的比热容与探头比热容相差较大，这意味着在相同条件下加厚模型测量不锈钢材料的初期温升数据要小于标准模型下的温升值，绝缘层吸收的热量也略有增加，从而导致了高导热系数材料的计算值相对误差较大，低导热系数材料的计算值相对误差较小这一现象。

4 结束语

本文根据TPS热物性分析仪在实际使用中存在的问题，提出了一种新型加厚探头，随后利用仿真软件COMSOL Multiphysics 5.6建立了加厚探头的实际双螺旋镍丝模型，并研究该探头在测量不同材料时的表现，并与标准探头进行了比较。结果表明：使用三维双螺旋结构的镍丝模拟时，未对误差因素进行修正，该模型的测量精度相较于现有研究中的二维模型有明显改善。加厚探头在导热系数测量精度方面相比标准探头有明显不足，主要是因为镍丝厚度的增加使得其本身吸收的热量增多，同时还会增大轴向方向上镍丝与绝缘材料的接触面积，热量损失占比加大从而进一步增大加厚探头的测量误差；随后提出针对性的探头热容修正模型，重新拟合温升曲线，最终将测量误差控制在1.5%以内，在提升TPS探头机械强度的同时，也满足了国际标准对于TPS法测量精度的要求，证明了该探头具备理论可行性和实际应用的潜力。但是加大镍丝厚度带来的探头电阻变化、镍丝和导线的连接方式和电压测量精度等问题仍亟待解决，这也为下一步的工作指明了方向。