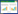文章信息
- 林也非
- LIN Yefei
- 110 GHz宽带同轴S参数标准装置设计
- Design of 110 GHz broadband coaxial S-parameter standard device
- 中国测试, 2024, 50(7): 131-137
- CHINA MEASUREMENT & TEST, 2024, 50(7): 131-137
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022120018
-
文章历史
- 收稿日期: 2022-12-05
- 收到修改稿日期: 2023-03-25
网络分析仪[1]是研制、生产、应用毫米波器部件的单位所必须的测量设备,其频率范围已可达110 GHz。为确保网络分析仪量值准确可靠,须利用校验件对其进行量值传递[2]。校验件通常包括用于传输相位校准的匹配同轴线和用于反射模值校准的失配同轴线[3]。在110 GHz频段下,国际上常见的微波产品厂家能提供的产品情况如下:Keysight公司的校验件85059 V,可实现DC~120 GHz频段的校验。根据是德公司提供的《操作与服务手册》[4],该款校验件“根据机械测量结果和材料特性进行了精确建模并推导了准确的电特性表达式”,但并未提供建模方法与计算过程;Anritsu公司的校验件3659为0.8 mm校验件,可实现DC~145 GHz频段的校验,根据安利公司提供的参考文献[5],提及了“需要对连接器装配、探索附件新材料等问题进行定量仿真研究”,但也未提供具体的方法。反观国内情况,仅有对110 GHz同轴线或同轴连接器[6]等产品的设计,目前尚无厂家研制、生产覆盖该频段的校验件。
在微波器件的设计工具方面,国内外业内主要依托于电磁仿真EDA工具,例如ANSYS公司的HFSS[7]、CST公司的仿真设计套件[8]、ALTAIR公司的FEKO[9]等。此类工具在建模和仿真计算方面都较为精确,但是计算时间和消耗的计算资源通常较多,尤其是在高频段对象尺寸以电长度衡量较大时面对的计算问题更是如此,在设计调试过程中敏捷计算能力较差。
本文研究并设计了10 MHz~110 GHz宽带同轴S参数标准装置,包含一个失配同轴线和一个匹配同轴线,分别作为反射模值的标准和传输相位的标准。根据项目任务要求,标准器须满足的技术指标为:反射模值(0~0.6):U=0.100(k=2);传输相位(–180°~180°):U=5°(k=2)。失配同轴线相对复杂,为三段分段均匀(又称“阶跃阻抗”、“Stepped Impedance”)同轴线的组合;匹配同轴线结构相对单纯,可认为是失配同轴线的特例(当失配段直径等于匹配段时)。因此本文的设计工作主要针对失配同轴线展开论述,匹配同轴线的设计同理。
在设计工具上,采用了基于Matlab实现的解析方法计算工具和有限元仿真工具HFSS。其中Matlab实现的解析方法优势在于计算快速且有一定准确度,对于关键参数的设计和调整能在1 min内完成重算。劣势在于方法基于了两个近似导致计算精确度不高:1)分段均匀同轴线阻抗以无限长均匀同轴线近似;2)数学模型不考虑结构阶跃处电磁场反射影响。而HFSS的优势在于精确建模和全波仿真可以得到高准确度的解,但是对于高频段(10波长以上电尺寸)需要较大的内存占用和时间开销,不利于频繁调整参数进行设计。
综合以上,本文在设计过程中结合了解析算法和有限元仿真的方法,利用解析算法敏捷的特点先大致确定关键参数的范围,再利用有限元仿真软件准确的特点进行精确建模,进一步进行参数调优和仿真考核。
1 解析方法与关键参数设计失配/匹配同轴线作为校准网络分析仪反射幅度的标准器,首先必须满足以下条件:
1) S11幅度曲线应在全频段有足够多周期。为了考核110 GHz内网络分析仪反射模值从0到峰值之间的测量准确度,周期数不应过少。
2) S11幅度曲线总体斜率不应太大。若斜率太大,则S11幅度对于频率敏感度过高,即在频率上细小的偏差将带来S11幅度的剧烈变化,不利于计量校准工作的开展。
3) S21相位曲线应在全频段有足够多周期。
综合上述因素的考虑,S11幅度周期数设计为约15个。而由于S21相位周期数仅与总长度有关,因此应在条件允许下尽可能长。出于加工的便利性以及标准装置的统一性,失配/匹配同轴线总长度设计为相等。
因为匹配同轴线可认为是失配同轴线特例,且匹配同轴线S21相位数学模型较为简单,且该模型可以较好地应用于网络分析仪校准[9],S21相位表达式为:
| $ {\rm Phase}({S_{21}}) = \frac{{2\pi d}}{\lambda } $ | (1) |
式中:d——匹配同轴线总长度;
λ——电磁波波长。
所以本文主要对分段均匀的失配同轴线进行数学模型的构建。参照同类产品,本文分段均匀的同轴线也设计为50 Ω-25 Ω-50 Ω的形式。几何模型如图1所示,外导体直径均匀,内导体由P1、P2、P3三部分组成,其中P1和P3为50 Ω,P2为25 Ω。内导体外径为ai,外导体内径为bi,长度为di(i=1,2,3)。
|
| 图 1 失配同轴线结构示意图 |
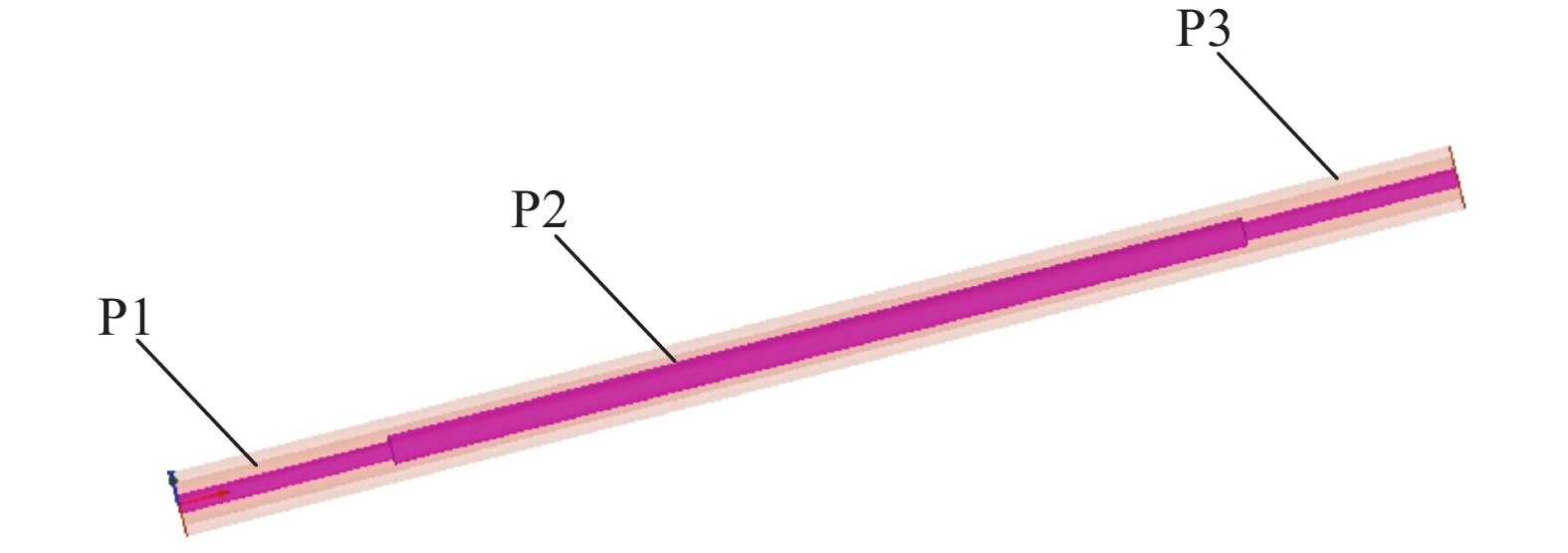
失配同轴线的微波等效电路模型如图2所示。
|
| 图 2 失配同轴空气线等效电路 |
其中左右端Z0为端接匹配负载,Z1、Z2和Z3分别表示三段的特征阻抗。Z1、Z2和Z3均可用下式计算:
| $ {Z_i} = \frac{{60}}{{\sqrt {{\varepsilon _r}} }}\ln \frac{{{b_i}}}{{{a_i}}} $ | (2) |
针对上述的阻抗网络,为了方便计算,增加了A、B节点,如图2所示。A左侧对应了结构图中P1,AB之间对应了结构图中P2,B右侧对应了结构图中P3。在该处沿着电磁场传播方向的阻抗记为ZA、ZB,反射系数为ΓA、ΓB。
在终端负载处有:
| $ {\varGamma _L} = \frac{{{Z_0} - {Z_3}}}{{{Z_0} + {Z_3}}} $ | (3) |
其中ΓL为在负载端的反射系数。
在特征阻抗Z3的导波系统中,A处的反射系数为:
| $ {\varGamma _A} = {\varGamma _L}{{\rm e}^{ - 2\gamma {d_3}}} = {\varGamma _L}{{\rm e}^{ - 2(\alpha + {\rm j}\beta ){d_3}}} $ | (4) |
其中γ为传播系数,可以复数展开为α+jβ,其中的衰减常数α=αc+αd。αc表示导体衰减,αd表示介质衰减。由于本模型为空气介质同轴线,因此α仅涉及导体衰减αc,其表达式为[10]:
| $ \alpha = {\alpha _c} = \frac{{{R_m}{Y_{\rm TEM}}}}{{2\ln \left( {b/a} \right)}}\left(\frac{{a + b}}{{ab}}\right) $ | (5) |
| $ {R_m} = \sqrt {\mu \omega /2\sigma } $ | (6) |
式中:Rm——表面电阻;
μ——磁导率,一般为常数4π×10–7 H/m;
σ——导电率。
在特征阻抗Z3的导波系统中,A处的阻抗为:
| $ {Z_A} = {Z_3}\frac{{1 + {\varGamma _A}}}{{1 - {\varGamma _A}}} $ | (7) |
以A左侧作为负载,以Z2为特性阻抗的反射系数
| $ {\varGamma _A^\prime} = \frac{{{Z_A} - {Z_2}}}{{{Z_A} + {Z_2}}} $ | (8) |
在特征阻抗Z2的导波系统中,B处的反射系数为
| $ {\varGamma _B} = {\varGamma _A^\prime }{{\text{e}}^{ - 2\gamma {d_2}}} $ | (9) |
在特征阻抗Z2的导波系统中,B处的阻抗为:
| $ {Z_B} = {Z_2}\frac{{1 + {\varGamma _B}}}{{1 - {\varGamma _B}}} $ | (10) |
以B左侧作为负载,以Z1为特性阻抗的反射系数:
| $ {\varGamma _B^\prime} = \frac{{{Z_B} - {Z_1}}}{{{Z_B} + {Z_1}}} $ | (11) |
在右端特征阻抗Z1的导波系统中,反射系数为:
| $ {\varGamma }_{理论}={\varGamma }_{B}^\prime {\rm e}^{-2\gamma {d}_{1}} $ | (12) |
当S11模值在频域周期性出现最小值(接近0)时,说明空气线在这些频率点上是阻抗匹配的,因此有
| $ \varGamma _B^\prime = \frac{{{Z_B} - {Z_1}}}{{{Z_B} + {Z_1}}} = 0 $ | (13) |
进一步推导出
| $ {Z_B} = {Z_1} $ | (14) |
代入公式(10)有
| $ {Z_1} = {Z_2}\frac{{1 + {\varGamma _B}}}{{1 - {\varGamma _B}}} $ | (15) |
推导出
| $ {\varGamma _B} = \frac{{{Z_1} - {Z_2}}}{{{Z_1} + {Z_2}}} $ | (16) |
代入公式(9)得
| $ \frac{{{Z_1} - {Z_2}}}{{{Z_1} + {Z_2}}} = \varGamma _A^\prime {{\rm e}^{ - 2\gamma {d_2}}} $ | (17) |
公式(8)代入公式(17)得
| $ \frac{{{Z_1} - {Z_2}}}{{{Z_1} + {Z_2}}} = \frac{{{Z_A} - {Z_2}}}{{{Z_A} + {Z_2}}}{{\rm e}^{ - 2\gamma {d_2}}} $ | (18) |
由于Z1为匹配段约为50Ω,根据公式(3)、(4)、(7)在Z0≈Z3条件下可导出ZA也约为50 Ω,因此从公式可得
| $ {{\rm e}^{ - 2\gamma {d_2}}} = 1 $ | (19) |
在公式(19)中,γ=α+jβ,由于导体外层镀金,因此代入金的电导率4.52×107 S/m,代入公式(5)、公式(6)可得α可以忽略不计,因此
| $ {{\rm e}^{ - 2{\rm j}\beta {d_2}}} = 1 $ | (20) |
所以有
| $ 2\beta {d_2} = 2n\pi $ | (21) |
因为
| $ \beta = \frac{{2\pi }}{\lambda } $ | (22) |
所以可以得到失配段长度d2与匹配点波长/频率的关系为
| $ {d_2} = \frac{{n\lambda }}{2} = \frac{{nc}}{f} $ | (23) |
考虑了n=15的条件,最终选择了d2=20 mm。根据上述推导,110 GHz内完整的周期数为14个,15个匹配点的取值如表1所示。
| GHz | |
| n | 匹配点频率 |
| 0 | 0 |
| 1 | 7.5 |
| 2 | 15 |
| 3 | 22.5 |
| 4 | 30 |
| 5 | 37.5 |
| 6 | 45 |
| 7 | 52.5 |
| 8 | 60 |
| 9 | 67.5 |
| 10 | 75 |
| 11 | 82.5 |
| 12 | 90 |
| 13 | 97.5 |
| 14 | 105 |
另一关键参数为总长度,即d1+d2+d3。由于该参数关联S21相位在110 GHz频段内出现的周期数,应尽可能长。一方面为满足上述d2=20 mm的条件,另一方面在国内圆柱深孔的加工直线度和粗糙度的工艺条件下[11],将同轴线总长度设计为30 mm。
经过参数的初步调整,确定了以表2所示的参数为失配同轴线的设计值。
| 类型 | 几何量 | 符号 | 几何量值/mm |
| 1 mm失配同轴线 | 外导体内径 | b | 1.000 |
| 内导体外径1 | a1 | 0.434 | |
| 内导体外径2 | a2 | 0.659 | |
| 内导体外径3 | a3 | 0.434 | |
| 长度1 | d1 | 5.000 | |
| 长度2 | d2 | 20.000 | |
| 长度3 | d3 | 5.000 | |
| 1 mm匹配同轴线 | 外导体内径 | b | 1.000 |
| 内导体外径 | a1 | 0.434 | |
| 长度 | d | 30.000 |
2 有限元仿真与参数调优 2.1 精细化建模与仿真关键参数设置
为了在有限元仿真中得到更精确的结果,在代入表2设计参数的基础上,另外考虑了加工制造中的两个因素:
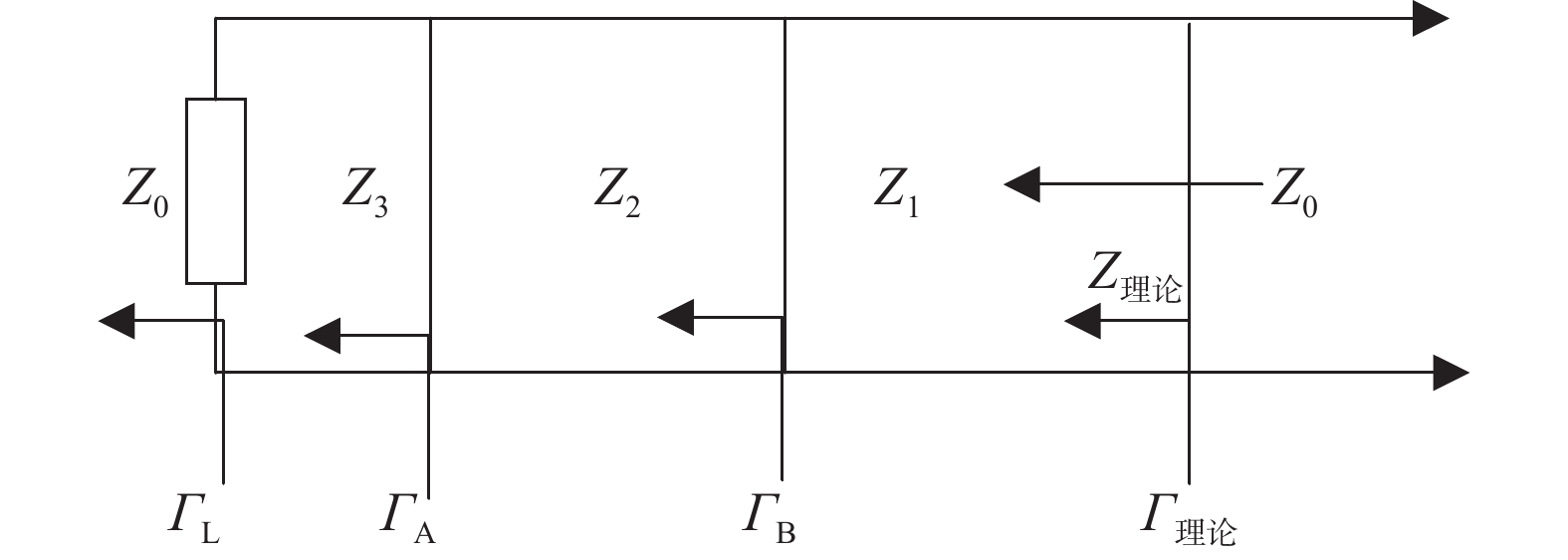
1) 插针深度
一般同轴线外导体全长大于内导体全长,这是因为在设计过程中“插针深度”[12]这一参数的存在射频同轴连接器为了避免连接器中心体的硬接触带来机械损伤,通常会要求连接器内导体到基准面之间工差预留一个很难小的负数,使连接状态下连接器内导体不会直接接触,即在图3中,G为一个很小的数。根据110 GHz转接头设计标准[13],作为计量设备使用的LPC级转接头插针深度不应超过13 μm。因此这里按照13 μm进行仿真设计,如图4所示。

|
| 图 3 连接器内导体间隙示意图。 |
|
| 图 4 插针深度的设计 |
2) 倒角
由于在实际加工中,结构的棱边会进行去毛刺处理[14],因此必然存在倒角半径。而倒角的处理在内导体的阶跃变化处会对阻抗失配带来一定的改善,从而影响整体反射系数。因此在仿真时,根据加工工艺设置了棱边倒角圆角半径为0.01 mm。
另一方面,考虑到有限元计算精确度与迭代收敛参数、离散剖分网格密度有密切关系。且计算资源、时间开销和计算精度应根据运算平台进行合理平衡,因此对仿真关键参数进行了如下配置:
1)求解分段
为了节约计算资源,避免在低频段应用密度过大的剖分网格导致冗余计算量,本问题中将全频带10 MHz~110 GHz分为10 MHz~40 GHz和40 ~ 110 GHz两段进行频率扫描。为了使整数GHz关键频点得到准确求解,避免插值算法引入数值误差,频率扫描方法选择了插值扫描,且以100 MHz为起点,110 GHz为终点,步进100 MHz;为了使得结果在频率间隔上保证一定的连续性,将插值的Error Tolerance值设置为0.01%。
2)求解频点与S参数最大残差设置
在两个分段中,为保证计算精度,分别设置最高频点(40 GHz和110 GHz)为求解频点。因此每个分段的最高频点在收敛时需要的网格密度会作为该段基准剖分尺度。该尺度一般而言密度足够大,将其应用于分段内各插值频点的计算中时通常能使迭代迅速收敛。
为了在保证精度的前提下减少对内存和时间的消耗,最重要的便是控制基准剖分尺度的密度。该密度通过收敛门限Max DeltS的进行控制。Max DeltS数学意义是两次迭代S参数相差的最大值。经考核,该模型下S参数残差在5次迭代之内能够到达0.01且在到达后开始在小于0.01的范围内震荡。因此MaxDeltS设置为0.01足以满足计算精度要求,且能够实现快速收敛,终止剖分网格的进一步加密。
2.2 仿真考核工差对电性能的影响由于制造过程存在工差(国内加工工差水平见表3),为了考核产品批产后是否会在因工差影响电性能一致性,利用HFSS的参数扫描功能对表3中10项工差进行了仿真。
| 类型 | 几何量 | 符号 | 设计值/mm | 工差/mm |
| 1 mm失配同轴线 | 外导体内径 | b | 1.000 | ±0.003 |
| 内导体外径1 | a1 | 0.434 | ±0.003 | |
| 内导体外径2 | a2 | 0.659 | ±0.003 | |
| 内导体外径3 | a3 | 0.434 | ±0.003 | |
| 长度1 | d1 | 5.00 | ±0.01 | |
| 长度2 | d2 | 20.00 | ±0.01 | |
| 长度3 | d3 | 5.00 | ±0.01 | |
| 1 mm匹配同轴线 | 外导体内径 | b | 1.000 | ±0.003 |
| 内导体外径 | a1 | 0.434 | ±0.003 | |
| 长度 | d | 30.00 | ±0.01 |
将工差带入模型后,考核与设计值的S11模值和S21相位偏差的结果见表4。这里的结果可以认为是对制造过程重复性的最差情况模拟。因此参考对重复性考核较为苛刻的计量标准器具技术报告编写要求[15],计量器具重复性须满足不大于合成不确定度uc的2/3。本文选择相同的判定条件(即设计要求扩展不确定度U的1/3),因此S11模值判定条件为不大于0.033,S21相位判定条件为不大于1.7°。由表4可见失配同轴线工差引入最大偏差为0.015,匹配同轴线工差引入最大偏差为1.3°,均能满足判定条件。由此可见在考虑最大加工工差的情况下,产品的电性能仍能够得到保证。
| 类型 | 分类 | 符号 | 设计值/ mm |
考察值/ mm |
S11模值 偏差值 |
| 1 mm失配同轴线 | 外导体内径 | b | 1.000 | 0.997 | 0.014 |
| 1.003 | 0.011 | ||||
| 内导体外径1 | a1 | 0.434 | 0.431 | 0.009 | |
| 0.437 | 0.008 | ||||
| 内导体外径2 | a2 | 0.659 | 0.656 | 0.010 | |
| 0.662 | 0.011 | ||||
| 内导体外径3 | a3 | 0.434 | 0.431 | 0.009 | |
| 0.437 | 0.008 | ||||
| 长度1 | d1 | 5.00 | 4.99 | 0.012 | |
| 5.01 | 0.015 | ||||
| 长度2 | d2 | 20.00 | 19.99 | 0.012 | |
| 20.01 | 0.015 | ||||
| 长度3 | d3 | 5.00 | 4.99 | 0.012 | |
| 5.01 | 0.015 | ||||
| 类型 | 分类 | 符号 | 设计值/ mm |
考察值/ mm |
S21相位 偏差值/(°) |
| 1 mm匹配同轴线 | 外导体内径 | b | 1.000 | 0.997 | 0.2 |
| 1.003 | 0.1 | ||||
| 内导体外径 | a1 | 0.434 | 0.431 | 0.0 | |
| 0.437 | 0.1 | ||||
| 长度 | d | 30.00 | 29.99 | 1.1 | |
| 30.01 | 1.3 | ||||
3 仿真结果与实测结果
在确认了产品满足了设计要求后进行了生产加工,见图5。随后使用110 GHz网络分析仪对样件进行了S11模值和S21相位的测试。

|
| 图 5 失配(右)/匹配(左)同轴线实物图 |
图6和图7分别为S11模值和S21相位的解析计算结果、仿真设计结果和实测结果。
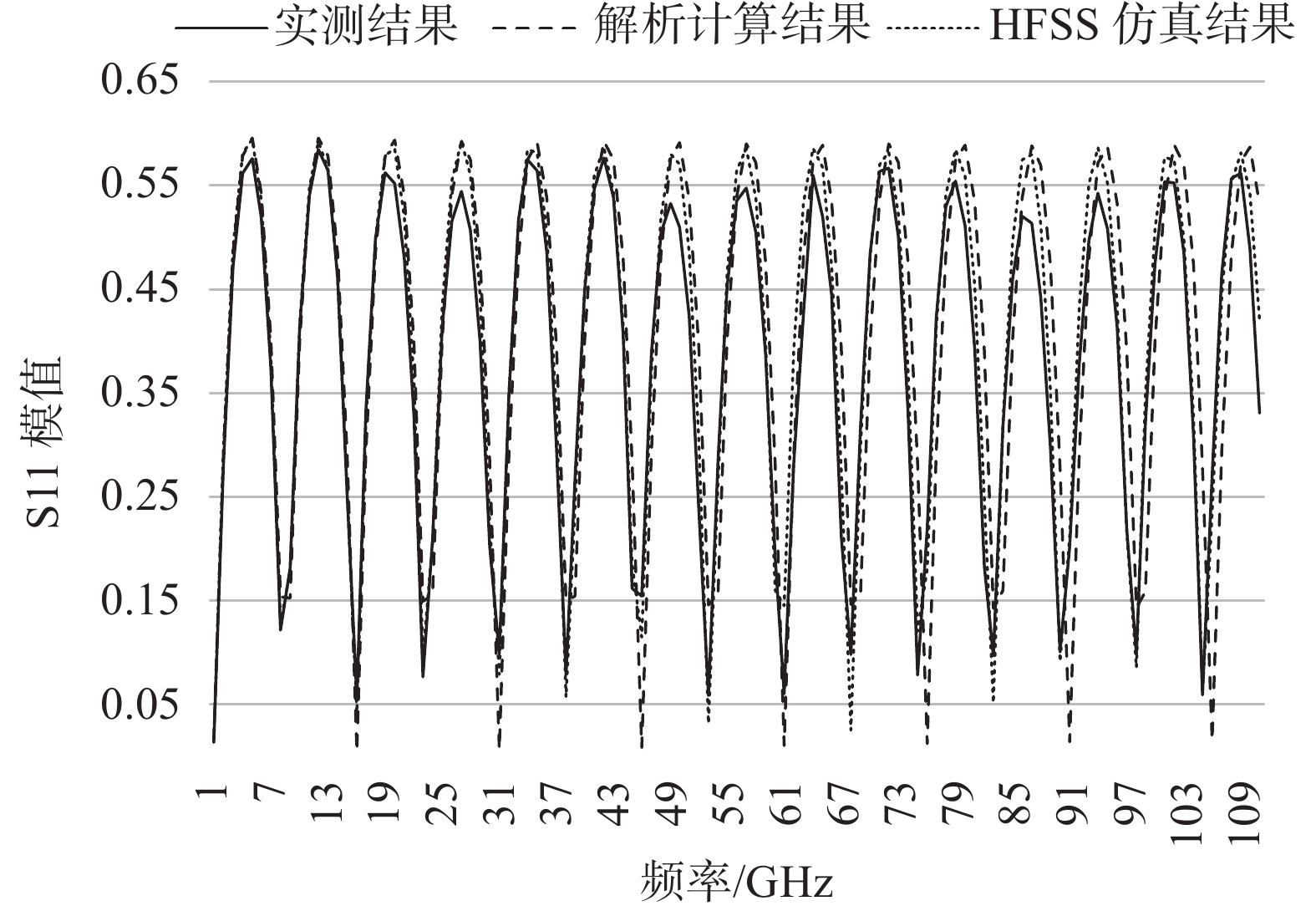
|
| 图 6 S11模值解析计算结果、仿真设计结果和实测结果 |
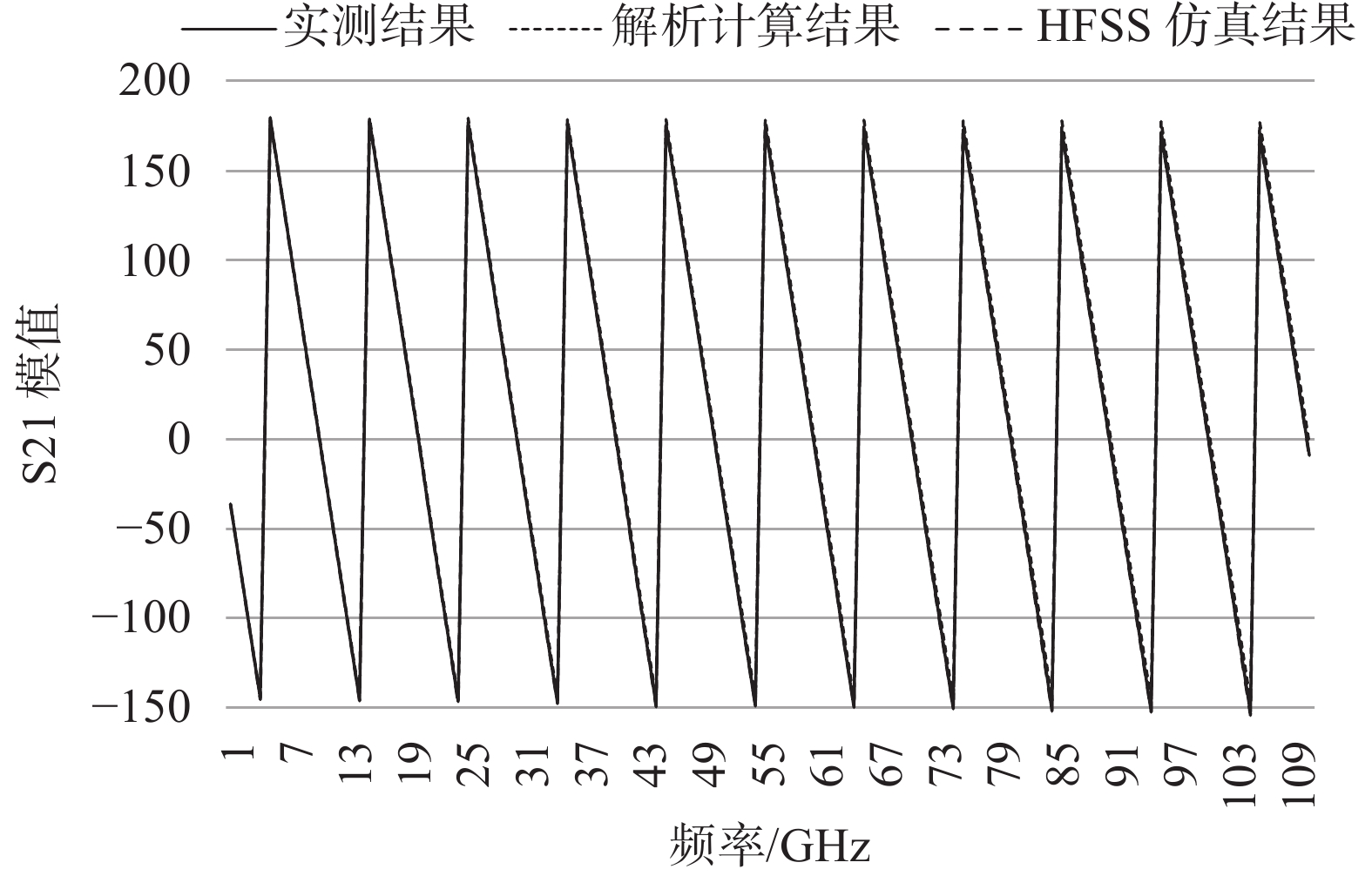
|
| 图 7 S21相位解析计算结果、仿真设计结果和实测结果 |
由结果对比可知,解析结果能够较好地计算出S参数在全频段的趋势。解析算法的S11模值计算时由于在阻抗计算时做了近似,高频段相较实测值在频域上发生了一定的偏差,但S21相位吻合度较高;而HFSS仿真结果无论S11模值还是S21相位在全频段的峰值和匹配点处都能与测试值较好吻合。从而证明了本文提出的设计方法的有效性。
4 结束语在110 GHz宽带同轴S参数标准装置设计中,将解析方法与有限元仿真方法结合可以实现设计过程中高效率与高准确度的平衡,该方法经过了实际测试的验证。相同的设计方法也可以应用在其他频段的同轴S参数标准装置的设计中。基于本文提出的数学模型,可以在此基础上构建S参数与不同几何量之间的偏微分关系,研究各参量引入的不确定度分量,为110 GHz宽带同轴S参数的计量标准建设和维护提供数学分析支撑。
| [1] |
明治中. 射频一体化网络仪原理及故障分析[J].
电子测量技术, 2018, 41(12): 105-108.
MING Z Z. Principle and fault analysis of RF integrated network instrument[J].
Electronic Measurement Technology, 2018, 41(12): 105-108.
|
| [2] |
王宏珍, 卜云平, 马迎春. 浅析矢量网络分析仪测量误差和误差修正[J].
中国测试, 2001, 27(5): 19-20.
WANG H Z, BU Y P, MA Y C. Analysis of measurement error and error correction in vector network analyzer[J].
China Measurement & Test, 2001, 27(5): 19-20.
DOI:10.3969/j.issn.1674-5124.2001.05.006 |
| [3] |
王怀念. 网络分析仪校验件设计和参数化过程[J].
机电元件, 2022, 42(5): 6.
WANG H N. Design and parameterization process of verification components for network analyzers[J].
Electromechanical Components, 2022, 42(5): 6.
DOI:10.3969/j.issn.1000-6133.2022.05.004 |
| [4] |
Operating and service manual 85059V 1.0 mm precision verification kit[M].Keysight Technologies, 2022.
|
| [5] |
TUMBAGA C . 0.8 mm connectors enable D-band coaxial measurements[J]. Microwave Journal, 2019, 62(MAR. SPEC. ): 6-12.
|
| [6] |
端木文乐. 毫米波射频同轴连接器的结构研究[D]. 北京:北京邮电大学, 2019.
DUANMU W L. Structural research on millimeter wave RF coaxial connectors [D]. Beijing: Beijing University of Posts and Telecommunications, 2019.
|
| [7] |
孙成芹, 胡永建, 李显义, 等. 基于HFSS仿真的感应耦合传输装置设计[J].
电子测量技术, 2021, 44(2): 32-35.
SUN C Q, HU Y J, LI X Y, et al. Design of inductive coupling transmission device based on HFSS simulation[J].
Electronic Measurement Technology, 2021, 44(2): 32-35.
|
| [8] |
邢蕾, 孔祥鲲, 徐千. 理论分析与电磁仿真结合的微波器件设计教学[J].
实验技术与管理, 2019, 36(3): 4.
XING L, KONG X K, XU Q. Teaching of microwave device design by combining theoretical analysis and electromagnetic simulation[J].
Experimental Technology and Management, 2019, 36(3): 4.
|
| [9] |
崔广新, 赵熙. 同轴空气线电长度计算在VNA传输相位校准中的应用[J].
中国测试, 2022, 48(S1): 149-153.
CUI G X, ZHAO X. Application of coaxial air line electrical length calculation in VNA transmission phase calibration[J].
China Measurement & Test, 2022, 48(S1): 149-153.
|
| [10] |
徐锐敏. 微波技术基础[M]. 北京:科学出版社, 2009.
XU R M. Fundamentals of Microwave Technology [M]. Beijing:Science Press, 2009.
|
| [11] |
陈俐华, 武文革, 于大国, 等. 深孔加工技术工艺分析[J].
工具技术, 2022(8): 56.
CHEN L H, WU W G, YU D G, et al. Process analysis of deep hole machining technology[J].
Tool Engineering, 2022(8): 56.
DOI:10.3969/j.issn.1000-7008.2022.08.011 |
| [12] |
柏雪崧. 110 GHz射频同轴连接器的研制[J].
机电元件, 2015, 35(4): 7.
BAI X S. Development of 110 GHz RF coaxial connectors[J].
Electromechanical Components, 2015, 35(4): 7.
|
| [13] |
Std I . 287-2007 - IEEE Standard for Precision Coaxial Connectors (DC to 110 GHz)[J]. IEEE, 2007.
|
| [14] |
董大鹏. 精密工作边磨削毛刺形成机理及其去除技术研究[D]. 上海:上海交通大学, 2016.
DONG D P. Research on the formation mechanism and removal technology of burrs in precision working edge grinding [D]. Shanghai:Shanghai Jiao Tong University, 2016.
|
| [15] |
国防军工计量标准器具技术报告编写要求: JJF(军工)3—2012[S]. 北京: 国家国防科技工业局, 2012.
Technical Requirements for National Defense and Military Metrology Standard Instruments: JJF (Military Industry) 3-2012 [S]. Beijing: National Defense Science and Technology Industry Bureau, 2012.
|
 2024, Vol. 50
2024, Vol. 50