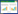文章信息
- 金涛涛, 崔秀慧, 王健, 苗沛
- JIN Taotao, CUI Xiuhui, WANG Jian, MIAO Pei
- 水下无人平台的模型参考自适应姿态控制研究
- Research on model reference adaptive attitude control for unmanned underwater platform
- 中国测试, 2024, 50(7): 107-114
- CHINA MEASUREMENT & TEST, 2024, 50(7): 107-114
- http://dx.doi.org/10.11857/j.issn.1674-5124.2023030166
-
文章历史
- 收稿日期: 2023-03-29
- 收到修改稿日期: 2023-05-18
2. 中冶京诚工程技术有限公司,北京 100176
2. Capital Engineering & Research Incorporation Limited, Beijing 100176 , China
海洋矿产资源丰富,深海探测、海洋资源开发已成为各国重点研究方向,有效推动了水下机器人的发展[1-2]。水下无人平台作为水下机器人的一种,可搭载多种设备在恶劣的海底工况下完成环境勘探和采样任务。为了更好地完成相关工作以及清晰、稳定的传输水下环境图像,水下无人平台的姿态控制稳定性至关重要[3-4]。
水下机器人控制系统早在上世纪八十年代就已经成为国内外研究学者的重点研究对象[5],其中姿态控制更是得到众多研究学者和机构的重点关注[6-7]。王鸿儒[8]等对水下机器人的姿态控制采用了基于奇异摄动法的串-并联PID控制,提高了系统抗扰动能力;骆晓玲[9]设计了模糊PID控制器应用于水下航行器,解决了因参数变化和环境干扰引起的水下机器人控制失稳的问题,NGUYEN Q H[10]使用自适应控制方法,通过识别水下机器人在工作中机械臂受力情况,进行载体反方向力的补偿,实现了水下机器人的稳定控制;陈巍[11]将滑模自适应控制运用到水下无人平台的姿态位置跟踪问题上,提高了控制系统稳定性。另外,有相关学者将常规PID控制应用于水下无人平台的姿态控制[12],制器不能很好地适应系统参数和环境的变化。
目前,大多数水下无人平台的姿态控制不能应对搭载不同设备所产生的运动模型变化问题,且多数姿态控制算法仅限于仿真层面[13]。而比较成熟的传统PID控制精度低,在环境干扰比较严重的情况下便无法满足应用需求。为了解决水下无人平台姿态控制问题,本文提出了一种模型参考自适应PID控制方法,算法环境适应性强,可保证水下无人平台面对水下复杂多变的环境以及搭载不同设备的情况下依然具有较好的动态性能和控制精度。
1 水下无人平台模型及分析 1.1 水下无人平台结构针对海底资源勘探问题,自主设计了水下无人平台,如图1所示。

|
| 图 1 水下无人平台 |
该设备主要分为四部分即主体模块、可视化模块、驱动模块和控制模块。其优点在于平台软硬件系统无需做较大更改的前提下,可以根据任务需求增加新的模块,满足搭载设备和作业任务多样化的需求。
1.2 水下无人平台运动学模型为了实现水下无人平台的姿态控制系统设计,首先对其运动学及动力学进行建模分析。这里采用的是国际拖曳水池会议(ITTC)以及造船与轮机工程学会(SHAME)术语公报推荐的体系,建立两种坐标系即固定坐标系(E-ξηζ)和运动坐标系(O-xyz),如图2所示。
|
| 图 2 固定坐标系和运动坐标系 |
固定坐标系(简称“定系”)以地球为参考,相对于地球固定。水下无人平台在定系中运动及力的参数定义如表1所示。
| 矢量 | 速度 | 角速度 | 航向角 | 外力 | 外力矩 |
| x轴 | |||||
| y轴 | |||||
| z轴 |
运动坐标系(简称“动系”)以水下无人平台为参考,和其一起运动[14]。水下无人平台在动系中运动的定义如表2所示。
运动坐标系不是一个惯性参考系,以水下无人平台为参照,相对于地面有角速度和加速度。用运动学牛顿定律不能得以求解。因此,在分析水下无人平台运动时,首先在定系中建立运动方程,通过转换关系,求出动系中的分量,从而便可得出水下无人平台在运动坐标系下的运动方程。同一矢量参数在定系和动系中各分量之间存在换算关系。坐标变换公式为[15]:
| $ {\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{\dot X}}}&{{\boldsymbol{\dot Y}}}&{{\boldsymbol{\dot Z}}} \end{array}} \right]^{\text{T}}}{\boldsymbol{ = S}}{\left[ {\begin{array}{*{20}{c}} {\boldsymbol{u}}&{\boldsymbol{v}}&{\boldsymbol{w}} \end{array}} \right]^{\text{T}}} $ | (1) |
基于通用的水下机器人6-DOF动力学模型,假设水下无人平台的浮力中心与运动坐标系的原点重合,则本文所研究的水下无人平台的动力学方程为:
| $ {\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \psi }&{\sin \phi \sin \theta \cos \psi - \cos \phi \sin \psi }&{\cos \phi \sin \theta \cos \psi + \sin \phi } \\ {\cos \theta \sin \psi }&{\sin \phi \sin \theta \sin \psi + \cos \phi \cos \psi }&{\cos \phi \sin \theta \sin \psi - \sin \phi \cos \psi } \\ { - \sin \theta }&{\sin \phi \cos \theta }&{\cos \phi \cos \theta } \end{array}} \right] $ | (2) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {\sum {F_X} = m\left[ {\dot u - vr + wq - {x_{\text{G}}}\left( {{q^2} + {r^2}} \right) + {y_{\text{G}}}(pq - \dot r) + {{\textit{z}}_{\text{G}}}(pr + \dot q)} \right]} \\ {\sum {F_Y} = m\left[ {\dot v - wp + ur - {y_{\text{G}}}\left( {{r^2} + {p^2}} \right) + {{\textit{z}}_{\text{G}}}(qr - \dot p) + {x_{\text{G}}}(qp + \dot r)} \right]} \\ {\sum {F_Z} = m\left[ {\dot w - uq + vp - {{\textit{z}}_{\text{G}}}\left( {{p^2} + {q^2}} \right) + {x_{\text{G}}}(rp - \dot q) + {y_{\text{G}}}(rp + \dot p)} \right]} \\ {\sum {M_K} = {I_x}\dot p + \left( {{I_{\textit{z}}} - {I_y}} \right)qr + m\left[ {{y_{\text{G}}}(\dot w + vp - uq) - {{\textit{z}}_{\text{G}}}(\dot v + ur - wp)} \right]} \\ {\sum {M_M} = {I_y}\dot q + \left( {{I_x} - {I_{\textit{z}}}} \right)rp + m\left[ {{{\textit{z}}_{\text{G}}}(\dot u + wq - vr) - {x_{\text{G}}}(\dot w + vp - uq)} \right]} \\ {\sum {M_N} = {I_{\textit{z}}}\dot r + \left( {{I_y} - {I_x}} \right)pq + m\left[ {{x_{\text{G}}}(\dot v + ur - wp) - {y_{\text{G}}}(\dot u + wq - vr)} \right]} \end{array}} \right. $ | (3) |
式中:
从流体力学角度对水下无人平台进行分析,水下无人平台外力(力矩)的数学描述如下:
| $ {{\boldsymbol{\tau }}_{{\text{RB}}}}{\boldsymbol{ = }}{{\boldsymbol{\tau }}_{\text{H}}}{\boldsymbol{ + \tau }} $ | (4) |
式中:
作用在水下无人平台的外部流体力和力矩可以表示为:
| $ {{\boldsymbol{\tau }}_{\text{H}}} = - {{\boldsymbol{M}}_{\text{A}}}\dot v - {{\boldsymbol{C}}_{\text{A}}}(v)v - {\boldsymbol{D}}(v)v - {\boldsymbol{g}}(\eta ) $ | (5) |
其中方程(5)中,惯性附加质量
| $ {{\boldsymbol{M}}_{\text{A}}} = - \left[ {\begin{array}{*{20}{c}} {{X_{\dot u}}}&{{X_{\dot v}}}&{{X_{\dot w}}}&{{X_{\dot p}}}&{{X_{\dot q}}}&{{X_{\dot r}}} \\ {{Y_{\dot u}}}&{{Y_{\dot v}}}&{{Y_{\dot w}}}&{{Y_{\dot p}}}&{{Y_{\dot q}}}&{{Y_{\dot r}}} \\ {{Z_{\dot u}}}&{{Z_{\dot v}}}&{{Z_{\dot w}}}&{{Z_{\dot p}}}&{{Z_{\dot q}}}&{{Z_{\dot r}}} \\ {{K_{\dot u}}}&{{K_{\dot v}}}&{{K_{\dot w}}}&{{K_{\dot p}}}&{{K_{\dot q}}}&{{K_{\dot r}}} \\ {{M_{\dot u}}}&{{M_{\dot v}}}&{{M_{\dot w}}}&{{M_{\dot p}}}&{{M_{\dot q}}}&{{M_{\dot r}}} \\ {{N_{\dot u}}}&{{N_{\dot v}}}&{{N_{\dot w}}}&{{N_{\dot p}}}&{{N_{\dot q}}}&{{N_{\dot r}}} \end{array}} \right] $ | (6) |
式(6)中的符号如
| $ {{\boldsymbol{C}}_{\text{A}}}(v){\text{ = }}\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{ - {f_3}}&{{f_2}} \\ 0&0&0&{{f_3}}&0&{ - {f_1}} \\ 0&0&0&{ - {f_2}}&{{f_1}}&0 \\ 0&{ - {f_3}}&{{f_2}}&0&{ - {f_6}}&{{f_5}} \\ {{f_3}}&0&{ - {f_1}}&{{f_6}}&0&{ - {f_4}} \\ { - {f_2}}&{{f_1}}&0&{ - {f_5}}&{{f_4}}&0 \end{array}} \right] $ | (7) |
式中:
| $ \begin{gathered} {f_1} = {X_{\dot u}}u + {X_{\dot v}}v + {X_{\dot w}}w + {X_{\dot p}}p + {X_{\dot q}}q + {X_{\dot r}}r \\ {f_2} = {X_{\dot v}}u + {Y_{\dot v}}v + {Y_{\dot w}}w + {Y_{\dot p}}p + {Y_{\dot q}}q + {Y_{\dot r}}r \\ {f_3} = {X_{\dot w}}u + {Y_{\dot w}}v + {Z_{\dot w}}w + {Z_{\dot p}}p + {Z_{\dot q}}q + {Z_{\dot r}}r \\ {f_4} = {X_{\dot p}}u + {Y_{\dot p}}v + {Z_{\dot p}}w + {K_{\dot p}}p + {K_{\dot q}}q + {K_{\dot r}}r \\ {f_5} = {X_{\dot q}}u + {Y_{\dot q}}v + {Z_{\dot q}}w + {K_{\dot q}}p + {M_{\dot q}}q + {M_{\dot r}}r \\ {f_6} = {X_{\dot r}}u + {Y_{\dot r}}v + {Z_{\dot r}}w + {K_{\dot r}}p + {M_{\dot r}}q + {N_{\dot r}}r \\ \end{gathered} $ |
一般来说,航行器在水下高速航行具有很强的非线性和复杂的耦合性。然而,本文研究的水下无人平台以低速运动,且有三个对称平面,附加质量矩阵内不在对角线上的元素可忽略不计。
因此,惯性附加质量矩阵
| $ \boldsymbol{M}_{\text{A }}=-\mathrm{diag}\left[X_{\dot{u}}\text{ },\text{ }Y_{\dot{v}}\text{ },\text{ }Z_{\dot{w}}\text{ },K_{\dot{p}}\text{ },\text{ }M_{\dot{q}}\text{ },N_{\dot{r}}\right] $ | (8) |
| $ {{\boldsymbol{C}}_{\text{A}}}(v){\text{=}}\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{ - {Z_{\dot w}}w}&{{\text{ }}{Y_{\dot v}}v} \\ 0&0&0&{{Z_{\dot w}}w}&0&{ - {X_{\dot u}}u} \\ 0&0&0&{ - {Y_{\dot v}}v}&{{X_{\dot u}}u}&0 \\ 0&{ - {Z_{\dot w}}w}&{{Y_{\dot v}}v}&0&{ - {N_{\dot r}}r}&{{M_{\dot q}}q} \\ {{Z_{\dot w}}w}&0&{ - {X_{\dot u}}u}&{{N_{\dot r}}r}&0&{ - {K_{\dot p}}p} \\ { - {Y_{\dot v}}v}&{{X_{\dot u}}u}&0&{ - {M_{\dot q}}q}&{{K_{\dot p}}p}&0 \end{array}} \right] $ | (9) |
| $ \begin{gathered}\boldsymbol{D}(\boldsymbol{v}) = \boldsymbol{D}_{\text{L}}\boldsymbol{+}\boldsymbol{D}_{\text{NL}}(\boldsymbol{v})=-\mathrm{diag}\left[X_u\text{ },\text{ }Y_v\text{ },\text{ }Z_w\text{ },K_p,\text{ }M_q\text{ },N_r\right]= \\ -\left[ \begin{array}{*{20}{c}}X_{u\left|u\right|}|u| & 0 & 0 & 0 & 0 & 0 \\ 0 & Y_{v\left|v\right|}|v| & 0 & 0 & 0 & 0 \\ 0 & 0 & Z_{w\left|w\right|}|w| & 0 & 0 & 0 \\ 0 & 0 & 0 & K_{p\left|p\right|}|p| & 0 & 0 \\ 0 & 0 & 0 & 0 & M_{q\left|q\right|}|q| & 0 \\ 0 & 0 & 0 & 0 & 0 & N_{r\left|r\right|}|r|\end{array} \right] \\ \end{gathered} $ | (10) |
式中:
由于平台在垂直方向上也受到重力
| $\begin{split} &{\boldsymbol{g(\eta )}}=\\ &\left[ {\begin{array}{*{20}{c}} {(W - B){\text{ }}\sin \theta } \\ { - (W - B){\text{ }}\sin \varphi \cos \theta } \\ { - (W - B)\cos \varphi \cos \theta } \\ { - ({y_{\text{G}}}W - {y_{\text{B}}}B){\text{ }}\cos \varphi \cos \theta + ({{\textit{z}}_{\text{G}}}W - {{\textit{z}}_{\text{G}}}B)\sin \varphi \cos \theta } \\ {({{\textit{z}}_{\text{G}}}W - {{\textit{z}}_{\text{G}}}B){\text{ }}\sin \theta + ({x_{\text{G}}}W - {x_{\text{B}}}B)\cos \varphi \cos \theta } \\ { - ({x_{\text{G}}}W - {x_{\text{B}}}B){\text{ }}\sin \varphi \cos \theta - ({y_{\text{G}}}W - {y_{\text{B}}}B)\sin \theta } \end{array}} \right] \end{split}$ | (11) |
在本研究中,推进器是成对排列的,如图3所示。

|
| 图 3 螺旋桨的分布示意图 |
因此,驱动力矩阵可被简化为:
| $ \begin{split} {\boldsymbol{\tau }} =& \left[ {{X_F},{Y_F},{Z_F},{K_F},{M_F},{N_F}} \right]{^{\text{T}}} =\\ & {\boldsymbol{S}}\left[ {{F_x},{F_y},{F_{\textit{z}}},{T_x},{T_y},{T_{\textit{z}}}} \right]{^{\text{T}}}= \\ & {\boldsymbol{S}}{\left[ {{F_1} + {F_2},0,{F_3} + {F_4},0,{F_3}{L_2} - {F_4}{L_2},{F_1}{L_1} - {F_2}{L_1}} \right]^{\text{T}}} \end{split}$ | (12) |
式中:
考虑到该平台主要工作是海底环境探测和沉物打捞,作业速度相对较慢。为了使模型更加简单,优化控制效果,对每个平面的运动进行单独分析,适当简化水下无人平台各个方向的动力学方程:
1) 前进和后退运动的控制方程
当水下无人平台只使用水平推进器来完成前进和后退的运动时,不考虑环境和垂直平面推进器的影响,即
| $ (m - {X_{\dot u}})\dot u - {X_u}u = {X_F} - (W - B)\sin \theta + {X_{u\left| u \right|}}{u^2} = {r_X} $ | (13) |
2) 恒定深度运动的控制方程
当水下无人平台在纵向垂直平面内做恒定深度运动时,只使用垂直推进器,不考虑其他力干扰情况,即
| $ (m - {Z_{\dot w}})\dot w - {Z_w}w = {Z_F} + (W - B)\cos \varphi \cos \theta + {Z_{w\left| w \right|}}{w^2} = {\text{ }}{r_Z} $ | (14) |
3) 横倾运动的控制方程
假设发生交叉倾斜的角度很小,即
| $ ({I_x} - {K_{\dot p}})\dot p{\text{ }} - {K_p}p = {\text{ }}{K_F} + {\text{ }}{K_{P\left| P \right|}}{p^2} = {\text{ }}{r_K}{\text{ }} $ | (15) |
4) 俯仰运动的控制方程
水下无人平台纵向垂直平面运动主要是指前进、后退、下潜、漂浮和俯冲,即
| $ ({I_y} - {M_{\dot q}})\dot q - {M_q}q = {M_F} + {M_{q\left| q \right|}}{q^2} = {\text{ }}{r_M}{\text{ }} $ | (16) |
5) 航向的控制方程
当船头转向运动仅由水下无人平台进行时,船头运动是缓慢的。假设无人平台的重心保持不变,不涉及前进、后退和横倾运动,即
| $ ({I_Z} - {N_{\dot r}})\dot r - {N_r}r = {N_F} + {N_{r\left| r \right|}}{r^{2{\text{ }}}} = {r_N}{\text{ }} $ | (17) |
水下无人平台主要在水平面和垂直面上进行运动。由于小型水下航行器的运行速度比较缓慢,模型的非线性项主要由阻力构成,这样会导致建模时难以求解,因此一般可作为模型的不确定性和干扰来处理。如果知道平台当前的运动状态,就可以得到外力(力矩)的大小,估计出平台在下一个采样周期的运动状态。据此便可构建水下无人平台的运动和控制模拟系统。
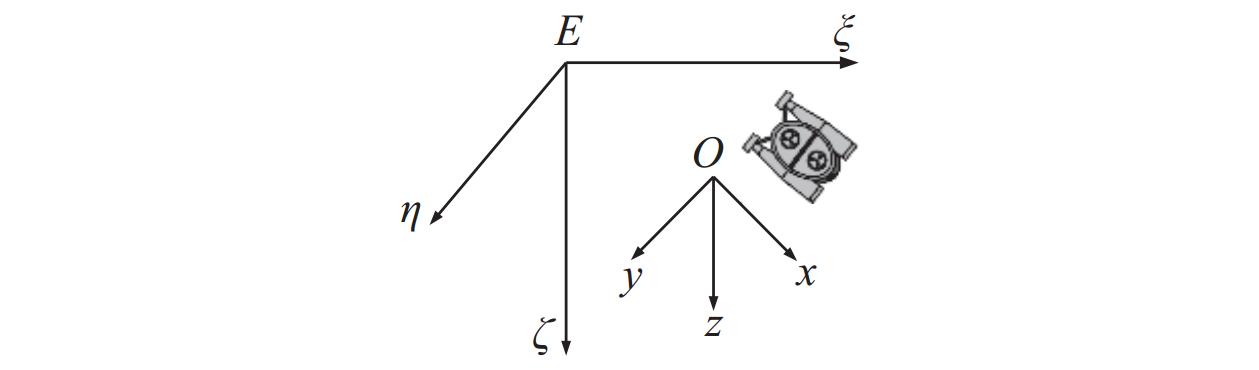
3 模型参考自适应PID姿态控制本文所使用的模型参考自适应控制(model reference adaptive control,MRAC)算法结构如图4所示。参考模型与控制对象和控制器并联,得到的结果通过自适应调节机构反馈到控制器,从而调整其参数,更正参考模型。由于在可调控制器中输入的参考信号在参考模型上也发挥作用,所以系统所期望的控制性能指标可用参考模型的输出状态来确定。
|
| 图 4 模型参考自适应控制系统结构框图 |
假设水下无人平台的运动和姿态控制系统为二阶传递函数模型:
| $ G(s) = \frac{b}{{{s^2} + {a_1}s + {a_2}}} $ | (18) |
若其与PID控制
| $ \begin{split} {G_{\text{C}}}(s) =& \frac{{{y_{\text{p}}}(s)}}{{r(s)}} = \frac{{G(s)C(s)}}{{1 + G(s)C(s)}}= \\ & \frac{{b({K_{\text{d}}}{s^2} + {K_{\text{p}}}s + {K_{\text{i}}})}}{{{s^3} + ({a_1} + b{K_{\text{d}}}){s^2} + ({a_2} + b{K_{\text{p}}})s + b{K_{\text{i}}}}} \end{split}$ | (19) |
式中:
根据上式所得系统传递函数取参考模型为:
| $ {G_{\text{m}}}(s) = \frac{{{y_{\text{m}}}(s)}}{{r(s)}} = \frac{{{b_{{\text{m}}1}}{s^2} + {b_{{\text{m2}}}}s + {b_{{\text{m}}3}}}}{{{s^3} + {a_{{\text{m1}}}}{s^2} + {a_{{\text{m2}}}}s + {a_{{\text{m3}}}}}} $ | (20) |
式中:
为了便于控制器参数计算,参考模型的阶数选取与实际系统模型相同。定义广义误差为:
| $ \varepsilon \left( t \right){\text{ }} = {\text{ }}{y_{\text{p}}}\left( t \right){\text{ }} - {\text{ }}{y_{\text{m}}}\left( t \right) $ | (21) |
设可调PID控制器参数为
| $ J(\theta ) = \frac{1}{2}{\varepsilon ^2} $ | (22) |
沿
| $ \dot \theta = \frac{{{\text{d}}\theta }}{{{\text{d}}t}} = - \gamma \frac{{\partial J}}{{\partial \theta }} $ | (23) |
式中:
将上述控制器参数调整律应用到PID控制器中则有:
| $ \left\{ \begin{gathered} \frac{{{\text{d}}{K_{\text{p}}}}}{{{\text{d}}t}} = - {\gamma _{\text{p}}}\frac{{\partial J}}{{\partial {K_{\text{p}}}}} = - {\gamma _{\text{p}}} \times \frac{{\partial J}}{{\partial \varepsilon }} \times \frac{{\partial \varepsilon }}{{\partial {y_{\text{p}}}}} \times \frac{{\partial {y_{\text{P}}}}}{{\partial {K_{\text{p}}}}} \\ \frac{{{\text{d}}{K_{\text{i}}}}}{{{\text{d}}t}} = - {\gamma _{\text{i}}}\frac{{\partial J}}{{\partial {K_{\text{i}}}}} = - {\gamma _{\text{i}}} \times \frac{{\partial J}}{{\partial \varepsilon }} \times \frac{{\partial \varepsilon }}{{\partial {y_{\text{p}}}}} \times \frac{{\partial {y_{\text{P}}}}}{{\partial {K_{\text{i}}}}} \\ \frac{{{\text{d}}{K_{\text{d}}}}}{{{\text{d}}t}} = - {\gamma _{\text{d}}}\frac{{\partial J}}{{\partial {K_{\text{d}}}}} = - {\gamma _{\text{d}}} \times \frac{{\partial J}}{{\partial \varepsilon }} \times \frac{{\partial \varepsilon }}{{\partial {y_{\text{p}}}}} \times \frac{{\partial {y_{\text{P}}}}}{{\partial {K_{\text{d}}}}} \\ \end{gathered} \right. $ | (24) |
式中:
| $ \frac{{\partial J}}{{\partial \varepsilon }} = \frac{{\partial ({\varepsilon ^2}/2)}}{{\partial \varepsilon }} = \varepsilon $ | (25) |
| $ \frac{{\partial \varepsilon }}{{\partial {y_{\text{p}}}}} = \frac{{\partial ({y_{\text{p}}}(t) - {y_{\text{m}}}(t))}}{{\partial {y_{\text{p}}}}} = 1 $ | (26) |
因此,PID控制器参数变化调整律为:
| $ \left\{ \begin{gathered} \frac{{{\text{d}}{K_{\text{P}}}}}{{{\text{d}}t}} = \frac{{{\gamma _{\text{p}}}\varepsilon s\displaystyle \sum\nolimits_{i = 0}^m {{b_i}{s^{m - i}}\left[ {r(s) - {y_{\text{P}}}} \right]} }}{{\displaystyle \sum\nolimits_{j = 0}^n {{a_j}{s^{n - j + 1}} + \displaystyle \sum\nolimits_{i = 0}^m {{b_i}{s^{m - i}}\left( {{K_{\text{d}}}{s^2} + {K_{\text{p}}}s + {K_{\text{i}}}} \right)} } }} \\ \frac{{{\text{d}}{K_{\text{i}}}}}{{{\text{d}}t}} = \frac{{{\gamma _{\text{i}}}\varepsilon \displaystyle \sum\nolimits_{i = 0}^m {{b_i}{s^{m - i}}\left[ {r(s) - {y_{\text{P}}}} \right]} }}{{\displaystyle \sum\nolimits_{j = 0}^n {{a_j}{s^{n - j + 1}} + \displaystyle \sum\nolimits_{i = 0}^m {{b_i}{s^{m - i}}\left( {{K_{\text{d}}}{s^2} + {K_{\text{p}}}s + {K_{\text{i}}}} \right)} } }} \\ \frac{{{\text{d}}{K_{\text{d}}}}}{{{\text{d}}t}} = \frac{{{\gamma _{\text{d}}}\varepsilon {s^2}\displaystyle \sum\nolimits_{i = 0}^m {{b_i}{s^{m - i}}\left[ {r(s) - {y_{\text{P}}}} \right]} }}{{\displaystyle \sum\nolimits_{j = 0}^n {{a_j}{s^{n - j + 1}} + \displaystyle \sum\nolimits_{i = 0}^m {{b_i}{s^{m - i}}\left( {{K_{\text{d}}}{s^2} + {K_{\text{p}}}s + {K_{\text{i}}}} \right)} } }} \\ \end{gathered} \right. $ | (27) |
本文的模型参考自适应PID控制是在自适应控制算法基础上提出的,PID控制器中的三个参数按照式(27)所推导的变化规律进行动态调整,以此来适应无人平台在水下工作时因运行环境或模型参数变化对姿态控制所带来的不利影响。由于控制器采用增量式算法更新控制参数,计算量较小,算法可以很方便地应用到嵌入式控制器中,充分满足实时控制的应用需求。
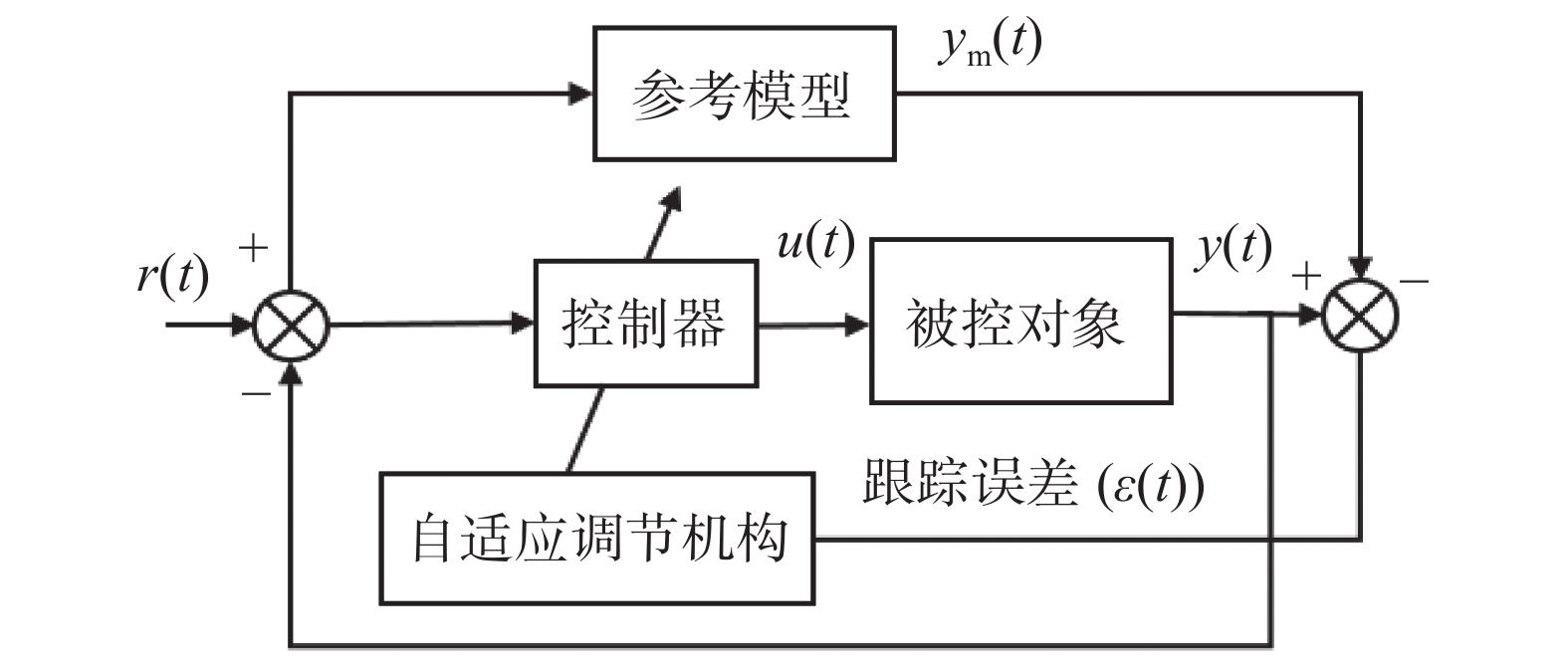
4 姿态控制系统仿真及分析为验证所设计的模型参考自适应PID控制算法是否有效,根据前文建立的水下无人平台模型,在Matlab/Simulink环境下模拟其运动控制姿态。为突显本文所设计控制算法的先进性,分别采用传统PID、模糊PID与模型参考自适应PID控制方法进行对比分析,其跟踪控制仿真结果如图5所示。
|
| 图 5 不同航向角的跟踪控制仿真结果对比 |
由图5可知,对于不同给定航向角的跟踪,三种控制算法均能达到较好的控制效果,对比如表3所示。
| 控制 模型 |
转向角度为3° | 转向角度为10° | |||
| 超调量/% | 调节时间/s | 超调量/% | 调节时间/s | ||
| MRAC-PID | 0 | 4.36 | 0 | 2.69 | |
| 传统PID | 30.8 | 10.41 | 30.7 | 8.94 | |
| 模糊PID | 14.3 | 13.8 | 14.2 | 12.52 | |
通过表3也可以看出:无论在超调量和调节时间上,模型参考自适应PID控制均优于其他两种控制算法,且算法具有更好的系统稳定性,还能补偿无人平台大范围运动时的模型不稳定问题。
由于水下无人平台运行环境复杂多变,搭载设备多种多样,这会导致其运动学模型发生较大变化。为了进一步验证所提出的控制算法能够适应无人平台水下工作时因模型参数变化对姿态控制所带来的不利影响,假设控制模型变化为:
| $ \frac{{\psi '(s)}}{{{{N'}_F}(s)}} = \frac{1}{{2{s^2} + 0.2s}} $ | (28) |
采用上述模型进行仿真,结果如图6所示。
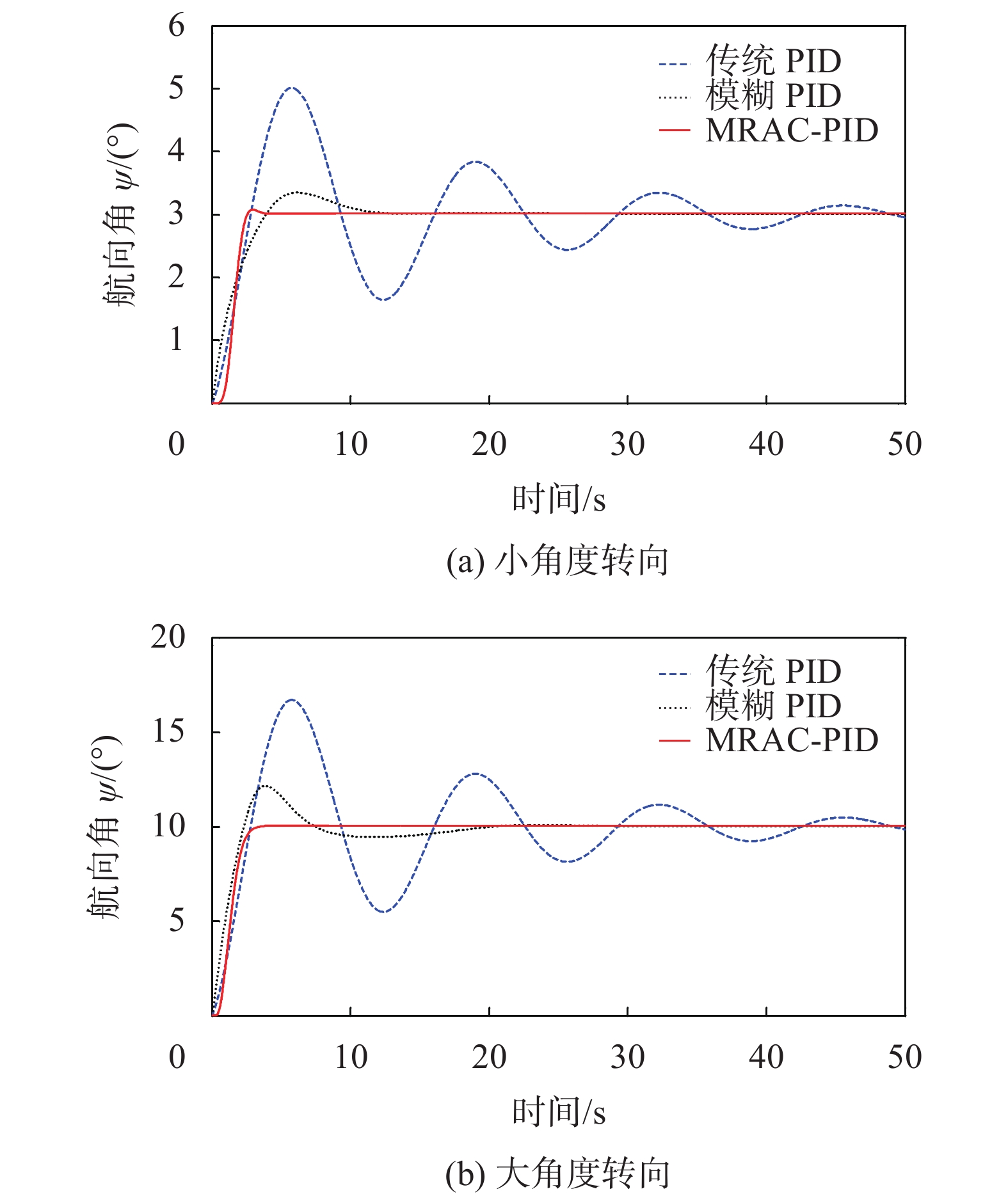
|
| 图 6 模型改变后的航向角控制仿真结果对比 |
从图中可以看出,当模型发生改变后,传统的PID控制已经无法实现正常操作;模糊PID控制虽具有一定的鲁棒性,且实现了给定目标的控制,但超调量和调节时间均差于模型改变之前,尤其是进行大角度转向时,其控制精度明显变差;(超调量:21.6%、调节时间:16.61 s);而模型参考自适应PID控制在模型参数发生改变前后无特殊变化,保持了较短的调节时间(3.05 s、2.68 s)和较小的超调量(2.16%、0%)。平台的俯仰控制、定深控制的方法与航向角控制方法相似,在此不再赘述,所提出的算法可保证水下无人平台在复杂多变的环境下依然具有良好的控制效果。
5 水下无人平台姿态控制试验为检验所开发的算法在实际环境下的控制效果,在野外开放水域下对水下无人平台进行了不同方向的运动控制试验,并测试了水下无人平台搭载不同工作装备情况下的水下控制效果,如图7所示。

|
| 图 7 水下无人平台运动控制测试试验 |
测试情况由安装在水下无人平台内部的传感器及前端的摄像头实时监测,结果如图8所示。图8(a)为改变航向的试验,从图中可以看出随着航向指令的改变,潜航器能够准确跟踪指令;图8(b)为静止状态下定航向试验,在波流等外力影响下,潜航器依旧能够保持航向稳定。
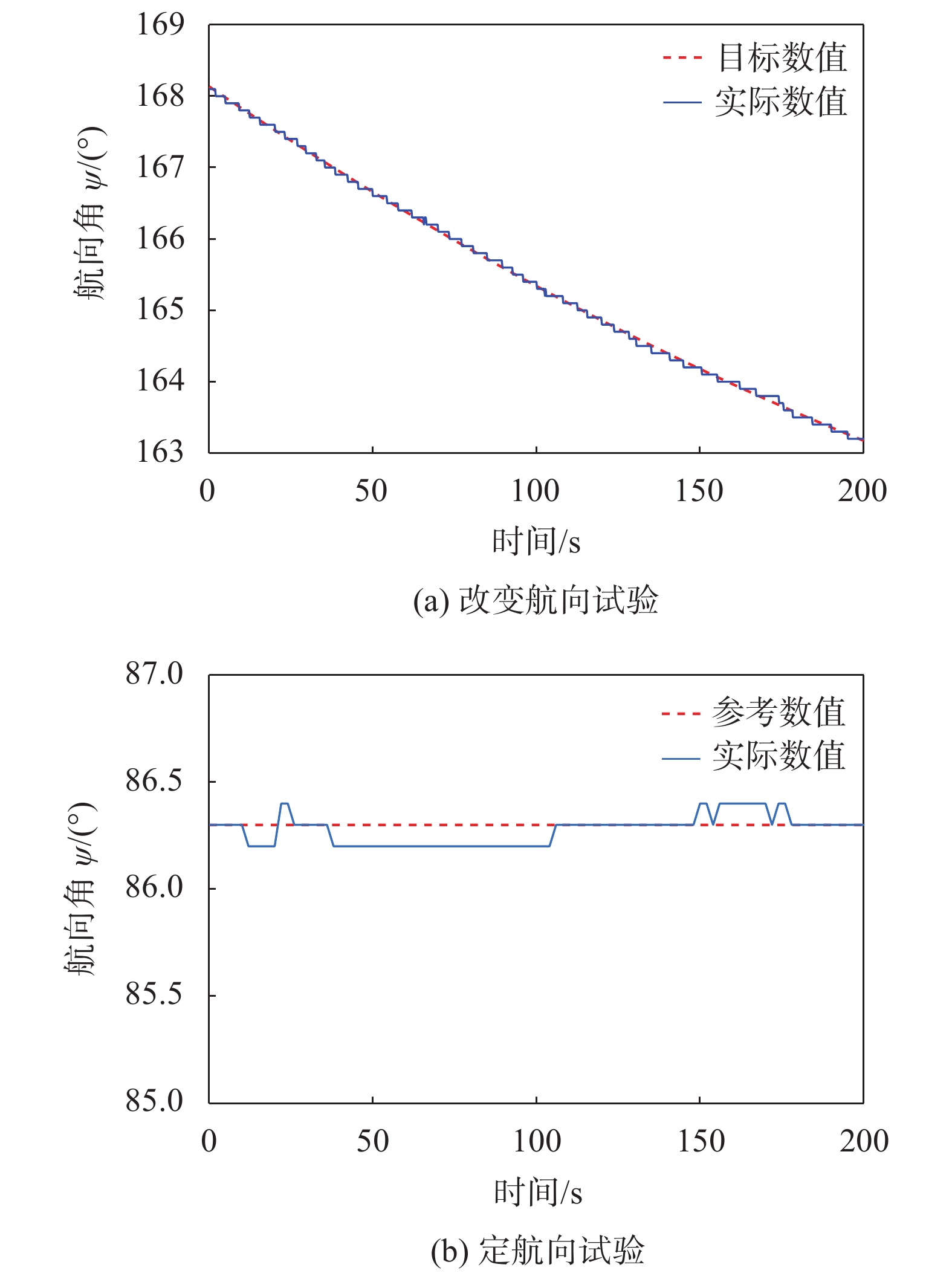
|
| 图 8 航向角控制试验结果 |
实际应用表明,针对水下无人平台姿态控制需求设计的模型参考自适应PID控制系统符合使用场景要求。平台能够根据给定的参考值快速调整运动姿态,系统稳定、响应快速,可满足平台搭载不同设备在复杂水域中的作业需求。
6 结束语针对水下无人平台姿态控制问题,运用了模型参考自适应PID控制,通过模型的仿真分析和实际试验操作验证了所提出控制策略的稳定性与可靠性。本文主要工作如下:
1)建立小型水下无人平台六自由度运动方程,通过分析设备水下受力情况,得到了水下无人平台动力学模型;
2)推导出适用于小型无人平台的模型参考自适应PID控制器参数变化调整律,控制器参数会按照所推导的规律进行动态调整,从而适应因工作环境发生变化以及搭载不同作业装备而导致的模型参数变化所引起的控制效果变差的问题。
3)运用Matlab/Simulink软件对所提出的控制算法进行仿真分析,得出了模型参考自适应PID控制策略在不同航向角的跟踪控制以及不同运动模型参数下的水下无人平台姿态控制均具有较好的控制效果。
4)在野外开放水域对无人平台进行了姿态控制测试。试验表明,所设计的模型参考自适应PID控制算法具有较强的适应性,在不同的水下情况下均可达到很好的控制效果,符合水下无人平台姿态控制的使用需求。本研究为水下平台快速准确部署、保持稳定姿态以及顺利开展水下的探测任务提供了可靠的技术保障。
| [1] |
吴伟, 曾庆军, 王阳, 等. 水下机器人多电机协同模糊滑模控制研究[J].
中国测试, 2021, 47(11): 101-106.
WU W, ZENG Q J, WANG Y, et al. Research on fuzzy sliding mode control of multi motor cooperative underwater robot[J].
China Measurement & Test, 2021, 47(11): 101-106.
|
| [2] |
任福深, 范玉坤. 基于小型两栖机器人横向定深控制研制[J].
电子测量技术, 2021, 44(9): 77-84.
REN F S, FAN Y K. Development of lateral depth control based on small amphibious robots[J].
Electronic Measurement Technology, 2021, 44(9): 77-84.
|
| [3] |
吴杰, 王志东, 凌宏杰, 等. 深海作业型带缆水下机器人关键技术综述[J].
江苏科技大学学报(自然科学版), 2020, 34(4): 1-12.
WU J, WANG Z D, LING H J, et al. A review of key technologies for deep-sea operation type cable underwater robots[J].
Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2020, 34(4): 1-12.
|
| [4] |
赵羿羽. 水下遥控机器人最新发展动向[J].
中国船检, 2020(8): 51-55.
ZHAO Y Y. The latest development trend of underwater remote-controlled robots[J].
China Ship Inspection, 2020(8): 51-55.
|
| [5] |
王永鼎, 王鹏, 孙鹏飞. 自主式水下机器人控制技术研究综述[J].
世界科技研究与发展, 2021, 43(6): 636-648.
WANG Y D, WANG P, SUN P F. A review of control technology for autonomous underwater robots[J].
World Science and Technology Research and Development, 2021, 43(6): 636-648.
|
| [6] |
YA X L, SHU X G, CHUN F Y. Preliminary concept of a novel spherical underwater robot[J].
International Journal of Mechatronics and Automation, 2015, 5(1): 11-21.
DOI:10.1504/IJMA.2015.068449 |
| [7] |
MI E V, MICHALIS M, SHU Z S G. An adaptive backstepping nonsingular fast terminal sliding mode control for robust fault tolerant control of robot manipulators[J].
IEEE Trans. Systems, Man, and Cybernetics: Systems, 2019, 49(7): 1-11.
DOI:10.1109/TSMC.2019.2917411 |
| [8] |
王鸿儒, 刘云平, 马金虎, 等. 基于奇异摄动法的水下机器人串-并联PID控制[J].
空间控制技术与应用, 2021, 47(3): 40-48.
WANG H R, LIU Y P, MA J H, et al. Series parallel PID control of underwater robots based on singular perturbation method[J].
Space Control Technology and Applications, 2021, 47(3): 40-48.
|
| [9] |
骆晓玲, 王子含. 基于模糊PID的水下航行器运动控制研究[J].
电子测量技术, 2020, 43(19): 53-56.
LUO X L, WANG Z H. Research on motion control of underwater vehicles based on fuzzy PID[J].
Electronic Measurement Technology, 2020, 43(19): 53-56.
|
| [10] |
NGUYEN Q H, EDWIN K. Adaptive PD-controller for positioning of a remotely operated vehicle close to an underwater structure: Theory and experiments[J].
Control Engineering Practice, 2006, 15(4): 411-419.
|
| [11] |
陈巍, 魏延辉, 曾建辉, 等. AUV纵倾角动态面滑模自适应控制[J].
火力与指挥控制, 2016, 41(6): 73-76.
CHEN W, WEI Y H, ZENG J H, et al. AUV pitch angle dynamic surface sliding mode adaptive control[J].
Firepower and Command Control, 2016, 41(6): 73-76.
|
| [12] |
付嘉忻. 基于PID控制的水下无人监测平台研制[D]. 北京: 北京林业大学, 2020.
|
| [13] |
张颖, 乔贵方, 王保升, 等. 基于优化位姿集的工业机器人运动学参数辨识方法研究[J].
中国测试, 2023, 49(3): 91-95.
ZHANG Y, QIAO G F, WANG B S, et al. Research on kinematics parameter identification method of industrial robot based on optimized pose set[J].
China Measurement & Test, 2023, 49(3): 91-95.
|
| [14] |
KABANOV A, KRAMAR V, ERMAKOV I. Design and modeling of an experimental ROV with six degrees of freedom[J].
Drones, 2021, 5: 113.
DOI:10.3390/drones5040113 |
| [15] |
王欢, 陈春俊, 杨露, 等. 模糊PID迭代学习气压模拟系统控制算法研究[J].
中国测试, 2021, 47(4): 77-82.
WANG H, CHEN C J, YANG L, et al. Research on control algorithm of air pressure simulation system based on fuzzy PID iterative learning[J].
China Measurement & Test, 2021, 47(4): 77-82.
|
 2024, Vol. 50
2024, Vol. 50