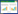文章信息
- 古亮, 蔡瑜, 陈新岗, 胡晓倩, 刘帮藩, 冯波
- GU Liang, CAI Yu, CHEN Xin’gang, HU Xiaoqian, LIU Bangfan, FENG Bo
- 基于小波能量熵的电磁式电压互感器绕组故障检测
- Interlayer insulation fault detection of electromagnetic voltage transformer winding based on wavelet energy entropy
- 中国测试, 2024, 50(7): 99-106
- CHINA MEASUREMENT & TEST, 2024, 50(7): 99-106
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022070131
-
文章历史
- 收稿日期: 2022-07-21
- 收到修改稿日期: 2022-09-18
2. 重庆市能源互联网工程技术研究中心,重庆 400054
2. Chongqing Energy Internet Engineering Technology Research Center, Chongqing 400054, China
电压互感器在电力系统中用于电压测控、电能计量和二次设备的保护,主要包含电磁式、电容式和电子式电压互感器三大类[1-3]。而电磁式电压互感器作为传统的电压互感器类型在电力系统中仍有大量应用。近年来,电压互感器的绕组绝缘故障多发,文献[4]介绍了一起电磁式电压互感器一次绕组放电故障引起母线停运的案例。若电压互感器在生产过程中绕组层间绝缘有皱褶或环氧树脂浇注有气泡,就容易导致绕组层间出现放电或短路故障[5]。因此,研究电磁式电压互感器绕组层间绝缘故障对保证电网安全运行具有实际工程意义。
目前,国内外学者针对绕组绝缘故障检测已展开大量研究工作。文献[6]以不同幅值雷电波对应电压、电流的广义相关系数作为判据,通过构建的非线性判别函数的数值大小进行故障判断,对绕组潜在的缺陷有较好的识别。文献[7]对绕组阻抗进行测量,将阻抗幅值和角度的变化作为特征参量,对绕组早期故障的诊断可靠性高,但在绕组电阻较小时误差较大。文献[8]使用直流高压对绕组进行激励,利用绕组末端电压振荡波的相关系数和欧几里德距离进行故障检测,与传统频率响应法相比,提高了绕组中部短路故障的灵敏度。文献[9]利用学习矢量量化(LVQ)网络对绕组短路故障进行诊断,以不同频段下电压的传递函数作为特征参数对LVQ网络进行训练,其训练后的LVQ网络故障诊断准确率达98%。文献[10]以故障绕组等效励磁电感的小波系数为特征参数,并采用C4.5算法进行数据分类和训练,对绕组轻微故障的检测率达96.67%。
综上,目前许多方法使用相关系数作为故障判据或采用数据分类和训练的方法进行故障检测,都需要较多的实验样本以消除数据的波动性,在样本数据较少时可能存在较大误差。本文针对上述问题提出基于电磁式电压互感器冲击响应电压小波能量熵的故障诊断方法。采用波形光滑的高压脉冲波对电压互感器进行冲击实验,正常情况和故障情况下原边的电压信号在高频段将出现差异。然后利用离散小波分解和重构消除噪声干扰,将冲击响应电压信号的小波能量熵作为特征参量,对绕组层间绝缘故障及类型进行诊断。
1 电磁式电压互感器高压绕组电路模型在工作原理上电磁式电压互感器与变压器相同,但结构上电压互感器的高压侧绕组细、匝数多,层数多、层间距离小。电压互感器运行过程中应考虑分布参数的影响,主要包括匝间电容、层间电容、对地电容等。针对

|
| 图 1 电磁式电压互感器高压绕组高频等值电路 |
其中,绕组自感
设电压互感器绕组绝缘层的介电常数为
| $ {C_{{\text{s}}ij}} = \frac{{2{\text{π}}\varepsilon {r_i}a}}{d} $ | (1) |
式中,
正常情况绕组每层电压分布均匀,对地电容为
| $ {C_{{\text{g}}ij}} = \frac{{2{\text{π}}\varepsilon a}}{d}\alpha $ | (2) |
| $ \alpha = \frac{{{r_i}}}{{{r_{{\text{Fe}}}}}} $ | (3) |
式中,
各层绕组之间的层间电容为
| $ C_{\text{p}ij}=\frac{1}{\left|j-i\right|}\frac{2\text{π}\varepsilon}{\ln\alpha},i\ne j;i,j\in[1,N] $ | (4) |
当绕组层间出现故障时,绕组的等效参数将会出现明显变化,使冲击响应在高频部分出现较大的差异[12]。因此,冲击响应电压信号的高频部分变化情况能在一定程度上反映绕组层间绝缘状态。
2 基于小波能量熵的故障特征量提取 2.1 小波变换小波变换能在时间和尺度上对信号进行变换,可以同时在时间和频率上反映信号的突变,适合分析正常信号中的反常突变,目前在故障检测领域被广泛使用[13-14]。
小波变换主要包括连续小波变换和离散小波变换。连续小波变换在分析数字信号时需要进行连续积分,运算复杂,在实际应用问题中常采用离散小波变换(DWT)[15],以消除和降低系数的冗余性。
对于函数
| $ {\int_{{\bf R}} {\left| {f(t)} \right|} ^2}{\text{d}}t < \infty $ | (5) |
如果
| $ {C_\psi } = {\int_{ - \infty }^{ + \infty } {\left| \omega \right|} ^{ - 1}}{\left| {\widehat \psi (\omega )} \right|^2}{\text{d}}\omega < \infty $ | (6) |
则称
| $ {\psi _{a,b}}(t) = {\left| a \right|^{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. } 2}}}\psi \left(\frac{{x - b}}{a}\right) $ | (7) |
离散小波变换需对伸缩因子
| $ {W_f}(j,k) = a_0^{ - \frac{j}{2}}\int_{ - \infty }^{ + \infty } {f(t)\overline {\psi (a_0^{ - j}t - k)} } {\text{d}}t $ | (8) |
熵能够反映物质的能量退化程度,本文对电压信号进行处理,可以表征冲击响应信号在离散小波分析下各个分量的小波能量变化程度[16]。
先对信号
| $ x(n) = {A_m}(n) + {D_m}(n) + {D_{m - 1}}(n) + \cdot \cdot \cdot + {D_1}(n) $ | (9) |
| $ x(n) = {A_m}(n) + \sum\limits_{i = 1}^m {{D_i}} (n) $ | (10) |
近似分量的小波能量定义为
| $ {E_{\text{a}}} = \sum\limits_{i = 1}^L {c{A_m}} {(i)^2} $ | (11) |
式中,
细节分量的小波能量定义为
| $ {E_{\text{d}}} = \sum\limits_{j = 1}^m {{E_{{{\text{d}}_j}}}} $ | (12) |
| $ {E_{{{\text{d}}_j}}} = \sum\limits_{k = 1}^{{L_{j}}} {c{D_j}} {(k)^2} $ | (13) |
式中,
信号的小波能量总和为
| $ E = {E_1} + {E_2} + {E_3} + \cdot \cdot \cdot + {E_{m + 1}} = {E_{\text{a}}} + {E_{\text{d}}} $ | (14) |
设
| $ S = \sum\limits_j {{{\lg }}} {p_j} $ | (15) |
本文将电压信号作为研究对象,首先采集电压互感器高压绕组冲击响应电压信号;其次,对电压信号进行离散小波分解,采用

|
| 图 2 故障检测流程图 |
3 电磁式电压互感器故障检测平台 3.1 实验原理与实验平台
实验原理如图3所示,实验电路由高压脉冲电路、电压互感器模型和测量装置构成,实验设备信息如表1所示。
|
| 图 3 实验原理图 |
| 设备 | 型号 | 厂家 | 主要参数 |
| 高压分压器 | FRC-50 | 豪泰电力 | 精度0.5% |
| 调压器 | TDGC2 | 华悦电器 | 调压范围0~250 V |
| 升压变压器 | GY-001 | 上海美星 | 变比220 V/3 kV |
| 示波器 | TO1102 | 麦科信 | 采样率250 MS/s |
实验电压互感器副边空载,高压脉冲电路产生高压脉冲对原边绕组进行冲击实验,示波器经分压器记录正常绕组和故障绕组的冲击响应电压波形。
其中,高压脉冲的产生由晶闸管控制,相比传统火花间隙高压脉冲电源,该电路输出的高压脉冲波形光滑可调,波形上升沿和下降沿可分别由波头电阻R2和波尾电阻R3的阻值进行调节。
实验平台实物如图4所示。

|
| 图 4 电压互感器故障检测平台 |
3.2 电压互感器故障模型
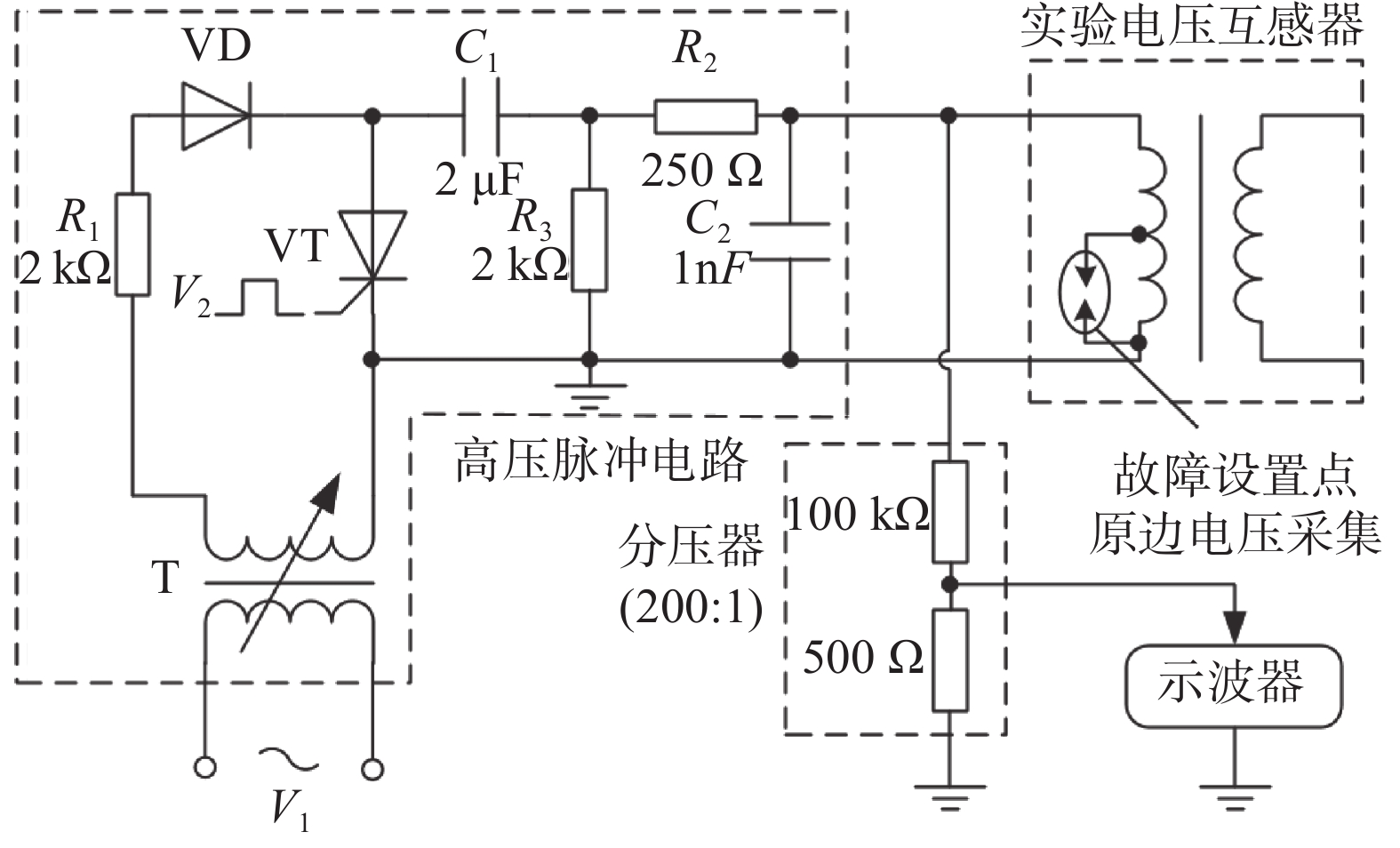
实验电压互感器高压绕组结构和抽头如图5所示。其中
|
| 图 5 高压绕组抽头示意图 |
绕制的实验电压互感器参数如表2所示。
电压互感器绕组层间故障模拟设置如表3所示,包括绕组层间放电故障和短路故障。针对层间放电故障,为使故障模拟可重复,采用短空气间隙模拟绕组在环氧树脂和绝缘纸之间的真实放电故障,通过调节间隙距离,整定放电电压值,放电电压范围为1~1.5 kV。针对短路故障,对间隙两电极进行短路连接。
4 故障诊断实验结果分析
首先对正常绕组进行不同电压等级下的冲击响应实验,然后对实验电压互感器设置不同部位的放电故障和短路故障,进行不同故障类型和故障程度的绕组层间故障模拟。
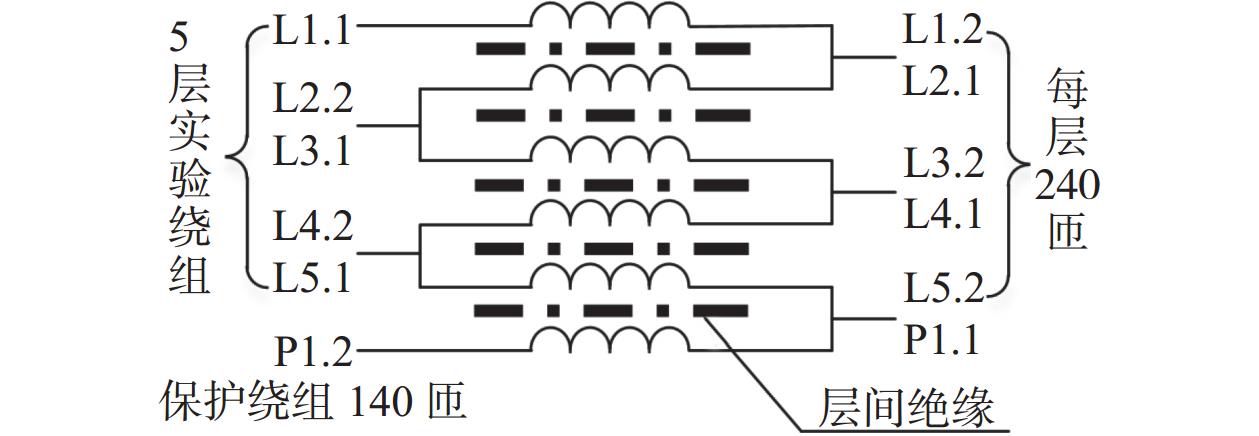
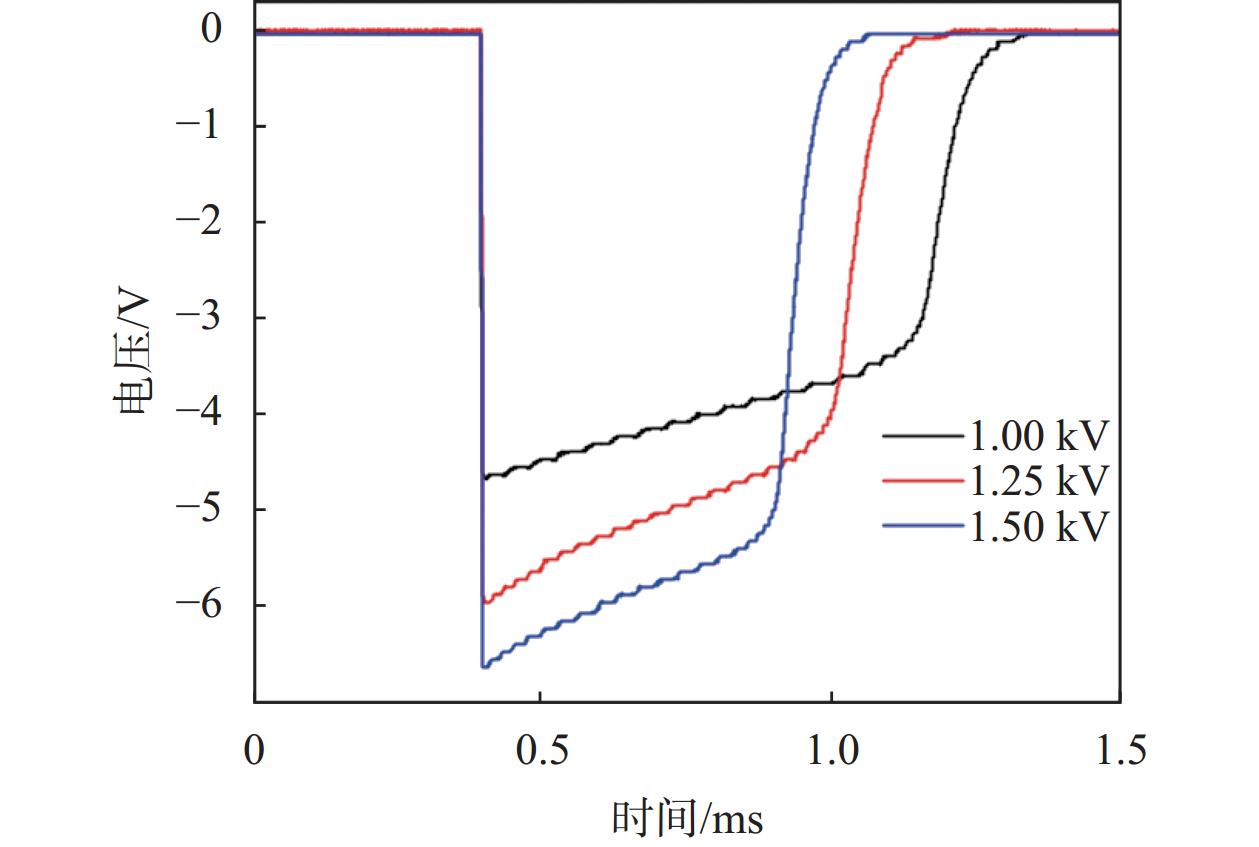
正常绕组冲击响应电压波形如图6所示,将其作为故障绕组冲击响应的对比标准。
|
| 图 6 正常绕组电压波形 |
4.1 绕组层间放电故障结果分析
如图7~图9是在三个电压等级下,不同绕组放电故障的冲击响应电压曲线,可以看到不同绕组放电故障电压曲线在放电时刻均有明显畸变。
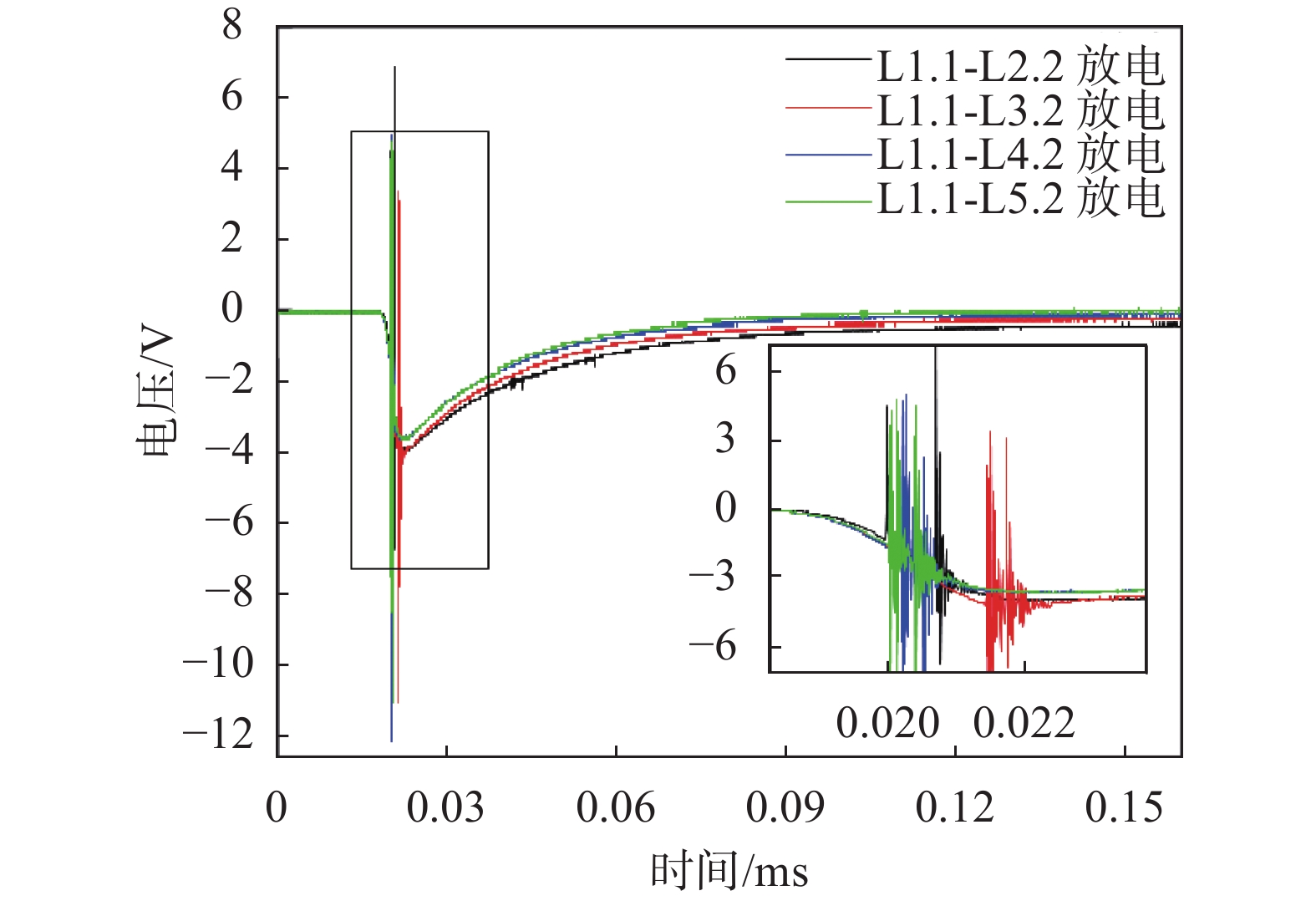
|
| 图 7 1.0 kV绕组层间放电故障电压波形 |
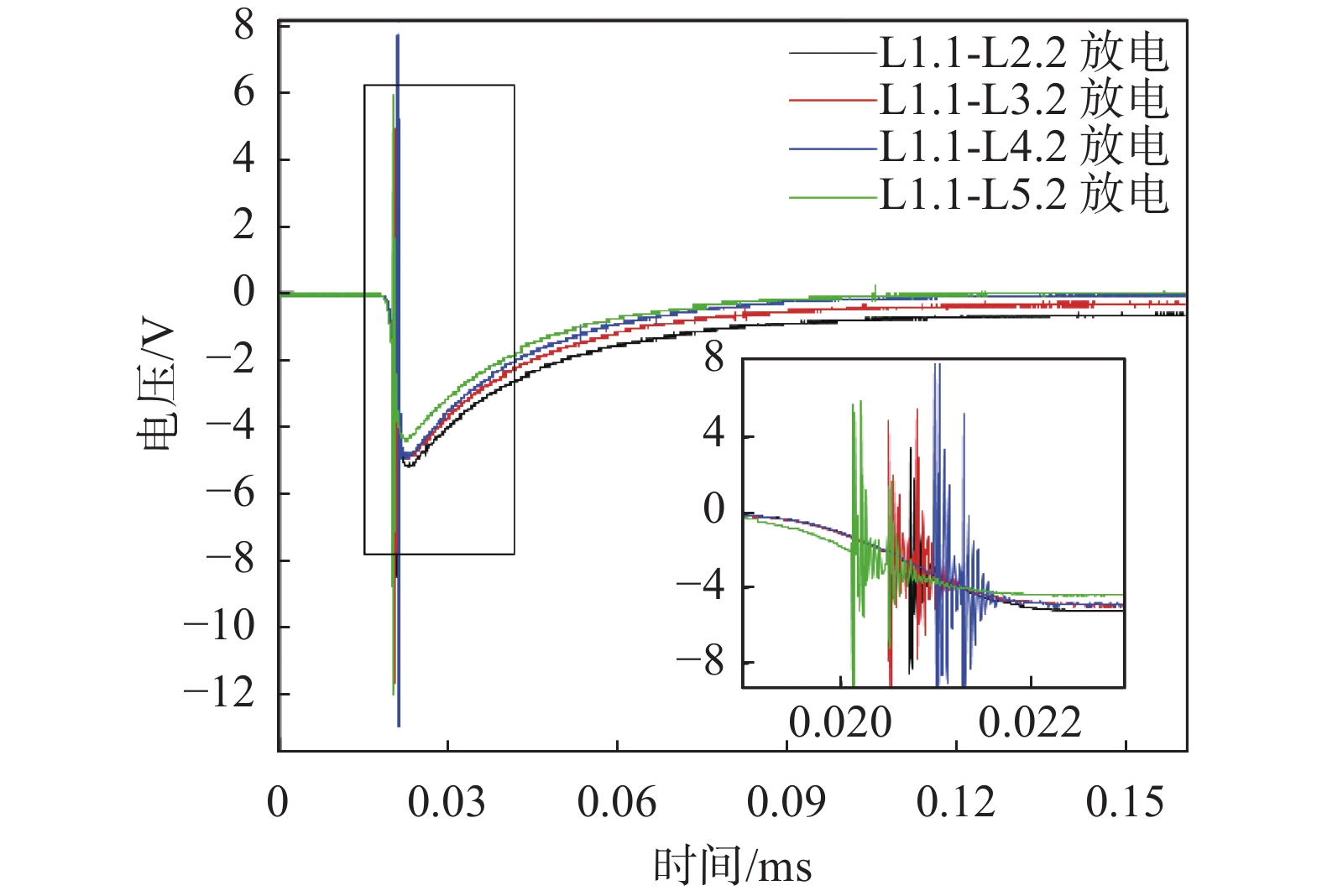
|
| 图 8 1.25 kV绕组层间放电故障电压波形 |
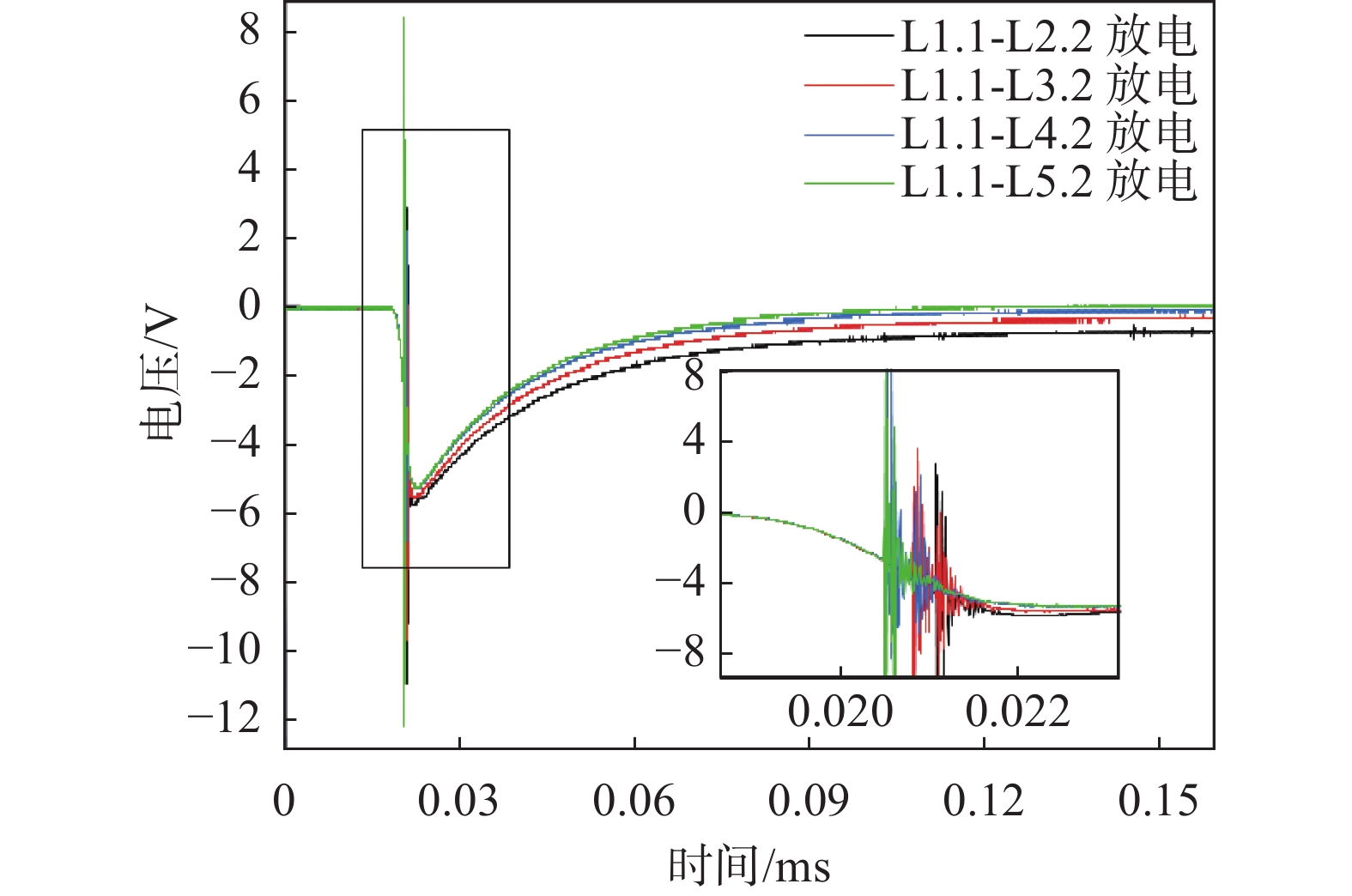
|
| 图 9 1.5 kV绕组层间放电故障电压波形 |
在三个电压等级下,随着故障严重程度的增加(
还可以看到放电故障波形的脉宽对比正常绕组的脉宽严重变窄,且随着故障严重程度的增加,波形脉宽逐渐减小。其原因是放电故障使绕组相比正常情况等效电容严重下降,维持电压的能力降低,故障越严重绕组的等效电容越小,当冲击电压到达峰值时就会快速的衰减,导致电压脉宽逐渐变窄。
对三个电压等级下的不同绕组层间放电故障电压采用sym4小波进行4层离散小波分解求得小波系数,最后计算出冲击响应电压波形近似分量的小波能量Ea和细节分量的小波能量Ed4、Ed3、Ed2、Ed1如表4~表6所示。
| 放电部位 | 小波能量 | ||||
| Ea | Ed4 | Ed3 | Ed2 | Ed1 | |
| 正常绕组 | 99.9956 | 0.0023 | 0.0012 | 0.0006 | 0.0003 |
| L1.1-L2.2 | 99.0912 | 0.4319 | 0.3489 | 0.0978 | 0.0301 |
| L1.1-L3.2 | 98.4012 | 0.8566 | 0.5996 | 0.1184 | 0.0242 |
| L1.1-L4.2 | 97.8828 | 0.9814 | 0.8596 | 0.2485 | 0.0276 |
| L1.1-L5.2 | 97.6746 | 1.4550 | 0.6658 | 0.1656 | 0.0389 |
| 放电部位 | 小波能量 | ||||
| Ea | Ed4 | Ed3 | Ed2 | Ed1 | |
| 正常绕组 | 99.9946 | 0.0029 | 0.0014 | 0.0007 | 0.0004 |
| L1.1-L2.2 | 99.6578 | 0.1802 | 0.1310 | 0.0262 | 0.0047 |
| L1.1-L3.2 | 98.9643 | 0.6492 | 0.2877 | 0.0731 | 0.0257 |
| L1.1-L4.2 | 98.4132 | 0.6842 | 0.7528 | 0.0837 | 0.0661 |
| L1.1-L5.2 | 97.9989 | 1.1821 | 0.6187 | 0.1692 | 0.0311 |
| 放电部位 | 小波能量 | ||||
| Ea | Ed4 | Ed3 | Ed2 | Ed1 | |
| 正常绕组 | 99.9979 | 0.0011 | 0.0005 | 0.0003 | 0.0002 |
| L1.1-L2.2 | 99.4324 | 0.2806 | 0.1931 | 0.0889 | 0.0050 |
| L1.1-L3.2 | 99.3685 | 0.3307 | 0.2238 | 0.0692 | 0.0079 |
| L1.1-L4.2 | 99.3315 | 0.2371 | 0.3623 | 0.0467 | 0.0224 |
| L1.1-L5.2 | 98.7637 | 0.7692 | 0.3251 | 0.1080 | 0.0340 |
可以看出每个电压等级下Ed4至Ed1依次降低,且Ed4在细节分量中占比最大,是反映细节分量能量分布的主要部分。放电故障的小波能量相比正常情况增加明显,其原因是绕组放电产生的波形畸变导致电压信号细节分量剧烈增加。
计算不同电压等级下放电故障冲击响应电压波形的小波能量熵如图10所示,正常绕组的小波能量熵值均较小,说明波形小波能量分布比较均匀,而放电故障的小波能量熵值明显大于正常绕组,说明放电故障引起的波形畸变使电压波形小波能量分布混乱。在各个电压等级下,随着故障严重程度的增加,小波能量熵值均逐渐增大,说明故障越严重,绕组等效参数变化越大,对电压波形的小波能量分布影响更强。
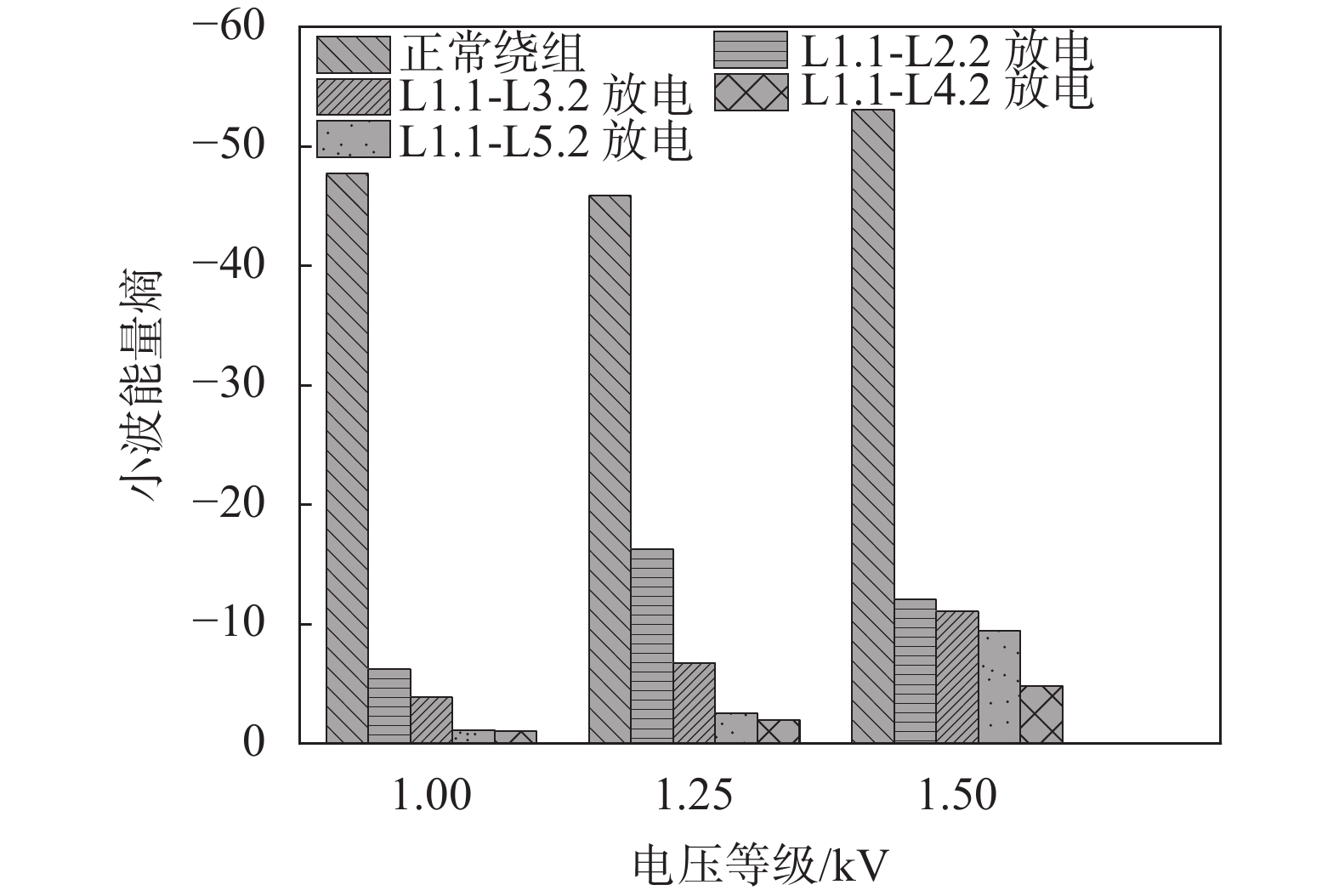
|
| 图 10 绕组层间放电故障小波能量熵 |
在1 kV、1.25 kV和1.5 kV电压下正常绕组与放电故障绕组的小波能量熵平均区分度为92.6%、84.6%和82.2%,总体平均区分度为86.5%,可见小波能量熵能够明显地区分绕组层间放电故障。
由实验电压互感器抽头结构可知,L1.1-L2.2放电等效于放电故障发生在最外层,远离铁芯,而L1.1-L5.2放电等效于放电故障发生在最里层,靠近铁芯。由图10可知,越远离铁芯的放电故障小波能量熵越小,越靠近铁芯的放电故障小波能量熵越大,其原因是越靠近铁芯发生故障,绕组的等效电气结构变化越大,电压信号的高频部分改变越大。所以,小波能量熵能够较好地反映放电故障发生的位置。
4.2 绕组层间短路故障结果分析如图11~图13是三个电压等级下不同绕组层间短路故障的冲击电压响应曲线。可以看到随着短路故障严重程度的增加,电压波形幅值逐渐降低,其原因是短路绕组匝数增加,短路绕组中储存的未释的放电压增加,导致电压幅值逐渐降低。随着故障严重程度的增加,波形脉宽逐渐减小,其原因是短路故障使得绕组等效电容减小,稳定电压的能力逐渐下降。
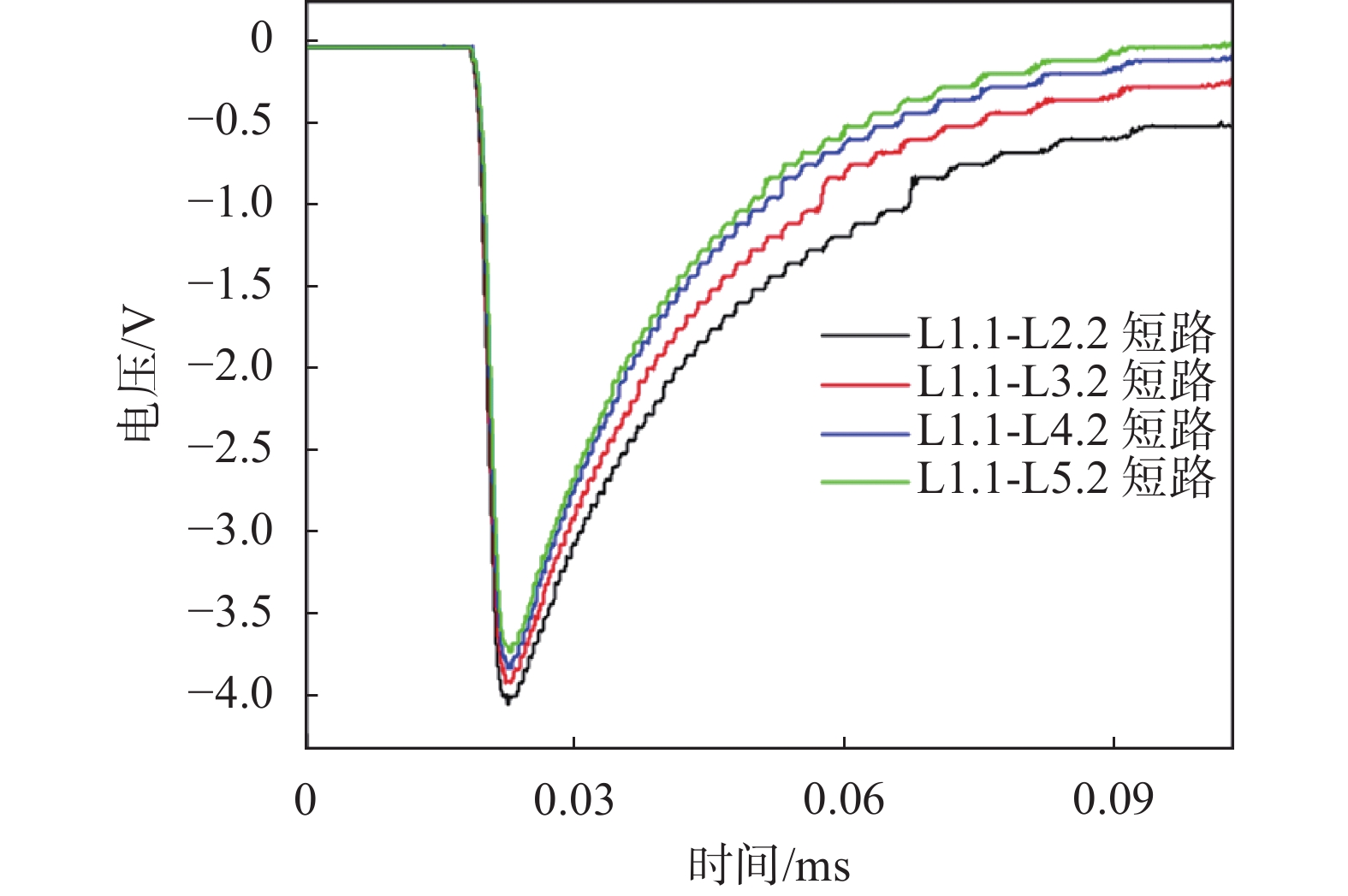
|
| 图 11 1.0 kV绕组层间短路故障电压波形 |

|
| 图 12 1.25 kV绕组层间短路故障电压波形 |
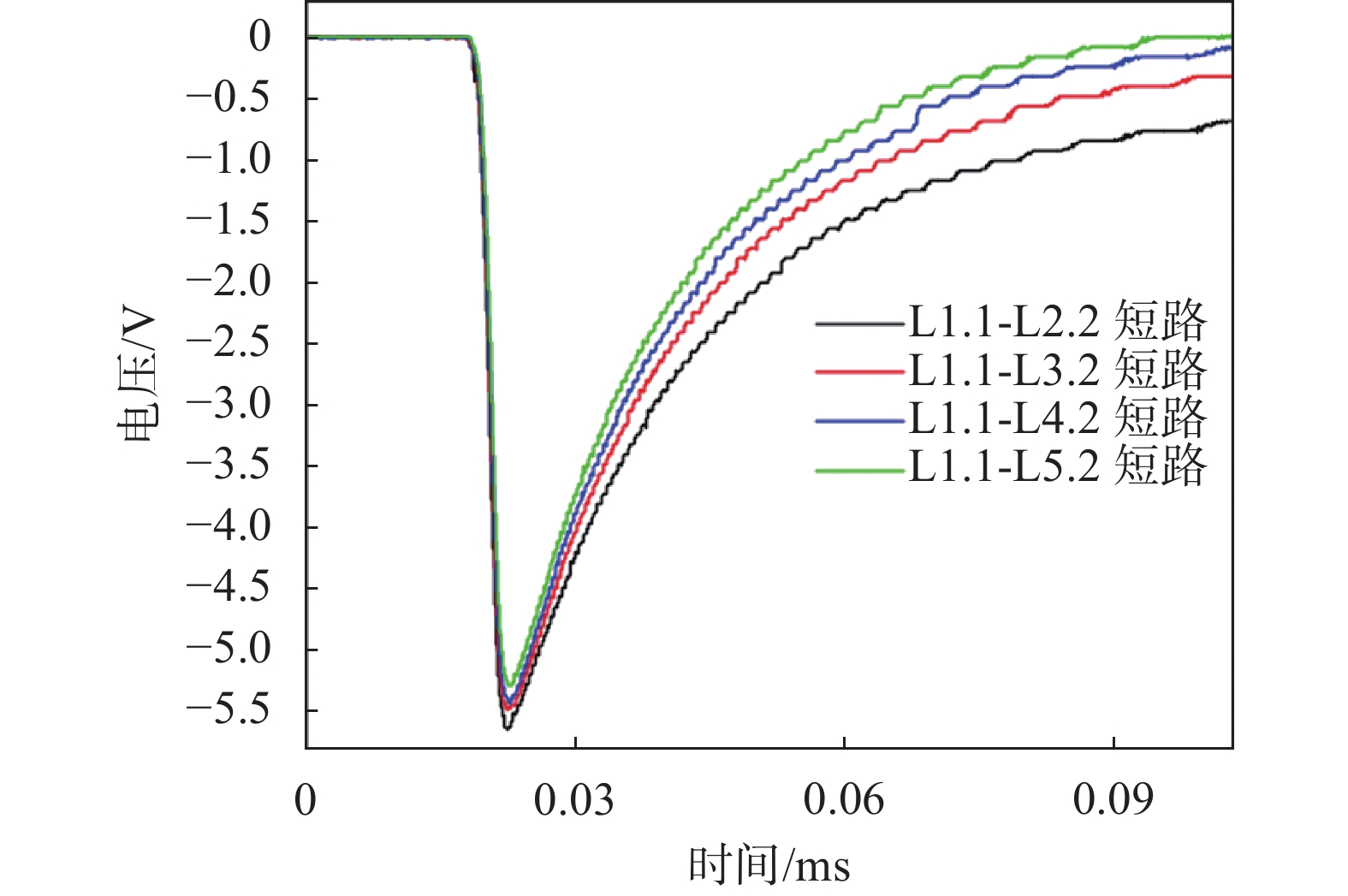
|
| 图 13 1.5 kV绕组层间短路故障电压波形 |
绕组层间短路故障的数据处理与层间放电故障一致,对三个电压等级下的层间短路故障冲击响应电压进行离散小波分解求得小波系数,最后计算出冲击响应电压波形近似分量的小波能量Ea和细节分量的小波能量Ed4、Ed3、Ed2、Ed1如表7~表9所示。
| 短路部位 | 小波能量 | ||||
| Ea | Ed4 | Ed3 | Ed2 | Ed1 | |
| 正常绕组 | 99.9956 | 0.0023 | 0.0012 | 0.0006 | 0.0003 |
| L1.1-L2.2 | 99.9808 | 0.0099 | 0.0053 | 0.0028 | 0.0013 |
| L1.1-L3.2 | 99.9730 | 0.0139 | 0.0071 | 0.0042 | 0.0019 |
| L1.1-L4.2 | 99.9692 | 0.0163 | 0.0081 | 0.0042 | 0.0022 |
| L1.1-L5.2 | 99.9678 | 0.0168 | 0.0086 | 0.0044 | 0.0024 |
| 短路部位 | 小波能量 | ||||
| Ea | Ed4 | Ed3 | Ed2 | Ed1 | |
| 正常绕组 | 99.9946 | 0.0029 | 0.0014 | 0.0007 | 0.0004 |
| L1.1-L2.2 | 99.9793 | 0.0108 | 0.0057 | 0.0028 | 0.0015 |
| L1.1-L3.2 | 99.9814 | 0.0097 | 0.0049 | 0.0023 | 0.0018 |
| L1.1-L4.2 | 99.9782 | 0.0117 | 0.0054 | 0.0031 | 0.0015 |
| L1.1-L5.2 | 99.9746 | 0.0134 | 0.0069 | 0.0033 | 0.0018 |
| 短路部位 | 小波能量 | ||||
| Ea | Ed4 | Ed3 | Ed2 | Ed1 | |
| 正常绕组 | 99.9979 | 0.0011 | 0.0005 | 0.0003 | 0.0002 |
| L1.1-L2.2 | 99.9872 | 0.0068 | 0.0031 | 0.0018 | 0.0010 |
| L1.1-L3.2 | 99.9865 | 0.0074 | 0.0033 | 0.0017 | 0.0010 |
| L1.1-L4.2 | 99.9836 | 0.0089 | 0.0041 | 0.0023 | 0.0011 |
| L1.1-L5.2 | 99.9806 | 0.0098 | 0.0056 | 0.0026 | 0.0015 |
可以看出,层间短路故障细节分量的小波能量与正常绕组有明显差距,总体分布规律和变化规律与层间放电故障一致,但其各个细节分量的小波能量均远低于放电故障,其原因是短路故障相比放电故障绕组的等效参数变化更稳定,对冲击响应高频部分影响较小,所以电压波形的细节分量变化相对较小。
计算不同电压等级下短路故障冲击响应电压波形的小波能量熵如图14所示,不同电压等级下短路故障的小波能量熵值与正常绕组有明显差异,但其差距普遍不如放电故障明显。在每个电压等级中随着故障严重程度的增加,小波能量熵值基本也随之增大,说明短路故障越严重,冲击响应电压的小波能量分布越混乱。

|
| 图 14 绕组层间短路故障小波能量熵 |
在1 kV、1.25 kV和1.5 kV电压下正常绕组与短路故障绕组的小波能量熵平均区分度为30.7%、24.7%和29.6%,总体平均区分度为28.3%,可见小波能量熵能够较好地区分绕组层间短路故障。
绕组层间短路故障的小波能量熵与放电故障变化趋势一致,随着故障位置远离铁芯,小波能量熵逐渐减小,反之,小波能量熵越大。所以,小波能量熵也能反映短路故障发生的位置,但在程度上不如放电故障那样明显。
5 结束语本文对电磁式电压互感器常见的绕组层间绝缘故障进行了模拟,采用高压脉冲波对实验电压互感器进行冲击实验,对正常绕组和故障绕组的电压波形进行特性分析,提出了基于小波能量熵的电压互感器绕组层间绝缘故障检测方法。实验较好地验证了该方法的有效性并得出以下结论:
1)绕组层间放电故障相比短路故障对绕组的电气结构影响更大,波形畸变更明显,小波能量分布更混乱。
2)绕组层间放电故障和短路故障的小波能量熵值与正常绕组小波能量熵的区分度分别为86.5%和28.3%,小波能量熵值能有效区分绕组的正常状态和故障状态。
3)同等电压、相同绕组放电故障比短路故障的小波能量熵值大,小波能量熵值能有效区分绕组层间绝缘故障类型。
4)小波能量熵能在一定程度上反映故障的位置,故障点离铁芯越近,小波能量熵越大,反之,越小。
| [1] |
姜春阳, 刘俭, 王雪, 等. 电磁式电压互感器谐波误差测量方法研究[J].
中国测试, 2021, 47(3): 163-168.
JIANG C Y, LIU J, WANG X, et al. Research on test method of harmonic measurement error of inductive voltage transformer[J].
China Measurement & Test, 2021, 47(3): 163-168.
|
| [2] |
赵鹏, 马克琪, 李红斌, 等. 计及一次电压波动的电压互感器误差状态在线评估方法[J].
高电压技术, 2022, 352(3): 1042-1051.
ZHAO P, MA K Q, LI H B, et al. On-line error evaluation method of instrument voltage transformers considering primary voltage fluctuations[J].
High Voltage Engineering, 2022, 352(3): 1042-1051.
|
| [3] |
刘俭, 姜春阳, 殷小东, 等. 谐波电压互感器宽频特性试验研究[J].
中国测试, 2021, 47(8): 130-136.
LIU J, JIANG C Y, YIN X D, et al. Study on frequency characteristics of harmonic voltage transformer[J].
China Measurement & Test, 2021, 47(8): 130-136.
|
| [4] |
何帅, 赵雨濛, 邰晨凡, 等. 一起半绝缘电压互感器故障原因分析及处理措施[J].
宁夏电力, 2020(3): 67-70.
HE S, ZHAO Y M, TAI C F, et al. Analysis and treatment of a fault of semi-insulated voltage transformer[J].
Ningxia Electric Power, 2020(3): 67-70.
DOI:10.3969/j.issn.1672-3643.2020.03.014 |
| [5] |
李良书, 韩彦华, 李晋, 等. 电容式电压互感器典型故障案例分析[J].
变压器, 2020, 57(9): 72-76.
LI L S, HAN Y S, LI J, et al. Typical fault case analysis of capacitor voltage transformer[J].
Transformer, 2020, 57(9): 72-76.
|
| [6] |
刘亮, 蒋鑫, 师普辛, 等. 发电机出口电压互感器绝缘缺陷检测方法[J].
电网技术, 2016, 40(12): 3966-3972.
LIU L, JIANG X, SHI P X, et al. A Novel methodology for insulation defect detection in voltage transformer in generator circuit[J].
Power System Technology, 2016, 40(12): 3966-3972.
|
| [7] |
HEWITT D A, HU R G, WANG J B. Early detection of turn-to-turn winding faults using a PWM ripple current based method[C]// IEEE The 10th International Conference on Power Electronics, 2020.
|
| [8] |
吴振宇, 周利军, 周祥宇, 等. 基于振荡波的变压器绕组故障诊断方法研究[J].
中国电机工程学报, 2020, 40(1): 348-357+401.
WU Z Y, ZHOU L J, ZHOU X Y, et al. Research on fault diagnosis method of transformer winding based on oscillatory wave[J].
Proceedings of the CSEE, 2020, 40(1): 348-357+401.
|
| [9] |
普子恒, 张宇娇, 方春华, 等. 雷电冲击下换流变压器绕组故障模拟与诊断方法[J].
中国电机工程学报, 2017, 37(5): 1552-1560.
PU Z H, ZHANG Y J, FANG C H, et al. Fault simulations and diagnosis methods of converter transformer windings under lightning impulse voltages[J].
Proceedings of the CSEE, 2017, 37(5): 1552-1560.
|
| [10] |
尹璇, 邓祥力, 游及第. 基于MODWT的变压器绕组轻微故障检测及分类研究[J].
电测与仪表, 2019, 56(14): 103-109.
YIN X, DENG X L, YOU J D, et al. Study on the detection and classification transformer winding slight fault based on MODWT[J].
Electrical Measurement & Instrumentation, 2019, 56(14): 103-109.
|
| [11] |
FAIFER M, LAURANO C, OTTOBOBI R, et al. Nonlinear behavioral modeling of voltage transformers in the frequency domain: comparing different approaches[J].
IEEE Transactions on Instrumentation and Measurement, 2020, 69(10): 8137-8145.
|
| [12] |
郭成, 叶壮, 孟贤, 等. 电容式电压互感器电路参数对暂态误差影响研究[J].
高压电器, 2021, 57(12): 131-139.
GUO C, YE Z, MENG X, et al. Study on influence of circuit parameters of capacitor voltage transformer on transient error[J].
High Voltage Apparatus, 2021, 57(12): 131-139.
|
| [13] |
张立石, 梁得亮, 刘桦, 等. 基于小波变换与逻辑斯蒂回归的混合式配电变压器故障辨识[J].
电工技术学报, 2021, 36(S2): 467-476.
ZHANG L S, LIANG D L, LIU H, et al. Fault identification of hybrid distribution transformer based on wavelet transform and logistic regression[J].
Transactions of China Electrotechnical Society, 2021, 36(S2): 467-476.
|
| [14] |
范国栋,李博涵.基于机器学习的工业机械设备故障预测方法[J].自动化与信息工程,2023,44(4):13-18.
FAN G D, LI B H. Fault prediction method of industrial machinery equipment based on machine learning[J]. Automation & Information Engineering, 2023,44(4):13-18.
|
| [15] |
刘红文, 王科, 林桐, 等. 基于离散小波的变压器绕组振荡波故障检测方法[J].
变压器, 2020, 57(1): 58-62.
LIU H W, WANG K, LIN T, et al. Detection method of transformer winding oscillation wave fault based on discrete wavelet transform[J].
Transformer, 2020, 57(1): 58-62.
|
| [16] |
DENG Y J, LIN S, FU L, et al. New criterion of converter transformer differential protection based on wavelet energy entropy[J].
IEEE Transactions on Power Delivery, 2019, 34(3): 980-990.
DOI:10.1109/TPWRD.2019.2893431 |
 2024, Vol. 50
2024, Vol. 50