0 引　言

近年来，随着我国城市轨道交通的快速发展，地铁因其方便、高效、安全等特点，已成为日运载量最大的城轨交通工具^[1]。尽管地铁系统为人们的出行提供了方便，但是其室内存在空气污染的问题，尤其是可吸入颗粒物（PM_2.5 ）严重影响通勤者和地铁工作人员的身体健康^[2]。因此，精准预测PM_2.5 浓度对于开发预警系统和调节通风系统以确保通勤者和地铁工作人员的健康具有重要的指导意义^[3]。

目前，虽然地铁环境监控系统能够监测PM_2.5 浓度的变化，但依然存在监控系统高成本、高功耗和低效率的问题^[4]。为了提高地铁站PM_2.5 监测的有效性和准确性，降低监测成本，有必要建立更合理的预测模型。目前用于时间预测的模型有人工神经网络（ANN）、支持向量回归（SVR）、自回归综合移动平均（ARIMA）和随机森林回归（RFR）等。Nouri等^[5]利用人工神经网络和主成分分析法来预测PM_2.5 的浓度，虽然利用了PM_2.5 的空间特征，但并未考虑PM_2.5 在时间和空间上依赖性，导致预测精度较低；Li等^[6]使用支持向量机回归（SVR）预测PM_2.5 。然而，由于PM_2.5 数据的不稳定特性，SVR很难达到高拟合度。刘拥民等^[7]使用XGBoost-ARIMA混合模型对城市中PM_2.5 浓度进行预测，但无法处理环境数据中随机不确定性，因此预测精度较低。Feng等^[8]结合随机森林回归（RFR）和RNN来分析和预测未来24 h的PM_2.5 ，但对于非线性PM_2.5 的预测，RFR存在过拟合的风险。由于地铁站室内空气环境的动态性质，递归神经网络（RNN）合适模拟PM_2.5 的时间演变，因为RNN可以处理任意输入序列，从而保证学习时间序列的能力^[9-10]。然而，当传统RNN存在长时间滞后时，它可能会遇到“梯度消失”和“梯度爆炸”等问题，这些基于RNN的方法也没有充分利用空间特征^[11-12]。此外，不同时间特征形成的状态也会对未来的PM_2.5 浓度产生不同的影响^[13]。LSTM的出现可以缓解RNN训练过程中的“梯度消失”和“梯度爆炸”问题。白盛楠 等^[14]使用LSTM预测空气污染物的变化，由于预测模型单一，对特征值的提取不够充分，难以实现高精度预测。赵彦明等^[15]提出基于时空相关性LSTM的PM_2.5 预测，但LSTM无法提取环境数据不同时间状态下的特征值，预测精度较低。现有的研究没有考虑过去不同时间的特征状态对地铁站内污染物的影响，而只提取了历史数据的时间相关特征，导致预测精度较低。

为了解决上述问题，本文提出了一种基于注意力机制（attention）的卷积神经网络(CNN)和改进长短期记忆(ILSTM)模型组合的CNN-ILSTM-attention混合神经网络模型，用于预测地铁站室内PM_2.5 的浓度。所提出的CNN-ILSTM-attention模型包括一维卷积神经网络(CNN)、改进长短期记忆(ILSTM)网络和注意力机制网络。为了克服传统RNN的“梯度消失”和“梯度爆炸”以及LSTM捕捉污染物相关时间序列数据的时空相关性和相互依赖性不充分的问题，对LSTM网络进行改进，删除了LSTM中的输出门，改进了LSTM中输入门和遗忘门，并引入CIM来防止学习过程中的过饱和现象。同时，结合一维CNN的目的是从地铁站室内空气中提取时空特征及局部空间相关性特征。注意力机制在预测模型中对过去的特征状态进行加权，以提高预测精度。因此，注意力机制应用于CNN-ILSTM模型，用于捕捉不同时间PM_2.5 浓度的过去特征状态。通过无锡某地铁站采集的环境数据进行验证，实验表明，所建立的PM_2.5 预测模型可以有效地提高预测精度和泛化能力。

1 基于注意力机制的CNN-ILSTM的PM_2.5 浓度预测 1.1 卷积神经网络（CNN）

CNN是一种多层神经网络结构，具有强大的网格数据处理能力和深度监督学习结构，能够处理时间序列数据和图像数据。典型的CNN结构主要包括输入层、卷积层、池化层、全连接层和输出层。输入层中的信息通过卷积层和池化层中的特征变换和提取进行处理，卷积层和池化层的本地信息由全连接层进一步集成，并通过输出层映射输出信号。图1为一维CNN的网络结构。卷积层是CNN中最重要、最独特的一层，因为它可以通过卷积核提取输入变量的特征，与全连接层的神经网络不同，CNN的卷积层只连接前一层的部分神经元，卷积核的规模小于输入矩阵的规模。卷积层使用卷积核运算而不是一般的矩阵运算来输出特征映射。变量特征中每个元素的计算公式如下式所示：

式中：${y}_{i,j}^{{\rm out}}$——变量特征第$ i $行和第$ j $列中的输出值；

${x}_{i+m,j+n}^{{\rm in}}$——输入矩阵第$ i $行和第$ j $列中的值；

${f}_{{\rm cov}}$——所选的激活功能；

$ {w}_{m,n} $——卷积核在$ m $行和$ n $列中的权重；

$ b $——卷积核的偏差。

输入矩阵通常使用多个核进行卷积运算。每个卷积核从输入矩阵中提取一个特征，并生成一个特征映射。之后，池化层减少了前一个特征映射的长度和宽度，并通过采样提高计算效率。

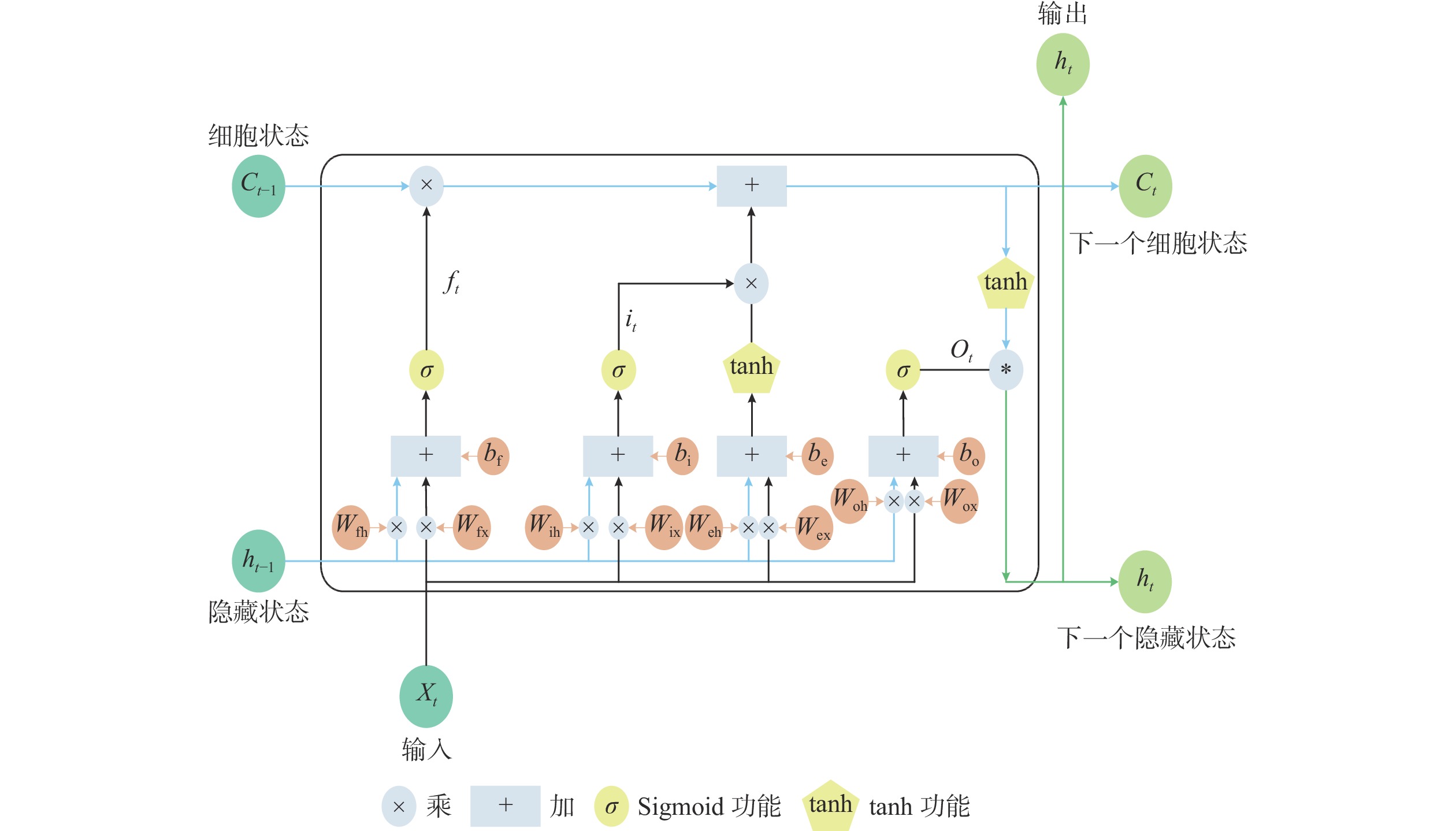
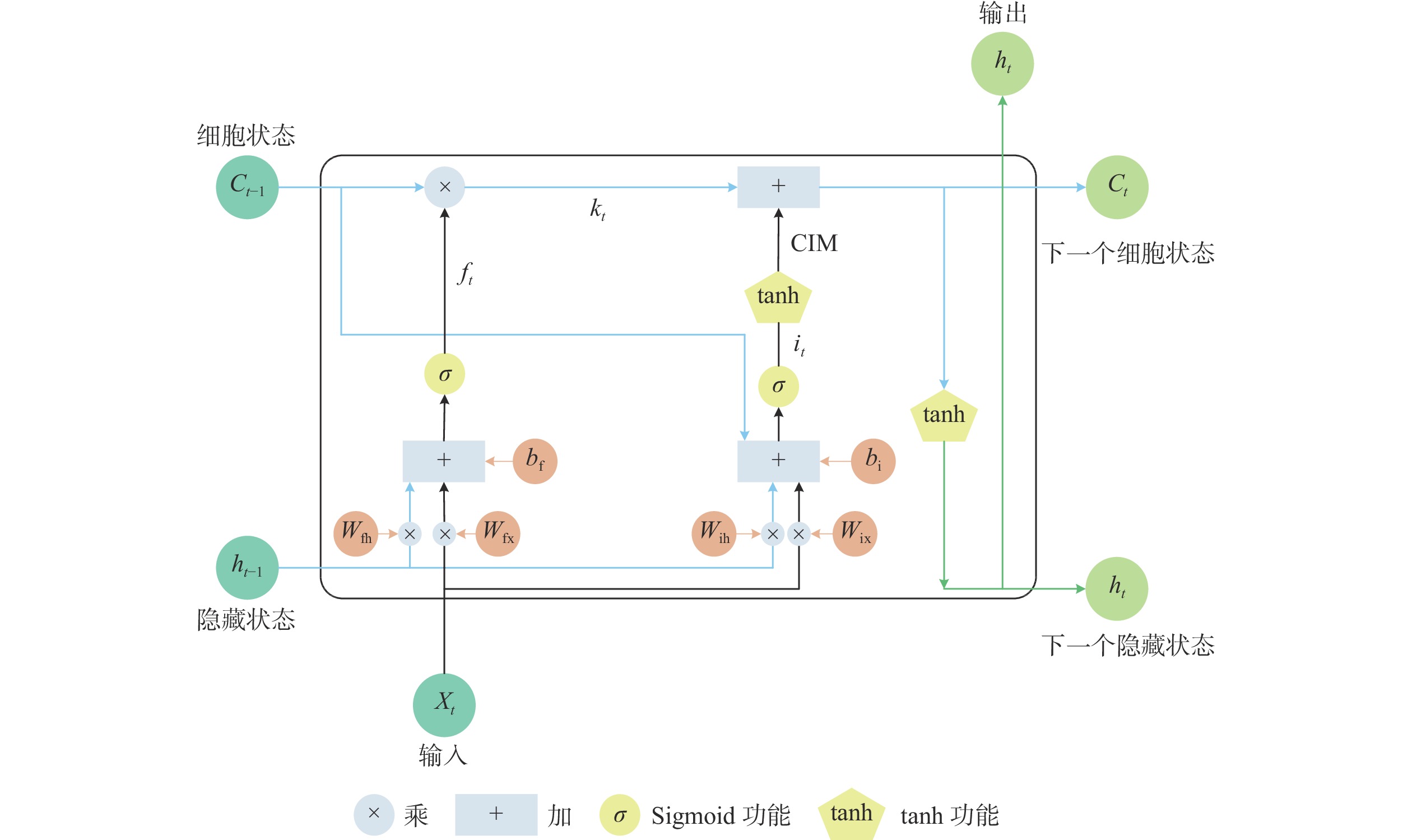
1.2 改进长短期记忆网络（ILSTM）

长短期记忆神经网络（LSTM）是一种特殊的RNN，LSTM模型具备了传统RNN的重复模块链式结构，区别于传统RNN的单一网络层，LSTM单元内部具有4个网络层。LSTM在挖掘序列数据的长期依赖关系方面具有很好的优势，将LSTM细胞加入神经元内部，即细胞中增加了门控结构，从而更新“细胞状态”。门控结构的作用是对流入的信息进行判断和甄别，来决定阻止或者允许信息的流入，从而选择性输入和丢弃信息，还能增加记忆单元，保存历史信息、神经元的长期状态。LSTM模型的内部结构如图2所示。门控递归单元（GRU）只有两个门。GRU将LSTM的输入门和遗忘门合二为一，称为更新门。基于门控技术，本文提出的ILSTM模型由输入门和遗忘门组成，如图3所示。与LSTM相比，ILSTM删除了输出门。与GRU相比，ILSTM结构更简单。LSTM、GRU和ILSTM的参数如表1所示。与LSTM相比，ILSTM将权重参数从8减少到4，将偏差参数从4减少到2。与GRU相比，ILSTM将权重参数从6减少到4，将偏差参数从3减少到2。

在算法方面，ILSTM将前一时刻的单元状态${C}_{t-1}$加入到遗忘门算法中生成主线遗忘$ {k}_{t} $，这将影响当前时间数据保留程度。此外，在更新当前时刻的细胞状态${C}_{t}$时，引入了信息转换模块（CIM）以防止学习过程中的饱和现象。ILSTM的遗忘门$ {f}_{t} $是ILSTM单元的主要组成部分，它可以控制哪些信息应该被保留，哪些信息应该被遗忘。$\sigma \left({x}\right)$是一个Sigmoid函数，如公式（2）所示。$ {x}_{t} $是第$ t $个时间步长的输入数据。$ {h}_{t-1} $是前一个时间步长$ t-1 $的隐藏层。${W}_{{\rm fh}}$是遗忘门$ {h}_{t-1} $的权重，${W}_{{\rm fx}}$是$ {x}_{t} $的权重。${b}_{{\rm f}}$是遗忘门的偏差，如公式（3）所示。

主线遗忘$ {k}_{t} $是由细胞状态${C}_{t-1}$和$ {f}_{t} $计算出来的。主线遗忘代表信息对当前细胞状态${C}_{t}$的影响，其中${C}_{t-1}$是从开始到前一刻的细胞状态信息，如下式所示：

输入门$ {i}_{t} $控制当前输入数据$ {x}_{t} $有多少流入存储单元，即有多少可以保存到${C}_{t}$。与LSTM的输入门相比，ILSTM在输入门算法中增加了${C}_{t-1}$，即截止到前一刻的单元状态信息。${C}_{t-1}$的引入使模型的输入门对当前时间的数据保留具有记忆效应，如下式所示：

其中$ {W}_{{\rm{ih}}} $和$ {W}_{{\rm{ix}}} $分别为输入门的$ {h}_{t-1} $和$ {x}_{t} $的权重，$ {b}_{{\rm{i}}} $是输入门的偏置。

由于Sigmoid激活函数的特性，当x的值在[–3,3]时，Sigmoid激活函数的值将进入过饱和区间。因此，在式（5）中，当输入数据进入输入门的过饱和区间时，其值不会发生明显变化，从而降低了学习的灵敏度。为了防止这种现象，在ILSTM模型中加入转换信息模块（CIM），如下式所示：

CIM输出的值将大大降低过饱和度，显著差异使模型计算更容易识别，从而使模型学习更灵敏。

式（7）表明，${C}_{t}$是从开始到现在保存的信息。

$ {h}_{t} $表示当前保存的信息。$ {C}_{t} $控制通过tanh函数可以保存多少信息，如下式所示：

ILSTM推导公式如下：ILSTM的提出是为了解决传统RNN的“梯度消失”和“梯度爆炸”以及LSTM捕捉污染物相关时间序列数据的时空相关性和相互依赖性不充分的问题，以提高模型的预测精度。输入门和遗忘门使用两个参数矩阵$ \left[{W}_{{\mathrm{fh}}},{W}_{{\mathrm{fx}}}\right] $和$ \left[{W}_{{\mathrm{ih}}},{W}_{{\mathrm{ix}}}\right] $。记$ {{\boldsymbol{W}}}_{f}=\left[{W}_{{\mathrm{fh}}},{W}_{{\mathrm{fx}}}\right] $，$ {{\boldsymbol{W}}}_{{\mathrm{i}}}=\left[{W}_{{\mathrm{ih}}},{W}_{{\mathrm{ix}}}\right] $和$ {\boldsymbol{W}}= [{W}_{{\mathrm{f}}}，{W}_{{\mathrm{i}}}] $。$ {\boldsymbol{W}} $的$ {L}_{t} $函数是对应$ {h}_{t} $的损失，$ L $表示总损失。至于$ {\boldsymbol{W}} $对$ L $的导数，如下式所示：

RNN通过下式更新$ {\boldsymbol{W}} $参数：

其中$ \dfrac{\partial {{L}}_{{t}}}{\partial \boldsymbol{W}} $可以写成：

式（11）可以简化为：

其中，${{C}}_{{t}}$的表达式为：

而$\text{CIM=}\mathit{\rm {{tan}h}}\left({i}_{t}\right)$，所以式（13）可以写成：

而${C}_{t}$的导数可以通过下式获得：

总损失可以写成：

此时记$ x $的表达式为：

那么$ {f}_{t} $可以写成：

记$ y $的表达式为：

那么$ {i}_{t} $可以写成：

那么式（16）可以写成：

此时记$ {\textit{z}}\left(x,y\right) $等于公式（22）：

那么公式（21）可以写成：

此时函数的梯度如公式（23）所示。函数的梯度为$\dfrac{\partial {{L}}_{{k}}}{\partial {{h}}_{{k}}}\dfrac{\partial {{h}}_{{k}}}{\partial {C}_{{k}}}\left(\displaystyle \prod _{{t}=2}^{{k}} \left(\textit z\left(x,y\right)\right)\right)\dfrac{\partial {C}_{{l}}}{\partial \boldsymbol{W}}$，当$ {\textit{z}}\left(x,y\right) $＞1时，随着数据量的增加，梯度可能过大。当$ {\textit{z}}\left(x,y\right) $太小时，梯度很容易消失。因此，ILSTM模型可以在很大程度上缓解“梯度消失”和“梯度爆炸”的问题。

1.3 注意力机制

在堆叠的ILSTM层特征中提取长期依赖关系后，其输出将被用作注意层的输入。每个隐藏状态的重要性由添加的注意层自动学习。注意机制可以简单地解释为加权总和。它首先计算输入特征的重要性；然后，应用softmax函数以确保所有权重之和为1。权重和输入特征会相应地相乘，最终将它们相加得到输出。

注意机制可以自动为不同时间阶段的不同特征分配不同权重，以区分它们的重要性，并且可以实现精确的时空可解释性。考虑过去状态不同特征时的PM_2.5 ，注意力机制允许模型捕捉PM_2.5 浓度最重要的部分。在提出的CNN-ILSTM-attention混合模型中，为了充分利用过去状态的信息，在ILSTM层中增加了一个注意层，它将过去不同特征状态的重要程度排序如下，其中${\boldsymbol H}=\left[{{\boldsymbol{h}}}_{1},{{\boldsymbol{h}}}_{2},\cdots ,{{\boldsymbol{h}}}_{t}\right]$是注意层中的特征状态矩阵，公式表示为：

式中：$ {{\boldsymbol{u}}}_{t} $和$ {\boldsymbol{v}} $——投影向量；

$ {\alpha }_{t} $——$ {{\boldsymbol{h}}}_{{\boldsymbol{t}}} $的归一化权重；

$ {\boldsymbol{s}} $——注意层的加权输出向量。

根据特征状态矩阵${\boldsymbol H}$中每个向量的重要性，式（24）和式（25）可以计算每个向量的归一化权重。式（26）给出了加权向量${\boldsymbol s }$。这实现了在不同时间测量PM_2.5 特征状态的重要性。最终，加权向量${\boldsymbol s }$通过一层完全连接的网络来获得PM_2.5 浓度预测任务的专注度。

1.4 基于注意力机制的CNN-ILSTM混合神经网络模型

CNN-ILSTM结合了CNN和ILSTM的优点，并在此基础上加入注意力机制，提出CNN-ILSTM-attention混合神经网络模型。该模型包括一个输入层、一个卷积层、两个ILSTM层、一个注意层和一个全连接层。设置一维CNN层卷积核为64，内核大小为32，并在一维CNN中添加最大池化层，激活函数为ReLU。卷积层和池化层中的stride=1。设置双层ILSTM网络，每层的隐藏单元个数为60，并在ILSTM网络中加入Dropout，设置其值为0.4，应用Dropout层可以防止模型过拟合。梯度下降的方式采用Adam训练算法，它能自动更新ILSTM网络的权重和偏置。本文提出的基于注意力机制的CNN-ILSTM模型具体实施步骤如下：首先，将数据输入模型，通过CNN的输入层、卷积层和池化层提取输入数据的特征，将得到的特征展平成一维阵列，作为时间序列输入ILSTM层。其次，CNN层的输出被送入第一个ILSTM层，该层捕获变量之间的长期依赖关系，并将每个ILSTM层的所有隐藏状态作为注意层的输入，注意层能够学习这些隐藏层状态的重要性。最后，通过全连接层得到PM_2.5 预测结果。图4为CNN-ILSTM-attention神经网络结构图。

2 基于注意力机制的CNN-ILSTM的PM_2.5 预测建模 2.1 数据来源和处理

本文采用的数据是无锡某地铁站内的环境传感器采集的空气质量数据，包括PM_2.5 、PM₁₀、一氧化碳、二氧化硫、温度和湿度。环境传感器以1 min为采集间隔，由传感器自动采集，共采集1440组数据。其中1120组数据作为训练样本，剩下320组数据作为测试样本检验CNN-ILSTM-attention模型对于PM_2.5 浓度预测的准确性。

一旦将未经处理的原始数据输入模型，训练速度就会减慢，预测结果也会受到影响，因此为了进一步提高模型的预测精度和模型的收敛速度，需要将输入量进行归一化处理。预测模型采用最大最小值标准化（min-max normalization），将数据归一化到[0,1]之间，其转换如下式所示：

式中：${\rm max}\left(x\right)$——数据样本中的最大值；

${\rm min}\left(x\right)$——数据样本中的最小值；

$ x $——数据样本中的任意值。

2.2 评估标准

为了评估CNN-ILSTM-attention模型的预测精度，选用均方根误差（RMSE）、平均绝对误差（MAE）和拟合度（r²）对算法模型进行评价。其计算公式如下式所示：

式中：$ {{\textit{z}}}_{t} $和$ {x}_{t} $——第$ t $次测试的真实值和算法模型输出值；

$ m $——测试总次数。

3 实验结果对比分析 3.1 不同时滞下的模型比较

一般的时间预测问题中，当面临长序列问题时，就会陷入瓶颈。一种解决方法就是引入注意力机制。注意力机制可以允许模型聚焦关注输入序列中所需要的部分。引入了注意力机制后的模型，它可以将输入序列中相关部分的作用进行放大，以实现比没有注意力的模型更好的效果。通常，注意力机制的表现形式可以看作是一种加权求和。在本文中，为了提高集成神经网络模型的可扩展性和准确性，将注意力机制引入CNN-ILSTM网络模型中。

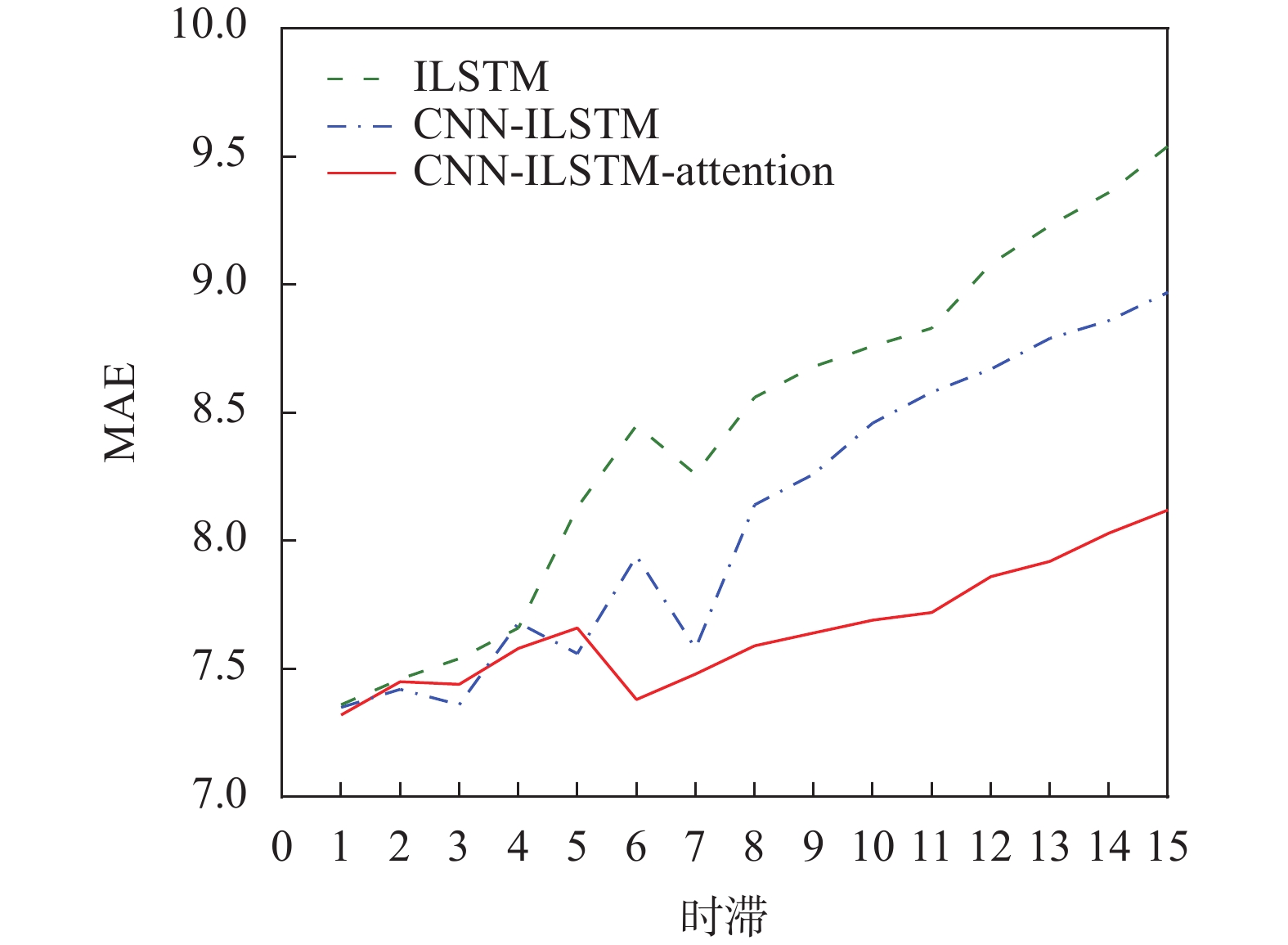
本文将CNN-ILSTM-attention模型、CNN-ILSTM模型和ILSTM模型在1~15之间的时滞进行对比，以研究注意机制的有效性。时滞越大，提取有用特征的难度就越大。从图5可以看出，随着时滞的增加，MAE变得越来越大。当时滞变大时，ILSTM模型和CNN-ILSTM模型都迅速退化，而CNN-ILSTM-attention模型性能保持稳定。结果表明，CNN-ILSTM-attention模型具有较强的稳定性和鲁棒性，这是因为注意机制考虑了不同隐藏状态的重要性，并将更多注意力集中在更重要的状态上。

3.2 预测模型收敛性比较

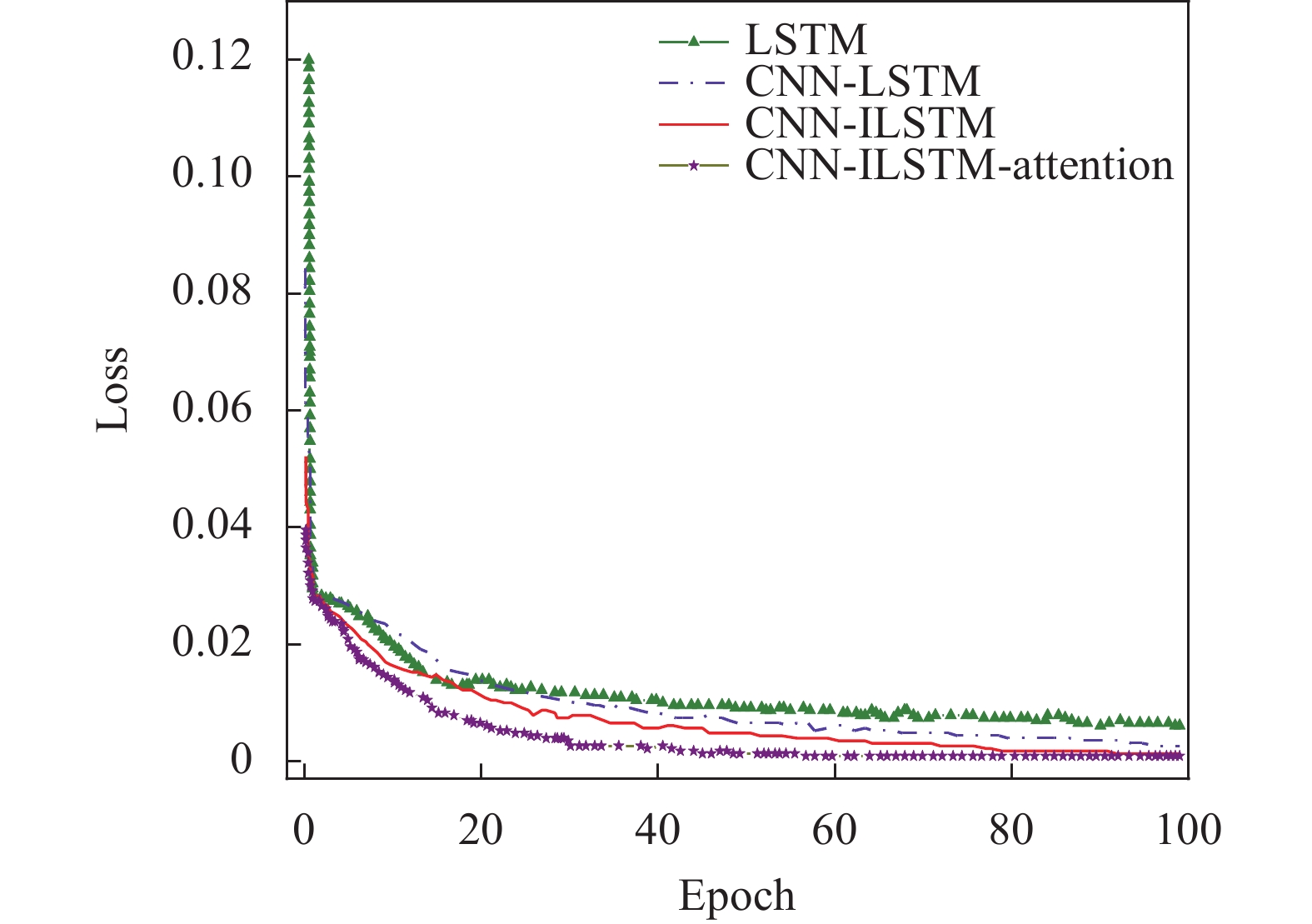
设置合适的模型参数后，需要验证CNN-ILSTM-attention在训练过程中是否收敛。因此，计算了CNN-ILSTM-attention模型在PM_2.5 浓度预测任务中的训练损失，并将结果与另外3种深度学习模型（LSTM、CNN-LSTM和CNN-ILSTM）进行了比较。所有预测模型的参数相同，使用数据归一化后的均方误差（MSE）作为损失函数进行训练。图6为4种模型训练损失函数。从图中可以看出，所有模型在Epoch=40处收敛。在预测过程中Epoch=40后，4个模型的MSE损失接近，但CNN-ILSTM-attention模型的MSE损失略小于LSTM、CNN-LSTM和CNN-ILSTM 3个模型，且拥有更快的收敛速度。因此，CNN-ILSTM-attention模型比ILSTM模型、CNN-LSTM和CNN-ILSTM模型具有更好的收敛结果。

3.3 预测模型性能比较

为了验证所提出的CNN-ILSTM-attention模型的有效性，本文从两个方面进行对比。

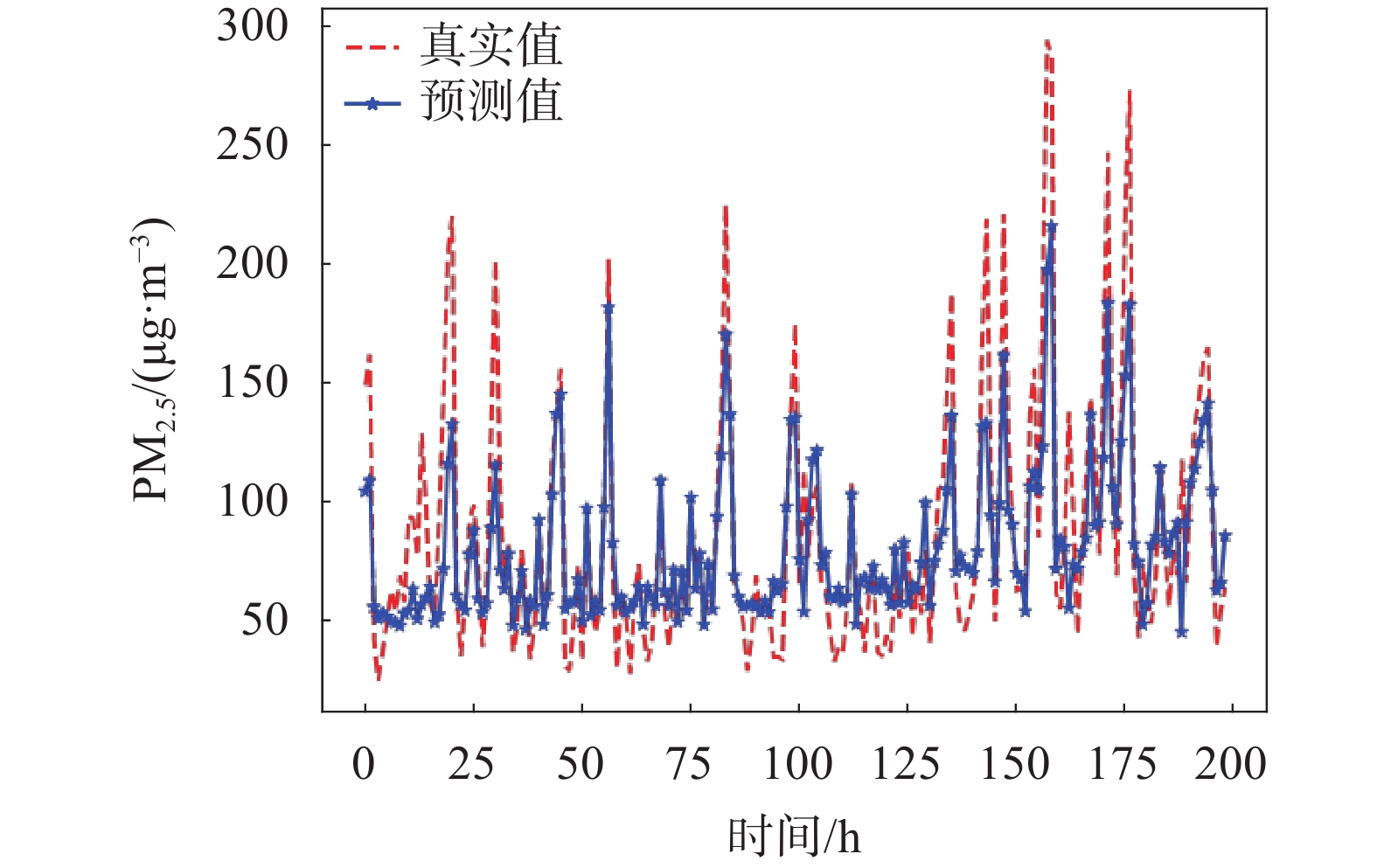
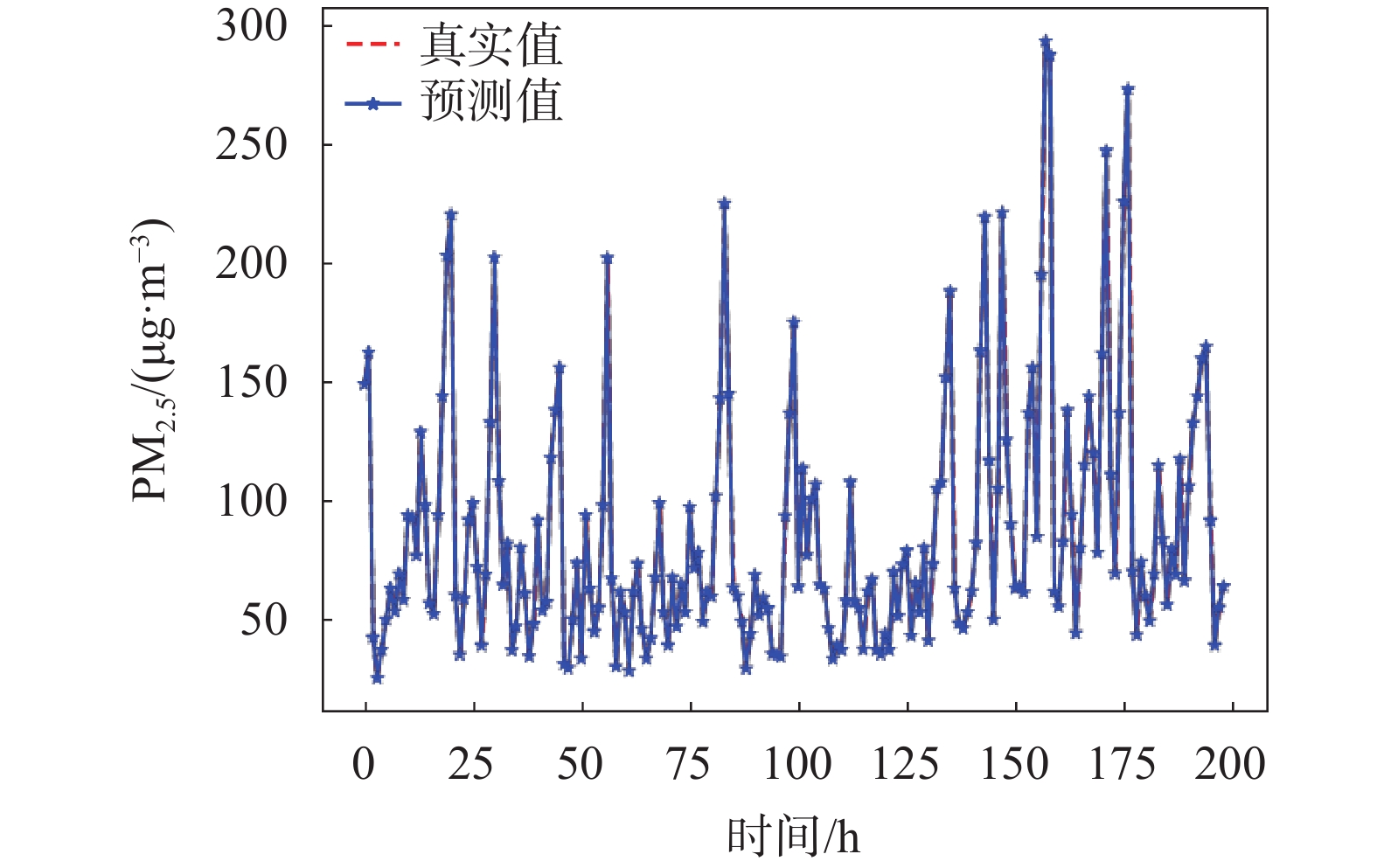
1）为了验证CNN-ILSTM-attention模型预测PM_2.5 浓度的准确性，本文引入传统的回归模型（ARIMA、SVR和MLP）作为对比模型。实验结果如图7~图10所示。从图中可以看出，传统的回归模型ARIMA、SVR和MLP的预测拟合度明显低于CNN-ILSTM-attention模型。

表2为4种模型评价指标的对比。从表中可以看出，CNN-ILSTM-attention预测模型的预测效果最好。与SVR模型相比，r²提高了24.9%，RMSE减少了15.04 μg/m³，MAE减少了11.1 μg/m³。与MLP模型相比，r²增加了14.2%，RMSE减少了10.28 μg/m³，MAE减少了9.92 μg/m³。与ARIMA模型相比，CNN-ILSTM-attention模型的r²提高了12.1%，RMSE减少了8.67 μg/m³，MAE减少了7.07 μg/m³。因此，相比较ARIMA、SVR和MLP模型，CNN-ILSTM-attention模型对PM_2.5 浓度的预测具有较高的准确性。

2）为了全面评估所提模型，本文选用基于门控技术的递归神经网络模型（LSTM）以及混合预测模型（CNN-LSTM、CNN-LSTM-attention、CNN-ILSTM）与本文所提模型进行对比。

图11为LSTM、CNN-LSTM、CNN-LSTM-attention、CNN-ILSTM以及CNN-ILSTM-attention5种算法模型预测PM_2.5 浓度结果对比图。图12为5种预测模型相对误差对比图。从图中可以发现，PM_2.5 实际浓度值在不停地变化，LSTM和CNN-LSTM两种预测模型能大致地捕捉PM_2.5 浓度变化规律，但依然存在预测误差较大的问题。CNN-LSTM-attention模型、CNN-ILSTM模型、CNN-ILSTM-attention模型都能够准确捕捉PM_2.5 浓度变化规律，但无法准确捕捉到当PM_2.5 浓度发生突然变化时的规律。在CNN-ILSTM-attention预测模型中，注意层能够通过输入数据提取和存储在记忆单元中来改善深度学习模型中的记忆性能。从图中可以看出，CNN-ILSTM-attention模型预测效果明显优于LSTM、CNN-LSTM、CNN-LSTM-attention和CNN-ILSTM这4种预测模型，能够更好地捕捉到PM_2.5 浓度突然变化规律，从而准确地预测PM_2.5 的浓度。

LSTM、CNN-LSTM、CNN-ILSTM、CNN-LSTM-attention、CNN-ILSTM-attention模型预测效果对比如表3所示。

从表中可以看出，CNN-ILSTM-attention模型拥有最高的拟合度以及最低的RMSE和MAE。在RMSE和MAE指标上，比LSTM模型和CNN-ILSTM模型降低了15.27 μg/m³、2.9 μg/m³和11.83 μg/m³、2.2 μg/m³。而CNN-ILSTM-attention模型在拟合度r²为98.5%，较LSTM模型和CNN-ILSTM模型分别提高了26%和6.2%。因此可以得出，CNN-ILSTM-attention模型预测效果优于其他4种预测模型，呈现出更高的预测精度。

4 结束语

为了提高预测精度，本文提出了一种基于注意力机制的CNN-ILSTM模型来预测地铁站PM_2.5 的浓度。卷积层能够提取局部特征，而改进LSTM层能够获取长期依赖关系，注意力机制可以根据过去的时间捕捉不同特征状态的重要程度。实验结果表明，本文所建立的CNN-ILSTM-attention模型能够捕捉局部和全局的依赖关系，相比典型的LSTM模型、CNN-LSTM模型以及CNN-ILSTM模型，具有更高的预测精度和泛化能力。这为精准预测PM_2.5 浓度提供理论和方法的支撑，对于未来开发预警系统和调节通风系统以确保通勤者和地铁工作人员的健康具有一定的指导意义。