文章信息
- 余浩, 马剑龙, 吕文春, 苏宏杰, 张鹏宇
- YU Hao, MA Jianlong, LÜ Wenchun, SU Hongjie, ZHANG Pengyu
- 基于等效刚度法优化的风力机叶片刚度计算
- Calculation of wind turbine blade stiffness based on equivalent stiffness method optimization
- 中国测试, 2024, 50(7): 47-52
- CHINA MEASUREMENT & TEST, 2024, 50(7): 47-52
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022080119
-
文章历史
- 收稿日期: 2022-08-22
- 收到修改稿日期: 2022-10-08
2. 内蒙古自治区高校可再生能源工程研究中心,内蒙古 呼和浩特 010051;
3. 风能太阳能利用技术教育部重点实验室,内蒙古 呼和浩特 010051;
4. 内蒙古机电职业技术学院科技与职教研究中心,内蒙古 呼和浩特 010070
2. Engineering Research Center of Renewable Energy at Universities of Inner Mongolia Autonomous Region, Hohhot 010051, China;
3. Key Laboratory of Wind Energy and Solar Energy Technology, Ministry of Education, Hohhot 010051, China;
4. Research Center of Technology and Vocational Education, Inner Mongolia Technical College of Mechanics and Electrics, Hohhot 010070, China
全球气候变暖的问题加重,使得清洁能源的开发利用成为当前能源行业发展的关注热点[1],风能发电已然成为能源行业重要的战略部署。叶片作为风力机能量转化的重要部件,其结构特性是保证风机稳定运行和提高风机能量转换率的关键,所以在设计初期对相应的叶片结构参数进行校核必不可少。刚度对叶片挠度安全性起着决定性作用,其大小将直接影响风机运行的可靠性[2],由于叶片结构与材质的不规则性,刚度的获取多以后期叶片实验为主[3]。因此,研究叶片的刚度计算方法对叶片设计初期的安全校核以及叶片优化前后的刚度评估有着重要意义[4]。
目前国内外对于叶片刚度的研究现状,将刚度与叶片的气动弹性相结合,探究不同程度的刚度对叶片运行的影响[5],其中在叶片刚度计算方面,多以简化叶片的数学模型或是简化叶片结构模型进行计算,多数为叶片截面刚度分布计算。例如通过研究叶片结构发现主梁帽刚度占据总刚度的90%以上,从而将叶片简化为工字梁结构进行刚度计算[6]。在叶片数学模型建模上,利用有限差分法和有限元法的数学方法,将叶片等效为变截面悬臂梁,再利用壳单元,简化叶片结构建立有限元模型,从而获得叶片刚度分布,为叶片刚度分析提供参考[7]。因为刚度直接影响挠度,所以以挠度作为中间参考值,用挠度参数代替刚度参数体现叶片刚度大小[8]。在截面刚度计算方面,利用截面刚度沿叶片展向分布曲线校核刚度[9],使用 Matlab优化工具箱计算出叶片各截面的参数,再结合材料力学理论计算挠度沿叶高的分布曲线,从而完成刚度校核[10]。
通过上述研究可知,叶片的刚度计算多以截面刚度分布曲线或是以挠度作为中间值进而分析叶片整体刚度,但刚度参考参数不够宏观直接。针对此现状问题,参考材料力学中变截面构件挠度计算的等效刚度法[11-12],根据风机叶片安装的边界条件以及叶片本身变截面的几何特征,将其简化成变截面悬臂梁,用等效刚度法求得的等效刚度值体现叶片刚度,相对刚度分布曲线而言,单一的刚度参数值,可以更加宏观直接地体现叶片刚度。但原始等效刚度法的线性近似用于叶片存在着误差较大的问题。针对该问题,以叶片的截面数据特征为基础对原始的等效刚度法进行优化,通过模拟实验得到叶尖位移值验证优化的可靠性[13],用优化后的算法计算得到的等效刚度值代表叶片整体刚度,为叶片设计初期的刚度提供参考值。
1 变截面悬臂梁的等效刚度法优化 1.1 变截面悬臂梁等效刚度法的基础原理等效刚度法是通过等效系统法将变刚度的梁用等刚度的梁来代替,其中等效系统的每一个挠曲线等于原来变刚度梁的挠曲线。若由一已知的变刚度梁得到了一个等效系统,就可用等效系统对原结构进行计算。
变截面构件的弹性曲线一般微分方程为
| $ \frac{{\text{d}}^{2}y}{ \text{d}{x}^{2}}=-\frac{{M}_{x}}{{E}_{x}{I}_{x}} $ | (1) |
积分二次得到变截面挠度曲线:
| $ y = \int {\left[ { - \int {\frac{{{M_x}}}{{{E_x}{I_x}}}} {\text{d}}x} \right]} {\text{d}}x + {C_2}\int {\text{d}} x + {C_1} $ | (2) |
则变刚度可表示为某一截面刚度与函数的乘积,如下式所示:
| $ {E_x}{I_x} = {E_1}{I_1}f(x) $ | (3) |
等刚度挠度曲线:
| $ y = \frac{1}{{{E_1}{I_1}}}\int {\left[ { - \int {\frac{{{M_x}}}{{f(x)}}} {\text{d}}x} \right]} {\text{d}}x + {C^\prime }\int {\text{d}} x + {C_2} $ | (4) |
由于式(2)、式(4)相同,且边界条件相同,所以
| $ {C_1} = C_1' \text{,} {C_2} = C_2' $ |
则有
| $ \int {\left[ { - \int {\frac{{{M_x}}}{{f(x)}}} {\text{d}}x} \right]} {\text{d}}x = \int {\left[ { - {M_{\text{e}}}{\text{d}}x} \right]} {\text{d}}x $ | (5) |
即
| $ {M_{\text{e}}} = \frac{{{M_x}}}{{f(x)}} $ | (6) |
通过上述讨论说明,一个变刚度的梁总是存在一个等刚度的等效系统,但这里的等刚度并不等于原结构的刚度,因为是通过改变弯矩从而达到刚度等效,也就是说,若
根据等效系统原理,变刚度与等效刚度的悬臂梁的叶尖挠度相同,可建立公式:
| $ f = \frac{{q{H^4}}}{{3E{I_{{\rm{eq}}}}}} = \frac{q}{E}\int_0^l {\frac{{{x^2}}}{{{I_x}}}} {\rm d}x $ | (7) |
其中
由式(7)即可推出等效刚度:
| $ E{I_{{\rm{eq}}}} = \frac{{E{H^4}}}{{4\displaystyle \int_0^l {\dfrac{{{x^3}}}{{{I_x}}}{\rm d}x} }} $ | (8) |
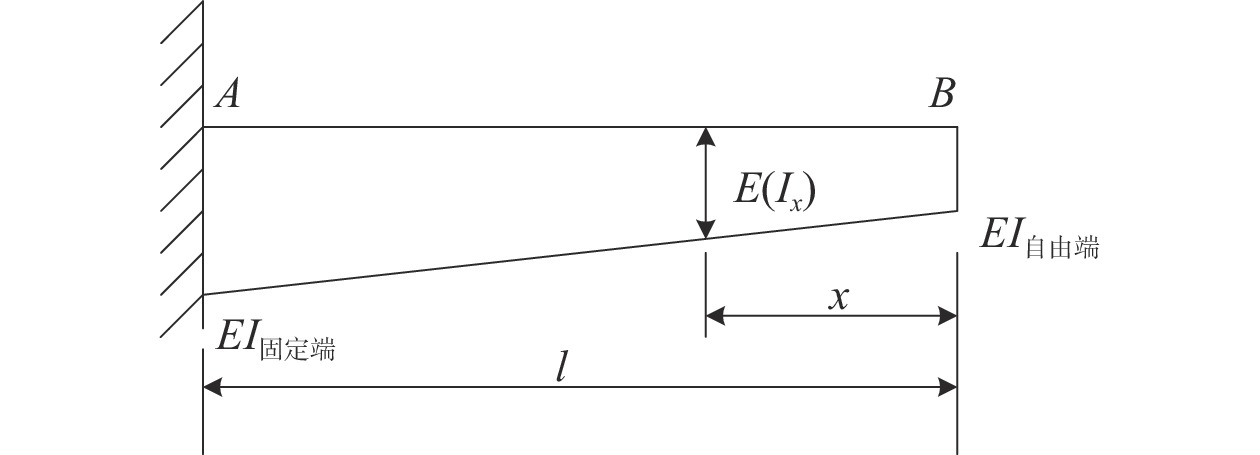
在经典的等效刚度法计算中,主要用于变刚度构件截面惯性矩形成的函数积分求解,数学计算坐标示意图,如图1所示。
|
| 图 1 变刚度构件示意图 |
原始的计算方法是通过取变截面悬臂梁的固定端和自由端的惯性矩值,将其近似成简单的线性函数,如式(9)所示,从而完成积分求值。然而叶片沿展向方向截面惯性矩变化程度大,若仍取叶片的固定端和自由端的惯性矩值进行线性近似会产生较大误差,并且不能反映叶片中间段的特殊翼型对叶片整体带来的刚度影响。因此利用叶片建模截面数据的特点以及原始等效积分法存在线性近似积分法误差过大的缺点,通过这两个方面进行基于叶片等效刚度法的计算优化。
| $ \begin{gathered} I(x) =\frac{1}{{1 + (n - 1){{\left( {1 - \dfrac{x}{l}} \right)}^2}}}n \\ n=\dfrac{{I}_{自由端}}{{I}_{固定端}} \end{gathered} $ | (9) |
式中:
根据叶片截面数据具有实验样本的数据特征并且呈现非线性,在积分法上可以选取梯形积分和辛普森积分,其次在区间分割相同的条件下,辛普森积分公式比梯形积分公式的计算精度高[13],但辛普森积分法仅适用于等分成偶数个小区间的区间上,所以根据叶片建模存在部分截面连续等间距和部分截面非等间距的特点,采用辛普森积分法和梯形积分法分别对等间距截面区间和非等间距截面进行分段积分求和,提高计算精度。
假设对函数
| $ \begin{split} {\displaystyle {\int }_{0}^{l}{y}_{i}{\mathrm{d}}x}=&{\displaystyle {\int }_{0}^{p}{y}_{i}{\mathrm{d}}x+{\displaystyle {\int }_{p}^{l}{y}_{i}{\mathrm{d}}x}}={\displaystyle {\int }_{0}^{p}\dfrac{{x}^{3}}{{I}_{x}}{\mathrm{d}}x}+{\displaystyle {\int }_{p}^{l}\dfrac{{x}^{3}}{{I}_{x}}{\mathrm{d}}x}=\\ &\dfrac{p\text{(}\dfrac{{p}^{3}}{{I}_{p}})}{2}+\dfrac{l-p}{6n}\left[\dfrac{{p}^{3}}{{I}_{p}}+\dfrac{{l}^{3}}{{I}_{l}}+4\left(\dfrac{{(p+h)}^{3}}{{I}_{p+h}}+\right.\right.\\ &\left.\dfrac{{(b+3\cdot h)}^{3}}{{I}_{b+3\cdot h}} +\cdots +\dfrac{{(b+(2n-1)\cdot h)}^{3}}{{I}_{b+(2n-1)\cdot h}}\right)+\\ &2\left(\dfrac{{(b+2\cdot h)}^{3}}{{I}_{b+2\cdot h}}+\dfrac{{(b+4\cdot h)}^{3}}{{I}_{b+4\cdot h}} +\cdots +\right.\\ &\left.\left.\dfrac{{(b+(2n-2)\cdot h)}^{3}}{{I}_{b+(2n-2)\cdot h}}\right)\right] \end{split} $ | (11) |
以小型风机的某S翼型叶片的摆振刚度计算为例,简述叶片建模初期的模型数据和特征以及如何应用优化后的等效刚度法对叶片取值的刚度计算。
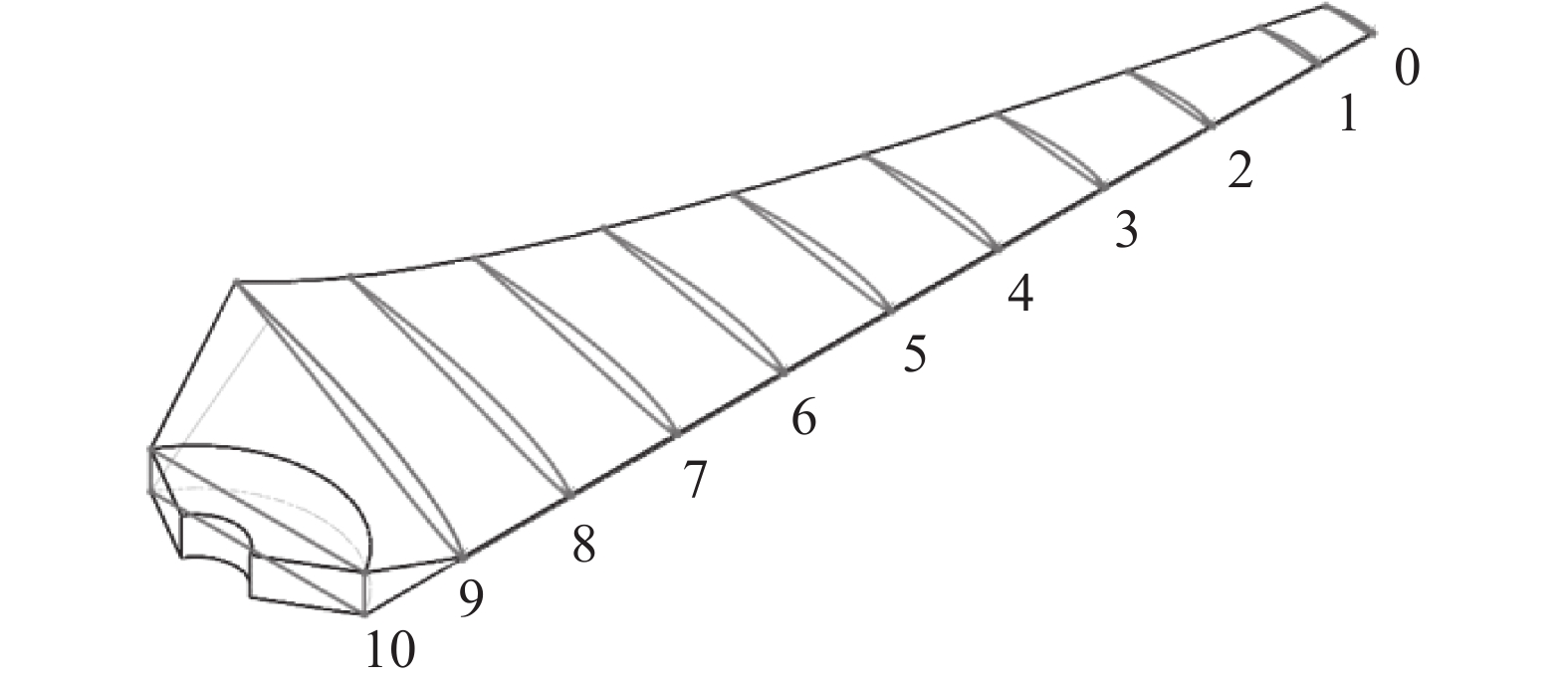
2.1 叶片模型及材料数据以某S翼型叶片为例,叶片结构总长700 mm,由10个特征翼型面组成,每个翼型面之间通过放样将其连接,其中0号和1号翼型面间距为35 mm,1号至9号翼型面相邻的面为等间距70 mm,叶根部位长度105 mm,叶片模型如图2所示,叶片材料参数如表1所示。
|
| 图 2 叶片模型 |
| 参数 | 数值 | 参数 | 数值 | |
| 密度 | 625 kg/m3 | 体积模量 | 4.7059×109 Pa | |
| 杨氏模量 | 4.8×109 Pa | 抗剪弹性系数 | 1.8045×109 Pa | |
| 泊松比 | 0.33 | 抗拉强度 | 1.2×106 Pa |
2.2 基于叶片的等效刚度法计算
由于叶片安装方式以及叶片主体的特点,将叶片近似成变截面悬臂梁模型,基于叶片的安装方式近似将10号截面作为固定端截面,0号截面作为自由端截面,以固定端为
|
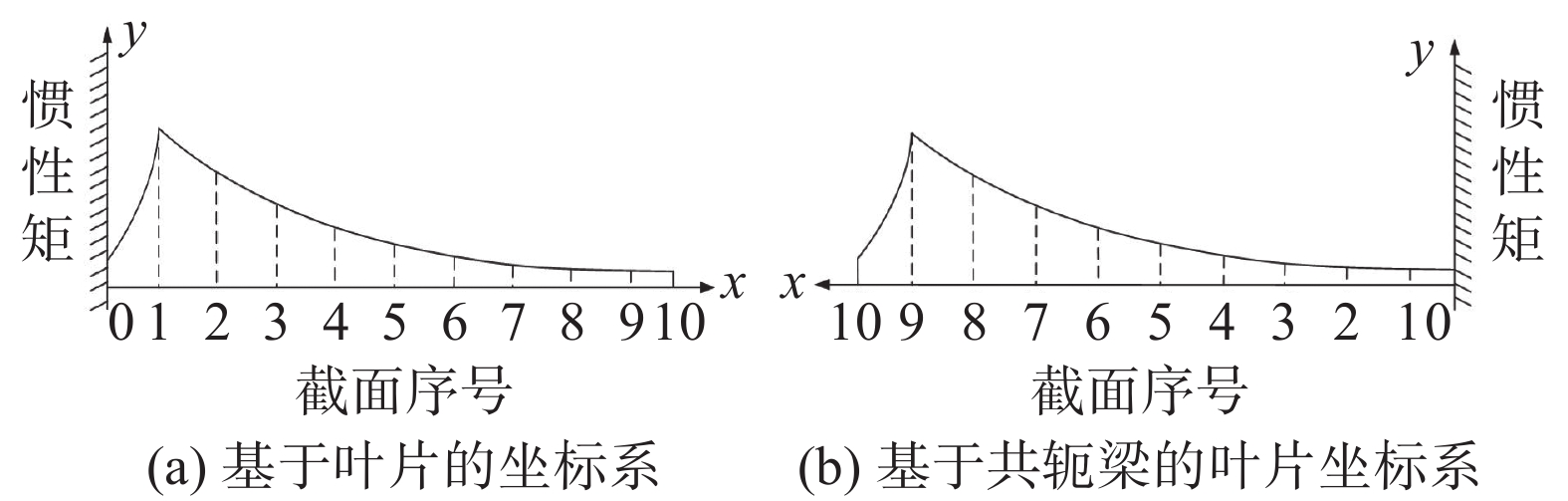
| 图 3 计算坐标系 |
由于等效刚度法的计算是基于挠度系统能量守恒推理得出,但在等效系统中采用共轭梁法计算挠度,原始的叶片坐标系会因为共轭梁系统建立从而发生对调,导致原来的固定端变成自由端,自由端变成固定端,变化后的坐标原点首尾互换,如图3(b)所示,导致截面的排列是从叶尖到叶根进行
| 截面 | 长度/ mm | 截面惯性矩/ mm4 | 截面 | 长度/ mm | 截面惯性矩/ mm4 | |
| 0 | 0 | 22.224 | 6 | 385 | 25626.121 | |
| 1 | 35 | 64.970 | 7 | 455 | 68816.307 | |
| 2 | 105 | 338.422 | 8 | 525 | 192520.433 | |
| 3 | 175 | 1115.888 | 9 | 595 | 577660.793 | |
| 4 | 245 | 3566.549 | 10 | 659.5 | 161621.13 | |
| 5 | 315 | 9690.902 |
根据叶片建模的截面间距的分布特点,0号至1号截面间距为35 mm和9号至10号截面间距为64.5 mm采用梯形积分法,1号至9号截面为8等分间距为70 mm采用辛普森积分法,加以分段积分求和,基于式(11)代入式(8)得到等效刚度的优化后叶片刚度的求解公式,如下式所示:
| $\begin{split} E{I}_{\text{eq}}=&\dfrac{E{H}^{4}}{4}{\displaystyle {\int }_{0}^{10}\dfrac{{x}_{i}{}^{3}}{{I}_{i}}{\mathrm{d}}x}=\\ &\dfrac{{H}^{4}}{4}\left({\displaystyle {\int }_{0}^{1}\dfrac{{x}_{i}{}^{3}}{{I}_{i}}{\mathrm{d}}x+{\displaystyle {\int }_{1}^{9}\dfrac{{x}_{i}{}^{3}}{{I}_{i}}{\mathrm{d}}x}}+{\displaystyle {\int }_{9}^{10}\dfrac{{x}_{i}{}^{3}}{{I}_{i}}{\mathrm{d}}x}\right)=\\ &\dfrac{E{H}^{4}}{4}\left\{\begin{array}{l}\dfrac{{x}_{1}^{3}}{2{I}_{1}}+\dfrac{1}{2}\left(\dfrac{{x}_{9}^{3}}{{I}_{9}}+\dfrac{{x}_{10}^{3}}{{I}_{10}}\right)({x}_{10}-{x}_{9})+\\ \dfrac{{x}_{9}-{x}_{1}}{24}\left[\begin{array}{l}\dfrac{{x}_{1}^{3}}{{I}_{1}}+\dfrac{{x}_{9}^{3}}{{I}_{9}}+4\left(\dfrac{{x}_{2}^{3}}{{I}_{2}}+\dfrac{{x}_{4}^{3}}{{I}_{4}}+\dfrac{{x}_{6}^{3}}{{I}_{6}}\right.\\ \left.+\dfrac{{x}_{8}^{3}}{{I}_{8}}\right)+2\left(\dfrac{{x}_{3}^{3}}{{I}_{3}}+\dfrac{{x}_{5}^{3}}{{I}_{5}}+\dfrac{{x}_{7}^{3}}{{I}_{7}}\right)\end{array}\right]\end{array}\right\} \end{split} $ | (12) |
式中:
计算求得该S翼型叶片的等效刚度156.19
叶片模型为某S翼型小型水平轴风力机叶片,长700 mm,通过10个特征翼型坐标在CAD中绘制翼型截面,将各翼型截面在Solidworks中结合截面间隔和法兰连接盘放样生成单只叶片,将三维模型导入ANSYS中,以

|
| 图 4 ANSYS叶片模型 |
3.2 网格划分
网格采用ANSYS Workbench中的mesh模块进行划分,由于风力机叶片结构的不规则和叶片表面曲度高,结构化网格对复杂外形的贴体网格生成较难,非结构化网格对于不规则的结构具有更好的适应性,所以采用非结构化网格对叶片实体的网格进行划分,非结构化的网格单元尺寸选取5 mm,网格数量与质量如表3所示,网格划分密度如图5所示,网格质量较为理想。

|
| 图 5 网格划分密度 |
3.3 计算类型选取和边界条件设置
叶片为三维实体结构,具有
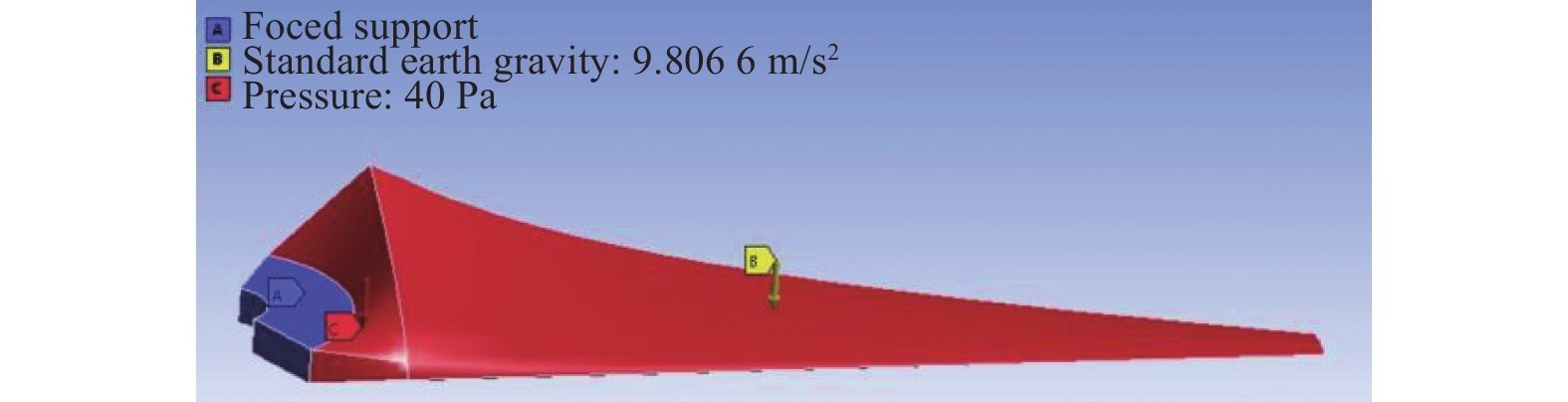
叶片等效成悬臂梁,所以边界条件的选取与叶片的安装方式相结合。由于法兰连接,所以选取圆盘处作为固定端,如图6所示。添加重力加速度,垂直于叶片平面施加均布载荷,在均布载荷的取值上,根据叶片的常规风速范围,取6 m/s,8 m/s,10 m/s,12 m/s这4个风速在20 ℃所对应的22.5 Pa,40 Pa,62.5 Pa,90 Pa风压值,风压计算公式如式(12)所示,计算获得的风压值作为均布载荷的压强值。
|
| 图 6 施加约束条件和均布荷载 |
| $ P = \frac{1}{2}\rho {v^2} $ | (13) |
式中:
用模拟试验的摆振方向位移值作为中间参数,验证摆振刚度计算值的可靠性,所以选取方向性位移计算板块,对叶片载荷方向下进行位移求解,可得叶片位移云图,如图7所示。

|
| 图 7 叶片位移云图(单位:mm) |
悬臂梁的自由端挠度为最大挠度,在叶片上对应的最大挠度就是叶尖位移,模拟结果可得到22.5、40、62.5、90 Pa下均布载荷的叶尖位移值如表4所示。
3.5 试验值与理论值的结果分析
以模拟试验的叶尖位移为中间值作为参考标准,验证优化后等效刚度法计算结果是否达到优化目的。在不同风压值下,用原等效刚度法得到的刚度值和优化后计算得到的等效刚度值代入式(7),即可获得优化前后相应的叶尖位移值如表5所示。将优化前后的等效刚度值与模拟试验的叶尖位移值对比可知,优化后的等效刚度法减小了该方法应用于叶片计算的误差,实现了量级式的误差减小,证明等效刚度法优化后应用于叶片的适用性。
| 均布载荷 值/Pa |
原方法位 移值/m |
优化后位 移值/m |
模拟实验 位移值/m |
误差值/ % |
| 90 | 0.87931 | 0.009072 | 0.00632 | 43.64 |
| 62.5 | 0.61063 | 0.006299 | 0.00448 | 40.48 |
| 40 | 0.39080 | 0.004032 | 0.00312 | 29.02 |
| 22.5 | 0.21983 | 0.002268 | 0.00207 | 9.68 |
| 注:1)定义误差值=(优化后计算值-实验值)/实验值×100%。 | ||||
优化后的等效刚度法计算的位移值与模拟试验的误差值如表5所示。由表中误差值可知,随着载荷值的增加误差值随之增大,误差最大为43.64%,在低载荷值22.5 Pa下的误差值达到最小为9.68%。
在计算方法和数据正确且不考虑数学计算本身存在的误差情况下,对误差的分析回归到叶片的数学建模问题,在对叶片采取梁的数学计算模型中包含相应的梁的假设,由于叶片在叶片的模拟试验时模型并未按照“平截面假设”后的计算模型进行计算,存在基于叶片的展向以及纵向两个方向的剪切变形量,由于纵向剪切变形的存在有效减弱了外部载荷的作用效果,在梁的计算中并未考虑剪切形变,并且剪切变形量与力呈线性关系,所以外加载荷增大剪切变形量越大的情况下,计算误差会随载荷增加而增大。由于梁作为特殊的平板模型,将叶片简化成梁在不考虑转角自由度的剪切变形时计算弯曲挠度是可行的。
所以优化后的等效刚度法估算叶片的弯曲刚度在不考虑叶片的剪切变形的情况下,对叶片的刚度评估是可靠的,可为叶片设计或优化提供新的刚度参数参考,为叶片的刚度计算提供新方法,方法简单,便于工程应用。
4 结束语1)提出了叶片新的刚度计算方法。基于材料力学的等效刚度法,根据叶片截面数据特征,改善原始等效刚度法的数学计算方法,使其在叶片的计算上减小误差,适用于叶片刚度计算。
2)验证了优化等效刚度法的可行性。通过均布载荷的模拟试验,将模拟实验计算的叶尖位移作为中间参考参数,在22.5 Pa的载荷下误差值达到9.68%,说明在减小剪切变形的影响下,误差在工程误差的允许范围内,即该方法计算得到的刚度值可为评估叶片刚度提供参考。
| [1] |
洪星. 基于气动性能与截面刚度特性的风力机翼型廓线设计研究[D]. 武汉: 湖北工业大学, 2019.
HONG X. Research on wind turbine airfoil profile design based on aerodynamic performance and cross section stiffness characteristics[ D ]. Wuhan: Hubei University of Technology, 2019.
|
| [2] |
白学宗, 安宗文, 侯运丰, 等. 低速冲击载荷下的风电叶片刚度退化规律[J].
太阳能学报, 2022, 43(1): 132-139.
BAI X Z, AN Z W, HOU Y F, et al. Stiffness degradation rule of wind turbine blade under low-velocity impact load[J].
Acta Energiae Solaris Sinica, 2022, 43(1): 132-139.
|
| [3] |
吕文春, 马剑龙, 陈雅男. 风轮固有频率随材质参数变化的规律研究[J].
中国测试, 2023, 49(7): 54-60,75.
LÜ W C, MA J L, CHEN Y N. Research on the law of natural frequency of wind turbine with different material parameters[J].
China Measurement & Testing, 2023, 49(7): 54-60,75.
|
| [4] |
钟贤和, 戚中浩, 曾明伍. 风电叶片刚度的影响因素和简化计算方法[C]//中国动力工程学会透平专业委员会2013年学术研讨会论文集, 2013.
ZHONG X H, QI Z H, ZENG M W. The influence and simplified calculation methods for stiffness of wind turbine blades[C]//Proceedings of the 2013 Academic Symposium of the Turbine Professional Committee of the Chinese Society of Power Engineering, 2013.
|
| [5] |
FERNANDEZ G, USABIAGA H, VANDEPITTE D. An efficient procedure for the calculation of the stress distribution in a wind turbine blade under aerodynamic loads[J].
Journal of Wind Engineering and Industrial Aerodynamics, 2018, 172: 42-54.
DOI:10.1016/j.jweia.2017.11.003 |
| [6] |
秦超, 侯彬彬, 陈康, 等. 大型分段式风电叶片刚度及模态有限元分析[J].
玻璃钢/复合材料, 2016(12): 34-37.
QIN C, HOU B B, CHEN K, et al. Stiffness and modal Large sectional type wind turbine blade finite element modeling and stiffiness and model analysis[J].
Composites Science and Engineering, 2016(12): 34-37.
|
| [7] |
王同光. 风力机叶片结构设计[M]. 北京: 科学出版社, 2015.
WANG T G. Structural design of wind turbine blade[M]. Beijing: Science Press, 2015.
|
| [8] |
胡丹梅, 孙凯, 张志超. 风力机模型叶片结构设计计算[J].
可再生能源, 2013, 31(6): 56-60, 65.
HU D M, SUN K, ZHANG Z C. The calculation of blade structure design for wind turbine model[J].
Renewable Energy Resources, 2013, 31(6): 56-60, 65.
|
| [9] |
邹家兴. 用等效刚度法计算变截面梁的变形[J].
农田水利与小水电, 1995(9): 36-38.
ZOU J X. Equivalent stiffness method is used to calculate the deformation of variable cross-section beams[J].
China Rural Water and Hydropower, 1995(9): 36-38.
|
| [10] |
李正良. 变刚度梁的计算[M]. 北京: 人民交通出版社, 1996.
LI Z L. Calculation of variable stiffness beams[M]. Beijing: China Communication Press, 1996.
|
| [11] |
何佳浩, 张文伟, 邓航, 等. 风电叶片静力试验配载优化与验证[J].
复合材料科学与工程, 2021(9): 18-21.
HE J H, ZHANG W W, DENG H, et al. Optimization and verification of static test for wind turbine blades[J].
Composites Science and Engineering, 2021(9): 18-21.
|
| [12] |
WALTERRUDIN, RUDIN, 赵慈庚, 等. 数学分析原理[M]. 北京: 机械工业出版社, 2004.
WALTERRUDIN, RUDIN, ZHAOC G, et al. Mathematical analysis principle[M]. Beijing: China Machine Press, 2004.
|
| [13] |
刘鸿文. 高等材料力学[M]. 北京: 高等教育出版社, 1985.
LIU H W. Higher mechanics of materials[M]. Beijing: Higher Education Press, 1985.
|
 2024, Vol. 50
2024, Vol. 50


 ,
,