0 引　言

传统的指向性校准是在自由场与远场条件下进行^[1]，但随着水声换能器工作频率的降低以及换能器体积尺寸的增加，使得其远场距离变大，实验室建造的消声水池狭小的空间已经难以满足测量所需要的自由场及远场条件^[2]，消声水池的造价昂贵，并且吸声材料无法对所有频段的反射波进行吸收，因此其声学参数的测量需要在开阔水域进行^[3]。开阔水域虽然解决了基阵工作频率低、尺寸过大导致自由场远场条件难以实现的问题，但是测量过程很难将基阵进行较深程度的吊放以减少水面反射的影响，需配备专门的吊装设备，设备维护工作量较大且测量的效率不高^[4]。同时，当基阵吊放至较深水域处难以获取基阵与标准声源的位姿，难以对基阵指向性进行标定。在指向性测量方面，国内外研究机构采用测量近场法测量换能器和阵的远场声特性^[5-8]，这种测量只需在被测对象的近场进行，但其工作效率较低，且存在测量区域选取不易和测量点数较多、运算量较大的问题。

针对大尺寸低频换能器其声学参数测量的局限性，文章采用超短基线定位技术，信号采用线性调频脉冲信号并结合脉冲压缩法对定位声源与基阵进行测距，发射伪随机编码脉冲信号配以复相关算法进行测向。通过对湖上定位精度的测试、湖上基阵指向性标定的静态试验、动态试验，对超短基线定位技术在基阵指向性标定中的应用效果进行了验证。

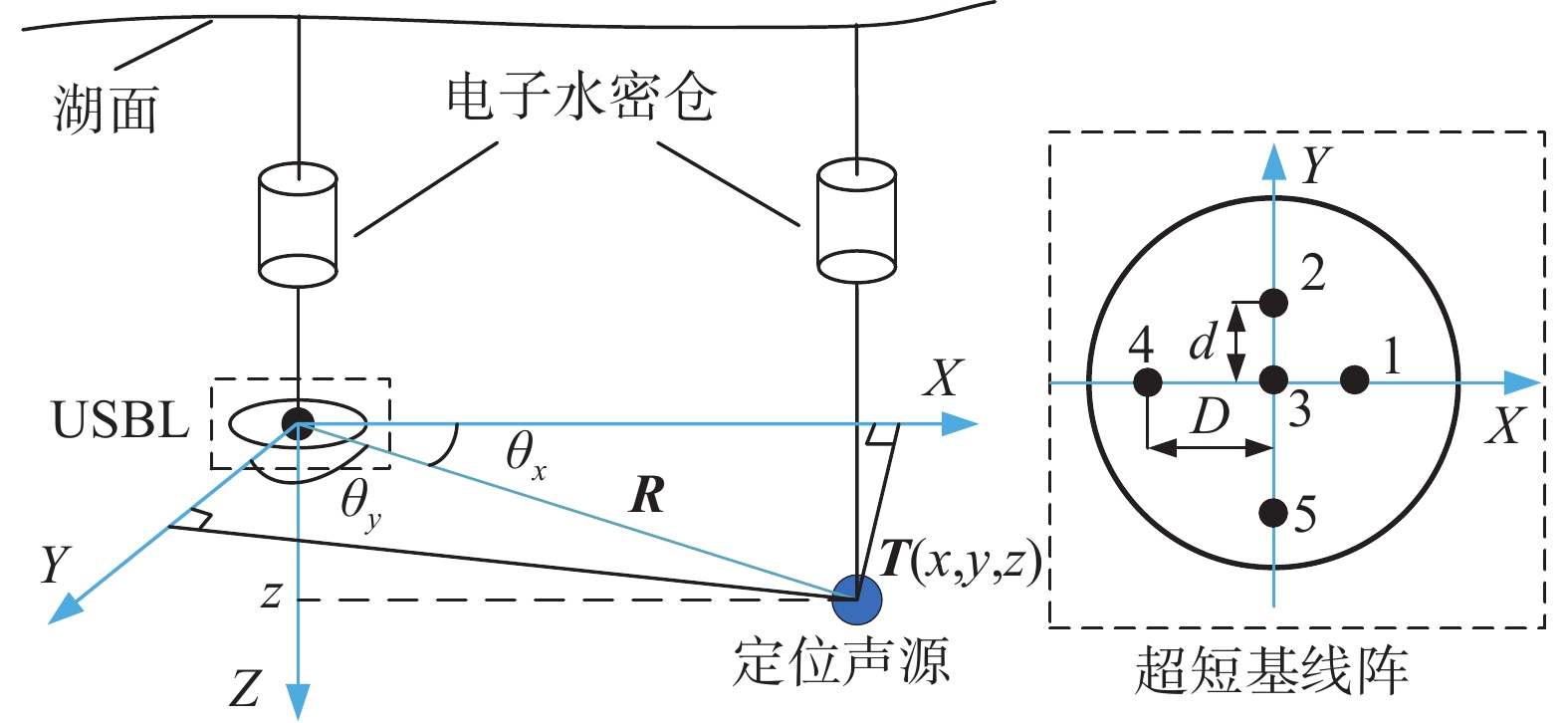
1 超短基线原理 1.1 超短基线定位理论

超短基线定位是通过测量信号到达接收基阵阵元之间的相位差和测量目标到基阵中心的斜距来实现定位^[9-10]。定位阵列由5个阵元按照如图1所示排列构成X、Y轴，每根轴上由三个阵元组成，最小阵元间距为d=150 mm，最大阵元间距D=Nd=450 mm。

假设声源为$ {\boldsymbol{T}}(x,y,{\textit{z}}) $。其矢量表示为：

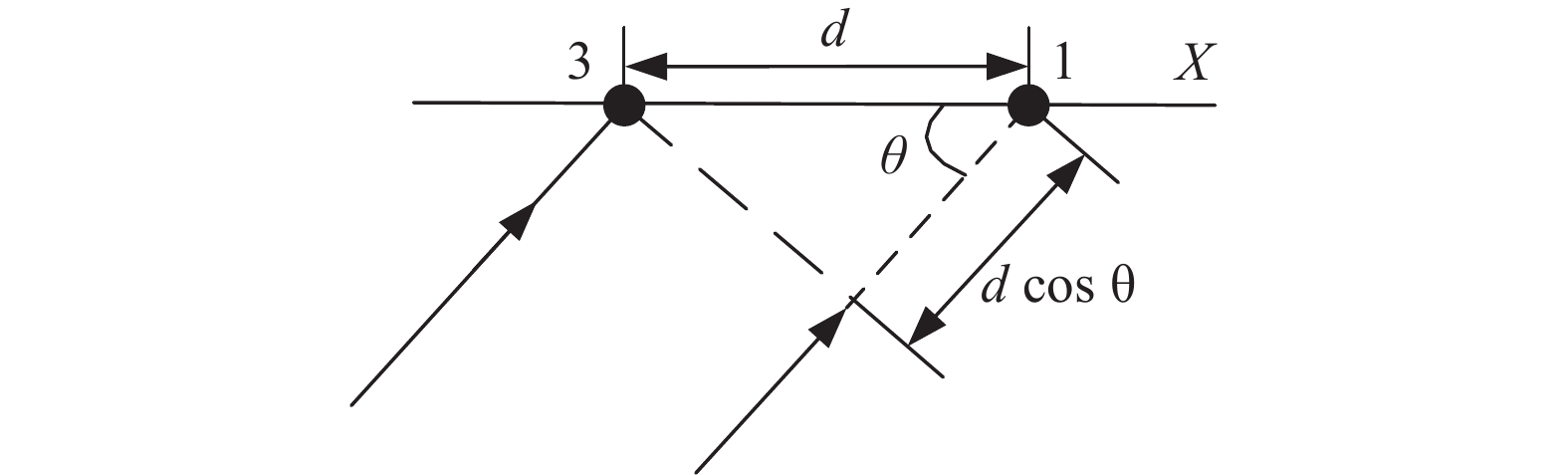
基阵阵元的尺寸较小，在远场条件下，入射到基阵阵元的声波线可认为近似平行，如图2所示。

则两阵元接收到的相位差可得如下关系：

式中：d——最小阵元间距；

$\theta $——信号入射角；

$d\cos \theta $——两阵元信号路程差；

c——水声声速；

$\lambda $——声信号波长。

可得到阵元1号和3号之间的相位差为：

同理，阵元2号和阵元3号之间的相位差为：

其中，$ {\theta _x} $为定位声源与X轴得夹角，$ {\theta _y} $为定位声源与Y轴的夹角。

将公式(2)、(3)、(4)代入公式(1)可得：

1.2 基于线性调频脉冲信号的测距算法

线性调频脉冲信号是应用最广泛的一种大带宽且适用于脉冲压缩技术的信号^[11]，经过脉冲压缩法匹配滤波器即可将能量汇聚从而得到较大的压缩比，增大信噪比^[12]。线性调频信号表示为：

式中：$ A $——信号的幅值；

$ {f_{\text{0}}} $——信号中心频率；

$ K $——信号的调频斜率。

$ K = B/T $，其中，$ B $为信号的带宽，$ T $为信号的脉宽。

脉冲压缩法是指对接收的调频或者扩频信号进行匹配滤波，能够通过聚拢带宽信号能量并抑制噪声信号使信噪比趋于最大的一种方法^[13]。其工作过程示意图如图3所示。

若匹配的滤波器输入信号为$s(t)$，输入噪声为$n(t)$，经过匹配滤波器后的信号为$ s_{\mathrm{o}}(t) $与信号$ n_{\mathrm{o}}(t) $相互叠加后的信号，假设当时间$ {t_m} $时输出信号的信噪比最大，利用频域表达可得输出信号为：

而白噪声平均功率为：

式中，N为噪声总功率。则匹配滤波器输出信号的噪声比带入式(7)、(8)可表示为：

借助柯西-施瓦茨不等式可得，当且仅当$ H({\text{j}}\omega ) = k{[S({\text{j}}\omega )\exp ({\text{j}}\omega {t_m})]^*} $时，信噪比为最大值。因此，最终得到的匹配滤波器为：

通过输入信号时域上反褶取其共轭设计匹配滤波器。信号输入匹配滤波器后即可实现脉冲压缩。则处理后的信号为：

其中$ * $表示为信号的卷积。

1.3 基于伪随机编码脉冲信号的测向算法

伪随机编码脉冲信号^[14]随着伪随机序列码元数的增加，自相关函数类比于冲激函数，具有很低的旁瓣，有利于微弱信号的检测。其中，伪随机编码脉冲信号可表示为：

式中：$ u(t) = a(t)\exp [{\text{j}}\phi (t)] $——信号的复包络函数；

$ \phi (t) $——相位调制函数。

二相编码信号的复包络可写成：

其中：P——码长；

$ {c_k} $——伪随机序列；

T——子脉冲宽度；

$ v(t) $——子脉冲函数。

对公式(13)进行傅里叶变换后可以得到频谱为：

假设定位阵列某阵元接收到直达波信号为：

式中：$ A $——幅度；

$\omega $——载波频率；

$ \varphi $——相位。

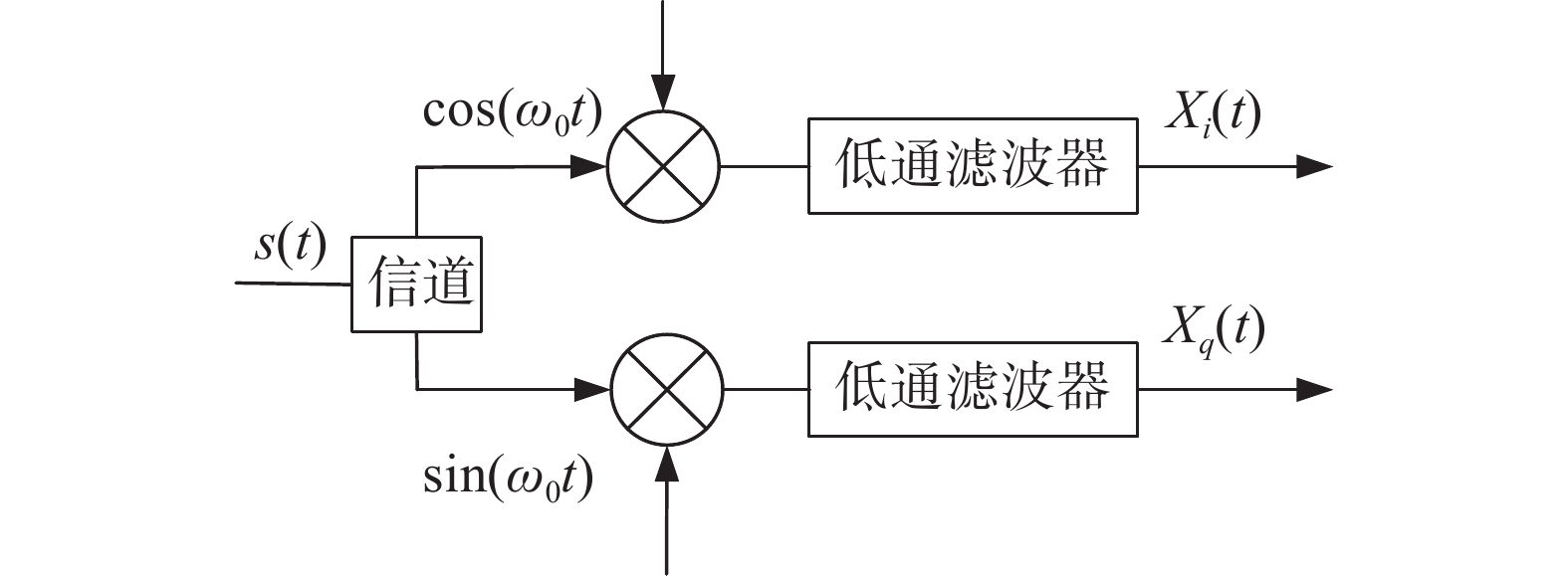
正交解调工作示意图如图4所示。

直达信号$ s(t) $经正交变换后，得到混频信号。当$ {\omega _0} $趋近于$ \omega $时，$ \omega + {\omega _0} $远远大于$ \omega - {\omega _0} $。因此，信号$ {X_i}(t) $和$ {X_q}(t) $经低通滤波器滤波后，其高频成分会被消除，仅保留低频成分，则输出信号表示为：

将其组合后即为直达波信号经过解调处理后的复数信号：

同理可得，测向两阵元接收到的信号可分别表示为$ {y_1}(t) $、$ {y_2}(t) $：

可以求得复相关函数$ R(\tau ) $：

代入公式(16)、(17)可得：

当正交解调处理时的载波频率已知时，复相关求得的相位值仅与测向信号的相关信号时延差有关，分析复相关函数的相位值就能得到测向信号的时延差。复相关函数的相位结果为：

式中：$ {{\mathrm{Im}}} {{R}}(\tau ) $——$ R(\tau ) $的虚部；

$ {{\mathrm{Re}}} R(\tau ) $——$ R(\tau ) $的实部。

因此测向信号的时延差可以表示为：

2 指向性标定实验 2.1 定位验证实验

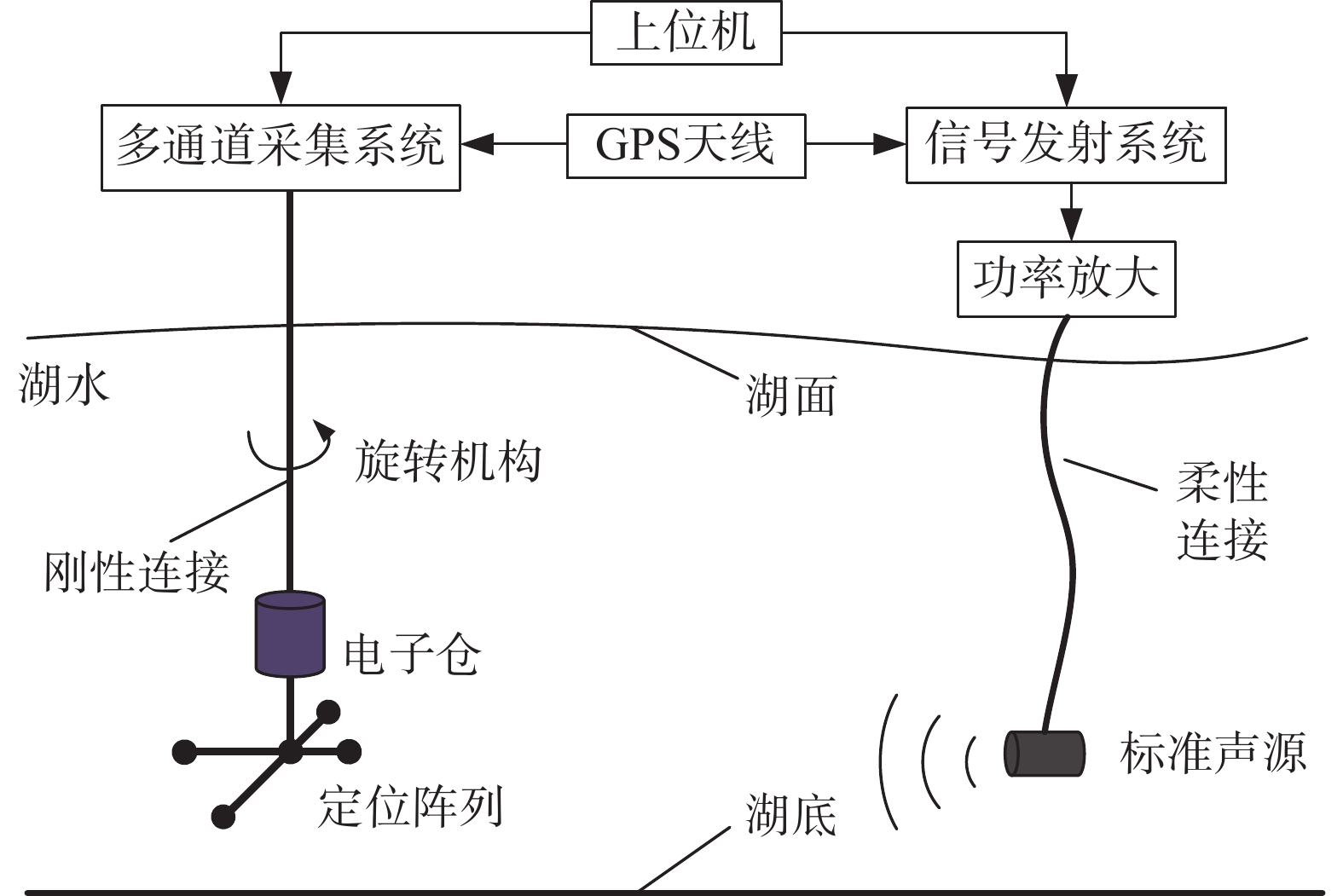
定位精度试验需要在已知角度的条件下进行，通过定位阵列获取的角度值对比理论结果实现定位精度的验证。其测量示意图如图5所示。

试验时，定位阵列通过旋转机构刚性连接于水下10 m处，通过旋转机构实现定位阵列的定角度转动，同时，相距10 m处的平台边缘吊放定位声源，用于超短基线定位，为保证接收信号信噪比达到测试要求，定位声源及定位阵列信噪比在测量频段内声源级达到170 dB，且定位声源发射脉宽为20 ms、频率为4 kHz的正弦脉冲信号、脉宽10 ms、带宽为2 kHz、中心频率为7 kHz的线性调频脉冲信号和码元数为16、中心频率为4 kHz的伪随机编码脉冲信号拼接而成的信号，步进角度为2°，声源经由功率放大器放大后发出声波信号，通过多通道采集系统将采集到的信号进行数据的处理分析。试验采用了型号为LPA-200的国产功率放大器，阻抗调节范围为8 Ω~1 kΩ，可对1 ~20 kHz频段的信号进行增益放大调节，并具有输出电压和电流监视的功能。信号发射系统采用NI公司型号为PXI-4461信号发射器，具有204.8 kS/s采样率的双通道动态信号生成；多通道信号采集系统选用NI公司型号为NI PXI-4462的采集卡，采样率高达204.8 kS/s，可同步采集4路模拟信号。

2.2 基阵指向性标定静态实验

静态试验用于校准低频基阵指向性，需在已知角度的情况下对接收阵列进行校准，其测试的结果作为参考的指标，旋转机构可实现模拟基阵的定角度转动。静态实验需将待测10阵元水听器阵列取代图5定位阵列并刚性吊放至同等深度。待测阵列的分布示意图如图6所示。

结构排布为线状，从左至右为1-10号阵元，坐标分别为–0.673 m，–0.423 m，–0.173 m，–0.113 m，–0.053 m，0.053 m，0.113 m，0.173 m，0.423 m，0.673 m。其现场测试图如图7所示。

模拟基阵刚性连接于旋转机构上，放至水深10 m处，标准声源相距10 m处同深度吊放至水下，标准声源发射频率为4 kHz、脉宽为20 ms的正弦脉冲信号与带宽为2 kHz、脉宽为10 ms、且中心频率为7 kHz的线性调频脉冲信号拼接后的信号，同时旋转机构的步进角度为2°。在GPS秒脉冲信号上升沿时，通过多通道采集系统采集经功率放大器放大后的接收阵列各阵元信号并且存储至上位机进行分析。GPS秒脉冲模块使用北微公司的BS-125模块，输出信号为周期1 s、占空比为10%的秒脉冲信号，用于实现测量端系统与定位端系统的时间同步。

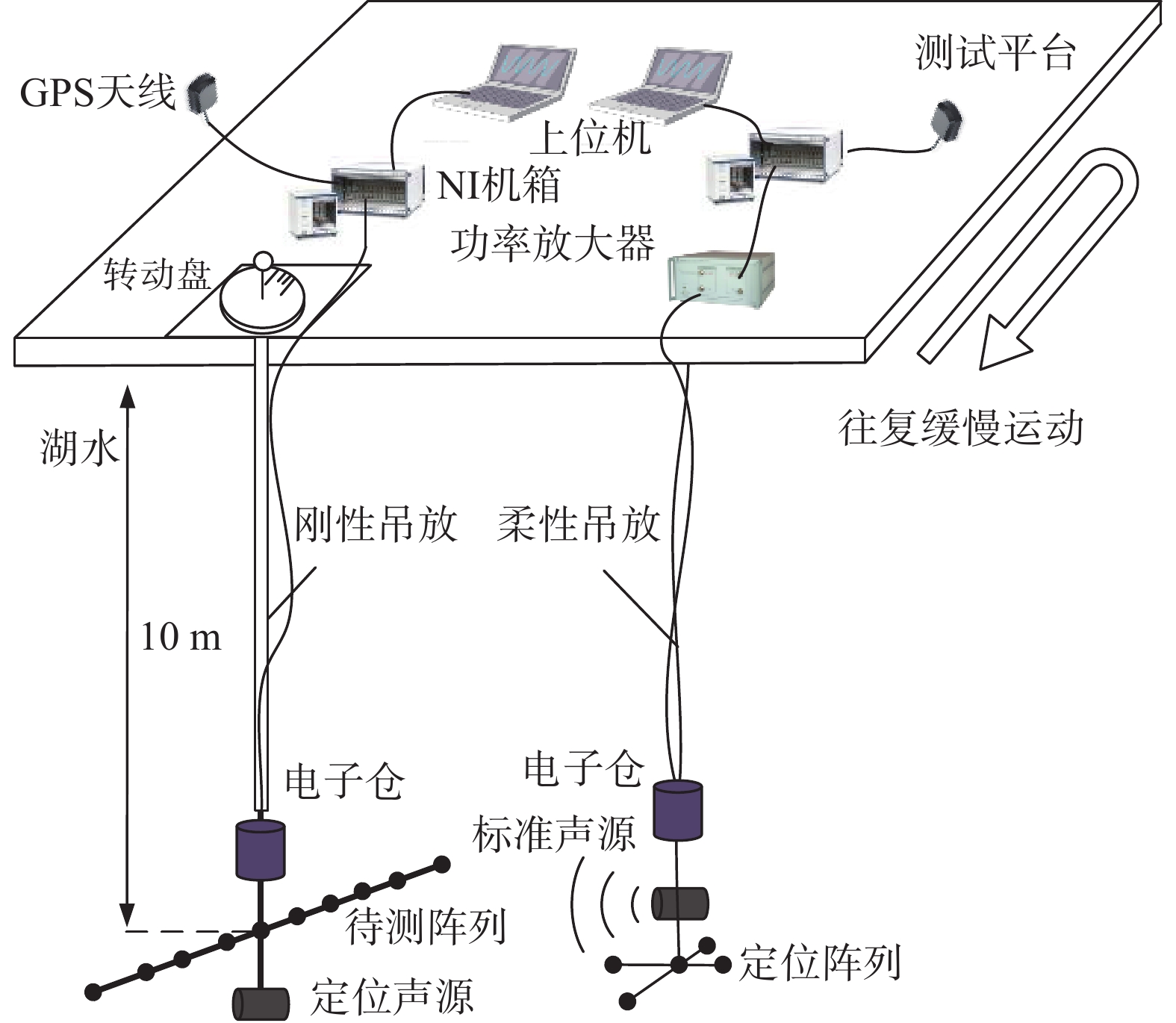
2.3 基阵指向性标定动态实验

其测量原理如图8所示，模拟基阵通过刚性连接放至水下10 m处，定位阵列同深度放至平台边缘作来回往返运动，标准声源发射脉宽为20 ms，频率为4 kHz的正弦脉冲信号与脉宽为10 ms，带宽为2 kHz、中心频率为7 kHz的线性调频脉冲信号和码元数为16、中心频率为4 kHz的伪随机编码脉冲信号拼接而成的校准信号。

当GPS偶数秒脉冲上升沿时，触发测量端生成信号，经由功放放大后发射，定位阵列同步采集阵元信号并上传至计算机进行实时计算显示和保存；在GPS奇数秒脉冲上升沿时，触发定位端信号发射系统生成待测频率的脉宽为20 ms的正弦脉冲信号与脉宽10 ms、带宽2 kHz、中心频率7 kHz的线性调频脉冲信号拼接而成的校准信号，校准信号的频率分别为2、4、6、8、10 kHz，同时进行信号数据采集。

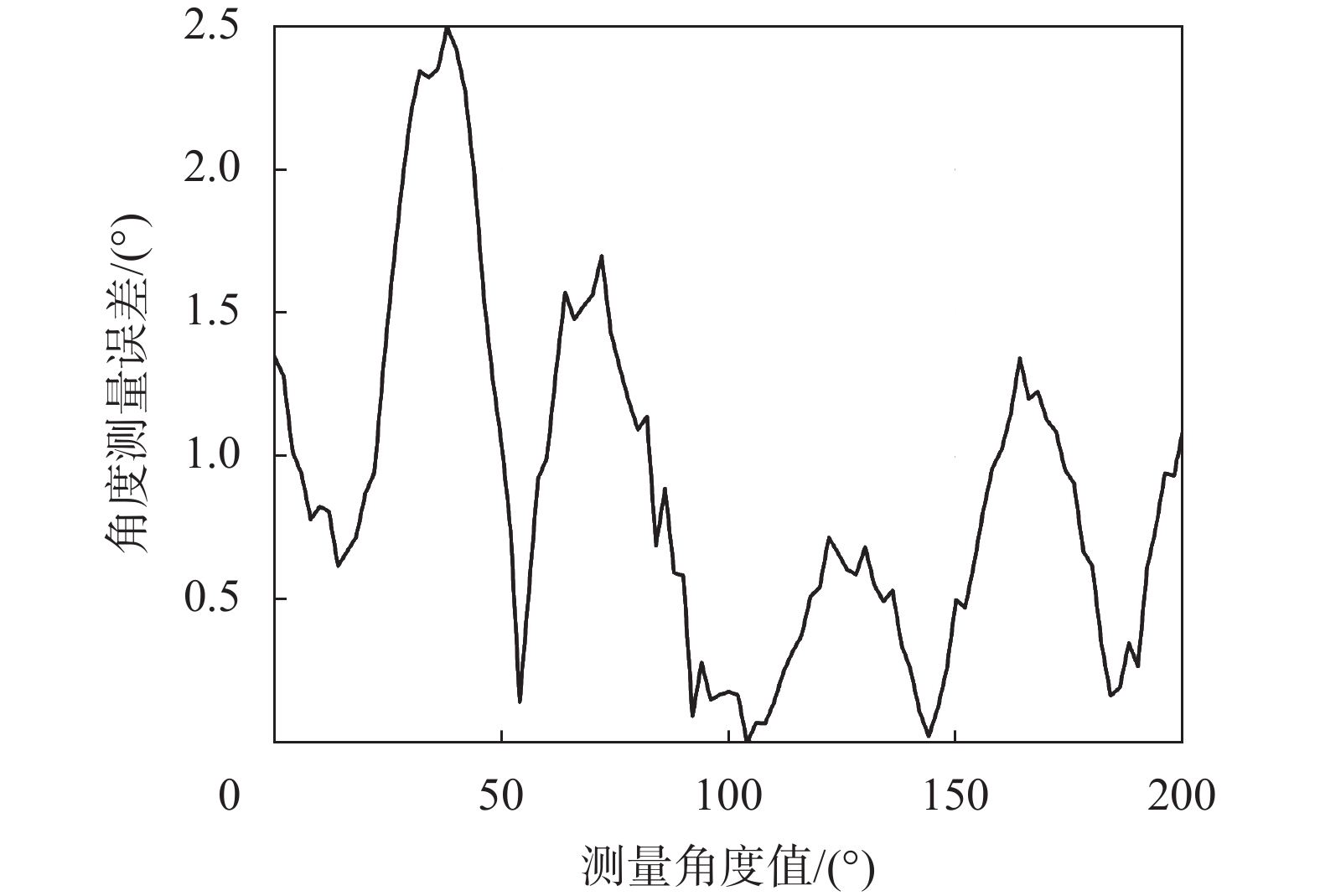
3 试验结果分析 3.1 定位精度试验结果分析

通过脉冲压缩法和复相关算法分别处理线性调频脉冲信号与伪随机编码脉冲信号，计算得到实际测量角度值对比理论结果得到其测量偏差曲线，其偏差曲线如图9所示。

由偏差结果分析可知，发射宽带信号进行超短基线定位时，最大角度偏差为2.5°。验证了超短基线定位应用于低频基阵指向性标定的可行性。

3.2 指向性标定对比结果

为了验证基阵指向性标定方法的有效性，分别对2、4、6、8、10 kHz的阵列仿真结果、基阵指向性标定静态试验结果与基于超短基线定位原理的基阵指向性标定动态试验结果进行比较，结果对比如图10所示。

阵列仿真、基阵指向性标定静态试验与超短基线用于基阵指向性标定的动态试验三者对比–6 dB波束宽度结果如表1所示。

由试验及仿真结果可知，在频率为2、4、6、8、10 kHz情况下，基于超短基线定位原理的标定试验得到的–6 dB波束宽度结果相较于静态测量法以及仿真结果得到的–6 dB波束宽度结果最大偏差为5.38%，其测试结果在误差范围10%之内。

4 不确定度分析

测量系统的不确定度由两部分组成，其一主要由重复性引入的测量不确定度，称为测量不确定度A类评定；其二由测量系统本身及测量方法不完善等因素引入，通过理论分析及进行评定，称为测量不确定度B类评定^[15]。

在该校准方法测量不确定度A类评定研究中，本次试验对指向性结果重复测量三次，由重复性引入的A类标准不确定度${u_{\text{A}}}$为：

测量系统的测量不确定度B类评定${u_{\text{B}}}$通过概率分布进行计算，常见有均匀分布和正态分布。

主要不确定度来源有采集卡引入的测量不确定度，测距、测向等由于时间和声速引入的测量不确定度，标听灵敏度准确性引入的不确定度，周围噪声引入的测量不确定度等。

系统中采用的采集卡的测量误差不超过0.05 dB，以均匀分布考虑，取k为$ \sqrt 3 $，其不确定度为：

测距有时间和声速两个影响量，由此带来的测距误差小于0.001 dB，服从均匀分布，计算其不确定度分量：

测向同测距相似，均有时间和声速影响，由此带来的测向误差小于0.2 dB，服从均匀分布，其不确定度分量为：

由标准水听器灵敏度引入的不确定度，服从正态分布，k取1.96。则不确定度分量为：

周围噪声引入的不确定度不应超过±0.1 dB，服从均匀分布，其不确定度分量约为：${u_{{\text{B5}}}} \approx 0.1\;{\text{dB}}$

则B类标准不确定度的结果约为：

通过合成标准不确定度公式计算结果约为：

取包含因子k=2，不确定度的置信水平约为95%，则指向性测量的扩展不确定度为：

5 结束语

本文提出了一种超短基线定位理论应用于开阔水域环境下基阵的指向性校准，信号上选用了线性调频脉冲信号与伪随机编码脉冲信号，并分别基于脉冲压缩法和复相关法实现距离和相位测量。通过湖上定位精度验证试验、基阵指向性标定的湖上静态试验以及基于超短基线定位理论的基阵指向性标定动态试验，通过对比两种测量方法的指向性测量结果同仿真趋势相同，–6 dB波束宽度测量误差满足水声指向性测量标准中测量误差低于10%的测量要求。实验结果证明，基于超短基线定位理论的基阵指向性标定试验测量结果准确度符合要求，可以广泛应用于开阔水域指向性校准测量。