0 引　言

转炉炼钢节约能源、效率高，是目前广泛应用的炼钢方法。转炉炼钢工艺流程是一个多元多相高温物理、化学反应过程，将氧气吹入熔池与铁水中各种元素发生氧化反应，完成脱碳等杂质任务，反应过程中放出的热量将钢液加热，在吹氧结束时，终点钢水碳含量和温度应满足出钢要求，否则会影响冶炼过程中的能量、合金元素收得率、炉衬使用寿命及出钢质量等技术经济指标，降低冶炼效率^[1-2]。整个工艺过程具有复杂性、非线性、时滞性等特点，难以建立准确的数学模型。建立转炉终点的预报模型可为转炉终点提供有力判断，能够有效提高钢厂生产效率、减少资源浪费。

目前，转炉终点碳温检测主要包括人工经验取样分析法、副枪检测法、烟气分析法、火焰图像处理法和基于数据驱动的软测量建模法等^[3]。人工经验法易受主观因素影响，终点命中率低。副枪检测与炉气分析测量存在滞后性，价格昂贵，难以广泛应用。徐刚等^[4]提出了利用烟气分析实时监测碳氧信息的数字孪生预测函数模型，因烟气易受空气影响产生预测误差。张彩军等^[5]提取了火焰光谱特征并进行叠加，反映了全光谱信息，结合极限学习机算法得到了高精度碳温动态预测模型。但火焰图像处理过程较为复杂，且易受环境影响。柴天佑等^[6]采用RBF与灰色模型相结合的方法用于转炉终点预报，同时解决了定量因素和非定量因素的影响，从而提高预报精度；COX I J等^[7]检测冶炼接近结束时的温度值，将测量值作为人工神经网络模型的输入，以预测补吹氧气和添加冷却剂量，使达到出钢条件；CEMALETTIN K等^[8]应用模糊建模方法控制转炉过程中的部分参数，实现炼钢过程的更优控制。HAN M等^[9]将基于经验的案例推理(CBR)模型与基于数据的支持向量机(SVM)模型相结合，获得了比单一模型更好的预测结果。

上述基于数据驱动的软测量建模方法重点考虑了过程数据输入变量与终点碳温之间关系，减少了其他因素的不利影响，但对于解决复杂问题泛化能力较差，难以选择最优参数。相较于其他模型，梯度提升决策树具有预测精度高、可解释性强、鲁棒性强的优点；贝叶斯优化算法相较于其他优化算法能够高效寻找超参数，本文将二者有机结合，提出了基于贝叶斯优化梯度提升决策树的转炉终点预测模型。通过分析对比转炉炼钢终点几种预测方法对某钢厂历史数据进行软测量建模。结果表明，本文提出的预测模型预报终点碳温精度高、误差小，满足实际生产要求。

1 转炉炼钢终点碳温预测模型

GBDT模型通过设置不同的可微损失函数处理各类学习任务，是一族可将弱学习器提升为强学习器的串行序列化算法，将所有学习器预测值加权结合生成预测结果^[10]。

本文将转炉炼钢过程装入铁水量、废钢量、耗氧量、生石灰等作为GBDT回归模型的输入变量，将转炉炼钢终点碳含量或温度作为输出变量，输入训练数据集为$ D = \left\{ {\left. {({x_1},{y_1}),({x_2},{y_2}),\cdots ,({x_N},{y_N})} \right\}} \right. $，其中$ {x_i} $（$ {x_i} \in X \subseteq {{\bf R}^n} $）为影响转炉终点碳含量或温度的因素，$ X $为输入样本空间；$ {y_i} $（$ {y_i} \in Y \subseteq {\bf R} $）为转炉终点实测碳含量或温度，$ Y $为输出样本空间；损失函数为$ L(y,h(x)) $，基分类器为$ {h_m}(x) $，输出最终决策树$ {h_M}(x) $。GBDT预测模型建模步骤如下^[11]：

1）初始化弱学习器：

2）对于基学习器$ {h_m}(x),m \in \{ 1,2,3,\cdots ,M\} $即建立的M棵回归树：

a.计算每一个样本对应的损失函数的负梯度：

b.将上步得到的梯度作为样本新的真实值，并将数据$ ({x}_{i},{r}_{m,i}) $作为下棵树的训练数据，得到第m棵树的叶结点区域$ {R_{m,j}},j = 1,2,3,\cdots ,J $，j为叶结点数量。

c.对叶子区域$ j = 1,2,\cdots ,J $，计算最佳拟合值：

d.更新当前强学习器：

3）得到最终回归树：

2 贝叶斯优化梯度提升决策树 2.1 贝叶斯优化算法

应用贝叶斯优化算法求解转炉炼钢终点目标函数表达式未知的复杂优化问题。对于给定优化目标函数，在参数空间内随机采样，初步得到目标函数分布，不断迭代寻找未知目标函数的最优解，直到采样点拟合分布大体与真实目标函数接近。贝叶斯优化的两个主要部分为概率代理模型和采集函 数^[12-13]。

由下式对先验概率修正，得到修正后的未知函数置信度：

式中：f——未知目标函数；

D−已采集的样本点集合($ D = \left\{ \left( {{x_1},{y_1}} \right), \left( {{x_2},{y_2}} \right), \cdot \cdot \cdot, \left( {{x_t},{y_t}} \right) \right\} $，x_t为观测到的参数，$ {y_t} = f({x_t}) + {\delta _t} $为观测值)；

p(D| f )——y的似然分布；

p(f |D)——f的后验概率；

p(f )——f的先验概率；

p(D)——边际似然分布。

本文概率代理模型选择非参数模型高斯过程，此过程是需要优化的GBDT模型的参数组合^[14]，如下式所示：

式中：f(x)——平均绝对误差；

p(f |D)——f的后验概率分布；

μ(x)——均值函数，一般设为0；

$ k(x,x') $——协方差函数。

为了避免贝叶斯优化陷入局部最优解，本文选择基于提升策略的EI(excepted improvement)函数作为采集函数。

2.2 贝叶斯优化梯度提升决策树回归模型建模过程（BOA_GBDT）

GBDT算法模型参数较多，主要考虑弱学习器的最大迭代次数、权重缩减系数、决策树最大深度和子采样比例。若最大迭代次数太小容易欠拟合，太大容易过拟合；弱学习器的权重缩减系数与最大迭代次数互相影响，对于同样的训练集拟合效果，较小的权重缩减系数需要的迭代次数更多，实际调参时常将两参数一起考虑；决策树最大深度太小容易欠拟合，太大会导致决策树模型过于复杂，容易过拟合，泛化能力下降；子采样比例取值会影响样本拟合偏差，但在一定程度上可以防止过拟合。

选择和调节模型参数理论尚未建成，需要人工调参，耗时长且存在不定性，合适的参数能极大程度地提高模型预测精度。因此，本文将贝叶斯优化算法引入到GBDT模型中，利用贝叶斯优化算法的超参数寻优获取模型最优参数。针对GBDT模型参数特性，模型参数范围设置如下：最大迭代次数、权重缩减系数、决策树最大深度和子采样比例的取值区间分别为[10,1000]、[0.001,0.1]、[1,100]、[0.1,1]。在这些区间随机生成初始化样本点，输入到高斯过程中以训练GBDT模型，利用GBDT模型目标函数输出的损失值对高斯模型进行修正，使高斯模型更加接近实际函数分布。然后，运用采样函数在修正后的高斯模型中选取下一组需要评估的样本点x_i，x_i作为GBDT模型输入进行训练，获得目标函数新的输出值y_i，以此来更新样本集合$ {D_t} = \left\{ \left( {{x_1},{y_1}} \right), \left( {{x_2},{y_2}} \right), \cdot \cdot \cdot, \left( {{x_t},{y_t}} \right) \right\} $和高斯模型^[15]。

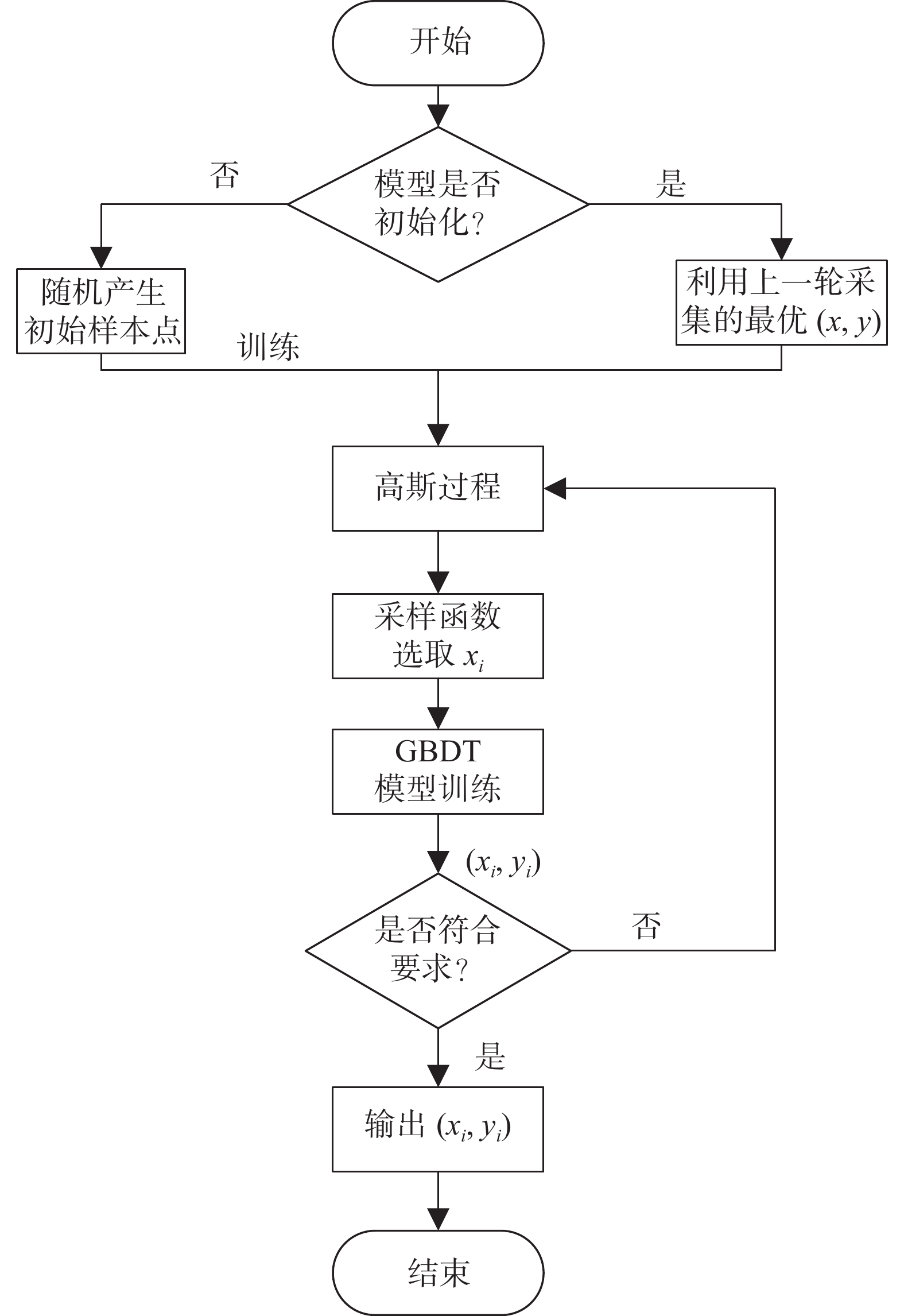
若新选取的样本点x_i对应的目标函数损失值符合要求，则终止算法执行并退出，输出当前选取的最佳参数组合；若不符合要求，则将(x_i,y_i)更新到D_t中，继续修正高斯模型，直到满足要求。最后，据此最佳参数组合训练GBDT模型，进而建立BOA_GBDT预报模型。图1为BOA_GBDT模型的工作流程图。

3 仿真实验及分析 3.1 数据处理

分析转炉终点预测原有机理模型和数据模型，并结合专家经验，本文选用A钢厂转炉生产2021年1月-6月内的部分实际生产数据，历史库数据样本400炉次，包括铁水装入量、废钢量、耗氧量、白灰、生白云石、吹氧量等，部分原始数据如表1所示。对实验数据进行缺失值填补、异常值剔除，利用特征选择^[16]结合专家经验选取与终点碳温相关性较高的特征，终点碳含量预测模型的输入特征主要包括装入废钢量、铁水温度、轻烧白云石、生白云石、补吹氧气量、主吹结束钢水温度、主吹结束钢水碳含量；终点温度预测模型的输入特征主要包括装入铁水量、铁水P含量、氧枪枪位、氧压、补吹氧气量、主吹结束钢水温度、主吹结束钢水碳含量。

为了消除不同评价指标之间的量纲影响，使各指标处于同一数量级，提升模型收敛速度及精度，对数据进行归一化处理^[17]：

式中：$ Z $——归一化后数据；

$ x $——原始数据；

$ \mu $——所有数据样本均值；

$ \delta $——所有样本数据标准差。

将处理完成后的优质数据选取270组作为训练集，100组作为测试集。

3.2 贝叶斯超参数优化结果

GBDT终点碳含量预测模型贝叶斯优化输出最优参数：权重缩减系数0.001、决策树最大深度47、最大迭代次数853和子采样比例1.0；终点温度预测模型贝叶斯优化输出最优参数：权重缩减系数0.001、决策树最大深度500、最大迭代次数920和子采样比例0.3。RBF终点碳预测模型贝叶斯优化输出最优参数：隐藏层节点数σ=35，终点温度预测模型输出最优参数：σ=40。SVM终点碳预测模型贝叶斯优化输出最优参数：惩罚系数C=184.1、选择径向基作为核函数自带的一个参数gamma=141；终点温度预测模型贝叶斯优化输出最优参数：C=711.4、gamma=445。

采用上述最优参数组合分别训练GBDT模型。

3.3 终点碳温预测实验结果

分别建立BOA_RBF、BOA_SVM、BOA_GBDT的转炉终点碳含量和温度预测模型，比较3种模型的误差和碳含量在±0.01%、温度在±10℃误差范围内的命中率。实验参数均由实际炼钢记录所得，输入数据为特征选择后并处理的铁水装入量、废钢量、轻烧白云石、生白云石等特征量，输出为转炉终点碳含量或温度。以模型的均方根误差（root mean square error，RMSE）和平均绝对误差（mean absolute error，MAE）、命中率（hit rate，HR）作为回归模型的评价指标。计算公式如下：

式中：n——测试样本数量；

$ {y}_{{\mathrm{true}},i}、{y}_{{\mathrm{pre}},i} $——转炉终点碳含量或温度实际值和预测模型输出值；

HS——预测误差，在命中区间时即为命中，值为1，其他情况记为0。

RMSE、MAE值越小，说明实验数据预测值与实际值越接近、拟合效果越好、预测模型描述的实验数据精确度较高。

碳含量预测误差范围S为±0.01%，温度预测误差范围S₁为±10℃，HR表示碳温在误差范围内的预测精度，该值越大表示该模型的预测性能越好。在pycharm2020.2.2X64环境下模型对比结果如表2所示。

由表2可得，优化的RBF终点预测模型的误差最大，命中率HR最低，预测效果最差；优化的SVM命中率略高于RBF，误差略小于优化的RBF；贝叶斯算法优化GBDT，即BOA_GBDT各项指标最优，碳含量预测模型的命中率最高，RMSE与MAE最小。

3个优化模型的转炉终点碳含量、终点温度的模型预测效果如图2、图3所示。

由图可知，优化的RBF和SVM预报模型预测效果较差，难以取得较好预测结果。相对来说，BOA_GBDT采用贝叶斯优化算法对GBDT模型参数寻优，效果最好。

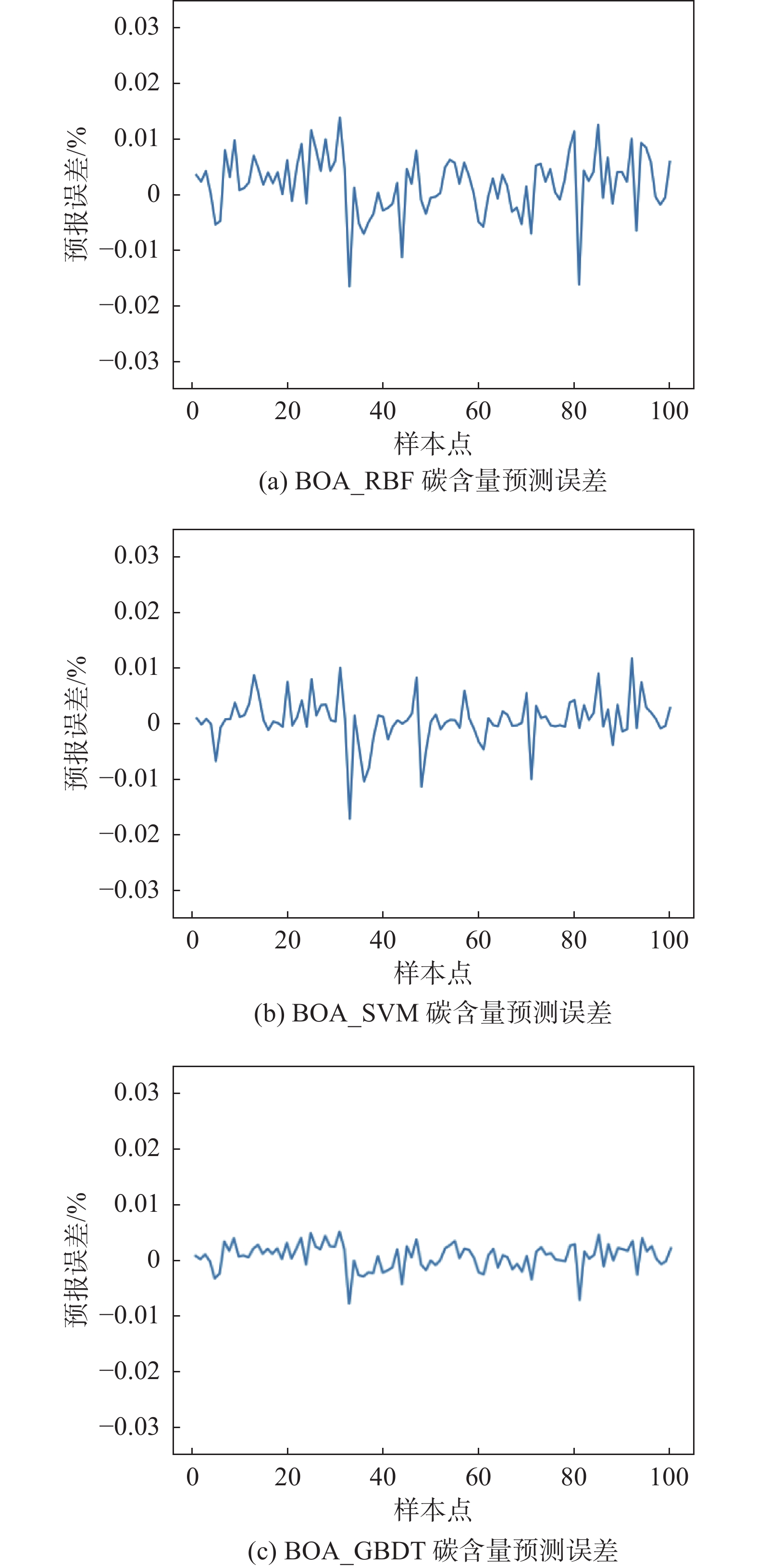
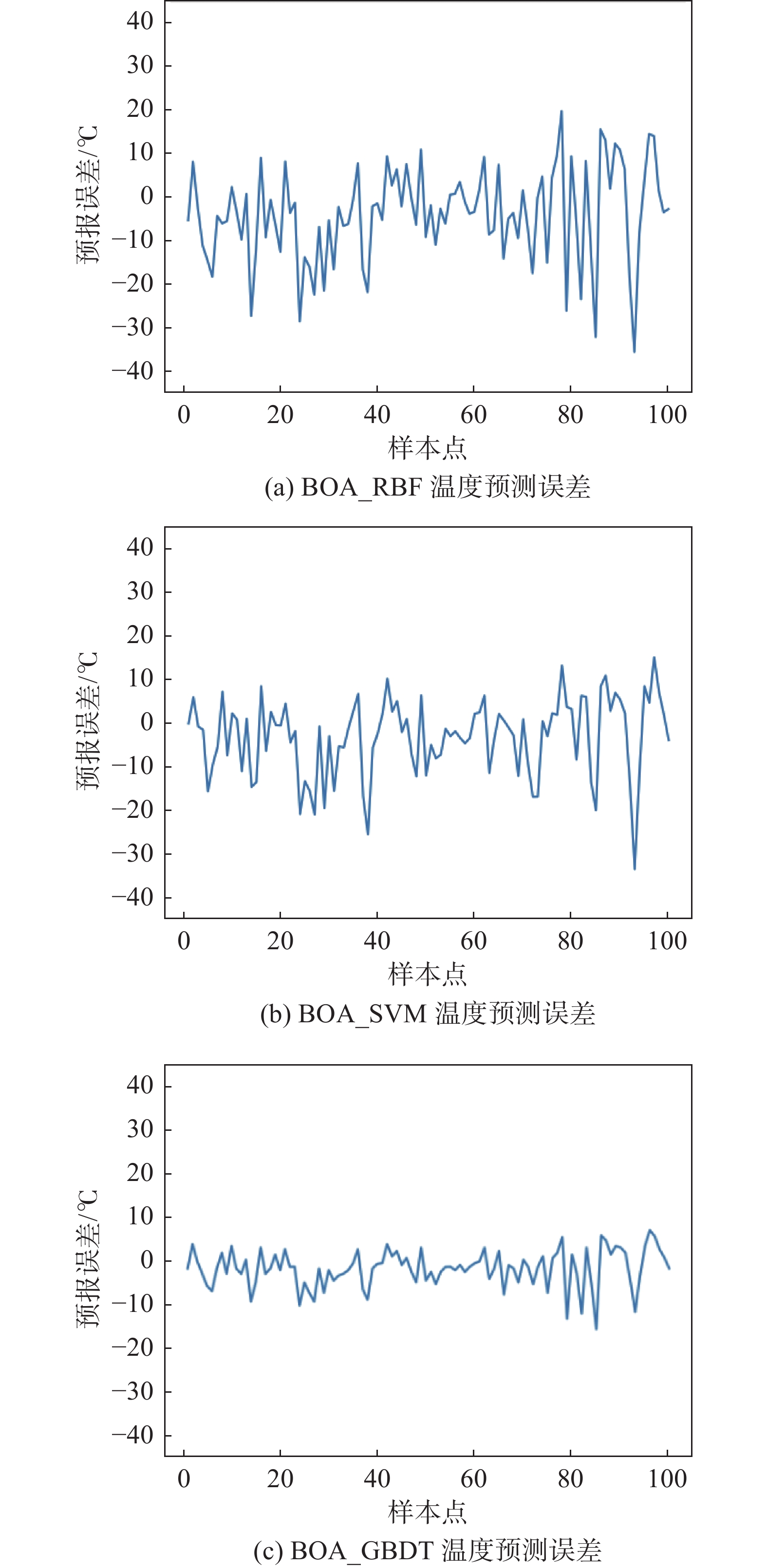
转炉终点碳含量、终点温度的模型预测误差如图4、图5所示。由图可知，BOA_GBDT预测模型在转炉终点碳含量、温度预测方面误差最小，效果最佳，更具优势。BOA可迅速并合理地选择最优模型参数，提高预测模型的准确性、稳定性和泛化能力。

将BOA_GBDT预测模型与RBF、SVM、GBDT预测模型进行对比，如表2、表3所示。由各项评价指标可知，BOA_GBDT模型预测碳温命中率最高，各项误差均最小。对于终点碳温预测模型，BOA_GBDT相比于GBDT模型RMSE与MAE均有所降低、碳含量HR提高了2.1%，温度HR提升了8.3%，说明贝叶斯优化算法能显著提高模型精度。

4 结束语

本文结合贝叶斯优化算法的全局寻优能力和梯度提升决策树的鲁棒性优点，提出了基于贝叶斯算法优化梯度提升决策树回归模型，可准确预测转炉终点碳含量和温度，为提高转炉终点命中率提供了新方法和思路。以A钢厂氧气顶吹转炉炼钢生产线采集的实际生产数据，对模型进行训练和测试，BOA_GBDT模型对转炉终点碳温预测结果与现场实际检测结果高度一致，转炉炼钢终点碳含在误差区间内的命中率达到96.2%，温度命中率达到92.1%，说明贝叶斯优化算法能显著提高模型预测性能，为转炉炼钢终点预报提供了合理的建模过程。