0 引　言

气液两相流广泛存在于能源、电力、化工、冶金等工业过程。其中，截面含气率是两相流研究领域内的重要参数之一^[1-2]。安全且准确地测量含气率对工业中两相流系统的稳定运行具有重要的意义^[3]。常用的含气率测量方法有很多，如快关阀法、射线法、光学法等^[4]。快关阀法指在一对阀门快速关闭后，测量封闭管段的液体流量，并经计算获得含气率，但阀门关闭会破坏两相流的流动状态。射线法是根据不同介质分布对射线的吸收程度不同来测量含气率，但射线具有辐射性，实验中存在安全隐患。光学法则是使光源穿过两相流体后，根据光学传感器获取的信号测量含气率，但此法的设备维护成本较高。上述方法很难满足工业要求，因此，需要一种非侵入式、适用性广且安全性高的含气率测量方法。ERT传感器具有非侵入性、适用广泛且信息获取速度快等优点，因此被广泛应用于多相流问题研究中^[5-6]。使用ERT技术获取截面含气率时，需先进行图像重建，再根据重建图像求取含气率。但该方法的效率较低，当研究较长时间内的含气率变化情况时，要不断地进行图像重建，并计算相应的含气率。

近年来，传感器信息结合机器学习的测量方法成为两相流参数测量问题研究的主要技术路线之一。文献[7]以电容层析成像传感器电容值为特征，使用最小二乘支持向量机测量了离散相浓度值。文献[8]根据压力信号结合BP神经网络实现了气液两相的流量测量。受到上述工作的启发，尝试一种ERT传感器信号结合机器学习的含气率测量方法。Elman神经网络作为一种经典机器学习方法，在故障诊断^[9]、参数预测^[10]等方面都表现出良好的性能。但Elman神经网络泛化能力会受到初始化参数的影响，故使用PSO算法为该网络寻找合适的初始参数。而PSO算法易陷入局部最优^[11]，因此对该算法的惯性权重和学习因子计算式进行改进，实现全局搜索能力与局部搜索能力的均衡，并加入遗传算法的交叉和变异行为，保证粒子多样性，得到搜索能力更强的IPSO算法。由于阵列电阻特征维度较高，需降维处理以避免数据冗余。PCA经正交变换将高维特征降为低维特征，可有效减少模型训练时间，并降低模型参数复杂度，常被用于数据降维^[12]。

综上，本文提出一种ERT传感器结合Elman神经网络的含气率测量方法。先使用PCA算法对归一化阵列电阻进行降维，然后使用IPSO算法优化Elman神经网络的初始参数并建立含气率测量模型。借助模型的泛化能力实现阵列电阻到含气率的映射，以省去ERT常规方法中的图像重建与图像处理过程。最后使用实验数据验证了所提方法的可行性。

1 ERT系统工作原理简介

ERT系统由传感器单元、数据采集单元、计算机单元组成^[13]。该系统的测量原理框图如图1所示。其中，传感器单元由一定数量的金属电极组成，使用时需将其安放于被测管道。经ERT系统可获取反映场域内介质分布规律的阵列电阻特征。获取过程如下，对任一极板施加激励，当管道中两相流动状态发生变化，那么敏感场中的电阻率分布也发生变化，则极板上的电阻发生改变。改变激励位置并测量不同极板的阵列电阻，经一周的激励后，得到ERT系统的一次完整测量值。测量过程描述如图2所示。

可以发现，一次完整测量获得的电阻数目取决于ERT传感器的电极数目，对于n电极的ERT传感器，经一次测量，可获得n(n-1)/2个独立电阻值。那么16电极ERT传感器经一周激励可获取120个电阻值。

2 IPSO算法优化Elman神经网络 2.1 Elman神经网络

Elman神经网络是一种反馈型神经网络。该网络结构包含输入层、隐含层、承接层与输出层。其中，承接层存储了隐含层前一时刻的输出信息，与输入一同参与下一次隐含层输出的运算，提高了信息的利用率。

Elman神经网络的运算表达式为：

式中：$ {u_{\mathrm{n}}}(k) $——网络的输入；

$ {x_{\mathrm{h}}}(k) $——隐含层输出；

$ {x_{\mathrm{c}}}(k) $——承接层输出；

$ y(k) $——输出层输出；

$ {w_1} $、$ {w_2} $、$ {w_3} $——承接层与隐含层、输入层与隐含层、隐含层与输出层之间的权值；

$ {b_1} $、$ {b_2} $——输入层与隐含层、隐含层与输出层之间的阈值；

$ F( * ) $和$ G( * ) $——隐含层和输出层的激活函数。

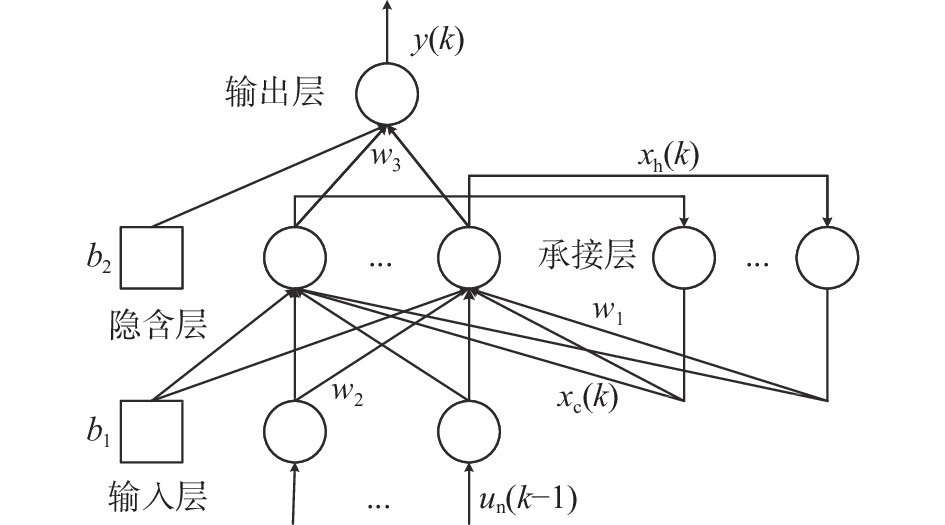
单隐含层的Elman神经网络结构如图3所示。Elman神经网络经随机初始化得到权值和阈值，这会导致网络的泛化能力不稳定，需使用搜索算法对网络参数进行优化。

2.2 PSO算法及改进

PSO算法的思想来自于鸟类觅食过程。该算法常被用于神经网络参数寻优^[14]。标准PSO算法位置和速度更新公式如下式所示：

式中：$ w $——惯性权重；

$ {c_1} $和$ {c_2} $——个体学习因子和社会学习因子；

$ {r_1} $和$ {r_2} $——0~1的随机数；

$ {v_{in}}(t) $——粒子当前飞行速度；

$ x(t) $——当前粒子位置；

$g_{\rm best}$和${\textit{z}}_{\rm best}$——个体最优位置和群体最优位置。

对PSO算法进行改进。惯性权重大小影响粒子当前速度对前一次粒子速度的保留程度。为了权衡粒子的全局搜索能力和局部搜索能力，引入一种自适应惯性权重，其计算式如下式所示：

式中：$ {f_n} $——第n个粒子的适应度；

$ {f_{\max }} $和$ {f_{\min }} $——当前粒子群中最大和最小适应度；

$ {w_{\max }} $和$ {w_{\min }} $——设定惯性权重的上限值和下限值；

$ i $——粒子现在的搜索次数；

$ m $——设定的最大搜索次数。

学习因子可以调节粒子向个体或群体学习的程度。在搜索前期，较大的个体学习因子会使粒子有较强的全局搜索能力。在搜索后期，较大的社会学习因子可使粒子向全局最优位置学习的比重变高，有助于粒子收敛到全局最优。因此，引入非线性变化学习因子，计算式如下式所示：

式中：$ {c_{1\max }} $和$ {c_{2\max }} $——个体学习因子和社会学习因子的上限值；

$ {c_{1\min }} $和$ {c_{2\min }} $——个体学习因子和社会学习因子的下限值。

同时，为了改善粒子群搜索速度，根据遗传算法的思想，加入了变异和交叉行为。变异行为即当随机值大于设定界限值，对粒子的某位置分量重新赋值。交叉行为指当随机值大于设定界限值，将粒子某位置分量与另一粒子位置分量相互交换。再根据交叉、变异前后适应度对比确定是否保留新的粒子。遗传算法的引入，保证了粒子位置的多样性，加快了PSO算法的寻优速度。

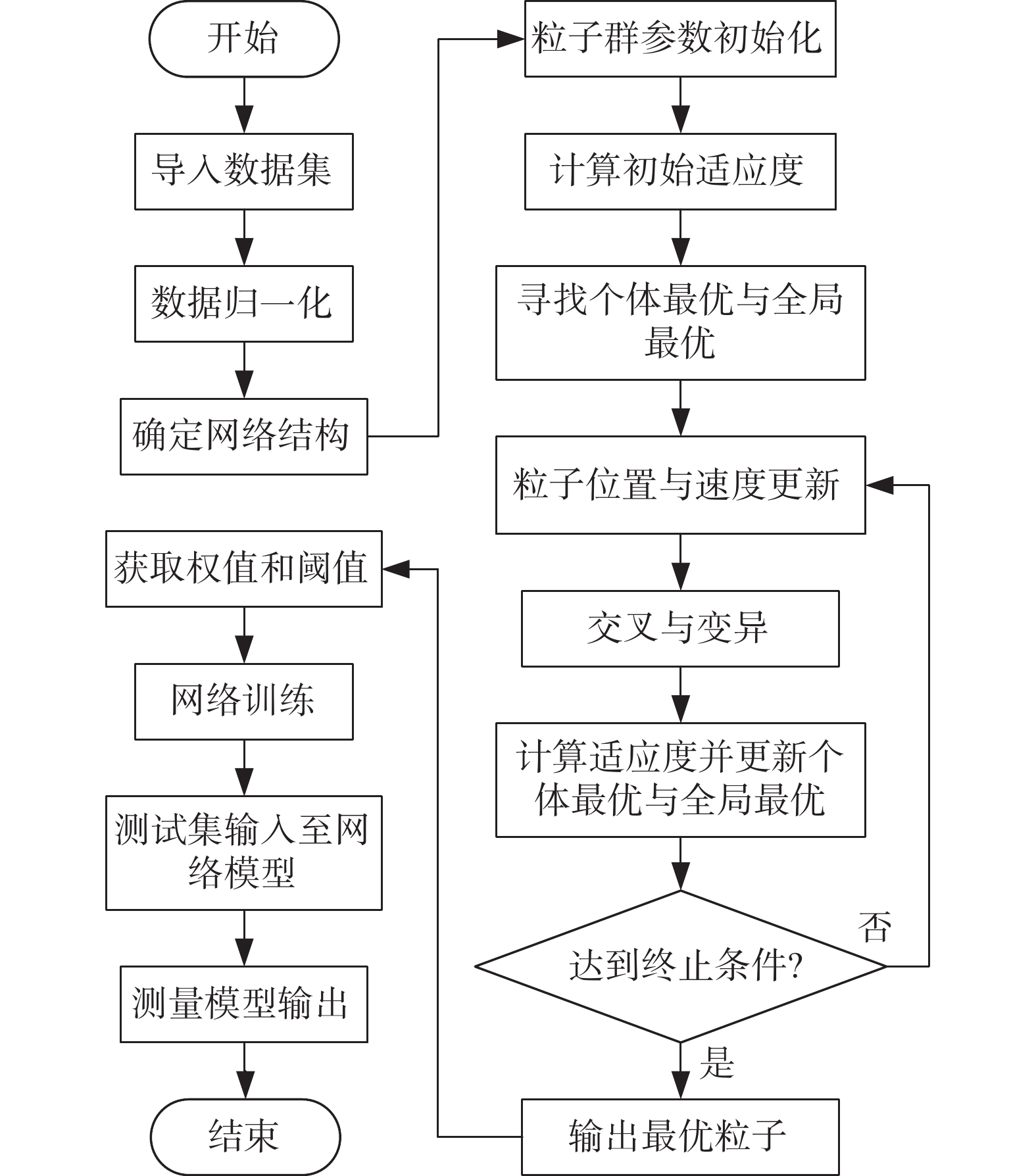
2.3 IPSO算法优化Elman神经网络

PSO算法经改进后其搜索能力得到增强，若使用改进后的PSO算法对Elman神经网络进行优化，可有效提升网络的泛化能力。优化流程如图4所示。

从图4可得算法过程描述如下：

1）导入数据集并进行数据预处理，然后初始化网络结构。

2）初始化IPSO算法参数后，生成粒子初始位置。其中，以下式计算粒子维数：

式中：$ {\mathrm{nu}}{{\mathrm{m}}_{{\mathrm{in}}}} $——输入层节点个数；

$ {\mathrm{nu}}{{\mathrm{m}}_{{\mathrm{hid}}}} $——隐含层节点个数；

$ {\mathrm{nu}}{{\mathrm{m}}_{{\mathrm{out}}}} $——输出个数。

3）求初始粒子适应度，并记录最优适应度，其中粒子适应度计算式如下式所示：

式中：$ {y_j} $——期望输出；

$ {\hat y_j} $——网络输出；

$ M $——样本个数。

4）根据改进公式计算下一代粒子速度和位置，并进行变异、交叉操作。计算最新种群的适应度，并对最优位置进行更新。

5）若完成规定迭代次数，则进入到步骤6）；否则重新回到步骤4）。

6）取出种群最优粒子，将其拆解并作为Elman神经网络的初始权值和阈值，然后进行网络的训练和测试。

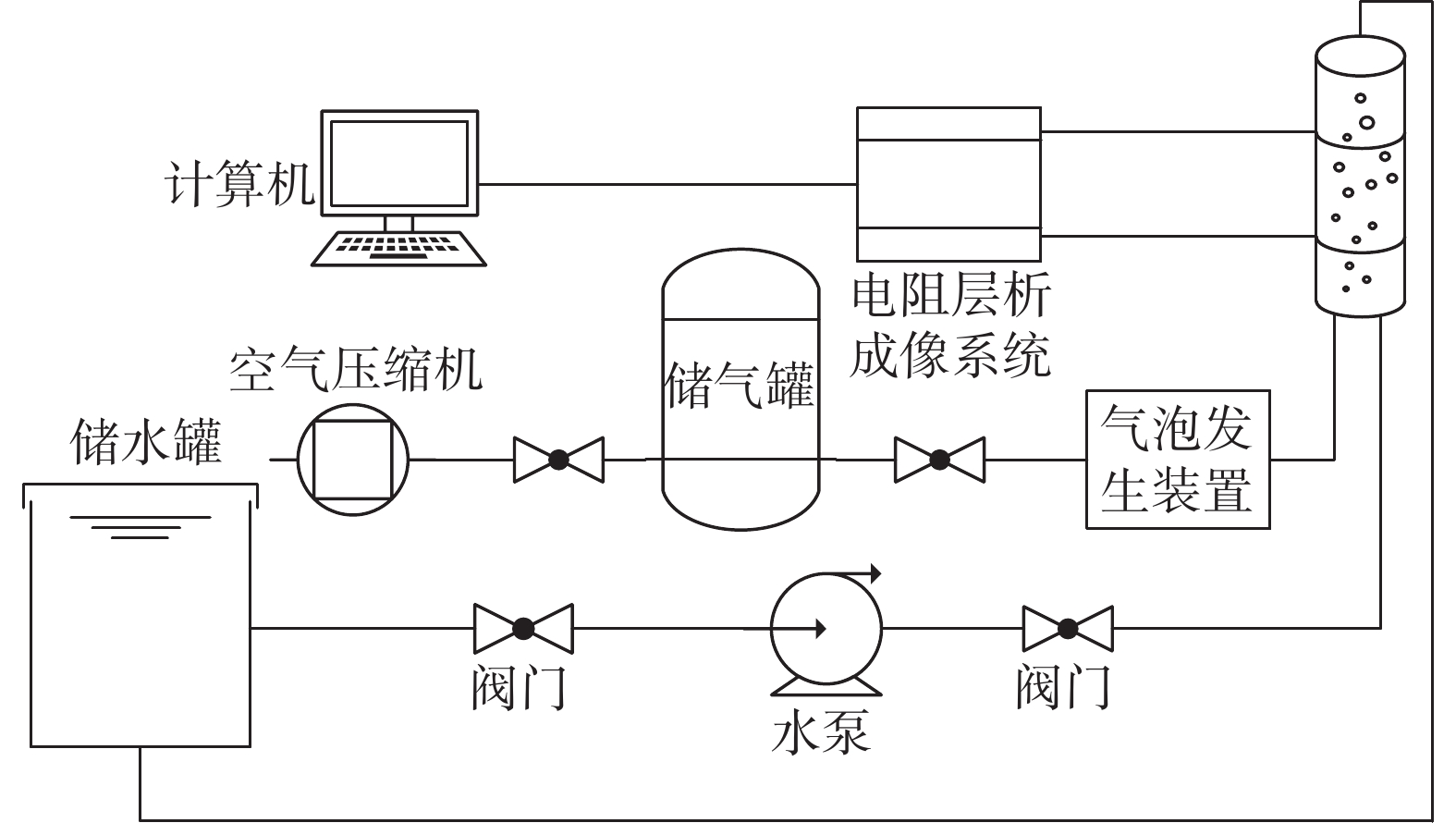
3 实验与分析 3.1 实验环境与数据采集

实验数据采集于气液两相流实验室，实验装置如图5所示。液体流动管道材质为不锈钢，内径为80 mm。在内径为60 mm的竖直有机玻璃管道上安装ERT系统的传感器电极。实验中气液相分别为空气和水。

实验过程如下：启动水泵后，等待水逐渐充满管道。调节气泡发生装置的进气量，空气与水在竖直管道中发展为不同的流动状态。进气量较小时，竖直管道流型为泡状流。不断增加进气量，并调整进气间隔，在竖直管道观察到弹状流。ERT系统配合计算机中的TJU-Etest软件不断采集竖直管道的阵列电阻。采集完毕后，在计算机上使用成像质量较好的Landweber迭代算法^[15]对被测管道截面进行图像重建，迭代次数为50。重建图像典型示例如图6所示。通过图像处理法可获取参考截面含气率。首先将重建图像转为灰度图，然后设定二值化阈值为0.3，将灰度图二值化，得到气液两相区分明显的黑白图。最后根据下式计算含气率参考值：

式中：A——管道截面像素总数；

A_gas——气相像素个数。

实验共采集了2100组阵列电阻值，其中泡状流1100组，弹状流1000组。截面含气率范围为0.1~0.45。从中选择2 000组数据用于模型训练，剩下的100组用于测试模型性能。

3.2 数据预处理与含气率测量模型建立

对数据初步分析后发现，不同阵列电阻值的数量级相差较大，需对数据归一化处理以保证神经网络能够快速收敛。选用最大最小值归一化方法处理数据。

由于阵列电阻特征维度为120，若不进行处理直接用于网络训练，易发生过拟合，且训练时间较长。需使用PCA算法对电阻特征降维。

PCA降维步骤如下：

1）数据去均值化。计算每个特征的平均值$ \bar v $，每个特征都减去相应的平均值得$ {\boldsymbol{T}} $。

式中：N——数据组数；

$ {v_e} $——某个特征下第e组数据对应的数值。

2）计算协方差矩阵$ {\boldsymbol{R}} $：

3）求协方差矩阵的特征值$ \lambda $及对应的特征向量，并由下式计算方差贡献率：

式中：$ {\lambda _i} $——第i个特征值；

${\lambda _{\rm s}}$——所有特征值之和。

4）选择较大的前q个特征值，直至其方差贡献率之和达到85%或以上。

5）将q个特征值对应的特征向量作为行向量构成变换矩阵$ {\boldsymbol{P}} $，根据下式获得维度为q的数据矩阵$ {\boldsymbol{U}} $：

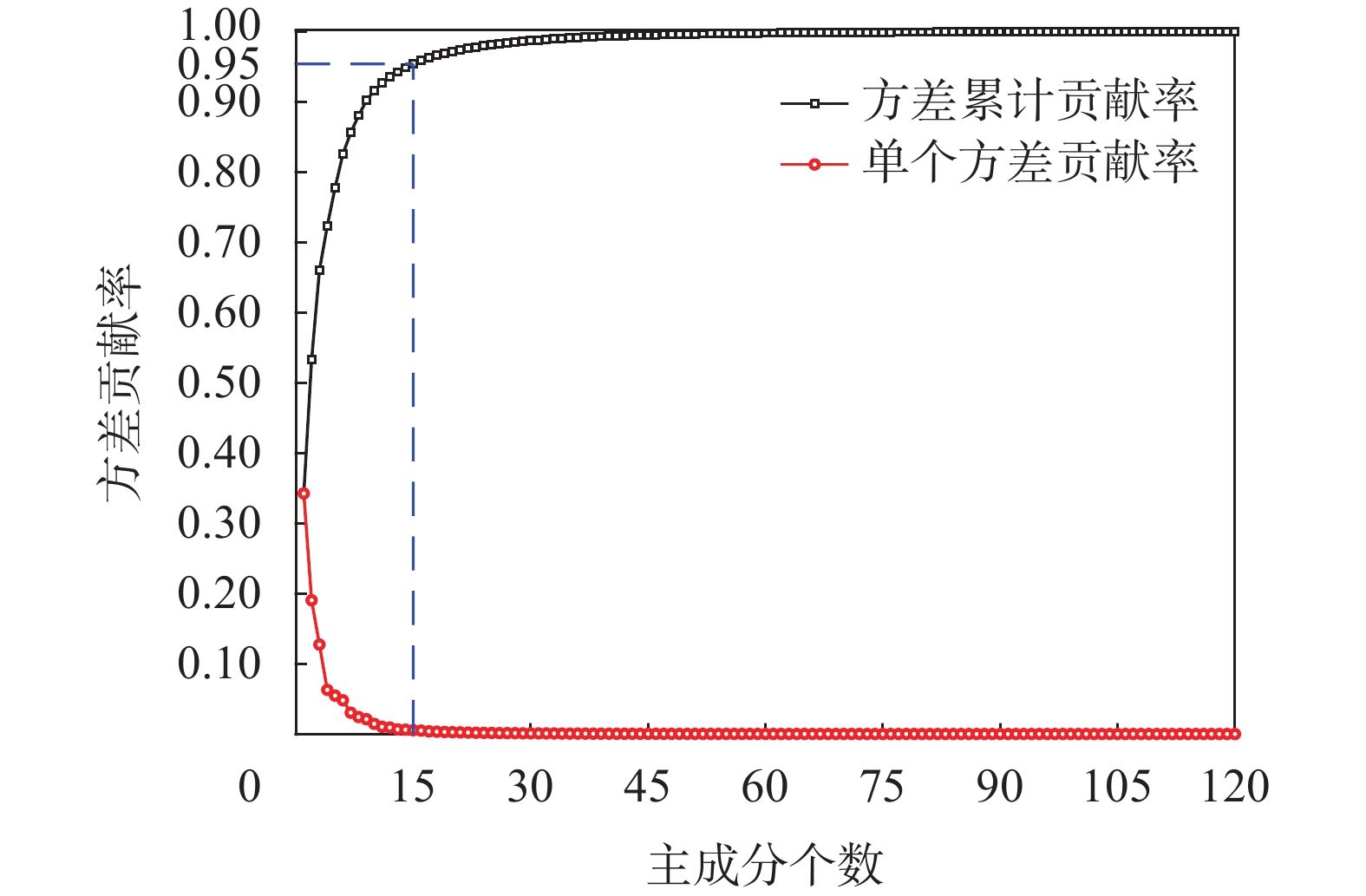
降维时，PCA算法的方差贡献率分布情况如图7所示。

由图可知，前15个主成分的方差累计贡献率达到0.95。若再增加变量个数，虽可以使方差累计贡献率继续增加，但也意味着数据维度的增加。在第15个主成分之后，其他主成分的方差贡献率均较小，故确定降维后特征维度为15。既可提取到原始特征中的重要特征，又可减小计算量。

结合上述内容可得最终的含气率测量模型如图8所示。

3.3 模型训练结果与分析

为了全面分析测量模型的性能，将从模型训练与含气率测量两个方面展开研究。

在训练含气率测量模型前，应先设定模型参数。其中，Elman神经网络的参数如下：训练次数为5000，学习率为0.01。IPSO算法参数中搜索次数为80；粒子群规模为30；惯性权重上下限分别为0.9和0.4；个体学习因子上下限分别为2和0.4；社会学习因子上下限分别为2和0.4；交叉界限为0.1；变异界限为0.9。

已知模型中的神经网络的输入输出个数分别为15、1。可经实验确定神经网络的隐含层节点个数。先通过经验公式确定隐含层节点数的大致范围，再将范围内的值代入Elman神经网络，并建立含气率测量模型，寻找测试集误差最小的模型所对应的隐含层节点数。经验公式如下式所示：

式中：$ k $——隐含层节点个数；

$ p $——输入层节点个数；

$ \tau $——整数，其范围为[0,10]。

当特征维度为15时，由经验公式得隐含层节点初始范围为[4, 14]，经上述方法最终确定使用降维特征的测量模型隐含层节点数为9。以同样的方法确定未降维处理的含气率测量模型的隐含层节点数为14。

确定好参数后，对模型进行训练。使用120维电阻特征建立Elman模型以及PSO、GA、IPSO算法优化的Elman模型作为对比。模型中涉及到相同算法时，其参数均保持一致。不同测量模型的训练时间如表1所示。

由表可得，Elman模型的训练时间最短，IPSO-Elman模型的训练时间最长，且加入优化算法的Elman模型训练时间均比未加优化算法的模型长。原因在于，经算法优化的Elman模型要在优化算法多次循环后才能得到合适的参数，神经网络需等待优化算法结束才开始最后的训练。

PCA-IPSO-Elman模型相较于未降维的IPSO-Elman模型，训练时间减少了68.8%。其原因在于，PCA降维减小了输入特征维度，而PSO算法粒子维度与输入特征维度有关，因此算法的运算速度与模型训练速度加快。

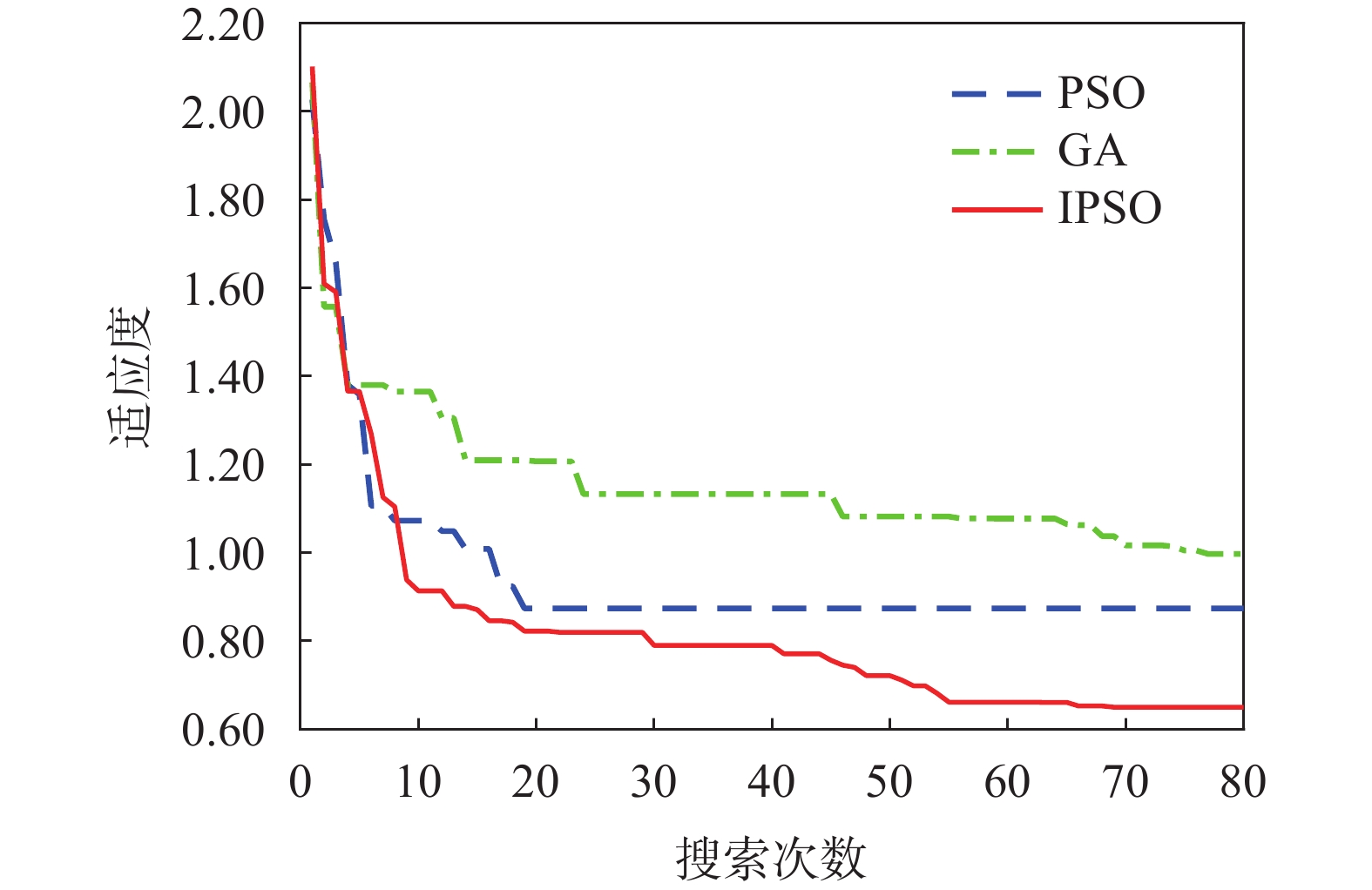
为了对比不同搜索算法的效果，在输入特征维度都为120时，观察不同算法优化的Elman模型中搜索算法的适应度变化情况，如图9所示。由图可知，PSO算法搜索至0.87附近，GA算法最终搜索到0.99附近。IPSO算法在前后期都表现出很好的搜索能力，最终搜索至0.65附近。表明IPSO算法经改进后搜索能力得到增强。

3.4 含气率测量结果

将测试集特征输入至测量模型得到含气率测量值。由不同算法构成的含气率测量模型的测量结果如图10所示。

不同模型的测量误差如图11所示。5种测量模型中，IPSO-Elman模型的测量效果最优，误差波动最小，PCA-IPSO-Elman模型测量效果与其相近。对比Elman模型和经搜索算法优化的Elman模型可知，优化算法为神经网络提供了更合适的网络参数，从而更好地描述了电阻特征与含气率的映射关系。

相较于PSO-Elman模型，IPSO-Elman模型有更好的测量结果。在对低含气率测量时，该模型也较好的测量效果，这是因为粒子群算法经改进后提高了搜索能力，改善了算法对Elman神经网络的优化效果。

为了客观评价含气率测量模型的测量结果，以均方误差（MSE）和平均绝对百分比误差（MAPE）作为评价标准，计算公式如下式所示：

式中：$ N $——样本个数；

$ {y_j} $——样本的期望值；

$ {\hat y_j} $——模型的测量值。

不同含气率测量模型的评价指标如表2所示。

由表可知，IPSO-Elman测量模型的平均绝对百分比误差最小，PCA-IPSO-Elman测量模型的均方误差最小。两种模型均实现了平均绝对百分比误差小于3%的含气率测量。

与Elman模型相比，PCA-IPSO-Elman模型的均方误差、平均绝对百分比误差分别下降了81.5%、46.9%；与PSO-Elman模型相比，分别下降了53.2%、27.7%；与GA-Elman模型相比，分别下降了67.7%、31.5%。说明降维后使用IPSO算法优化Elman进行含气率测量，测量效果好于上述对比模型。

可以看出，经PCA降维的IPSO-Elman测量模型的MAPE值比未降维的IPSO-Elman模型稍高。这是因为PCA算法虽提取到阵列电阻的主要特征，仍存在特征损失，但经降维处理再建立测量模型可有效解决优化算法带来的耗时长的问题。

因此，本文提出的含气率测量方法是有效的，该方法兼顾了模型训练速度快与测量误差小的特点，可实现含气率的安全且非侵入式测量。

4 结束语

本文提出一种以阵列电阻为特征输入的气液两相流截面含气率测量方法。对特征降维后建立IPSO-Elman含气率测量模型，经对比实验验证模型的性能后，得出以下结论：

1）PCA降维加快了模型的训练速度，避免了数据冗余引起的过拟合。

2）自适应惯性权重和非线性学习因子实现了PSO算法全局搜索能力与局部搜索能力的平衡，交叉和变异行为则加快了算法的搜索速度。IPSO算法为Elman神经网络寻到合适的参数，更好地实现了阵列电阻向含气率的映射。

3）非侵入式的ERT传感器与机器学习方法结合，为含气率的测量研究提供了一种思路。

本文工作仍存在一些不足，由于实验环境限制，仅采集了0.1~0.45范围内的含气率数据，下一步工作将尝试对更大范围内的含气率测量进行研究。