文章信息
- 董莉娜, 张志劲, 王茂政
- DONG Lina, ZHANG Zhijin, WANG Maozheng
- 基于历史天气的区域电网负荷预测
- Research on regional power grid load forecasting based on historical weather
- 中国测试, 2024, 50(6): 183-190
- CHINA MEASUREMENT & TEST, 2024, 50(6): 183-190
- http://dx.doi.org/10.11857/j.issn.1674-5124.2021020069
-
文章历史
- 收稿日期: 2021-02-22
- 收到修改稿日期: 2021-05-25
2. 国家电网重庆市电力公司市区供电分公司,重庆 400015
2. State Grid Chongqing Electric Power Company, Chongqing 400015, China
随着社会的不断进步和科技的不断发展,以及我国电力系统和电网管理趋于复杂化、智能化和完善化,电力系统负荷预测已成为现代人工智能电力系统科学中一个重要研究领域,引起越来越多国内外学者的关注[1]。为保证电力系统安全稳定、经济运行,避免造成不必要的能源浪费,必须掌握各种负荷的变化规律和发展趋势。特别是区域电网负荷预测的精度,显著影响安全校核与日、月、年供电计划,区域电网负荷是制定日、月、年供电工作计划与安全校核的基础。积极开展区域电网负荷预测,精益研究区域电网负荷变化规律,准确进行预测,有助于调度运行部门更好地控制和驾驭电网。
国内外对中长期负荷预测进行了大量研究,杨楠等[2]使用改进灰色模型对中长期负荷进行预测,其预测精度比传统灰色预测模型高;黄俊铭等[3]通过将径向基函数神经网络应用于中长期负荷预测中,基本消除了电力负荷的动态微分变化过程对中长期负荷预测的影响;Li等[4]提出一种基于Elman的人工神经网络的复合载荷模型;Shi等[5]提出一种基于改进遗传神经网络的长期负荷预测模型;李冬辉等[6]提出一种基于果蝇优化算法的广义回归神经网络的负荷预测模型,消除了预测结果因神经网络扩展参数选择不当而陷入局部最优的问题;Yang等[7]提出基于负荷类型识别的深度负荷预测方法,可以根据不同的负荷类型,建立不同的深度信念网络模型,负荷预测准确率比人工神经网络更高。目前的研究都是通过对单一模型改进进行电网负荷预测[8-10],难以降低极端数据的影响,本文通过将多种预测模型归一化处理,得到归一化模型进行负荷预测,降低了极端数据的影响。
本文针对重庆市区供电分公司供电区域电网中长期负荷预测的需求,采用多气象因素智能处理开展电网中长期负荷预测研究。首先,应用统计学理论,建立气象负荷与单气象因素的关联模型,对重庆市区供电分公司供电区域电网负荷中的气象负荷与当地温度、湿度、风速、降雨量等气象因素的关联关系进行研究;然后,结合己有电网负荷预测方法,提出考虑多气象因素的重庆市区供电分公司供电区域电网中长期负荷预测改进方法并进行区域电网中长期负荷的预测,建立基于不同算法的多种预测模型,通过归一化处理,将区域电网中长期负荷预测结果与实际区域电网负荷进行对比分析。
1 区域电网负荷与气象因素的关联 1.1 区域电网负荷分解区域电网负荷不仅会受到气象因素(温度、相对湿度、降雨量、风速等)的影响,也会受到社会活动、经济情况和一般随机误差的影响[11-13]。在分析区域电网负荷与气象因素的关联时,首先提取受气象因素影响的气象负荷,将气象负荷与气象因素进行关联分析,得到真实可靠的结论。
将区域电网负荷(M)分解为不受气象因素影响的趋势负荷(Mt)和受气象因素影响的气象负荷(Ml):
| $ M={M}_{t}+{M}_{l} $ | (1) |
式中:Mt——不受气象因素影响的趋势负荷;
Ml——受气象因素影响的气象负荷。
趋势负荷Mt可以线性关系拟合,即:
| $ {M}_{t}=at+b $ | (2) |
式中:t——时间;
a、b——系数。
根据最小二乘法可得:
| $ \left\{\begin{array}{l}a=\dfrac{n{\displaystyle \sum} _{i=1}^{n}{t}_{i}{M}_{{t}_{i}}-{\displaystyle \sum} _{i=1}^{n}{t}_{i}{\displaystyle \sum} _{i=1}^{n}{M}_{{t}_{i}}}{n{\displaystyle \sum} _{i=1}^{n}{t}_{i}^{2}-{\left({\displaystyle \sum} _{i=1}^{n}{t}_{i}\right)}^{2}}\\ b=\dfrac{{\displaystyle \sum} _{i=1}^{n}{M}_{{t}_{i}}}{n}-\dfrac{a{\displaystyle \sum} _{i=1}^{n}{t}_{i}}{n}\end{array}\right. $ | (3) |
求出趋势负荷Mt后,用总负荷M减去趋势负荷Mt即可得到气象负荷Ml,图1为总负荷及趋势负荷的折线图。
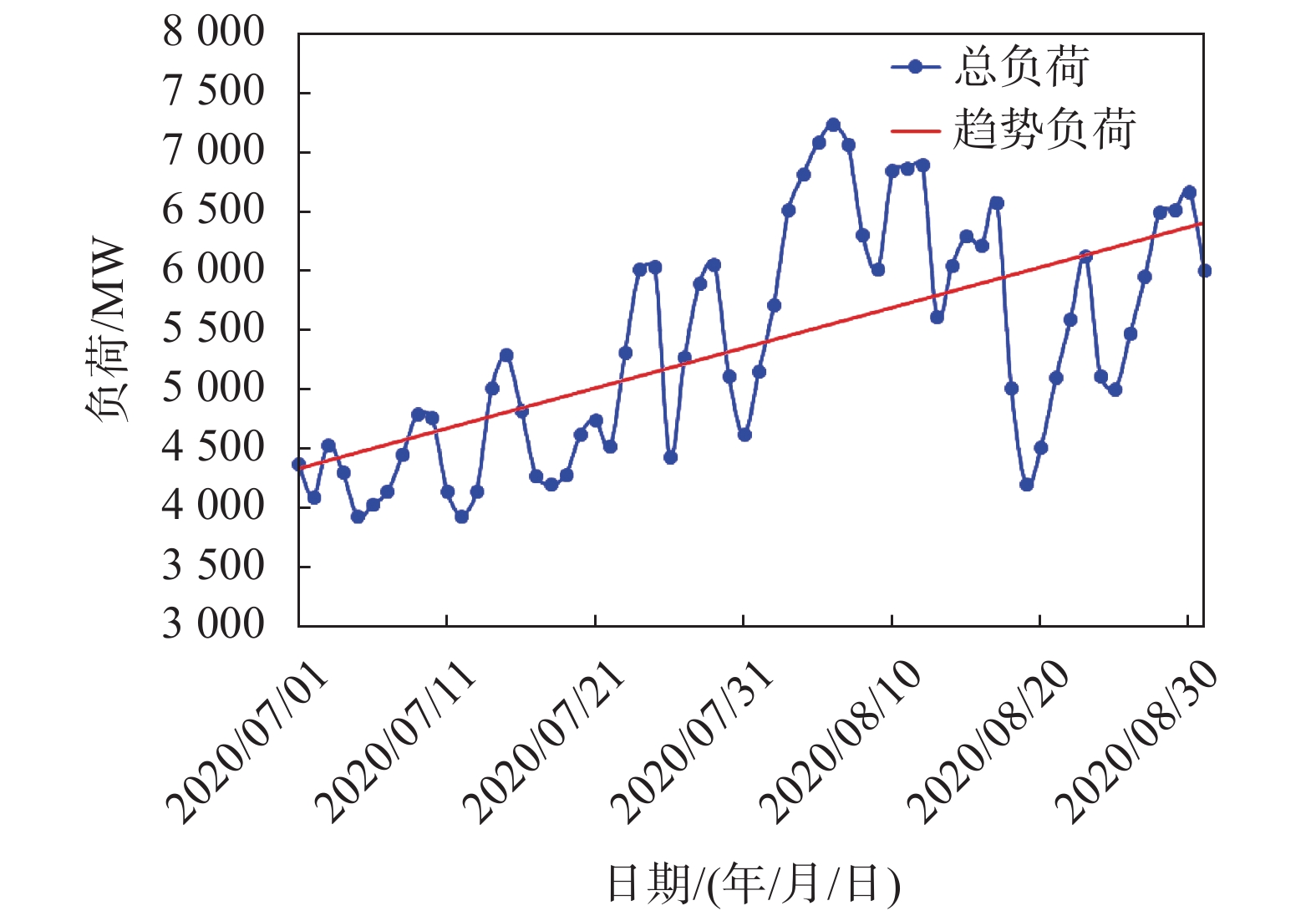
|
| 图 1 总负荷及趋势负荷折线图 |
1.2 单气象因素关联
根据式(4)计算各个单气象因素与气象负荷以及单气象因素间的Pearson相关系数,并根据相关系数的大小和正负较准确地判断单气象因素与气象负荷之间的关联性关系,即:
| $ r=\frac{1}{n-1}\sum _{i=1}^{n}\left(\frac{{X}_{i}-\bar{X}}{{S}_{x}}\right)\left(\frac{{Y}_{i}-\bar{Y}}{{S}_{y}}\right) $ | (4) |
式中:Xi——每天的单气象条件值;
Sx——单气象条件值的标准差;
Yi——每天的气象负荷值;
Sy——气象负荷值的标准差;
表1为各个单气象因素与气象负荷的相关系数,表2为各个单气象因素之间的相关系数。
| 相关性 | 最高温度 | 最低温低 | 平均温度 | 相对湿度 | 降雨量 | 风速 |
| 最高温度 | 1.000 | 0.830 | 0.990 | –0.815 | –0.602 | 0.103 |
| 最低温度 | 0.830 | 1.000 | 0.910 | –0.551 | –0.359 | 0.055 |
| 平均温度 | 0.990 | 0.910 | 1.000 | –0.749 | –0.540 | 0.089 |
| 相对湿度 | –0.815 | –0.551 | –0.749 | 1.000 | 0.750 | –0.274 |
| 降雨量 | –0.602 | –0.359 | –0.540 | 0.750 | 1.000 | –0.178 |
| 风速 | 0.103 | 0.055 | 0.089 | –0.274 | –0.178 | 1.000 |
由表1可知:最高温度、最低温度和平均温度的相关系数与气象负荷正相关,且最低温度与气象负荷的相关性最强;相对湿度和降雨量的相关系数与气象负荷是负相关;风速则与气象负荷几乎没有相关性。
由表2可知:最高温度和相对湿度受降雨量的影响很大,由于降雨过后,空气相对湿度增大,最高温度也有所下降;风速与其他气象因素的相关性都不大。
然后可采用趋势拟合法展现各气象因素与气象负荷之间的变动趋势。首先将各个气象因素数据和气象负荷标准化,本文根据式(5)和式(6)采用z-score法对其数据进行标准化;然后将各个气象因素与气象负荷进行趋势拟合,从而可得二者之间的关系,如图2~图7所示。
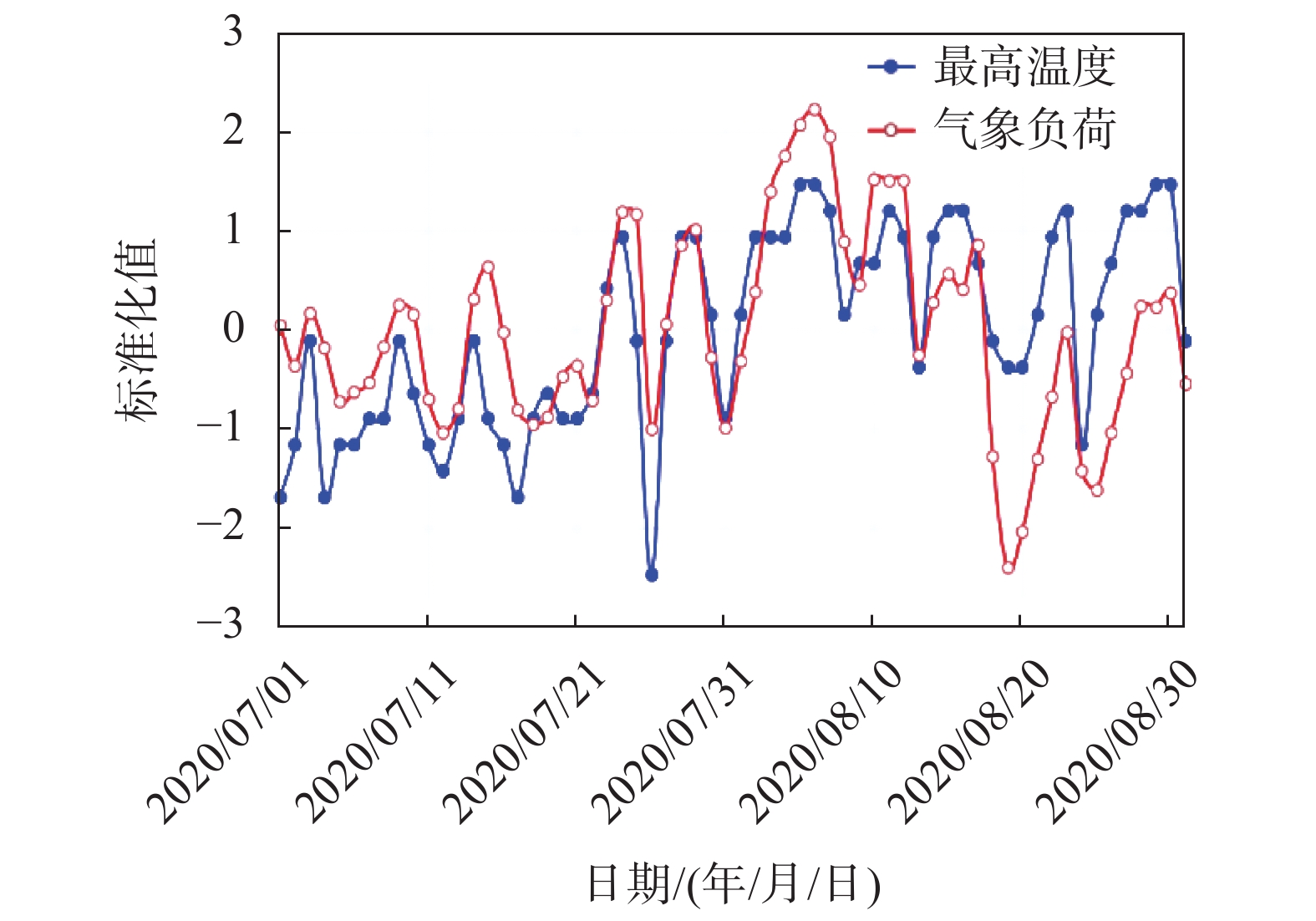
|
| 图 2 最高温度和气象负荷标准化折线图 |

|
| 图 3 最低温度和气象负荷标准化折线图 |

|
| 图 4 平均温度和气象负荷标准化折线图 |

|
| 图 5 相对湿度和气象负荷标准化折线图 |
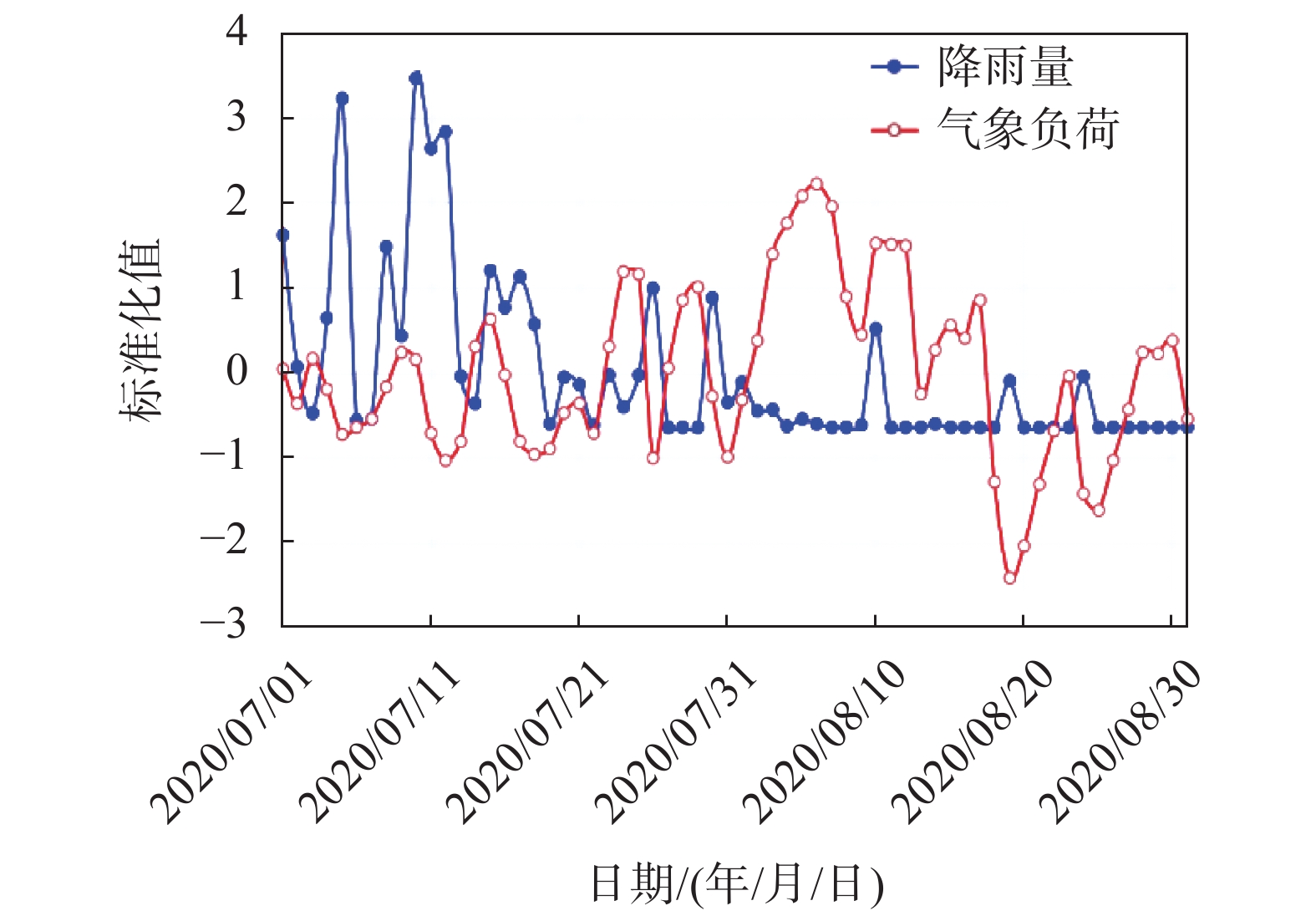
|
| 图 6 降雨量和气象负荷标准化折线图 |
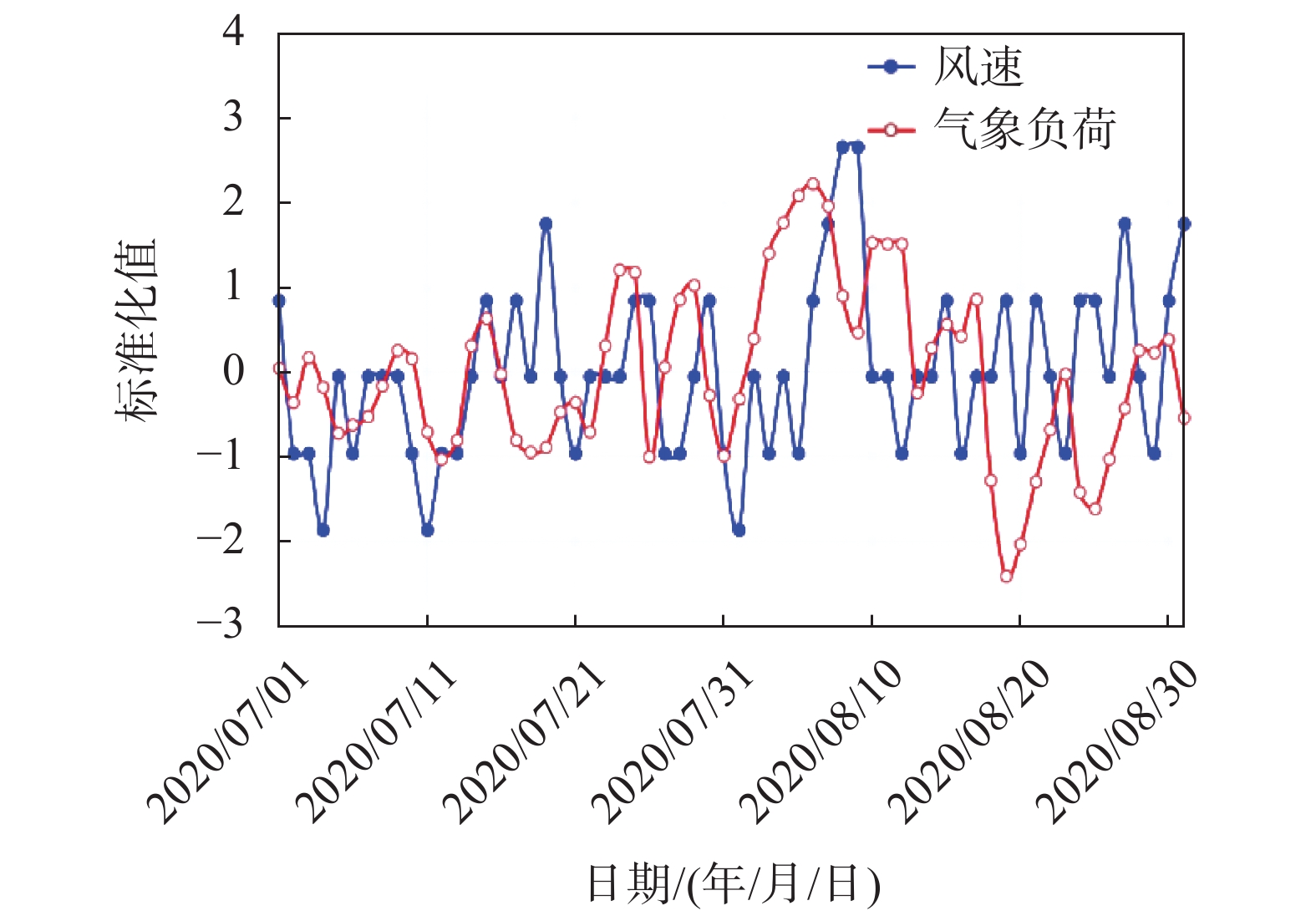
|
| 图 7 风速和气象负荷标准化折线图 |
| $ {\sigma}=\sqrt{\frac{1}{N}{\sum}_{i=1}^N(X_i-\mu)^2} $ | (5) |
| $ \text{z}_i=\frac{X_i-\mu}{\sigma} $ | (6) |
式中:μ——数据均值;
σ——数据标准差。
由图2~图4可知最高温度、最低温度、平均温度和气象负荷呈现同增同减的正相关关系;由图5~图6可知相对湿度、降雨量和气象负荷在某些程度上有一定的负相关关系;由图7可知风速和气象负荷的相关性很低。各个气象因素与气象负荷的标准化折线图呈现的相关性与计算得到的相关性相互印证,其中温度和气象负荷呈现同增同减的正相关关系,其原因是重庆市夏季高温,空调用电占比大,温度升高,空调的使用时间就会增多,用电量就会增加,气象负荷就会增大;降雨量、湿度和气象负荷有一定的负相关关系其原因是有降雨时,降雨量增加,空气湿度就会增加,温度就会降低,因此空调使用就会减少,气象负荷就会降低。
2 区域电网负荷预测实例 2.1 区域电网负荷预测方法与步骤本文提出一种新的预测区域电网中长期负荷的方法,即基于前12个月历史天气条件和区域电网负荷关联关系的多元非线性拟合的特征参数因子曲线的区域电网中长期负荷预测方法。其预测流程如图8所示。

|
| 图 8 区域电网负荷预测流程图 |
由该方法实现区域电网中长期负荷预测的步骤如下:
1) 确定电网负荷的区域范围,并根据实际情况划分子负荷单位或子供电区域,制定地理位置关系网络拓扑结构图,见图9。
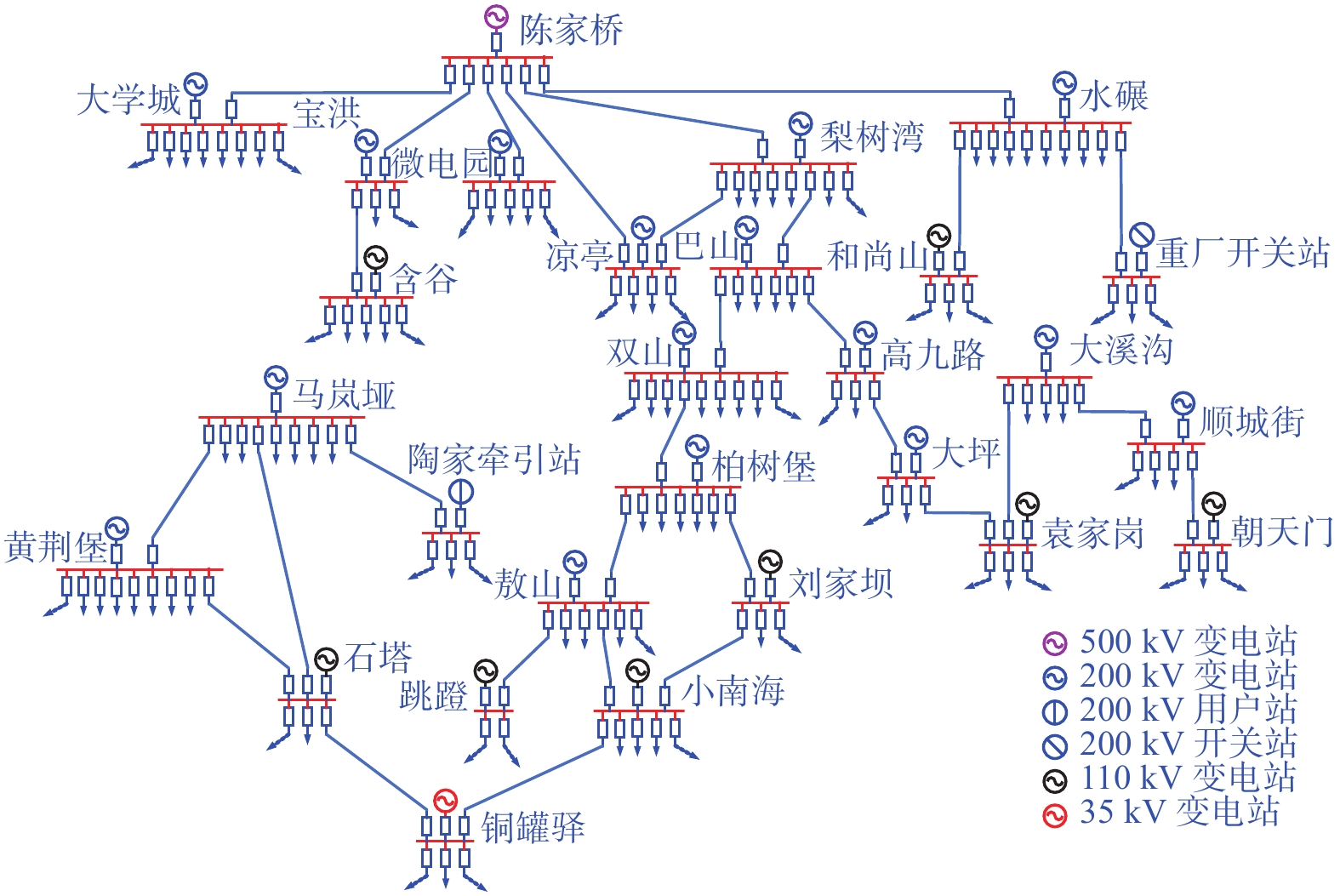
|
| 图 9 重庆市区供电局供电区域网络拓扑图 |
2) 按网络拓扑结构,以子负荷单位为区间,输入重庆市2019年12个月按日均值的天气条件,如相对湿度、降雨量、风速、温度(最低、最高与平均)等基本参数,形成拓扑网络结构的天气数据库。
3) 对历史负荷数据进行卡尔曼滤波,以去除系统中的噪声和干扰的影响,而后利用主成分分析方法,对数据进行降维处理。
卡尔曼滤波(Kalman filtering)是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
系统的状态方程为:
| $ {x}_{k}=A{x}_{k-1}+B{u}_{k-1}+{w}_{k-1} $ | (7) |
其中:A、B是系数,uk-1为系统控制量,
观测方程:
| $ {{\textit{z}}}_{k}=H{x}_{k}+{v}_{k} $ | (8) |
其中:
4) 以非线性多元拟合和BP神经网络方法,综合确定天气及其子因素影响用电负荷的加权子因素,确定负荷性质的加权子因子。
BP神经网络是一种按误差反向传播算法训练的多层前馈网络,应用较为广泛,具有较强的泛化能力和容错能力。BP神经网络具有学习和存储大量输入-输出关系映射,学习规则是最速下降法,通过反向传播,不断调整网络的权值和阈值,从而使误差的平方和最小。
BP神经网络模型拓扑结构包括输入层、隐含层和输出层,见图10。
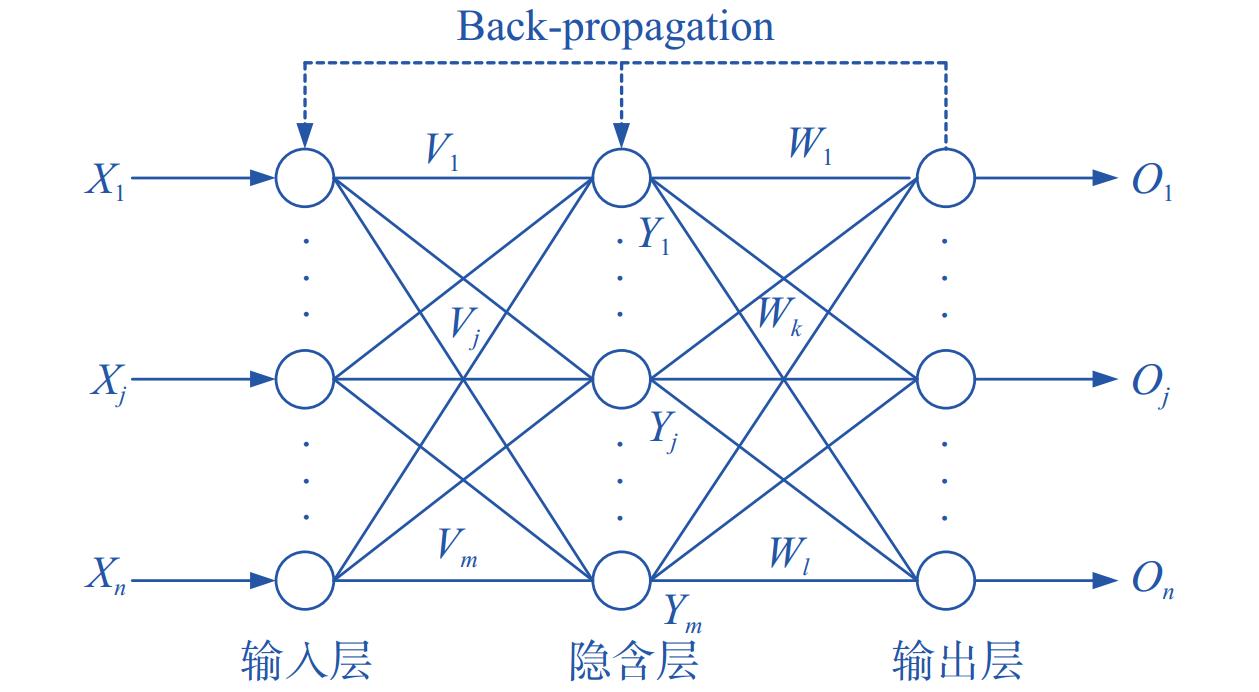
|
| 图 10 BP神经网络拓扑结构图 |
设输入变量为X,隐含层输出变量Y,输出层变量为O;期望输出变量为D;输入层到隐含层间的权值矩阵为V;隐含层到输出层的权值矩阵为W。
对于输出层:
| $ o_k=f\left(\mathrm{net}_k\right),k=1,\mathrm{ }2,\mathrm{ }\cdots,l $ | (9) |
| $ \mathrm{net}_k={\sum}_{j=0}^nW_{ij}y_j,k=1,2,\cdots,l $ | (10) |
对于隐含层:
| $ y_j=f\left(\mathrm{net}_j\right),j=1,\mathrm{ }2,\mathrm{ }\cdots,m $ | (11) |
| $ \mathrm{net}_j={ \sum}_{i=0}^nV_{ij}x_i,j=1,\mathrm{ }2,\mathrm{ }\cdots,m $ | (12) |
对于输出误差E定义:
| $ E=\frac{1}{2}(D-O)^2=\frac{1}{2}\sum_{k=1}^l(d_k-o_k)^2 $ | (13) |
进一步展开代入,得:
| $ \Delta W_{jk}=\eta\delta_k^oy_j=\eta(d_k-o_k)o_k(1-o_k)y_j $ | (14) |
| $ \Delta {V}_{ij}=\eta {\delta }_{j}^{y}{y}_{i}=\eta \left({\sum }_{k=1}^{l}{\delta }_{j}^{y}{W}_{jk}\right){y}_{j}\left(1-{y}_{j}\right){x}_{j} $ | (15) |
定义信号误差为:
| $ \delta_k^o=-\frac{\partial E}{\partial\mathrm{net}_k} $ | (16) |
| $ \delta_j^y=-\frac{\partial E}{\partial\mathrm{net}_j} $ | (17) |
其中,学习步长
5) 建立基于不同算法的多种预测模型,并进行归一化处理;以加权因子分解重庆市区供电分公司2019年12个月的区域电网负荷,并以天气因子值标幺值乘以其加权因子,得到重庆市区供电分公司2019年12个月按月度的区域电网负荷预测标幺值。
6) 根据重庆市区供电分公司2019年12个月的历史区域电网负荷标幺值,采用多元非线性拟合方法得到优化重庆市区供电分公司2019年12个月的区域电网负荷变化曲线和拟合关系。
7) 根据区域电网中长期负荷曲线,给出重庆市区供电分公司2020年每6天的区域电网负荷。
根据重庆市区供电局2020年每6天的实际区域电网负荷检验和修正,最后对本论文提出的区域电网中长期负荷预测方法进行评价。
2.2 单一模型区域电网负荷预测2020年全年总共有366天,为充分利用全年每一天的数据,本文以6天为一组,使用多种单一模型和归一化模型对重庆市区供电分公司每6天的区域电网负荷进行预测,得到如下预测结果。
表3所示是单一模型区域电网负荷预测的平均绝对百分比误差(MAPE)、均方差(MSE)、归一化均方差(NMSE)和最大百分比误差(MAXPE)。
| 编号 | 模型 | MAPE /% | MSE /MW2 | NMSE | MAXPE /% |
| 1 | LGBM | 1.079 | 1.239×105 | 0.250×10–3 | 9.682 |
| 2 | RFR | 1.259 | 1.450×105 | 0.293×10–3 | 9.891 |
| 3 | XGB | 1.169 | 1.300×105 | 0.263×10–3 | 9.775 |
| 4 | LSTM | 1.124 | 1.260×105 | 0.255×10–3 | 9.723 |
| 5 | ADB | 1.304 | 1.540×105 | 0.311×10–3 | 9.938 |
| 6 | MLP | 1.234 | 1.410×105 | 0.285×10–3 | 9.842 |
| 7 | LSVR | 1.146 | 1.270×105 | 0.257×10–3 | 9.754 |
| 8 | GBM | 1.191 | 1.347×105 | 0.272×10–3 | 9.797 |
由表3可知,用轻量级梯度提升算法模型(LGBM)进行区域电网负荷预测的各项误差最小,平均绝对百分比误差(MAPE)为1.079%、均方差(MSE)为1.239×105 MW2、归一化均方差(NMSE)为0.250×10–3、最大百分比误差(MAXPE)为9.682%。
2.3 归一化模型区域负荷预测极端数据对单一模型区域电网负荷预测的精度影响非常大,为降低极端数据的影响,基于加权平均算法,本文根据各种单一模型区域电网负荷预测的误差赋予该模型类似加权平均的加权因子,以此降低极端数据对单一模型区域电网负荷预测的精度影响,然后将各种单一模型区域电网负荷预测结果接入神经网络层MATE,通过神经网络算法进行类似加权平均的归一化处理,以此建立归一化模型。
基于前面不同算法的多种区域电网中长期负荷预测模型,然后将全部区域电网中长期负荷预测模型通过归一化处理,最后采用归一化模型进行区域电网中长期负荷预测,具体过程如图11所示,本文采用归一化模型进行区域电网中长期负荷预测时,采用META法处理数据,处理数据示意图如图12所示。

|
| 图 11 归一化模型负荷预测流程 |
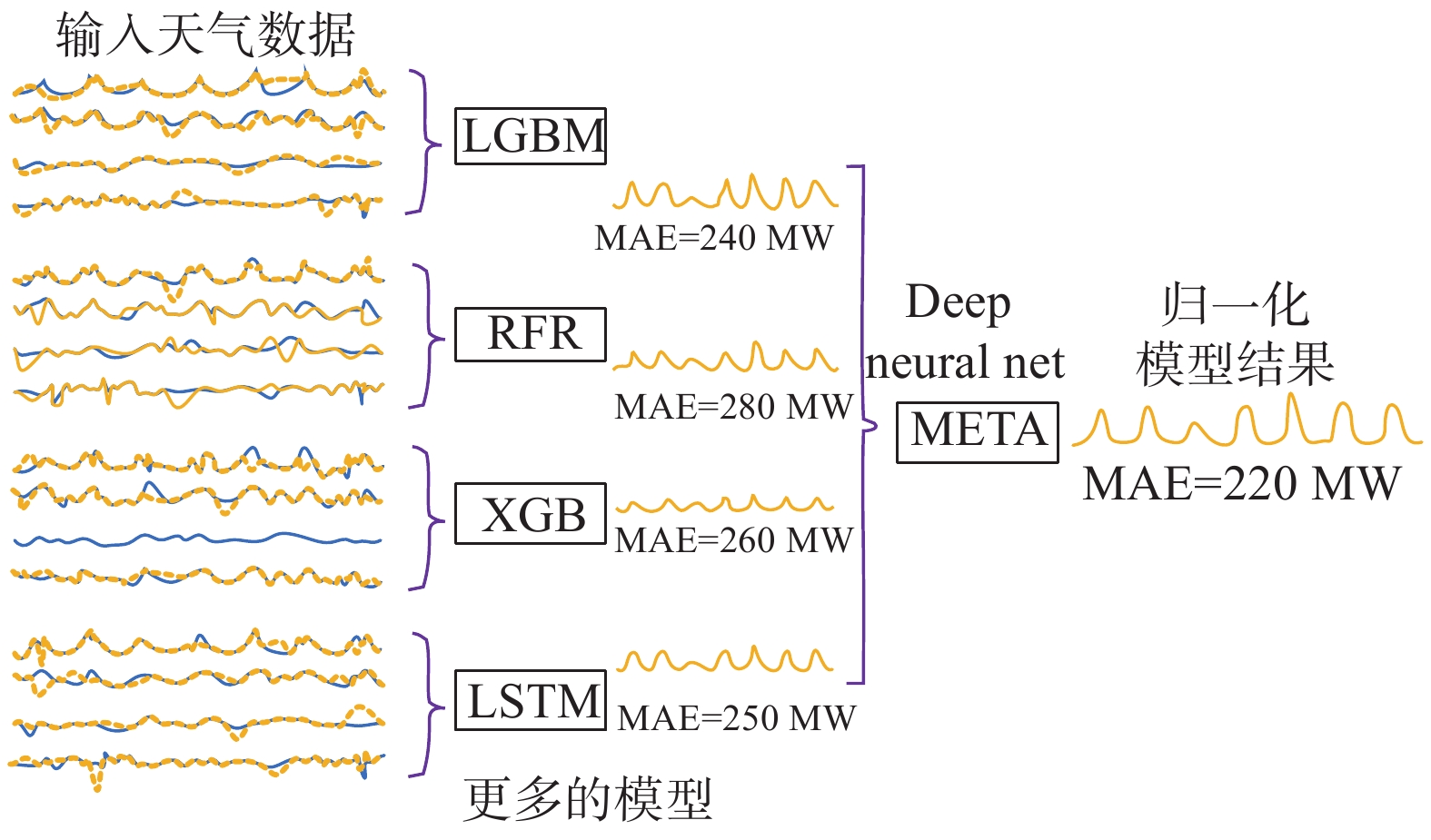
|
| 图 12 META法处理数据示意图 |
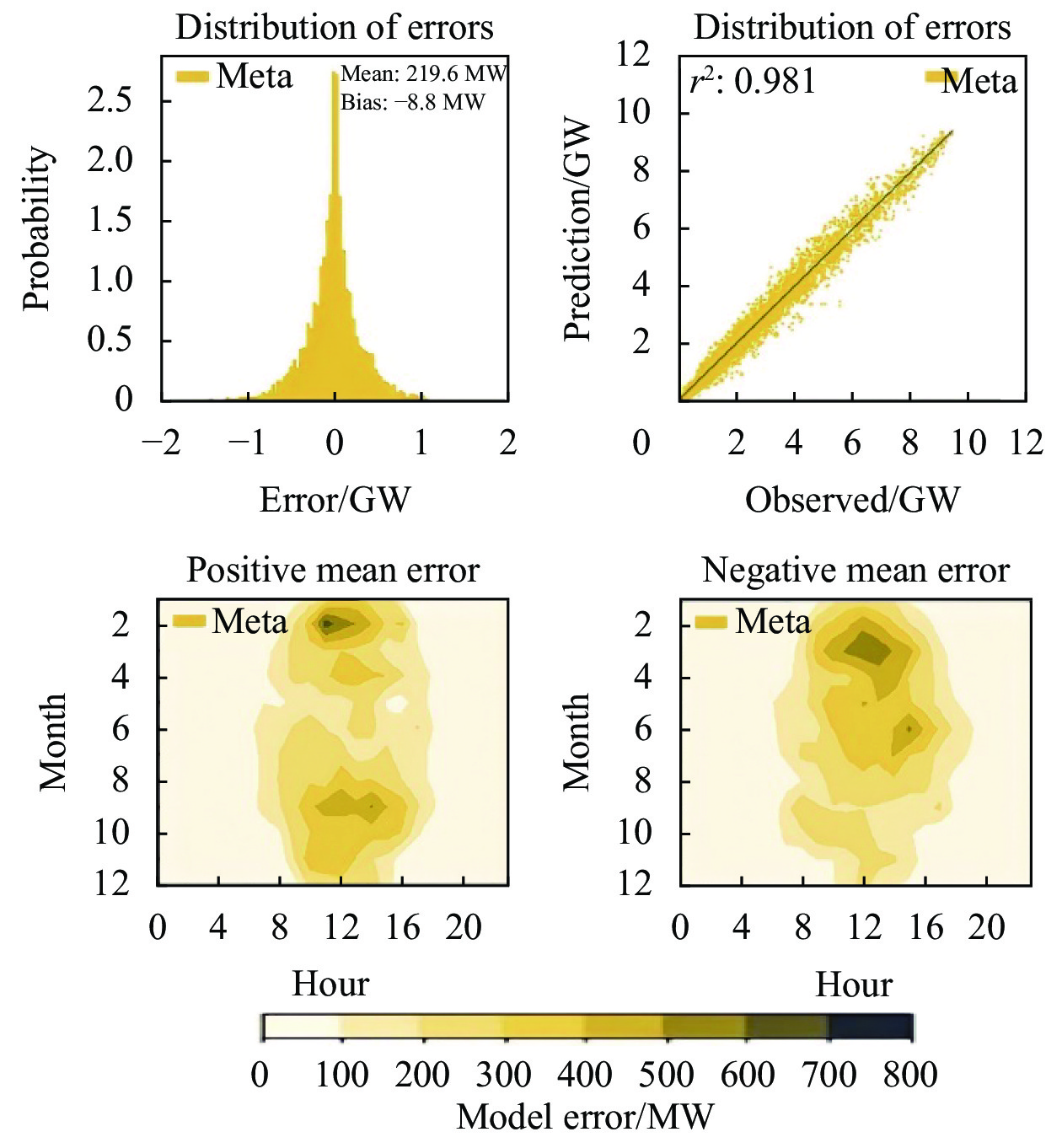
采用META法处理归一化模型数据,得到如表4所示的归一化模型区域电网中长期负荷预测的平均绝对百分比误差(MAPE)、均方差(MSE)、归一化均方差(NMSE)和最大百分比误差(MAXPE),采用META法处理归一化模型数据误差如图13所示,利用K-Fold交叉验证方法的区域电网负荷预测模型误差分布如图14所示。

|
| 图 13 归一化模型数据误差 |
|
| 图 14 区域电网负荷预测模型误差分布 |
采用归一化模型进行区域电网中长期负荷预测的平均绝对误差(MAE)为219.6 MW,均方根误差(RMSE)为311.1 MW,平均绝对百分比误差(MAPE)为0.987%,均方差(MSE)为0.967×105 MW2,归一化均方差(NMSE)为0.195×10–3,最大百分比误差(MAXPE)为8.469%。归一化模型的预测精度相较于单一模型区域电网负荷预测精度得到了提升,表明归一化处理对降低极端数据的影响有一定作用。
3 结束语本文提出基于前12个月历史天气条件和区域电网负荷关联关系的多元非线性拟合的特征参数因子曲线的区域电网中长期负荷的预测方法,并建立不同算法的多种预测模型,通过归一化处理,得到归一化模型。负荷预测结果表明:
1) 归一化模型负荷预测精度优于单一模型负荷预测精度,归一化模型降低了极端数据的影响;
2) 本文所提出的区域电网中长期负荷的预测方法的精度高,预测效果好,对于区域电网中长期负荷预测分析具有重要参考利用价值。
| [1] |
李冰洁. 多气象因素智能处理的区域电网母线负荷预测研究[D]. 北京: 华北电力大学, 2016.
LI B J. The bus load forecasting of regional power grid based on the intelligent processing of multi meteorological factors[D]. Beijing: North China Electric Power University, 2016.
|
| [2] |
杨楠, 李宏圣, 袁景颜, 等. 计及灰色关联度分析的中长期负荷灰色预测方法[J].
电力系统及其自动化学报, 2018, 30(6): 108-114.
YANG N, LI H S, YUAN J Y, et al. Medium- and long-term load forecasting method considering grey correlation degree analysis[J].
Proceedings of the CSU-EPSA, 2018, 30(6): 108-114.
|
| [3] |
黄俊铭, 朱建全, 庄远灿. 基于动态RBF神经网络的广义电力负荷建模[J].
电网技术, 2018, 42(2): 591-597.
HUANG J M, ZHU J Q, ZHUANG Y C. Generalized power load modeling based on dynamic RBF neural network[J].
Power System Technology, 2018, 42(2): 591-597.
|
| [4] |
LI X R, WANG L D, LI P Q. The study on composite load model structure of Artificial neural network[C]//2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies. Nanjing, China: IEEE, 2008: 1564-1570.
|
| [5] |
SHI Y L, YANG H S, DING Y W. Research on long term load forecasting based on improved genetic neural network[C]//2008 IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application. Wuhan, China: IEEE, 2008: 80-84.
|
| [6] |
李冬辉, 尹海燕, 郑博文. 基于MFOA-GRNN模型的年电力负荷预测[J].
电网技术, 2018, 42(2): 585-590.
LI D H, YIN H Y, ZHENG B W. An annual load forecasting model based on generalized regression neural network with multi-swarm fruit fly optimization algorithm[J].
Power System Technology, 2018, 42(2): 585-590.
|
| [7] |
YANG J J, WANG Q. A deep learning load forcasting method based on load type rcognition[C]//2018 International Conference on Machine Learning and Cybernetics(ICMLC). Chengdu, China: IEEE, 2018: 173-177.
|
| [8] |
杨鹤, 王良, 修世军. 基于深度玻尔兹曼机的并行电力负荷预测算法[J].
辽东学院学报(自然科学版), 2020, 27(3): 178-183.
YANG H, WANG L, XIU S J. Parallel power load forecasting algorithm based on deep boltzmann machine[J].
Journal of Liaodong University(Natural Science Edition), 2020, 27(3): 178-183.
|
| [9] |
王激华, 仇钧, 方云辉, 等. 基于深度长短期记忆神经网络的短期负荷预测[J].
广东电力, 2020, 33(8): 62-68.
WANG J H, QIU J, FANG Y H, et al. Short term load forecasting based on deep LSTM neural network[J].
Guangdong Electric Power, 2020, 33(8): 62-68.
DOI:10.3969/j.issn.1007-290X.2020.008.008 |
| [10] |
吴福疆, 范晟, 王振达, 等. 基于门控递归神经网络的电网日峰值负荷预测[J].
计算技术与自动化, 2020, 39(4): 20-26,56.
WU F J, FAN S, WANG Z D, et al. Daily peak load forecasting based on gating recurrent neural network[J].
Computing Technology and Automation, 2020, 39(4): 20-26,56.
|
| [11] |
DEHALWAR V, KALAM A, KOLHE M L, et al. Electricity load forecasting for urban area using weather forecast information[C]//2016 IEEE International Conference on Power and Renewable Energy (ICPRE): IEEE Press, 21: 355-359.
|
| [12] |
AMJADY N. Short-term hourly load forecasting using time-series modeling with peak load estimation capability[J].
IEEE Transactions on Power Systems, 2001, 16(4): 798-805.
DOI:10.1109/59.962429 |
| [13] |
丁斌, 邢志坤, 王帆, 等. 基于Stacking模型集成的LSTM网络短期负荷预测研究[J].
中国测试, 2020, 46(7): 40-45.
DING B, XING Z K, WANG F, et al. Short-term load forecasting of LSTM network based on Stacking model integration[J].
China Measurement & Test, 2020, 46(7): 40-45.
DOI:10.11857/j.issn.1674-5124.2020040146 |
 2024, Vol. 50
2024, Vol. 50