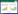文章信息
- 郭光, 王海元, 彭潇, 王智, 梁睿琪, 赵景波
- GUO Guang, WANG Haiyuan, PENG Xiao, WANG Zhi, LIANG Ruiqi, ZHAO Jingbo
- 基于学习排序的计量装置故障严重程度评估方法
- Fault severity assessment method of metering device based on learning ranking
- 中国测试, 2024, 50(6): 176-182
- CHINA MEASUREMENT & TEST, 2024, 50(6): 176-182
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022060150
-
文章历史
- 收稿日期: 2022-06-22
- 收到修改稿日期: 2022-08-16
2. 智能电气量测与应用技术湖南省重点实验室,湖南 长沙 410000;
3. 东南大学信息科学与工程学院,江苏 南京 210096;
4. 湖南大学电气与信息工程学院,湖南 长沙 410082
2. Hunan Province Key Laboratory of Intelligent Electrical Measurement and Application Technology, Changsha 410000, China;
3. College of Information Science and Engineering,Southeast University , Nanjing 210096, China;
4. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China
电能表的精准可靠稳定运行关系到电力供给侧的信任度和经济利益。复杂的供电拓扑结构、多样化的电力设备以及分布式新能源并网使得电能计量装置的运营与维护更加复杂。电能计量装置作为电网故障分析、故障定位、故障处理的数据来源,需要以高效的维护手段来保证装置的稳定运行[1]。实际工作中,绝大多数的故障对用户的正常用电并不会产生影响。例如,极端天气导致电压异常、大功率设备导致电流异常、临时计量数据异常等,其相应的措施只是进行一些微调。如果电能表内部的计量部件出现损坏,导致计量装置出现长期故障,则会对电力系统的稳定性造成影响,并导致较大的经济损失。因此,对电能计量装置故障的严重程度进行分级对于提高电能计量装置运维水平具有重要意义。
针对电能计量装置故障诊断问题,国内外学者主要采用的方法有基于傅里叶变换等传统信号处理方法和基于神经网络等机器学习的方法。例如,肖勇等提出异频导纳法实现对电流出现二次回路的诊断[2]。杨世海等利用数据挖掘技术建立故障特征和故障数据的对应关系,实现对电流出现二次回路故障的实时判别[3]。危阜胜等利用智能电网中的上传的数据构建专家诊断系统,同时结合多线程的方式实现故障的远程诊断[4]。
针对电能计量装置运行状态在线分析的要求,国内外学者主要通过分析设备工作过程中的电压、电流和设备工况等数据,建立相应的理论评估模型来实现。例如,杜卫华等将电能表的状态评价指标划分性能、可靠性、部件配置和工况环境等4中指标,其中涉及到电能表的多种数据,包括不局限于出厂设置数据、标定数据和故障数据[5]。程瑛颖等提出基于专家系统和模糊分析法的电能表状态评估方法[6]。
目前,国内外对电网中电能计量器件的状态监测取得了较好的研究成果。但上述研究均未涉及电能计量装置故障严重程度的区分或排序问题。在实际的检修任务中,检修工作者对器件故障程度的判别往往是通过器件中某些固定的参数指标,例如电压值和电流值等。然而,由于这些指标往往是孤立的,仅仅根据某些特定的参数来对电能计量装置的故障程度进行划分是不合理的,存在很大的局限性[7-8]。此外,导致电能表某些数据指标产生跳变的原因可能是些暂态因素 [9]。而电能计量装置监测数据指标多,数据量大,很难用特定的公式和准则去评价其故障程度,导致电能计量装置故障严重程度难以评估。
学习排序方法可以根据标注数据训练相应的评价模型,进而实现对数据的排序。学习排序既不依赖孤立的指标,也不同于公式化的评价。学习排序可以依据训练数据格式的不同划分为单文档、文档对和文档列表三种方法[10]。单文档方法对每个单一样本进行绝对标注,但标注标签的标准难以统一;文档对方法则是通过两两对比进行标注,比较方便且可避免出现样本标注不同,但是相应的缺陷就是工作量大;列表方法无法适应电能计量装置故障数据量巨大的特点。结合电能计量装置故障的标注一致的需求特点,本文采用文档对方法研究电能计量装置故障排序的解决方案。
针对电能计量装置运维中的非紧急故障处理和异常检修工作排序科学难题,本文主要对电能计量装置的电压、电流等数据进行分析,首先,设计相应特征提取方法,从电能表的监测数据中提取出反映运行状态和故障程度的特征;然后,结合神经网络对电能计量装置故障进行分类,根据故障程度对分析样本排序;最后,建立电能计量装置故障严重度排序方法,帮助检修人员实现高效的电能计量装置的检修。
1 电能计量装置运行数据的特征提取三相电能表包括电压、电流互感器及相应的二次回路、电能表,典型的故障包括失压、失流和压降超差等电能表故障。电能计量装置的运行监测数据主要包括电压、电流和分相功率等十余个物理量,各个物理量均为采样时间间隔为15 min的时域序列,十余组相互独立的时域序列构成了复杂高维时空序列,很难作为各种分类算法的数据输入。本文依据电能表故障判别需求,设计了表1所示的电能计量装置运行监测特征参数字段表,反映各指标的大小、波动情况以及波形特征。
| 类型 | 字段1 | 字段2 | 字段3 | 字段4 |
| 电压 | A相电压 | B相电压 | C相电压 | |
| 电流 | A相电流 | B相电流 | C相电流 | |
| 有功功率 | A相 有功功率 |
B相 有功功率 |
C相 有功功率 |
总有功 功率 |
| 无功功率 | A相 无功功率 |
B相 无功功率 |
C相 无功功率 |
总无功 功率 |
| 功率因数 | 当前A相 功率因数 |
当前B相 功率因数 |
当前C相 功率因数 |
当前总 功率因数 |
| 其他 | 三相 不平衡度 |
负载率 |
由表1可见,电能计量装置运行监测参数的每个类型字段的时域序列均为独立的一维数组,因此所有监测字段参数构成了一个复杂的高维数组,无法作为分类算法的输入,需要对数据进行降维,本文通过特征提取方式进行处理。
本文引入的特征向量如下:
| $ \begin{split} {\boldsymbol{X}} = &({N_0},{N_1},{N_2},{R_{\rm AB}},{R_{\rm AC}},{R_{\rm BC}}, \\ & S,{N_3},{N_4},{E_{\rm A}},{E_{\rm B}},{E_{\rm C}},L,{N_{\rm S}}) \end{split} $ | (1) |
其中,公式(1)中各个参数的定义如下:
式中:N0——iun大于Umax的时间点的个数,Umax是判断iun是否过大的阈值;
N1——imax大于
N2−imin大于
RAB−
RAC−
RBC——
S——三相电压中电压曲线的复杂程度。
参数S定义为,三相电压的近似熵的最大值:
| $ S = \max \{ {\rm ApEn}({{\boldsymbol{U}}_{\rm{A}}}), {\rm ApEn}({{\boldsymbol{U}}_{\rm{B}}}), {\rm ApEn}({{\boldsymbol{U}}_{\rm{C}}})\} $ | (2) |
式中:UA,UB,UC——三相电压向量;
N3——vmax大于
N4——vmin小于
1)EA = mean(UA),EB= mean(UB),EA = mean(UC),其中mean(
2)L,平均负载率;
3)N5,一天中重载的采样点数。
以上特征参数中,相间电流的欧氏距离可以反映三相电流的平衡度,欧氏距离越大,三相不平衡度越高。阈值参数可以反映电能计量装置是否处于超重载状态,结合三相电压的近似熵参数可反映电压是否存在异常。综合考虑以上参数基本能够描述三相电流不平衡、电能计量装置超重载以及电压异常等故障特征。
2 电能计量装置故障严重程度排序方法电能计量装置故障严重程度的学习排序主要通过训练模型,实现某个故障样本排序高于另一样本的概率预测,同时会有一个评分函数与所得的概率进行映射。排序越靠前的故障样本,对应的故障程度也就越严重。可用于学习排序的训练模型有很多,没有具体的算法限制,包括但不局限于神经网络[11]、梯度提升决策树(gradient boosted decision tree,GBDT)[12]等。
在训练过程中,需要为训练模型中的评分制定一个损失函数,然后利用梯度下降法对电能计量装置的故障严重程度评分模型进行训练,其中,模型训练过程中常用的损失函数是极大似然准则。采用梯度下降法则提高排在其他样本之前的故障样本对应的排名分数,对于排在其他样本之前的故障样本,则梯度下降法就将其对应的分数减少。其中,样本增加和减少的分数与样本间的分数差相关联。在实际工况中,往往优先考虑故障程度最严重的电能计量装置,所以必须保证排序靠前的样本的排序准确性。一般的解决方案是使用加权损失函数,即利用某些有用的特征对损失函数进行加权。
由于在训练过程中,需要进行概率和评分的转换,所以在对代价函数进行定义时,需要附加条件对概率函数进行限制。假设模型对第i个样本的评分为si,概率函数的性质如下:
1)两个样本对应的概率与样本的得分之间为正相关的关系。
2)样本概率为0.5表示有两个具有相同得分的样本。
3)概率函数为对称函数。
Sigmoid函数符合上述三个要求,且可以微分,即:
| $ P({\rm rank}(i) > {\rm rank}(j)) = \frac{1}{{1 + {{\rm e}^{ - ({s_i} - {s_j})}}}} $ | (3) |
由于采用Sigmoid函数后,概率P随si–sj的变化是单调的,本文中损失函数取该概率的负对数,即:
| $ {J_{ij}} = - \lg \left( {\frac{1}{{1 + {{\rm e}^{ - ({s_i} - {s_j})}}}}} \right) = \lg (1 + {{\rm e}^{ - ({s_i} - {s_j})}}) $ | (4) |
其曲线如图1所示。如图1所示,当si-sj> 0时,Jij的值几乎等于0,即当第i个样本排在第j个样本之前,第i个样本得分也要比第j个样本高,而此时对应的损失函数值非常小,反之则损失函数的值随着分数差值增大而变大。
|
| 图 1 损失函数随分数差的变化 |
在电能计量装置故障严重程度排序训练数据集D中,故障样本成对出现,即(samplei, samplej),其中samplej的严重程度低于samplei,因此,代价函数的优化目标在训练模型时应该为
| $ \min J = \sum\limits_{(i,j) \in D} {{J_{ij}}} $ | (5) |
设θk为评分函数中的参数,采用梯度下降法调节评分模型,则损失函数Jij对θk求导:
| $ \begin{split} \frac{{\partial {J_{ij}}}}{{\partial {\theta _k}}} =& \frac{{\partial {J_{ij}}}}{{\partial {s_i}}}\frac{{\partial {s_i}}}{{\partial {\theta _k}}} + \frac{{\partial {J_{ij}}}}{{\partial {s_j}}}\frac{{\partial {s_j}}}{{\partial {\theta _k}}} = \frac{{ - {{\rm e}^{{s_j} - {s_i}}}}}{{1 + {{\rm e}^{{s_j} - {s_i}}}}}\frac{{\partial {s_i}}}{{\partial {\theta _k}}} + \frac{{{{\rm e}^{{s_j} - {s_i}}}}}{{1 + {{\rm e}^{{s_j} - {s_i}}}}}\frac{{\partial {s_j}}}{{\partial {\theta _k}}}= \\ & \frac{{ - {{\rm e}^{{s_j} - {s_i}}}}}{{1 + {{\rm e}^{{s_j} - {s_i}}}}}\left( {\frac{{\partial {s_i}}}{{\partial {\theta _k}}} - \frac{{\partial {s_j}}}{{\partial {\theta _k}}}} \right) = {\lambda _{ij}}\left( {\frac{{\partial {s_i}}}{{\partial {\theta _k}}} - \frac{{\partial {s_j}}}{{\partial {\theta _k}}}} \right)\\[-18pt] \end{split}$ | (6) |
其中,
| $ \frac{{\partial J}}{{\partial {\theta _k}}} = \sum\limits_{(i,j) \in D} {\frac{{\partial {J_{ij}}}}{{\partial {\theta _k}}}} = \sum\limits_{(i,j) \in D} {{\lambda _{ij}}\left( {\frac{{\partial {s_i}}}{{\partial {\theta _k}}} - \frac{{\partial {s_j}}}{{\partial {\theta _k}}}} \right)} $ | (7) |
对于单个样本,损失函数的梯度为
| $ \begin{split} \sum\limits_{(i,j) \in D} {{\lambda _{ij}}\left( {\frac{{\partial {s_i}}}{{\partial {\theta _k}}} - \frac{{\partial {s_j}}}{{\partial {\theta _k}}}} \right)} =& \sum\limits_{\{ j|(i,j) \in D\} } {{\lambda _{ij}}\frac{{\partial {s_i}}}{{\partial {\theta _k}}}} - \sum\limits_{\{ i|(i,j) \in D\} } {{\lambda _{ij}}\frac{{\partial {s_j}}}{{\partial {\theta _k}}}}= \\ & \sum\limits_l {\left( {\sum\limits_{\{ j|(l,j) \in D\} } {{\lambda _{lj}}} - \sum\limits_{\{ i|(i,l) \in D\} } {{\lambda _{il}}} } \right)} \frac{{\partial {s_l}}}{{\partial {\theta _k}}} \end{split}$ | (8) |
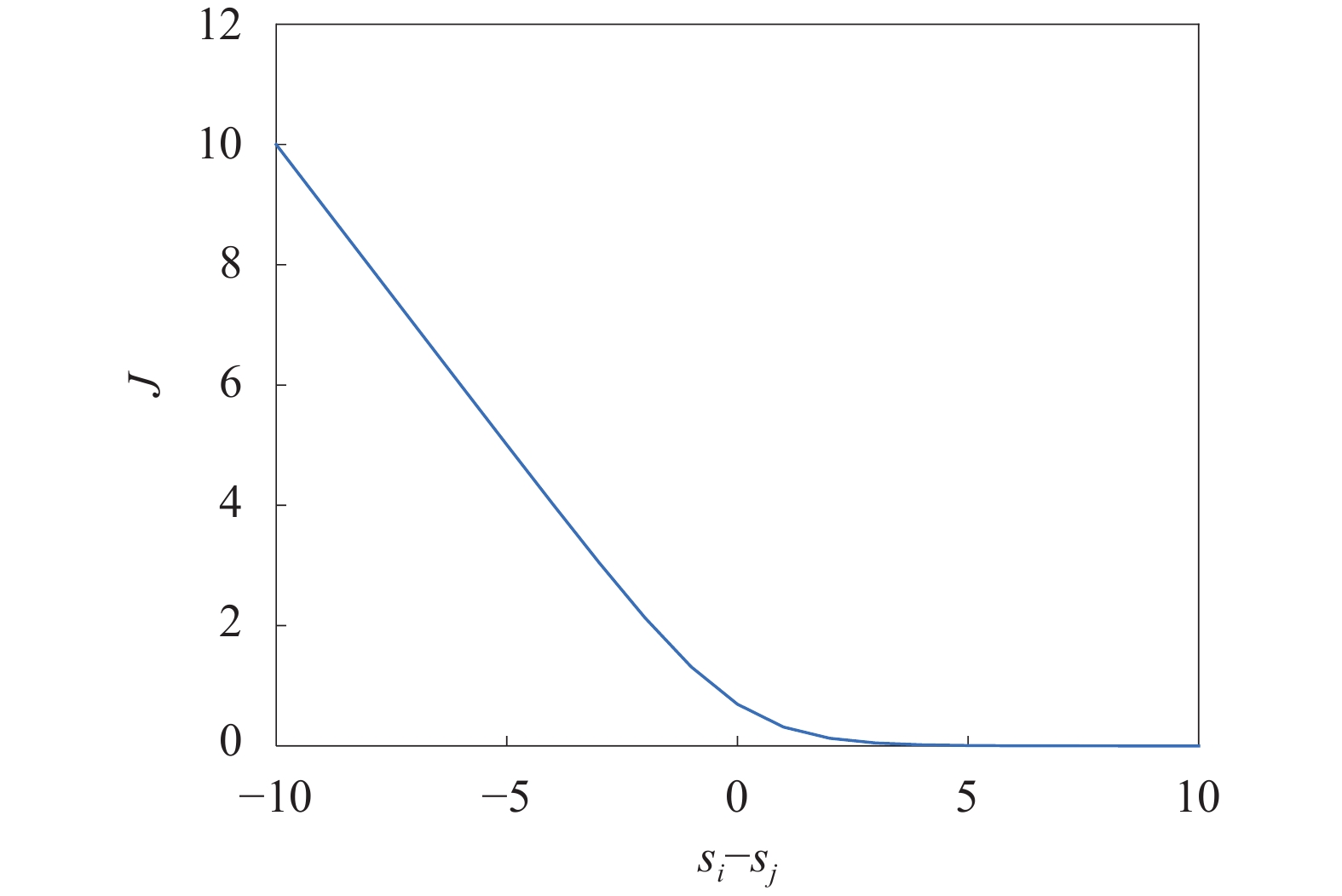
这表明,在数据集所有的故障样本对中,对于任意的一个故障样本,排在其前面的故障样本分数减少,而排在其后面的故障样本分数增加,分数的差值决定了变化的范围。单个样本(排序4的样本)的评分调节原理如图2所示。
|
| 图 2 单个样本的评分调节原理图示 |
图2中,左侧的1-8代表排序值,排序4的样本与排序1-3、5-8的样本分别可以组成7个样本对。在每个样本对中,排序4样本分数变化情况均不一样。例如,在排序1-3的样本与排序4的样本组成的样本对中,因排序4的样本排在后,其分数将增加,而排序1-3的样本分数将减少。基于此,电能计量装置故障严重程度评分模型就能实现对故障样本的评分,进而得到排序结果。
3 实验结果与分析本文实验中采用国家电网公司某省2020年度-2021年度部分地区电能计量装置运行监测数据,涵盖部分城市、乡镇电能计量装置运行故障情况。根据电能计量装置运行特点,其中最严重的故障类型是电压异常,例如电压骤升或骤降的情况,其次是持续性的三相不平衡。根据实际检修数据中,计量装置故障类别占比与监测字段数据统计分析,本文采用的电能计量装置故障程度对应的评分函数为:
| $ f({{\boldsymbol{X}}_i}) = {\boldsymbol{P}} \cdot {\boldsymbol{X}}_i^{\rm{T}} $ | (9) |
其中,P = (2,1,1,0.5,0.5,0.5,2,3,3,0.5,0.5,0.5,2,2),系数为监测字段对应的归一化故障占比,Xi是第i个样本归一化后的特征向量。
由于上述评分函数是基于特定区域的计量装置维护数据计算得出的,对于大范围、多种类的电能计量装置欠缺一定的普适性,以本文中所采用的数据集仅能反应特定区域的计量装置故障特征,如需得到更为泛化的训练模型,则需要增加不同区域与不同种类计量装置的相关数据进行训练。电能计量装置实际故障数据通过以上评分函数进行排序后,根据式(9)所示的评分函数对部分电能计量装置故障进行初步排序后的电压电流曲线如图3所示。

|
| 图 3 初步排序前三的三相电流和三相电压曲线 |
图3中所示的排序前三的电能计量装置故障情况均存在持续性低电压、三相电流不平衡和单相断电异常状况。经计量专家评估,在实际计量现场中这些故障程度均属于很严重类别,这在一定程度上说明式(9)的合理性。图3的结果也表明,通过评分函数对电能计量装置故障进行初步排序,能够为合理区分电能计量装置故障严重程度提供有效支撑。
由于实际运行中故障类型各不相同,导致一方面难以积累有效的大量故障样本,另一方面确实存在不同故障类型的样本数量严重不平衡的问题。由于所采集的数据中故障样本占比较低,为提高训练效率,丰富故障样本类型,确保模型对各类型故障有全局较平衡的响应能力,本研究采取基于少量故障样本的随机组合的方案得到训练所需的额外故障样本。
这些特征向量均经过标准化处理,并使用f(X)进行评分。考虑样本对的数据标注格式,从数据集中随机抽取样本,计量专家根据现场情况,对不同类型故障进行评估,区分不同故障类型的严重程度,进而设置属性标签,为后续人工智能模型的训练提供依据。标签种类分三种,(+1,0,–1)分别代表紧急、严重、一般三个程度。若
本文采用两部分四层全连接神经网络进行评分模型训练,输入为数据样本对应的特征向量,损失函数的参数为神经网络的两个输出的差值。
所采用的全连接神经网络参数如下:输入层一共有14个神经元(对应特征向量维度是14),隐含层一共有三层,其中第一层包括128个神经元,第二层包括64个神经元,第三层包括32个神经元。学习过程使用误差反向传播方法来训练,对同一个排序下的所有样本对全部代入全连接神经网络进行前向反馈,然后计算总差分并进行误差反向传播,可减少误差反向传播的次数。
训练集包含2万组数据样本,测试集包含1万组数据样本。训练集与测试集中的故障样本均来源与实际故障样本以及通过随机组合方案生成的拓展故障样本。利用本文所建立的基于神经网络和RankNet算法在训练集上训练得到的电能计量装置故障严重程度评分模型测试集和训练集上的测试结果如表3所示,其中,正确数量表示电能计量装置故障严重程度评分模型判别结果与样本标注相同,如果两者不相同,则看做判别错误,对于0标签样本对,都统计为判别错误。
| 样本 | 判断正确 样本对数 |
判断错误 样本对数 |
准确率/% |
| 训练集(20000) | 19648 | 352 | 98.24~99.95 |
| 测试集(10000) | 9769 | 231 | 97.69~100 |
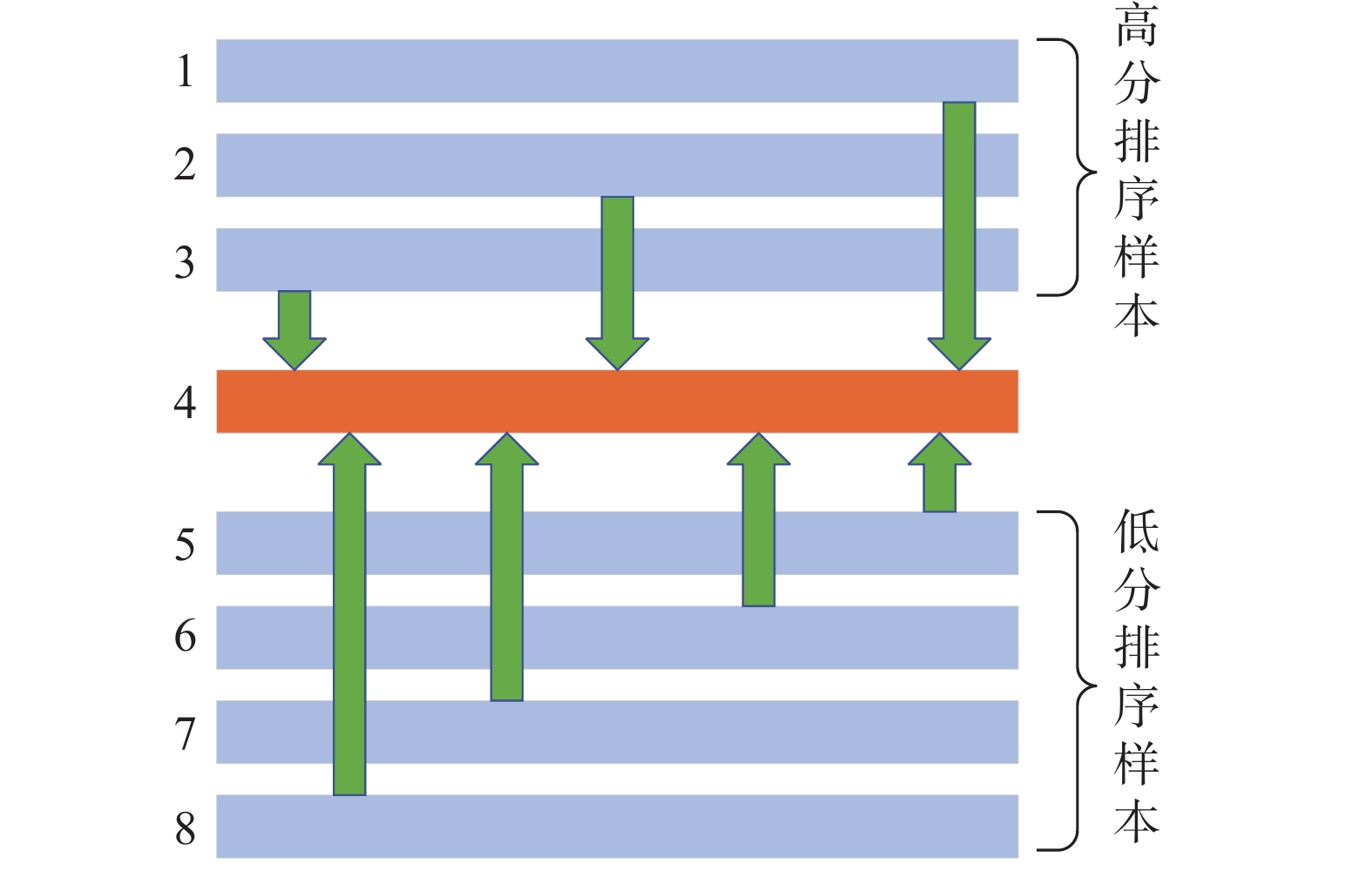
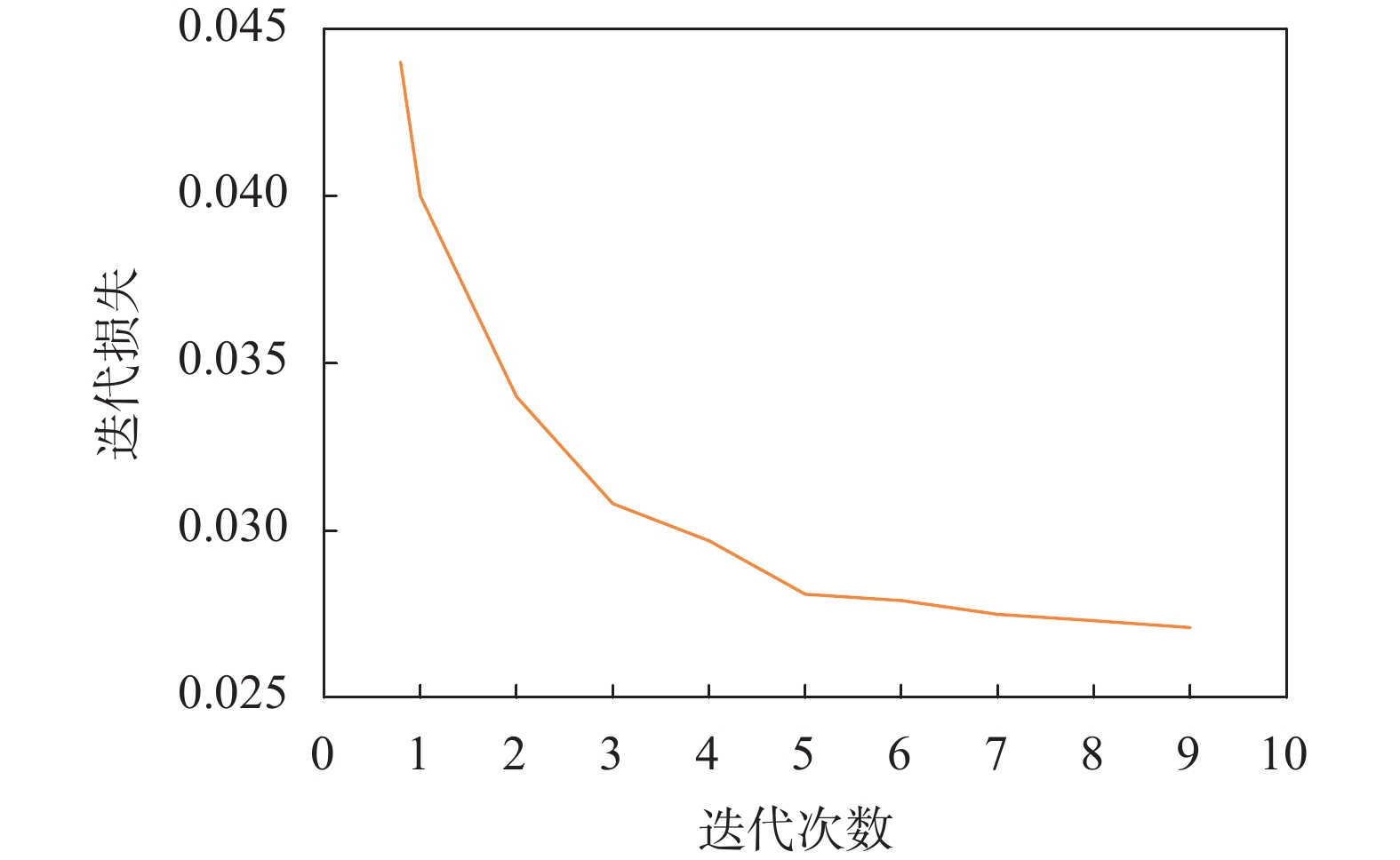
如表3所示,如果不考虑0标签的样本对,电能计量装置故障严重程度评分模型在基于RankNet算法的情况下,在训练集和测试集上的判别准确率几乎接近于100 %。电能计量装置故障严重程度评分模型训练的Epoch损失如图4所示,其中当RankNet算法中的Epoch Number等于10、神经网络学习速率为0.1的时候,epoch loss的收敛速度非常快。
|
| 图 4 RankNet的Epoch损失 |
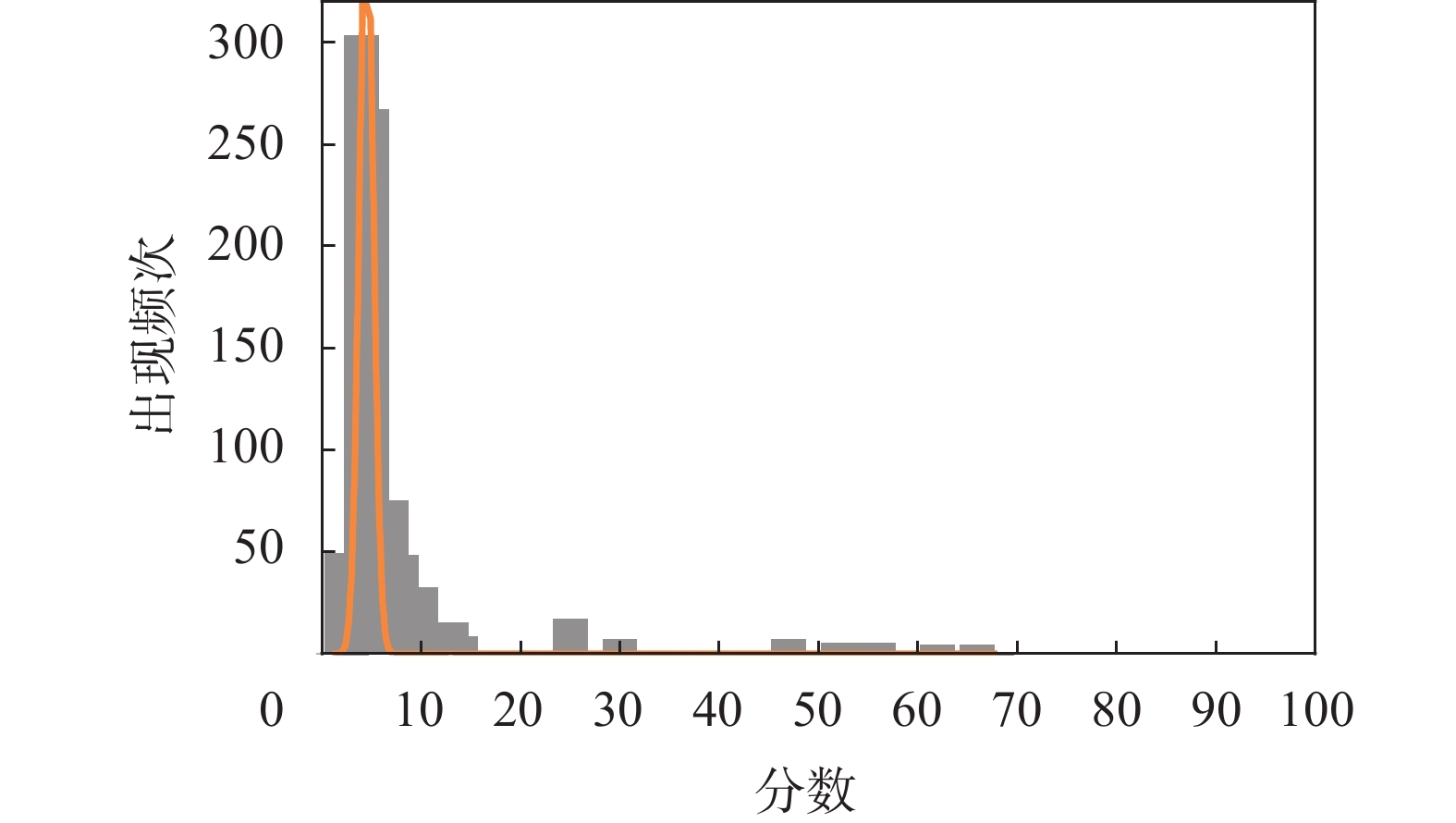
当验证集是实际电能计量装置故障数据时,故障样本总数为702个,采用评分函数f(X)进行打分,对应的分数分布如图5所示,验证集样本模型所得分数的分布如图6所示。
|
| 图 5 验证集样本实际分数的分布 |
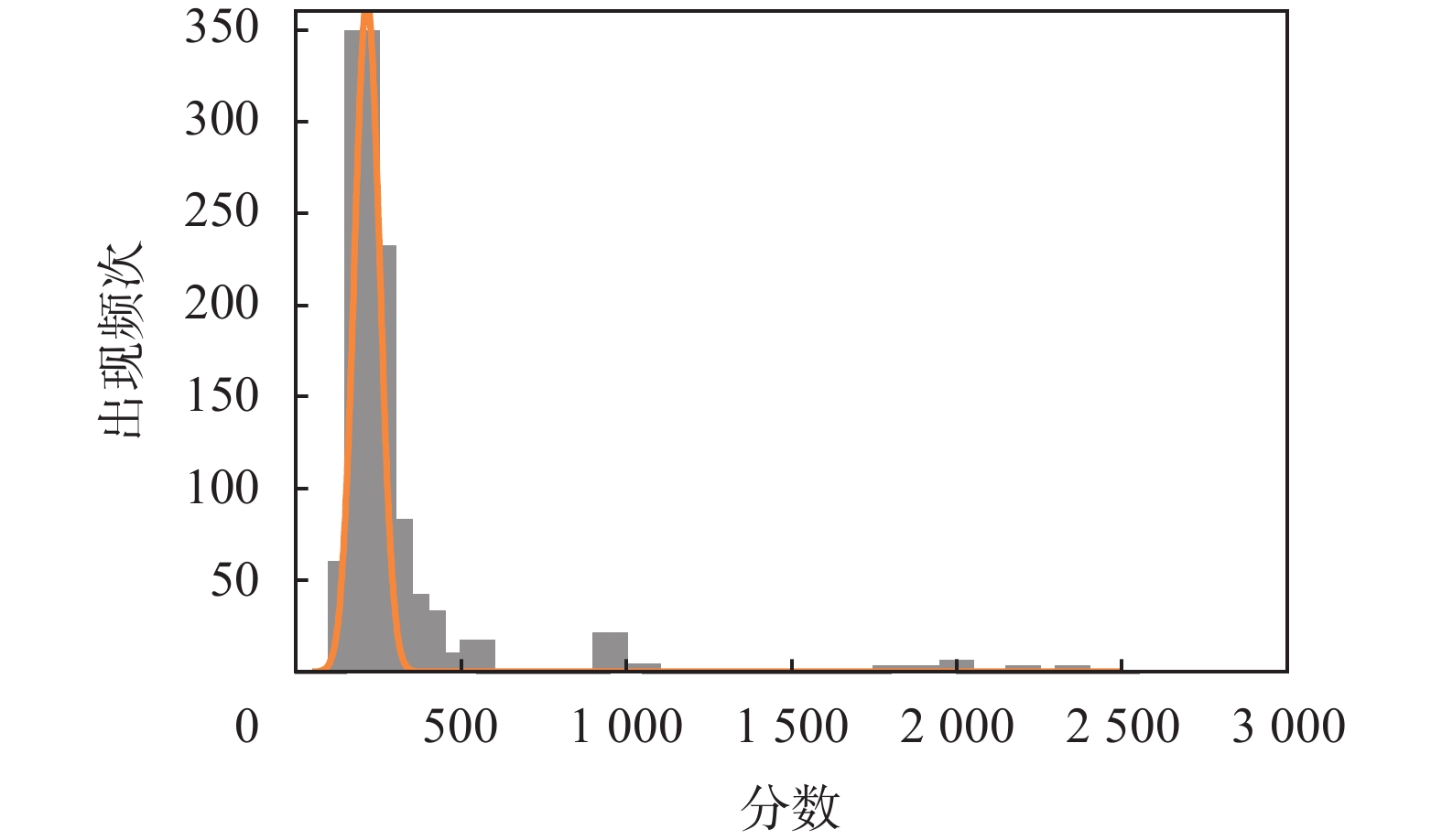
|
| 图 6 验证集样本模型所得分数的分布 |
图5和图6横坐标的分数反映了样本的故障严重程度评分结果。图5是采用评分函数f(X)进行打分的结果,图6是在数据集所有的故障样本组成的样本对进行评分调节后的值,也就是根据图2的调节原理得到的结果。因采用的评分函数不同,两图在分数值上存在较大差异。但需要指出的是,不同方法得到不同的分值对严重程度评估结果影响甚微,这是因为严重程度评估依赖的是样本评分值的相互比较结果。比较图5和图6,尽管两者在分数值上存在差异,但是在分数相对值的分布上还是具有一定的相似性。通过电能计量装置故障严重程度评分模型评分得到相应故障样本的排列,计算排列的平均偏移量,即对故障样本真实的顺序与通过电能计量装置故障严重程度评分模型得到的顺序差值求加权平均值,得到的结果如表4所示。
从表4的结果可知,对于前50个故障样本,由电能计量装置故障严重程度评分模型得到的排序与故障样本的真实顺序相差很小,平均排序偏移量为0.96,小于1,说明本文提出的电能计量装置故障严重程度评分模型对于排序靠前的故障具有很好的排序效果。但对于后续的样本,基于RankNet算法的模型则存在较大的排序偏差。
产生这个的原因是由于偏序靠前的故障样本故障差异较大,故障样本的分数差值也同样较大,而排序在后面的故障样本故障差异较小,所以故障样本的分数差值同样较小,因此导致模型得到的平均排序偏移量较大。在实际的电能计量装置的检修任务中,检修人员首先需要安排检修的是排序靠前故障程度比较严重的电能表,所以本文提出的算法可以有效的提高检修人员的检修效率。
4 结束语本文提出一种电能计量装置故障严重程度评分及排序方法。设计了包括4个字段和14个特征的三相电能计量装置运行监测数据数组,实现了数据的降维处理;采用Sigmoid函数的负对数进行排序概率和评分的转换,运用全连接神经网络(输入层14个神经元对应14个特征),对RankNet模型进行训练,实现了计量装置故障程度的分级。通过随机组合的方式拓展故障样本,实现了故障样本不足的情况下的网络模型训练。训练集包含2万组数据样本,测试集包含1万组数据样本,训练集样本准确率为98.24 %~99.95 %,测试集样本准确率为97.69 %~1。实验结果表明,本文提出的评分模型可实现对不同程度故障的精确的排序,从而实现计量装置故障严重程度的高效评估。
| [1] |
朱少斌, 许素安, 马宗彪, 等. 基于BSO-BPNN模型的电能计量装置异常诊断方法研究[J].
中国测试, 2022, 48(1): 141-146.
|
| [2] |
肖勇, 周尚礼. 电流互感器二次回路故障智能检测方法研究与设计实现[J].
电力系统保护与控制, 2010, 38(12): 115-120.
|
| [3] |
杨世海, 戴太文, 卢树峰, 等. 基于数据挖掘的计量装置在线监测与故障诊断系统设计[J].
电子设计工程, 2016, 24(23): 108-111.
|
| [4] |
危阜胜, 肖勇, 陈锐民. 故障诊断技术在计量自动化系统中的应用[J].
电测与仪表, 2013, 50(8): 93-97.
|
| [5] |
杜卫华, 曹袆, 厉达. 状态评估技术在关口电能计量装置管理上的应用[J].
华东电力, 2013, 41(10): 2107-2110.
|
| [6] |
程瑛颖, 吴昊, 杨华潇, 等. 电能计量装置状态模糊综合评估及检验策略研究[J].
电测与仪表, 2012, 49(12): 1-6.
|
| [7] |
XU L, CAO M, SONG B, et al. Open-circuit fault diagnosis of power rectifier using sparse autoencoder based deep neural network[J].
Neurocomputing, 2018, 311: 1-10.
DOI:10.1016/j.neucom.2018.05.040 |
| [8] |
CHEN T, HILL D J, WANG C, et al. Distributed fast fault diagnosis for multimachine power systems via deterministic learning[J].
IEEE Transactions on Industrial Electronics, 2020, 67(5): 4152-4162.
DOI:10.1109/TIE.2019.2917367 |
| [9] |
黎海生, 许明柱, 唐坚钊, 等. 全模块化防窃电低压计量装置及其关键技术研究[J].
中国测试, 2021, 47(S1): 117-121.
|
| [10] |
胡非, 刘志刚, 何士玉, 等. 一种基于模型的低压配电网故障诊断搜索算法[J].
电力自动化设备, 2013, 33(1): 81-84.
|
| [11] |
BURGES C J, SHAKED T, RENSHAW E L, et al. Learning to rank using gradient descent. Proceedings of the 22nd international conference on Machine learning. August 2005: 89–96.
|
| [12] |
FRIEDMAN, JEROME H. Greedy function approximation: a gradient boosting machine[J].
Annals of Statistics, 2001, 29(5): 1189-1232.
DOI:10.1214/aos/1013203450 |
| [13] |
HU Z, WANG Y, PENG Q, et al. Unbiased lambdamart: an unbiased pairwise learning-to-rank algorithm[C]. the web conference, 2019: 2830-2836.
|
| [14] |
梁睿琪. 基于大数据的电力系统故障与异常分析[D]. 南京: 东南大学, 2020.
LIANG R Q. Analysis of power system faults and abnormalities based on big data [D]. Nanjing: Southeast University, 2020.
|
 2024, Vol. 50
2024, Vol. 50