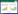文章信息
- 康利改, 袁小雪, 曹紫霖, 高晓霞, 沈仁东, 赵军
- KANG Ligai, YUAN Xiaoxue, CAO Zilin, GAO Xiaoxia, SHEN Rendong, ZHAO Jun
- 储能协调下负荷密集区分布式综合能源系统优化研究
- Optimization of distributed integrated energy system in load intensive area under energy storage coordination
- 中国测试, 2024, 50(6): 167-175
- CHINA MEASUREMENT & TEST, 2024, 50(6): 167-175
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022070064
-
文章历史
- 收稿日期: 2022-07-11
- 收到修改稿日期: 2022-09-28
2. 河北省岩土与结构体系防灾减灾技术创新中心(筹),河北 石家庄 050018;
3. 智能低碳装配式建筑技术研究中心,河北 石家庄 050018;
4. 河北省科学院能源研究所,河北 石家庄 050081;
5. 华北电力大学动力工程系,河北 保定 071003;
6. 中低温热能高效利用教育部重点实验室(天津大学),天津 300072
2. Innovation Center of Disaster Prevention and Mitigation Technology for Geotechnical and Structural Systems of Hebei Province (Preparation), Shijiazhuang 050018, China;
3. Engineering Technology Research Center for Intelligent & Low-carbon Assembled Building, Shijiazhuang 050018, China;
4. Institute of Energy Sources, Hebei Academy of Science, Shijiazhuang 050081, China;
5. Department of Power Engineering, North China Electric Power University, Baoding 071003, China;
6. Key Laboratory of Efficient Utilization of Low and Medium Grade Energy (Tianjin University), MOE, Tianjin 300072, China
习近平主席在第75届联合国大会上发表“二氧化碳排放力争于2030年达到峰值,努力争取2060年前实现碳中和”重要讲话[1]。应对全球气候变化,加速全社会绿色低碳转型,尽早实现碳中和,是全人类的共同期望。与此同时,各国城市化与电气化水平也在不断提高,造就了建筑行业能源消耗的不断上升,也导致城市中负荷聚集效应不断增强,冷热电负荷持续升高,负荷峰谷差进一步拉大,导致供应分配矛盾不断加深。因此,需要寻求新的解决方案来破解这一难题。
分布式综合能源系统的发展大致划分为孕育、概念、起航和升华4个阶段。孕育阶段,主要是基于能的梯级利用的天然气冷热电联产系统;概念阶段,主要是基于能的因地制宜的分布式能源系统;起航阶段,主要是基于能的多能互补的综合能源系统;升华阶段,主要是基于能的互联互济的能源互联网[2]。近几年,分布式综合能源系统的结构研究越来越复杂。以王江江研究团队为例,最初构建的分布式综合能源系统为动力机发电,高温余热驱动换热器/溴化锂制冷机组供热/冷[3],2010年开始,研究的系统构成复杂化,加入蓄热/冷装置,采用遗传算法对蓄能容量等参数进行优化[4]。此外,一些学者也提出了新的结构,李剑锋等[5]在分布式综合能源的基础上加入了储热和储电设备,降低了碳的排放量;龚逊东[6]将电转气设备耦合到分布式能源系统中,以提高风电利用率来提高系统的灵活性。
国内外学者对江水源热泵进行了一系列研究,Si等[7]提出了新的冷却水单元优化模型,采用主元分析法对江水源热泵模型进行评价,用于河水源热泵系统的仿真模拟和能耗;Li等[8]提出了一种基于系统仿真的太阳能混合热泵冷热系统多目标优化模型,提高了系统的能源、经济和环境性能;吴杰等[9]以重庆市某能源站为研究对象,分析了在 20%、50%、80%与100%四种开发规模对系统蓄冰/蓄热优先和机组优先运行模式的影响;龙天河等[10]针对包含包括内燃机、烟气热水型吸收式制冷机组、江水源热泵机组的冷热电三联供和江水源热泵组成的复合联供系统,对其进行优化分析。
通过文献综述分析可以发现,国内外针对综合供能系统架构和规划的研究多集中在冷热电联供系统或水源热泵分供系统上,提出的系统结构形式较为单一。大多将江水源热泵和分布式综合能源系统分开进行评价,没有针对整个基于江水源热泵的供能系统架构和运行方式的评价方法。因此,文中构建了基于储能协调下的负荷密集区综合能源系统,采用多目标优化方法进行评价。
1 负荷密集区分布式综合能源系统的构建 1.1 系统的构建文中构建了包含光伏、江水源热泵和储能系统的负荷密集区分布式综合能源系统,如图1所示。
|
| 图 1 负荷密集区分布式综合能源系统图 |
由图1可知,传统分供系统中,建筑物电力供应由电网满足,供热/冷需求由冷水机组满足。负荷密集区分布式综合能源系统中,建筑物电力供应由光伏提供,同时能够驱动江水源热泵满足供冷/供热需求。当江水源热泵不能满足供冷/供热需求时,储能系统放能;反之,储能系统储能。当光伏发电量高于建筑电负荷和江水源热泵电耗时,多余电量售卖给电网;反之,从电网买电来满足供电需求。
1.2 数学模型的建立 1.2.1 江水源热泵的数学模型为了确定相关参数对容量和功耗的影响,利用EnergyPlus提供的水源热泵[11]的性能曲线,建立了数学模型,其性能曲线由三条曲线组成,分别为:
1)制冷能力曲线
该曲线定义为冷却水和冷冻水出口温度与最大制冷量的关系。
| $ \begin{split} {\rm {CAP_{FT}}} = & {a_1} + {b_1} \times {T_{\rm{ ch,o}}} + {c_1} \times T_{\rm{ ch,o}}^2 + \\ & {d_1} \times {T_{\rm{co,o}}} + {e_1} \times T_{\rm{co,o}}^2 + {f_1} \times {T_{\rm{ch,o}}} \times {T_{\rm{co,o}}} \end{split}$ | (1) |
式中:Tch,o、Tco,o——冷冻水、冷却水出水温度,℃;
a1、b1、c1、d1、e1、f1——系数。
因此,在Tch,o和Tco,o工况下运行的最大制冷量:
| $ {Q_{\max }} = {Q_{\rm eq}} \times \rm{CA{P_{FT}}} $ | (2) |
式中:Qmax——最大制冷量,kW;
Qeq——额定制冷量,kW。
2)性能系数与运行水温条件关系曲线
该曲线定义为最大负荷下的COP随冷却水出口温度和冷冻水出口温度的变化。
| $ \begin{split} \rm{CO{P_{FT}}} =& 1/({a_2} + {b_2} \times {T_{\rm{ch,o}}} + {c_2} \times T_{\rm{ch,o}}^2 + \\ &{d_2} \times {T_{\rm{co,o}}} + {e_2} \times T_{\rm{co,o}}^2 + {f_2} \times {T_{\rm{ch,o}} \times {T_{\rm{co,o}}}}) \end{split}$ | (3) |
3)性能系数与部分负荷系数关系曲线
该曲线定义为COP随部分负荷系数的变化。
| $ \begin{split} \rm{CO{P_{Fr}}} =& 1/({a_3} + {b_3} \times {T_{\rm{co,o}}} + {c_3} \times T_{\rm{co,o}}^2 + \\ &{d_3} \times r + {e_3} \times {r^2} + {f_3} \times {T_{\rm{co,o}}} \times r + {g_3} \times {r^3}) \end{split} $ | (4) |
| $ r = Q/{Q_{\max }} $ | (5) |
式中:r——部分负荷系数;
Q——实际制冷量,kW。
根据三条曲线得到冷水机组的功耗数学模型:
| $ {P_{{\text{comp }}}} = \frac{{{Q_{\max }}}}{\rm {CO{P_{eq}}}} \times \frac{1}{\rm{CO{P_{FT}} \times \rm{CO{P_{Fr}}}}} $ | (6) |
其中:Pcomp为冷水机组功率,kW;COPeq为额定性能系数。式(1)~(6)中热泵性能参数如表1所示。
| 符号 | 数值 |
| Qeq | 724 kW |
| a1 | –0.111601 |
| b1 | –0.1058351 |
| c1 | –0.001829692 |
| d1 | 0.09677921 |
| e1 | –0.02169221 |
| f1 | 0.00499866 |
| a2 | 0.589916 |
| b2 | 0.01976846 |
| c2 | 0.000875509 |
| d2 | –0.007564222 |
| e2 | 0.000877513 |
| f2 | –0.002036856 |
| a3 | 0.364549 |
| b3 | 0.00273214 |
| c3 | –5.35677×10–5 |
| d3 | 0.1212025 |
| e3 | 0.549175 |
| f3 | 0.000208394 |
| g3 | –0.07516191 |
| Tch,o | 5.56 ℃ |
| Tco,o | 31.44 ℃ |
1.2.2 光伏发电系统的数学模型
光伏发电系统的发电量受光伏转换效率、太阳辐射量、环境温度和安装面积的影响,因此,光伏的输出功率数学模型[12]为:
| $ {E_{\rm PV}} = {A_{\rm PV}} \cdot {\eta _{\rm PV}} \cdot I \cdot \left( {1 - 0.005 \times \left( {{t_0} - 25} \right)} \right) $ | (7) |
式中:ηPV——光伏发电系统转换效率;
I——太阳辐射量,kW/m2;
t0——环境温度,℃;
APV——安装面积,m2。
1.2.3 储能系统的数学模型储能系统可以在时间上解耦能源的生产和消耗,提高系统经济效益,建立储能系统设备的储能和放能模型[13],其连接到系统后,充能时,可认为是冷/热负荷;放能时,可认为是系统的冷/热源,如下所示:
| $ {E_{{\text{st}},i}}(t) = {E_{{\text{st}},i,0}} + \sum\limits_{t \in {\phi _{{\text{in}}}}} {{P_{{\rm{st}},i}}(t){\eta _{{\rm{in}},i}}} \Delta t + \sum\limits_{t \in {\phi _{\rm out}}} {\frac{{ - {P_{{\rm{st}},i}}(t)}}{{{\eta _{{\rm{out}},i}}}}} \Delta t $ | (8) |
式中:i−储能设备类型,i为1,2分别表示储热、储冷设备;
Est,i(t),Est,i,0——储能设备t时段、初始时段储能量;
Pst.i(t)——t时段储能设备储能或放能功率;
ηin,i——储能设备储能效率;
ηout,i——储能设备放能效率;
Δt——相邻时段的时间间隔。
2 优化方法 2.1 评价指标评价指标是否合理、是否能反映系统的关键性能对能源系统综合性能的分析起着至关重要的作用。目前,对能源系统的性能评价主要集中在经济、能源和环境这三个层面。将从这三个大的层面中选取相应的评价指标,为负荷密集区分布式综合能源系统的多目标优化奠定基础。
2.1.1 经济指标经济指标是评价一个系统能否得到实施的重要指标,选取年度总费用节约率(ATCR)作为系统的经济指标[14-15]。负荷密集区分布式综合能源系统的年度总费用(ATC)包括系统的运行费用(OC)和年度均化费用(IC)。
| $ \mathrm{ATC=OC+IC} $ | (9) |
1)系统的运行费用为从电网购电费用和向电网售电费用,其表示为:
| $ \mathrm{OC}=C\mathrm{_{\mathrm{e},b}}-C_{\text{e},\mathrm{s}} $ | (10) |
| $ {C_{\rm e,b}} = \mathop \sum \limits_{i = 1}^{8\;760} \left( {{c_{{\rm{e,b}},i}}{E_{{\rm{e,b}},i}}} \right) $ | (11) |
| $ {C_{\rm e,s}} = \mathop \sum \limits_{i = 1}^{8\;760} \left( {{c_{{\rm{e,s}},i}}{E_{{\rm{e,s}},i}}} \right) $ | (12) |
式中:OC——年运行费用,元;
Ce,b、Ce,s——从电网购电、售电费用,元;
ce,b,i、ce,s,i——购电、售电价格,元;
Ee,b,i、Ee,s,i——从电网的购电、售电量,kW·h。
2)系统的年度均化费用包括各个设备的初投资,其费用年值为:
| $ \mathrm{IC}=R\sum\limits_{j=1}^kc_jN_j $ | (13) |
| $ R = \frac{{l{{(1 + l)}^n}}}{{{{(1 + l)}^n} - 1}} $ | (14) |
式中:IC——年度均化费用,元;
R——投资回收因子;
Nj和cj−第j个设备装机容量和单位容量初投资费用,元;
l和n——年利率和工程年限,年利率取0.06,工程年限取20。
对于传统分供系统,其年度总费用为:
| $ \mathrm{ATC_{SP}=OC_{SP}+IC_{SP}} $ | (15) |
| $ {\rm{O{C_{SP}}}} = \mathop \sum \limits_{i = 1}^{8\;760} \left( {{c_{{\rm{SP,e,b}},i}}{E_{{\rm{SP,e,b}},i}}} \right) $ | (16) |
| $ \mathrm{IC}_{\text{SP}}=R\sum\limits_{j=1}^kc_jN_j $ | (17) |
其中:ATCSP,OCSP和ICSP分别为分供系统的年度总费用(元),年度运行费用(元)和系统初投资年度均化费用(元)。
因此,该系统相对于传统的分供系统的年度总费用节约率可表示为:
| $ \mathrm{ATCR=(ATC_{SP}-ATC)/ATC_{SP}} $ | (18) |
若ATCR>0,则表示负荷密集区分布式综合能源系统的经济性比分供系统的经济性好。
2.1.2 能效指标系统的一次能源利用率(PESR)可以很好的表征系统在运行时能量是否被充分利用,选取年度一次能源利用率作为负荷密集区分布式综合能源系统的能耗评价指标。年度一次能耗(PEC)为[14-15]:
| $ \mathrm{PEC}=\sum\limits_{i=1}^{8\;760}\left(\beta E_{\mathrm{e},\mathrm{b},i}\right) $ | (19) |
式中:PEC——系统全年一次能耗,kg;
β——电网购电的一次能耗系数,kg/kWh;
Egr,i——从电网购电量,kW·h。
因此,该系统相对于传统的分供系统的一次能源节约率PESR可表示为:
| $ \mathrm{PESR=\frac{(PEC_{\text{SP}}-PEC)}{PEC_{SP}}} $ | (20) |
其中,PECSP为分供系统的全年一次能耗。若PESR>0,则负荷密集区分布式综合能源系统相较分供系统节能性好。
2.1.3 环境指标随着人们对全球变暖、气候变化等问题关注的深入,能源系统的减排性能越来越受到重视。负荷密集区分布式综合能源系统主要碳排放来源是从电网购电的排放。因此,选取年度CO2减排率(CDER)作为系统的评价指标[14-15]。其年度CO2排放量(CDE)为:
| $ \mathrm{CDE}=\sum\limits_{i=1}^{8\;760}\lambda E_{\mathrm{e},\mathrm{b},i} $ | (21) |
式中:CDE——系统全年CO2排放量,kg;
λ——碳排放系数,kg/kWh。
因此,该系统相对于传统的分供系统的CO2减排率为:
| $ \mathrm{CDER=(CDE_{SP}-CDE)/CDE_{SP}} $ | (22) |
其中,CDESP为分供系统的全年CO2排放量。若CDER>0,则负荷密集区分布式综合能源系统相较分供系统CO2排放量小。
2.2 多目标决策选取层次分析法进行多目标决策,该方法具有系统性、简洁性和适用性等优点。首先,考虑系统综合性能作为整个系统的优化决策目标,在其下层的综合影响因素有能源、经济、环境,可得到相应的层次结构模型。
其次,根据阅读文献和问卷调查,建立三个影响因素的两两比较判断矩阵,如表2所示。
该判断矩阵表示在决定系统综合性能时,经济因素比能源因素稍微重要,经济因素相对于环境因素的重要性介于同样重要和稍微重要之间,环境因素相对于能源因素的重要性介于同样重要和稍微重要之间。据层次分析法一致性检验,得到一致性指数为0.0088,小于判断值0.1,证明矩阵一致性检验通过。其中,特征值计算公式:
| $ \Omega=\frac{1}{n}\sum\limits_{i=1}^n\frac{(\boldsymbol{AW})_i}{\omega_i} $ | (23) |
式中:n——判断矩阵的阶数;
A——n阶判断矩阵;
W——n维权重向量;
ωi——W中的第i个元素,表示第i种方案的权重。
最后得出环境、经济、能源三个影响因素的权重指标分别为0.2970、0.5396和0.1634。
2.3 目标函数以系统的设备容量为自变量,系统容量配置优化的目标函数为
| $ \begin{split} &{\max {\mathrm{IP}}\left( {{N_j},j = 1,2, \cdots ,k} \right)} \\ &{{\mathrm{IP}} = {\omega _1}{\mathrm{ATCR}} + {\omega _2}{\mathrm{PESR}} + {\omega _3}{\mathrm{CDER}}} \\ &{{\omega _1} + {\omega _2} + {\omega _3} = 1} \end{split} $ | (24) |
式中:Nj——各设备的装机容量,kW;
IP——综合性能;
ω1,ω2,ω3——经济、能源和减排权重系数。
2.4 约束条件1)设备运行条件约束
| $ {N_{j,\min }} \leqslant {N_j} \leqslant {N_{j,\max }}\quad j = 1,2, \cdots ,k $ | (25) |
2)系统平衡条件约束
①电平衡约束。建筑物的电负荷和江水源热泵的用电量可由光伏发电系统和电网提供。
| $ E_{\mathrm{rwshp}}+E\mathrm{_{load}}=E_{\text{g}\mathrm{rid}}+E_{\mathrm{PV}} $ | (26) |
式中:Erwshp——江水源热泵的用电量,kW·h;
Eload——建筑所需电负荷,kJ;
Egrid——电网提供的电负荷,kJ。
②热平衡约束。建筑物的热负荷由江水源热泵和储能系统来满足。
| $ Q_{\mathrm{h}}(t)=Q_{\rm{r}wshp-h}(t)+Q_{\mathrm{st},1}(t) $ | (27) |
式中:Qh(t)——t时段建筑物的热负荷需求,kJ;
Qrwshp-h(t)——t时段江水源热泵提供的热负荷,kJ;
Qst,1(t)——t时段储能系统储/放能,大于0为储能系统放热,小于为储能系统储热。
③冷平衡约束。建筑物的冷负荷由江水源热泵和储能系统来满足。
| $ {Q_{\text{c}}}(t) = {Q_{\rm rwshp-c}}(t) + {Q_{\rm st,2}}(t) $ | (28) |
式中:Qc(t)——t时段建筑物的冷负荷需求,kJ;
Qrwshp-c(t)——t时段江水源热泵提供的冷负荷,kJ;
Qst,2(t)−t时段储能系统储/放能,大于0为储能系统放冷,小于0为储能系统储冷。
3 案例分析 3.1 负荷模拟研究的负荷密集区由10栋住宅建筑、2栋办公楼建筑、1栋酒店建筑和1栋商场建筑构成。其中住宅建筑总建筑面积为18270 m2,每栋建筑有6层,每层层高2.8 m,包含有客厅、厨房、卧室、卫生间等主要房间类型。办公建筑总建筑面积为7112 m2,每栋建筑有6层,每层层高3.6 m,包含有办公室、密集办公室以及会议室三个不同类型的房间。酒店建筑包含有大厅门厅、多功能厅以及酒店客房三类主要房间类型,整个酒店建筑共10层,每层层高2.8 m,其建筑总面积为1650 m2。商场建筑总建筑面积为4592 m2,每层层高5.5 m,共有3层,第一层为大型的超市,第二层以及第三层则为一般商店店铺、高档商店店铺。采用清华大学研发的DeST软件对负荷密集区建筑进行能耗模拟,其建筑全年累计冷热电负荷如图2所示。

|
| 图 2 建筑全年累计负荷 |
由图2可知,由于酒店建筑人员在室率较低,全年累计负荷最少,商场建筑长时间有人在室内,加之设备较多,因此,全年累计负荷最高;此外,由于商场建筑晚上几乎处于无人使用的状态,而其用电设备相对较多,所以商场建筑的热电比最低;而住宅建筑则因为晚上居住时冷热负荷均比较高,而用电相对较少,其热电比最高。
3.2 四类典型建筑分布式综合能源系统优化结果分析如表3所示为四类典型建筑分布式综合能源系统在有储能系统和无储能系统时的供能系统最优配置结果和综合性能指标。
| 建筑 类型 |
项目 | 无储能 | 有储能 |
| 办公 建筑 |
江水源热泵的装机容量/kW | 200 | 100 |
| 光伏的装机容量/kW | 157.50 | 157.50 | |
| 储能装置容量/(kW·h) | – | 80.43 | |
| 初投资/万元 | 55.50 | 59.59 | |
| ATCR/% | 21.00 | 20.81 | |
| PESR/% | 27.20 | 28.50 | |
| CDER/% | 27.20 | 28.50 | |
| IP/% | 23.40 | 24.35 | |
| 酒店 建筑 |
江水源热泵的装机容量/kW | 100 | 100 |
| 光伏的装机容量/kW | 21.87 | 21.87 | |
| 储能系统容量/(kW·h) | – | 12 | |
| 初投资/万元 | 16.37 | 18.77 | |
| ATCR/% | –0.09 | –0.28 | |
| PESR/% | 11.90 | 14.30 | |
| CDER/% | 11.90 | 14.30 | |
| IP/% | 5.43 | 6.43 | |
| 住宅 建筑 |
江水源热泵的装机容量/kW | 350 | 250 |
| 光伏的装机容量/kW | 104.62 | 104.62 | |
| 储能系统容量/(kW·h) | – | 72 | |
| 初投资/万元 | 62.93 | 65.33 | |
| ATCR/% | 3.92 | 3.87 | |
| PESR/% | 7.15 | 7.52 | |
| CDER/% | 7.15 | 7.52 | |
| IP/% | 5.41 | 5.55 | |
| 商场 建筑 |
江水源热泵的装机容量/kW | 600 | 500 |
| 光伏的装机容量/kW | 193.75 | 193.75 | |
| 储能系统容量/(kW·h) | – | 84 | |
| 初投资/万元 | 84.45 | 89.25 | |
| ATCR/% | 6.39 | 5.86 | |
| PESR/% | 14.26 | 15.28 | |
| CDER/% | 14.26 | 15.28 | |
| IP/% | 10.01 | 10.20 |
由表3可知,办公建筑中,负荷密集区分布式综合能源系统相比于传统的分供系统,PEC、CDE、ATC分别减少27.20%,27.20%,21.00%。若系统中加入储能系统,则江水源热泵的装机容量有所下降,但无论是否加入储能系统,光伏的装机容量都为157.50 kW,其面积为1260 m2。还可以看出,加入储能系统,使得系统初投资小幅度增加,从而导致系统的ATCR由21.00%降低到20.81%。值得注意的是,储能系统能够提升系统的IP,从23.40%增加到了24.35%。其中,住宅建筑和商场建筑分布式综合能源系统的优化结果与办公建筑类似,不再赘述。
对于酒店建筑而言,无论是否加入储能系统,光伏与江水源热泵的装机容量都不变,分别为21.87 kW和100 kW。PESR、CDER和IP分别为11.90%,11.90%,5.43%,由于其全年累计负荷很低,ATCR仅为–0.09%,表示该系统在酒店使用不经济。但值得一提的是,储能系统把系统的IP从5.43%提升到6.43%,因此,加入储能系统还是有利的。
3.3 负荷密集区分布式综合能源系统优化结果分析如表4所示为负荷密集区分布式综合能源系统与四类建筑叠加的分布式综合能源系统在有储能系统和无储能系统时的容量配置优化结果和综合性能指标。
| 项目 | 负荷密集区整体 | 四类建筑叠加 | ||
| 有无储能 | 无储能 | 有储能 | 无储能 | 有储能 |
| 江水源热泵的装机容量/kW | 1150 | 900 | 1250 | 950 |
| 光伏的装机容量/kW | 456.34 | 456.34 | 477.75 | 477.75 |
| 储能系统容量/(kW·h) | – | 230.56 | – | 248.43 |
| 初投资/万元 | 292.24 | 299.71 | 306.55 | 316.79 |
| ATCR/% | 45.76 | 45.21 | 30.77 | 29.47 |
| PESR/% | 58.89 | 65.43 | 40.26 | 45.28 |
| CDER/% | 58.89 | 65.43 | 40.26 | 45.28 |
| IP/% | 51.81 | 54.51 | 35.14 | 36.75 |
由表4可知,当分布式综合能源系统加入储能系统后,江水源热泵装机容量较无储能系统时的装机容量减小,但是系统初投资小幅度增加。无论是否加入储能系统,当建筑负荷密集的地区作为一个整体时的建筑供能系统整体优化比当能源系统分别服务于每种类型的建筑分类优化结果好。未加入储能的分布式综合能源系统的江水源热泵以及光伏装机容量比分类优化分别低8%和4.5%,初投资节约14.31万元。加入储能的分布式综合能源系统的江水源热泵以及光伏装机容量比分类优化分别低5.3%和4.5%,初投资节约17.08万元。在经济、能源、环境与综合性能四个方面,仍为整体优化优于分类优化,当没有储能系统时,系统的ATCR、PESR、CDER和IP整体优化分别优于分类优化14.99%,18.63%,18.63%,16.67%;当加入储能系统时,分别优于分类优化15.74%,20.15%,20.15%和17.76%。还可以看出,由于系统加入储能系统,无论是分类优化还是整体优化ATCR都降低,分别降低了1.30%和0.55%,PESR和CDER都增加,分类优化均增加了5.02%,整体优化均增加了6.54%,值得注意的是,分类优化和整体优化的IP分别增加了1.61%和2.7%。
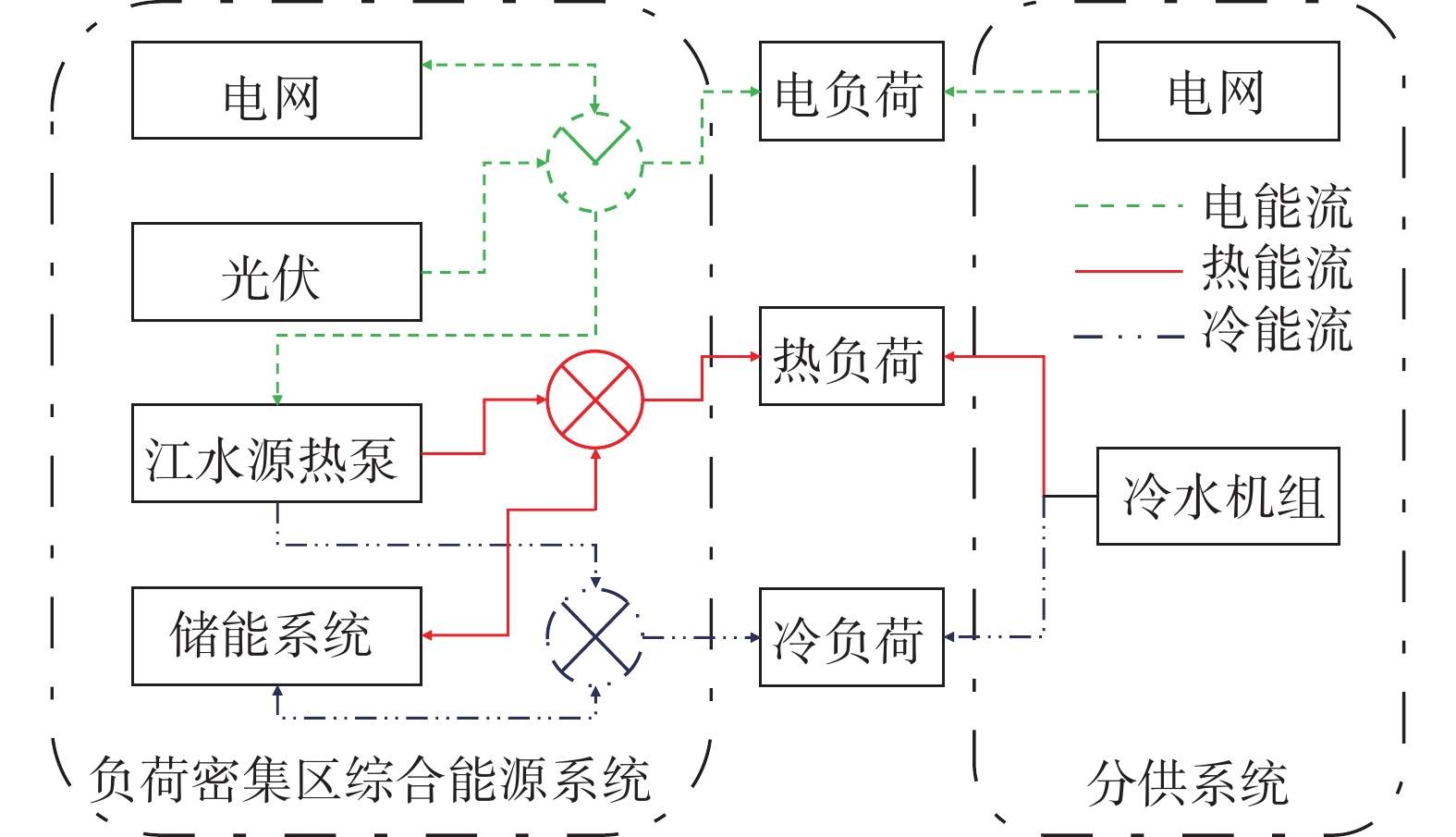
3.4 政策影响分析 3.4.1 光伏初投资影响分析初投资补贴即针对能源系统投资之初按照系统驱动装置的装机容量给予一定的补贴,在一定程度上减少初投资费用,吸引投资。主要研究光伏初投资补贴对分布式综合能源系统的影响。其中,光伏初投资补贴对年度总费用、光伏装机容量和系统性能的影响如图3所示。
|
| 图 3 光伏初投资补贴对年度总费用、光伏装机容量和系统性能的影响 |
由图3(a)可知,随着光伏系统初投资补贴的增加,其装机容量和年度总费用都不断增加。光伏初投资补贴每增加500元,装机容量增加约14%,年度总费用增加约18%。由图3(b)可知,随着光伏初投资补贴的变化,系统的性能也不断变化。其中,经济性小幅度升高,CDER和PESR相较于ATCR显著升高。光伏初投资补贴从0元增加到3000元时,ATCR、PESR和CDER相应增加1.29%、5.41%和7.55%。
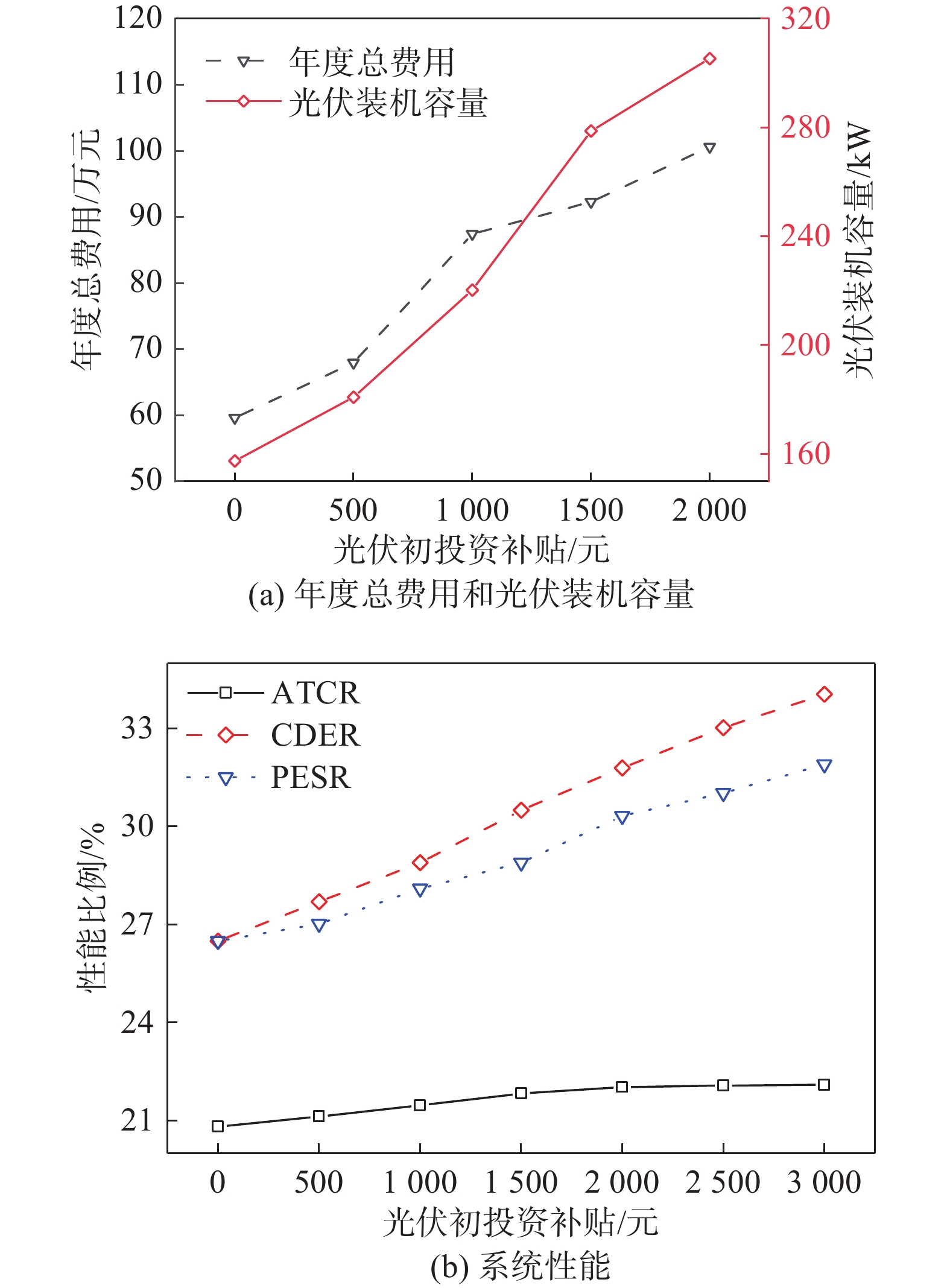
3.4.2 上网电价影响分析上网电价政策作为目前能源系统发展的阻碍之一,上网与否以及上网电价的多少必然会影响到系统的设计值以及综合性能。因此,研究了上网电价对分布式综合能源系统的影响,其中,上网电价价格比例对年度总费用、光伏装机容量和系统性能的影响如图4所示。
|
| 图 4 上网电价价格比例对初投资、光伏装机容量和系统性能的影响 |
由图4(a)可知,随着上网电价价格比例的增加,系统装机容量和初投资都增加。上网电价比例为0到40%时,光伏系统容量和初投资增加较缓慢,分别增加4.99 kW和7.39万元;比例为40%到100%时,光伏装机容量增加幅度较大,分别增加35.01 kW和53.03万元。当上网电价比例超过100%后,光伏装机容量不再增加,达到算法设定值,此时系统配置几乎可以在离网的情况下运行。如图4(b)可知,随着上网电价价格比例不断增加,系统的ATCR、PESR和CDER也不断增加,相比于上网电价比例为0时,上网电价100%时的ATCR、PESR和CDER各增加1.96%,3.73%,11.82%,上网价格超过100%后,ATCR、PESR和CDER则有所降低,大量电力被送往电网,这时系统更像是对外的电站而非是以对内供能为主的能源站。
4 结束语该研究构建了储能协调下的分布式综合能源系统,建立了该系统的数学模型与评价指标体系。用能耗模拟软件DeST进行建筑负荷模拟,并对比分析了负荷密集区四类建筑分别单独设置供能系统和考虑四类建筑负荷耦合互补设置一套供能系统时的系统容量配置优化以及在相关政策影响下的系统性能,得出以下结论:
1)从系统优化结果分析,四类建筑中碳减排性能和节能性能相较于经济性好,无论是否加入储能系统,考虑四类建筑负荷耦合互补设置一套供能系统时的系统性能优于四类建筑分别单独考虑时的性能,且经济、能耗和环境性能都优于传统系统;当加入储能系统时,不仅两种系统的经济性和能耗性都优于不加储能系统的分布式综合能源系统,还降低了江水源热泵的出力。
2)从光伏初投资补贴角度分析,随着初投资的增加,其整体装机容量增加。系统性能对初投资补贴具有良好反馈。在光伏初投资补贴从0元增加到3000元时,系统的ATCR、PESR、CDER相应增加1.29%,5.41%,7.55%。
3)从上网电价角度分析,随上网电价的增加,系统性能、光伏装机容量和初投资都会增加。但是,当上网电价为40%的比例后,光伏容量增加幅度较大,超过100%后,光伏装机容量不再增加,达到算法设定值,此时系统配置几乎可以在离网的情况下运行,其系统性能也会略有降低。
| [1] |
高庆先, 高文欧, 马占云, 等. 大气污染物与温室气体减排协同效应评估方法及应用[J].
气候变化研究进展, 2021, 17(3): 268-278.
GAO Q X, GAO W O, MA Z Y, et al. The synergy effect assessment method and its application for air pollutants and greenhouse gases reduction[J].
Climate Change Research, 2021, 17(3): 268-278.
|
| [2] |
王永真, 康利改, 张靖, 等. 综合能源系统的发展历程、典型形态及未来趋势[J].
太阳能学报, 2021, 42(8): 84-95.
WANG Y Z, KANG L G, ZHANG J, et al. Development history, typical form and future trend of integrated energy system[J].
Acta Energiae Solaris Sinica, 2021, 42(8): 84-95.
|
| [3] |
WANG J, JING Y, ZHANG C. Optimization of capacity and operation for CCHP system by genetic algorithm[J].
Applied Energy, 2010, 87(8): 1325-1335.
|
| [4] |
WANG J, ZHAI Z, JINNG Y, et al. Particle swarm optimization for redundant building cooling heating and power system[J].
Applied Energy, 2010, 87(6): 3668-3679.
|
| [5] |
李剑锋, 郝晓光, 曾四鸣, 等. 考虑碳排放的综合能源系统储能优化配置研究[J].
中国测试, 2022, 48(7): 83-89.
LI J F, HAO X G, ZENG S M, et al. Research on optimal energy storage configuration of integrated energy system considering carbon emissions[J].
China Measurement & Test, 2022, 48(7): 83-89.
|
| [6] |
龚逊东, 薛溟枫, 毛晓波, 等. 电转气成本特性对电-气-热综合系统调度的影响[J].
中国测试, 2020, 46(7): 33-39.
GONG X D, XUE M F, MAO X B, et al. Influence of power-to-gas cost characteristics on scheduling of power-gas-heating integrated system[J].
China Measurement & Test, 2020, 46(7): 33-39.
|
| [7] |
SI P, LI A, RONG X, et al. New optimized model for water temperature caculation of river-water source heat pump and its application in simulation of energy consumption[J].
Renewable Energy, 2015, 84(5): 65-73.
|
| [8] |
LI R, DAI Y, CUI G. Multi-objective optimization of solar powered adsorption chiller combined with river water heat pump system for air conditioning and space heating application[J].
Energy, 2019, 189(15): 116141.
|
| [9] |
吴杰, 李妤姝, 卢军. 重庆某江水源热泵性能影响因素分析[J].
制冷与空调(四川), 2020, 34(5): 581-587.
WU J, LI Y S, LU J. Analysis of factors affecting the performance of a water source heat pump in a river in Chongqing[J].
Refrigeration & Air Conditioning, 2020, 34(5): 581-587.
|
| [10] |
龙天河, 张伟. 燃气三联供和江水源热泵复合系统数学模型的建立和分析[J].
制冷与空调(四川), 2018, 32(2): 125-130.
LONG T H, ZHANG W. Mathematical modelling and studying of the composite system of CCHP and river water source heat pump[J].
Refrigeration & Air Conditioning, 2018, 32(2): 125-130.
|
| [11] |
康利改, 杨俊红, 赵军, 等. 基于温度控制的空调系统能耗和IPLV研究[J].
电气应用, 2016, 35(7): 59-66.
KANG L G, YANG J H, ZHAO J, et al. Power consumption and study on IPLV of the air conditioning system based on terminal temperature control[J].
Electrotechnical Application, 2016, 35(7): 59-66.
|
| [12] |
YANG G, ZHAI X. Optimal design and performance analysis of solar hybrid CCHP system considering influence of building type and climate condition[J].
Energy, 2019, 174(3): 647-663.
|
| [13] |
耿健, 杨冬梅, 高正平, 等. 含储能的冷热电联供分布式综合能源微网优化运行[J].
电力工程技术, 2021, 40(1): 25-32.
GENG J, YANG D M, GAO Z P, et al. Optimal operation of distributed integrated energy microgrid with CCHP considering energy storage[J].
Electric Power Engineering Technology, 2021, 40(1): 25-32.
|
| [14] |
KANG L, WU X, YUAN X, et al. Influence analysis of energy policies on comprehensive performance of CCHP system in different buildings[J].
Energy, 2021(2): 121-159.
|
| [15] |
KANG L, YUAN X, SUN K, et al. Feed-forward active operation optimization for CCHP system considering thermal load forecasting[J]. Energy, 2022, 254(1): 124234.
|
 2024, Vol. 50
2024, Vol. 50