文章信息
- 缪欣, 张忠锐, 郭威, 侯思祖
- MIAO Xin, ZHANG Zhongrui, GUO Wei, HOU Sizu
- 基于信号图像化和CNN-ResNet的配电网单相接地故障选线方法
- Single-phase ground fault line selection method for distribution network based on signal imaging and CNN-ResNet
- 中国测试, 2024, 50(6): 157-166
- CHINA MEASUREMENT & TEST, 2024, 50(6): 157-166
- http://dx.doi.org/10.11857/j.issn.1674-5124.2023070038
-
文章历史
- 收稿日期: 2023-07-07
- 收到修改稿日期: 2023-09-15
2. 北方工业大学电气与控制工程学院,北京 100144;
3. 华北电力大学电气与电子工程学院,河北 保定 071003
2. School of Electrical and Control Engineering, North China University of Technology, Beijing 100144, China;
3. School of Electrical and Electronic Engineering,North China Electric Power University, Baoding 071003, China
在我国,35 kV以下的配电网一般采用中性点非有效接地方式,其中单相接地故障占总故障数的80%以上[1]。当小电流接地系统发生单相接地故障时,如果不能及时清除故障,将会造成绝缘击穿,引发更严重的故障,影响配电网安全可靠运行[2]。随着分布式电源的接入,配电网的拓扑结构更加复杂,零序电流信号呈现较强的随机性和非线性,传统的故障选线方法难以准确选出故障线路。因此,亟需提出一种新的故障选线方法,提高故障选线准确率。
准确地选择出故障线路,是故障隔离的前提。现有的配电网故障选线方法主要分为三种方式:稳态选线法[3]、暂态选线法[4]、注入信号法[5]。当配电网发生单相接地故障时,稳态特征含量微弱,难以有效提取。注入信号法需要额外的注入设备,价格昂贵,且有可能对电网造成冲击[6]。相比稳态特征选线法,暂态特征含量丰富,且不受消弧线圈的影响。文献[7]利用经验模态分解算法提取零序电流信号的五次谐波,通过混沌振子的混沌状态辨识正常线路与故障线路。但是经验模态分解算法存在模态混淆问题,影响故障选线的结果。文献[8]通过比较正常线路与故障线路的磁场差异,确定故障点位置,但是所用方法较为复杂,难以有效应用在实际的配电网故障选线中。部分学者将智能算法应用到配电网的故障诊断中[9-11],但是智能算法容易陷入局部最优解,出现错误判断。随着人工智能技术的快速发展,机器学习方法也广泛应用到电力系统数据分析之中[12-13]。文献[14-15]采用机器学习算法进行故障选线,但是机器学习算法需要人工提取特征向量,需要有较强的研究经验。文献[16-17]利用现代信号处理的方法获得信号的时频特征图,通过深度学习方法进行故障选线,但是该方法忽略了零序电流信号本身具有的时序相关性和特征。
目前关于故障选线方法的研究大多是单一的故障诊断模型,不能充分挖掘配电网的故障特征。因此,本文从数据的输入方式和自主挖掘故障特征角度出发,提出一种基于图转换和CNN-ResNet的配电网故障选线方法,可以充分地融合零序电流信号的一维和时频特征图的二维特征。通过理论分析和仿真建模验证方法的有效性,可以在采样时间不同步、高阻接地、中性点接地方式改变等情况下准确选择出故障线路,为配电网故障选线提供新思路。
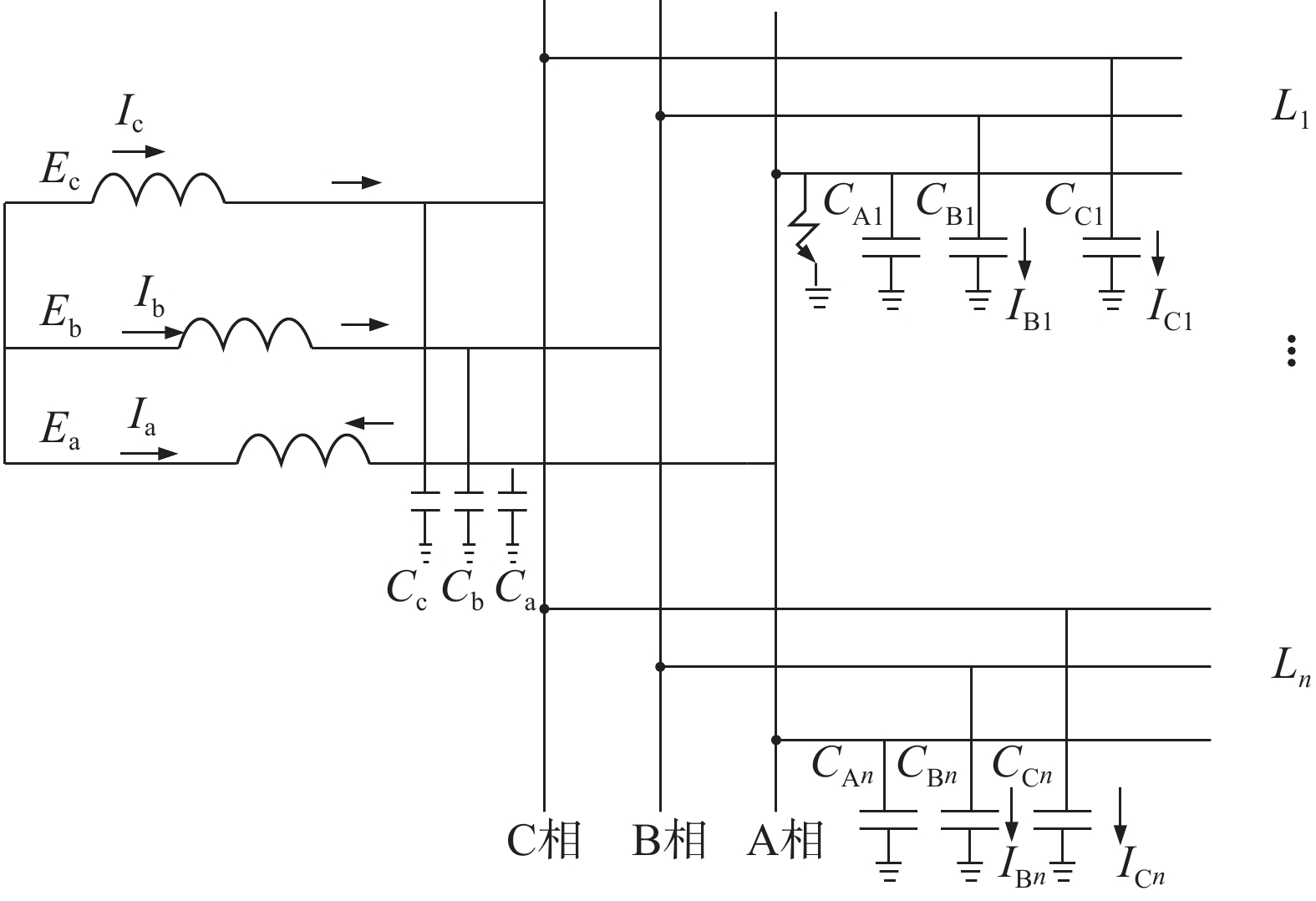
1 接地故障分析图1为不接地系统的单相接地故障结构图,假设线路1的A相发生单相接地故障,“→”表示系统中的电容电流分布。当A相发生单相接地故障,故障相电压降为0,非故障相电压升高为原来相电压的
|
| 图 1 不接地系统单相接地故障结构图 |
| $ {I_{({\mathrm{fault}})}} = - \sum\limits_{i = 1}^n {{I_{{\mathrm{C}}(i)}}} + {I_{{\mathrm{C}}({\mathrm{fault}})}} = - \sum {{I_{0({\mathrm{normal}})}}} $ | (1) |
式中:I(fault)——故障线路的零序电流;
IC(fault)−故障线路中正常相对地的电容电流;
IC(i)——线路i对地电容电流;
I0(normal)——正常线路的零序电流。
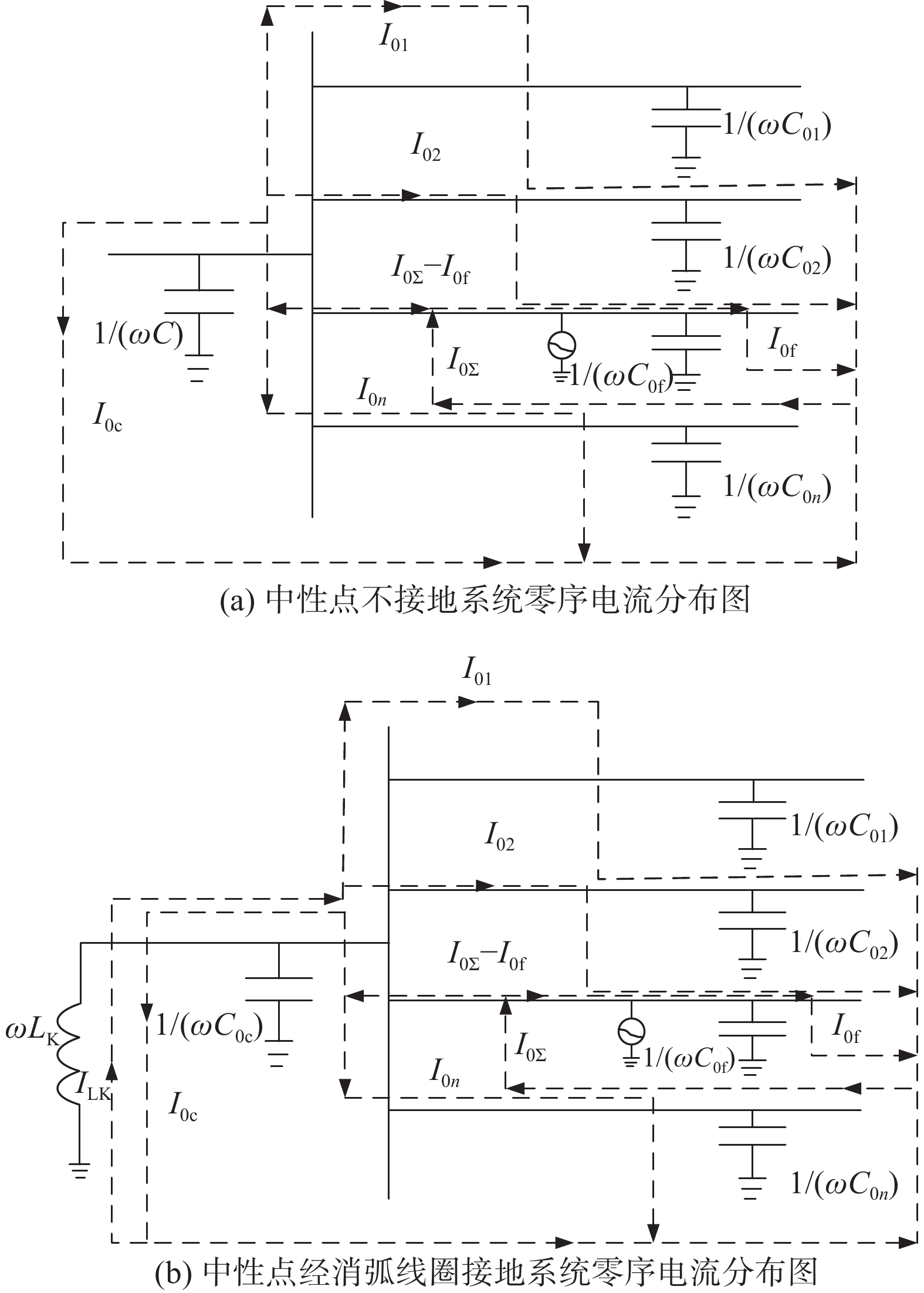
中性点不接地和中性点经消弧线圈接地系统发生单相接地故障时零序电流分布如图2所示。可以看出,当配电网发生单相接地故障后,故障线路的零序电流等于所有健全线路的零序电流之和,且正常线路与故障线路零序电流的极性相反,正常线路与故障线路的零序电流存在差异,因此可以通过比较各个线路的零序电流特征实现故障选线。
|
| 图 2 零序电流分布情况 |
2 排列熵优化的VMD算法
短时傅里叶变换(short-time Fourier transform,STFT)存在边界效应和频谱泄漏问题。S变换通常需要大量计算资源,特别是在对信号进行高分辨率时,可能会导致计算成本较高。小波变换(wavelet transform,WT)对信号的非平稳性处理能力有限,且需要选择合适的小波基函数,选择错误的基函数可能导致分析结果不准确。因此,本文选择VMD算法,能够有效地分离信号中的低频和高频成分,对于理解信号的不同频率分量之间的关系以及对不同频率分量的独立分析非常重要。VMD算法通过求解变分问题,将一维信号分解成一系列固有模态函数(intrinsic mode function,IMF),可以缓解经验模态分解算法的模态混淆问题。但是在分解信号前,需要人为设定分解层数k,如分解层数设置不恰当,将会影响信号分析的结果。因此,本文利用排列熵对VMD算法的分解层数k进行参数优化。
2.1 排列熵排列熵[17]通过比较时间序列相邻数据的特征,实现信号的随机性检测,具有较好的计算效率,具体计算原理如下:
对时间序列x(i)进行相空间重构:
| $ \begin{gathered} X(1) = \{ x(1),{\text{ }}x(1 + \tau ),{\text{ }} \cdots ,x(1 + (m - 1)\tau )\} \\ X(i) = \{ x(i),{\text{ }}x(i + \tau ),{\text{ }} \cdots ,x(i + (m - 1)\tau )\} \\ \vdots \\ X(N - (m - 1)\tau ) = \{ x(N - (m - 1)\tau ),{\text{ }} \cdots ,x(N)\} \end{gathered} $ | (2) |
式中:τ和m——时间延迟、相空间嵌入维数;
N——时间序列的长度。
将X(i)中的向量按照升序进行排列:
| $ x(i+({j}_{1}-1)\tau )\leqslant x(i+({j}_{2}-1)\tau ) \leqslant\cdots \text{ } \leqslant x(i+({j}_{m}-1)\tau ) $ | (3) |
每一个X(i)可以获得一个信号序列:
| $ S(g) = [{j_1},{\text{ }}{j_2},{\text{ }} \cdots ,{j_m}] $ | (4) |
S(g)是m!种序列的一种,则序列号出现的概率为:
| $ {P_i} = \frac{l}{k} $ | (5) |
其中,l为S(g)出现的频次,则时间序列x(i)的排列熵为:
| $ {H_p}(m) = - \sum\limits_{g = 1}^k {{P_g}} \ln {P_g} $ | (6) |
将式(6)进行标准化:
| $ {P_E} = \frac{{{H_p}(m)}}{{\ln (m!)}} $ | (7) |
其中,PE的大小在0~1之间,越接近1,说明信号越复杂,越接近0,信号越稳定。
2.2 变分模态分解算法通过变分模态分解算法,可以将一维信号分解成含有丰富频率和幅值信息的固有模态函数。设f(t)为原始时间序列,
| $ \begin{gathered} \mathop {\min }\limits_{\left\{ {{u_k}} \right\},\left\{ {{\omega_k}} \right\}} \left\{ {\sum\limits_k {\left\| {{\partial _t}\left[ {(\delta (t) + \frac{{\mathrm{j}}}{{\pi t}}) * {u_k}(t)} \right]{{\mathrm{e}}^{ - {\mathrm{j}}{\omega _k}t}}} \right\|_2^2} } \right\} \\ {\mathrm{s.t.}}\sum\limits_k^{} {{u_k} = f} (t) \\ \end{gathered} $ | (8) |
式中:
引入增广拉格朗日函数求解式(8):
| $ \begin{split} & L\left( {\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\},\lambda } \right) = \alpha \sum\limits_k {\left\| {{\partial _t}\left[ {(\delta (t) + \frac{{\mathrm{j}}}{{\pi t}})*{u_k}(t)} \right]{{\mathrm{e}}^{ - {\mathrm{j}}{\omega _k}t}}} \right\|_2^2} + \\ &\qquad \quad \left\| {f(t) - \sum\limits_k {{u_k}(t)} } \right\|_2^2 + \left\langle {\lambda (t),f(t) - \sum\limits_k {{u_k}(t)} } \right\rangle \\[-1pt] \end{split}$ | (9) |
其中,
| $ \hat u_k^{n + 1}\left( \omega \right) = \frac{{\hat f\left( \omega \right) - \displaystyle \sum\limits_{i \ne k} {\hat u_i^n\left( \omega \right) + {{\hat \lambda }^n}\left( \omega \right)/2} }}{{1 + 2\alpha {{\left( {\omega - \omega _k^n} \right)}^2}}} $ | (10) |
| $ \omega _k^{n + 1} = \frac{{\displaystyle \int_0^\infty {\omega |\hat u_k^{n + 1}\left( \omega \right){|^2}{\mathrm{d}}\omega } }}{{\displaystyle \int_0^\infty {|\hat u_k^{n + 1}\left( \omega \right){|^2}{\mathrm{d}}\omega } }} $ | (11) |
式中:
n——迭代次数。
具体步骤如下:
1) 对
2) 根据式(10)和式(11)迭代更新
3) 更新拉格朗日乘法算子:
| $ \hat \lambda _{}^{n + 1}(\omega ) \leftarrow \hat \lambda _{}^n(\omega ) + \tau \left( {\hat f(\omega ) - \sum\limits_k {{{\hat u}_k}^{n + 1}(\omega )} } \right) $ | (12) |
4) 反复执行步骤2)、步骤3),直到满足式(13),迭代停止:
| $ \sum\nolimits_k {\left\| {\hat u_k^{n + 1} - \hat u_k^n} \right\|_2^2/\left\| {\hat u_k^n} \right\|_2^2} < \varepsilon $ | (13) |
式中
5) 按照高频到低频的顺序输出k个模态函数。
2.3 排列熵优化VMD算法分解层数k取值过大,算法出现过分解现象,会得到复杂分量[17-19],复杂信号的排列熵值大于正常信号的排列熵值。因此,可以利用排列熵对VMD算法进行优化。文献[20]建议排列熵阈值取值在0.55~0.6范围内。本文取500组信号,以0.01步长为间隔,当排列熵阈值取0.6时,确定分解层数k的效果最佳,因此本文排列熵阈值取0.6,即当信号的排列熵值大于0.6时,判定该信号为异常信号。
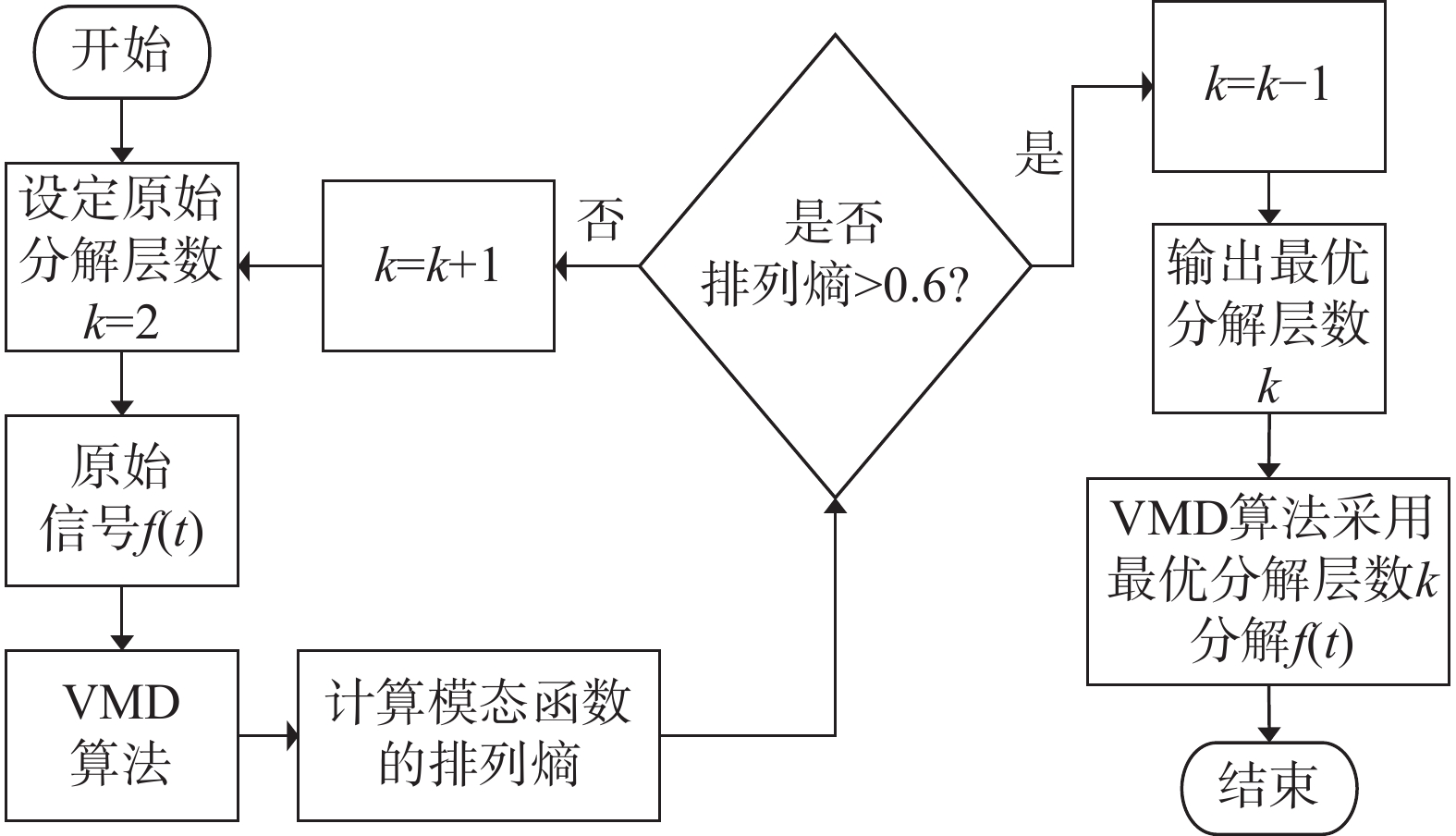
排列熵优化VMD算法具体步骤如图3所示,设VMD算法初始分解层数k=2,若分解得到的固有模态函数的排列熵小于0.6,则k=k+1,继续进行VMD算法分解,直到出现固有模态函数大于0.6,令k=k–1,停止分解。
|
| 图 3 排列熵优化VMD算法流程图 |
2.4 优化算法有效性验证
利用式(14)仿真信号验证优化算法的有效性,其中x1、x2、x3分别为正弦信号、调幅信号、间歇噪声信号,x为x1、x2、x3合成信号,各信号时域波形如图4所示。

|
| 图 4 仿真信号 |
| $ \left\{ \begin{gathered} {x_1} = 5\sin (2 \times 30\pi t + \pi /2) \\ {x_2} = (t + 1.5)\sin (2 \times 10\pi t + \pi /3) \\ {x_3} = [{\mathrm{zeros}}(1,300),0.{\text{5}} \times {\mathrm{randn}}(1,600), {\mathrm{zeros}}(1,300), \\ \qquad 0.{\text{5}} \times {\mathrm{randn}}(1,500),{\mathrm{zeros}}(1,300)] \\ x = {x_1} + {x_2} + {x_3} \\ \end{gathered} \right. $ | (14) |
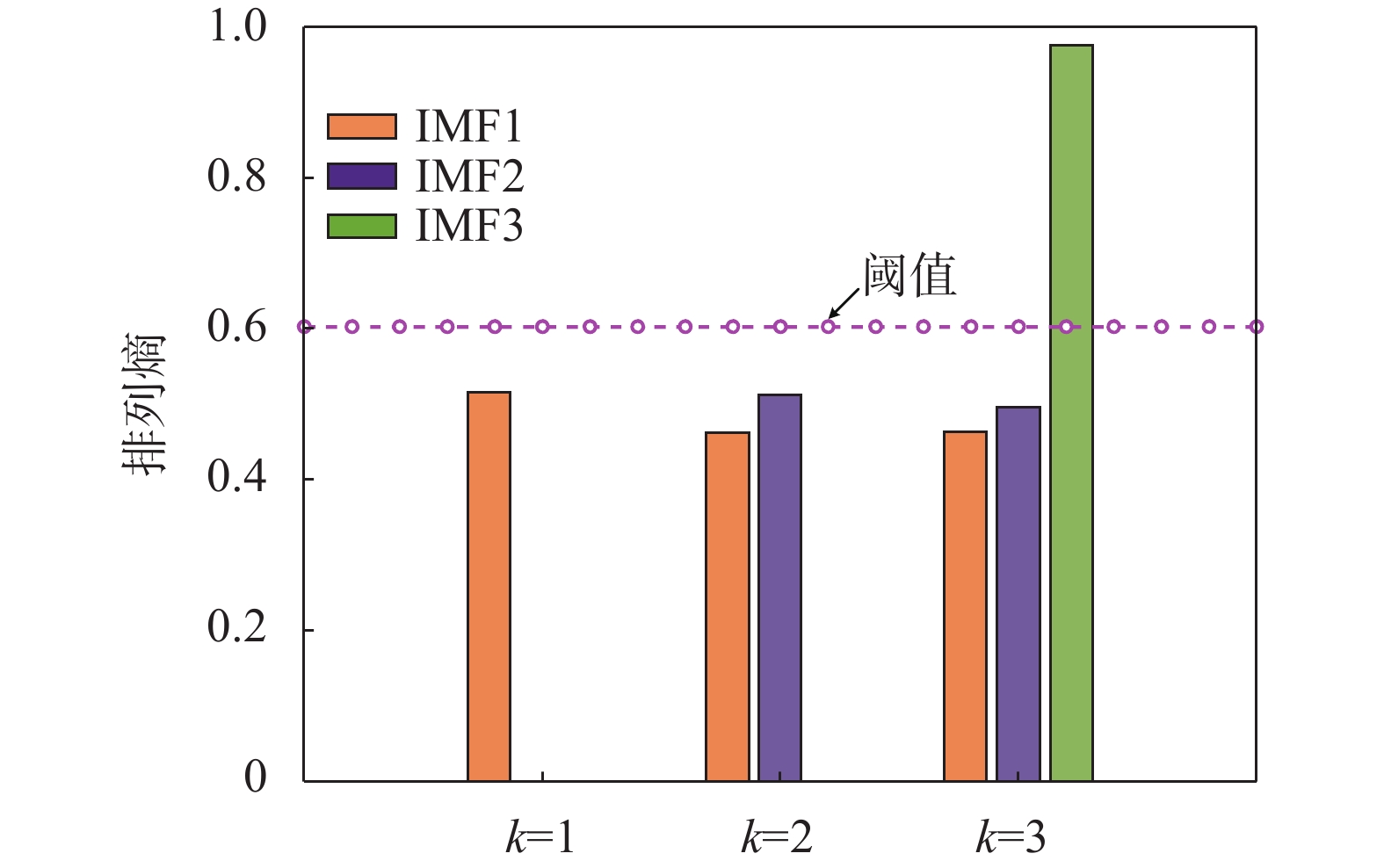
按照排列熵优化VMD算法流程,对合成信号x进行分解,所得结果如图5所示。从图5可以看出,当k=3时,第三固有模态函数大于0.6,为异常分量,因此最终的分解层数为k–1=2,与给定的仿真信号相符。可以看出,参数优化后的VMD算法能够保留原始信号的有效成分,并且抑制噪声分量。
|
| 图 5 各固有模态函数的排列熵值 |
将VMD算法的分解层数k设为2,分别利用经验模态分解(empirical mode decomposition,EMD)和优化的VMD算法对合成信号x进行分解,所得结果如图6所示。从图6可以看出,EMD算法在分解合成信号x时,出现了模态混淆问题,并且出现了大量的伪分量。参数优化的VMD算法能够提取原始信号的有效成分,且没有出现伪分量和模态混淆问题。为了比较各算法的时频特征,利用Hilbert-Huang谱分析各分解算法的时频效果。

|
| 图 6 不同算法分解结果 |
如图7所示,EMD算法出现了模态混淆问题,并且出现了大量的伪分量,瞬时频率较为不稳定。参数优化VMD算法能够提取原始信号的有效成分,分解得到的模态函数瞬时频率较为稳定。因此,可以利用参数优化的VMD算法分解电网的零序电流信号,得到一系列IMF,模态函数是含有幅值信息和频率信息的数据矩阵。若通过一种有效的方式将时频数据矩阵转成具有图像性质的像素矩阵,将可以为深度学习故障选线提供良好的样本素材。

|
| 图 7 不同算法的Hilbert-Huang谱 |
3 信号到图像转换方法
利用参数优化的VMD算法分解信号,可以获得一维信号的时频矩阵,时频矩阵含有丰富的频域特征和幅值特征。参照文献[21]将时频数据矩阵转成具有图像性质的像素矩阵,可以让深度学习方法在“视觉上”对数据进行分析和识别,其中数据矩阵转像素矩阵如下式所示:
| $ P(m,{\text{ }}n) = {\text{round}}\left[ {\frac{{{x_i} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} \times 255} \right] $ | (15) |
式中:m,n——第m行,第n列;
round[∙]——函数取整;
P——像素值。
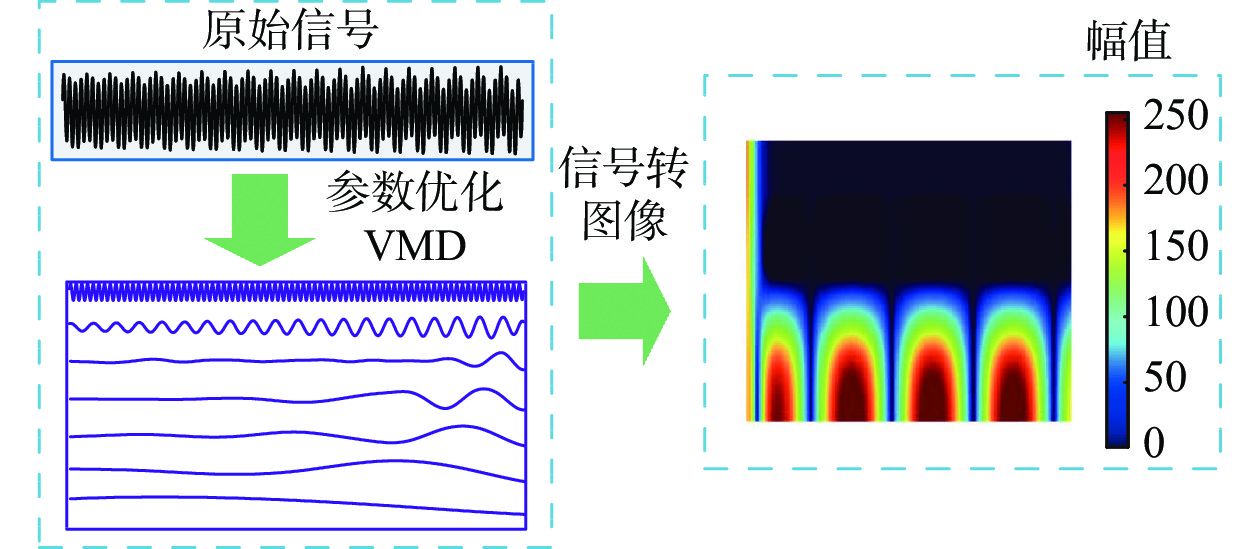
通过式(15)可以将参数优化VMD算法得到的时频数据矩阵转成像素矩阵,取值范围0~255之间。该方法可以在无任何定义的情况下,将一维信号转成二维图像,为深度学习故障诊断方法提供良好素材,不同零序电流信号的特征图具有不同的纹理参数和形状特征,具体信号转图像流程如图8所示。
|
| 图 8 信号转图像流程 |
4 基于CNN-ResNet的故障选线方法
当配电网发生单相接地故障时,零序电流信号受过渡电阻、中性点接地方式、噪声等因素影响,难以有效地建立故障诊断数学模型。因此,本文通过深度学习方法实现故障诊断,免去数学建模过程。通过一维卷积网络提取零序电流信号的相关性和特征,利用ResNet18网络提取时频特征图的特征,如图9所示。其中,一维处理模块利用一维卷积神经网络挖掘时域信号的特征,该模块由一维卷积层、批量标准层、激活函数层、展平层和全连接层构成。利用网格搜索算法和交叉验证方法确定卷积核尺寸为5效果最佳,第一层卷积包含32个卷积核,第二层卷积包含64个卷积核。利用Dropout层提高网络的泛化能力。经过展平层后,与全连接层相连,通过最后一层全连接层输出128个特征向量。考虑到过深的网络容易过拟合,利用ResNet18网络提取时频特征图的特征,并将提取的特征与一维卷积神经网络提取的特征相互混合作为最终的特征。

|
| 图 9 基于CNN-ResNet故障选线模块 |
配电网发生单相接地故障选线具体流程如下:
1) 当配电网发生单相接地故障时,采集各线路首端的零序电流信号作为待分析信号。
2) 通过参数优化VMD算法分解零序电流信号,获取零序电流信号的时频数据矩阵,通过信号转图像方法将时频数据矩阵转成具有图像性质的特征图。
3) 将零序电流信号和时频特征图一起作为混合卷积神经网络的输入,通过深度学习方法实现故障选线。
本文提出的基于信号图像化和CNN-ResNet的故障选线方法具有以下优势:①利用参数优化算法将零序电流转成二维图像,可以增加原始信号的不可见信息,包括颜色特征、纹理特征、时频特征等;②ResNet网络在传统的卷积神经网络中引入残差模块[22],可以化简网络的复杂程度,有利于网络的训练[23];③同时利用一维卷积神经网络和ResNet18网络挖掘零序电流信号和时频特征图特征,可以充分发挥两种网络的优势,有利于提升故障选线模型的准确度和泛化能力。
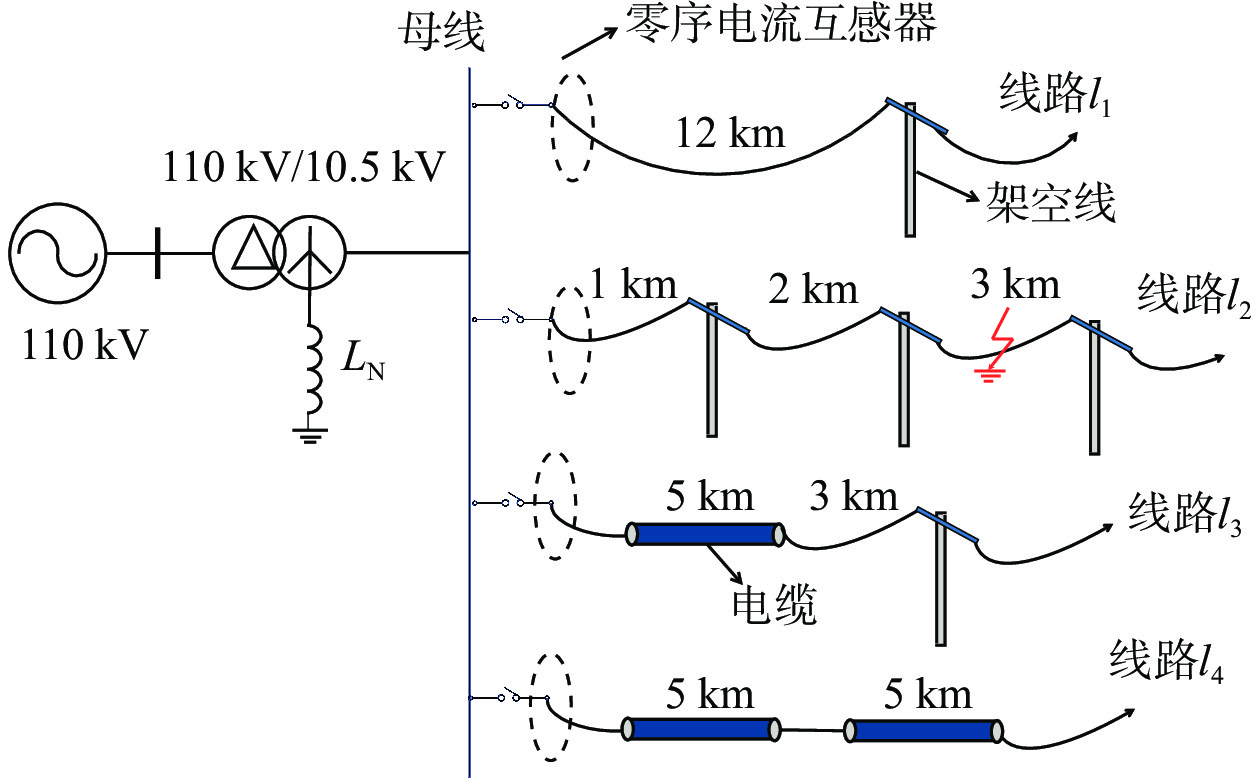
5 实验分析 5.1 实验数据集以图10辐射状配电网为研究对象,中性点采用消弧线圈接地方式,包含四条线路,线路长度分别为12 km架空线线路、6 km架空线线路、8 km线缆混合线路、10 km电缆线路。
|
| 图 10 辐射状配电网 |
单位长度架空线的正序和零序参数如下:
| $ \left\{ \begin{gathered} {R_0} = 0.262\;{{\Omega /{\mathrm{km}}, }} \,{L_0}{\text{ = 4}}{\text{.660}} \times {\text{1}}{{\text{0}}^{ - 3}}\;{\text{H/km}} \\ {C_{\text{0}}}{\text{ = 0}}{\text{.005\,8}} \times {\text{1}}{{\text{0}}^{ - 6}}\;{\text{F/km, }}{R_1} = 0.188\;{{\Omega /{\mathrm{km}}}} \\ {L_1}{\text{ = 1}}{\text{.252}} \times {\text{1}}{{\text{0}}^{ - 3}}\;{\text{H/km, }}{C_1}{\text{ = 0}}{\text{.009\,8}} \times {\text{1}}{{\text{0}}^{ - 6}} \;{\text{F/km }} \\ \end{gathered} \right. $ | (16) |
单位长度电缆线路的正序和零序参数如下:
| $ \left\{ \begin{gathered} {R_0} = 2.850\;{{\Omega /{\mathrm{km}}, }}\,{L_0}{\text{ = 1}}{\text{.218}} \times {\text{1}}{{\text{0}}^{ - 3}}\;{\text{H/km}} \\ {C_{\text{0}}}{\text{ = 0}}{\text{.490}} \times {\text{1}}{{\text{0}}^{ - 6}}\;{\text{F/km, }}{R_1} = 0.288\;{{\Omega /{\mathrm{km}}}} \\ {L_1}{\text{ = 0}}{\text{.266}} \times {\text{1}}{{\text{0}}^{ - 3}}\;{\text{H/km, }}{C_1}{\text{ = 0}}{\text{.538}} \times {\text{1}}{{\text{0}}^{ - 6}}\;{\text{F/km }} \\ \end{gathered} \right. $ | (17) |
在辐射状配电网不同位置设置故障点采集样本数据,故障类型包括AG、BG、CG和间歇性电弧故障,详细样本数据分布情况如表1所示。
| 故障参数 | 参数取值 |
| 故障线路 | l1, l2, l3, l4 |
| 故障位置 | 每0.15 km设置一个故障点 |
| 故障类型 | AG, BG, CG, 间歇性电弧接地 |
| 故障相角 | 0°, 30°, 60°, 90°, 120°, 150° |
| 过渡电阻 | 0~1500 Ω |
| 训练样本数量 | 8000 |
| 测试样本数量 | 3525 |
当线路3距离母线2 km处,发生C相接地故障,接地电阻为纯金属接地,每个线路的特征图如图11所示。从图11可以看出,当配电网发生单相接地故障时,故障线路与正常线路的特征图具有一定差异,可以作为深度学习良好的样本。

|
| 图 11 低阻接地各线路特征图 |
当线路1的A相发生1000 Ω接地故障时,各线路的信号到图像转换结果如图12所示。从图12可以看出,当线路1发生高阻接地故障时,各线路的特征图有明显的不同,将信号转成图像,可以扩充原始信号不可见的信息,转换后的图像有利于作为深度学习方法的输入,通过深度学习方法自助挖掘图像特征就可以实现端到端配电网故障诊断。

|
| 图 12 高阻接地各线路特征图 |
5.2 模型对比
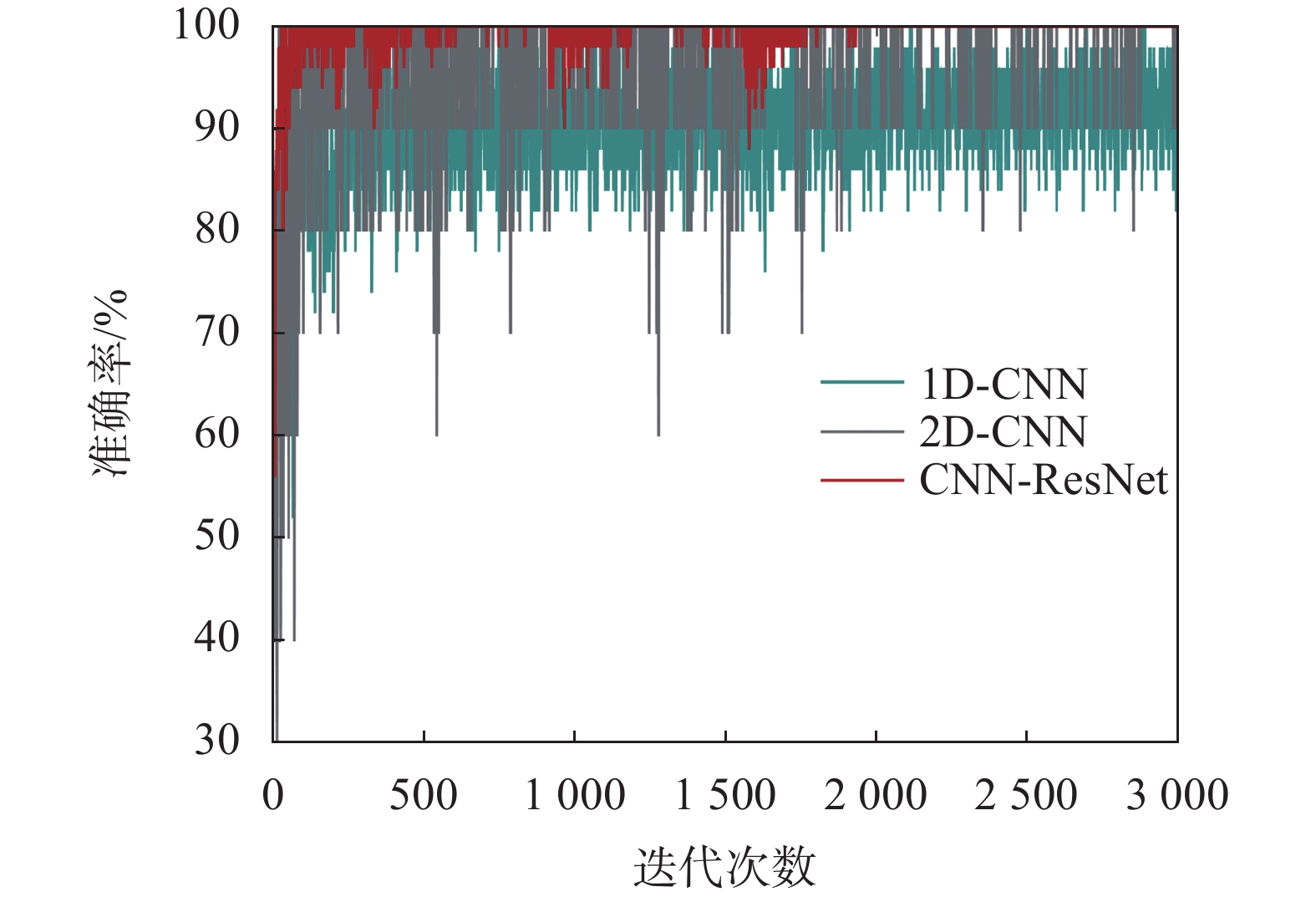
对比一维卷积神经网络(1D-CNN)、二维卷积神经网络(2D-CNN)和CNN-ResNet三种网络的训练过程,其中1D-CNN是只输入零序电流信号,2D-CNN是只输入特征图,CNN-ResNet是同时输入零序电流信号和特征图,训练过程曲线如图13所示。可以看出,1D-CNN和2D-CNN训练曲线均有较大的波动,而CNN-ResNet的训练过程随着训练次数的增加,准确率稳定到达100%,说明所提方法训练效果优于单输入的训练网络,可以保证较高的故障诊断准确率。
|
| 图 13 三种网络训练过程 |
对混合卷积神经网络的特征进行降维可视化,所得结果如图14所示。可以看出,输入层的特征向量相互交错,难以区分,随着卷积池化的操作,相同故障的线路特征聚集到一起,具有明显的区分度。

|
| 图 14 不同层特征可视化结果 |
5.3 测试样本准确率分析
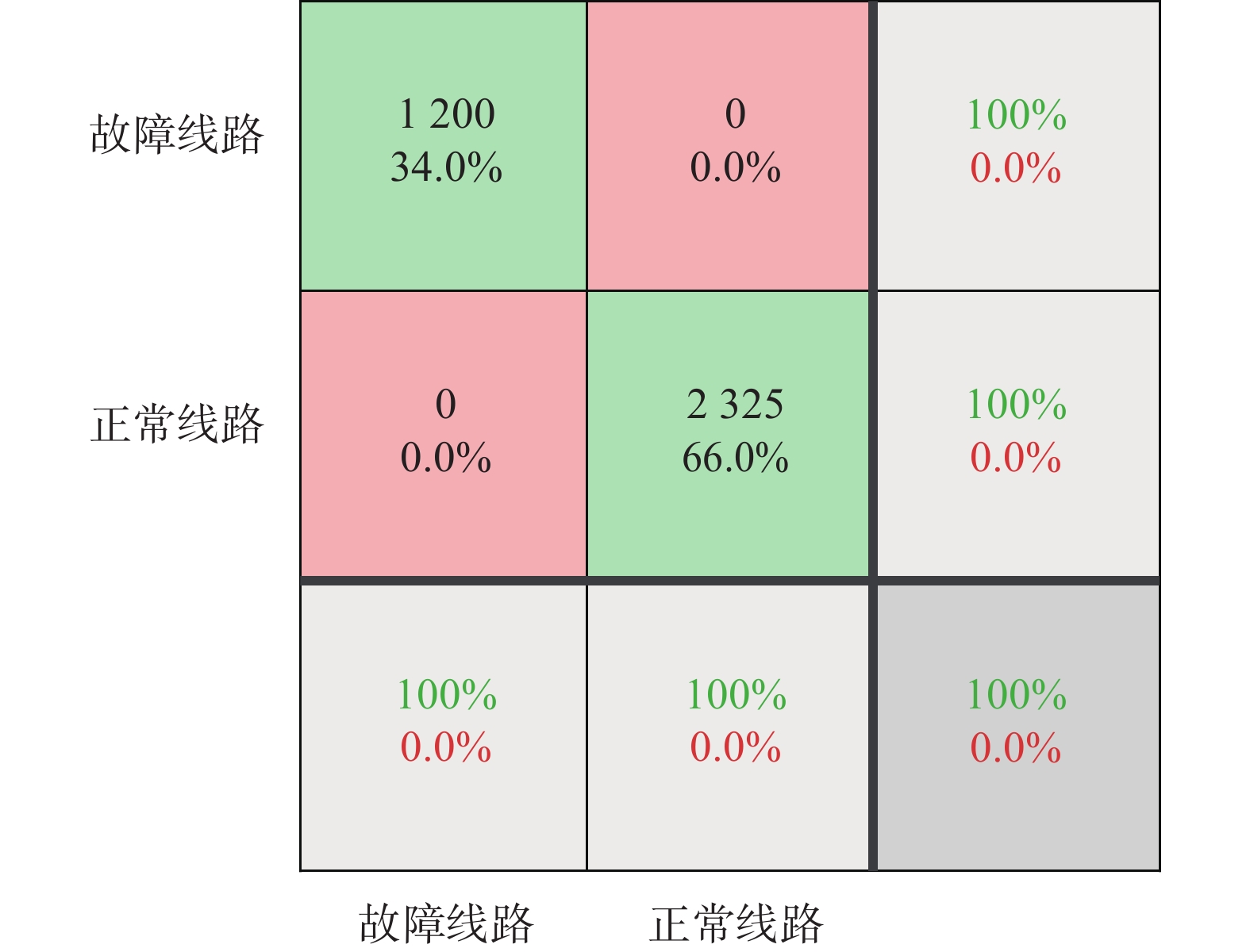
网络训练好以后,对3525个测试样本进行测试,所得混淆矩阵如图15所示,其中主对角线元素代表分类正确的样本数量。从图15可以看出,无论是正常线路还是故障线路,所提方法均没有出现误判,具有较高的故障选线准确率。
|
| 图 15 测试样本混淆矩阵 |
5.4 噪声干扰分析
实际现场有大量噪声的存在,会影响故障选线的准确性,因此故障选线方法要有一定的抗噪能力。向零序电流中加入不同信噪比噪声,对比不同选线方法的故障选线抗噪性能,如表2所示。可以看出,所提方法在抗噪能力方面,优于其他故障选线方法。
5.5 采样时间不同步分析
当各线路采样时间不同步时,会影响故障选线结果。表3比较了不同方法在采样时间不同情况下故障选线结果。从表中可以看出,本文方法在采样时间不同步,接地电阻较大的情况下,依然可以准确地选择出故障线路。
5.6 改变中性点接地方式分析
在配电网实际运行过程中,可能改变中性点运行方式,训练样本采用中性点经消弧线圈接地方式,测试样本采用中性点不接地方式,所得结果如表4所示,可以看出本文方法对中性点不接地方式同样适用。
5.7 动模实验
由于仿真实验数据与实际情况具有一定差异,因此利用图16所示动模实验平台验证所提方法的准确性。利用动模实验平台进行实验,可以更加接近真实的故障环境。通过动模实验平台获取测试样本,故障选线模型无需重新训练,所得结果如表5所示,从表5可以看出,所提方法在动模实验平台上依然能够准确地选择出故障线路,没有出现误判。

|
| 图 16 动模实验平台 |
5.8 故障选线时间分析
小电流接地系统在发生单相接地故障时,可以带故障运行2~3 h,本文通过排列熵优化VMD算法和颜色编码的方式将零序电流信号转成图像用时0.25 s,通过深度学习判断图像是否为故障线路用时0.102 s,整体故障选线时间小于0.4 s,可以满足工程实际的需求。
6 结束语本文提出了一种基于信号图像化和CNN-ResNet 的配电网单相接地故障选线方法,并在辐射配电网上进行了实验验证,得出如下结论:
1) 利用排列熵优化的VMD算法,可以根据信号自身的复杂程度,自适应地确定分解层数,可以在一定程度上抑制EMD算法的模态混淆问题。
2) 利用信号转图像的方法,图像的颜色、点、线、面可以丰富一维信号的特征,扩充信号的不可见信息。
3) 将一维卷积神经网络和ResNet网络相互混合,挖掘一维零序电流信号和二维图像特征,可以实现端到端故障诊断,效果优于仅使用单一网络。
4) 所提故障选线方法具有较高的故障诊断准确率,并且具有一定的抗噪能力,可以在高阻接地、采样时间不同步等情况下实现故障选线。在动模实验平台上也可以准确地选择出故障线路。
| [1] |
余晓, 吕飞鹏, 张国星, 等. 循环神经网络输电线路双端故障测距方法[J].
中国测试, 2021, 47(9): 119-125.
YU X, LV F P, ZHANG G X, et al. Two-terminal fault location algorithm for transmission lines based on recurrent neural network[J].
China Measurement & Test, 2021, 47(9): 119-125.
DOI:10.11857/j.issn.1674-5124.2020100065 |
| [2] |
陈博帆, 孙岩洲, 王彬. 基于改进SSA-VMD和多尺度模糊熵的接地故障选线方法[J].
国外电子测量技术, 2023, 42(1): 28-34.
CHEN B F, SUN Y Z, WANG B. Line selection of grounding fault based on improved SSA-VMD and multi-scale fuzzy entropy[J].
Foreign Electronic Measurement Technology, 2023, 42(1): 28-34.
|
| [3] |
侯思祖, 郭威, 王子奇, 等. 基于小波AlexNet网络的配电网故障区段定位方法[J].
电测与仪表, 2022, 59(3): 46-57.
HOU S Z, GUO W, WANG Z Q, et al. Fault segment location method for distribution network based on wavelet AlexNet network[J].
Electrical Measurement & Instrumentation, 2022, 59(3): 46-57.
|
| [4] |
WANG D, PSARAS V, EMHEMED A, et al. A novel fault let-through energy based fault location for LVDC distribution networks[J].
IEEE Transactions on Power Delivery, 2021, 36(2): 966-974.
DOI:10.1109/TPWRD.2020.2998409 |
| [5] |
侯思祖, 郭威. 基于自适应陷波滤波器和混沌振子的配电网故障选线[J].
电测与仪表, 2020, 57(6): 61-66.
HOU S Z, GUO W. Fault line selection in distribution network based on adaptive notch filter and chaos oscillator[J].
Electrical Measurement & Instrumentation, 2020, 57(6): 61-66.
|
| [6] |
刘宝稳, 曾祥君, 张慧芬, 等. 注入电流馈线分布特征及其在接地故障检测中的应用[J].
电网技术, 2021, 45(7): 2731-2740.
LIU B W, ZENG X J, ZHENG H F, et al. Distribution model of injection current in feeder and its application in single phase to ground fault detection[J].
Power System Technology, 2021, 45(7): 2731-2740.
|
| [7] |
张淑清, 翟欣沛, 董璇, 等. EMD及Duffing振子在小电流系统故障选线方法中的应用[J].
中国电机工程学报, 2013, 33(10): 161-167.
ZHANG S Q, ZHAI X P, DONG X, et al. Application of EMD and duffing oscillator to fault line detection in un-effectively grounded system[J].
Proceedings of the CSEE, 2013, 33(10): 161-167.
|
| [8] |
郭亮, 杜欢, 王晓卫, 等. 基于磁场检测与多判据融合的架空线路接地故障定位方法[J].
电力系统保护与控制, 2022, 50(17): 24-34.
GUO L, DU H, WANG X W, et al. Single phase to ground fault location method of an overhead line based on magnetic field detection and multi-criteria fusion[J].
Power System Protection and Control, 2022, 50(17): 24-34.
|
| [9] |
严太山. 基于人类进化算法的配电网故障定位[J].
仪器仪表学报, 2015, 36(3): 694-700.
YAN T S. Fault location for distribution network based on the human evolutionary algorithm[J].
Chinese Journal of Scientific Instrument, 2015, 36(3): 694-700.
|
| [10] |
高杰, 程启明, 程尹曼, 等. 基于量子遗传双稳态系统的配电网故障选线方法[J].
电力自动化设备, 2018, 38(5): 164-170.
GAO J, CHENG Q M, CHENG Y M, et al. Faulty line selection method based on quantum genetic bistable system for distribution network[J].
Electric Power Automation Equipment, 2018, 38(5): 164-170.
|
| [11] |
李霆, 方志坚, 罗义旺, 等. 基于改进蚁群算法的配电网故障定位研究[J].
微型电脑应用, 2020, 36(9): 86-88.
LI T, FANG Z J, LUO Y W, et al. Research on fault location of distribution network based on improved ant colony algorithm[J].
Microcomputer Applications, 2020, 36(9): 86-88.
DOI:10.3969/j.issn.1007-757X.2020.09.027 |
| [12] |
马磊, 黄伟, 李克成, 等. 基于Attention-LSTM的光伏超短期功率预测模型[J].
电测与仪表, 2021, 58(2): 146-152.
MA L, HUANG W, LI K C, et al. Photovoltaic ultra-short-term power prediction model based on Attention-LSTM[J].
Electrical Measurement & Instrumentation, 2021, 58(2): 146-152.
|
| [13] |
王阳, 乐健, 周谦, 等. 基于小波包分析与神经网络的变压器区内外故障判断方法[J].
电测与仪表, 2020, 57(7): 1-7+15.
WANG Y, LE J, ZHOU Q, et al. Inner and outer zone fault diagnosis method of transformer based on wavelet packet analysis and neural network[J].
Electrical Measurement & Instrumentation, 2020, 57(7): 1-7+15.
|
| [14] |
彭华, 朱永利. 基于apFFT频谱校正和XGBoost的风电场集电线路单相接地故障测距[J].
电工技术学报, 2020, 35(23): 4931-4939.
PENG H, ZHU Y L. Single phase grounding fault location for power lines of wind farm based on apFFT spectrum correction and XGBoost algorithm[J].
Transactions of China Electrotechnical Society, 2020, 35(23): 4931-4939.
|
| [15] |
LUO G M, TAN Y J, LI M, et al. Stacked auto-encoder-based fault location in distribution network[J].
IEEE Access, 2020, 8: 28043-28053.
DOI:10.1109/ACCESS.2020.2971582 |
| [16] |
程文傲, 徐明, 高金峰. 小电流接地系统单相接地故障选线空间域图像生成及融合方法[J].
电力自动化设备, 2021, 41(7): 97-103.
CHENG W A, XU M, GAO J F. Spatial domain image generation and fusion method of single-phase grounding fault line selection for small current grounding system[J].
Electric Power Automation Equipment, 2021, 41(7): 97-103.
|
| [17] |
戴洪德, 陈强强, 戴邵武, 等. 基于样本分位数排列熵的故障诊断方法[J].
振动与冲击, 2019, 38(23): 152-156.
DAI H D, CHEN Q Q, DAI S W, et al. Fault diagnosis method based on sample quantile permutation entropy[J].
Journal of Vibration and Shock, 2019, 38(23): 152-156.
|
| [18] |
刘长良, 武英杰, 甄成刚. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J].
中国电机工程学报, 2015, 35(13): 3358-3365.
LIU C L, WU Y J, ZHEN C G. Rolling bearing fault diagnosis based on variational mode decomposition and fuzzy c means clustering[J].
Proceedings of the CSEE, 2015, 35(13): 3358-3365.
|
| [19] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J].
IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
DOI:10.1109/TSP.2013.2288675 |
| [20] |
郑近德, 程军圣, 杨宇. 改进的EEMD算法及其应用研究[J].
振动与冲击, 2013, 32(21): 21-26.
ZHENG J D, CHENG J S, YANG Y. Modified EEMD algorithm and its applications[J].
Journal of Vibration and Shock, 2013, 32(21): 21-26.
DOI:10.3969/j.issn.1000-3835.2013.21.004 |
| [21] |
WEN L, LI X, GAO L, et al. A new convolutional neural network-based data-driven fault diagnosis method[J].
IEEE Transactions on Industrial Electronics, 2018, 65(7): 5990-5998.
DOI:10.1109/TIE.2017.2774777 |
| [22] |
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]//Proc of IEEE Conference on Computer Vision and Pattern Recognition. Washington DC: IEEE Computer Society, 2016: 770-778.
|
| [23] |
林旭梅, 胡川, 朱广辉, 等. 一种改进ADAM-CNN模型的钢筋混凝土腐蚀检测方法[J].
中国测试, 2023, 49(2): 8-14.
LIN X M, HU C, ZHU G H, et al. An improved ADAM-CNN model for corrosion detection of reinforced concrete[J].
China Measurement & Test, 2023, 49(2): 8-14.
|
 2024, Vol. 50
2024, Vol. 50


 ,
,