文章信息
- 江帆, 许巍, 张俊, 仇念源, 卢杨, 叶晖, 王明琨
- JIANG Fan, XU Wei, ZHANG Jun, QIU Nianyuan, LU Yang, YE Hui, WANG Mingkun
- 响应面法纤维网格布强化混凝土配比设计
- Mix design of fiber mesh reinforced concrete based on response surface method
- 中国测试, 2024, 50(6): 148-156, 190
- CHINA MEASUREMENT & TEST, 2024, 50(6): 148-156, 190
- http://dx.doi.org/10.11857/j.issn.1674-5124.2021110076
-
文章历史
- 收稿日期: 2021-11-11
- 收到修改稿日期: 2022-05-26
2. 空军工程大学航空工程学院,陕西 西安 710038;
3. 95979部队,山东 泰安 271000
2. College of Aeronautical Engineering, Air Force Engineering University, Xi′an 710038, China;
3. PLA Unit 95979, Tai′an 271000, China
机场道面混凝土在使用期间,易受到机轮磨耗、干湿冻融循环、高温尾喷、紫外线照射和盐类侵蚀等外部作用,导致混凝土表层受损,出现裂纹产生松动与剥落,严重影响跑道的正常使用,降低跑道的使用寿命,甚至会对机场混凝土道面结构强度造成不利影响[1]。特别是随着我军航空装备的更新换代,主战装备向荷载重型化发展,致使机场道面所承受荷载不断增大,新型飞机对道面性能的要求与日俱增,挑战也越来越大[2]。因此对研究如何有效增强道面混凝土,特别是表层抵抗上述外部作用能力的需求十分迫切。
混凝土表层是水泥砂浆层,该层结构对道面混凝土表面性能影响重大,因此可以从优化混凝土表层砂浆层组份和在表层砂浆层中布设纤维网格布两种方式增强道面混凝土表面性能[1-3]。朱懋江等[2]提出采用将纤维、聚合物乳液掺入混凝土以及在混凝土表面喷涂硅烷等方式来增强道面混凝土的表面性能,冻融与磨耗试验结果表明三种方式都能有效提升混凝土表面性能。胡成等[1]对玄武岩纤维网格布和玻璃纤维网格布强化混凝土在不同环境因素作用下的抗冻性能进行了对比研究,结果发现纤维网格布可有效增强混凝土抗冻性能,其中玄武岩纤维网格布效果更好。李悦媛等[4]对比研究了不同规格的碳纤维网格布、芳纶纤维网格布和玄武岩纤维网格布表层强化混凝土的早期开裂特性,结果发现网格尺寸为3 mm×3 mm的玄武岩纤维网格布增强效果最好。言兴[5]采用玻璃纤维网格布和聚丙烯纤维对混凝土进行复合加固,研究了其轴压性能,结果表明玻璃纤维网格布和聚丙烯纤维都能大幅度提高构件的延性,延缓裂缝的展开。丁一宁等[6]研究了钢纤维和玻璃纤维网格布对混凝土板的增强作用,发现耐碱玻璃纤维网格布可将板的极限承载力提高59%。封雷等[7]研究了玻璃纤维网格布增强复合保温墙板的抗弯和抗压性能,发现玻璃纤维网格布增强后板的极限荷载平均提高了14.98%。刘敬福等[8]通过正交试验研究了各因素对玻璃纤维网格布增强聚合物矿物混凝土抗压强度影响规律,发现影响由大到小依次是黏合剂用量、玻璃纤维网格布加入量、网格布网眼尺寸、填料用量。王庆轩等[9]研究了玄武岩纤维网格布对混凝土方板的双向增强效果,结果表明玄武岩纤维网格布可以改善方板的内力重分布,显著提高其承载力,但是破坏时脆性特征明显。廖瑜等[10]研究了聚脲和玻璃纤维网格布联合加固钢板的抗冲击力学性能,发现经复合加固后钢板峰值动能相比纯聚脲层加固最大可降低28%,内能可达到2.75倍。张勇超[11]研究发现纤维网格布提高了混凝土吸收能量的能力,且玻璃纤维网格布的增强作用优于玄武岩纤维网格布。姜乐等[12]以抗冻和耐磨耗性能为指标对水灰比、砂率、细度模数和含泥量四个参数进行了优选,取得了一定的成果。但试验没有考虑纤维网格布尺寸与砂率、细度模数之间交互作用,无法指导纤维网格布强化混凝土配合比设计。
响应面法(response surface methodology, RSM)是一种试验设计方法和统计方法,可拟合得到不同因素的关系式,并寻取最优值[13-14]。与正交法相比,响应面法设计试验不但能够分析几种因素的共同作用并取得最优组合,还可以得到响应值与自变量之间的回归模型,有利于进行更为详细精确的试验研究[14-15]。因此本文采用响应面法,对玄武岩纤维网格布强化混凝土在飞机尾喷和紫外线照射作用下的耐磨耗和抗冻性能进行对比研究,分析了网格尺寸大小、砂率和细度模数对强化混凝土性能的影响,得到了最优的纤维网格布强化混凝土配合比。
1 试验概况 1.1 试验材料试验用水泥为PO-42.5 R硅酸盐水泥且掺量固定为320 kg/m3。砂是优质天然河砂,配制范围为2.8~3.2的细度模数。粗集料为石灰石碎石,分5~10 mm,10~20 mm和20~40 mm三种级配,比例2∶3∶6。玄武岩纤维网格布分3 mm×3 mm、5 mm×5 mm和10 mm×10 mm三种,性能参数见表1。
| 密度/ (kg∙m–3) |
比热容/ (J∙kg–1∙K–1) |
热传导率/ (W·m–1·K–1) |
断裂伸 长率/% |
泊松比 | 拉伸强 度/MPa |
弹性模 量/GPa |
| 3000 | 0.94 | 0.04 | 2.2 | 0.28 | 1575 | 26.2 |
1.2 试件准备
磨耗试验试件为150 mm×150 mm×75 mm的半立方体,冻融循环试验试件为100 mm×100 mm×400 mm的小梁。试件制作按照试模准备、拌合混凝土、浇筑与振捣、布设纤维网格布及养护的流程进行。其中纤维网格布的布设方法是:振捣结束之后,将备好的纤维网格布平铺至试模上方。首先通过人工提浆的方式将网格布初步埋入水泥砂浆层当中,随后再次开启振动台30 s,振动期间使用水泥刀再次对试模进行提浆,完全将网格布铺入水泥砂浆层当中,振动完毕之后,使用水泥刀进行精准抹平,之后将试件静置。如图1所示。

|
| 图 1 纤维网格布形态 |
1.3 试验方法
1)环境作用处理
以飞机尾喷作用和紫外线照射作用作为环境因素,其中飞机尾喷采用火焰喷射枪进行模拟,如图2(a)所示,紫外线照射采用紫外线老化试验机进行模拟,如图2(b)所示。

|
| 图 2 环境作用处理 |
2)磨耗试验
磨耗试验如图3(a)所示,试件成型后置于标准养护箱养护27 d,之后进行12 h自然干燥和12 h烘箱干燥。在第一次环境处理后称取质量m0,随后在200 kN配重下进行30圈预磨,量取质量m1和磨耗深度h1,而后每5圈,测量一次质量,每10圈测量一次磨耗深度,当磨耗60圈后,停止试验。试验以单位面积磨耗量(

|
| 图 3 试验方法 |
| $ {G_c} = \left({{{m_0} - {m_1}}}\right)/{{0.012\;5}} $ | (1) |
式中:
0.0125——试件的磨耗面积,m2。
3)冻融循环试验
冻融试验如图3(b)~(c)所示,采用单面冻融法,养护及干燥程序同磨耗试验,进行环境处理后开展冻融试验。一次冻融循环总时间为24 h,分为4个阶段,第1个阶段为20 ℃恒温3 h,第二个阶段为通过4 h将温度从20 ℃降到–20 ℃,第三个阶段为–20 ℃恒温1 h,第四个阶段为通过4 h将温度从–20 ℃升到20 ℃。每进行完4次冻融循环后,进行1次环境处理。以单位面积累计剥落量mn (g/m2)和相对动弹模量
| $ {m_n} = {{\displaystyle \sum\limits_{i = 1}^n {\Delta {m_i}} }}/{{0.04}} $ | (2) |
| $ \Delta {E_i} = {{{E_{di}}}}/{{{E_{d0}}}} $ | (3) |
式中:
1)响应面法
响应面法(response surface methodology, RSM)是一种试验设计方法和统计方法,可拟合得到不同因素的关系式,并寻取最优值,本文首选的是二次多项式模型,如式(4)所示。
| $ \begin{split} {{y}} = & g({X_1},{X_2}, \cdots \cdot \cdot \cdot {X_n}) =\\ & {\partial _0} + \sum\limits_{i = 1}^n {{\partial _i}{X_i} + } \sum\limits_{i = 1}^n {{\partial _{ii}}{X_{ii}}^2} + \sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i}^n {{\partial _{ij}}{X_i}{X_j}} } \end{split} $ | (4) |
式中:y——预测响应值;
n——影响因子。
2)方案设计
本文选用砂率、细度模数和纤维网格布尺寸大小作为设计因素,以纤维网格布强化混凝土耐磨耗和抗冻性能作为控制目标,通过响应面法对试验配比进行设计,试验方案见表2。
| 序号 | 水泥/ (kg·m–3) |
水灰比 | 砂率/% | 细度模数 | 网格布尺寸/ (mm×mm) |
| 1 | 320 | 0.43 | 32 | 3.2 | 5×5 |
| 2 | 320 | 0.43 | 28 | 3.2 | 5×5 |
| 3 | 320 | 0.43 | 30 | 3.0 | 5×5 |
| 4 | 320 | 0.43 | 28 | 2.8 | 5×5 |
| 5 | 320 | 0.43 | 30 | 3.2 | 10×10 |
| 6 | 320 | 0.43 | 32 | 3.0 | 3×3 |
| 7 | 320 | 0.43 | 28 | 3.0 | 10×10 |
| 8 | 320 | 0.43 | 28 | 3.0 | 3×3 |
| 9 | 320 | 0.43 | 30 | 3.0 | 5×5 |
| 10 | 320 | 0.43 | 30 | 3.0 | 5×5 |
| 11 | 320 | 0.43 | 30 | 3.0 | 5×5 |
| 12 | 320 | 0.43 | 30 | 2.8 | 10×10 |
| 13 | 320 | 0.43 | 30 | 2.8 | 3×3 |
| 14 | 320 | 0.43 | 32 | 2.8 | 5×5 |
| 15 | 320 | 0.43 | 30 | 3.0 | 5×5 |
| 16 | 320 | 0.43 | 32 | 3.0 | 10×10 |
| 17 | 320 | 0.43 | 30 | 3.2 | 3×3 |
2 结果分析与讨论 2.1 耐磨耗性能
1)响应面函数拟合
按照试验方案开展的磨耗与抗冻试验结果如表3所示,以式(4)作为拟合模型进行多元回归拟合,分别得到单位面积磨耗量和磨耗深度与网格尺寸、砂率和细度模数之间的二次多项式方程如式(5)和式(6)所示,其中
| 序号 | 砂率/% | 细度模数 | 网格布尺寸/(mm×mm) | 单位面积磨耗量/(kg·m–2) | 磨耗深度/mm | 相对动弹模量/% | 单位面积剥落量/(g·m–2) |
| 1 | 32 | 3.2 | 5×5 | 2.545 | 3.30 | 75.89 | 12987.8 |
| 2 | 28 | 3.2 | 5×5 | 2.415 | 3.25 | 69.12 | 14330.8 |
| 3 | 30 | 3.0 | 5×5 | 2.307 | 3.11 | 63.78 | 15897.6 |
| 4 | 28 | 2.8 | 5×5 | 1.986 | 2.97 | 64.12 | 15768.6 |
| 5 | 30 | 3.2 | 10×10 | 3.124 | 3.70 | 76.31 | 12912.3 |
| 6 | 32 | 3.0 | 3×3 | 1.787 | 2.88 | 70.02 | 14289.6 |
| 7 | 28 | 3.0 | 10×10 | 2.812 | 3.53 | 75.01 | 13068.8 |
| 8 | 28 | 3.0 | 3×3 | 1.543 | 2.77 | 63.16 | 15989.6 |
| 9 | 30 | 3.0 | 5×5 | 2.327 | 3.19 | 64.96 | 15686.5 |
| 10 | 30 | 3.0 | 5×5 | 2.312 | 3.14 | 67.86 | 14689.2 |
| 11 | 30 | 3.0 | 5×5 | 2.317 | 3.16 | 69.89 | 14310.3 |
| 12 | 30 | 2.8 | 10×10 | 2.711 | 3.44 | 68.25 | 14523.4 |
| 13 | 30 | 2.8 | 3×3 | 1.467 | 2.58 | 72.12 | 13967.6 |
| 14 | 32 | 2.8 | 5×5 | 2.223 | 3.02 | 71.25 | 14131.5 |
| 15 | 30 | 3.0 | 5×5 | 2.319 | 3.19 | 77.12 | 12814.5 |
| 16 | 32 | 3.0 | 10×10 | 2.989 | 3.61 | 70.12 | 14258.8 |
| 17 | 30 | 3.2 | 3×3 | 1.643 | 2.91 | 70.24 | 14233.9 |
| $ \begin{split} {G_{60}}{\text{=}}&2.67{\text{ + }}0.65{X_1}{\text{ + }}0.096{X_2}{\text{ + }}0.18{X_3}-0.013{X_1}{X_2}+\\ &{\text{0}}{\text{.046}}{X_1}{X_3}-0.027{X_2}{X_3}-0.40{X_1}^2{\text{ + }}0.011{X_2}^2-\\ &0.035{X_3}^2\\[-1pt] \end{split}$ | (5) |
| $\begin{split} {h_{60}} = &3.36 + 0.39{X_1} + 0.038{X_2} + 0.14{X_3} - 0.002{X_1}{X_2} -\\ &0.018{X_1}{X_3} - 0.17{X_1}^2 + 0.010{X_2}^2 - 0.032{X_3}^2\\[-1pt] \end{split} $ | (6) |
对上述两种模型进行方差分析,单位面积磨耗量结果如表4所示,磨耗深度分析同理。从表4中可以看出,模型的P值小于0.0001,表明此模型极为显著;但失拟项对应的P值小于0.05,因此需要调整模型的阶数。采用三次式模型重新对试验结果进行拟合并进行方差分析后发现三次式模型拟合效果较好。三次式模型拟合结果如表5所示,其中,模型的P值<0.0001,表明此模型极为显著。因子对应的P值表明
| 来源 | 平方和 | 自由度 | 均方差 | F值 | P值 |
| 模型 | 3.70000 | 9 | 0.41161 | 169.20000 | < 0.0001 |
| X1 | 3.37000 | 1 | 3.37480 | 1387.31000 | < 0.0001 |
| X2 | 0.06800 | 1 | 0.06770 | 27.82900 | 0.00120 |
| X3 | 0.23000 | 1 | 0.23230 | 95.49300 | < 0.0001 |
| X1 X2 | 0.00070 | 1 | 0.00070 | 0.28919 | 0.60740 |
| X1 X1 | 0.00937 | 1 | 0.00937 | 3.85160 | 0.09050 |
| X1 X3 | 0.00286 | 1 | 0.00286 | 1.17660 | 0.31400 |
| X12 | 0.40101 | 1 | 0.40101 | 164.85000 | < 0.0001 |
| X22 | 0.00053 | 1 | 0.00053 | 0.21615 | 0.65610 |
| X32 | 0.00525 | 1 | 0.00525 | 2.15990 | 0.18510 |
| 失拟项 | 0.01680 | 3 | 0.00560 | 98.59802 | 0.00030 |
| 来源 | 平方和 | 自由度 | 均方差 | F值 | P值 |
| 模型 | 3.72000 | 12 | 0.31010 | 5459.58589 | <0.0001 |
| X1 | 1.86000 | 1 | 1.85641 | 32683.20863 | <0.0001 |
| X2 | 0.01400 | 1 | 0.01398 | 246.20688 | <0.0001 |
| X3 | 0.11000 | 1 | 0.11379 | 2003.33445 | <0.0001 |
| X1 X2 | 0.00112 | 1 | 0.00112 | 19.75792 | 0.0113 |
| X1 X3 | 0.01400 | 1 | 0.01404 | 247.22271 | <0.0001 |
| X2 X3 | 0.00286 | 1 | 0.00286 | 50.39173 | 0.0021 |
| X12 | 0.40000 | 1 | 0.40101 | 7060.03252 | <0.0001 |
| X22 | 0.00002 | 1 | 0.00002 | 0.39984 | 0.5615 |
| X32 | 0.00919 | 1 | 0.00919 | 161.84544 | 0.0002 |
| X1 X2 X3 | 0.00000 | 0 | 0.00000 | 0.00000 | 0.00000 |
| X12 X2 | 0.00078 | 1 | 0.00078 | 13.79002 | 0.0206 |
| X12 X3 | 0.00795 | 1 | 0.00795 | 140.02341 | 0.0003 |
| X1X22 | 0.00807 | 1 | 0.00806 | 141.98063 | 0.0003 |
| X1 X32 | 0.00000 | 0 | 0.00000 | 0.00000 | 0.00000 |
| X22 X3 | 0.00000 | 0 | 0.00000 | 0.00000 | 0.00000 |
| X2X32 | 0.00000 | 0 | 0.00000 | 0.00000 | 0.00000 |
| X13 | 0.00000 | 0 | 0.00000 | 0.00000 | 0.00000 |
| X23 | 0.00000 | 0 | 0.00000 | 0.00000 | 0.00000 |
| X33 | 0.00000 | 0 | 0.00000 | 0.00000 | 0.00000 |
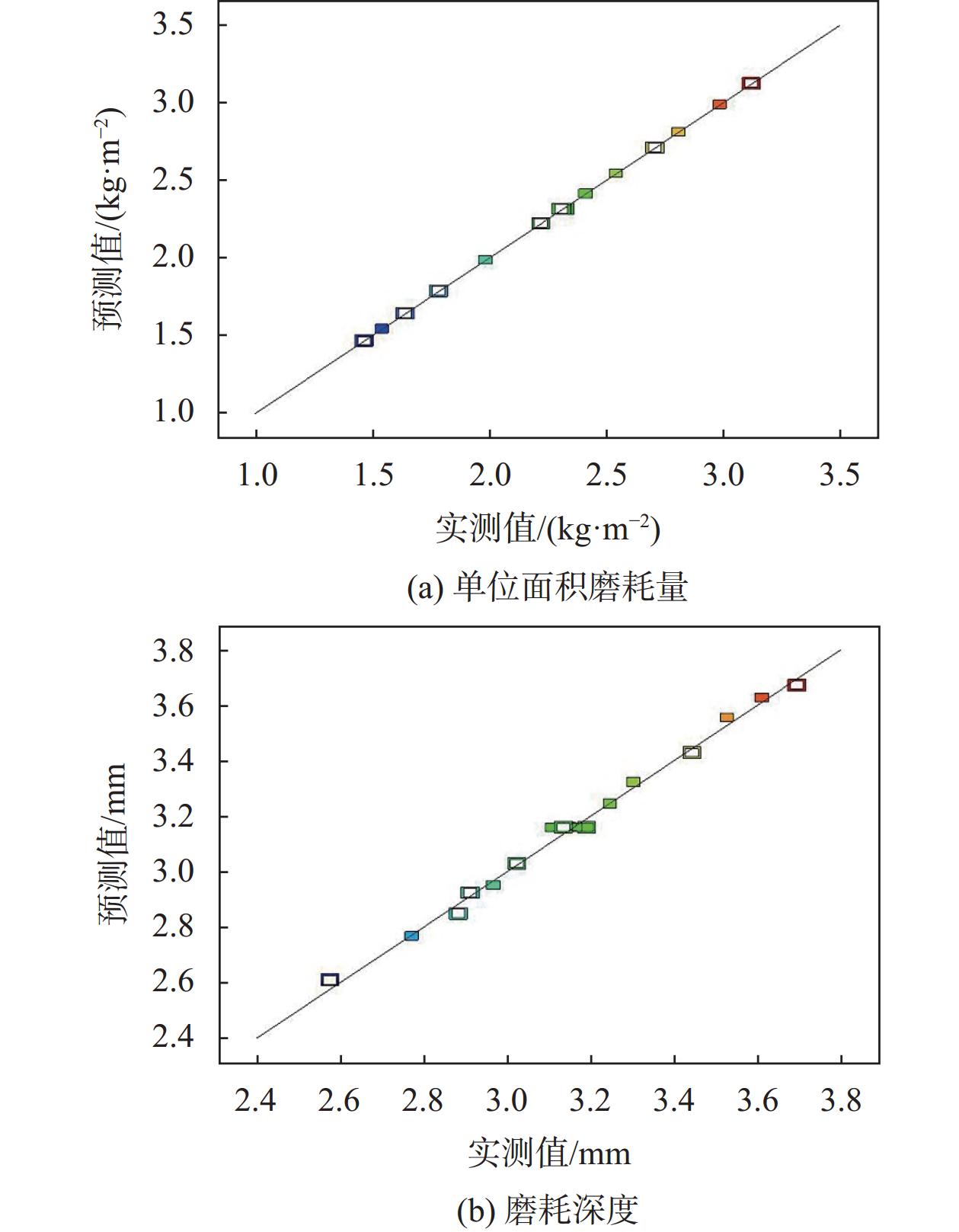
|
| 图 4 预测数据与实测数据比较 |
| $ \begin{split} {G_{60}}{\text{ = }}&2.67{\text{ + }}0.65{X_1}{\text{ + }}0.096{X_2}{\text{ + }}0.23{X_3} - \\ &0.017{X_1}{X_2}{\text{ + }}0.059{X_1}{X_3}{\text{ - 0}}{\text{.027}}{X_2}{X_3}- \\ &0.40{X_1}^2 - 0.049{X_3}^2{\text{ + }}0.025{X_1}^2{X_2} - \\ &0.081{X_1}^2{X_3} -0.064{X_1}{X_2}^2 \end{split} $ | (7) |
磨耗深度的方差分析结果表明,模型的P值小于0.0001,失拟项对应的P值为0.3992,大于0.05,表示模型与试验数据极其相关;各因子对应P值表明,
| $ {h_{60}} = 3.36 + 0.39{X_1} + 0.038{X_2} + 0.14{X_3} - 0.17{X_1}^2 $ | (8) |
2)响应面参数对耐磨耗性能的影响
为了分析砂率、细度模数和网格尺寸大小对纤维网格布表层强化混凝土耐磨耗性能的影响,应用以下三维响应面图进行分析。根据多元回归方程方程式(6)和式(7)得出任意两个因素对纤维网格布表层强化混凝土耐磨耗性能的响应面曲线图(图5和图6),曲线的陡峭程度代表其对性能的影响程度[13-15]。从图5中可看出,三种因素当中,纤维网格布网格尺寸对单位面积磨耗量影响最大,砂率和细度模数的影响相近,细度模数影响程度稍大于砂率,这和姜乐[10]所得试验结果是一致的。图5(a)和图5(b)所示曲面扭曲明显,表明纤维网格布尺寸和砂率、纤维网格布尺寸和细度模数的交互作用影响明显,而图5(c)中所示曲面基本无扭曲,表明砂率和细度模数对单位面积磨耗量的交互作用影响甚微。

|
| 图 5 各因素对单位面积磨耗量影响的三维响应面图 |

|
| 图 6 各因素对磨耗深度影响的三维响应面图 |
同时,从图6中可以看出,三种因素对磨耗深度的影响规律相似,纤维网格布尺寸对磨耗深度影响最大,砂率和细度模数的影响相近,纤维网格布尺寸和砂率、纤维网格布尺寸和细度模数的交互作用影响明显,而砂率和细度模数的交互作用对磨耗深度影响甚微。
其机理可通过纤维网格布加筋混凝土受载破坏过程来进行分析。纤维网格布可看作混凝土的“结构钢筋”,纤维网格布可以分散并承担一定外部约束使混凝土产生的拉应力。承受外加荷载时,纤维网格布同混凝土共同承担。随着荷载逐渐增大,纤维网格布通过界面粘结力阻止裂缝传递内力,应力重新分布,混凝土仍能继续承载。载荷继续增加,纤维网格布与混凝土粘结界面破坏,进而纤维网格布脱粘、脱落,但此过程中吸收大量能量,提高混凝土的强度及断裂韧性。网格尺寸越小,在试样横截面上分布的网格数目越多,经向和纬向结合点多,单独网格所包含的水泥砂浆面积更小,从而网格布能够分担更多约束拉应力[1-4, 9, 11]。
2.2 抗冻性能1)响应面函数拟合
按照试验方案开展的抗冻试验结果如表3所示,以第28次冻融循环后试件的相对动弹模量和单位面积累计剥落量作为控制目标,对拟合后的二次多项式方程进行方差检验发现单位面积累计剥落量对应失拟项的P值为0.03小于0.05,因此改用三次式模型对单位面积累计剥落量进行拟合,最终得到两控制目标的拟合多项式如式(9)和式(10)所示。
| $ \begin{split} \Delta E{{=}}&66.67{{ - }}6.04{X_1}{{ + }}0.24{X_2}{{ + }}1.35{X_3}{{ - }}0.043{X_1}{X_2}{{ + }}\\ &0.24{X_1}{X_3}{{ - 0}}{{.12}}{X_2}{X_3} + 3.38{X_1}^2{{ - }} \\ &0.023{X_2}^2 + 0.015{X_3}^2 \end{split} $ | (9) |
| $ \begin{split} m =& 15\;025.67 + 1448.20{X_1} - 96.49{X_2} + 316.06{X_3} -\\ &13.38{X_1}{X_2} + 12.20{X_1}{X_3} - 0.48{X_2}{X_3} - 655.15{X_1}^2 - \\ &21.05{X_2}^2 + 19.33{X_3}^2 + 45.36{X_1}^2{X_2} - \\ &176.71{X_1}^2{X_3} - 6.67{X_1}{X_2}^2\\[-1pt] \end{split} $ | (10) |
其中,
试件的相对动弹模量拟合模型方差分析结果表明,模型对应的P值小于0.0001,表明此模型极为显著。各因子对应的P值表明,
| $ \Delta E{\text{ = 66}}{\text{.67 - 6}}{\text{.04}}{X_{\text{1}}} + 1.35{X_3} + 3.38{X_{\text{1}}}^2 $ | (11) |
试件的单位面积累计剥落量拟合模型方差分析结果表明,模型对应的P值小于0.0001,表明此模型极为显著。各因子对应的P值表明,
| $ \begin{split} m =& 15\;025.67 + 1\;448.20{X_1} - 96.49{X_2} + 316.06{X_3} - \\ &13.38{X_1}{X_2}+ 12.20{X_1}{X_3} - 0.48{X_2}{X_3} - 655.15{X_1}^2 + \\ &19.33{X_3}^2 + 45.36{X_1}^2{X_2} - 176.71{X_1}^2{X_3} - \\ &6.67{X_1}{X_2}^2\\[-1pt] \end{split} $ | (12) |
2)响应面参数对抗冻性能的影响
根据多元回归方程方程式(11)和式(12)得出任意两个因素对纤维网格布强化混凝土抗冻性能的响应面曲线图(图6和图7),从图6中可看出,三种因素当中,纤维网格布网格尺寸对相对动弹模量影响最大,砂率和细度模数的影响相近,细度模数影响程度稍大于砂率,这和姜乐等[12]所得试验结果也是一致的。图7(a)和图7(b)所示曲面扭曲明显,表明纤维网格布尺寸和砂率、纤维网格布尺寸和细度模数的交互作用影响明显,而图7(c)中所示曲面基本无扭曲,表明砂率和细度模数对相对动弹模量的交互作用影响甚微。同时,从图8中可以看出,三种因素对单位面积累计剥落量的影响规律相似,纤维网格布尺寸对磨耗深度影响最大,砂率和细度模数的影响相近,纤维网格布尺寸和砂率、纤维网格布尺寸和细度模数的交互作用影响明显,而砂率和细度模数的交互作用对磨耗深度影响甚微。上述分析所得出的结论与磨耗试验得出的结论一致。

|
| 图 7 各因素对相对动弹模量影响的三维响应面图 |

|
| 图 8 各因素对单位面积累计剥落量影响的三维响应面图 |
从上述分析可以看出,纤维网格布的加入可以有效提高水泥混凝土抗冻性能,且网格布尺寸和砂率、网格布尺寸和细度模数的交互作用影响明显,通过合理组合设计能够有效提高水泥混凝土抗冻性能。
2.3 基于响应面的参数优选从前面的分析可知,纤维网格布尺寸对混凝土耐磨耗和抗冻性能影响最大,网格布尺寸为3 mm×3 mm时,耐磨耗和抗冻性能最好,但考虑到3 mm×3 mm玄武岩纤维网格布不是市场目前大批量生产对象,使用成本较高,因此工程实际中也可以采用5 mm×5 mm玄武岩纤维网格布。在前面已经拟合得到以单位面积磨耗量、磨耗深度、相对动弹模量和单位面积累计剥落量为控制目标的多项式模型,因此可通过对多项式模型进行求解分析,得出各网格布尺寸相应砂率和细度模数的最优值。使用Design Expert 8.0软件,可依据式(13)所示的约束和相应多项式模型求解出相应控制目标总体最优时对应各响应面参数值,计算结果如表6和表7所示。
| 方案 | 砂率 | 细度 模数 |
相对动弹 模量/% |
单位面积累计 剥落量/(g·m–2) |
单位面积磨耗 量/(kg·m–2) |
磨耗深 度/mm |
| 1 | 0.29 | 2.80 | 77.32 | 12849 | 1.403 | 2.58 |
| 2 | 0.29 | 2.80 | 77.33 | 12847.4 | 1.405 | 2.58 |
| 3 | 0.29 | 2.80 | 77.31 | 12851.2 | 1.402 | 2.58 |
| 4 | 0.29 | 2.80 | 77.29 | 12853.9 | 1.400 | 2.57 |
| 5 | 0.28 | 2.80 | 77.26 | 12860.8 | 1.397 | 2.57 |
| 6 | 0.30 | 2.80 | 77.63 | 12809.6 | 1.491 | 2.61 |
| 7 | 0.31 | 2.80 | 77.71 | 12805 | 1.528 | 2.62 |
| 方案 | 砂率 |
细度 模数 |
相对动 弹模量/% |
单位面积累计 剥落量/(g·m–2) |
单位面积磨 耗量/(kg·m–2) |
磨耗深 度/mm |
| 1 | 0.29 | 2.80 | 73.65 | 13517.2 | 1.753 | 2.79 |
| 2 | 0.29 | 2.80 | 73.66 | 13516 | 1.754 | 2.79 |
| 3 | 0.29 | 2.80 | 73.65 | 13518.8 | 1.752 | 2.79 |
| 4 | 0.29 | 2.80 | 73.68 | 13511.4 | 1.757 | 2.79 |
| 5 | 0.29 | 2.80 | 73.68 | 13509.8 | 1.758 | 2.79 |
| 6 | 0.30 | 2.80 | 73.85 | 13471.6 | 1.797 | 2.80 |
| 7 | 0.30 | 2.80 | 73.88 | 13464.5 | 1.807 | 2.81 |
| 8 | 0.30 | 2.80 | 74.00 | 13442.7 | 1.846 | 2.82 |
| 9 | 0.31 | 2.80 | 74.07 | 13431.1 | 1.876 | 2.83 |
| 10 | 0.31 | 2.80 | 74.08 | 13430.4 | 1.878 | 2.83 |
| $ \left\{\begin{array}{l}0.28\leqslant 砂率\leqslant 0.32\\ 2.8\leqslant 细度模数\leqslant 3.2\\ 网格尺寸=3\;{\mathrm{mm}}\times 3\;{\mathrm{mm}}或5\;{\mathrm{mm}}\times 5\;{\mathrm{mm}}\\ 63.16{\text{%}}\leqslant 相对动弹模量\leqslant 77.12{\text{%}}\\ 12\;814.5\;\text{g}/{{\mathrm{m}}}^{2}\leqslant 单位面积剥落量\leqslant 15\;989.6\;\text{g}/{{\mathrm{m}}}^{2}\\ 1.467\;\text{kg}/{{\mathrm{m}}}^{2}\leqslant 单位面积磨耗量\leqslant 3.124\;\text{kg}/{{\mathrm{m}}}^{2}\\ 2.576\;\text{mm}\leqslant 磨耗深度\leqslant 3.696\;{\mathrm{mm}}\end{array}\right. $ | (13) |
本文基于响应面法对试验进行设计,以飞机尾喷和紫外线照射作为环境作用,探究了网格尺寸、砂率和细度模数三种因素对混凝土抗冻性能和耐磨耗性能的影响,并拟合得到了对于不同控制目标的响应面函数,最后基于响应面函数对混凝土配合比进行了优化。得到结论如下:
1)可使用响应面法对纤维网格布强化混凝土进行优化设计,二项式或三项式模型拟合效果较好,方差分析结果表明模型极为显著。
2)网格尺寸、砂率和细度模数都对玄武岩纤维网格布强化混凝土耐磨耗和抗冻性能有一定影响,其中网格布尺寸影响最大,其次是细度模数,最后是砂率。网格尺寸和砂率、网格尺寸和细度模数的交互作用较为明显,而砂率和细度模数的交互作用不够明显。
3)设置约束条件,依据所得四个模型,以四个控制目标总体最优为目标条件,对混凝土配合比进行了优化设计,当纤维网格布尺寸为3 mm×3 mm,砂细度模数为2.8,砂率为0.28~0.31时,强化混凝土性能最好。
4)本文仅对玄武岩纤维网格布进行了研究,且结论主要通过室内小试件试验所得,下一步还应开展多种纤维网格布对比研究以及足尺试验验证。
| [1] |
胡成, 翁兴中, 朱懋江, 等. 纤维网格布表层强化混凝土抗冻性能[J].
河海大学学报(自然科学版), 2021, 49(1): 84-92.
HU C, WENG X Z, ZHU M J, et al. Frost resistance performance of surface reinforced concrete with fiber mesh[J].
Journal of Hohai University (Natural Sciences), 2021, 49(1): 84-92.
|
| [2] |
朱懋江, 翁兴中, 高瑞, 等. 机场道面混凝土表面强化材料的性能研究[J].
山东农业大学学报(自然科学版), 2018, 49(2): 295-302.
ZHU M J, WENG X Z, GAO R, et al. Study on performance of reinforced concrete material for airport pavement[J].
Journal of Shandong Agricultural University (Natural Science Edition), 2018, 49(2): 295-302.
|
| [3] |
陈首, 石少卿, 肖颖杰, 等. 金属网增强混凝土抗低速冲击试验与数值模拟研究[J].
中国测试, 2021, 47(4): 136-143.
CHEN S, SHI S Q, XIAO Y J, et al. Experimental and numerical study on low speed impact resistance of metal mesh reinforced concrete[J].
China Measurement & Test, 2021, 47(4): 136-143.
|
| [4] |
李悦媛, 许巍, 张俊, 等. 纤维网格布表层强化混凝土的早期开裂特性[J]. 河海大学学报(自然科学版), 2022, 50(6): 114-122.
LI Y Y, XU W, ZHANG J, et al. Early cracking characteristics of concrete strengthened with fiber mesh[J]. Journal of Hohai University (Natural Sciences), 2022, 50(6): 114-122.
|
| [5] |
言兴. GRC网格布与聚丙烯砼复合加固短圆柱试验研究及理论分析[D]. 长沙: 湖南科技大学, 2018.
YAN X. Experimental study and theoretical analysis of short cylinder reinforced with GRC mesh and polypropylene concrete[D]. Changsha: Hunan University of Science and Technology, 2018.
|
| [6] |
丁一宁, 菅淑敏, 李冬. 玻璃纤维网格布的耐碱性能及其对混凝土板双向受弯性能的影响[J].
复合材料学报, 2019, 36(4): 954-963.
DING Y N, JIAN S M, LI D. Alkaline resistance of glass fiber meshes and its effect on biaxial flexural behavior of concrete slabs[J].
Acta Materiae Compositae Sinica, 2019, 36(4): 954-963.
|
| [7] |
封雷, 封叶, 王庆华. 玻璃纤维网格布增强复合保温墙板的保温性能和力学性能研究[J].
新型建筑材料, 2016, 3: 73-76.
FENG L, FENG Y, WANG Q H. Study on insulation and mechanical properties of the composite insulation wallboard reinforced by fiberglass mesh[J].
New Building Materials, 2016, 3: 73-76.
|
| [8] |
刘敬福, 徐平, 于英华. 玻璃纤维网格布增强聚合物矿物混凝土组分优化[J].
非金属矿, 2014, 37(5): 8-10.
LIU J F, XU P, YU Y H. Optimization of component in polymer mineral concrete reinforced by glass fiber mesh[J].
Non-Metallic Mines, 2014, 37(5): 8-10.
|
| [9] |
王庆轩, 丁一宁. 玄武岩纤维耐碱性能及其网格布对混凝土的增强效应[J].
建筑材料学报, 2021, 24(1): 54-62.
WANG Q X, DING Y N. Alkali resistance of basalt fiber and strengthening effect of its textile on concrete[J].
Journal of Building Materials, 2021, 24(1): 54-62.
|
| [10] |
廖瑜, 石少卿, 梁朝科, 等. 聚脲-编织玻璃纤维网格布复合材料加固钢板抗冲击力学性能研究[J].
兵工学报, 2018, 39(10): 1988-1996.
LIAO Y, SHI S Q, LIANG C K, et al. Dynamics performances of polyurea-woven fiberglass mesh composite reinforced steel plate subjected to shock waves[J].
Acta Armamentarii, 2018, 39(10): 1988-1996.
|
| [11] |
张勇超. 纤维网格布的耐腐蚀性及其对混凝土力学性能的影响[D]. 大连: 大连理工大学, 2016.
ZHANG Y C. Investigation on fiber mesh corrosion resistance and its effect on mechanical properties of concrete[D]. Dalian: Dalian University of Technology, 2016.
|
| [12] |
姜乐, 翁兴中, 李强, 等. 基于表面性能导向的机场道面混凝土最优配合比设计[J].
公路工程, 2017, 42(6): 94-99.
JIANG L, WENG X Z, LI Q, et al. Optimum mix retio design of airport pavement concrete based on surface performance oriented[J].
Highway Engineering, 2017, 42(6): 94-99.
|
| [13] |
LONG X, CAI L, LI W. RSM-based assessment of pavement concrete mechanical properties under joint action of corrosion, fatigue, and fiber content[J].
Construction and Building Materials, 2019, 197: 406-420.
DOI:10.1016/j.conbuildmat.2018.11.157 |
| [14] |
刘雪, 吴莉蔚, 杨勇, 等. 牦牛酸奶加工工艺参数优化及其品质分析[J]. 中国测试, 2023, 49(6): 68-74.
LIU X, WU L W, YANG Y, et al. The processing parameter optimization of yak yogurt and its quality analysis[J]. China Measurement & Test, 2023, 49(6): 68-74.
|
| [15] |
吴永根, 张泽垚, 刘庆涛, 等. 运用响应面法的无机聚合物混凝土性能分析[J].
空军工程大学学报(自然科学版), 2017, 18(3): 92-98.
WU Y G, ZHANG Z Y, LIU Q T, et al. Study on performance of inorganic polymer concrete based on response surface methodology[J].
Journal of Air Force Engineering University (Natural Science Edition), 2017, 18(3): 92-98.
|
 2024, Vol. 50
2024, Vol. 50