文章信息
- 李练兵, 康伟伟, 范辉, 梁纪峰, 曾四鸣
- LI Lianbing, KANG Weiwei, FAN Hui, LIANG Jifeng, ZENG Siming
- 改进VSG控制的储能系统并网优化策略
- Grid connected optimal strategy of energy storage system based on improved VSG control
- 中国测试, 2024, 50(6): 139-147
- CHINA MEASUREMENT & TEST, 2024, 50(6): 139-147
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022060020
-
文章历史
- 收稿日期: 2022-06-04
- 收到修改稿日期: 2022-08-05
2. 国网河北省电力有限公司,河北 石家庄 050000;
3. 国网河北省电力有限公司电科院,河北 石家庄 050000
2. State Grid Hebei Electric Power Co., Ltd., Shijiazhuang 050000, China;
3. State Grid Hebei ElectricPower Research Institute, Shijiazhuang 050000, China
可再生能源在人们生产生活中应用越来越广泛,传统变换器并网时不具备惯量、阻尼特性,对电网电压及频率难以支撑,电网调度作用发挥不到最优,从而引来一系列安全稳定问题,所以分布式电源友好并网的研究广受青睐。将并网变流器加入优化控制策略,增强控制的稳定性,与电网友好兼容,通过将VSG技术运用到并网中,其可以模拟同步发电机惯性、阻尼和下垂特性,也具备机电特性和电磁特性,使电力电子变换器性能更佳,并在风电、储能等分布式电源领域应用广泛[1-2]。将VSG控制技术运用到储能系统中,控制手段更为灵活,研究前景且应用价值颇好。而目前对储能系统并网的研究,多为逆变器并网时采用 PQ 控制,孤网时采用 VF 控制[3-4],这种方法利用电网的瞬时U/I来控制,动态性能较好,但其进行模式切换会产生较大暂态电压电流,且不易在调试时模拟该类问题,实验操作难度较大。文献[5]中分布式电源为主源,提出了微网内将各模块的频率协调控制,储能系统利用频率自适应器调节频率偏差,但缺乏惯量阻尼控制,系统鲁棒性较差,大功角时功率耦合严重。文献[6]提出了前馈自抗扰控制的车载储能系统协调控制策略,利用市电与柴油发电机(DG)配合,储能环节利用蓄电池电流与调频电流合成并网电流,该方式在并网上产生较大无功环流。文献[7]提出储能变流器为微源,DG并网采用PQ模式,当储能蓄电池 SOC 低于30%时调节DG转速,提高DG输出功率,并为蓄电池进行充电,维持储能UPS状态,然而增加通信线,线路产生干扰导致信号不稳定,降低了系统的可靠性。文献[8-11]通过采用VSG策略,使逆变器具备惯量阻尼特性,实现并网、孤岛转换,但在负载波动下算法同样存在频率偏移问题,暂态特性差。文献[12]利用虚拟同步机控制提高暂态性能指标的自适应扰动的控制参数计算方法,运用到电压源逆变器,并提出将频率阻尼加在有功功率环中,频率偏移得以补偿,但未形成闭环,仍然无法完全消除频率偏移。文献[13-14]建立虚拟同步机P-F、Q-U小信号模型,得出虚拟同步机并网系统的静态稳定问题,虚拟同步机控制方法中的转动惯量、下垂系数和系统阻尼等控制参数与同步发电机的参数不同,根据具体工况自适应调整,因此对VSG控制参数的灵活设置极为重要。然而目前这些研究都是针对 VSG 本体,缺乏对储能单元的考虑,不能真实模拟储能系统并网的真实运行情况,难以应对突发状况带来的影响,并且不便于控制算法开发和移植。文献[15]利用RT-LAB进行虚拟同步发电机控制程序以及硬件电路,突破客观实验条件的束缚,且解决硬件损坏等问题,对储能变流器的并网研究提供基础。
为了解决上述问题,本文提出一种将具有虚拟同步机特性的分布式逆变电源与储能系统相结合的方法,通过在VSG有功-频率环节加入前馈补偿,在无功-电压环节加入功角对无功的补偿,利用非线性变化惯性权重的改进PSO算法进行设计参数迭代求解得到控制参数的控制策略。解决由于功率差额带来的电网频率暂态扰动的问题,同时改善大功角时无功功率的动态响应,降低有功功率与无功功率的耦合。在Matlab中建立VSG储能系统仿真验证并网性能优化,并通过RT-LAB半实物仿真实验验证所提出控制策略的可行性和有效性。
1 控制基本原理分布式电源大规模运用到电力系统中,其带来的波动性和随机性对电网稳定运行造成了巨大的影响。在传统的电力系统中,由于同步发电机的控制,使转动惯量变化、系统频率波动、电压调节控制对并网性能造成影响,因此可以在分布式电源系统中增加带VSG控制策略的储能装置改善并网系统的稳定性。通过对分布式电源采取改进VSG的控制算法,使得分布式逆变电源从外特性上与同步发电机的频率和电压特性一致,同时具备惯量阻尼特性,并且将功角变化对无功环节的影响进行补偿,来实现良好并网,为模仿真实的储能系统,采用RT-LAB半实物实时仿真平台验证所提策略的有效性,见图1。

|
| 图 1 储能系统总控制框图 |
由光伏发电单元、蓄电池以及柴油发电机组成的储能并网系统,三者是整个系统的功率输入端,通过交错并联Boost升压至直流母线上,而储能装置主要作用是协调输入功率与负载功率的稳定,达到动态功率平衡。当系统中有功负荷发生变化时,不平衡的输入机械功率和电磁功率会带来系统频率波动,其主要由同步发电机机械惯性和阻尼引起的比较缓慢的状态,同步发电机通过频率的变化量调节输入的机械功率,也就是改变发电机的转速,使系统功率平衡,这是一次有差调频过程,还需要人为改变输入机械功率来将频率调整到额定值,即二次无差调节。同理,系统无功功率负载变化引起同步发电机进行励磁调节来体现系统电压变化调节,所以从这两个控制环节着手,进行优化,实现储能系统并网运行,主要解决有功功率变化对系统频率的影响以及功角变化对无功环节的作用,通过无功功率的变化对电压产生的影响构造控制器,计算储能系统功率缺额,补偿电压变化带来的干扰,提升电网频率暂态扰动时的支撑能力,改善大功角时无功功率的动态响应,降低有功功率与无功功率的振荡,利用RT-LAB半实物仿真实验平台来验证所提控制策略的稳定有效性,提升储能系统并网性能。
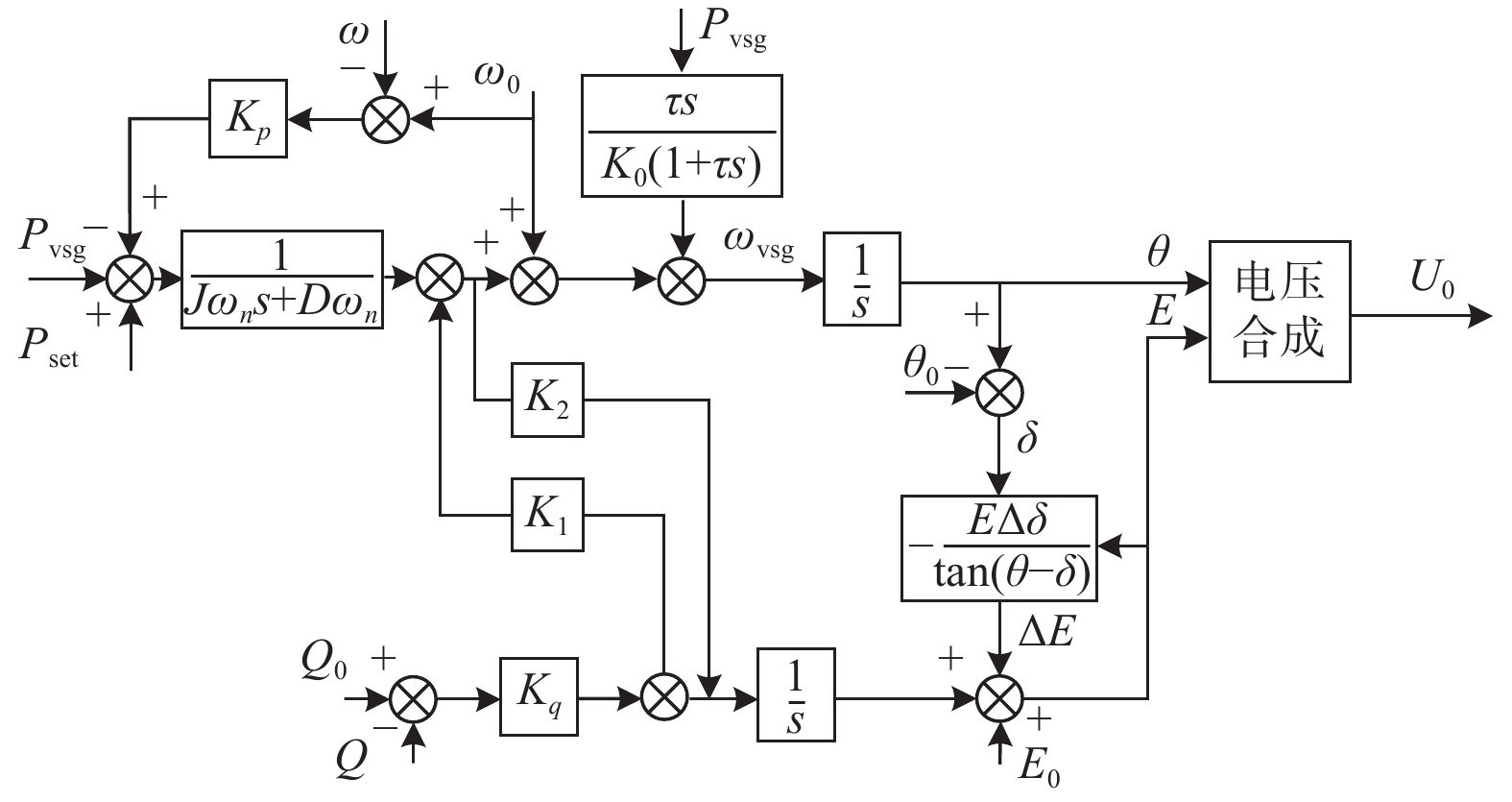
2 VSG的优化控制策略改进VSG优化控制总框图如图2所示。虚拟同步发电机较同步发电机的控制灵活性更高,暂态性能更佳。因此,在负载发生突变时,VSG可根据功率差额,抑制功率波动,完成电网频率的主动支撑,但电压的变化会对有功环节产生影响,频率的波动也会使有功功率和无功功率形成耦合,故分别在有功控制和无功控制环节上各增加一个补偿环节。通过对相关参数的设计,减少有功控制和无功控制环节中的干扰,从而抑制功率振荡。该方法的主要实现方式如下:
|
| 图 2 基于改进VSG控制总框图 |
| $ \omega=\frac{-K_{p} \Delta \omega+\Delta P}{J s \omega_{0}+D \omega_{0}}+\omega_{0}-K_{1}\left(U_{0}-U_{{\rm{e}}}\right) $ | (1) |
式中:
| $ U_{{\rm{m}}}=K_{q}\left(Q_{{\rm{ref}}}-Q\right)+U_{0}-K_{2}\left(\omega_{0}-\omega\right) $ | (2) |
式中:
通过补偿后在有功控制环节将负载波动功率作为输入量前馈至功率控制回路,进行功率前馈,实现VSG对电网频率的主动支撑,如图2所示。通过高通滤波器提取负荷扰动分量,将负荷扰动分量前馈至虚拟同步发电机的有功控制环节中,提高暂态响应能力,改善同步发电机的频率稳定性。
图中,
| $ \begin{split} {\omega _{{\text{vsg}}}}{\text{ = }}&{\omega _{\text{n}}} + \frac{{{P_{{\text{set}}}} + {K_{{p}}}({\omega _{\rm{n}}} - {\omega _{{\text{vsg}}}}) - {P_{{\text{vsg}}}}}}{{J{\omega _{\text{n}}}s + D{\omega _{\text{n}}}}} + \\ & \frac{{\tau s}}{{{K_0}\left( {1 + \tau s} \right)}}{P_{{\text{vsg}}}} - {K_1}({U_0} - {U_{\rm{e}}}) \end{split}$ | (3) |
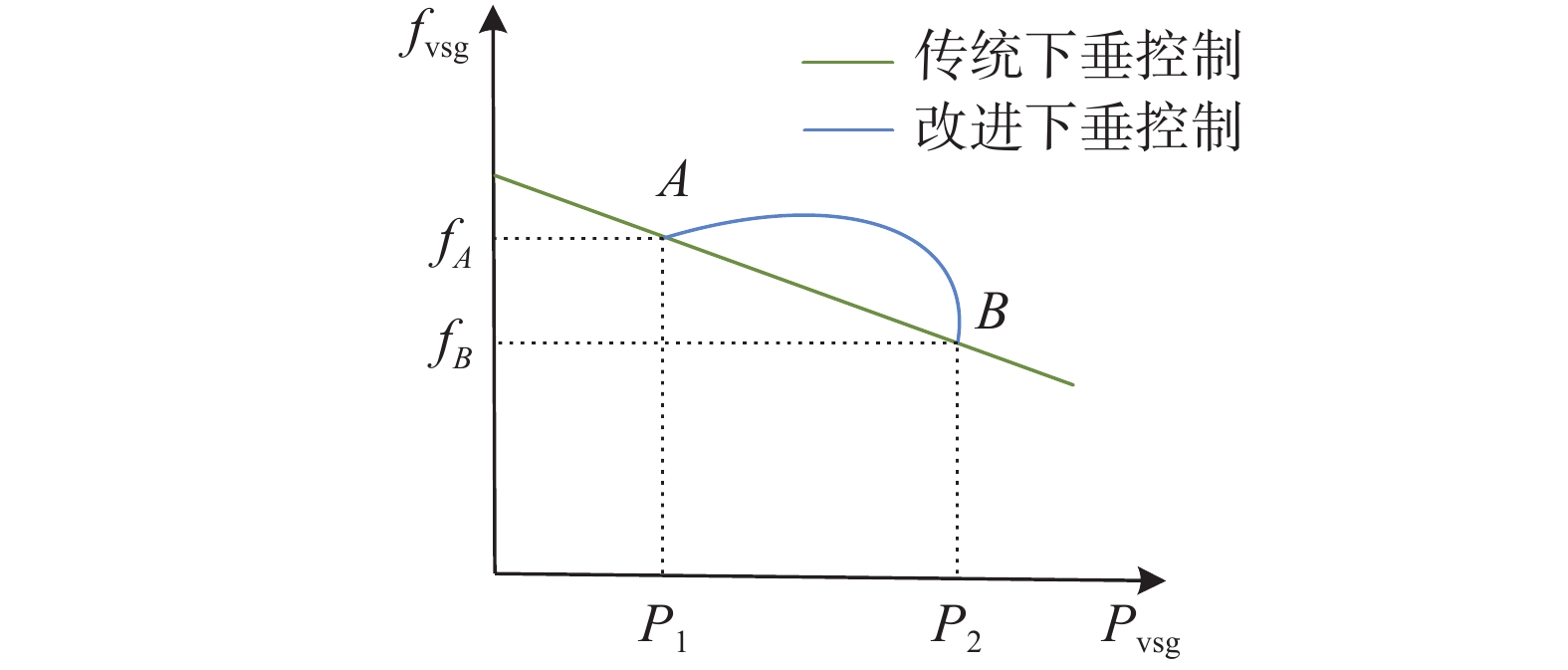
传统P-f下垂与所提主动频率支撑策略的频率输出特性对比如图3所示。
|
| 图 3 暂态过程中的频率输出特性 |
在图3中,当负载增加时,系统频率变化曲线由A点运行到B点,可以看出,改进控制策略的频率曲线在系统负载突变时更为平滑,表明所提主动频率支撑策略改变了暂态过程中的VSG频率输出特性,实现对电网频率的主动支撑。
由于负载波动造成功角的变化,从而使得无功功率发生振荡,需要对无功环节进行改进,由于逆变器的
| $ \left\{\begin{array}{l} \Delta P=-\dfrac{3 E U_{\rm{g}} \cos \delta}{X_{\rm{g}}} \Delta \delta+\dfrac{3 U_{\rm{g}} \sin \delta}{X_{\rm{g}}} \Delta E \\ \Delta Q=\dfrac{3 E U_{\rm{g}} \sin \delta}{X_{\rm{g}}} \Delta \delta+\dfrac{3 U_{\rm{g}} \cos \delta}{X_{\rm{g}}} \Delta E \end{array}\right. $ | (4) |
式中:
根据式(4)分别作关于

|
| 图 4 功角变化对功率耦合的影响 |
基于上述分析可知,相角对
| $ Q=Q_{0}+\Delta Q=Q_{0}+\frac{\partial Q}{\partial \delta} \Delta \delta+\frac{\partial Q}{\partial E} \Delta E $ | (5) |
其中
功率耦合就是当
| $ \Delta Q=\frac{\partial Q}{\partial \delta} \Delta \delta+\frac{\partial Q}{\partial E} \Delta E=0 $ | (6) |
将
| $ \begin{split} \Delta E = & -\dfrac{\dfrac{\partial Q}{\partial \delta}}{\dfrac{\partial Q}{\partial E}} \Delta \delta=-\dfrac{\dfrac{3 E U_{\rm{g}}}{Z_{\mathrm{g}}} \cos (\theta-\delta)}{\dfrac{3 U_{{\rm{g}}}}{Z_{\mathrm{g}}} \sin (\theta-\delta)} \Delta \delta= \\ &-\dfrac{1}{\tan (\theta-\delta)} E \Delta \delta \end{split} $ | (7) |
改进无功电压环节的VSG控制原理图如图2所示。当改变
在改进虚拟同步发电机控制策略中,要保证储能系统具有良好的动态特性和稳定性,参数

|
| 图 5 改进PSO算法流程图 |
在经典粒子群算法中,每个粒子都是该搜索区域的一个解,其速度代表征其运动快慢,位置表代表移动方向。粒子最初为搜索区域里的一系列随机解,每个粒子在其区域搜索最优解,将其存储,并将其优化效果与其他粒子进行比较取优。然后根据该解调整各自位置及速度。所以速度及位置更新速度方程可以表示为:
| $ \begin{split} {v_{ij}}(t + 1) =\;& {v_{ij}}(t) + {c_1}{r_1}\left( {x_{ij}^P(t) - {x_{ij}}(t)} \right)+ \\ \;& {c_2}{r_2}\left( {x_{gj}^G(t) - {x_{ij}}(t)} \right) \end{split}$ | (8) |
| $ {x}_{i j}({t}+1)={x}_{i j}({t})+{v}_{i j}({t}+1) $ | (9) |
在原有基础上增加了惯性权重,速度更新方程为:
| $ \begin{split} v_{i j}(t+1)= & w^{2} v_{i j}(t)+c_{1} r_{1}\left(x_{i j}^{P}(t)-x_{i j}(t)\right)+ \\ & c_{2} r_{2}\left(x_{gj}^{G}(t)-x_{i j}(t)\right) \end{split} $ | (10) |
当
| $ w=w_{\min }\left(\dfrac{w_{\min }}{w_{\max }}\right)^{t_{\max }^2\left(t_{\max }+K t\right)}+\dfrac{w_{\min }^2\left(\dfrac{1}{2}-c_3\right)}{K w_{\max }^2} $ | (11) |
式中:
根据计算可得改进PSO算法参数设置值,如表1所示。
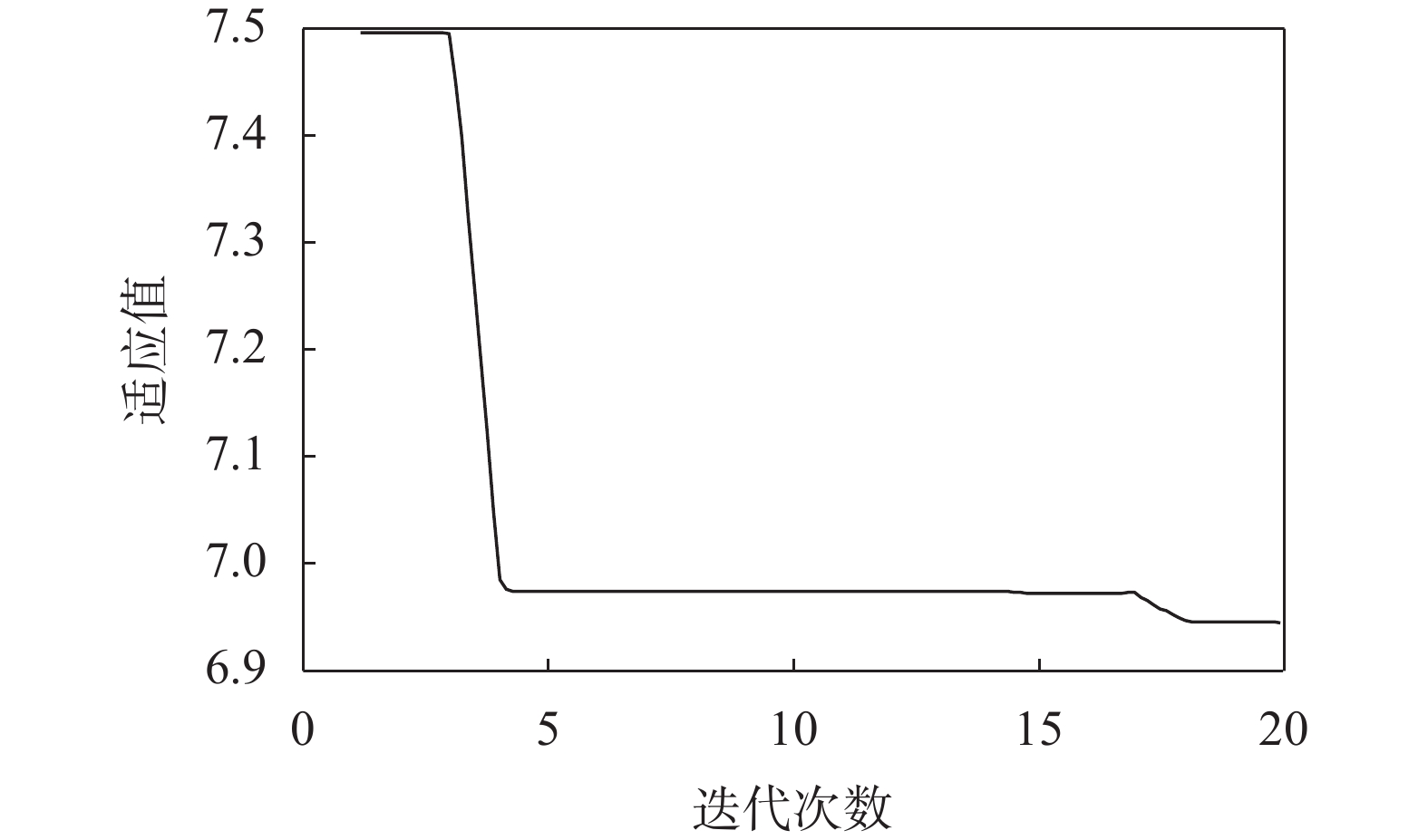
从图6中可以看出,运用改进PSO算法其适应值在迭代次数超过4代后有一个快速下降过程,之后便一直稳定在6.9832,直到迭代次数超过18 代后,适应值降低到6.8356。从仿真优化过程中可以得知,大于10次优化迭代内全局最优区域就能被快速找到。
|
| 图 6 适应值变化曲线 |
迭代优化结果如表2所示。
4 储能系统并网RT-LAB实验平台
为了验证改进VSG储能系统策略的有效性及动态性能,硬件系统主要由控制板和采样板组成,控制板和采样板通过排线连接。控制板采用以ARM为核心数字控制器的嵌入式开发板,主控芯片采用国产GD32F407ZET6,开关频率和采样频率均为10 kHz。采用三相三线制变流器带交流负载,储能电池采用160S5P-512V18AH-9.2kWh锂离子电池进行功率转换,控制板直流24 V由直流源提供,通过RS232进行上位机控制,利用电能质量分析仪观察实验波形。其中,储能模块、柴油发电机、三相全桥控制,储能装置、直流接触器,交流继电器、交流负载和大电网等主电路部分利用RT-LAB半实物仿真平台搭建,控制部分则利用VSG并网控制器来实现。首先在Matlab中建立VSG储能系统仿真,利用RT-LAB搭建半实物实验平台,搭建容量为50 kW的储能系统,分别采用Droop控制与改进VSG控制策略。实验平台及上位机监控界面如图7所示,实验参数如表3所示。

|
| 图 7 实验平台及上位机监控界面 |
| 参数 | 数值 | 参数 | 数值 | |
| 有功指令 | 0.5 p.u. | 无功指令值 | 0 p.u. | |
| 调速器比例 | 1/(2π) | 空载电压/V | 230 | |
| 虚拟阻尼 | 2 | 无功下垂系数 | 8 | |
| 虚拟惯量 | 0.2 | 逆变器侧滤波电感/mH | 500 | |
| 电流环比例系数 | 0.15 | 网侧滤波电感/mH | 300 | |
| 电流环积分系数 | 0.01 | 电网角频率/(rad·s–1) | 314 | |
| 电压环比例系数 | 0.2 | 角频率指令值/(rad·s–1) | 314 | |
| 电压环积分系数 | 0.02 | 线路等效电阻 |
1 | |
| 滤波电容/μF | 1200 | 功率基准值/kW | 50 |
VSG运行于并网模式下,通过改进VSG控制经过所提PSO算法计算得到参数值,0.3 s时VSG进入并网模式,0.5 s时Pm由10 kW变化为至25 kW,0.8 s时有功指令值Pm由25 kW阶跃至40 kW,并网有功功率、无功功率跟随指令值变化。
图8是加功率前馈补偿优化策略前后系统频率的变化图。由图可知,加入改进后的系统频率随负载波动是调节速度快,波动较小,暂态性能提升明显,Droop控制下系统频率波动较大,系统稳定性不足。
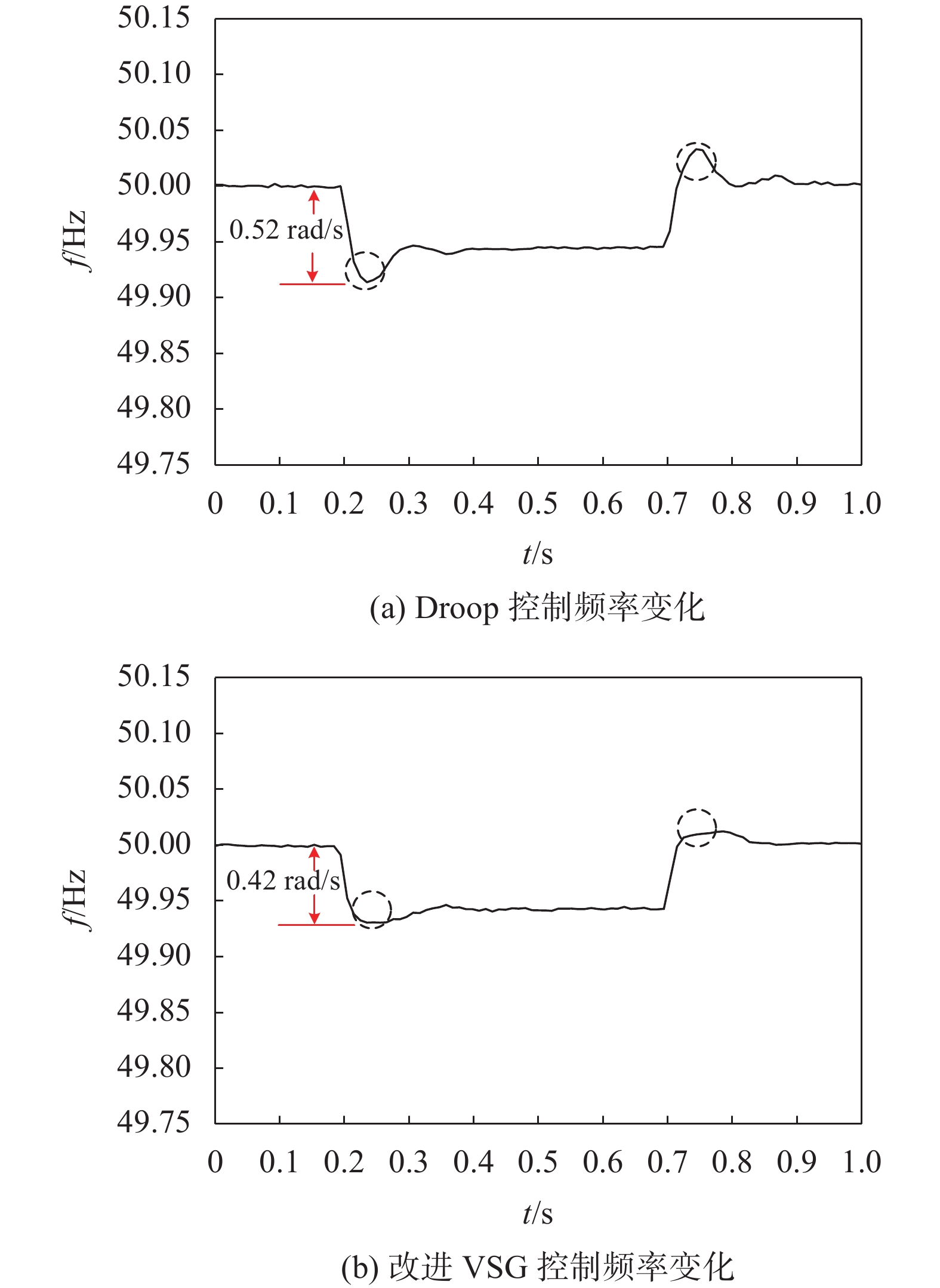
|
| 图 8 Droop/改进VSG控制频率变化 |
图9、图10是加入改进控制策略后,VSG输出电压、电流以及并网输出有功功率、无功功率图。可以看出,经过改进优化后,VSG输出电流波形良好,调节时间短,响应速度快,并网输出的有功功率无功功率波动小,均分精度高,并网功率随设定值变化,储能系统并网运行稳定。
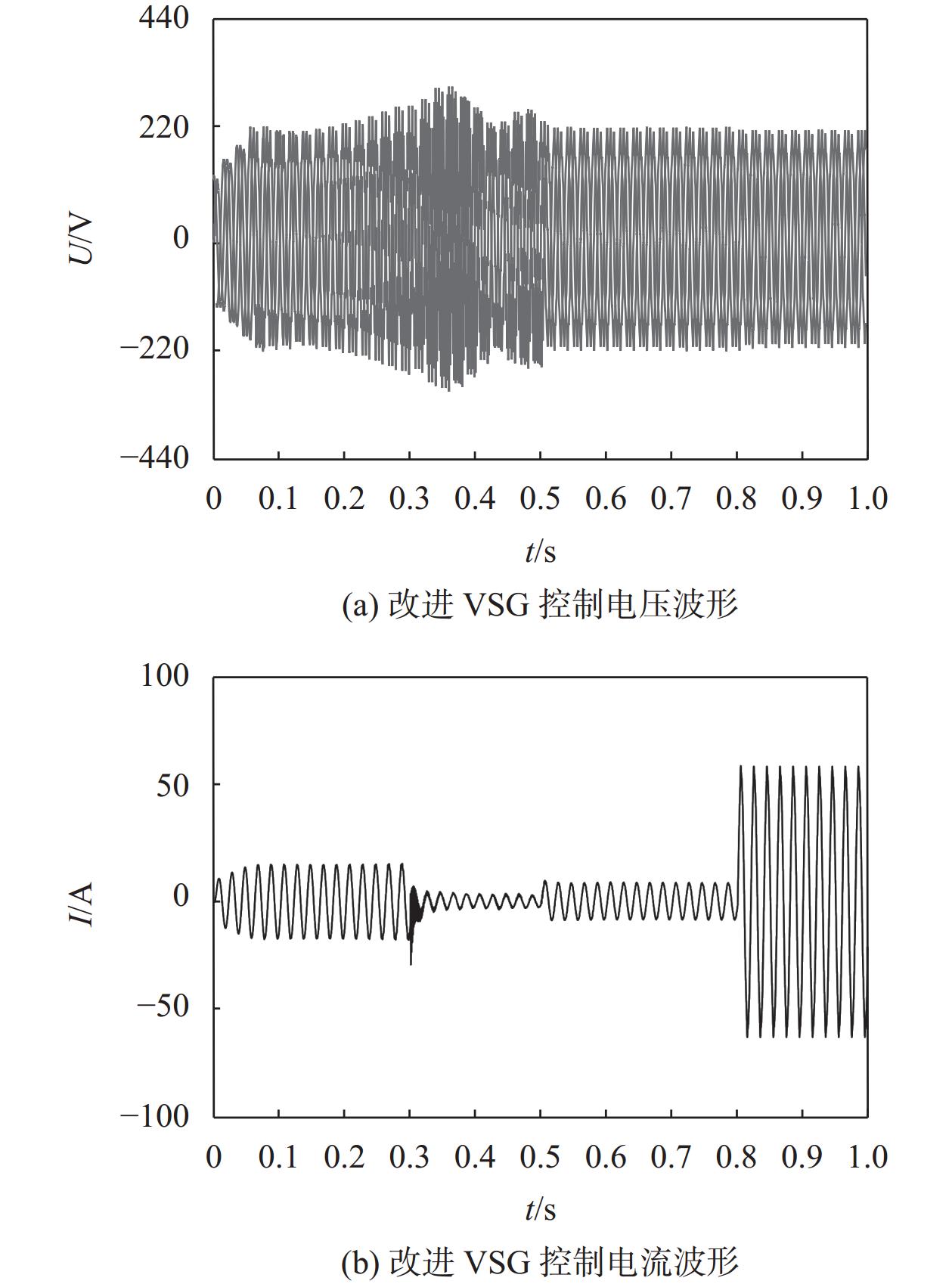
|
| 图 9 VSG电压电流波形 |
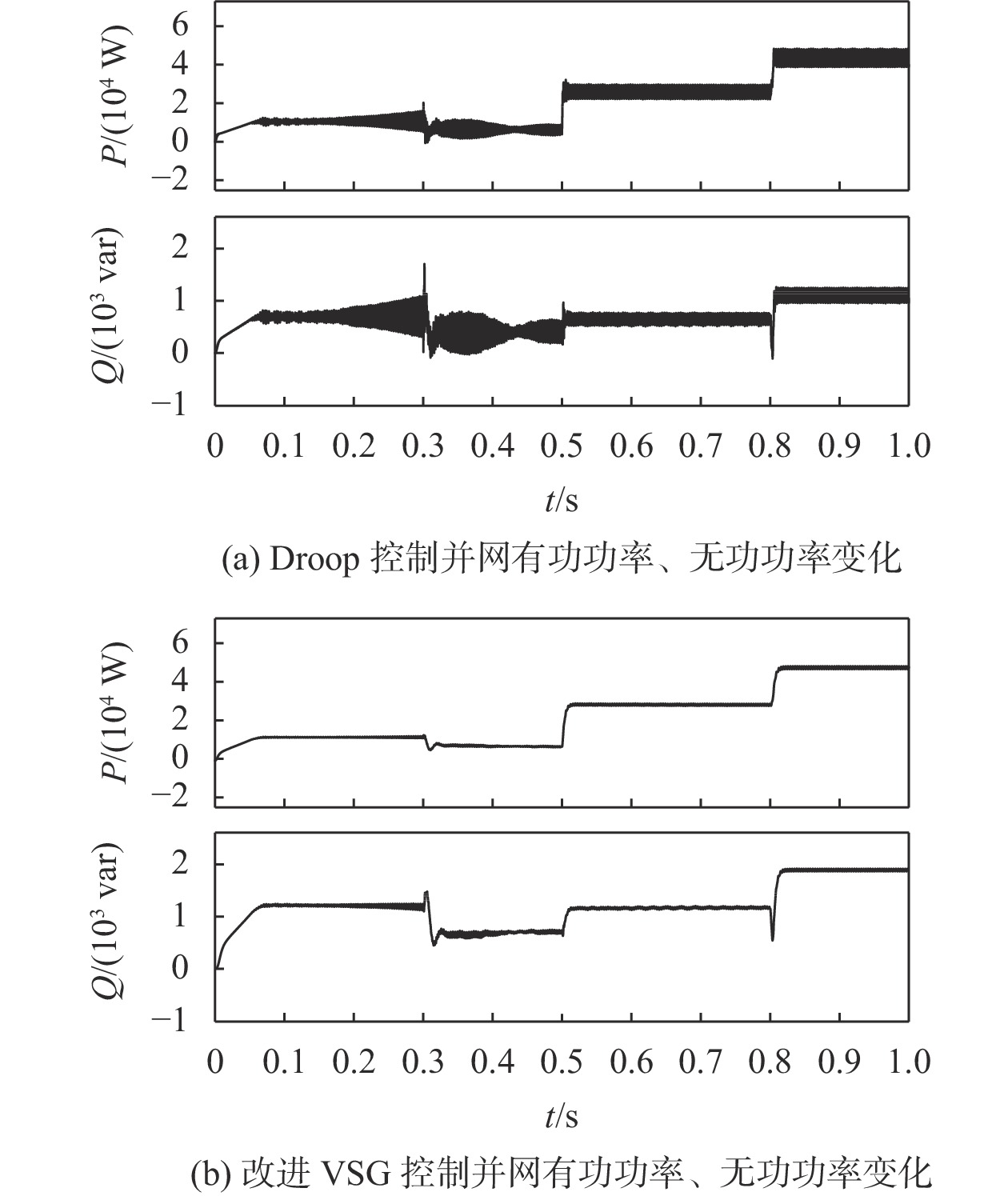
|
| 图 10 Droop/改进VSG控制并网有功功率、无功功率变化 |
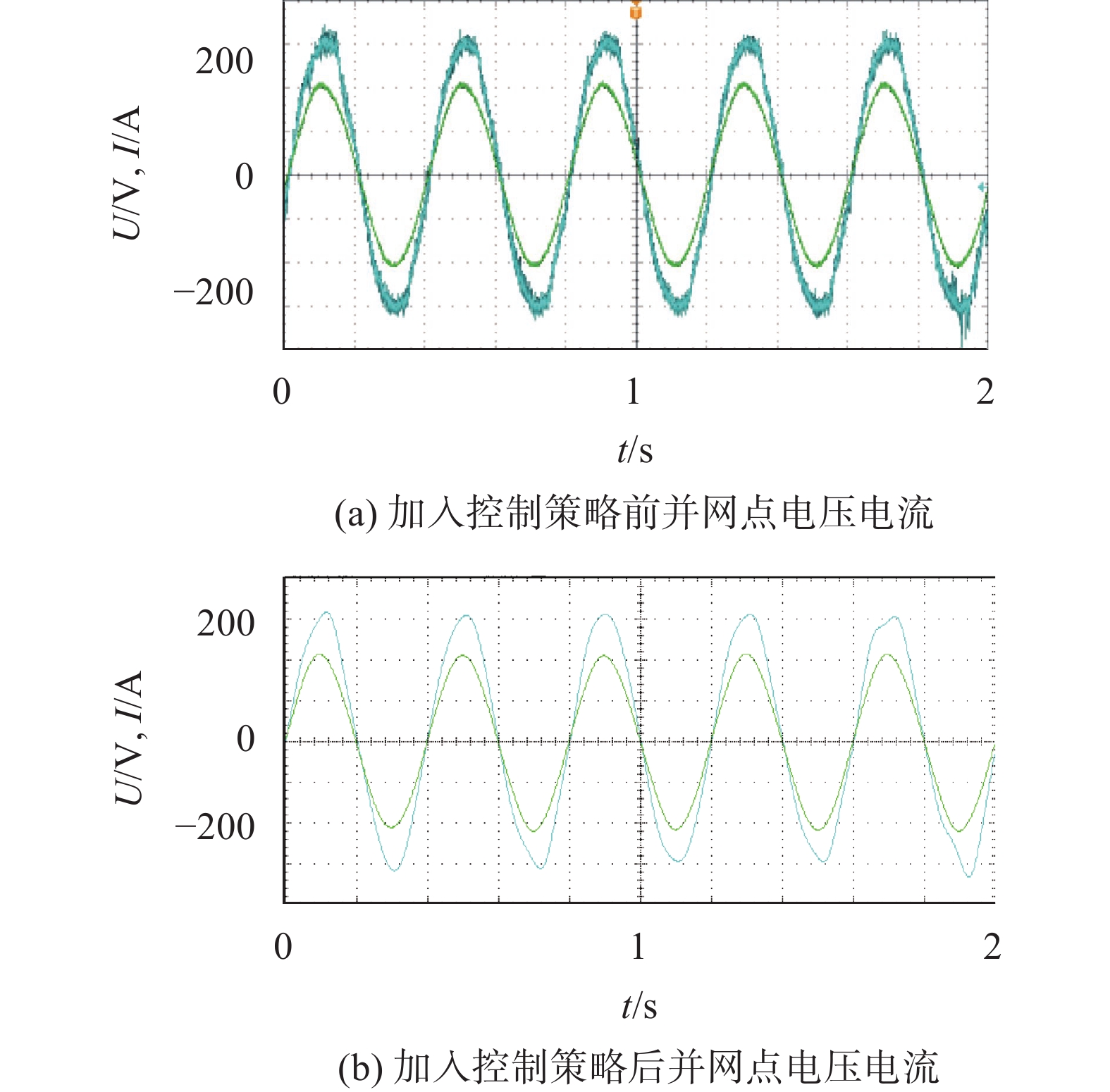
图11是加入控制策略前后直流母线电压波形。可知,加入改进VSG控制策略后,母线电压随负载增加跌落幅度减小,波形稳定。图12是加入控制策略前后输出电压电流波形,经过功角对无功功率的补偿,电网电压和并网电流同相,能够有效减少电网中无功功率的占比,提高电网的功率因数,有功功率和无功功率耦合度减少。图13为三相电压波形矢量图,可得出其幅值相位均较好。图14是加入控制策略前后并网点电压电流。加入控制策略后系统在负载波动时,并网电压电流波形良好,谐波减小,波形良好,并网性能提升。

|
| 图 11 加入优化控制策略前后母线电压 |

|
| 图 12 加入控制策略前后输出电压电流 |
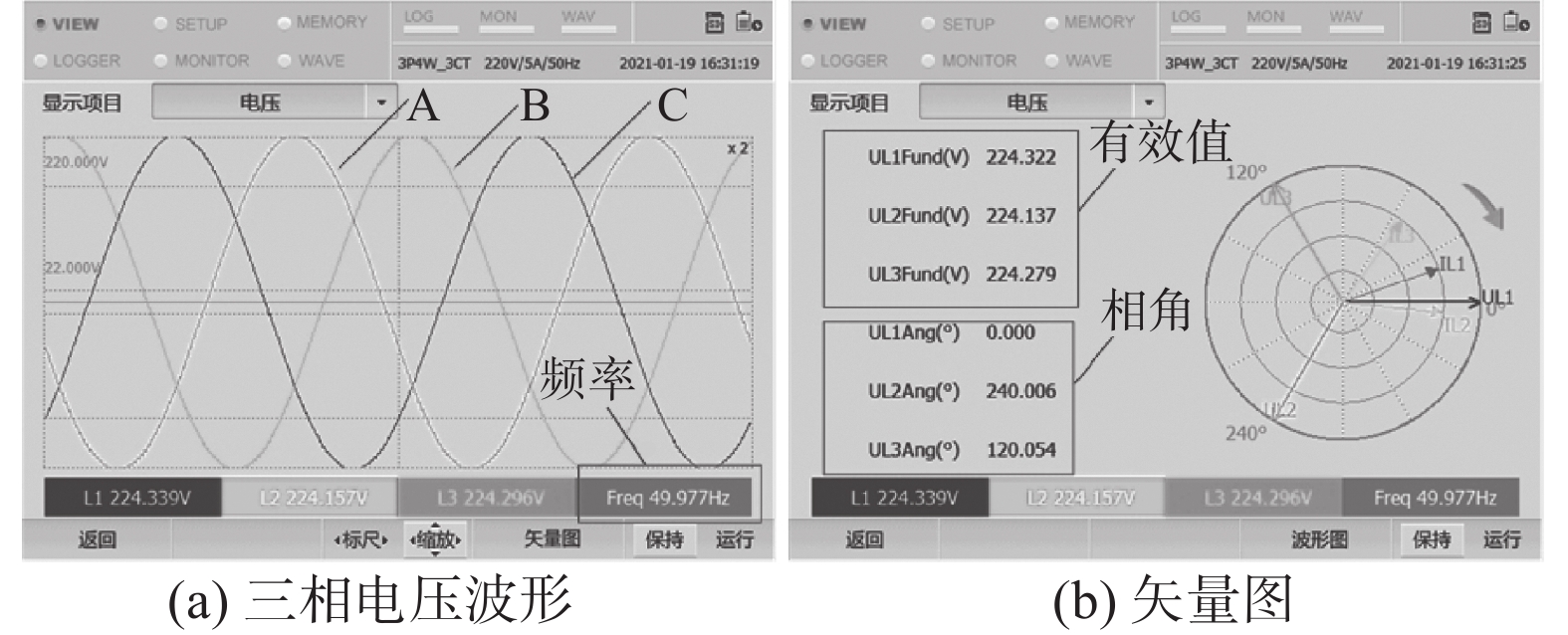
|
| 图 13 三相电压波形及矢量图 |
|
| 图 14 加入控制策略前后并网点电压电流 |
实验结果如表4所示,将具有虚拟同步机特性的分布式逆变电源与储能系统相结合的方法,通过在VSG有功-频率环节加入前馈补偿,计算功率缺额,补偿电压变化带来的干扰,在无功-电压环节加入功角对无功的补偿策略,提升电网频率暂态扰动时的支撑能力,改善大功角时无功功率的动态响应,降低功率的振荡,同时将频率波动对无功的影响利用补偿环节进行削弱,利用非线性变化惯性权重的改进PSO算法进行设计参数迭代求解进而并网性能得到了优化,并网电压电流波形良好,储能并网系统运行效果得到很好的提升。
5 结束语
根据储能系统同步发电机自身特性,降低了并网逆变器对电网频率的支撑能力,且功角变化对无功影响较大,造成功率振荡,提出改进VSG控制的储能系统并网优化控制策略。
1) 针对并网逆变器缺乏对电网频率的支撑的问题,提出在VSG有功-频率环节加入前馈补偿,计算功率缺额,提高电网频率系统暂态扰动时主动支撑能力。
2) 针对功角变化对无功功率影响较大,造成有功功率无功功率振荡,影响并网稳定性问题,提出在无功-电压环节加入功角对无功的补偿策略,提升电网频率支撑能力,改善大功角时无功功率的动态响应,降低
3) 利用非线性变化惯性权重的改进PSO算法进行设计参数迭代求解得到最优控制参数,在Matlab中建立VSG储能系统仿真验证并网性能优化,并通过RT-LAB硬件在环实验验证所提优化控制策略的可行性和有效性。
| [1] |
万晓凤, 詹子录, 廖志鹏, 等. 虚拟同步发电机并离网无缝切换策略研究[J].
电子测量与仪器学报, 2018, 32(5): 33-40.
WAN X F, ZHAN Z L, LIAO Z P, et al. Research on seamless switching strategy of virtual synchronous generator[J].
Journal of Electronic Measurement and Instrumentation, 2018, 32(5): 33-40.
|
| [2] |
李皓然, 王茜, 李怡萌, 等. 一种微网电压不平衡下虚拟同步发电机的控制方法[J].
电子测量技术, 2019, 42(11): 5-9.
LI H R, WANG Q, LI Y M, et al. Control method of virtual synchronous generator under microgrid voltage imbalance[J].
Electronic Measurement Technology, 2019, 42(11): 5-9.
|
| [3] |
王亚维, 刘邦银, 段善旭, 等. 虚拟同步控制的暂态特性优化策略研究[J].
中国电机工程学报, 2019, 39(20): 5885-5893.
WANG Y W, LIU B Y, DUAN S Y, et al. research on transient characteristic optimization of virtual synchronization generator control strategy[J].
Proceedings of the CSEE, 2019, 39(20): 5885-5893.
|
| [4] |
张继红, 冀伟成. 基于改进遗传算法的光伏系统储能优化配置[J].
中国测试, 2021, 47(1): 160-168.
ZHANG J H, JI W C. Optimal allocation of energy storage in photovoltaic system based on improved genetic algorithm[J].
China Measurement & Test, 2021, 47(1): 160-168.
DOI:10.11857/j.issn.1674-5124.2020070092 |
| [5] |
单锁兰, 谷志锋, 李宏城, 等. 混合储能系统分散自适应强扭曲虚拟阻抗控制[J].
中国测试, 2021, 47(1): 127-132.
SHAN S L, GU Z F, LI H C, et al. Decentralized adaptive super-twisting virtual impedance control for hybrid energy storage system[J].
China Measurement & Test, 2021, 47(1): 127-132.
|
| [6] |
刘志坚, 李晓磊, 梁宁, 等. 基于前馈自抗扰控制方法的蓄电池储能控制策略[J].
电机与控制应用, 2020, 47(6): 97-102.
LIU Z J, LI X L, LIANG N, et al. Battery energy storage control strategy based on feedforward active disturbance rejection control method[J].
Electric Machines & Control Application, 2020, 47(6): 97-102.
DOI:10.12177/emca.2020.034 |
| [7] |
KIM Y S, KIM E S, MOON S I. Frequency and voltage control strategy of standalone microgrids with high penetration of intermittent renewable generation systems[J].
IEEE Transactions on Power Systems, 2016, 31(1): 718-728.
DOI:10.1109/TPWRS.2015.2407392 |
| [8] |
LI Z, JIA X. An improved VSG control strategy based on the amplitude-frequency characteristics of virtual power[J].
IEEE Access, 2019, 7: 101096-101105.
DOI:10.1109/ACCESS.2019.2930623 |
| [9] |
阳建, 刘勇, 盘宏斌, 等. 基于虚拟同步机的微网逆变器无频差控制[J].
电网技术, 2016, 40(7): 2001-2008.
YANG J, LIU Y, PAN H B, et al. Method of frequent deviation-free control of microgrid inverter based on virtual synchronous generator control[J].
Power System Technology, 2016, 40(7): 2001-2008.
|
| [10] |
胡超, 张兴, 石荣亮, 等. 独立微电网中基于自适应权重系数的VSG协调控制策略[J].
中国电机工程学报, 2017, 37(2): 516-525.
HU C, ZHANG X, SHI R L, et al. VSG coordinated control based on adaptive weight factors in islanded microgrids[J].
Proceedings of the CSEE, 2017, 37(2): 516-525.
DOI:10.13334/j.0258-8013.pcsee.160834 |
| [11] |
党克, 郑玉浩, 严干贵. 电网电压不平衡下光伏并网逆变器的同步技术[J].
仪器仪表学报, 2015, 36(1): 87-94.
DANG K, ZHENG Y H, YAN G G. Synchronization technique of grid-connected PV inverter under unbalanced grid voltage[J].
Chinese Journal of Scientific Instrument, 2015, 36(1): 87-94.
|
| [12] |
颜湘武, 张伟超, 崔森, 等. 基于虚拟同步机的电压源逆变器频率响应时域特性和自适应参数设计[J]. 电工技术学报, 2021, 36: 241-254.
YAN X W, ZHANG W C, CUI S, et al. Frequency response characteristics and adaptive parameter tuning of voltage-sourced converters under VSG control[J]. Transactions of China Electrotechnical Society, 2021, 36: 241-254.
|
| [13] |
LIU J, MIURA Y, BEVRANI H, et al. Enhanced virtual synchronous generator control for parallel inverters in microgrids[J].
IEEE Transactions on Smart Grid, 2017, 8(5): 2268-2277.
DOI:10.1109/TSG.2016.2521405 |
| [14] |
曹昕鸷, 韩珏. 新能源虚拟同步机多参量自适应控制策略[J].
电力电子技术, 2022, 56(3): 43-46.
CAO X Z, HAN J. Multi-parameter adaptive control strategy for new source virtual synchronous generator[J].
Power Electronics, 2022, 56(3): 43-46.
|
| [15] |
王彩冉. 基于硬件在环的虚拟同步机并/离网控制研究[D]. 北京: 北京交通大学, 2018.
WANG R C. Hardware-in-loop-based research on virtual synchronous generator under connected and off grid states[D]. Beijing: Beijing Jiaotong University, 2018.
|
 2024, Vol. 50
2024, Vol. 50