文章信息
- 谢文举, 薛贵军, 史彩娟, 李水清
- XIE Wenju, XUE Guijun, SHI Caijuan, LI Shuiqing
- 基于遗传粒子群优化的热负荷预测方法
- Heat load prediction method based on genetic particle swarm optimization
- 中国测试, 2024, 50(6): 131-138, 147
- CHINA MEASUREMENT & TEST, 2024, 50(6): 131-138, 147
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022080128
-
文章历史
- 收稿日期: 2022-08-24
- 收到修改稿日期: 2022-11-24
2. 华北理工大学智能仪器厂,河北 唐山 063210;
3. 华北理工大学人工智能学院,河北 唐山 063210
2. Instrument Factory, North China University of Technology, Tangshan 063210, China;
3. College of Artificial Intelligence, North China University of Technology, Tangshan 063210, China
近些年,随着人民生活水平持续提升,工业水平的不断发展,我国能源消耗剧烈增加。其中能源带来的环境问题也逐渐显现出来,特别是北方冬季地区雾霾严重的问题饱受国内外争议。集中供热作为北方普遍的供热手段,其主要供热方式仍然采用消耗煤炭能源来获得热量。根据相关研究发现,能源消耗与环境之间存在很大关联[1],因此提高能源利用率,早日实现碳达峰对减少环境污染具有重大意义。
由于不同时间段的用热习惯差异,供热负荷呈现非线性、时变性、时滞性等特点,当热用户需求产生大量变化时,需对一次网供水热量进行合适的调节,才能满足换热站与二次网的热量交互。供热负荷预测技术的发展大致可以分为三个阶段:第一阶段主要采用热能相关知识以及统计模型来进行预测;文献[2]结合环境因素构建了基于递归最小二乘的热负荷预测方法。基于统计模型的热负荷预测模型具有计算简单、解释性好的优点,但是对数据要求非常苛刻,需要提供大量连续的热负荷数据来进行拟合,且对异常数据非常敏感,泛化性能较差;第二阶段随着机器学习的兴起,供热负荷预测主要采用热负荷数据与机器学习相结合进行建模。文献[3]根据天气影响因素和历史热负荷数据对供热系统二次网热负荷进行了建模,提出了基于热传递搜索以及果蝇优化算法的广义回归神经网络。以上学者所提的模型都是基于神经网络的热负荷预测模型,在数据集较少的情况下,有着速度快,精度高的特点。但人工神经网络预测模型属于浅层神经网络,在复杂特征提取以及模型参数确定上具有一定挑战,且人工神经网络少有考虑热负荷数据在时间序列上的特征相关性;第三阶段在大数据与人工智能的驱使下,深度学习在热负荷预测中更为高效、精准。文献[4]针对供热负荷时间规律,建立了基于长短时记忆网络(long short-term memory,LSTM)的居民短时供热负荷预测模型,实验结果表明基于居民短时供热负荷的LSTM模型相比自回归积分滑动平均模型(autoregressive integrated moving average model,ARIMA)以及支持向量回归(support vector regression,SVR),在时间序列特征提取中拥有更好的表现力。文献[5]提出了利用卷积神经网络(convolutional neural networks,CNN)与LSTM网络相结合的网络预测模型,实验表明CNN层与LSTM相结合,能够有效提高不同变量之间的相关性的同时,还能考虑时间序列所带来的影响,且变量的选取与最后预测结果有很大的影响关系。但CNN-LSTM网络参数难以确定,不同参数对最后的预测结果都有所不同。虽然以上学者都对热负荷时间序列进行研究和探讨,但是供热系统仅仅考虑时间上所带来的影响是远远不够的。
目前,集中供热负荷预测研究主要集中于天气影响因素以及换热站至二次网热负荷预测研究颇多[2-4],而针对换热站内部自身影响因素以及一次网热负荷预测文章较少。同时对于模型参数的选择,大多数都是鉴于主观意识的判别,无法考虑到参数不同对热负荷预测的影响结果。针对以上不足,本文提出了一种基于GAPSO优化的CNN-BiLSTM模型。一方面,GAPSO优化算法可以针对CNN-BiLSTM网络结构参数进行寻优,减少人为主观判断带来的偏差。另一方面,采用CNN-BiLSTM网络模型,不仅能够提取供热负荷影响因素上的空间特征,而且还能提取供热负荷上的时间序列特征,从而实现提高供热负荷预测精度。对于供热负荷数据,呈现非平稳性、非线性、时滞性等特点,本文提出了CEEMDAN-SE的分解方法,从而实现降低供热负荷序列复杂性,减少由分解过多所带来的时间损耗,并对不同分解情况下的预测结果进行探讨与研究。
1 CEEMDAN-SE原理与方法 1.1 CEEMDAN分解CEEMDAN是在经验模态分解(empirical mode decomposition,EMD)与集合经验模态分解(ensemble empirical mode decomposition,EEMD)的基础上改进而来的,能够在挖掘不同尺度历史特征的同时,又保持原始数据的特性。此类方法常用于解决非线性和非平稳数据的问题如:故障诊断、经济数据预测、图像处理等领域[6-7]。由于EMD分解容易出现模态混叠现象,Huang等人在EMD分解的基础上提出了EEMD的方法,通过在原始数据中添加白噪音,使其降低原始数据的信噪比,从而解决了模态混叠的问题。但EEMD并无法完全消除添加的白噪音,从而导致原始特征信息出现偏差。为了解决白噪声无法消除的问题,Torres等[8]人提出了CEEMDAN分解,通过引入额外的信噪比来压制噪声水平,与EMD、EEMD相比CEEMDAN特征提取更为准确,分解效率更高。供热负荷的CEEMDAN具体分解步骤如下[9]:
设供热负荷原始序列为f(t),IMFk(t)为第k次时CEEMDAN分解的结果,EMDj(t)为第j次的EMD分解的结果。
1)在原始序列f(t)添加信噪比为ε0的白噪音ωi(t)如式(1)所示,将得到的数据用于第一次分解。
| $ {f^i}(t) = f(t) + {\varepsilon _0}{\omega ^i}(t),i = 1,2,3,\cdots ,n $ | (1) |
式中,f i(t)为添加白噪音后的原始序列。
2)利用EMD对step1中f i(t)进行n次分解,根据公式(2)计算其均值,其结果作为第一次CEEMDAN的分量,之后根据公式(3)计算出残差分量r(t)。
| $ {\overline {{\mathrm{IMF}}} _1}(t) = \frac{1}{n}\sum\limits_{i = 1}^n {{\mathrm{IMF}}_1^i(t) = \frac{1}{n}{\mathrm{EM}}{{\mathrm{D}}_1}} ({f^i}(t)) $ | (2) |
| $ {r_1}(t) = f(t) - {\overline {{\mathrm{IMF}}} _1}(t) $ | (3) |
式中:
EMD1(f i(t))——对f i(t)进行第一次EMD分解;
r1(t)——第一次分解后的剩余残差分量。
3)在第一次的残差分量r1(t)中添加自适应白噪音,再以新的序列为基准进行EMD分解并求均值得到第二次的CEEMDAN分量如公式(4)所示,根据公式(5)计算出第二次残差分量r(t)。如此类推进行CEEMDAN分解直至残差分量满足终止条件。
| $ {\overline {{\mathrm{IMF}}} _2}(t) = \frac{1}{n}\sum\limits_{i = 1}^n {{\mathrm{EMD}}{}_1({r_1}(t) + {\varepsilon _1}{\mathrm{EM}}{{\mathrm{D}}_1}({\omega ^i}(t))} $ | (4) |
| $ {r_2}(t) = {r_1}(t) - {\overline {{\mathrm{IMF}}} _2}(t) $ | (5) |
式中:
r2(t)——第二次分解后的剩余残差分量。
1.2 样本熵原理样本熵是由学者Richman和Moorman基于近似熵改进而来的,样本熵利用计算总和对数减少近似熵误差[10]。样本熵已在时间序列复杂程度评估中被广泛使用,样本熵数值越大,时间序列复杂程度越高。样本熵具体步骤如下:
1)设时间序列Xm表达式如公式(6)所示,其中N表示序列个数,m表示数据长度。
| $ {{\boldsymbol{X}}}_{m}(i) = [x(i),x(i+1),\cdots ,x(i+m-1)]\text{,}i = 1,2,\cdots ,N-m+1 $ | (6) |
2)计算向量Xm(i)与Xm(j)之间最大距离Lm。
| $ \begin{split} {{\boldsymbol{L}}_m}[{{\boldsymbol{X}}_m}(i),{{\boldsymbol{X}}_m}(j)] =& \max [{{\boldsymbol{X}}_m}(i + k) - \\ & {{\boldsymbol{X}}_m}(j + k)],0 \leqslant k \leqslant m - 1 \end{split}$ | (7) |
3)设定给定阈值r,计算Lm[Xm(i), Xm(j)]≤r与Lm+1[Xm+1(i), Xm+1(j)]≤r的个数,分别记为vm和wm+1,则m个点的匹配率与m+1个的点的匹配率可表示为:
| $ {{{A}}^m}(r) = \frac{1}{{n - m}}\sum\limits_{i = 1}^{n - m} {\frac{1}{{n - m + 1}}} {w^{m + 1}}(i) $ | (8) |
| $ {{{B}}^m}(r) = \frac{1}{{n - m}}\sum\limits_{i = 1}^{n - m} {\frac{1}{{n - m + 1}}} {v^m}(i) $ | (9) |
4)最后样本熵表达式可表示为:
| $ {\mathrm{SampEn}}(m,r) = \mathop {\lim }\limits_{n \to \infty } \left( - \ln \frac{{{{{A}}^{{m}}}(r)}}{{{{{B}}^{{m}}}(r)}}\right) $ | (10) |
式中,m与r为样本熵参数,根据文献[7]中的研究成果并进行反复实验,本文样本熵参数m=1,r=0.2std,计算的样本熵具有更好的特征。
2 GAPSO-CNN-BiLSTM热负荷预测模型 2.1 遗传粒子群优化算法粒子群(particle swarm optimization,PSO)与遗传算法算法(genetic algorithm,GA)都属于自然生物群智能算法的范畴。PSO算法通过不断更新局部最优和全局最优粒子,保留局部和全体最优信息,收敛速度快,但容易陷入局部最优。GA算法通过对粒子进行交叉变异操作,丰富种群多样性,避免过早成熟现象。根据GA与PSO算法各自优缺点,引入共同进化概念构建GA-PSO优化算法,改变传统寻优方式避免陷入局部最优和早熟收敛的缺陷[11],算法流程图如图1所示,GAPSO优化的CNN-BiLSTM具体步骤如下。

|
| 图 1 GAPSO-CNN-BiLSTM算法流程 |
1)初始化杂交概率pc、变异概率pm、学习率范围、BiLSTM隐含层神经元个数等参数。
2)搜寻全局最优和个体最优,根据目标函数计算适应度值fitness。目标函数公式如下:
| $ {\mathrm{fitness}}{\text{ = }}\sqrt {\frac{{\text{1}}}{n}{{({{{y}}_{{\mathrm{hat}}}} - {{y}})}^2}} $ | (11) |
式中:n——样本长度;
yhat——仿真数据;
y——真实数据。
3)根据粒子适应度将粒子分为优势粒子和劣势粒子两类,保留优势粒子进入下一代。
4)在优势粒子中随机挑选两个粒子进行交叉,更新粒子速度与位置。
5)在交叉完的粒子中随机选择两个粒子进行变异。
6)更新变异后粒子的适应度值、全局最优、个体最优。
7)判断是否达到要求,达到输出最优参数,反之返回步骤2)。
2.2 CNN层在很多的研究工作中都有强调CNN网络拥有强大的特征捕捉能力和复杂函数的逼近能力[12-13],它将高维输入数据映射为局部特征并组成关系更为紧密的低维特征。CNN网络主要由卷积层、池化层、全连接层共同组成,算法主要核心是卷积操作,其作用是生成特征映射,防止数据过拟合。池化方式一般选用最大池化,在起到降低数据维度的同时还不改变数据特征映射结构。
2.3 BiLSTM层LSTM是一种改进的递归神经网络[13],常用于解决RNN在长时间输入数据间隔中,容易造成梯度消失所使用的方法。LSTM主要由输入门、遗忘门、输出门共同组成,其数学表达式如下所示:
| $ f_{t}=\operatorname{sigmoid}\left(W_{f} \times\left[h_{t-1}, x_{t}\right]+b_{f}\right) $ | (12) |
| $ \bar{L}_{t}=\operatorname{sigmoid}\left(W_{i} \times\left[h_{t-1}, x_{t}\right]+b_{i}\right) $ | (13) |
| $ g_{t}=\tanh \left(W_{g} \times\left[h_{t-1}, x_{t}\right]+b_{g}\right) $ | (14) |
| $ C_{t}=\left(C_{t-1} \otimes f_{t}\right) \oplus\left(g_{t} \otimes \bar{L}\right) $ | (15) |
| $ O_{t}=\operatorname{sigmoid}\left(W_{o} \times\left[h_{t-1}, x_{t}\right]+b_{o}\right) $ | (16) |
| $ h_{t}=\tanh \left(C_{t}\right) \otimes O_{t} $ | (17) |
式中,Wf、Wi、Wg、bf、bi、bg为遗忘门、输入门、临时细胞状态的权重和偏置。
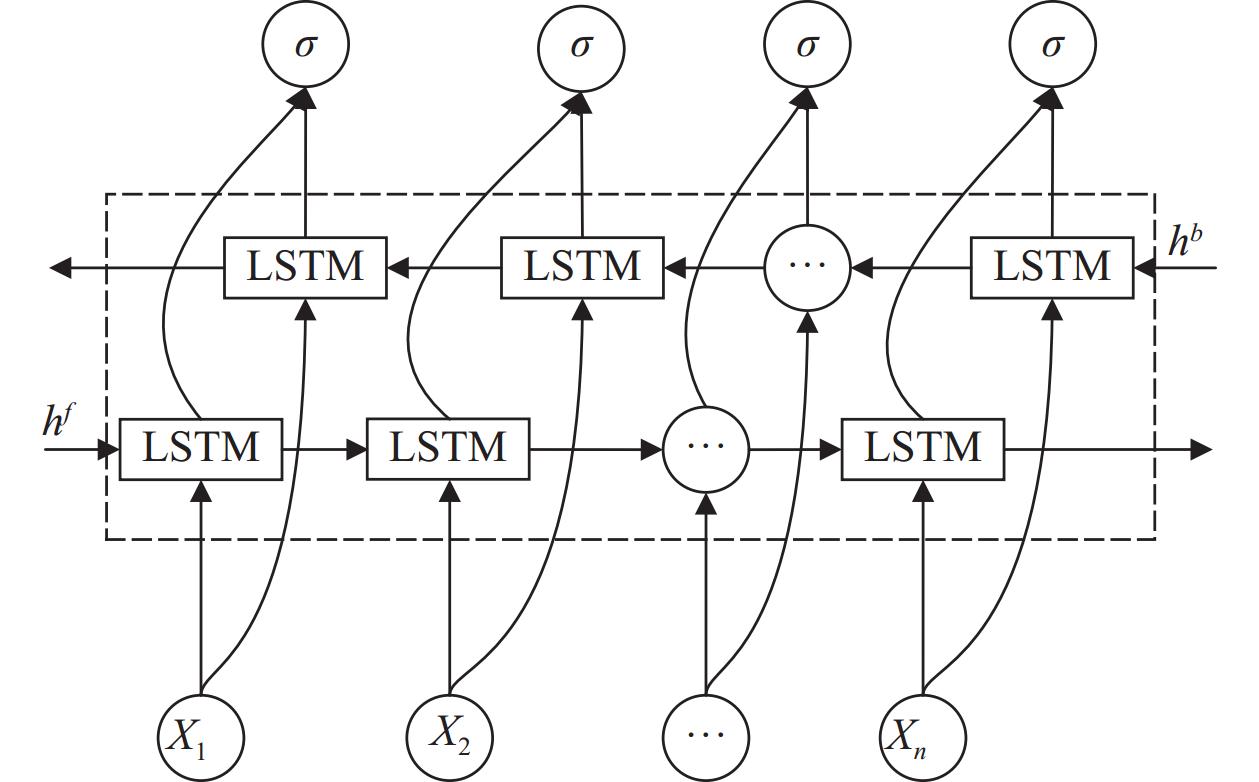
如图2所示,为了增强传统LSTM的学习能力和泛化能力,BiLSTM引用双向处理的网络结构,在LSTM隐含层的基础上增加前后通道,通过对前后通道隐含层的加权拼接获取额外的前后时间关联信息[14]。BiLSTM隐含层数学表达式如下所示:
|
| 图 2 BiLSTM结构图 |
| $ {h_t} = \alpha h_{}^f + \beta h_{}^b $ | (18) |
| $ {y_t} = \sigma ({h_t}) $ | (19) |
式中:α——向前因子;
β——向后因子,且α+β=1;
hf——向前隐含层加权求和;
hb——向后隐含层加权求和。
2.4 GAPSO-CNN-BiLSTM预测模型GAPSO-CNN-BiLSTM模型主要由CEEMDAN-SE与GAPSO-CNN-BiLSTM两个模块共同组成。首先,针对供热负荷复杂序列进行CEEMDAN分解,并根据样本熵评估每一条序列复杂程度,将复杂程度相近的序列进行二次重组构成GAPSO-CNN-BiLSTM网络输入。其次,利用CNN卷积层对多维度数据进行特征卷积,将高维数据汇集成较低的一维输数据,再利用池化层进一步降低数据复杂程度,增加数据特征多样性。最后,将输出的一维数据输入至BiLSTM层,并利用GAPSO优化算法对BiLSTM超参数进行寻优。CNN在负荷预测中起到捕捉短期固有特征的作用,BiLSTM有效保存前后时间序列关联,避免长时间序列所造成的梯度消失。图3为GAPSO-CNN-BiLSTM模型框架图。

|
| 图 3 GAPSO-CNN-BiLSTM模型框架 |
3 算例分析 3.1 模型参数设置及评价标准
根据在河北唐山地区换热站2021年1月1日至2021年1月8日提供的历史供热负荷数据,以每10 min为采样频率进行采样,一共采样1148个数据点,前1004个数据样本作为训练数据,后144个点作为检测模型准确率。首先将换热站一次网历史洪流流量、供水温度、供水回温、供水压力、供水回压,全部归一化作为网络特征输入,保证数据在同一参考范围之内,其次利用CEEMDAN将原始序列进行分解,并利用SE对相似复杂度的进行合并,降低网络复杂程度。最后根据预测不同的子分量,还原合并出预测值。GAPSO-CNN-BiLSTM网络参数经过多次尝试后确定为表1中所示。当PSO学习因子c1、c2均为1.5,杂交概率pc与变异概率pm分别为0.5与0.05时,CNN-BiLSTM具有较好的拟合效果。在实验中为了公平对比不同模型之间的差异,选用均方根误差(root mean squared error,RMSE)、平均绝对误差(mean absolute error,MAE)、均方误差(mean squared error,MSE)以及决定系数r2作为评判标准。其评价指标公式如式下所示。
| 方法 | 参数 | 数值 |
| GAPSO | c1、c2 | 1.5 |
| pc | 0.5 | |
| pm | 0.05 | |
| CNN-BiLSTM | filtersize | [2 1] |
| learning rate | 0.001:0.01 | |
| numhiddenunits | 20:200 | |
| optimzier | adam | |
| SampEn | m | 1 |
| r2 | 0.2 |
| $ {\mathrm{RMSE}} = \sqrt {\frac{{\text{1}}}{n}{{\sum\limits_{i = 1}^n {({{\hat y}_i} - y{}_i)} }^2}} $ | (20) |
| $ {\mathrm{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{{\hat y}_i} - y{}_i} \right|} $ | (21) |
| $ {\mathrm{MSE}} = \frac{1}{n}{\sum\limits_{i = 1}^n {({{\hat y}_i} - y{}_i)} ^2} $ | (22) |
| $ r^2=\left(1-\frac{\displaystyle\sum\limits_{i=1}^n(\hat{y}_i-y_i)^2}{\displaystyle\sum\limits_{i=1}^n(\hat{y}_i-\overline{y})^2}\right)\times100\text{%} $ | (23) |
式中:
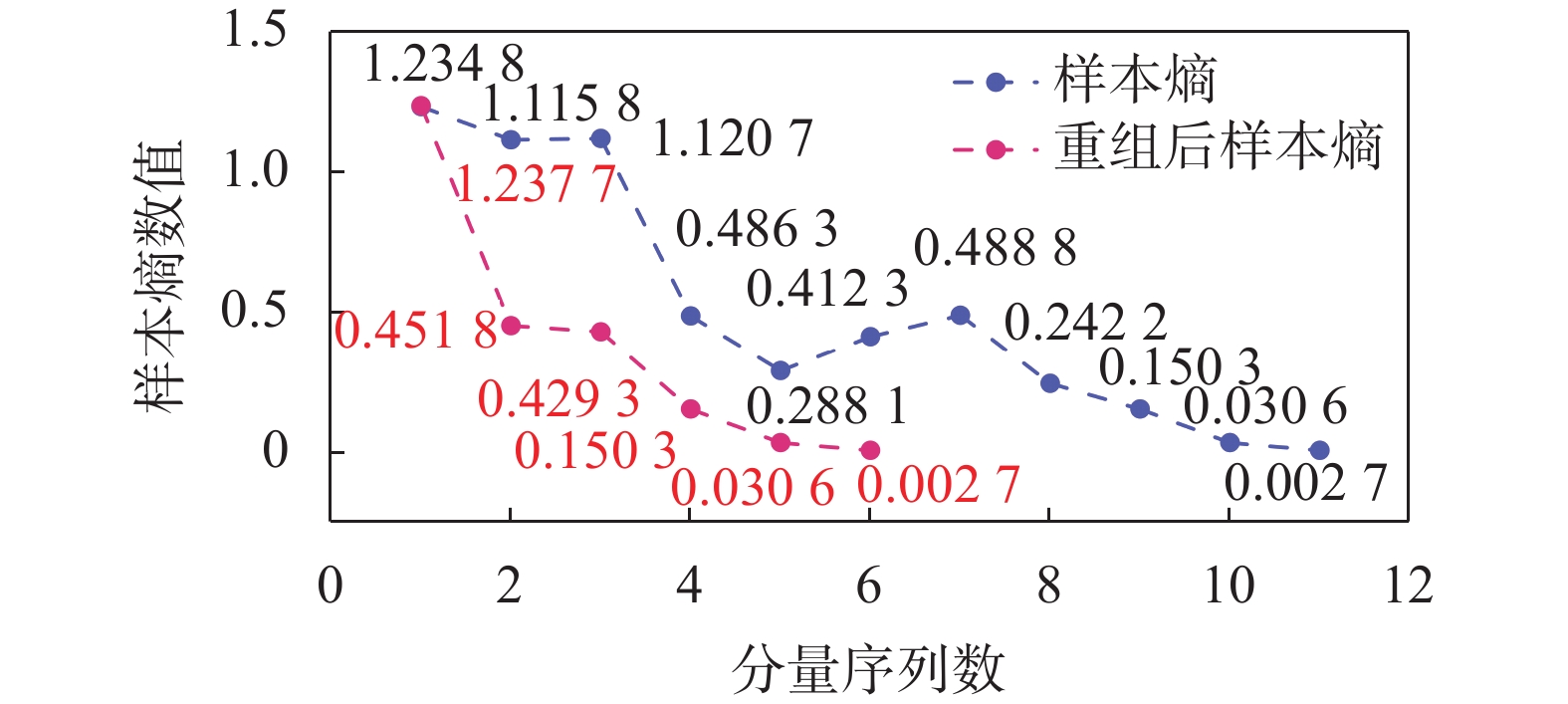
对每一个IMF分量进行样本熵计算如图4所示。观察图5可知,供热负荷原序列呈现非线性、非平稳性的特点,为了降低供热负荷预测难度,凸显供热负荷序列特征,采用CEEMDAN对供热负荷进行分解。原始供热负荷序列被分解为多个不同尺度的IMF分量,且每个分量都保持着一定的规律。如果直接使用GAPSO-CNN-BiLSTM网络预测则计算规模庞大,耗时较长。根据图4与图5可知IMF1至IMF3在数据波动与复杂程度上类似,IMF4、IMF6、IMF7拥有相似的复杂程度,IMF5、IMF8样本熵复杂程度差异较小,对于此类序列按照表2进行重组,构成新的CEEMDAN分解。图6反应了重组之后的序列,不同分量之前保持着原有的规律性,且分解数量相比之前减少了5次,在保证原有序列规律性与复杂程度的同时又减少了网络预测所需要的时间。
|
| 图 4 样本熵数值对比 |

|
| 图 5 CEEMDAN热负荷时间序列分解 |

|
| 图 6 重构后CEEMDAN热负荷分解 |
3.3 模型对比
为了分析各个模型的优劣性,首先以LSTM、CNN-LSTM进行分析比较,验证混合模型的优越性。其次再通过比较CNN-LSTM、PSO-CNN-LSTM与GAPSO-CNN-BiLSTM,验证GAPSO优化模型性能更优,最后比较各个模型在不同分解下的预测结果,验证CEEMDAN-SE的适用性。
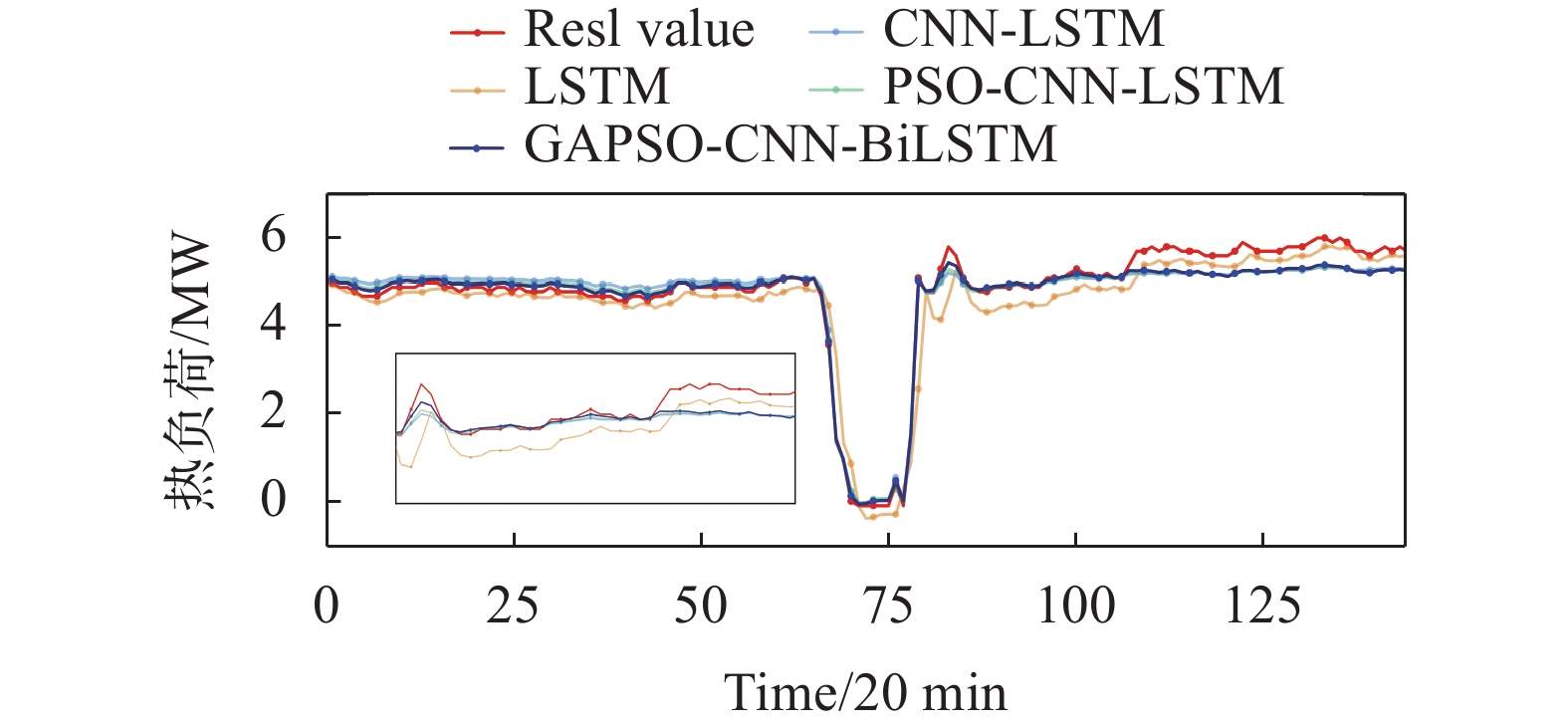
不同模型的热负荷预测结果如图7所示,评价指标如表3所示。从图中可以看出四个模型在热负荷中都取得了良好的预测结果,虽然存在不同程度的误差但是整体趋势与热负荷趋势一致,反应了供热负荷的基本特点。从LSTM与CNN-LSTM的预测结果中可以看出CNN-LSTM的预测结果明显好于LSTM的预测结果,特别是在热负荷变化趋势较大的情况下,GAPSO-CNN-BiLSTM整体预测结果优于其他模型,根据表3所示,GAPSO-CNN-BiLSTM的RMSE、MAE和MSE都低于其他模型,R2也更加接近1,拟合效果更优。对比PSO-CNN-LSTM与GAPSO-CNN-BiLSTM的预测结果,GAPSO-CNN-BiLSTM预测模型在供热负荷初始阶段,拟合更接近真实负荷。BiLSTM的对于捕捉供热负荷时序关系,相比LSTM更为精准。
|
| 图 7 不同模型热负荷预测结果 |
| 网络模型 | RMSE/% | MAE/% | MSE/% | r2 |
| LSTM | 0.404 | 0.273 | 0.163 | 0.992 |
| CNN-LSTM | 0.305 | 0.246 | 0.093 | 0.996 |
| PSO-CNN-LSTM | 0.287 | 0.214 | 0.082 | 0.996 |
| GAPSO-CNN-BiLSTM | 0.256 | 0.191 | 0.065 | 0.997 |
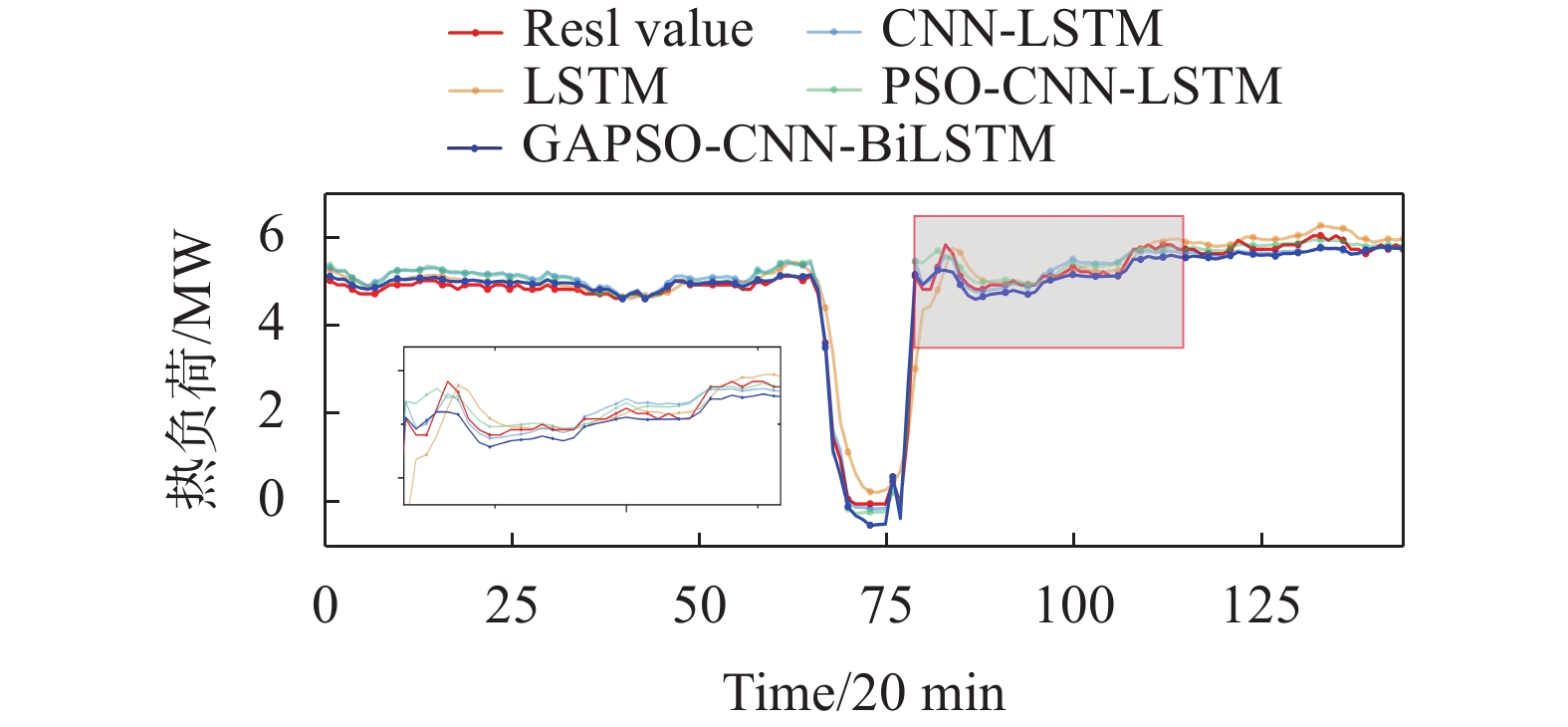
根据观察表3中误差和离散值可发现,使用单一模型进行热负荷预测精度非常有限,且图7中波峰预测结果都出现了不少误差。为了进一步提高预测精度,增强热负荷特征提取,采用不同分解方法对热负荷数据进行分解重构,挖掘热负荷内部的潜在变化趋势。根据观察图8、图9所示,混合预测模型相比单一模型更有很大优势,采用样本熵合并的CEEMDAN预测模型性能优于采用EEMD和EMD的模型,其RMSE、MAE、MSE最低,拟合效果最优,且因为采用了样本熵合并,降低了原有算法的复杂程度,模型运算时间也得以缩减。从图9中不难发现,采用EMD分解的模型精度提升不明显,造成这种原因的主要因素是由于EMD分解难免会出现模态混叠的现象,而EEMD与CEEMDAN都能够有效缓解模态混叠的出现,对于热负荷精度都有显著提高效果。
|
| 图 8 CEEMDAN-SE热负荷预测结果对比 |

|
| 图 9 各类不同分解预测结果对比 |
综合分析,所提混合预测模型能够有效的挖掘热负荷内外特征信息,提高热负荷预测性能,具有一定参考价值。
4 结束语通过分析集中供热系统一次网热负荷预测提出了GAPSO-CNN-BiLSTM混合预测模型,并对实际换热站一次网进行了实验,得出如下结论:
1)对于供热负荷序列呈现非线性和非平稳性的特点,提出CEEMDAN-SE分解方法。引入样本熵的概念,降低了子序列过多而造成的模型时间过长的问题。根据实验结果所示,所提CEEMDAN-SE相比EEMD-SE和EMD-SE预测精度得到了显著提高。
2)相比传统模型参数难以确定的问题,所提结合优化算法的混合模型能够结合优化算法,匹配最优模型参数,避免模型结构的盲目性。
3)针对供热系统一次网热负荷预测研究,为供热系统调节循环水泵,提高供热效率铺垫了基础。
| [1] |
江亿, 唐孝炎, 倪维斗,等. 北京PM2.5与冬季采暖热源的关系及治理措施[J].
中国能源, 2014, 36(1): 7-13+28.
|
| [2] |
VOGLER–FINCK P J C, BACHER P, MADSON H. Online short-term forecast of greenhouse heat load using a weather forecast service[J].
Applied Energy, 2017, 205: 1298-1310.
DOI:10.1016/j.apenergy.2017.08.013 |
| [3] |
顾伟, 薛贵军, 李水清. 结合天气因素的HTS-FOA-GRNN短期热负荷预测研究[J].
机械设计与制造, 2022(1): 81-83+87.
|
| [4] |
许裕栗, 姜娜, 陈卓, 等. 基于LSTM网络的居民区供热负荷短时预测[J].
自动化仪表, 2018, 39(10): 1-5+10.
|
| [5] |
KIM T Y, CHO S B. Predicting residential energy consumption using CNN-LSTM neural networks[J].
Energy, 2019, 182: 72-81.
DOI:10.1016/j.energy.2019.05.230 |
| [6] |
CAO J, LI Z, LI J. Financial time series forecasting model based on CEEMDAN and LSTM[J].
Physica A:Statistical mechanics and its applications, 2019, 519: 127-139.
DOI:10.1016/j.physa.2018.11.061 |
| [7] |
ZHOU F, HUANG Z, ZHANG C. Carbon price forecasting based on CEEMDAN and LSTM[J].
Applied Energy, 2022, 311: 118601.
DOI:10.1016/j.apenergy.2022.118601 |
| [8] |
TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]//2011 IEEE international conference on acoustics, speech and signal processing (ICASSP). IEEE, 2011: 4144-4147.
|
| [9] |
石琳,刘文慧,曹富军,等.基于CEEMDAN-SVM-LSTM的高炉煤气利用率组合预测[J].中国测试,2023,49(1):86-91.
SHI L, LIU W H, CAO F J, et al. Combination prediction of blast furnace gas utilization based on CEEMDAN-SVM-LSTM [J].China Measurement& Test, 2023,49 (1): 86-91.
|
| [10] |
张林, 刘继春. 基于EEMD-SE和PSO-KELM的短期负荷区间预测方法[J].
中国电力, 2021, 54(3): 132-140.
|
| [11] |
徐岩, 靳伟佳, 朱晓荣. 基于遗传粒子群算法的光伏并网逆变器参数辨识[J].
太阳能学报, 2021, 42(7): 103-109.
|
| [12] |
党建武, 从筱卿. 基于CNN和GRU的混合股指预测模型研究[J].
计算机工程与应用, 2021, 57(16): 167-174.
DOI:10.3778/j.issn.1002-8331.2004-0236 |
| [13] |
RAFI S H, DOOBA S R, HOSSAIN E. A short-term load forecasting method using integrated CNN and LSTM network[J].
IEEE Access, 2021, 9: 32436-32448.
DOI:10.1109/ACCESS.2021.3060654 |
| [14] |
廖清阳, 王军, 胡凯强,等. 基于深度并行CNN-BiLSTM的能源互联网电负荷和热负荷联合预测模型[J].
中国测试, 2022, 48(4): 146-153.
|
 2024, Vol. 50
2024, Vol. 50


 ,
,