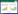文章信息
- 滕飞
- TENG Fei
- 轴向应变放大式谐振温度传感器研究
- Research on resonant temperature sensor with axial strain amplification
- 中国测试, 2024, 50(6): 111-116
- CHINA MEASUREMENT & TEST, 2024, 50(6): 111-116
- http://dx.doi.org/10.11857/j.issn.1674-5124.2023120082
-
文章历史
- 收稿日期: 2023-12-25
- 收到修改稿日期: 2024-02-26
近年来,试验机改装重心自动调节系统、舱内温度控制系统、航空燃油温度监测系统等专用系统的装配已成为开展民机适航试飞的重要手段之一,为了能够进一步提高系统性能,需要具有高精度高可靠性的微型温度传感器。微机电系统(MEMS)技术已经成功实现了包括惯性传感器、生物传感器和温度传感器在内的传感器的小型化、低成本与低能耗。基于MEMS技术的谐振器因具有优异的信号分辨率与高灵敏度,在未来拥有广泛前景。特别是对于温度变化,基于MEMS谐振传感元件的小型化,如几微米厚的长谐振梁和较低的热时间常数,微小的温度波动可以直接而迅速地影响到MEMS谐振器的机械结构。因此,MEMS谐振器是温度传感的优良器件之一[1-3]。
将基于硅绝缘体的谐振式温度传感器与玻璃层相结合,再将玻璃层与封装相连,由封装向玻璃层进行热传导,进而使器件层产生应变,实现频移,以完成对外界温度变化的检测[4];通过在基底采用氧化物材料以及在复合层采用不同热膨胀系数的材料,提高了温度变化过程中梁固定端的轴向载荷,实现了高灵敏度的固-固梁式谐振式温度传感器。然而,以上研究仍存在问题。一方面,中间层不仅延迟了从封装到结构层的热传导,增加了热滞后,而且由于其热膨胀系数接近于封装层的热膨胀系数,导致应力放大退化,限制了温度灵敏度的提高;另一方面,极大的轴向载荷会引起谐振梁的非线性形变,这将导致相应频率-温度模型的精度降低,从而影响温度传感器的性能。
因此,本文提出了一种新的轴向应变放大结构。当外界温度变化时,通过将不同热膨胀系数材料[5]制成的基底与封装直接相连,使结构层上的谐振梁产生较大的轴向应变,器件的谐振频率产生较大偏移,从而提高了温度传感器的灵敏度。同时,本文还建立了频率-温度模型,推导了频率温度系数(CTf)作为衡量器件灵敏度的物理量,并通过仿真分析与误差修正,使所建模型与仿真模型具有较高一致性。
1 器件结构设计谐振式温度传感器的结构设计如图1所示,由谐振梁、电极、锚和放置在SOI晶片器件层的应变放大结构组成。其中,电极用于激励谐振梁产生振动,谐振梁用于感测由温度变化引起的频率变化,锚杆分别与梁的两端连接。整个装置分为三个部分。第一部分和第三部分的硅基底与不同热膨胀系数材料的封装表面固定在一起,第二部分的基底对于封装处于自由状态。当外部温度变化时,热量通过封装和基底层传递到结构层。由于谐振器和封装的材料具有不同的热膨胀系数,悬挂在结构层上的谐振梁的轴向应变将被放大,这将导致器件的谐振频率随温度变化而产生较大的偏移,意味着温度传感器获得了更高的灵敏度。

|
| 图 1 谐振器结构 |
2 频率-温度建模与分析
当外部温度变化时,由于封装和器件之间材料的热膨胀系数不同,谐振梁会发生形变。频率温度系数(CTf)用于描述理想谐振器的灵敏度。具体推导如下:
由于谐振器的谐振频移
首先,谐振器的模型需要被简化。考虑到两个应变放大结构之间长度为
根据振动力学的经典理论,谐振梁
| (∫Lt0ρSi Abeam Φ2(x)dx+mpΦ2(Lt2))¨q(t)+(∫Lt0ESiIbeam (∂2Φ(x)∂x2)2dx+∫Lt0F(∂Φ(x)∂x)2dx)q(t)=0 | (1) |
式中:
根据动力学理论,推导了基于等式(1)的梁的等效质量和等效刚度。等式(1)可以写成如下:
| meff=∫Lt0ρSiAbeamΦ2dx+mpΦ2x=Lt/2 | (2) |
| keff=∫Lt0ESiIbeam(∂2Φ(x)∂x2)2dx+∫Lt0F(∂Φ(x)∂x)2dx | (3) |
根据等式(2)、(3),梁的谐振频率表示为:
| f(F)=12π√keffmeff=√f2273\,K+4.85F4π2meffLt | (4) |
在参考温度为273 K时,谐振频率为
根据等式(4)可以看出,谐振频率
当温度升高时,谐振器和封装逐渐膨胀。由于材料的热膨胀系数不同,热膨胀系数为
| {δSi(ΔT,F)=αSiΔT+FESiAeffδAl(ΔT,F)=αAlΔT−FEAlAAl | (5) |
式中:
封装的压缩应变与梁的压缩应变相似。
由于梁和封装之间的固-固连接,应变
| δSi=δAl | (6) |
根据等式(5)和等式(6),轴向力
| F(ΔT)=(αAl-αSi)ΔT1/(EAlAAl)+1/(ESiAeff) | (7) |
根据等式(4)和等式(7),谐振频率
| f(ΔT)=√f2273\,K+4.85(αAl-αSi)ΔT4π2meffLt(1/(EAlAAl)+1/(ESiAeff)) | (8) |
此外,频率温度系数可以如下给出:
| CTf(ΔT)=dfdΔT1f273\,K=4.858π2meffLt1f273\,Kf(ΔT)F(ΔT)ΔT | (9) |
根据等式(8)、(9)计算了谐振频率和频率温度系数随温度的变化关系,如图2所示。在模型仿真中,未对模型设置固定、位移等力学边界条件,同时,对器件整体赋予相同的温度,未设置温度梯度(文中所有仿真条件均相同)。基于上述模型计算,当温度从273 K升高到293 K时,谐振频率从18967 Hz增加到22996 Hz,频率温度系数的变化范围为11750×10–6~9691×10–6 K–1,平均值10565×10–6 K–1。
|
| 图 2 谐振梁频率-温度曲线 |
3 模型验证与误差修正
为了验证上述数学模型,本文建立了包括谐振器和封装在内的器件仿真模型(如图3所示),并首先模拟了温度变化时的应变,其次分别给出了谐振频率和频率温度系数的数值模拟结果。

|
| 图 3 器件仿真模型 |
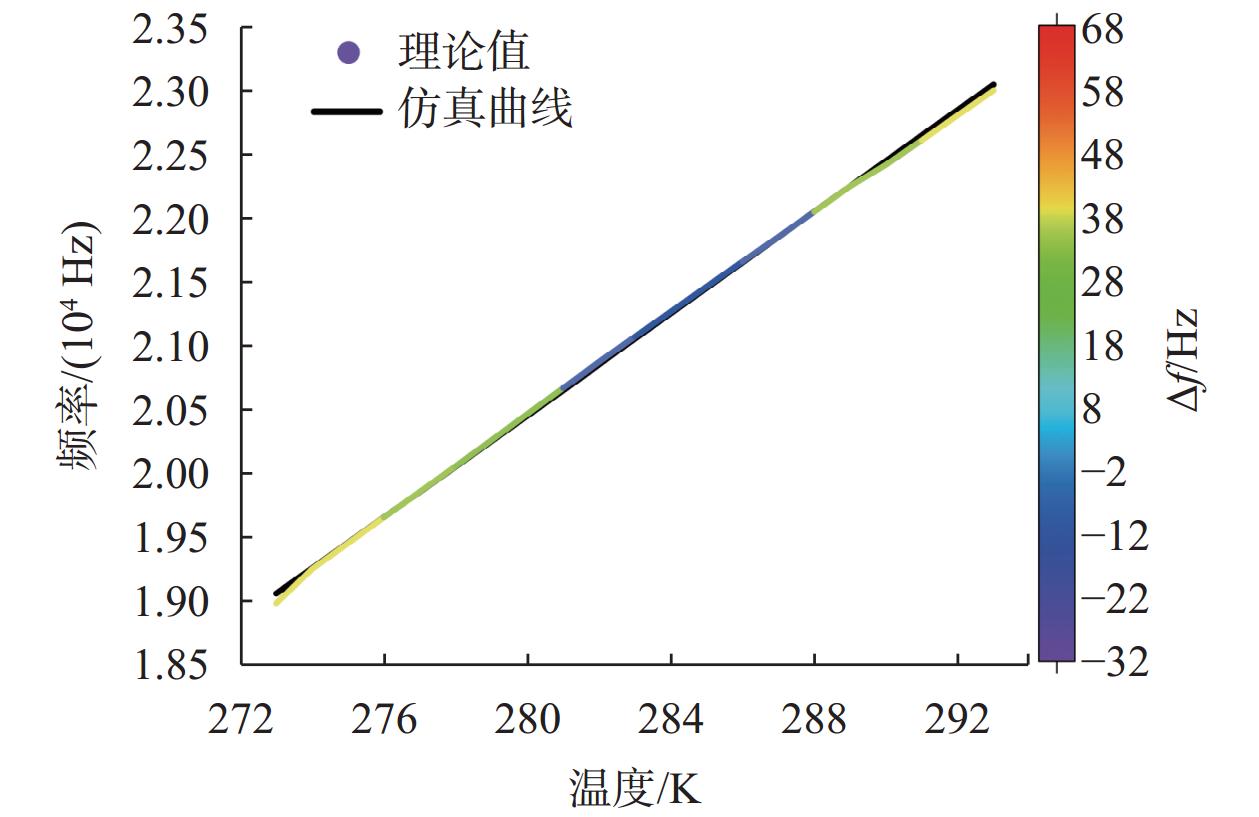
根据数值仿真与模拟,图4所示的平均频率温度系数为12935×10–6 K–1,与第二节中建立的数学模型的计算值(10565×10–6 K–1)比较,相对误差为22.4%,这表明所建立的数学模型存在较大的误差。为修正所建模型,需确定该模型的主要误差来源。
|
|
图 4
仿真、计算对比图 |
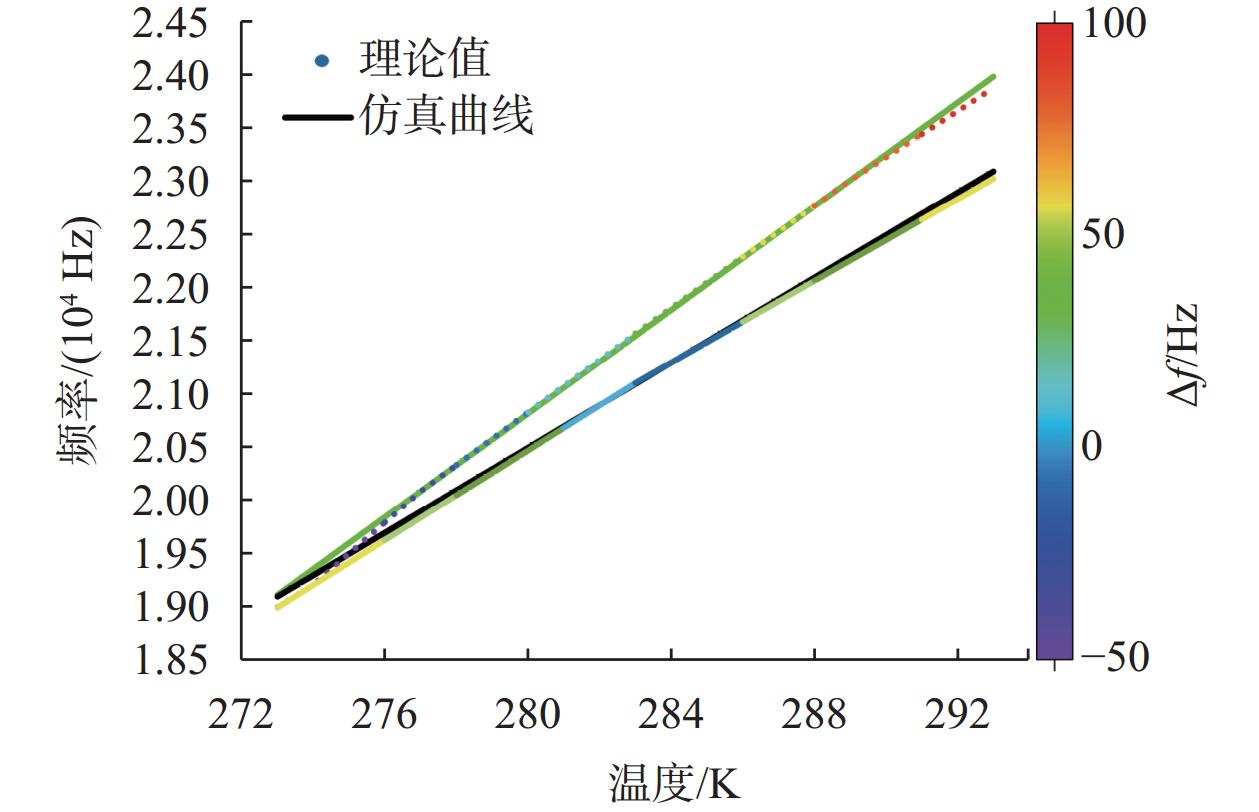
等式(4)中的
|
|
图 5
仿真、计算对比图 |
进一步对仿真模型进行分析,模拟了端部梁与同一横截面处封装的应变,如图6所示。图中着色表示物理量为各点x方向位移,在同一截面处,梁的位移大于封装的位移,相差约22%,即在认定封装受力固定的情况下,梁产生了位移。这表明梁的应变大于封装在同一截面处的应变,故在分析此类器件时,当处于固-固约束条件下,等式(6)中的应变相等是无效的。
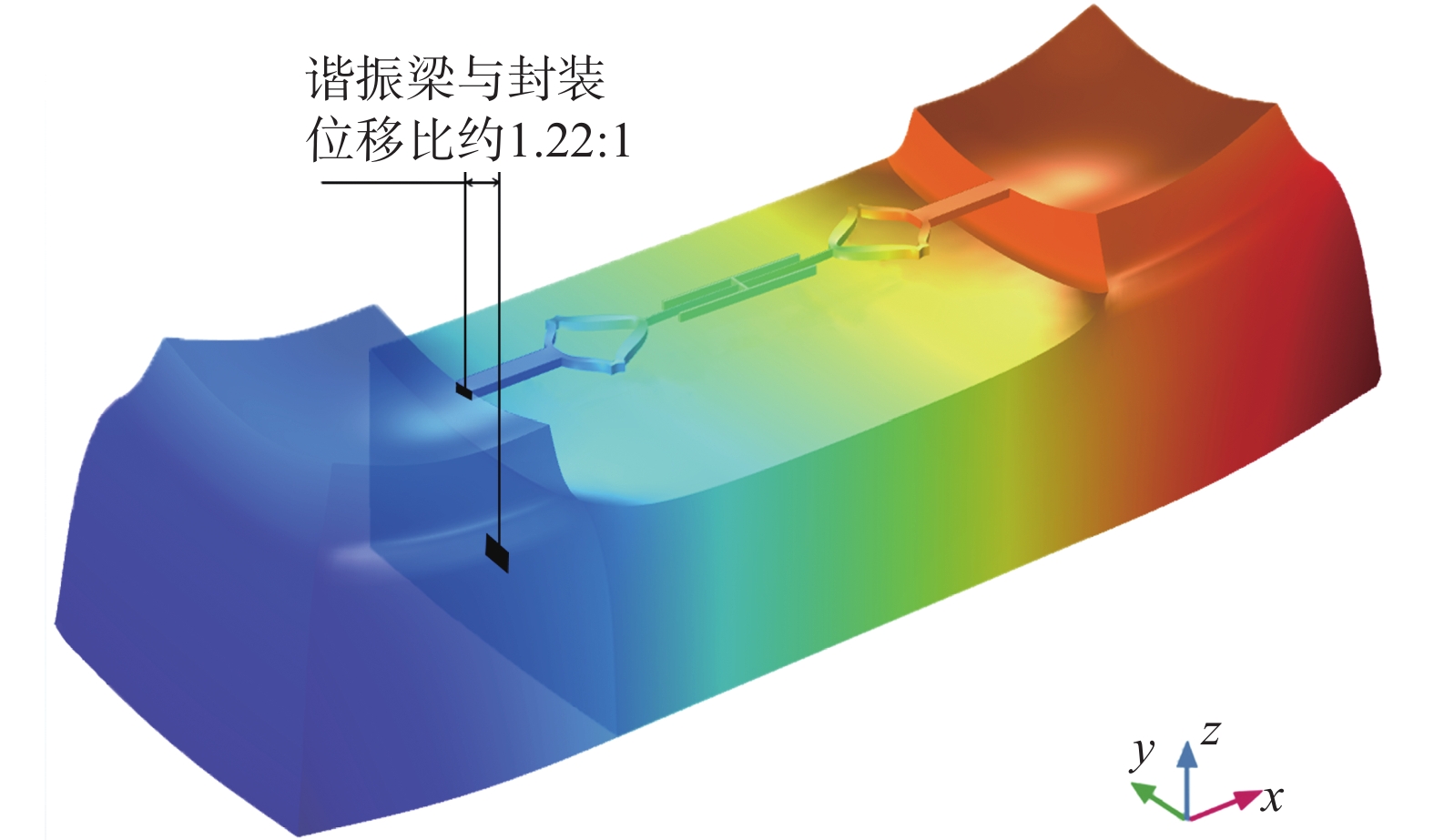
|
| 图 6 端部梁与封装应变仿真图 |
基于数学模型,本文发现锚不能被视为梁和封装的理想固定约束。为了实现足够的键合强度,本文在硅基板和铝封装之间设计了一个大的接触面积,导致了梁与封装不同的位移。鉴于以上差异,谐振梁的应变等于1.22倍同一截面处封装的应变,故等式(6)需要修改为:
| δ′Si=1.22δ′Al | (10) |
将等式(10)代入等式(7),轴向力与温度的函数校准模型可以写为:
| F(ΔT)=(1.22αAl-αSi)ΔT1.22/(EAlAAl)+1/(ESiAeff) | (11) |
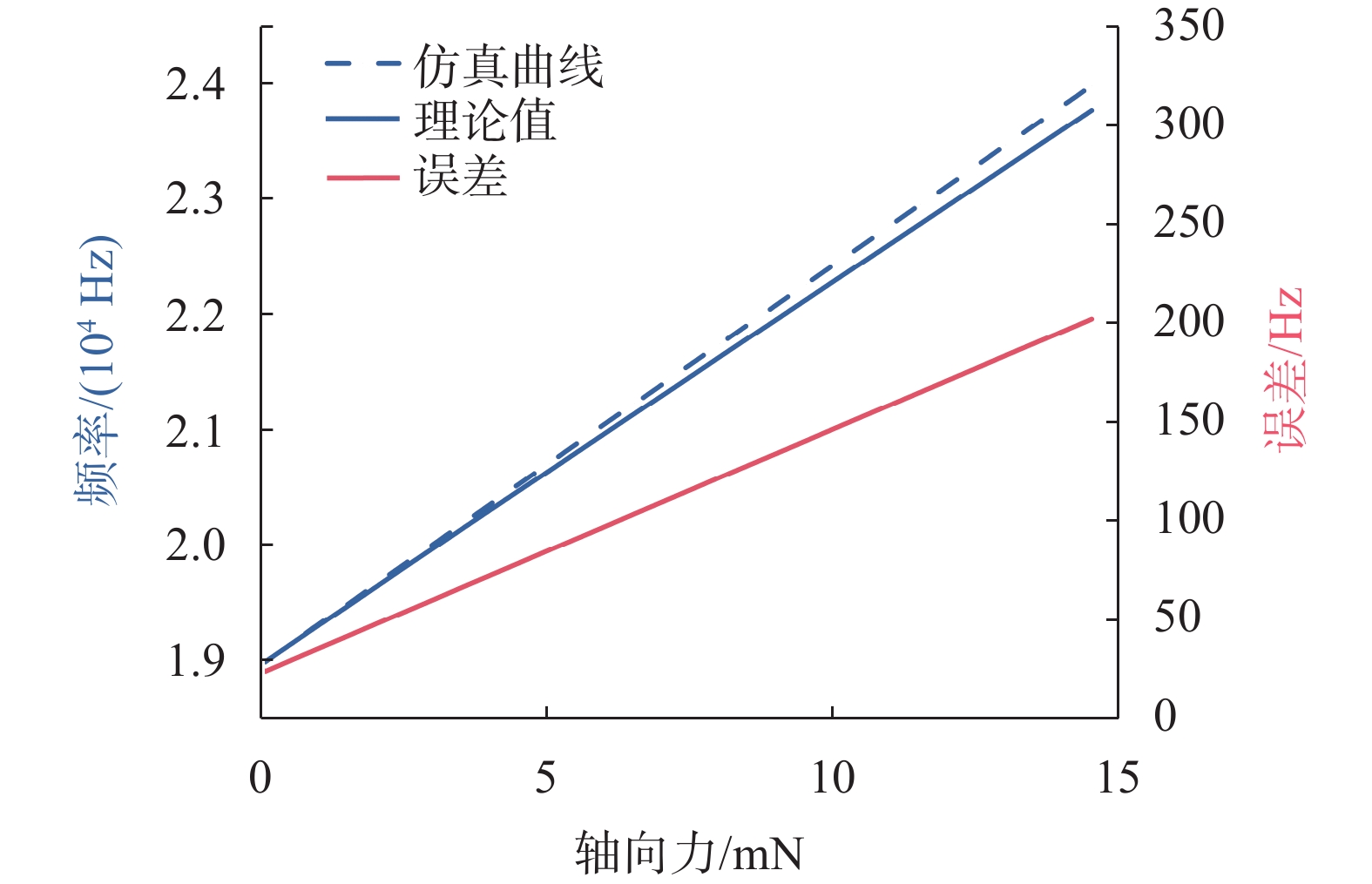
此外,基于等式(11)重新计算的谐振频率(
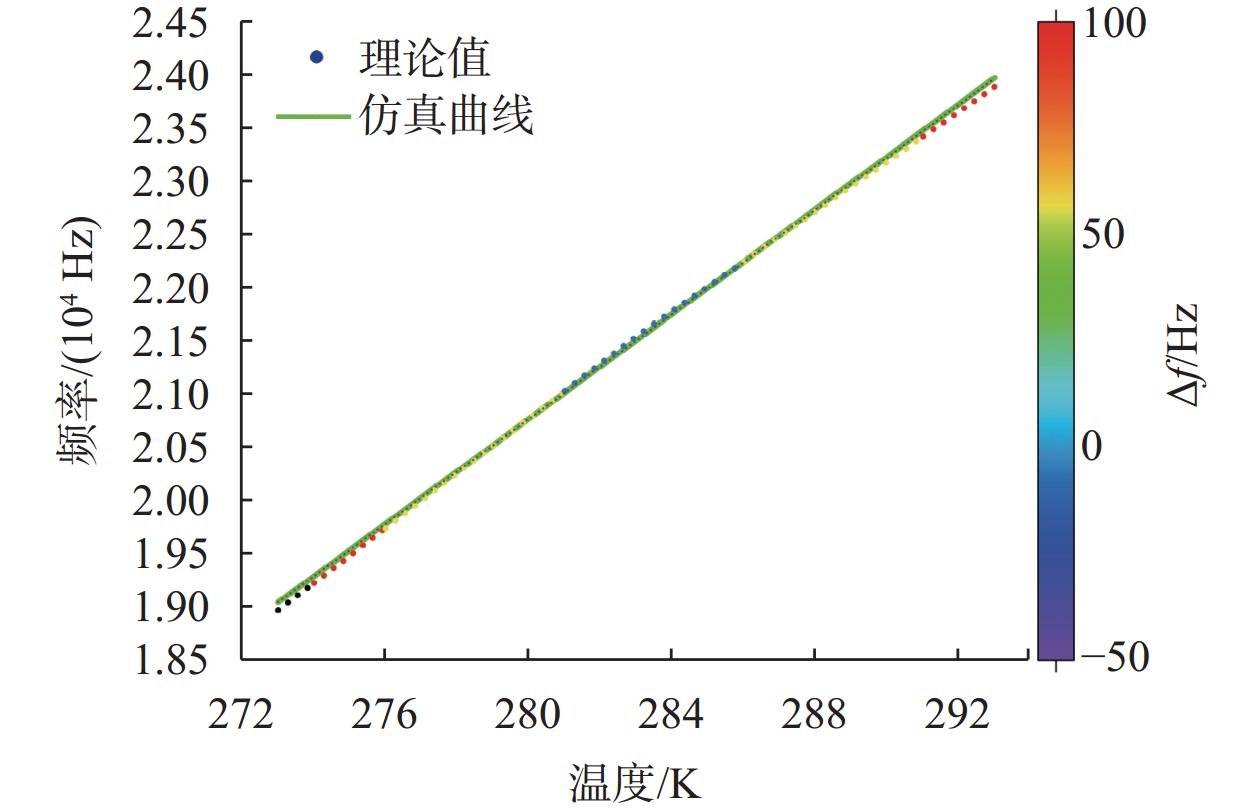
|
|
图 7
修正后仿真、计算对比图 |
进一步,针对0~100 ℃温度变化范围内器件的频率变化进行仿真,仿真结果如图8所示。根据仿真结果进行分析,在0~20 ℃温度变化范围内,器件的线性度为0.01;在20~100 ℃温度变化范围内,线性度为0.05。
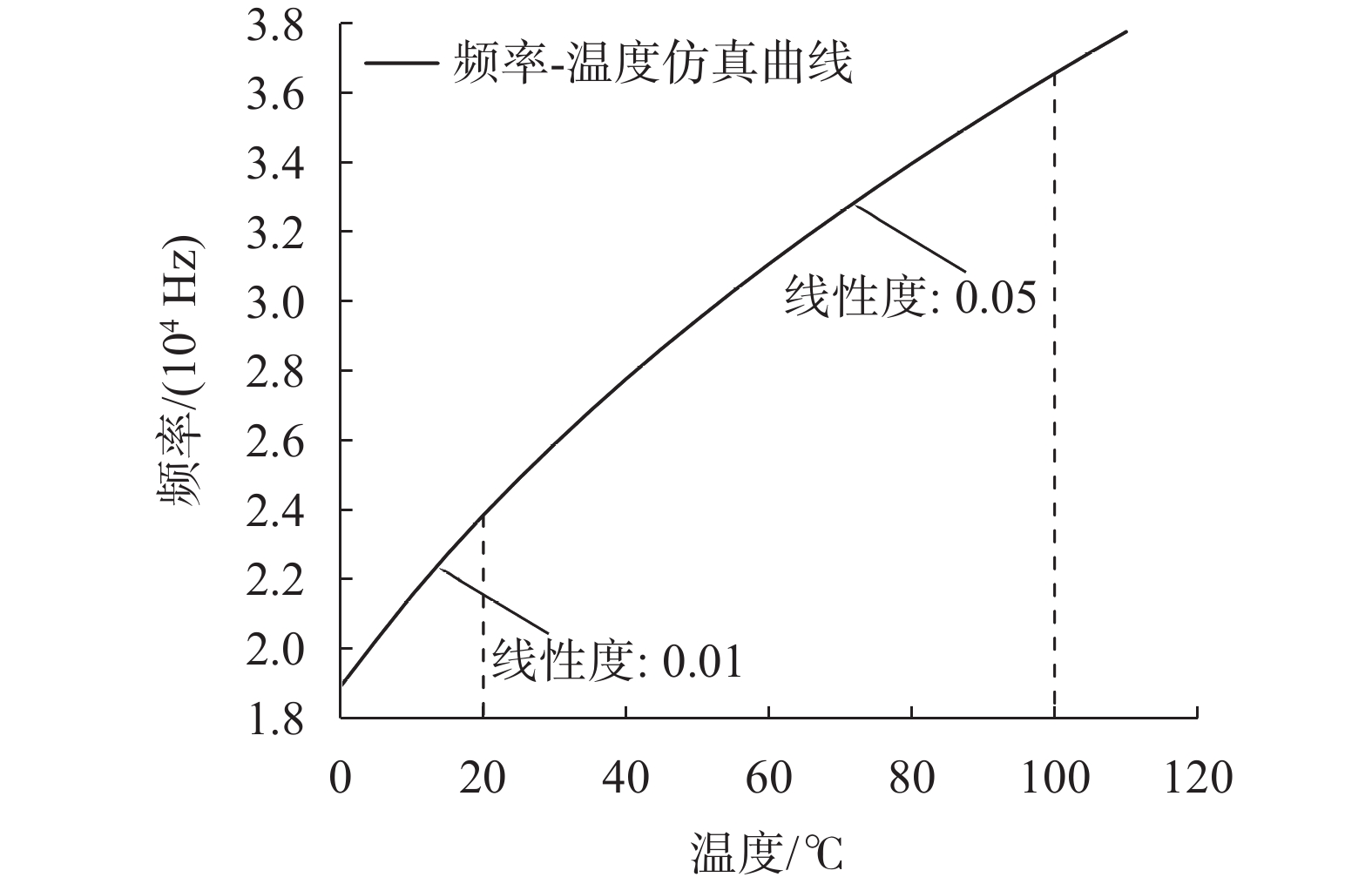
|
| 图 8 器件频率-温度仿真曲线图 |
4 器件测试与结果分析
本文主要制造流程如图9所示。整个器件采用厚度为460 μm的SOI晶片,相应的器件和基底层的厚度分别为60 μm和400 μm。首先,通过一些主要步骤蚀刻SOI晶片的基底层以形成三个部分,如图9(a)~(g)所示。其次,使用典型的蚀刻工艺在器件层上形成谐振器,如图9(h)~(i)所示。最后,获得所制造的器件,如图10所示。

|
| 图 9 器件制备工艺图 |

|
| 图 10 器件的SEM照片 |
器件共分为三部分,由谐振梁、电极、锚与应变放大结构组成,电极激励谐振梁产生振动,谐振梁感测由温度变化引起的频率变化,锚杆分别与梁的两端连接。图10中,左上角为器件完整示意图,右上角为应变放大结构局部示意图。下方两张图分别为谐振梁以及梁两侧携带梳齿,可根据外界温度变化产生振动,改变器件谐振频率。
器件对于温度变化的频率响应测试方式为:将器件放置于恒温箱中持续工作,由示波器记录其振荡频率。测试所用到的主要仪器为恒温箱与示波器,分别进行温度控制与频率测量。为保证测试的准确性,设置温度变化步长为0.1 ℃,每个温度保持4 min,期间采用示波器对器件谐振频率多次测试,使用平均值作为测试结果;整个测试过程持续15 h,温度从0 ℃变化到23 ℃。
测试结果如图11所示。当外界温度在273~293 K范围内变化时,修正后理论模型计算所得器件频率温度系数为12876×10–6 K–1,仿真模拟所得器件频率温度系数为12935×10–6 K–1,实际测试器件频率温度系数为13104×10–6 K–1。经过对比,器件的测试结果与仿真结果、理论结果误差较小(与仿真结果相比误差为1.3%,与理论计算结果相比误差为1.8%),这表明该模型可用于高灵敏度温度传感器的优化设计。
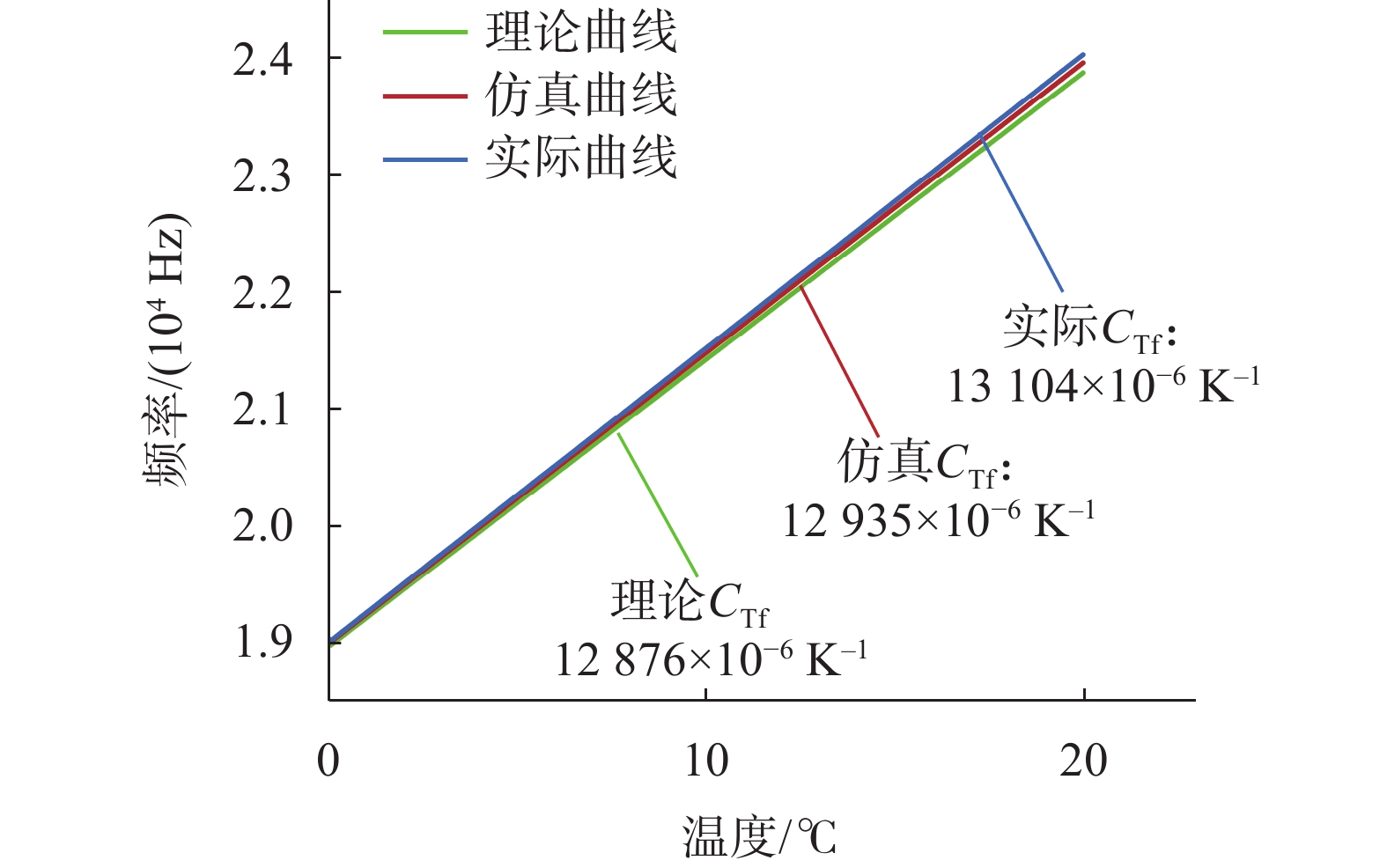
|
| 图 11 测试结果图 |
与诸多谐振式温度传感器相比,本文设计的轴向应变放大结构,使温度变化下器件的谐振梁轴向应变放大,导致器件谐振频率随温度变化而大幅偏移,获得了较高的频率温度系数(13104×10–6 K–1),极大程度提高了器件的灵敏度,具体性能对比如表1所示。
5 结束语
本文提出了一种轴向应变放大结构,并根据经典理论推导了谐振器的频率温度系数(CTf)并进行了有限元建模与仿真,将二者比较。随后根据仿真结果观察到的现象对理论模型进行了校准,并进一步探究不同器件尺寸对热应力造成的形变带来的影响。最后,本文采用SOI工艺加工了该器件,并对传感器样机进行测试,得到的测试结果为频率温度系数13104×10–6 K–1,仿真结果为12935×10–6 K–1,二者相较误差为1.3%,相比于以往谐振式温度传感器,灵敏度提高了4~83倍。基于应变放大方法,本文为改装专用系统实现了高灵敏度的谐振式温度传感器。
| [1] |
JIANG B, HUANG S, ZHANG J, et al. Analysis of frequency drift of silicon MEMS resonator with temperature[J].
Micromachines, 2020, 12(1): 26.
DOI:10.3390/mi12010026 |
| [2] |
SHCHEGLOV K, EVANS C, GUTIERREZ R, et al. Temperature dependent characteristics of the JPL silicon MEMS gyroscope[C]//2000 IEEE Aerospace Conference. IEEE, 2002.
|
| [3] |
梁嘉琪, 董浩斌, 葛健. 多传感器高准确度便携式温度测量仪[J]. 中国测试, 2016, 42(5): 70-74.
LIANG J Q, DONG H B, GE J, et al. High-precision portable temperature measurement system based on three kinds of sensors[J]. China Measurement & Test, 2016, 42(5): 70-74.
|
| [4] |
PRIKHODKO I P, TRUSOV A A, SHEKEL A M. Compensation of drifts in high-Q MEMS gyroscopes using temperature self-sensing[J]. Sensors and Actuators A: Physical, 2013, 201:517-524.
|
| [5] |
FILIPE A, VINCENT M, VOLANT V, et al. Impact of die-attachmaterials on MEMS gyro performance[C]//International Symposium on Inertial Sensors and System. Laguna Beach, 2014.
|
| [6] |
徐军, 孟月霞, 刘春花, 等. 石英音叉温度传感器测试系统[J].
哈尔滨理工大学学报, 2017, 22(2): 44-49.
XU J, MENG Y X, LIU C H, et al. Testsystem for quartz tuning fork temperature sensor[J].
Journal of HARBIN University of Science and Technology, 2017, 22(2): 44-49.
|
| [7] |
李城鑫. 基于参数泵浦调制的谐振式MEMS温度传感器[D]. 武汉: 华中科技大学, 2021.
LI C X. Resonant MEMS temperature sensor based on parametric modulation[D]. Wuhan: Huazhong University of Science and Technology, 2021.
|
| [8] |
薛程颢. 钼铼合金超声导波谐振式温度传感器及系统设计[D]. 太原: 中北大学, 2022.
XUE C H. Design of ultrasonic guided wave resonance temperature Sensor and system based on Mo-Re alloy[D]. Taiyuan: North University of China, 2022.
|
| [9] |
田力. 超声导波谐振测温仪设计[D]. 太原: 中北大学, 2021.
TIAN L. Design of ultrasonic guided wave resonant thermometer[D]. Taiyuna: North University of China, 2021.
|
| [10] |
KOSE T, AZGIN K, AKIN T. Design and fabrication of a high performance resonant MEMS temperature sensor[J].
Journal of Micromechanics and Microengineering, 2016, 26(4): 045012.
DOI:10.1088/0960-1317/26/4/045012 |
| [11] |
李飞龙. 基于RF MEMS压电谐振器的无线传感技术研究[D]. 成都: 电子科技大学, 2022.
LI F L. Research on wireless sensing technology based on rf mems piezoelectric resonator[D]. Chengdu: University of Electronic Science and Technology of China, 2022.
|
| [12] |
LI Z K, HEBIBUL R, ZHAO L B, et al. Capacitive micromachined ultrasonic transducer as a resonant temperature sensor[J]. Instrumentation, 2014, 1(3): 67-74.
|
 2024, Vol. 50
2024, Vol. 50