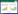文章信息
- 王鹏宇, 高磊, 程娟, 刘翠兰, 张英德, 李兆杰
- WANG Pengyu, GAO Lei, CHENG Juan, LIU Cuilan, ZHANG Yingde, LI Zhaojie
- 旋转式室温磁制冷机用永磁系统的设计与数值计算
- Design and numerical simulation of magnetic field system for rotary room-temperature magnetic refrigerator
- 中国测试, 2024, 50(6): 106-110
- CHINA MEASUREMENT & TEST, 2024, 50(6): 106-110
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022050130
-
文章历史
- 收稿日期: 2022-05-19
- 收到修改稿日期: 2022-07-26
近年来,室温磁制冷技术成为制冷领域的研究热点,许多大学、研究机构以及企业都投入大量的科研力量来研制室温磁制冷机,如斯洛文尼亚的卢布尔雅那大学、日本中部大学、法国的格勒诺布尔电气工程实验室以及中国的包头稀土研究院[1-4]。目前所研制的磁制冷机根据其磁场系统和磁工质的相对运动模式,主要分为往复式以及旋转式。相比气体压缩制冷,磁制冷具有高能效(磁制冷:卡诺循环的30%~60%,气体压缩制冷:卡诺循环的5%~10%)、环境友好和运行可靠等优点,已成为有望替代气体压缩制冷的热门制冷技术之一[5-7]。磁工质(磁制冷材料、磁热材料、磁卡材料)处于变化磁场中时,磁熵发生变化而引起吸放热的现象称为“磁热效应”,其强弱可用等温磁熵变和绝热温变这两个关键参数来表征[8-11]。磁制冷技术基于磁工质的磁热效应实现制冷。当外加磁场的变化越大时,磁热效应就越强。磁工质的磁热性能在很大程度上决定了磁制冷设备的制冷温跨和制冷能力,而目前实用型磁工质的磁热效应受限,难以研发出低成本、高磁感应强度的磁场系统[12]。并且,旋转式磁制冷机的旋转式磁场系统,有利于实现磁制冷机的高频工作,而频率是影响磁制冷机效率的重要因素之一。因此,设计性能优良的旋转式磁场系统对磁制冷技术的发展有重要意义。本文选用NdFeB永磁体作为磁场系统的主要组成部分,设计了旋转式室温磁制冷机用磁路。永磁系统中间位置的磁体由电动机带动绕定轴转动。在转动过程中,空间磁场分布发生变化,磁工质实现励磁与退磁。并且,利用有限元方法(COMSOL Multiphysics软件)对磁场分布进行了数值计算,计算结果与实测的结果相吻合,误差在30 mT以内。
1 磁路设计磁路设计与仿真模拟是近年来的研究热点[13-14]。现已研制的磁制冷设备所用磁场包括超导磁系统、电磁系统和永磁系统[15]。相比于超导磁系统和电磁系统,永磁系统具有结构简单、价格便宜和易装配等特点,在磁制冷装置中得到广泛的应用[16-19]。因此,基于磁场矢量叠加原理,设计了旋转式室温磁制冷机用永磁系统。与BaO·6Fe2O3和SrO·6Fe2O3等铁氧体、Sm-Co永磁材料、AlNiCo系和AlNiCo系铸造永磁材料相比,烧结NdFeB永磁材料具有高饱和磁感应强度、高剩磁和大矫顽力等优点,因此选用NdFeB永磁体提供磁场。为了屏蔽周围空间的磁场,选用高磁导率钢作为磁轭。永磁系统的三维示意图见图1。其中,棕色区域(1、4、5、8区域)代表钢轭,灰色区域(2、3、6、7区域)代表NdFeB永磁体,圆筒状磁工质(9区域)包围在磁场系统中间部分的外部。永磁系统两端(1、2、7、8区域)固定在距离控制架上,通过转动螺纹杆实现两端NdFeB永磁体沿y轴方向的移动和距离的调节,进而实现磁场空间范围的连续可调。中间位置区域(3、4、5、6区域)固定在电机上,电机的转速由程序控制,通过电机的转动带动中间位置区域做定轴转动。中间位置区域的转动,或者磁工质做定轴转动,引起磁工质的励磁与退磁。
|
| 图 1 设计永磁系统的三维示意图 |
2 数值计算方法
在磁场分布的数值计算中,有限元法是一种可准确求解的重要方法,通常包括几何结构的建立、材料属性的参数设定、求解方程的选用和边界条件的设定、网格的精细剖分、求解模型的选择以及结果的计算与后处理等。为了节约计算时间成本且考虑到对磁场分布结果影响较小,构建几何结构时忽略距离控制架。构建一个长方体作为周围空气区域,以长方体的体心为坐标原点。在材料参数设定环节,NdFeB的剩余磁感应强度
| $ \nabla \cdot {\boldsymbol{B}} = 0 $ | (1) |
| $ \nabla \times {\boldsymbol{H}} = 0 $ | (2) |
其中,
| $ {\boldsymbol{H}} = - \nabla {V_{\text{m}}} $ | (3) |
假定无限远处的磁势为0。NdFeB永磁体所满足的本构方程为
| $ {\boldsymbol{B}} = \mu_{\text{r}}\mu_0{\boldsymbol{H}} + {\boldsymbol{B}}_{\rm{r}} $ | (4) |
周围空气和磁轭满足的本构方程为
| $ {\boldsymbol{B}}' = \mu_{\text{r}}\mu_0{\boldsymbol{H}} $ | (5) |
式中:μr和μ0——各自材料的相对磁导率和真空磁导率;
在求解过程中,先计算出几何区域中每个点的磁势Vm,再利用式(3)~式(5)计算出磁场强度
| $ {\boldsymbol{B}} \cdot {\boldsymbol{n}} = 0 $ | (6) |
其中
在网格剖分过程中,逐渐细化网格,直至对计算的影响可忽略。结合求解模型,选用直接求解器进行计算求解。
3 数值计算结果未填充磁工质时的永磁系统在xy平面的投影如图2所示。永磁系统中心位置O沿y轴方向到外侧NdFeB永磁体块的距离为L。圆M的半径为磁工质内外半径和的1/2。中心O点指向圆M上各点的矢量与y轴正方向沿顺时针方向所形成的角度为θ。设置NdFeB永磁体的剩余磁感应强度

|
| 图 2 永磁系统在xy平面的投影图 |
3.1 距离L对磁场分布的影响
以圆M上各点的磁场变化为例,研究了不进行旋转时参数L的变化对磁场分布的作用规律。对于多晶磁制冷工质材料,磁工质的磁热效应和磁场大小有关,而对磁场的方向不敏感。因此,研究了参数L和圆M上各点的磁感应强度值的关系,关系曲线图见图3。参数L的取值分别为79~159 mm,间隔为10 mm。

|
| 图 3 当L为不同值时圆M上各点的磁感应强度的分布曲线 |
由图3可知,在不同L条件下,圆M上磁感应强度值的分布关于φ = π对称,这是由几何对称性和均匀磁化假设所导致的。相应条件下磁感应强度的最大值B1和最小值B2与参数L的关系见图4。分析图4可知,随着参数L的逐渐增大,磁感应强度的最大值B1降低,最小值B2升高,磁场变化范围变小。磁工质的等温磁熵变和绝热温变与磁场变化范围的大小呈正相关。因此,减小参数L有利于提高单位质量磁工质的磁热效应,但同时意味着所能填充的磁工质的质量降低,制冷效率下降,在实际应用中应根据实际需求调节参数L的大小。

|
| 图 4 圆M上磁感应强度的最大值B1和最小值B2与参数L的关系 |
3.2 旋转角度α对磁场分布的影响
计算模拟了当L为79 mm时,不同旋转角度α下圆M上各点磁感应强度的分布,计算结果见图5。分析图5可知,两端的NdFeB永磁体(图1中2、7区域)以及中间NdFeB永磁体(图1中3、6区域)形成的空间磁场都为非匀强磁场,中间位置区域的定轴转动引起的非匀强磁场以不同的方向叠加,导致圆M上各点的磁感应强度值变化范围不相同。在旋转过程中,永磁系统形成的空间磁场的最大值约为1265 mT,最小值约为32 mT。

|
| 图 5 当L为79 mm时不同旋转角度α下圆M上各点的磁感应强度的分布曲线 |
为了更加直观地体现该永磁系统磁场的空间分布,进一步模拟计算了L为79 mm,旋转角α为0°时磁场的空间分布,模拟结果见图6。图中不同颜色的曲面代表不同大小磁感应强度的等值面,箭头的方向代表磁感应强度的方向。

|
| 图 6 当L为79 mm且α为0°时的磁场空间分布模拟图 |
在计算模型中,假设每块NdFeB永磁体被均匀磁化,即NdFeB永磁体中每个点的磁感应强度大小相等,方向相同。并且,假定NdFeB永磁体、钢轭以及周围空气都是匀质材料,在同种材料中各点的磁导率μ取同一个值。因此,永磁系统所产生的磁场关于xy平面(z = 0)和yz平面(x = 0)对称。分析图6可知,磁工质所处区域为非匀强磁场。因此,磁工质做定轴转动过程中,各点的磁感应强度不断变化,引起温度的升高与降低,并与换热流体进行充分热交换,利用换热流体的循环实现制冷的目的。
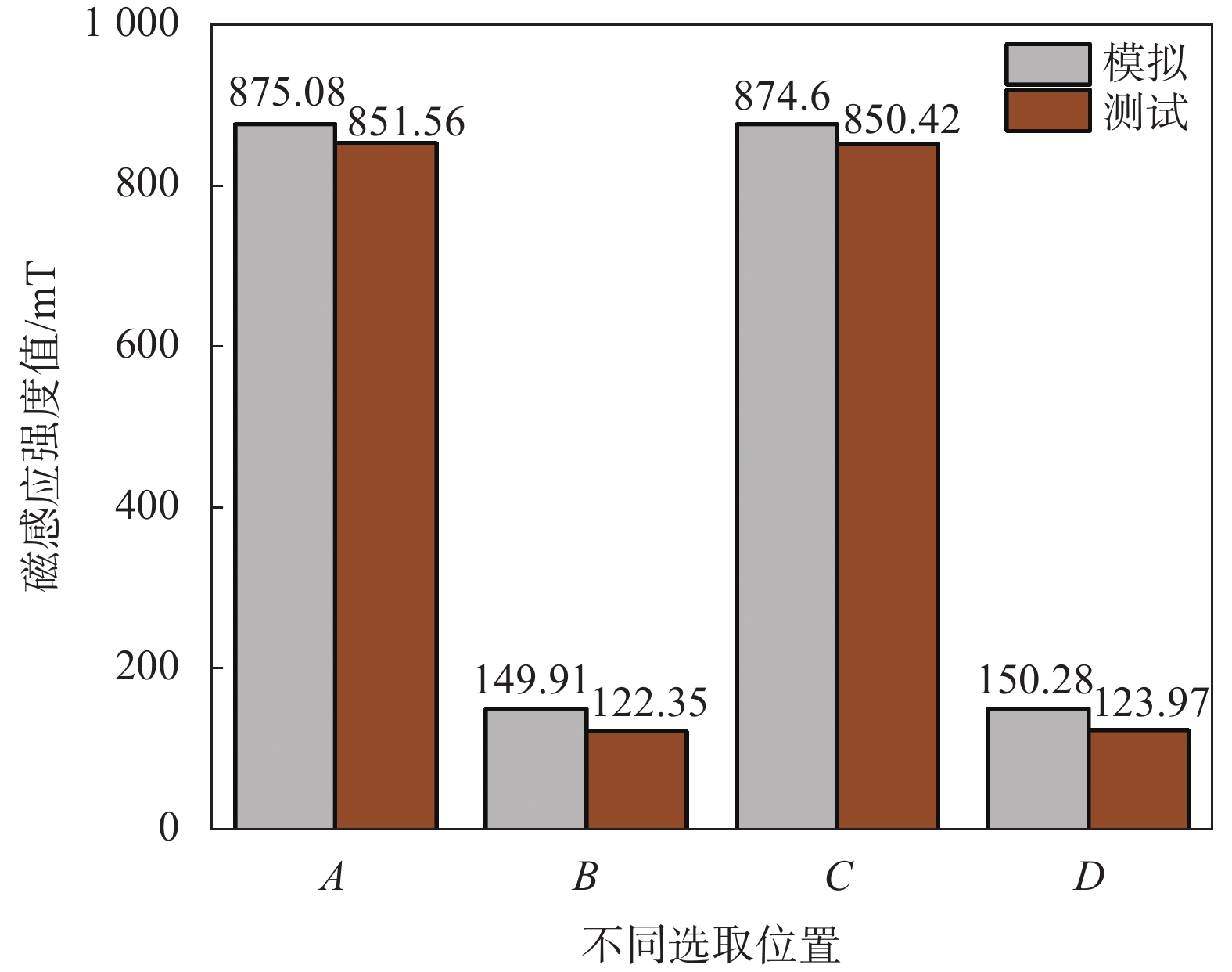
为了验证数值计算的准确性,利用高斯计测量了在距离L为79 mm、旋转角α为0°时A、B、C和D 4个位置(图2中给出)的磁感应强度,将测量结果和计算结果(图3或图5中数据)进行对比,如图7所示。由图可知,测试结果和计算结果的差值在30 mT以内,并且磁感应强度较小时差值较大,这是由测试误差引起的。
|
| 图 7 当L为79 mm且α为0°时A、B、C和D位置上的磁感应强度的测量结果和模拟结果 |
4 结束语
本文设计了旋转式室温磁制冷机用永磁系统,并利用有限元法对磁场分布进行了数值计算。设计的永磁系统主要由NdFeB永磁块、高磁导率钢轭和距离控制架构成。距离控制架能改变两端NdFeB永磁体的距离,实现磁场空间范围的调节。中间部分的NdFeB永磁体固定在电机上,电机的转动带动其做定轴转动,实现磁工质的励磁与退磁。模拟结果表明,两端NdFeB永磁体以及中间位置的NdFeB永磁体所产生的空间磁场均为非匀强磁场。中间位置的NdFeB永磁体做定轴转动,引起非匀强磁场以不同的方向进行叠加,使磁工质所处位置的磁场发生变化。在旋转过程中,永磁系统形成的空间磁场的最大值约为1265 mT,最小值约为32 mT。并且,参数L的减小使磁场强度范围变大,有利于磁工质磁热效应的提高。A、B、C和D 4点磁感应强度值实测和计算结果吻合较好,差值在30 mT以内。
| [1] |
TUŠEK J, ZUPAN S, ŠARLAH A, et al. Development of a rotary magnetic refrigerator[J].
International Journal of Refrigeration, 2010, 33(2): 294-300.
DOI:10.1016/j.ijrefrig.2009.11.003 |
| [2] |
YAMAGUCHI S, EMOTO M, YAMAMOTO N, et al. Refrigeration process to realize a multistage and gas-cooled current lead[J].
IEEE Transactions on Applied Superconductivity, 2013, 23(3): 4802304.
DOI:10.1109/TASC.2013.2243896 |
| [3] |
YU B F, LIU M, EGOLF P W, et al. A review of magnetic refrigerator and heat pump prototypes built before the year 2010[J].
International Journal of Refrigeration, 2010, 33(6): 1029-1060.
DOI:10.1016/j.ijrefrig.2010.04.002 |
| [4] |
HUANG J H, LIU J R, JIN P Y, et al. Development of permanent magnetic refrigerator at room temperature[J].
Rare Metals, 2006, 25(6): 641-644.
DOI:10.1016/S1001-0521(07)60164-8 |
| [5] |
司晓东, 刘永生, 徐娟, 等. 室温磁制冷材料研究进展[J].
磁性材料及器件, 2015, 46(4): 67-73.
SI X D, LIU Y S, XU J, et al. Research progress of room-temperature magnetic refrigeration materials[J].
Journal of Magnetic Materials and Devices, 2015, 46(4): 67-73.
DOI:10.3969/j.issn.1001-3830.2015.04.017 |
| [6] |
李振兴, 李珂, 沈俊, 等. 室温磁制冷技术的研究进展[J].
物理学报, 2017, 66(11): 110701.
LI Z X, LI K, SHEN J, et al. Progress of room temperature magnetic refrigeration technology[J].
Acta Physica Sinica, 2017, 66(11): 110701.
|
| [7] |
APREA C, GRECO A, MAIORINO A. Magnetic refrigeration: a promising new technology for energy saving[J].
International Journal of Ambient Energy, 2016, 37(3): 294-313.
DOI:10.1080/01430750.2014.962088 |
| [8] |
CAPOVILLA M S, LOZANO J A, TREVIZOLI P V, et al. Performance evaluation of a magnetic refrigeration system[J].
Science and Technology for the Built Environment, 2016, 22(5): 534-543.
DOI:10.1080/23744731.2016.1181510 |
| [9] |
LI L W, YAN M. Recent progresses in exploring the rare earth based intermetallic compounds for cryogenic magnetic refrigeration[J].
Journal of Alloys and Compounds, 2020, 823: 153810.
DOI:10.1016/j.jallcom.2020.153810 |
| [10] |
包立夫, 武荣荣, 张虎. 室温磁制冷材料的研究现状及发展前景[J].
材料导报, 2016, 30(3): 17-22.
BAO L F, WU R R, ZHANG H. Recent development and prospect of room-temperature magnetic refrigeration materials[J].
Materials Reports, 2016, 30(3): 17-22.
|
| [11] |
郭立君, 冯再, 吴卫. 磁制冷材料绝热温变测试数据自动控制分析系统[J].
中国测试技术, 2006, 32(2): 8-11.
GUO L J, FENG Z, WU W. Control and analysis system of the adiabatic temperature changes testing of magnetic refrigerants[J].
China Measurement & Testing Technology, 2006, 32(2): 8-11.
|
| [12] |
ALAHMER A, AL-AMAYREH M, MOSTAFA A O, et al. Magnetic refrigeration design technologies: State of the art and general perspectives[J].
Energies, 2021, 14(15): 4662.
DOI:10.3390/en14154662 |
| [13] |
李建, 张斌, 马锦程, 等. Lamb波电磁超声换能器三维仿真研究[J].
中国测试, 2020, 46(9): 90-95.
LI J, ZHANG B, MA J C, et al. Research on 3D simulation of electromagnetic ultrasonic transducer based on Lamb wave[J].
China Measurement & Test, 2020, 46(9): 90-95.
|
| [14] |
杜海龙, 王琦, 周振宇, 等. 单边核磁共振Halbach磁体结构设计[J].
中国测试, 2019, 45(6): 96-100.
DU H L, WANG Q, ZHOU Z Y, et al. The structural design method of Halbach magnets for unilateral nuclear magnetic resonance[J].
China Measurement & Test, 2019, 45(6): 96-100.
|
| [15] |
BJØRK R, BAHL C R H, SMITH A, et al. Review and comparison of magnet designs for magnetic refrigeration[J].
International Journal of Refrigeration, 2010, 33(3): 437-448.
DOI:10.1016/j.ijrefrig.2009.12.012 |
| [16] |
TREVIZOLI P V, LOZANO J A, PEIXER G F, et al. Design of nested Halbach cylinder arrays for magnetic refrigeration applications[J].
Journal of Magnetism and Magnetic Materials, 2015, 395: 109-122.
DOI:10.1016/j.jmmm.2015.07.023 |
| [17] |
TEYBER R, TREVIZOLI P V, CHRISTIAANSE T V, et al. Permanent magnet design for magnetic heat pumps using total cost minimization[J].
Journal of Magnetism and Magnetic Materials, 2017, 442: 87-96.
DOI:10.1016/j.jmmm.2017.06.039 |
| [18] |
YOU Y H, GUO Y, XIAO S F, et al. Numerical simulation and performance improvement of a multi-polar concentric Halbach cylindrical magnet for magnetic refrigeration[J].
Journal of Magnetism and Magnetic Materials, 2016, 405: 231-237.
DOI:10.1016/j.jmmm.2015.12.077 |
| [19] |
ARNOLD D S, TURA A, RUEBSAAT-TROTT A, et al. Design improvements of a permanent magnet active magnetic refrigerator[J].
International Journal of Refrigeration, 2014, 37: 99-105.
DOI:10.1016/j.ijrefrig.2013.09.024 |
 2024, Vol. 50
2024, Vol. 50