文章信息
- 赵树昌, 庞茂, 张紫建
- ZHAO Shuchang, PANG Mao, ZHANG Zijian
- 基于机器视觉的苹果体积测算研究
- Research on apple volumetric calculation based on machine vision
- 中国测试, 2024, 50(6): 49-55
- CHINA MEASUREMENT & TEST, 2024, 50(6): 49-55
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022070012
-
文章历史
- 收稿日期: 2022-07-02
- 收到修改稿日期: 2022-12-30
目前,中国苹果分选大部分还是经由人工筛选,成本高、效率低[1]。近年来,机器视觉技术逐渐应用在食品无损检测领域[2]。由于我国水果检测技术还达不到现代化标准,对于苹果无损检测还存在一定的片面性,进而降低了苹果的价值[3]。苹果商品性状影响着我国苹果市场的健康发展和在国际苹果市场上的竞争力[4]。关于水果等农产品的品质鉴定和分级研究,主要涉及大小、形状、颜色等,国外对水果等农产品的分级研究比较早[5]。TAO Y 等采用多变识别技术实现对苹果和马铃薯的颜色识别,识别准确率高但效率较低[6]。BAIGVAND M 等设计的无花果干分级系统,实现了对无花果干的实时检测[7]。VENKATESH G V等人研究了基于图像处理的轴对称水果的体积,并探究了体积与质量之间的关系[8]。吴明清等人由二维图像的轮廓构建三维多轮廓模型对红枣体积进行快速测量,为红枣分级装备的开发提供技术参考[9]。刘云等人改进了一种基于RGB彩色分量算术运算的背景分割算法,对苹果缺陷进行检测,取得了较高的准确率 [10]。林静等人通过机器视觉技术设计的水果姿态图像自动采集训练检测仪,满足水果姿态自动采集及检测需求[11]。谢洪起利用机器视觉技术对猕猴桃体积进行预测,结果表明预测体积与实际体积高度相关 [12]。基于以上研究,文中提出一种基于机器视觉和积分法的苹果体积测算方法,通过微元法将苹果轮廓细分为薄片进行积分求取其体积,同时研究苹果位姿倾斜时该方法误差情况,采用投影变换对位姿倾斜苹果进行位姿矫正,使其满足使用本文所提苹果体积测算方法的要求。结果表明该文所提测算苹果体积方法误差低于2%,准确度较高且位姿矫正满足该方法测算苹果体积的要求。
1 基于积分法苹果体积测算系统 1.1 积分法测算体积的原理苹果是不规则球体,若将其按照球体体积计算,误差较大。为此本文提出,采用积分法测算苹果体积:将苹果细分为若干薄片,计算出每一个薄片的体积再相加即可得到所求苹果体积。此法来源于微元思想,如图1所示为微元法细分苹果示意图。

|
| 图 1 微元法细分苹果示意图 |
将苹果轮廓分割为无数个高为h的小矩形,每个小矩形即为每个苹果薄片在平面的投影,矩形长即是薄片的直径d,即每个薄片的体积为:
| $ {V_i} = h\pi {\left( {\frac{{{d_i}}}{2}} \right)^2} $ | (1) |
将所得到的所有苹果薄片体积相加,即可表示为下式,就得到了整个苹果的体积。
| $ V = \mathop {\lim }\limits_{h \to 0} \sum\nolimits_{i = 1}^n {\left[ {h\pi {{\left( {\frac{{{d_i}}}{2}} \right)}^2}} \right]} $ | (2) |
本实验系统主要由工业相机、光源和图像采集计算机等组成,如图2所示。其中,2台垂直布置的相机可分别获取被测苹果的水平和垂直轮廓投影图像,水平投影用于苹果轮廓获取并使用积分法进行体积测算;垂直投影用于获取苹果垂向旋转角度并使用投影变换进行位姿矫正。

|
| 图 2 苹果图像采集系统 |
系统中所采用的相机为200万像素1/1.8"CMOS的彩色千兆以太网,工业面阵相机,全局快门,相机分辨率1624 pixel×1240 pixel,像元尺寸4.5 μm ×4.5 μm。镜头选用焦距16 mm的高分辨率镜头,光圈为手动光圈。光源为白色环形光源,亮度适中,光照均匀,相机曝光时间设置为3000 μs。
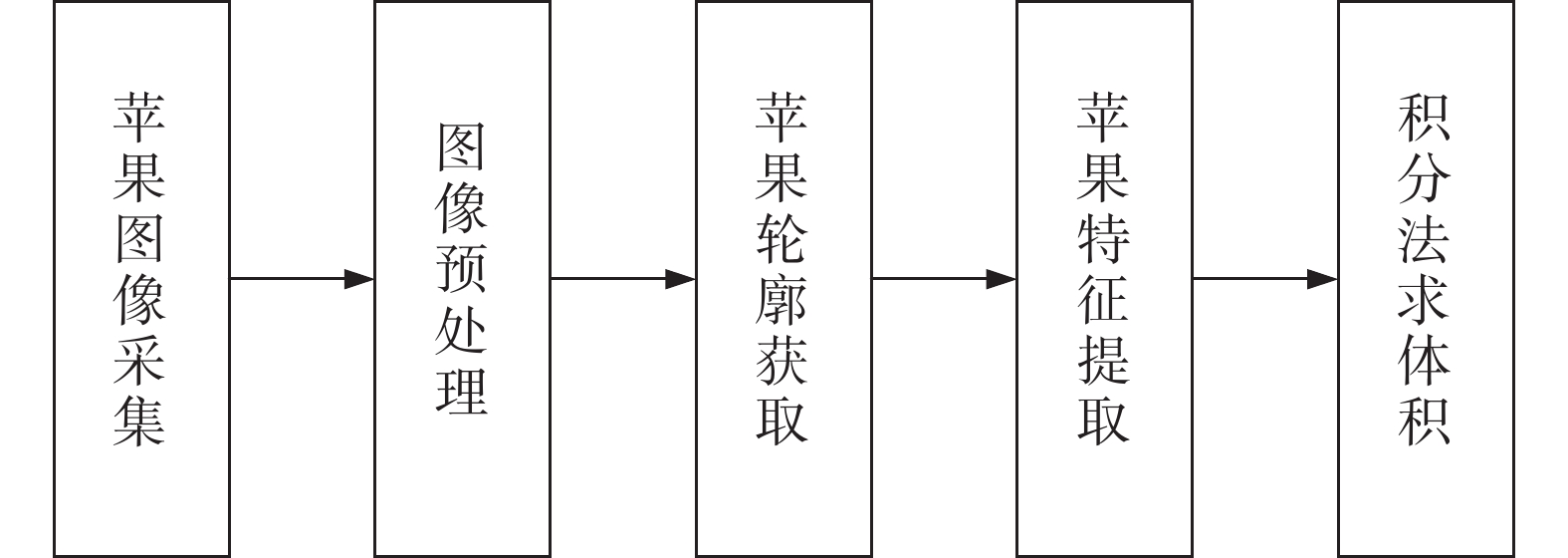
1.3 体积测算流程苹果体积测算系统主要由:苹果图像采集模块、图像预处理模块、苹果轮廓模块、积分法求体积模块组成,如图3所示为苹果体积测算流程图。
|
| 图 3 苹果体积测算流程图 |
在图3中,采集苹果图像后,为保证各个图像具有统一性,首先进入预处理模块。在处理过程中按照流程对苹果做灰度化、滤波、二值化等初步处理,将采集的彩色苹果图像转换为像素值为0的黑色背景和像素值为1的目标区域图像,进而再进行轮廓提取,最后使用积分法对苹果体积进行测算。
2 图像预处理及体积测算 2.1 高斯滤波积分法测算苹果体积时,首先需对获取的苹果图像进行预处理。为减少噪声干扰,获得更为完整的轮廓信息,使用高斯滤波对获取的图像进行高斯平滑处理。
高斯滤波的实质是构建一个平滑滤波器,通过二维零均值离散高斯函值实现,使用(5,5)的卷积扫描图像中的每一个像素,用卷积确定领域内像素的加权平均灰度值去代替卷积中心像素点的值,从而达到去除图像噪声的目的[13]。其中二维零均值离散高斯函数可表示成:
| $ G(x,y) = \frac{1}{{2\pi {\sigma ^2}}}{{\rm e} ^{ - \left( {\frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}} \right)}} $ | (3) |
式中:σ——高斯分布参数,高斯滤波器的宽度就是通过σ确定;
x——横向像素点数;
y——纵向像素点数。
图4为滤波前后的图像对比,其中图4(a)是原图,图4(b)是高斯滤波后的图像。对比发现,滤波后图像平滑了。这是由于σ越大,权重分布越均匀,图像越平滑,能较好消除图像的噪声,有利于后续的轮廓提取。

|
| 图 4 苹果图像高斯滤波前后对比 |
2.2 去边缘阴影
苹果为立体物体且表面反光,在实际现场分级筛选场景中,成像时容易产生边缘阴影,造成轮廓提取时将阴影部分识别为轮廓,增大了轮廓区域,使测算结果不准确。为消除图像采集过程中由于光照不均等原因导致的边缘阴影。通过研究发现对图像使用对数变换后即图像遍历每个像素点的对数变换,可以有效去除图像边缘阴影[14]。
对数变换公式如下:
| $ S = C \cdot {\lg}(1 + r) $ | (4) |
其中,C为常数,r≥0。
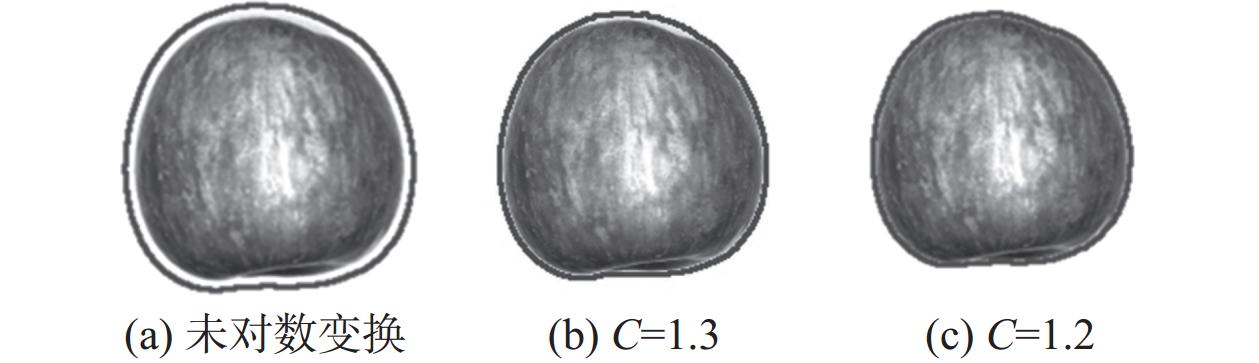
由于处理彩色三通道的数据较为复杂,造成计算量过大导致计算时间增加,故首先将图像进行灰度化处理。在灰度化过程中,阴影部分因像素值较低会被保留,如不去除,导致在后续轮廓识别时将其识别成苹果部分,造成轮廓变大。因为对数曲线在像素值较低的区域斜率较大,反之像素值较高区域斜率较低,所以对图像进行对数变换之后,阴影区域对比度得到提升像素值接近白色背景像素值,故轮廓识别时不会将其误识别为苹果。其中常数C的大小直接影响除阴影的效果,经多次实验发现本实验使用C=1.2时,去除阴影识别轮廓效果最佳,图5为对数变换前后图像对比,其中图5(a)为原图图像轮廓,图5(b)为C=1.3对数变换后的图像轮廓,图5(c)为C=1.2的图像轮廓。
|
| 图 5 苹果图像对数变换前后对比 |
图5为苹果原图轮廓与对数变换后轮廓对比,经图5对比可见,使用对数变换能有效去除边缘阴影,获取更准确的轮廓信息。
2.3 边缘提取图像预处理最终的目的是为了获取苹果的清晰边缘轮廓,边缘是图像局部灰度差异明显的区域,由灰度突变引起。本实验对比了Canny算子、Sobel算子、Laplacian算子对苹果边缘的提取效果,最终选用效果最好的Canny算子进行边缘提取[15]。
使用Canny算子提取边缘,首先要使用高斯滤波对图像进行平滑处理,同时增大边缘宽度。其次计算梯度幅值和方向,使用一阶微分来计算平滑后的图像
| $ {G_x} = \frac{{I(i,j + 1) - I(i,j) + I(i + 1,j + 1) - I(i + 1,j)}}{2} $ | (5) |
| $ {G_y} = \frac{{I(i,j) - I(i + 1,j) + I(i,j + 1) - I(i + 1,j + 1)}}{2} $ | (6) |
此时与此对应的
| $ G(i,j) = \sqrt {G_x^2(i,j) + G_y^2(i,j)} $ | (7) |
| $ \theta (i,j) = \arctan \left[ {\frac{{{G_x}(i,j)}}{{{G_y}(i,j)}}} \right] $ | (8) |
在高斯滤波的过程中,边缘可能被放大,使用非极大抑制NMS来消除边缘误检:遍历梯度矩阵上所有点,保留边缘方向上具有极大值的像素,如下式所示。目的是为将模糊的边界变得清晰,就是保留每个像素点的梯度强度的极大值,删掉其他值。
| $ M_T(i, j)=\left\{\begin{array}{l}M(i, j) ,\;\text { if } M(i, j)>T \\ 0 ,\;\text { otherwise }\end{array}\right. $ | (9) |
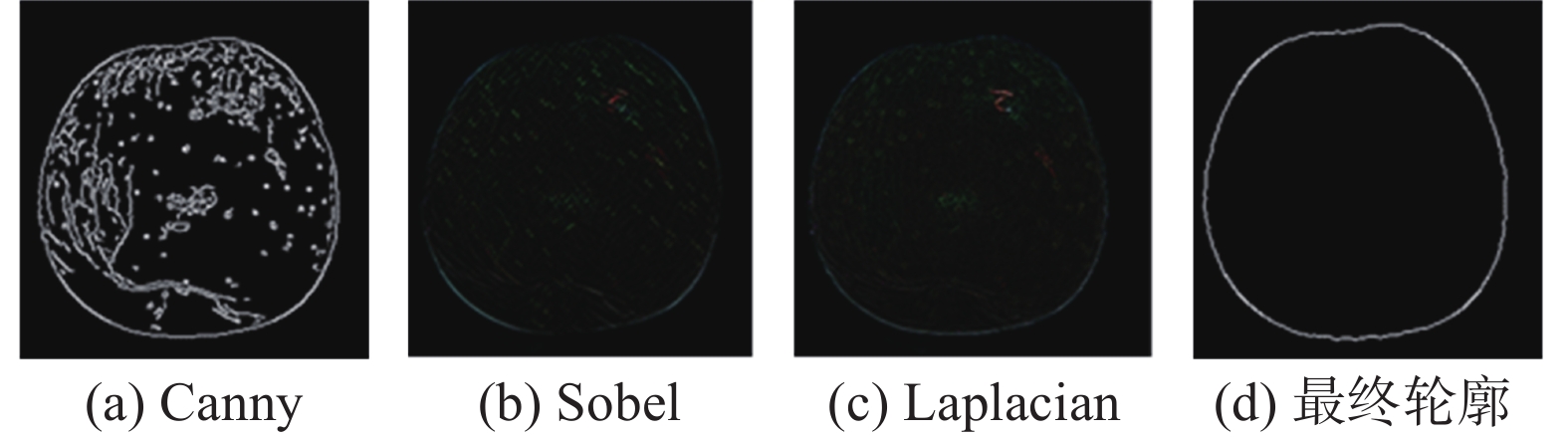
同时,使用双阈值来检测和连接最终边缘。如图6所示为三种算子提取得到的苹果边缘比较以及苹果最终的轮廓提取结果。
|
| 图 6 边缘轮廓 |
由图6可见,Sobel边缘检测和Laplacian边缘检测效果较为相似,部分区域边缘不够明显,而Canny边缘检测结果更清晰,保留了更多的细节,在后续提取最终轮廓时,保留边缘更完整,故本文采用Canny算子对苹果边缘进行识别检测。
2.4 苹果特征提取(长、宽)经图像预处理得到苹果轮廓后,提取苹果的腰径D(宽)和高度H(长),用于积分法测算苹果体积。本文使用最小外接矩形法获取苹果的长宽与实际长宽对比,如表1所示。实际人工测量使用剖面法:将苹果纵向剖开,采用准确度为0.02 mm游标卡尺测量腰径和高,每个苹果测三次取其平均值。
| mm | ||||||
| 序号 | 本文长 | 实际长 | 绝对误差 绝对值 | 本文宽 | 实际宽 | 绝对误差 绝对值 |
| 1 | 62.21 | 59.90 | 2.31 | 71.84 | 73.34 | 1.50 |
| 2 | 62.98 | 62.26 | 0.72 | 72.57 | 71.98 | 0.59 |
| 3 | 62.30 | 59.32 | 2.98 | 72.36 | 74.98 | 2.62 |
| 4 | 65.92 | 65.64 | 0.28 | 68.26 | 68.10 | 0.16 |
| 5 | 66.02 | 65.10 | 0.92 | 71.17 | 69.82 | 1.35 |
| 6 | 62.89 | 62.30 | 0.59 | 73.64 | 73.30 | 0.34 |
| 7 | 63.03 | 61.60 | 1.43 | 76.42 | 74.72 | 1.70 |
| 8 | 61.78 | 60.30 | 1.48 | 78.29 | 77.20 | 1.09 |
| 9 | 63.21 | 64.20 | 0.99 | 70.28 | 68.70 | 1.58 |
| 10 | 62.52 | 64.72 | 2.2 | 71.01 | 70.80 | 0.21 |
由表1可见,在线检测的腰径与人工检测的实际腰径平均误差绝对值为1.114 mm,高度平均相对误差绝对值1.39 mm,误差值较小,表明基于机器视觉获取的苹果特征参数与实际参数接近度高,故能够准确反应苹果实际特征。
2.5 测算苹果体积经图像预处理及获取苹果特征尺寸后,使用1.1节所提到的积分法测算体积对苹果体积进行测算。如表2所示,为部分样本使用积分法测算体积与实际体积进行对比,实际体积采用人工排水法进行测量,每个苹果测量三次,取其平均值。
| 序号 | V(实际)/ cm3 |
V(积分法)/ cm3 |
V(绝对误差 绝对值)/ cm3 |
V(相对误差 绝对值)/% |
| 1 | 180 | 174.47 | 5.53 | 0.032 |
| 2 | 163 | 161.23 | 1.77 | 0.011 |
| 3 | 163 | 164.12 | 1.12 | 0.007 |
| 4 | 180 | 181.98 | 1.98 | 0.011 |
| 5 | 178 | 176.82 | 1.18 | 0.007 |
| 6 | 182 | 180.18 | 1.82 | 0.010 |
| 7 | 168 | 172.04 | 4.04 | 0.023 |
| 8 | 178 | 178.62 | 0.62 | 0.003 |
| 9 | 170 | 171.09 | 1.09 | 0.006 |
| 10 | 181 | 181.51 | 0.51 | 0.003 |
由表2部分样本可知,积分法体积测算与实际体积最大绝对误差绝对值不超过6 cm3,平均相对误差不超过2 %,误差值较小,表明基于机器视觉和积分法的体积测量与实际测量接近度高,能够真实反映苹果体积。90个样本进行视觉测算体积用时400 s,误差1.61 %,人工用时1500 s,误差5.65 %。结果表明,视觉检测较人工检测效率明显提升,误差也较小,满足苹果在线分拣。
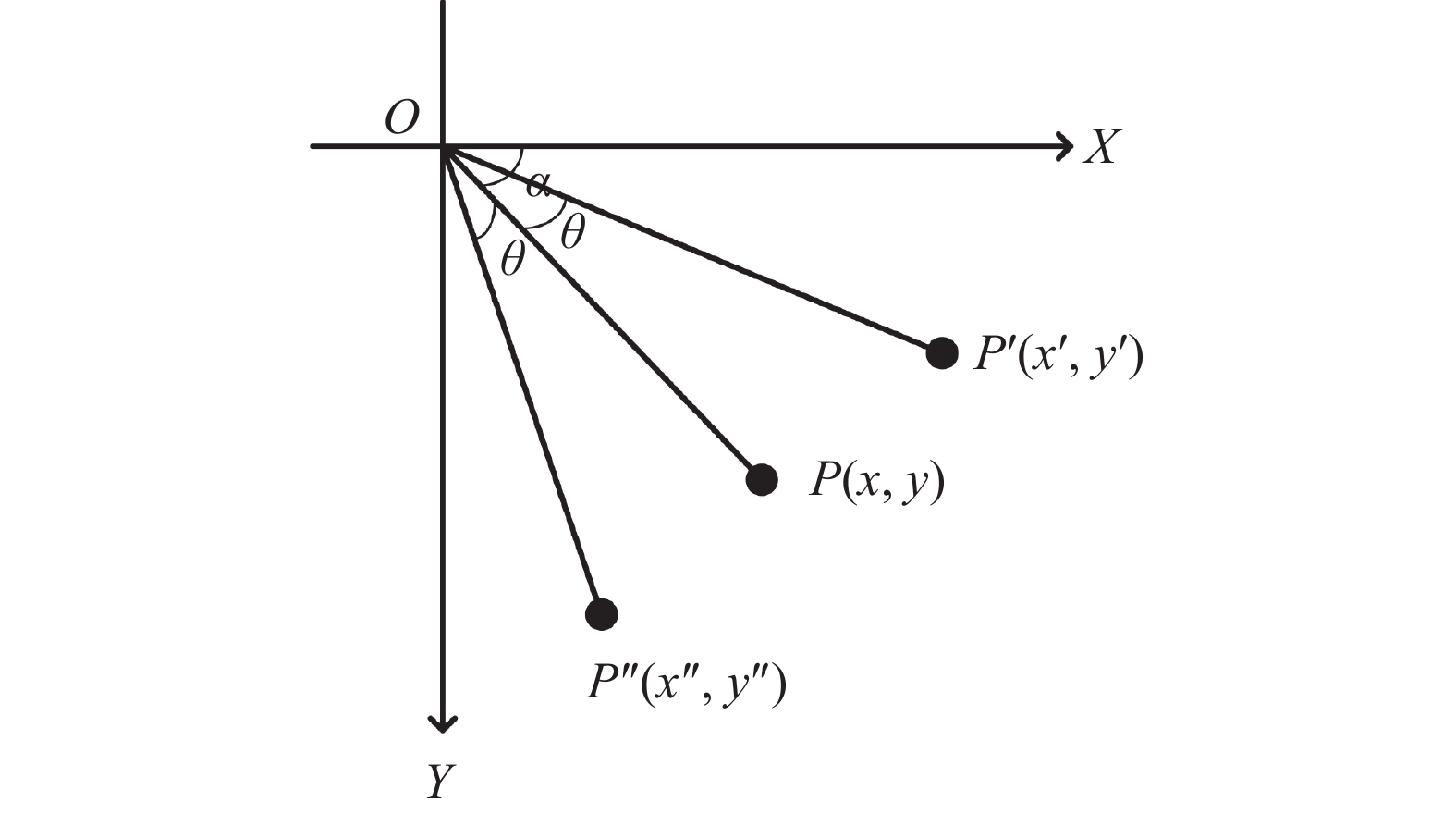
3 苹果位姿矫正 3.1 苹果角度获取苹果在积分法测算体积分拣过程中存在垂向位姿偏转的情形,针对本文采用模板匹配及仿射变换获取苹果位姿偏转角度。以逆时针方向为正,量角器量取实际角度为0°时,在苹果轮廓中画一条轴线作为基准,将不同位姿的苹果与0°姿态进行模板匹配及仿射变换从而得到相应位姿苹果轴线角度。本文使用的仿射变换原理图如图7所示。
|
| 图 7 仿射变换 |
其中,O为原点坐标,点
| $\left\{\begin{array}{l}x=\cos \alpha \\ y=\sin \alpha\end{array}\right.$ | (10) |
顺时针时:
| $ \left\{\begin{array}{l}x^{\prime \prime}=\cos (\alpha-\theta)=x \cdot \cos \theta+y \cdot \sin \theta \\ y^{\prime \prime}=\sin (\alpha-\theta)=y \cdot \cos \theta-x \cdot \sin \theta\end{array}\right. $ | (11) |
R为单位矩阵,则顺时针旋转矩阵R''为:
| $ {\boldsymbol{R}}''=\left[\begin{array}{cc}\mathrm{cos}\theta & \mathrm{sin}\theta \\ -\mathrm{sin}\theta & \mathrm{cos}\theta \end{array}\right] $ | (12) |
通过上述放射变换的旋转后,得到苹果角度,如图8所示为苹果角度检测效果图,其中前者为实际偏转角度,后者为视觉测量角度。

|
| 图 8 苹果角度检测效果图 |
90个样本使用仿射变换测量倾斜角度,与实际倾斜角度绝对误差均在5°以内,平均绝对误差为3.026°,误差较小,表明机器视觉测量的角度与实际角度接近,采用仿射变换能够准确反映苹果位姿。与此同时,由于苹果位姿的改变,导致苹果腰径和高发生变化,以及积分法测算体积误差增大,以2.5节绝对误差绝对值超过6 cm3为积分法失效。本文研究了苹果在不同角度时使用积分法测算体积的变化,表3为部分样本苹果不同角度时,实际体积与积分法体积的对比。
| cm3 | |||||
| 序号 | |||||
| 1 | 182 | 185.03 | 3.03 | 189.03 | 7.03 |
| 2 | 163 | 166.05 | 3.05 | 172.66 | 9.66 |
| 3 | 163 | 167.19 | 4.09 | 172.38 | 9.38 |
| 4 | 180 | 182.73 | 2.73 | 186.87 | 6.87 |
| 5 | 178 | 181.09 | 3.09 | 186.25 | 8.25 |
经统计90个样本得,在苹果垂向倾斜角度达到15°时,体积平均绝对误差为7.712 cm3,故垂向倾斜角度超过15°时,积分法求苹果体积失效,若继续使用本文积分法求体积,需进行位姿矫正。为方便描述将垂向倾斜定义为X轴倾斜。
同时,为验证本文所提出的积分法测算苹果体积的准确性,现将苹果放置在可旋转的滚筒架内,滚筒架一端可加高调整到使苹果沿X轴倾斜0°、10°和15°。直流电机通过皮带和齿轮带动滚筒转动且旋转方向为Y轴方向,从而实现苹果可在Y轴任意角度的转动,同时相机进行连续的图像采集。最终分别获取0°、10°和15°时的任意角度的苹果腰径D和苹果体积,并与实际腰径和体积进行对比,分析不同的D对体积误差的影响,滚筒架如图9所示。

|
| 图 9 滚筒架 |
其中,同一苹果不同X轴角度时Y轴任意旋转角度的腰径D与体积误差对比如表4所示。
| 角度 | 腰径D/mm | 体积V | |||||
| 实测 | 视觉 测量 |
绝对误差 绝对值 |
实测/cm3 | 积分法/cm3 | 相对 误差/% |
||
| 0° | 70.06 | 71.50 | 1.44 | 170 | 171.78 | 0.0104 | |
| 10° | 70.62 | 71.87 | 1.25 | 170 | 172.39 | 0.0139 | |
| 15° | 71.46 | 72.59 | 1.13 | 170 | 175.16 | 0.0295 | |
由表4可知,同一苹果不同X轴角度时Y轴任意旋转角度的腰径D误差不超过1.5 mm,误差较小;体积绝对误差5.16 cm3小于6 cm3,且相对误差不超过3%,误差较小。实验结果表明,积分法测算苹果体积时由于腰径D的变化使沿Y方向旋转时确实存在误差,但误差较小,不影响本文所提积分法测算苹果体积的准确性。
3.2 苹果图像位姿矫正以实际角度0°图像为模板,使用模板匹配判断苹果垂向倾斜角度是否超过15°,因超过15°时积分法求体积失效,故需进行位姿矫正,不超15°的直接进行积分法求体积,图10为检测苹果垂向倾斜角度是否超过15°,是否需进行位姿矫正的流程图,本文所使用投影变换原理图如图11所示。
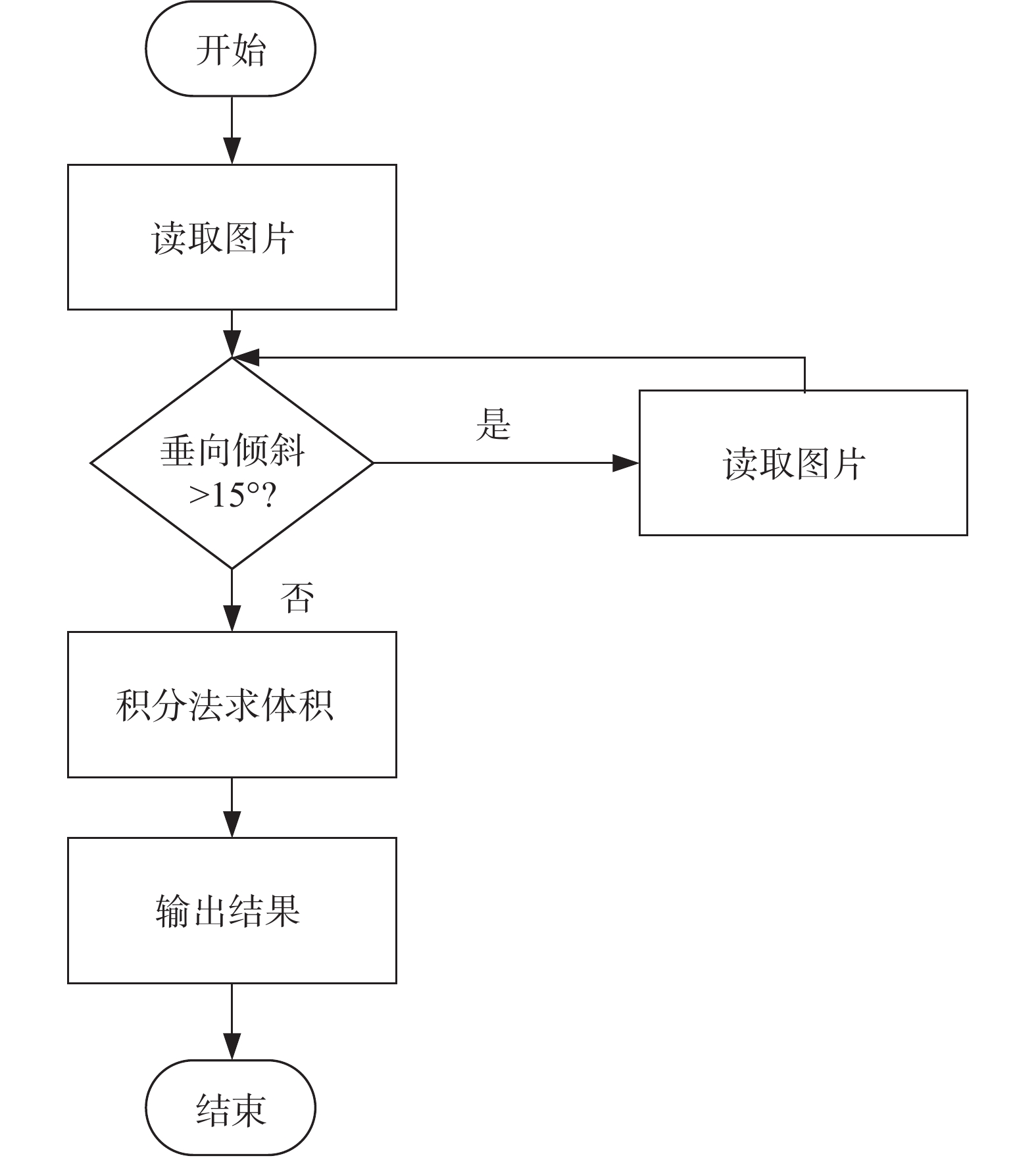
|
| 图 10 位姿矫正检测流程图 |
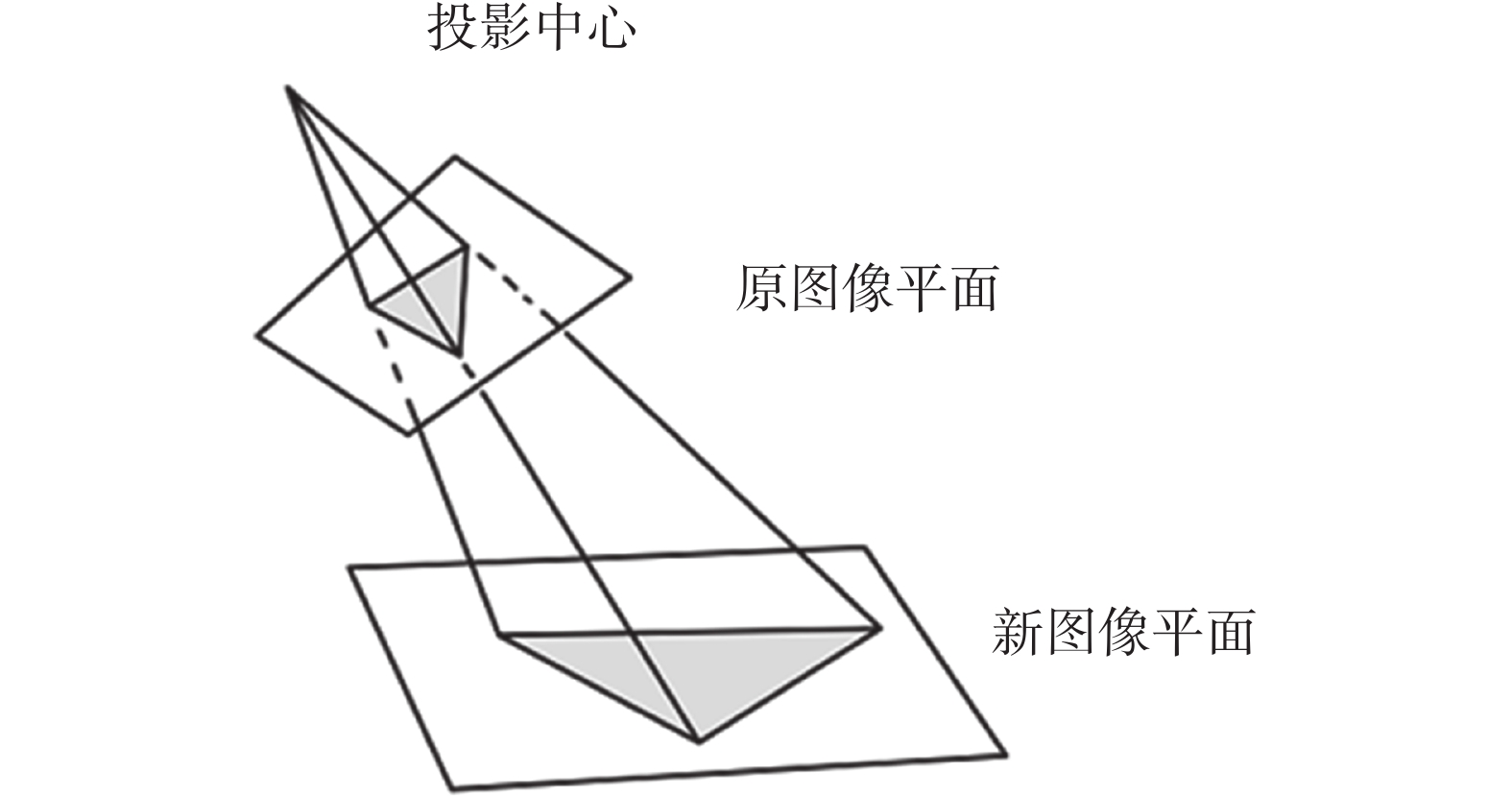
|
| 图 11 投影变换原理图 |
其中,变换公式为:
| $ \left[ {\begin{array}{*{20}{c}} X \\ Y \\ Z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}} \\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}} \\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_0}} \\ {{y_0}} \\ 1 \end{array}} \right] $ | (13) |
其中,

|
| 图 12 投影变换前后对比 |
为验证针对本文采用的投影变换位姿矫正的效果,现将一苹果垂向倾斜30°时,向0°进行矫正,矫正前后对比如表5所示。
| 0° | 30° | 30°(变) | V(0°)/ cm3 |
V(30°)/ cm3 |
V变(30°)/ cm3 |
|||||
| 长/mm | 宽/mm | 长/mm | 宽/mm | 长/mm | 宽/mm | |||||
| 62.50 | 71.09 | 69.59 | 71.37 | 62.71 | 70.54 | 181.51 | 189.87 | 184.39 | ||
通过对比可知,变换后与0°对比体积相对误差为1.56 %,绝对误差为2.88 cm3小于6 cm3,对比其他样本,误差均在6 cm3以内,故本文采用的投影变换位姿矫正可以有效对苹果位姿进行矫正。
4 结束语传统苹果体积测算效率低且视觉检测时对于发生垂向倾斜情境下的苹果进行体积测算误差大,不能满足苹果在线分选。本文提出的积分法测算体积与实际体积相对误差低于2 %,最大绝对误差不超过6 cm3,检测准确性较高;苹果沿垂向倾斜角度达到15°时,测算体积与实际体积绝对误差为7.712 cm3大于6 cm3,故积分法失效;对垂向倾斜角度超过15°的苹果,进行位姿矫正后平均误差为3.376 cm3小于6 cm3,验证了该位姿矫正方法适用于积分法测算体积。文中所提积分法测算苹果体积极大提高了苹果体积测量精度,为苹果分级提供了有利技术参考。
| [1] |
高辉, 马国峰, 刘伟杰. 基于机器视觉的苹果缺陷快速检测方法研究[J].
食品与机械, 2020, 36(10): 125.
|
| [2] |
汤钦林. 禽蛋食品在线智能品质检测控制系统研究与设计[J].
食品工业, 2020, 41(5): 223.
|
| [3] |
赵丹丹, 艾医. 基于计算机视觉的苹果大小检测方法研究[J].
农机化研究, 2022, 44(7): 206.
|
| [4] |
王心悦, 迟馨, 杜晓云, 等. 苹果商品性状的表观指标及影响因素[J].
中国果菜, 2019, 39(5): 28-31.
|
| [5] |
倪云峰, 叶健, 樊娇娇. 基于图像识别的水果分拣系统[J].
江苏农业科学, 2021, 49(10): 170-176.
|
| [6] |
TAO Y, HEINEMANN P H, VARGHESE Z, et al. Machine vision for color inspection of potatoes and apples[J].
Transactions of the ASAE, 1995, 38(5): 1555-1561.
DOI:10.13031/2013.27982 |
| [7] |
BAIGVAND M, BANAKAR A, MINAEI S, et al. Machine vision system for grading of dried figs[J].
Computers and Electronics in Agriculture, 2015, 119: 158-165.
DOI:10.1016/j.compag.2015.10.019 |
| [8] |
VENKATESH G V, IQBAL S M, GOPAL A, et al. Estimation of volume and mass of axi-symmetric fruits using image processing technique[J].
International Journal of Food Properties, 2014, 18(3): 608-626.
|
| [9] |
吴明清, 弋晓康, 罗华平, 等. 基于多轮廓模型的红枣体积和表面积在线测量方法[J].
农业工程学报, 2019, 35(19): 283-90.
|
| [10] |
刘云, 杨建滨, 王传旭. 基于卷积神经网络的苹果缺陷检测算法[J].
电子测量技术, 2017, 40(3): 108-112.
|
| [11] |
林静, 徐月华. 水果姿态图像自动采集训练检测仪设计[J].
中国测试, 2021, 47(7): 119-124.
|
| [12] |
谢洪起. 基于RGB-D相机的猕猴桃外形和体积检测方法研究[D]. 杨凌: 西北农林科技大学, 2018.
XIE H Q. Research on kiwifruit shape and volume detection method based on RGB-D camera [D]. Yang Ling: Northwest A&F University, 2018.
|
| [13] |
谈杰, 范乃吉, 白斌, 等. 高斯滤波对规则斑点图像的亚像素匹配精度影响研究[J].
中国测试, 2022, 48(4): 6-11.
|
| [14] |
丰远远, 高贤君, 杨元维, 等. 改进对数变换联合局部增强的高分遥感影像阴影自动补偿方法[J].
激光与光电子学进展, 2020, 57(20): 67-75.
|
| [15] |
周志宇, 刘迎春, 张建新. 基于自适应Canny算子的柑橘边缘检测[J].
农业工程学报, 2008(3): 21-24.
|
 2024, Vol. 50
2024, Vol. 50


 ,
,