文章信息
- 李睿智, 杨芳华, 张伟, 周旗开
- LI Ruizhi, YANG Fanghua, ZHANG Wei, ZHOU Qikai
- 基于ShuffleNet-DELM的轴承故障诊断研究
- Research on bearing fault diagnosis based on ShuffleNet-DELM
- 中国测试, 2024, 50(6): 42-48
- CHINA MEASUREMENT & TEST, 2024, 50(6): 42-48
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022050075
-
文章历史
- 收稿日期: 2022-05-12
- 收到修改稿日期: 2022-07-06
在各种机械中,滚动轴承是一种常见的结构,它承担着力矩传递的重要作用,是整个机电系统中的关键器件,同时也最易发生故障。据不完全统计,在全世界每年发生的机械故障中,因滚动轴承引发的占到约30%[1]。轴承一旦发生故障,设备往往被迫停机,甚至还会造成整体损坏。由于轴承是一种封闭性的结构,直接观测故障难以实现。因此,人们对其振动信号进行监测,此类信号中包含轴承运行的丰富状态信息,能够有效地监测轴承的运行状态。
轴承的振动信号均有非平稳、非线性的特性[2],通常为时域信号。传统的故障诊断方法中,常见的是提取人工设计的特征信息,严重依赖专家的经验,且泛化能力有限,适用性不强。随着硬件的发展和深度学习技术的突破,在图像分类领域的卷积神经网络(convolutional neural networks,CNN)和相关技术也被应用于分类任务中[3-4]。2012年,Alex等首次证明了神经网络自行学习到的数据特征能够优于专家人为提取的特征,其卷积层加池化层的基本结构被后续的研究人员沿用和借鉴。后续出现的新模型有些叠加卷积层数量,加深网络深度,如VGG系列;或者增加并行模块,拓宽网络宽度,如GoogLeNet、Inception等。
然而,传统的卷积神经网络深度和宽度增加后带来庞大的计算量和过高的硬件需求。为此,许多学者使用新卷积模型,如轻量级架构Xception、MobileNet、ShuffleNet[5]等,为故障特征提取提供强有力的技术支撑。也有的与传统机器学习方法相结合,或尝试引入新的功能模块。杨劼立等[6]使用MED强化冲击特征,再与原信号融合后作为CNN的输入,在噪声环境下对列车轴承故障进行分类,取得了良好效果。雷亚国等[7]提出了一种深度归一化卷积神经网络(DNCNN),并在不平衡数据下对滚动轴承的故障进行识别,取得了较好的效果。
在以上研究以及当前大多数方法中,对于充足数据量下同类别故障的分类识别准确率普遍已经高于99%,对于工程实际而言,再提高的意义有限。相比之下,模型或者方法的运行效率、泛化能力和抗噪声能力更加重要。基于以上考虑,本文通过改进的轻量级ShuffleNetV2模型提取故障特征,再使用DELM方法进行分类,以较少的参数量和运算数实现了不同工况下轴承故障诊断较强的泛化能力和强噪声干扰下较高的故障识别精度。
1 基本理论 1.1 ShuffleNetV2基本结构ShuffleNetV2在ShuffleNetV1的基础上进行了较大改动,其连接方式借鉴了残差网络的典型方法,基本结构中重点包含了深度卷积(Depthwise Conv)和通道混洗(Channel Shuffle)机制。
标准卷积中每个卷积核的通道单独做卷积运算后相加[8]。深度可分离卷积分为深度卷积和点卷积(Pointwise Conv),深度卷积中一个卷积核只负责一个通道的计算;点卷积会将上一步骤深度卷积输出的特征图在深度方向进行加权混合,生成新的特征图。深度卷积与标准卷积的区别如图1所示。
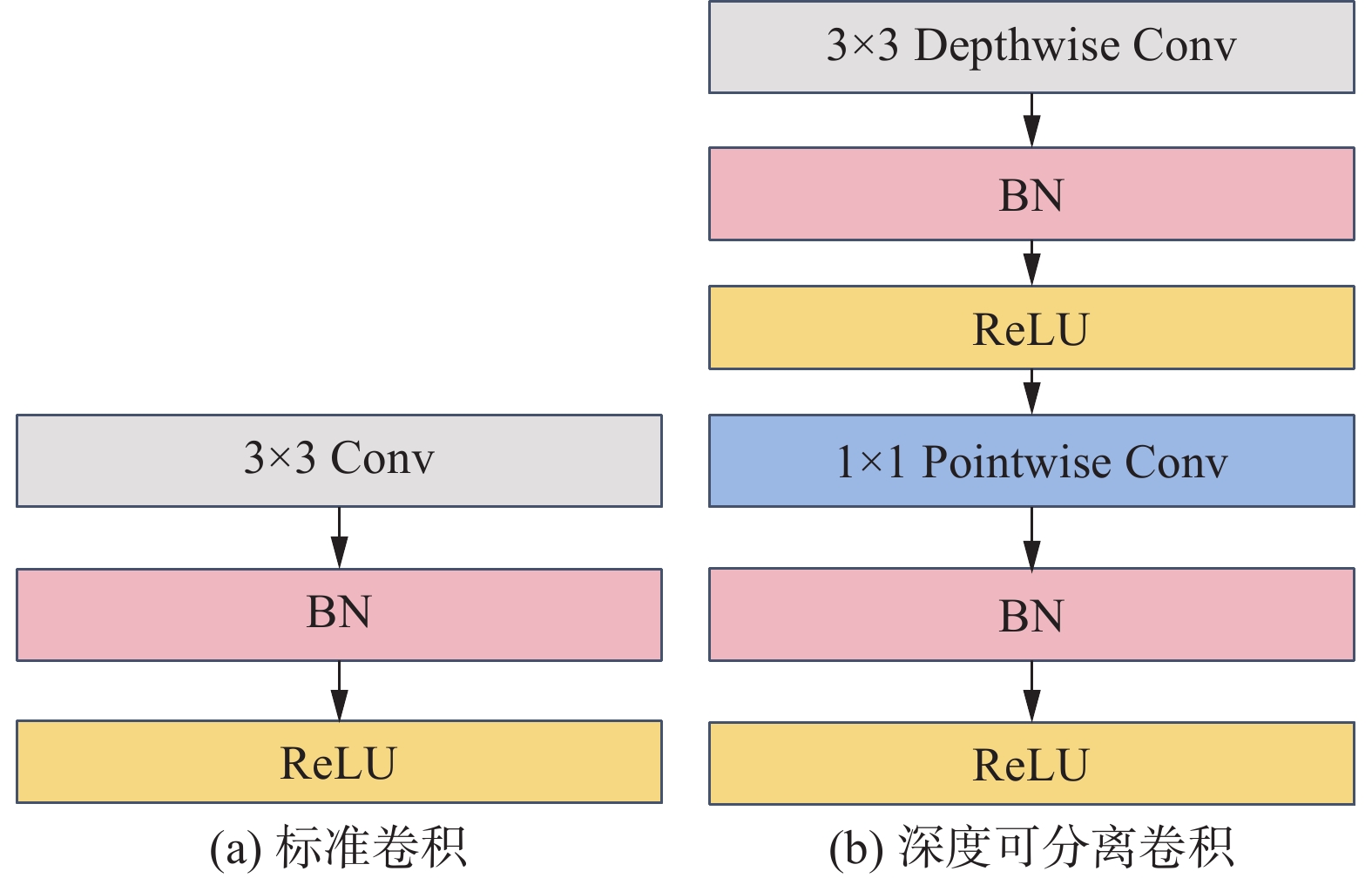
|
| 图 1 标准卷积与深度可分离卷积 |
与标准卷积相比,深度可分离卷积能够显著减少参数量(Parameters)和浮点运算数(FLOPs),二者比值公式如下:
| $ \frac{{{P_{{\text{DS}}}}}}{P} = \frac{{{F_{{\text{DS}}}}}}{F} = \frac{1}{N} + \frac{1}{{{K^2}}} $ | (1) |
式中:
该方法在效果相同的情况下,可以使运算速度大幅提升。
通道混洗基本原理如图2所示。其目的是将经由深度卷积的独立通道进行充分混合,以实现信息交流[5]。

|
| 图 2 通道混洗示意图 |
ShuffleNetV2包含两种基本单元,基本结构如图3所示。其中基本单元1的输入特征图与输出特征图有相同的通道数,该单元一般连接在单元2之后。特征图首先通过Channel Split,分成两个具有相同通道数的分支。左边分支恒定不变,右边分支经过3个步长为1的卷积,其中两个1×1卷积是普通卷积,3×3卷积是深度卷积。卷积完成后,将两个分支进行Concat操作,通道数重新合并,最后使用通道混洗使通道充分融合。在单元2中,将特征图在两个分支中并行处理,其中3×3深度卷积的步长为2,用以实现特征降维,减少计算量。接着,同样进行Concat操作,通道数翻倍,网络的宽度增加,最后同样进行通道混洗。
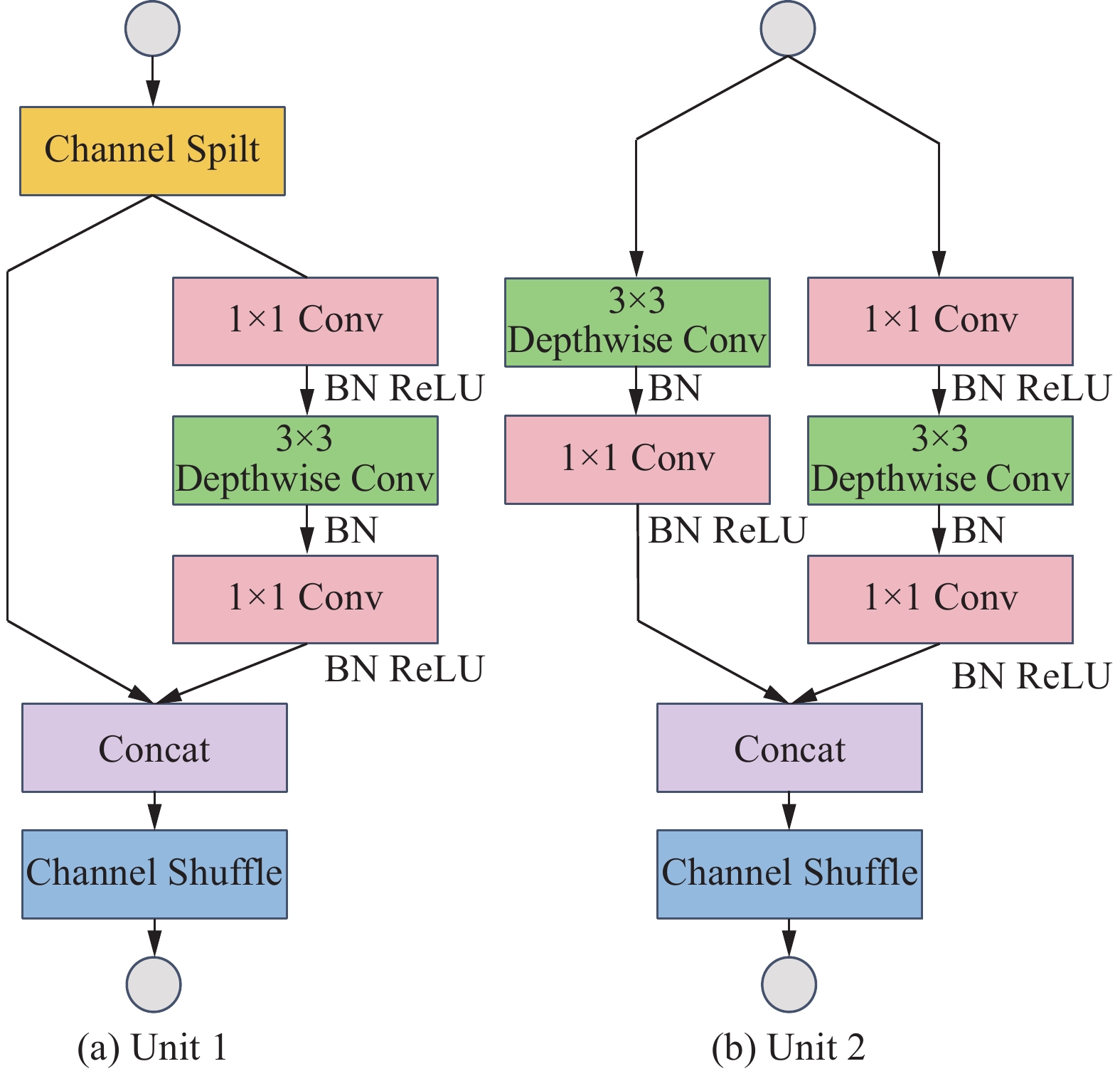
|
| 图 3 两种典型的ShuffleNetV2单元 |
ShuffleNetV2最大的特点在于应用了文献[5]中提出的4条设计准则,该准则既兼顾了减少浮点运算数,又着重缩减了内存访问成本,因而能够达到同等精度模型中极致的运行速度。
1.2 深度极限学习机极限学习机(extreme learning machine,ELM)是一种单隐层前馈神经网络,其隐藏层的输入权重和阈值可以随机产生,并不需要和现在普遍使用的梯度下降法一般对参数进行反向传播,逐步更新,而是可以通过广义逆矩阵理论一次性算出输出权重并完成学习,因此具有学习速度快和泛化能力强等优点。自动编码器(autoencoder,AE)是一种无监督学习算法。本文将二者相结合形成ELM-AE网络,如图4所示。
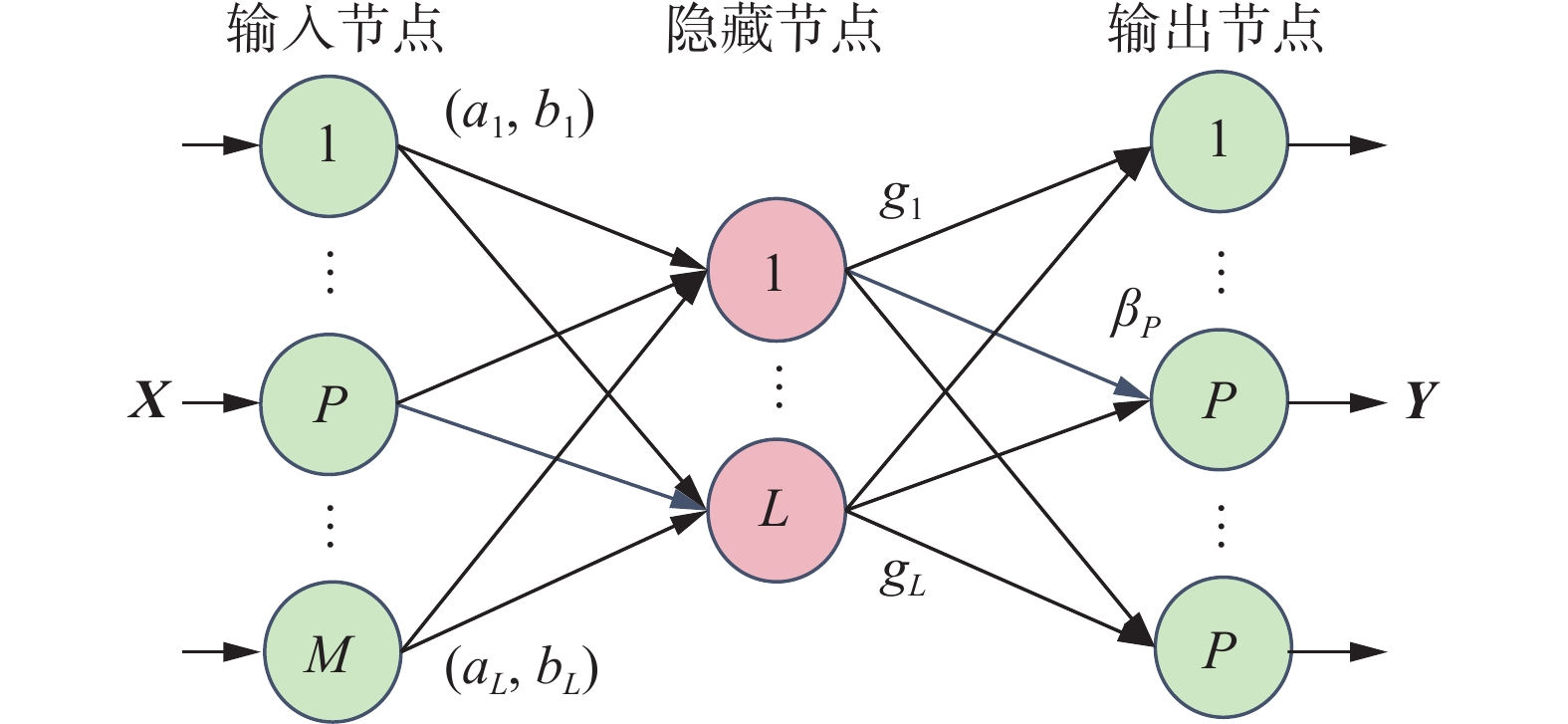
|
| 图 4 ELM-AE网络结构图 |
通过控制图中M和L的大小关系,ELM-AE能够实现维度缩放或者恒等映射,相当于一个通用的逼近器。隐藏层的输出权重
| $ {\boldsymbol{\beta}} = \left( {{\boldsymbol{H}}{{\boldsymbol{H}}^{\text{T}}} + \frac{1}{N}} \right){{\boldsymbol{H}}^{\text{T}}}{\boldsymbol{X}} $ | (2) |
式中:
深度极限学习机通常由多个ELM-AE单元堆叠而成,本文处理的是经由ShuffleNetV2提取出的特征张量,因而计算复杂度相对较低,综合考虑运行效率,使用单层DELM已经能够达到较为理想的效果。
2 基于ShuffleNet-DELM的诊断方法本文使用的ShuffleNet-DELM基本结构和方法如图5所示。该模型在原ShuffleNetV2的基础上进行了大量简化。输入特征图大小为32×32×1,先通过一个大小为3×3,步长为1,通道为24的标准卷积;接着连接一个3×3,步长为1的最大池化层。再接3个ShuffleNetV2模块,每个模块由1个单元2和1个单元1连接而成。3个Stage通道数分别为32、64、128。随后再连接1个卷积层,全局均池化层和全连接层。

|
| 图 5 ShuffleNet-DELM方法示意图 |
训练过程中,首先使用训练集进行训练,将模型参数调整至最优。该过程使用经典梯度下降法进行参数迭代更新,与常规的深度学习算法一致,DELM不进行参与。训练结束后,从全局平均池化层中提取训练数据的特征张量,输入DELM进行训练,其隐藏层数设置为800。最后,将测试集输入模型,此时该模型有2个结果,1个经由全连接层输出,1个经由DELM输出,可以很方便地对最终结果进行比对。
3 实验验证和性能分析 3.1 数据集处理本文使用的轴承数据集选自美国西储大学(CWRU)轴承试验台[9],电机近似转速为1730~1797 r/min。选取来自驱动端采样频率为12 kHz的数据,包括正常、内圈故障、滚动体故障和外圈故障(选择6点钟方向)4种典型状态,每种故障有3种损伤尺寸,因此一共将数据集分为10种类型。
依据工况的不同将驱动端数据分为A、B、C 3个数据集,分别对应原始数据的1、2、3工况。以2 048个采样点为一个样本,约等于轴承自转的5个周期。采用步长为128个点的滑动时间窗口法进行取值,按照约7:1.5:1.5的比例划分训练集、验证集和测试集,每个类别得到训练样本650个,验证样本140个,测试样本140个。数据集A具体情况如表1所示,数据集B、C除工况外划分方法均与A相同。
| 故障 类型 | 损伤尺寸/mm | 标签 | 训练 样本 | 验证 样本 | 测试 样本 |
| 正常 | – | 0 | 650 | 140 | 140 |
| 内圈 | 0.178 | 1 | 650 | 140 | 140 |
| 0.356 | 2 | 650 | 140 | 140 | |
| 0.533 | 3 | 650 | 140 | 140 | |
| 外圈 | 0.178 | 4 | 650 | 140 | 140 |
| 0.356 | 5 | 650 | 140 | 140 | |
| 0.533 | 6 | 650 | 140 | 140 | |
| 滚动体 | 0.178 | 7 | 650 | 140 | 140 |
| 0.356 | 8 | 650 | 140 | 140 | |
| 0.533 | 9 | 650 | 140 | 140 |
随机选取数据集A中每个状态各一个样本,均为一维时域数据,将其进行0-1标准化后如图6所示。将每个样本分别加汉明窗后进行快速傅里叶变换,获得频域特征数据,因其对称性的特点,取1024个点为一个样本,0-1标准化后结果如图7所示。

|
| 图 6 不同状态的轴承样本时域图 |

|
| 图 7 不同状态的轴承样本频域图 |
相比之下,频域数据更能反映轴承的故障特征,其不同状态的特点区分更为显著,且不易受噪声干扰,有利于模型的识别分类。在最后的输入模型前使用Python自带的reshape函数将大小为1×1024的输入向量在列的方向进行纵向堆叠,此时一维数据变换为大小32×32的二维数据,以符合卷积神经网络的计算要求。
本文中所有实验均在Windows11环境下完成,CPU为AMD Ryzen 7 5800H with Radeon Graphics,GPU 为NVIDIA GeForce RTX 3060,所用语言为 Python3.8,代码使用深度学习框架Tensorflow 2.4.1编写。
3.2 实验验证过程 3.2.1 不同工况准确率测试使用本文模型依次在A、B、C 3个数据集上进行训练,并用训练好的模型在另外2个数据集上直接进行预测。使用文献[10]中的人工特征+SVM模型、文献[11]中的WDCNN以及本文的ShuffleNetV2作为对比实验。均进行10次并取平均值,如表2所示。
| % | ||||
| 方法 | 人工特征+SVM | WDCNN | ShuffleNetV2 | ShuffleNet-DELM |
| A-B | 86.80 | 92.20 | 99.13 | 99.26 |
| A-C | 71.00 | 91.00 | 93.64 | 93.94 |
| B-A | 92.80 | 95.10 | 95.22 | 95.40 |
| B-C | 79.40 | 91.50 | 90.54 | 90.78 |
| C-A | 63.80 | 78.10 | 93.21 | 94.02 |
| C-B | 70.80 | 85.10 | 98.91 | 99.42 |
| 均值 | 77.10 | 90.00 | 95.11 | 95.47 |
从结果中可以看出,本文使用的ShuffleNetV2有明显优势,在6个预测结果中没有明显短板,相比之下,其余2种参照方法在C-A的预测中有明显不足。这是由于ShuffleNetV2中的深度卷积相当于使卷积核提取特征空间的相关性与通道的相关性进行解耦[12],而混洗机制则使特征实现充分融合,从而使特征的学习更加充分,最终的准确率更好。
随机选取C-A预测的一次结果,生成如图8所示的混淆矩阵。从混淆矩阵分析可得,较多标签为7和9的滚动体故障误判为同样是滚动体故障的标签8。从故障机理上讲,滚动体在转动时,既有自转也有公转,且故障部位与内外圈均有碰撞,还受到保持架影响;同时,故障冲击振动传播路径长,过程中受到的影响干扰最多,故障特征微弱,理论上识别困难是最高的。
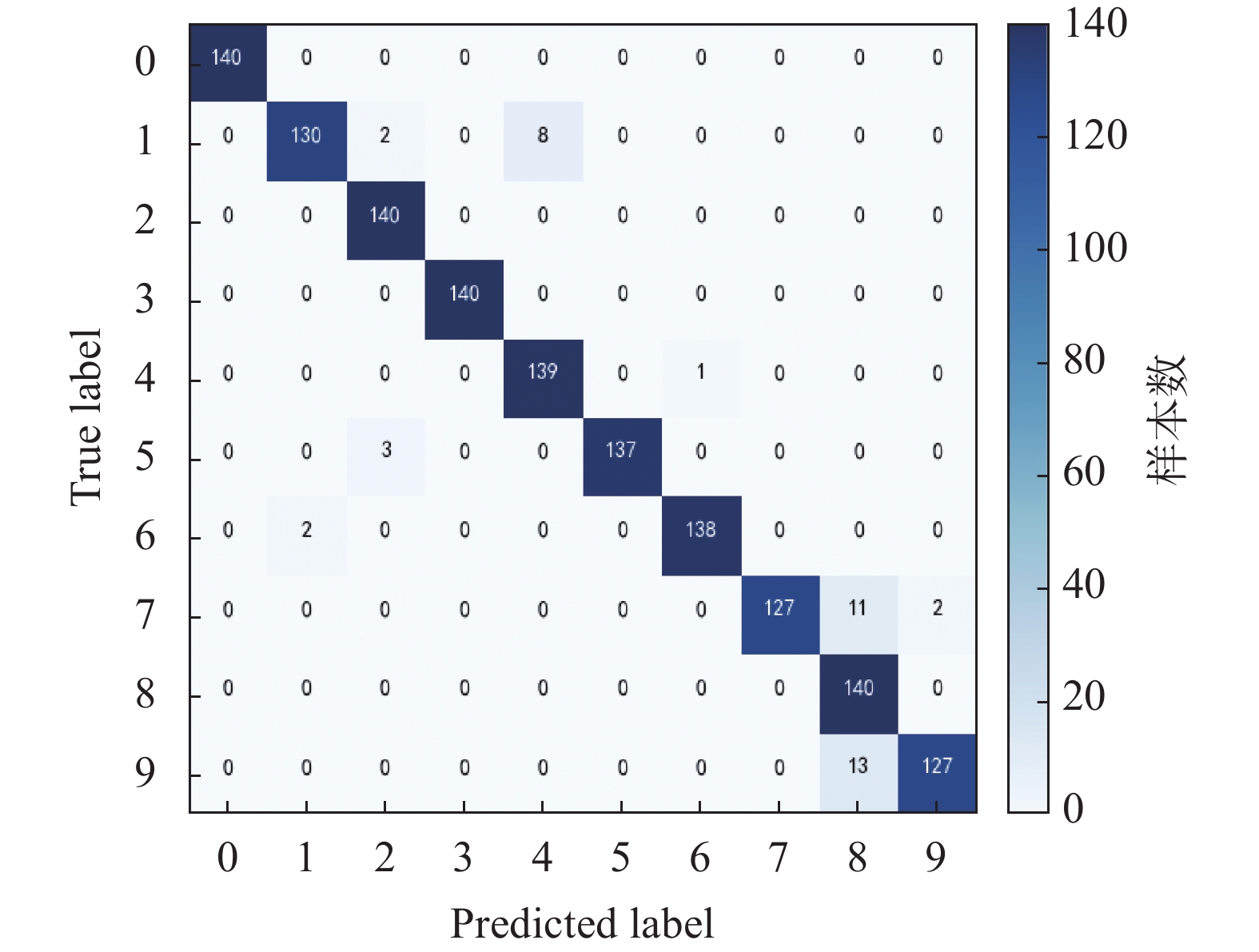
|
| 图 8 本文方法在C-A分类上的混淆矩阵 |
3.2.2 高噪声环境下性能验证
选取数据集A,在训练集、验证集和测试集中均加入逐步增强的高斯白噪声,信噪比SNR分别设置为–2 dB到–10 dB,步长为2。选取文献[13]的模型TICNN和文献[14]的DCVAEN进行比对,分别进行10次取平均值,结果如表3所示。其中TICNN使用的是原始一维时序数据作为输入,DCVAEN使用的是一维频域数据作为输入,超参数均已调整至最优。
| % | ||||
| SNR/dB | DCVAEN | TICNN | ShuffleNet V2 |
ShuffleNet– DELM |
| –2 | 97.05 | 88.61 | 99.88 | 99.99 |
| –4 | 96.26 | 86.27 | 99.86 | 97.46 |
| –6 | 94.64 | 85.09 | 99.67 | 92.23 |
| –8 | 91.03 | 76.80 | 98.84 | 87.98 |
| –10 | 85.33 | 26.01 | 95.49 | 71.40 |
从以上实验结果可以看出,随着加入噪声不断增强,本文的ShuffleNetV2抗噪声能力最好且稳定,而加入DELM后的抗噪声能力在SNR为–4 dB之前有一定的提升,但在噪声逐渐增大后数据波动剧烈,效果反而变差,说明DELM在具体应用中还应视情况而使用。
4 结束语针对传统轴承故障诊断方法结构冗余、运行效率低、泛化能力不足的问题,提出了改进的ShuffleNet-DELM故障诊断方法。实验结果表明,该模型在轴承故障诊断中具有良好的性能。主要结论如下:
1)改进后的ShuffleNetV2模型以及ShuffleNet-DELM方法能够有效地进行变工况条件下的轴承故障诊断。
2)将一维数据直接变换成二维数据,并使用图像分类的模型和方法对轴承振动数据进行处理是可行且有效的。
3)本文数据集使用的快速傅里叶变换丢失了时间信息,后续可以尝试对小波变换生成的时频图进行分类,并比对效果。对于DELM抗噪声能力不足的机理也需进一步研究测试。
| [1] |
GAN M, WANG C, ZHU C. Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings[J].
Mechanical Systems and Signal Processing, 2016, 72-73: 92-104.
DOI:10.1016/j.ymssp.2015.11.014 |
| [2] |
CERRADA M, SANCHEZ R , LI C, et al. A review on data-driven fault severity assessment in rolling bearings[J]. Mechanical Systems & Signal Processing, 2018, 99: 169-196.
|
| [3] |
赵朋成, 冯玉田, 涂云轩. 基于高倍特征深度残差网络的手写数字识别[J].
电子测量技术, 2018, 41(6): 86-89.
ZHAO P C, FENG Y T, TU Y X. Handwritten digital recognition based on high times feature deep residual network[J].
Electronic Measurement Technology, 2018, 41(6): 86-89.
DOI:10.19651/j.cnki.emt.1701304 |
| [4] |
张西宁, 郭清林, 刘书语. 深度学习技术及其故障诊断应用分析与展望[J].
西安交通大学学报, 2020, 54(12): 1-13.
ZHANG X N, GUO Q L, LIU S Y. Analysis and prospect of deep learning technology and its fault diagnosis application[J].
Journal of Xi'an Jiaotong University, 2020, 54(12): 1-13.
|
| [5] |
MA N, ZHANG X, ZHENG H T, et al. Shufflenet v2: Practical guidelines for efficient CNN architecture design[C]//Proceedings of the European conference on computer vision (ECCV), 2018.
|
| [6] |
杨劼立, 林建辉, 谌亮. 基于MED辅助特征提取CNN模型的列车轴承故障诊断方法[J].
中国测试, 2020, 46(10): 124-129.
YANG J L, LIN J H, CHEN L. Fault diagnosis method for train bearings based on MED-assisted feature extraction CNN model[J].
China Measurement & Testing Technology, 2020, 46(10): 124-129.
|
| [7] |
雷亚国, 贾峰, 孔德同, 等. 大数据下机械智能故障诊断的机遇与挑战[J].
机械工程学报, 2018, 54(5): 94-104.
LEI Y G, JIA F, KONG D T, et al. Opportunities and challenges of machinery intelligent fault diagnosis in big data era[J].
Journal of Mechanical Engineering, 2018, 54(5): 94-104.
|
| [8] |
牛罡, 张凯, 郭祥富, 等. 格拉米角场和图卷积神经网络识别复杂电能质量扰动[J].
中国测试, 2022, 48(7): 169-176.
NIU G, ZHANG K, GUO X F, et al. Complex power quality disturbance identification based on Gramian angular field and graph convolution neural network[J].
China Measurement & Test, 2022, 48(7): 169-176.
DOI:10.11857/j.issn.1674-5124.2020020031 |
| [9] |
Case Western Reserve University Bearing Data Center [EB/OL]. [2018-02-25]. http://csegroups.case.edu/bearingdatacenter/pages/download-data- file.
|
| [10] |
邓佳林, 邹益胜, 张笑璐, 等. 一种改进CNN在轴承故障诊断中的应用[J].
现代制造工程, 2020(4): 142-147.
DENG J L, ZOU Y S, ZHANG X L, et al. Application of an improved CNN in fault diagnosis of bearings[J].
Modern Manufacturing Engineering, 2020(4): 142-147.
|
| [11] |
ZHANG W, PENG G L, LI C H, et al. A new deep learning model for fault diagnosis with good antinoise and domain adaptation ability on raw vibration signals[J].
Sensors, 2017, 17(2): 425.
DOI:10.3390/s17020425 |
| [12] |
CHOLLET F. Xception: Deep learning with depthwise parable convolutions[C]//Proceedings of the IEEE conference on computer vision and pattern recognition, 2017.
|
| [13] |
ZHANG W, LI C H, PENG G L, et al. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load[J]. Mechanical Systems and Signal Processing, 2018, 100: 439-453.
|
| [14] |
佘博, 田福庆, 梁伟阁. 基于深度卷积变分自编码网络的故障诊断方法[J].
仪器仪表学报, 2018, 39(10): 27-35.
SHE B, TIAN F Q, LIANG W G. Fault diagnosis based on a deep convolution variational autoencoder network[J].
Chinese Journal of Scientific Instrument, 2018, 39(10): 27-35.
|
 2024, Vol. 50
2024, Vol. 50
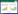


 ,
,