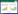文章信息
- 赵泽毅, 周福强, 王少红, 徐小力
- ZHAO Zeyi, ZHOU Fuqiang, WANG Shaohong, XU Xiaoli
- 应用双通道卷积神经网络的交通标识识别方法
- Traffic sign recognition method based on dual channel CNN
- 中国测试, 2024, 50(6): 35-41, 48
- CHINA MEASUREMENT & TEST, 2024, 50(6): 35-41, 48
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022070097
-
文章历史
- 收稿日期: 2022-07-18
- 收到修改稿日期: 2022-12-02
现如今,卷积神经网络[1-2](convolutional neural network, CNN)已广泛应用于各领域的研究,特别是在图像相关任务上表现的十分优异,如图像分类[3-4]、图像语义分割[5-6]、图像检索[7]、物体检测[8-9]。在智慧交通领域,交通标志识别问题的本质就是多图像分类问题,准确的交通图像标识识别对于无人驾驶以及无人机器人的可行性起着至关重要的作用,所以现在对交通标识分类的研究日益增多。
揭伟等人提出一种HOG-MBLBP特征融合算法[10]。齐朗晔等人在分块核函数的基础上提出了基于多个图像特征进行组合决策的识别方法,其分类准确率为94.67 %[11]。邓翔宇等人提出了一种利用边缘走势统计特征反映目标形状特征的新算法,并将其与神经网络相结合用于交通标识形状的识别,但是该算法对圆形和正八边形存在一定的误识率[12]。
通过对现有的研究成果发现,传统的交通标识识别存在实用性不强,准确率不高,在小尺度交通图像上不容易识别等问题。针对以上问题,本文提出一种基于LeNet-5卷积神经网络[13-14](LeNet-5 convolution neural network)改进的双通道网络结构与多尺度[15]思想相互结合的方案,使用较小的网络层数,在较短的时间内,提高交通标识识别准确率。
1 卷积神经网络卷积神经网络的基本组件包括卷积层、池化层、全连接层。一个卷积层包含多个卷积核,卷积核以扫描窗的方式对图像进行卷积操作,主要作用是提取局部特征和权重参数学习,工作原理如图1所示。
|
| 图 1 卷积核示意图 |
池化层是非线性下采样的一种形式,主要作用是特征融合,减小特征图,从而减小参数与权值,并且在池化层中无需进行参数的学习,其中池化层包含的参数有尺寸,步长,主要的计算方法有平均池化和最大池化两种方法,本文采用最大池化的方法。作为卷积神经网络的最后一层,全连接层将卷积层和池化层的特征空间映射到样本标记空间,转化为一个一维向量进行输出。
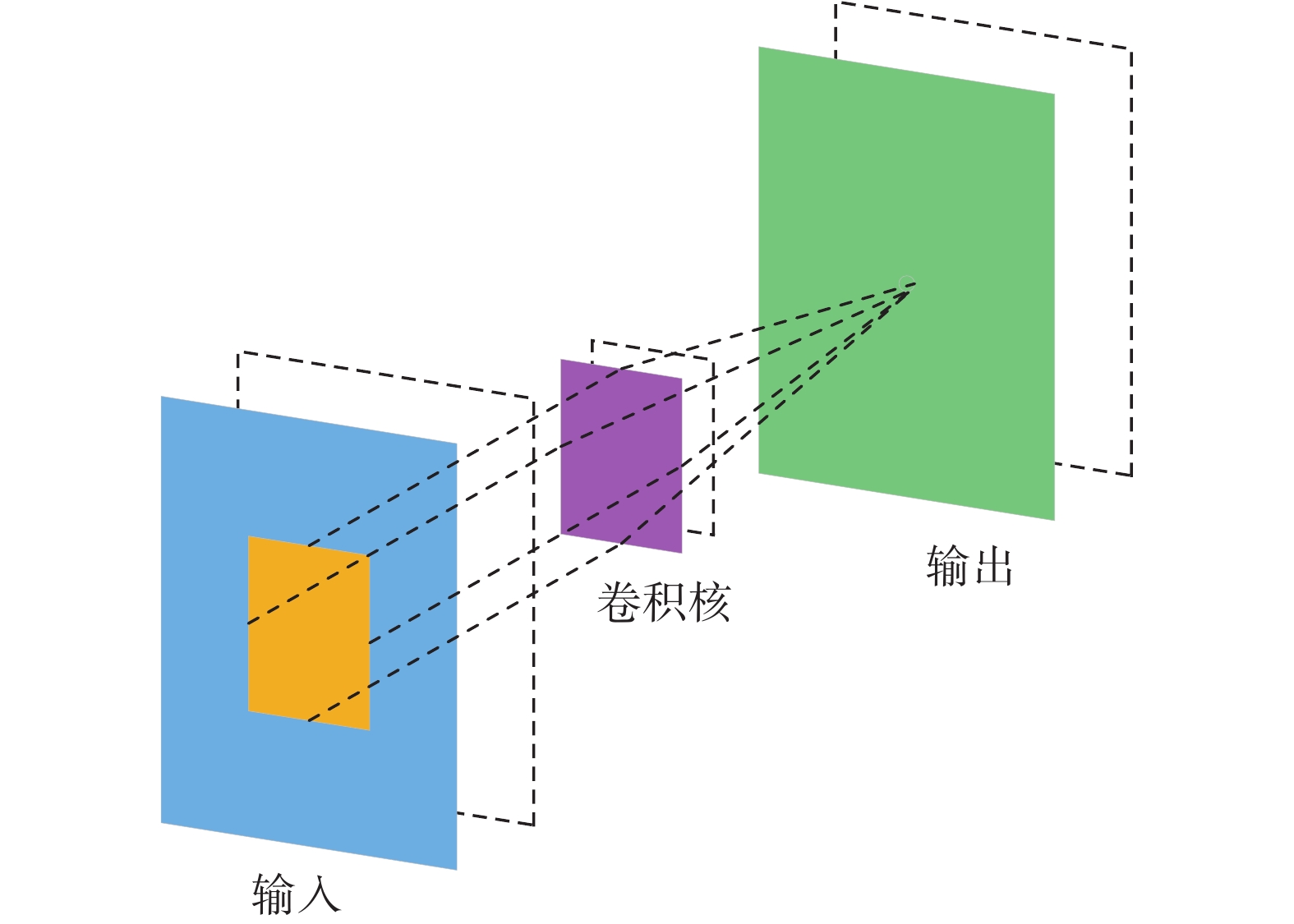
2 LeNet-5网络结构 2.1 传统LeNet-5结构如图2为LeNet-5网络结构示意图。LeNet-5网络结构共有7层,具体包含3个卷积层(C1、C3、C5),2个池化层(S2、S4),2个全链接层(Fc1、Fc2)。
|
| 图 2 LeNet-5网络结构示意图 |
2.2 存在的问题
使用传统LeNet-5网络模型进行交通标识的训练结果,其准确率为80 %~81.50 %,准确率并不高,归结原因如下:
传统LeNet-5网络模型结构适用于手写数据集的识别,而手写数据集的训练图像简单,提取少量的图像特征即可进行识别操作。但相对于交通标识图像而言,其背景复杂多变,需要提取大量的图像特征进行训练。
在实际应用中,无人车或无人机器人在每秒内获取的交通标识图像大小不一并且每秒获取的图像相对角度也不一样,所以在训练之前,需要对训练数据集进行数据预处理操作。
手写数据集最终仅有10个分类,在本文中交通标识最终分类为43类,分类越多难度越大。
结合其他因素,如梯度下降方式的选择,选取相对较好的学习率,更改原来的激活函数等因素来提高改进后网络的整体性能。
3 改进LeNet-5网络结构 3.1 基于交通标志识别问题的改进针对上述问题,本文做出了如下改进:
为了在不同尺度图像上捕获信息,增加卷积层之间特征图的联系,高效利用特征图。本文以传统的LeNet-5网络结构为基础构建了2个相对独立的卷积神经网络结构,并在每个通道上引入了多尺度化,即具有双通道多尺度的卷积神经网络结构(见图3)。

|
| 图 3 改进LeNet-5卷积神经网络结构 |
更改卷积核大小。原LeNet-5网络结构中卷积核大小为5×5,其提取特征图效果并不理想,分别更改不同通道中每层卷积层卷积核大小,实现对同一张图像不同特征的提取。
增加卷积核的个数。原LeNet-5网络结构中每层卷积层中卷积核数量并不能满足对交通标识的识别,为了满足对43类交通标识的分类,增加卷积核数量是十分必要的。
更改激活函数。式(1)为Sigmoid函数公式,原LeNet-5中使用的激活函数Sigmoid[16]反向传播求误差梯度时涉及除法操作,计算量大,容易出现梯度消失的情况。本文采用ReLu激活函数[17]替代Sigmoid激活函数,式(2)为ReLu函数公式。通过对比两个激活函数公式,明显得出ReLu激活函数计算量小,不涉及除法;且导数为1,有效避免梯度消失和梯度爆炸;其中为0的神经元可以减少参数之间的依赖,从而有效缓解过拟合问题。
| $ s\left( x \right) = {\text{Sigmoid}}\left( x \right) = \frac{1}{{1 + {{\rm e}^{ - x}}}} $ | (1) |
| $ r\left( x \right) = {\text{Relu}}\left( x \right) = {\text{max}}\left( {0,x} \right) $ | (2) |
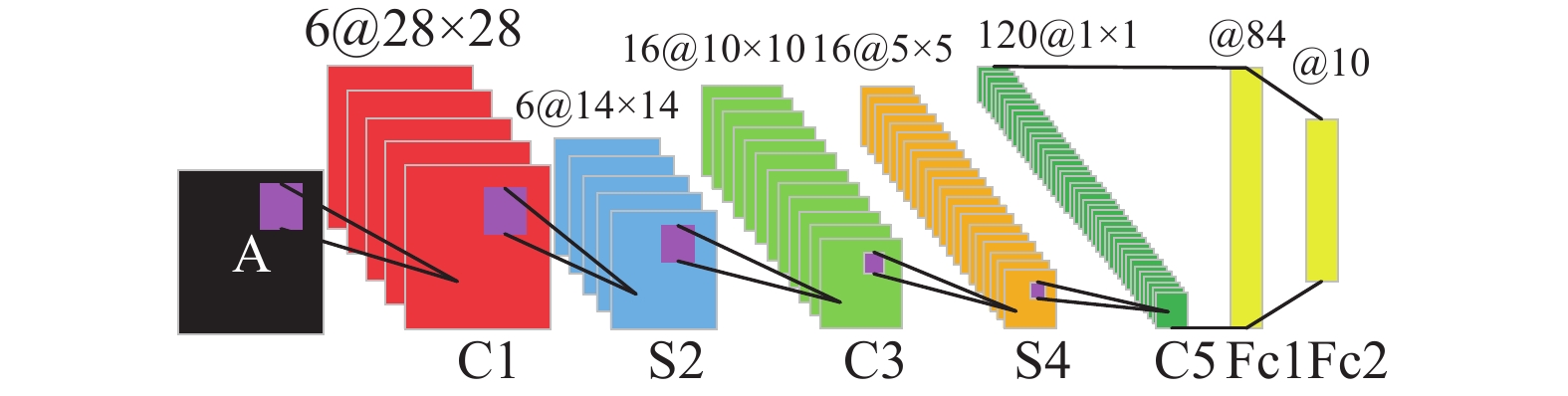
更改梯度下降算法,将随机梯度下降算法(stochastic gradient descent, SGD)更改为Adam(adaptive moment estimation, Adam)算法[18-19],Adam算法流程如图4所示。
|
| 图 4 Adam算法流程图 |
| $ {m_0} = 0,{v_0} = 0,t = 0 $ | (3) |
| $ t = t + 1,{g_t} = {\nabla _\theta }{f_t}\left( {{\theta _{t - 1}}} \right) $ | (4) |
| $ {m_t} = {\beta _1}{m_{t - 1}} + \left( {1 - {\beta _1}} \right){g_t} $ | (5) |
| $ {v_t} = {\beta _2}{v_{t - 1}} + \left( {1 - {\beta _2}} \right)g_t^2 $ | (6) |
| $ {{\hat m_t}} = \frac{{{m_t}}}{{1 - \beta _1^t}}, {{\hat v_t}} = \frac{{{v_t}}}{{1 - \beta _2^t}} $ | (7) |
| $ {{{\theta }}_{{t}}} = {{{\theta }}_{{{t - 1}}}} - \frac{\partial }{{\left( {\sqrt {{{\hat v }_{{t}}}} + \varepsilon } \right)}}{\hat m _{{t}}} $ | (8) |
式(3)~式(8)分别对应图4中的初始化参数、计算梯度、更新偏一阶矩估计,更新偏二阶矩估计、偏差修正、更新参数的计算公式。其中,
更改全连接层输出特征数量,因为交通标志识别图像量级大,原有84维向量不足以满足现在的要求,现更改为400维向量,softmax层输出更改为43维向量,以满足交通标识识别的要求。
3.2 改进的双通道网络结构参数描述在改进的结构中,输入层图像尺度为32×32。在通道1中,进行3次卷积操作,C1对应的卷积核大小为7×7,个数为16个;C2对应的卷积核大小为5×5,个数为32个;C3对应的卷积核大小为3×3,个数为64个;S1层池化尺寸是2×2,步长为2,S2层池化尺寸是3×3,步长为3,都采用最大池化的方式。在通道1中,使用大卷积核目的是提取更具全局特性的特征,防止遗漏或忽略交通标识图像重要的边缘信息,从而提高识别率。在通道2中,同样进行3次卷积操作,C4对应的卷积核大小为3×3,个数为32个;C5对应的卷积核大小为1×1,个数为64个;C6对应的卷积核大小为3×3,个数为128个;S3层池化尺寸是2×2,步长为2,S4层池化尺寸是3×3,步长为3,采用最大池化的方式。在通道2中,采用小卷积核和增大卷积核数量的方法,使特征提取更加细致。通道1和通道2都产生了2个不同的分支(见表1),每次不同尺度大小的图像进行卷积都会和全连接层相连,加强浅表层图像特征的提取。详细改进网络结构参数信息见表2,表3。
| 分支名称 | 输入层 | 中间层 | 输出层 |
| 通道1 | |||
| 分支1-1 | Input | (C1,S1,C2,S2) | Fc1 |
| 分支1-2 | Input | (C1,S1,C2,S2,C3) | Fc1 |
| 通道2 | |||
| 分支2-1 | Input | (C4,S3,C5,S4) | Fc1 |
| 分支2-2 | Input | (C4,S3,C5,S4,C6) | Fc1 |
| Layer层 | 特征图数目 | 输出特征图尺度 | 卷积核/池化 | 步长 |
| Input | 3 | 32×32 | - | - |
| 分支1-1 | ||||
| C1 | 16 | 26×26 | 7×7 | 1 |
| S1 | 16 | 13×13 | 2×2 | 2 |
| C2 | 32 | 9×9 | 5×5 | 1 |
| S2 | 32 | 3×3 | 3×3 | 3 |
| 分支1-2 | ||||
| C1 | 16 | 26×26 | 7×7 | 1 |
| S1 | 16 | 13×13 | 2×2 | 2 |
| C2 | 32 | 9×9 | 5×5 | 1 |
| S2 | 32 | 3×3 | 3×3 | 3 |
| C3 | 64 | 1×1 | 3×3 | 1 |
| Layer层 | 特征图数目 | 输出特征图尺度 | 卷积核/池化 | 步长 |
| Input | 3 | 32×32 | - | - |
| 分支2-1 | ||||
| C4 | 32 | 30×30 | 3×3 | 1 |
| S3 | 32 | 15×15 | 2×2 | 2 |
| C5 | 64 | 15×15 | 1×1 | 1 |
| S4 | 64 | 5×5 | 3×3 | 3 |
| 分支2-2 | ||||
| C4 | 32 | 30×30 | 3×3 | 1 |
| S3 | 32 | 15×15 | 2×2 | 2 |
| C5 | 64 | 15×15 | 1×1 | 1 |
| S4 | 64 | 5×5 | 3×3 | 3 |
| C6 | 128 | 3×3 | 3×3 | 1 |
4 实 验 4.1 GTSRB数据集
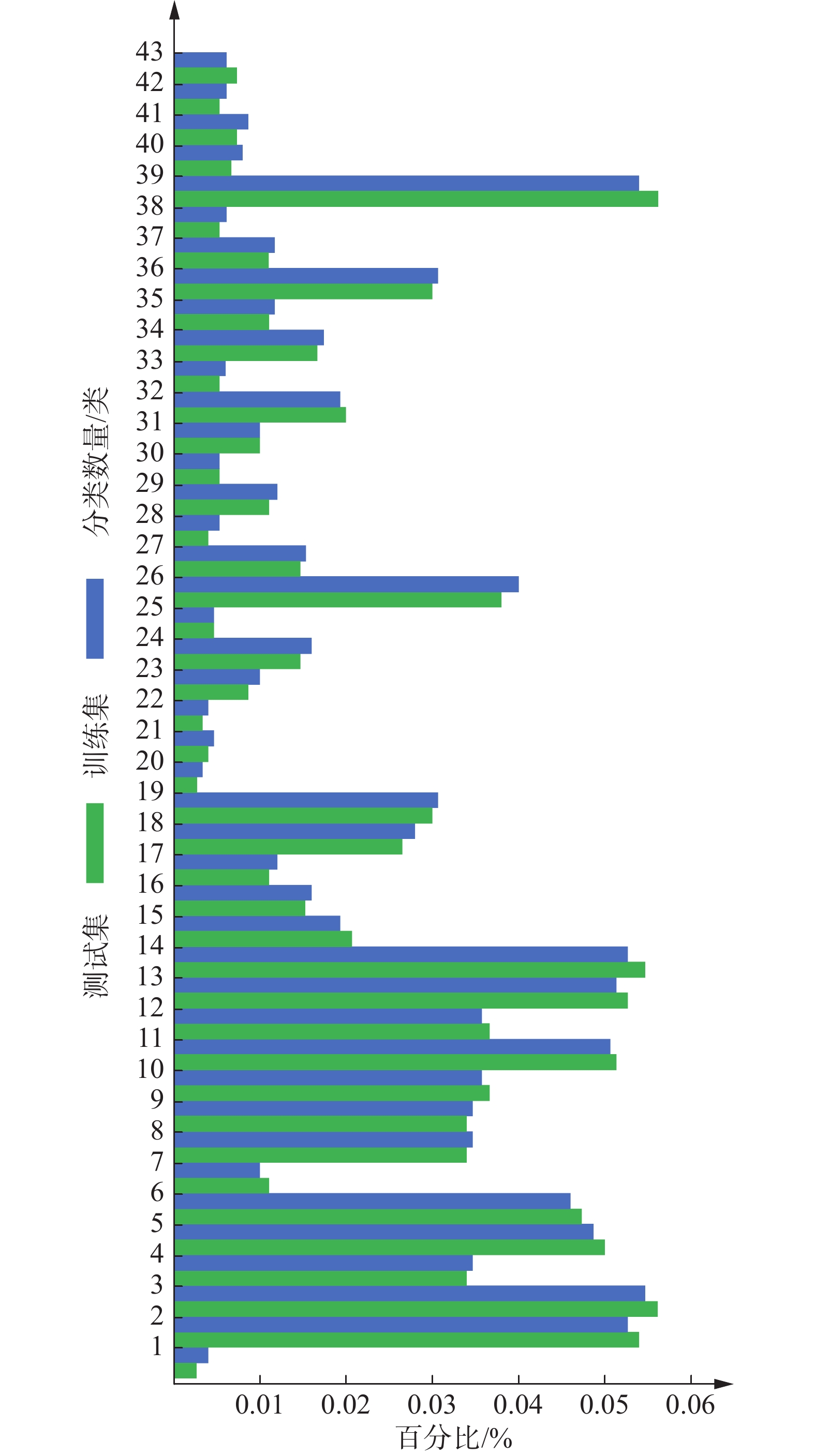
本文选取德国交通标识标准数据库(GTSRB)为数据集来验证改进后的LeNet-5网络结构模型对于交通标识识别的性能,该数据库包含43类交通标识图像,且每类图像囊括了强光照,雨雪天,黑夜等(图5)。共有39209张训练集交通标识图像以及12630张测试集交通标识图像。在训练数据集和测试数据集中,每种类的交通标识图像占比基本一致(图6),说明该训练数据集满足日常生活中的交通标识,可以应用到实际场景。

|
| 图 5 每个种类随机显示一个样本数据 |
|
| 图 6 每类数据在训练集和测试集中的占比 |
4.2 数据预处理
本文对训练集数据进行了数据增强操作,比如旋转、移位、翻转等微小的改变(见图7)。为防止天气因素以及物理因素的影响,又对数据集进行了降噪处理(见图8),并在训练之前将图像数据归一化为32×32像素。

|
| 图 7 数据增强样本展示 |

|
| 图 8 降噪前后对比 |
4.3 实验平台
实验所用计算机配置为i7-7900x处理器,显卡为NVIDIA GeForce GTX 1660,内存为16 GB,使用TensorFlow框架搭建训练平台,初始学习率设置为0.001,优化算法选用Adam算法,每次迭代次数设置为500次。
4.4 实验结果与分析 4.4.1 验证单通道和双通道的识别准确率实验1:为了验证基于LeNet-5网络结构所改进的双通道结构优于单通道结构,对本文中通道1,通道2和双通道结构分别做了12次训练,随机采样4次作为样本数据,实验结果如表4所示。
| % | ||||
| 网络结构 | 通道1 | 通道2 | 双通道 | |
| 训练结果 | 第1组 | 96.41 | 91.92 | 99.07 |
| 第2组 | 95.89 | 92.38 | 98.88 | |
| 第3组 | 95.91 | 91.85 | 99.01 | |
| 第4组 | 96.12 | 93.35 | 98.72 | |
| 平均值 | 96.08 | 92.37 | 98.91 | |
由表4可知,对本文中通道1,通道2和双通道结构随机采样的4次结果中,双通道网络结构训练效果最佳,说明双通道网络结构的可行性。
4.4.2 不同迭代次数的训练结果实验2:验证改进网络结构在不同迭代次数下对于交通识别精确度的影响,表5展示不同迭代次数对网络结构的影响,表6展示不同迭代次数下的损失值。
| % | |||||
| 迭代次数 | 第1次 | 第2次 | 第3次 | 第4次 | 平均值 |
| 1500 | 97.67 | 97.97 | 97.88 | 97.56 | 97.77 |
| 2000 | 98.56 | 98.61 | 97.98 | 97.86 | 98.25 |
| 3000 | 98.88 | 98.92 | 98.35 | 98.27 | 98.60 |
| 3500 | 98.72 | 98.88 | 98.56 | 98.83 | 98.75 |
| 4000 | 99.07 | 99.01 | 98.89 | 98.88 | 98.96 |
| 迭代次数 | 第1次 | 第2次 | 第3次 | 第4次 | 平均值 |
| 1500 | 0.0930 | 0.0814 | 0.0826 | 0.0925 | 0.0873 |
| 2000 | 0.0702 | 0.0475 | 0.0914 | 0.0982 | 0.0768 |
| 3000 | 0.0459 | 0.0456 | 0.0527 | 0.0586 | 0.0507 |
| 3500 | 0.0406 | 0.0429 | 0.0489 | 0.0517 | 0.0460 |
| 4000 | 0.0337 | 0.0350 | 0.0422 | 0.0489 | 0.0400 |
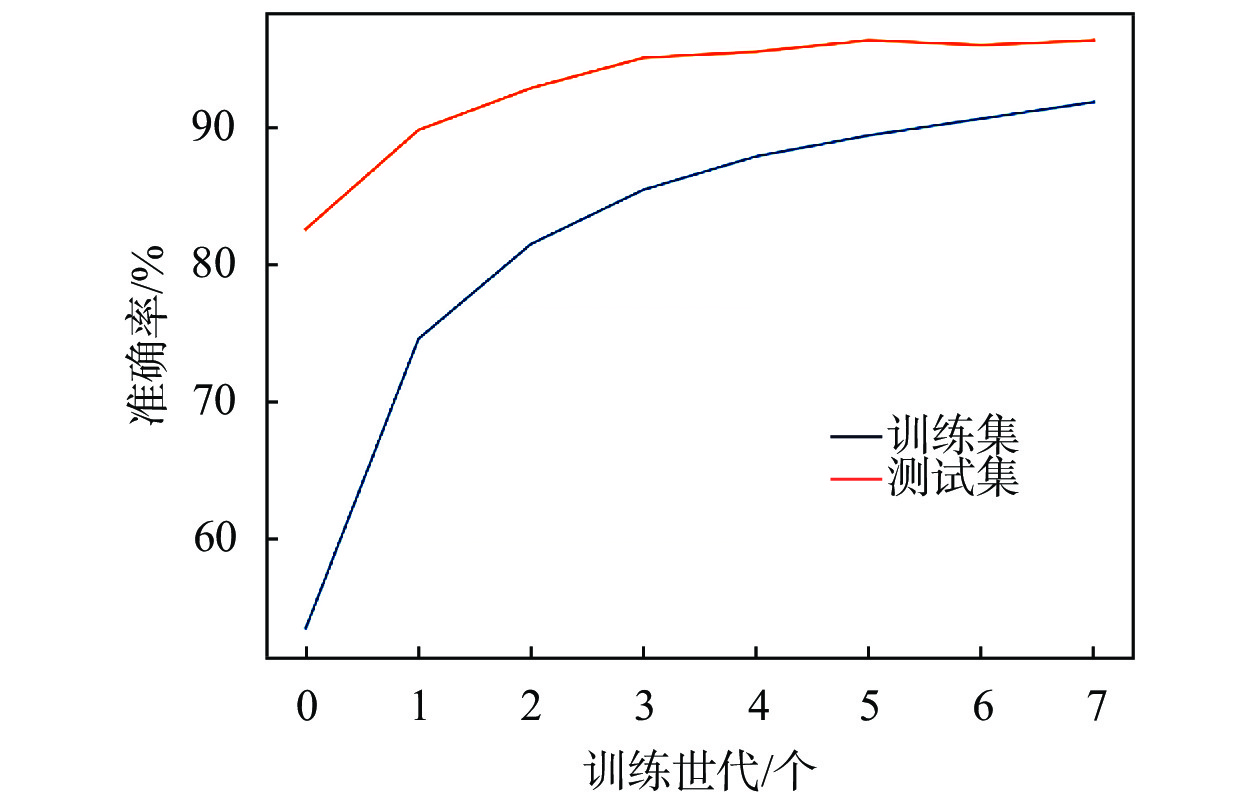
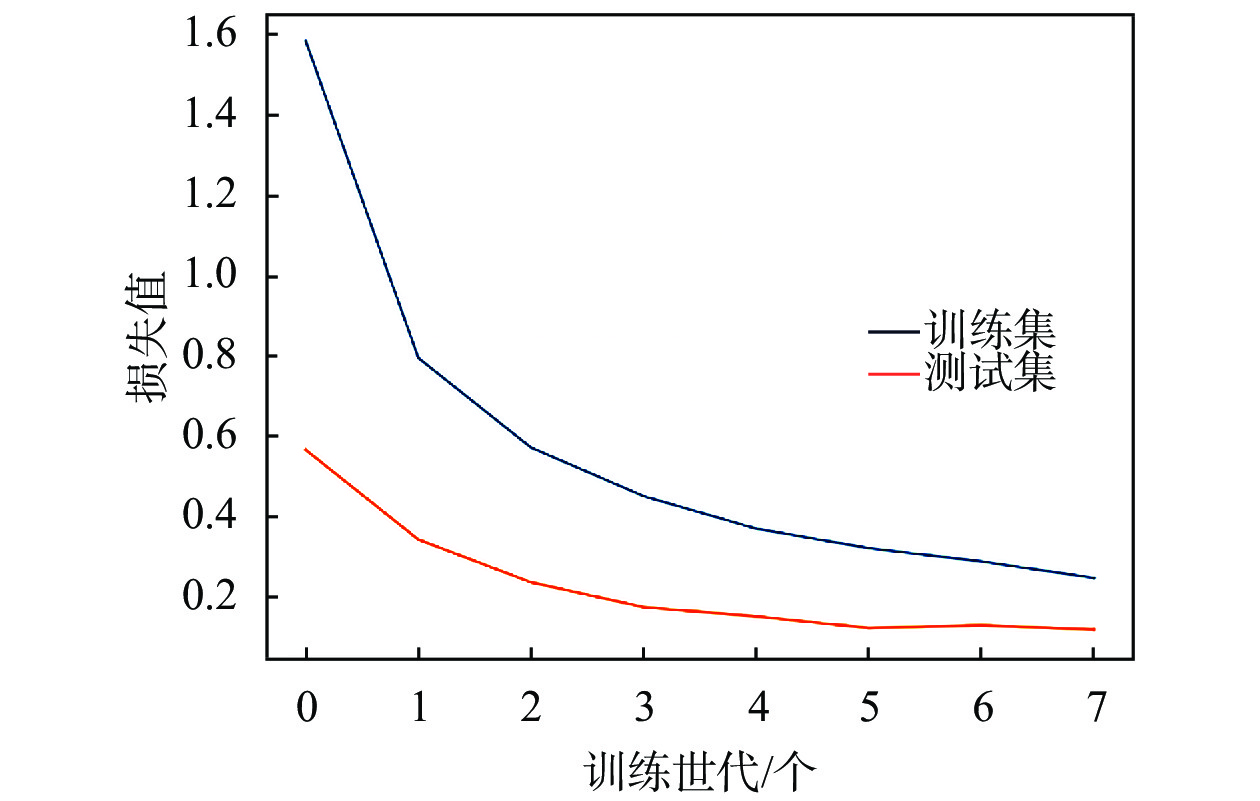
由表5,表6可知,随着迭代次数的增加和损失值的下降,本文网络结构对于交通标识的识别率在提升,虽然在1500次和2000次迭代时的识别率不高也不稳定,且损失值相对较高,但在3000~4000次迭代的识别率均值分别为98.60 %,98.75 %,98.96 %,损失值均值分别为0.0507,0.0460,0.0400说明样本数据已趋近于收敛,不会有大幅度的波动。图9,图10分别展示本文模型在训练集和测试集上的准确率,损失值。分析可知,经过一定迭代次数之后,模型准确率大幅度提高,且准确率曲线慢慢趋近于平滑,说明该模型在逐步收敛。
|
| 图 9 准确率展示 |
|
| 图 10 损失值展示 |
4.4.3 Dropout层对于识别准确率的影响
实验3:在添加Dropout层和未添加Dropout层数据中分别随机采样4组数据,对比其准确率(表7)。
| % | ||
| 网络结构 | 训练结果 | |
| 添加Dropout | 未添加Dropout | |
| 第1组 | 99.01 | 97.86 |
| 第2组 | 98.72 | 97.22 |
| 第3组 | 98.98 | 98.46 |
| 第4组 | 98.64 | 98.89 |
| 平均值 | 98.83 | 98.10 |
分析表7可知,在随机采样的4组训练数据中,添加Dropout层比不添加Dropout层的训练结果均值高0.73 %,说明添加Dropout层对交通标识的识别率起到一定的作用。
4.4.4 不同梯度下降算法对于识别准确率的影响实验4:在本文网络结构中,将梯度下降算法由SGD算法更改为Adam算法,随机分别选择1组实验数据展示在不同的迭代次数下SGD算法与Adam算法的识别准确率与损失值(表8)。
| 迭代次数 | 准确率/损失值 (SGD算法) |
准确率/损失值 (Adam算法) |
| 1500 | 69.65%/1.0018 | 97.03%/0.0930 |
| 2000 | 76.80%/0.7448 | 98.64%/0.0475 |
| 3500 | 84.86%/0.5229 | 98.72%/0.0350 |
| 4000 | 90.10%/0.3251 | 99.08%/0.0346 |
分析表8可知,在相同的迭代次数下,本文网络结构所使用的Adam算法不论是在识别准确率还是在损失值上其性能远远高于原LeNet-5网络结构使用的SGD算法。
4.4.5 不同算法的比较结果实验5:本文通过复现文献[15]中的网络结构、AlexNet网络结构、LeNet-5网络以及本文网络来对比其准确率(表9)。
分析表9可知,本文的网络结构相比于传统的AlexNet网络结构,LeNet-5网络结构以及文献[15]中所提出的网络结构识别率分别提高了约3.02 %,3.2 %以及2.37 %。
5 结束语本文使用卷积神经网络,设计并实现基于LeNet-5模型结构改进的双通道多尺度的网络模型结构算法。经过多次验证,本文结构具有较高的鲁棒性,该算法在两个通道的基础上,每个通道又实现了双分支结构,且通道1和通道2使用不同的卷积核大小来提取图像特征,通过全连接层将不同尺度的图像特征相互融合,从而获取更加丰富的图像特征。进一步工作,将本文网络结构所训练出来的参数信息,应用到无人机器人中,再通过实际情况,调整其训练参数,使其识别准确率进一步的提升。
| [1] |
周飞燕, 金林鹏, 董军. 卷积神经网络研究综述[J].
计算机学报, 2017, 40(6): 1229-1251.
DOI:10.11897/SP.J.1016.2017.01229 |
| [2] |
孙志军, 薛磊, 许阳明, 等. 深度学习研究综述[J].
计算机应用研究, 2012, 29(8): 2806-2810.
DOI:10.3969/j.issn.1001-3695.2012.08.002 |
| [3] |
段建, 翟慧敏. 深度卷积神经网络在Caltech-101图像分类中的相关研究[J].
计算机应用与软件, 2016, 33(12): 165-168.
DOI:10.3969/j.issn.1000-386x.2016.12.040 |
| [4] |
王昕, 赵飞, 蒋佐富, 等. 迁移学习和卷积神经网络电力设备图像识别方法[J].
中国测试, 2020, 46(5): 108-113.
DOI:10.11857/j.issn.1674-5124.2019040050 |
| [5] |
李英杰, 张惊雷. 基于全卷积网络的图像语义分割算法[J].
计算机应用与软件, 2020, 37(8): 213-218.
DOI:10.3969/j.issn.1000-386x.2020.08.037 |
| [6] |
顾攀, 张烽栋. 基于神经网络的图像弱监督语义分割算法[J].
计算机应用与软件, 2018, 35(2): 284-288.
DOI:10.3969/j.issn.1000-386x.2018.02.051 |
| [7] |
彭晏飞, 陶进, 訾玲玲. 基于卷积神经网络和E2LSH的遥感图像检索研究[J].
计算机应用与软件, 2018, 35(7): 250-255.
DOI:10.3969/j.issn.1000-386x.2018.07.045 |
| [8] |
彭伟康, 陈爱军, 吴东明, 等. 基于改进Faster R-CNN的水准泡缺陷检测方法[J].
中国测试, 2021, 47(7): 6-12.
DOI:10.11857/j.issn.1674-5124.2020090072 |
| [9] |
郭雨青, 曾庆军, 夏楠, 等. 图像增强水下自主机器人目标识别研究[J].
中国测试, 2021, 47(11): 47-52.
DOI:10.11857/j.issn.1674-5124.2021070003 |
| [10] |
揭伟, 李为相, 李为. 基于多特征融合的交通标识实时分类与识别[J].
现代电子技术, 2019, 42(11): 50-53.
|
| [11] |
齐朗晔, 张重阳, 何成东. 基于多特征组合的交通标识识别[J].
计算机工程与科学, 2015, 37(4): 776-782.
DOI:10.3969/j.issn.1007-130X.2015.04.024 |
| [12] |
邓翔宇, 张屹南, 杨雅涵. 一种用于交通标识分类的形状识别算法[J].
计算机工程与科学, 2021, 43(2): 322-328.
|
| [13] |
赵志宏, 杨绍普, 马增强. 基于卷积神经网络LeNet-5的车牌字符识别研究[J].
系统仿真学报, 2010, 22(3): 638-641.
|
| [14] |
王秀席, 王茂宁, 张建伟, 等. 基于改进的卷积神经网络LeNet-5的车型识别方法[J].
计算机应用研究, 2018, 35(7): 2215-2218.
DOI:10.3969/j.issn.1001-3695.2018.07.072 |
| [15] |
SERMANET P, LECUN Y. Traffic sign recognition with multi-scale Convolutional Networks[C]// International Joint Conference on Neural Networks. IEEE, 2011: 2809-2813.
|
| [16] |
张焕, 张庆, 于纪言. 激活函数的发展综述及其性质分析[J/OL]. 西华大学学报(自然科学版): 1-10.1-08-11.
ZHANG H, ZHANG Q, YU J Y. Development review and property analysis of activation functions [J/OL]. Journal of Xihua University (Natural Science Edition): 1-10.1-08-11.
|
| [17] |
陈超, 齐峰. 卷积神经网络的发展及其在计算机视觉 领域中的应用综述[J].
计算机科学, 2019, 46(3): 63-73.
DOI:10.11896/j.issn.1002-137X.2019.03.008 |
| [18] |
杨观赐, 杨静, 李少波, 等. 基于Dropout与ADAM优化器的改进CNN算法[J].
华中科技大学学报(自然科学版), 2018, 46(7): 122-127.
|
| [19] |
王功鹏, 段萌, 牛常勇. 基于卷积神经网络的随机梯度下降算法[J].
计算机工程与设计, 2018, 39(2): 441-445.
|
 2024, Vol. 50
2024, Vol. 50