0 引　言

随着新能源汽车技术的快速发展，对永磁电机中磁瓦的质量要求越来越高。受制造技术和运输条件限制，磁瓦在生产过程中不可避免地产生各种表面缺陷，并呈现出不同的图像特征，根据损伤原因和形状，缺陷可分为五类：气孔、裂纹、磨损、断裂和不均匀缺陷，其中，裂纹和气孔占据的比例最大^[1]。

金属表面较为光滑，具有镜面反射特点，平行光容易造成CCD曝光饱和，淹没缺陷特征。机器视觉检测时，多采用均匀散射光成像，具有照射面积大和光路非定向的优点，但是图像会存在对比度低、局部光照不均、高斯噪声大等问题。同时，磁瓦加工过程留下的切削纹理，会产生不规则亮条干扰。对磁瓦图像进行增强处理，过滤噪声、弱化干扰、凸显缺陷，可以显著降低后续缺陷识别和检测难度，提高准确率和实时性，对提高永磁电机的制造品质具有重要意义。磁瓦图像的增强算法成为近年来的研究热点。

利用频谱分析和统计学原理进行缺陷图像增强是一个重要的研究方向。Xie等人^[2]提出了一种基于多尺度几何分析shearlet变换的磁瓦图像缺陷分割方法，在气孔缺陷增强上表现突出。Li等人^[3]提出使用快速离散curvelet变换和纹理分析方法，有效增强了磁瓦图像中低对比度裂纹缺陷。华泽锋等人^[4]提出一种利用小波域高频系数特征实现发动机叶片微缺陷自动检测系统。Yang等人^[5]提出了一种基于非降采样shearlet变换NSST和包络灰度梯度EGLG的新算法，用于增强光照不均磁瓦图像中的低对比度裂纹。朱志勋^[6] 和项新建^[7]提出了一种改进的同态滤波与连续均值量化变换相结合的磁瓦表面缺陷图像增强算法，有效改善了磁瓦表面缺陷图像的光照不均匀、提高了图像的对比度、增强了图像的纹理细节信息。以上线性滤波增强算法的最大不足在于将噪声和边缘都归入高频信号，因此在增强边缘的同时，也会放大噪声，在过滤噪声的同时，不可避免地破坏边缘信息。

利用人工智能方法进行缺陷增强是另外一个研究思路。徐佳乐等人^[8]利用生成对抗网络对轴承图像进行重构，实现轴承表面缺陷定位。Huang等人^[9]介绍了一种称为MCuePush U-Net的多模块神经网络模型，该模型能实现光照不均下的磁瓦缺陷增强。谢舰等人^[10]提出了一种基于卷积神经网络的缺陷增强与分割网络，解决了部分缺陷前景面积占比太小，导致网络难以收敛的问题。祝礼佳等人^[11]提出了一种基于轻量级NASNet卷积神经网络的磁瓦表面缺陷增强与识别算法，实现了小样本多类别磁瓦表面缺陷的识别。基于人工智能算法虽在磁瓦表面缺陷的增强上效果较好，但其对样本数量要求大，不适用小批量生产，且计算量巨大，实时性差，限制了其用于现场检测的可行性。

基于偏微分方程（PDE）的非线性各向异性扩散方法是第三个研究方向。此类方法能较好区分图像边缘和平滑区域，并采用不同的滤波策略，从而克服了线性滤波的不足，且不需要大量样本进行训练，其计算效率也优于卷积神经网络。Perona和Malik^[12]首次提出了二维非线性扩散PM模型，能够在边缘区域和非边缘区域进行不同的扩散操作，从而同步实现过滤背景和保护细节。张天祥^[13]在研究了PM模型的不足后，提出了一种具有锐化功能的扩散系数函数，实现了增强边缘细节的效果。

1 PM模型及其改进算法

Perona和Malik（PM）的初衷是保留图像前景内容，而使背景内容尽可能扩散和平滑。他们根据图像梯度信息设计了各向异性过程，具有强梯度的边缘区域尽可能减少扩散，而弱梯度的背景区域则加大扩散。据此设计出偏微分方程，其扩散系数与梯度幅值成递减函数关系。其表达式如式(1)所示。

式中：$ \boldsymbol{I} $——输入图像；

x和y——其像素坐标；

t——图像重建的迭代时间变量；

$ \mathrm{d}\mathrm{i}\mathrm{v} $()——散度函数；

$\nabla $——不同像素空间的梯度；

$ g\left(\right) $——自适应扩散系数函数，具有严格非负递减特性。

PM模型在产品表面缺陷增强中取得了较好的效果，但由于低对比度图像中的边缘和噪声依然得不到较好区分，扩散过程甚至会出现阶梯效应和孔洞效应，产生虚假边缘。一些研究者为了抑制扩散过程对缺陷边缘的破坏，在PM模型基础上进行了改进。Chao和Tsai^[14]提出一种具有缺陷边缘锐化的各向异性扩散模型（SSAD）。其设计思想是对边缘区域进行反扩散，也就是锐化。其差分方程如公式(2)所示。

式中：$ {\nabla \boldsymbol{I}}_{t}^{i}\left(x,y\right) $——t时刻坐标$ \left(x,y\right) $像素点的$ i $方向梯度；

$ g\left(\right) $——PM模型中的扩散系数函数；

$ v\left(\right) $——锐化权重函数。

将4个不同方向梯度均值作为计算值，其定义为公式(3)。

式中，$ \mathrm{\alpha } $为权重因子，决定了边缘锐化的程度。然而，由于SSAD算法依然没有解决噪声和边缘的区分问题，所以当对比度较低，噪声严重时，噪点被误判为边缘，继而被锐化为虚假边缘，导致严重错误。

为消除噪声干扰问题，Chao和Tsai^[15]提出一种结合局部灰度方差和梯度幅值信息的改进扩散模型（LVAD）。其设计思想是根据局部方差来判断边缘和噪声。对扩散系数函数进行进一步改进，表达式为：

式中：$ g\left(\right) $——改进扩散系数函数；

$ \sigma $——局部灰度方差。

其计算区域以当前像素为中心，覆盖r×r(r=3,5,7)的邻域，$ {k}_{0} $为调整常数。

LVAD算法克服了SSAD对噪声敏感和产生过度加强的问题，并在低对比度的星云图像加强中，取得了较好的应用效果。但LVAD算法受局部方差区域形状影响，会出现将裂缝等条状缺陷误判为噪声的现象。

2 局部亮区抑制扩散模型

永磁电机磁瓦的成像特点，导致其图像对比度低，噪声严重。同时其曲面结构和切削纹理还会产生不规则亮条纹干扰。本文结合磁瓦图像缺陷和噪声信号的特点，在PM模型的基础上，提出一种具有局部亮区抑制功能的非线性各向异性扩散模型。以实现对磁瓦表面缺陷低分辨率图像的增强。

2.1 局部亮区特征描述

为了增强缺陷区域，平滑和过滤噪声及明亮条纹，用数值方法描述出亮区图像特征，并嵌入扩散方程中。因此，本文定义了局部亮区差值$ P_{\mathrm{\mathit{s}}} $及其特征描述符$ F_{\mathrm{\mathit{s}}} $。如公式(5)和公式(6)所示。

式中：$ {N}_{s} $——像素点$ I $的尺寸为(2S+1)的邻域像素和；

$ {P}_{s} $——邻域均值与中心点$ {I}^{*} $的差值。

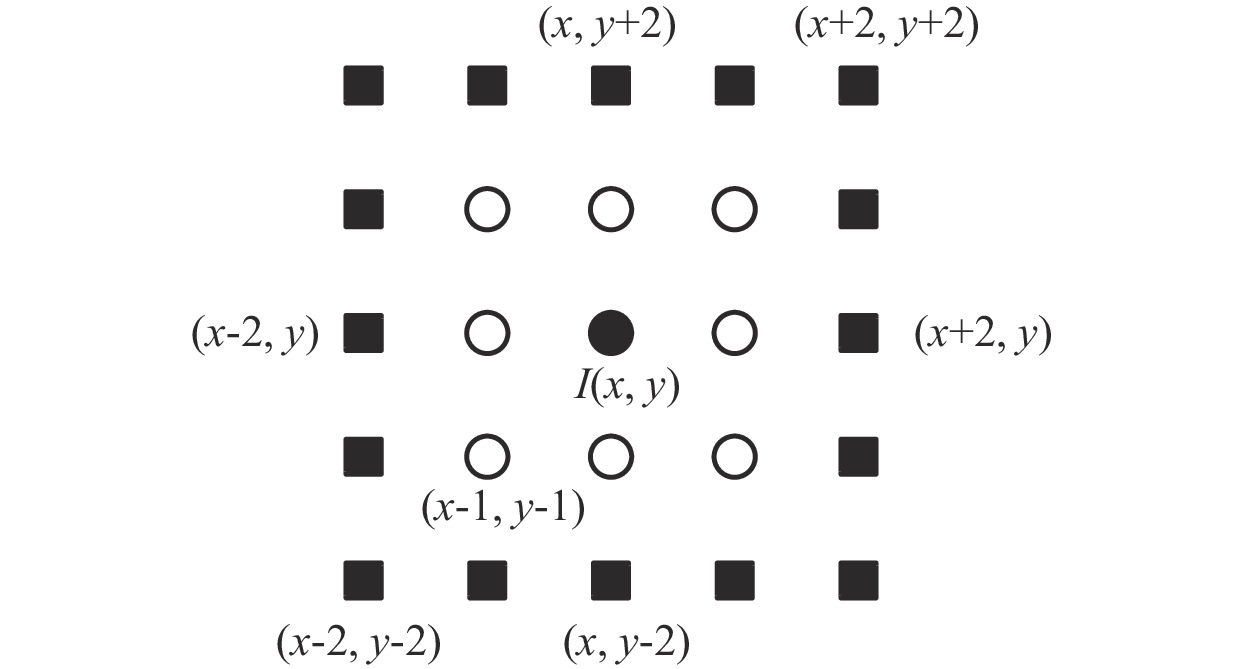
图1展示了尺寸为2的邻域结构图。

式中，特征描述符$ {F}_{s} $根据$ {P}_{s} $符号而定，如果为正，则保留当前值，如果为负，则赋成零。

为更准确地描述出像素点与其邻域均值的关系，可适当扩大邻域取样范围，再统计其均值。在本文磁瓦表面缺陷实验图像中，亮条形状长度均值约为23像素，因此取样范围$ S $可取{2, 8, 16, 24}。最后将4个不同的局部亮区特征$ {F}_{s} $求和并归一化，得到$ F $值，如公式(7)所示。

需要指出的是，在计算每个像素的$ F $特征时，涉及大量重复的矩阵区域求和计算，为减少计算量，提高处理的实时性，可以采用动态规划算法，在矩阵迭代重建过程中建立多张局部区域像素和的映射表^[16]，以空间换时间。特别是当检测图像较大时，时间复杂度将大为减少。

2.2 改进PM偏微分方程

局部亮区特征表达的是该像素点在局部区域中的明暗特征，在磁瓦图像中，气孔、裂纹等缺陷都是呈暗区，而亮区不是缺陷区域，应该增大扩散系数，加速平滑，对其进行过滤。反之，判定为暗区，则有可能是缺陷区域，应该降低扩散系数，保护其边缘。因此，亮区特征$ F $与PM模型中的局部梯度具有相近的功能，可以将两者进行组合，形成新的扩散系数函数$ g\left(x\right) $：

式中，当局部亮区特征$ F $值越大，扩散系数函数$ g\left(x\right) $值越大，该区域的扩散程度加大，滤波效果明显。而在缺陷区域，$ F $值较小，$ g\left(x\right) $值也变小，扩散减弱，缺陷区域得到保留。从而起到亮区抑制功能，反之，若要实现暗区抑制，亮区加强，则可以将$ (1-F) $更改为$ F $。

因此，具有局部亮区抑制功能的PM扩散方程表达式可以重写为：

公式(8)的扩散系数为$ g\left(x\right) $函数，其值只能为正，因此该扩散模式只能起到保护缺陷边缘的作用，而起不到锐化和增加边缘效果，这种模式称之为保护扩散模式。当缺陷与背景对比度较大时，这种扩散模式能将两者区分开。而磁瓦检测场景，缺陷与背景的对比度较低，这种扩散模式的缺陷增强不明显，会给后续识别环节带来困难，检测效果不佳。因此，本文继续改进具有增强缺陷边缘的扩散模式。其形式如公式(10)所示。

式中，$ v\left(x\right) $函数为锐化权重函数，其表达式为$ v\left(\nabla \boldsymbol{I},F\right)=\alpha [1-g\left(\left|\nabla \boldsymbol{I}\right|,F\right)] $，$ \alpha $为锐化权重因子，控制边缘锐化强度。可以看出，$ v\left(x\right) $的单调性与$ g\left(x\right) $相反，当$ g\left(x\right) $取值较大时，对应背景或亮条区域，这时$ v\left(x\right) $取值接近零，不会对扩散造成影响。而当$ g\left(x\right) $取值较小时，对应缺陷边缘区域，此时$ v\left(x\right) $取值较大，扩散系数为负值，扩散方向为逆扩散，缺陷边缘将得到锐化，这种模式称之为锐化扩散模式。

图2和图3分别展示了保护扩散和锐化扩散模式下，扩散系数与局部梯度幅值$ \left|\nabla \boldsymbol{I}\right| $以及局部亮区特征$ F $的关系。

从图2和图3可以看出，$ g\left(\left|\nabla \boldsymbol{I}\right|,F\right) $函数对平滑区域具有更强的扩散效果，而对边缘区域只有保护，没有锐化作用。$ g\left(\left|\nabla\boldsymbol{I}\right|,F\right) $函数则刚好相反，其在平滑区域的扩散效果有所减弱，而出现的负值则代表着能对边缘区域产生锐化作用。

3 实验结果与分析

本文在中科院自动化研究所公布的开源磁瓦缺陷图像集上开展测试，该数据集有1344张图像，根据不同缺陷类型分为6组，组名分别为气孔(blowhole)、裂纹(crack)、磨损(fray)、断裂(break)、不平(uneven)和无缺陷(free)。本文主要针对缺陷比例最大的气孔和裂纹进行实验。

实验所用计算机主要配置CPU为i5 8600，内存为32 GB，Windows10 64位版本平台下进行。编程语言采用Matlab。实验中用到的参数值为$ \alpha =0.03 $，$ \varepsilon =0.03 $，$ \Delta t=0.25\ \mathrm{s} $。

3.1 背景平滑实验

扩散模型的目标是将背景区域平滑，而保留或锐化前景。背景平滑程度是衡量扩散算法质量的一个重要指标。我们给出了不同滤波方法的比较结果。实验用到的磁瓦表面缺陷有气孔和裂纹。图4显示了不同扩散模型的结果。第一列为原始磁瓦图像，第二列为Perona-Malik方法（PM）的结果，第三列为SSAD方法，第四列为LVAD方法，最后一列为本文所提算法。

从图4可以看出，使用仅考虑梯度幅值信息的传统PM扩散模型，如第二列所示。不能有效地消除由不均匀照明引起的明亮形状，并且扩散的区域不均匀，呈色块状分布，增强效果不明显，这将对后续的目标识别带来干扰。对于第三列中的SSAD算法结果，与PM扩散方法一样，可以看到无法抑制亮线和改善对比度，但该算法能对缺陷边缘进行适当锐化处理。与PM和SSAD方法相比，LVAD是一种带局部噪声判别的扩散方法。从第四列结果可以看出，LVAD模型的结果具有较好的增强效果，背景扩散更光滑，图像对比度更大，缺陷轮廓也得到较好的保护。但是亮线干扰没有得到有效抑制。

最后一列为本文所提方法的扩散结果。从图中可以看出，背景区域中的亮条干扰和噪声被有效平滑，图像对比度得到增强。同时，缺陷的形状特征得到了较好的保护。图像增强的效果比较理想。

以上是从主观视觉效果进行对比，接下来再从客观参数指标进行对比研究。主要包括对比度、灰度均值、标准差、平均梯度和处理时间五个指标。表1列出了裂纹缺陷处理结果各项指标对比情况。

从上表可以看出，本文提出的具有亮区条纹抑制功能的改进扩散模型，相比同类算法，能有效提升原始图像的亮度和标准差，达到了凸显了缺陷的效果。但对比度增加并不明显，平均梯度还出现了下降，主要原因是亮区条纹和背景噪声得到了平滑，降低了对比度和梯度均值。在处理时间上，本文算法由于多了亮区参数计算过程，耗时比同类算法有所增加，但依然可满足实时处理的时间要求。

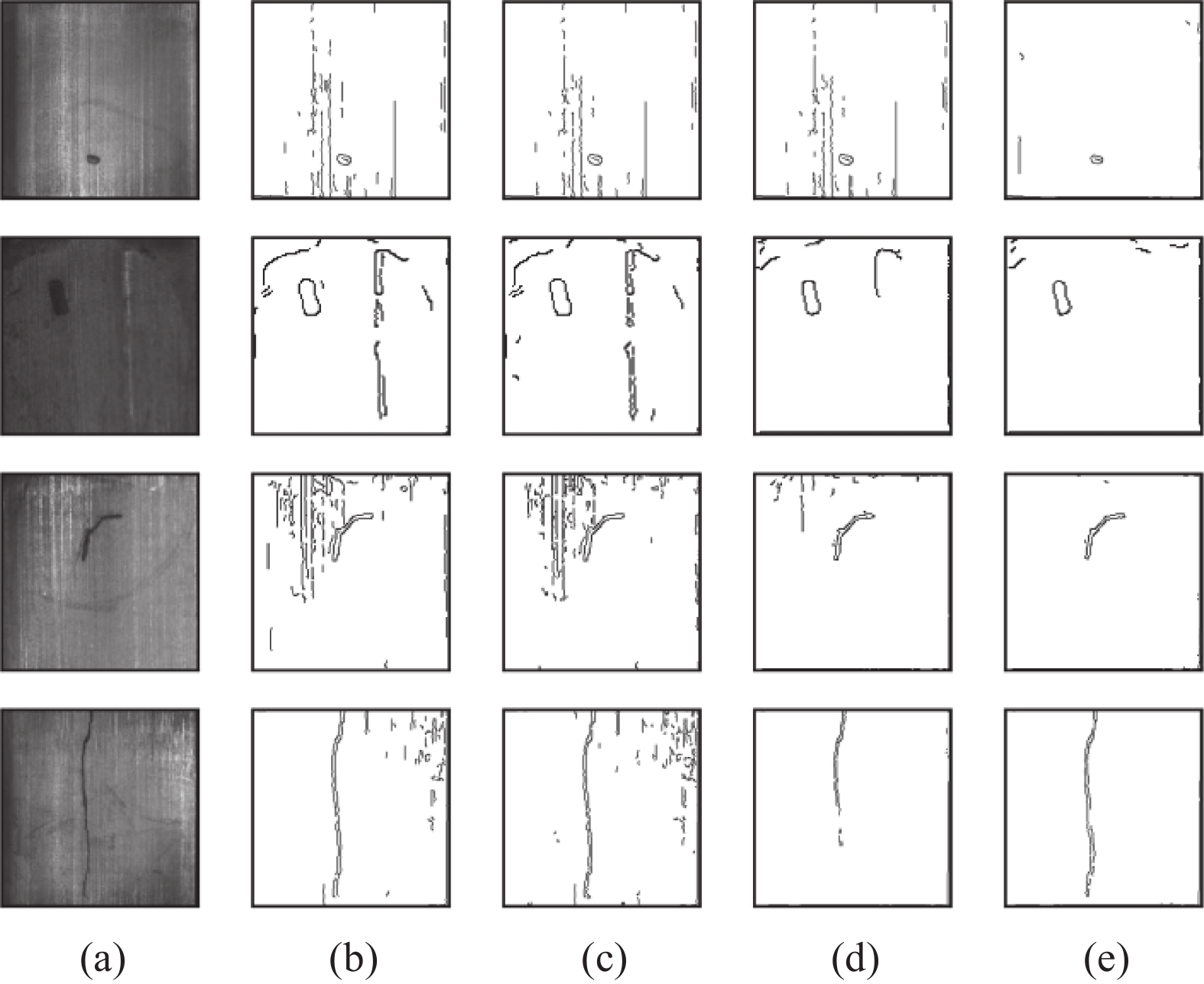
3.2 缺陷边缘检测与分割实验

边缘检测和图像分割是图像增强的常见后续处理步骤，通过该环节实验可以验证增强处理的效果。本实验在上述扩散结果的基础上，采用Canny算法进行边缘检测。图5显示了不同扩散模型的缺陷边缘检测结果。从（b）和（c）列的效果可以看出，PM和SSAD方法受噪声和亮条区域干扰严重，产生较多虚假边缘和噪点。尤其当缺陷区域面积较小时，PM模型甚至会将缺陷平滑，导致漏检。（d）列由于加入了噪声判别机制，检测效果较好，但其在裂纹缺陷增强时，出现了将裂纹误判为噪声进行平滑的情况，且其无法抑制亮条区域的干扰。而采用本文策略的边缘检测算法，由于有了亮区判别和抑制机制，则较好地实现了扩散背景和加强边缘的双重目标，缺陷轮廓保留清晰。进一步验证了本文增强算法的效果。

图6为在上述扩散结果基础上，进行磁瓦缺陷分割的结果，实验结果再次印证本算法在抑制亮区和扩散背景效果上的优势。

3.3 缺陷检测实验

为进一步验证增强后的图像对于缺陷检测结果的影响，在上述实验的基础上，进一步进行缺陷检测实验。实验采用最常用的模板匹配算法进行缺陷识别和检测。其中准确率和召回率分别如表2和表3所示。

从上表可以看出，经过本文提出的亮区抑制扩散模型增强后，仅使用简单的比对算法就可以实现较高的准确率和召回率。比同类的增强算法有了较大的性能提升。对于降低识别算法难度，提升检测速度，都具有重要意义。

4 结束语

1)提出了局部亮区描述算子，能较好地描述图像表面中的亮条纹特征，特别适用于金属表面缺陷的检测图像。

2)提出一种具有亮区抑制功能的各向异性扩散模型，该模型能根据亮区描述特征自适应地调整扩散系数。通过对磁瓦缺陷图库进行实验，结果表明，所提出的扩散方法可以有效地过滤背景噪声和亮条纹理干扰，并增强缺陷边缘。在仅使用图案比对算法情况下，便可实现对气孔和裂纹缺陷准确检测，其精确率分别达到95%和89%，比同类增强算法有较大提升。