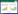文章信息
- 胡以怀, 李从跃, 沈威, 崔德馨, 张成, 芮晓松
- HU Yihuai, LI Congyue, SHEN Wei, CUI Dexin, ZHANG Cheng, RUI Xiaosong
- 基于VMD-多尺度排列熵和SVM的船用空压机故障诊断方法
- Fault diagnosis of marine air compressor based on VMD multi-scale permutation entropy and SVM
- 中国测试, 2024, 50(6): 20-27
- CHINA MEASUREMENT & TEST, 2024, 50(6): 20-27
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022040145
-
文章历史
- 收稿日期: 2022-04-21
- 收到修改稿日期: 2022-07-09
2. 招商局鼎衡造船有限公司,江苏 扬州 225217
2. China Merchants Dingheng Shipbuilding Co., Ltd., Yangzhou 225217, China
船用往复式空压机是船用辅助机械关键设备。船用往复式空压机结构复杂,工作环境恶劣,易发生一二级活塞环断裂、进排气阀片断裂以及地脚螺栓松动等故障。仅通过热工参数的变化很难及时准确地对空压机进行故障诊断,并且空压机振动激励源众多,使振动信号具有非平稳性和非线性等特点。
目前,传统的对非线性非平稳性的空压机振动信号提取特征信息进行故障诊断的研究较多,如短时傅里叶变换,但不能进行自适应调整;小波变换,但不能根据信号局部时频特性选择小波基[1]。经验模态分解(empirical mode decomposition, EMD)产生的分解高度依赖于极值点的搜寻方法、载波包络线的插值和终止条件,使EMD存在模态混叠及分解停止准则等问题[2],且EMD数学理论基础差, 鲁棒性和泛化能力低。虽然集合经验模态(ensemble empirical mode decomposition, EEMD)在分析非线性、非平稳信号具有良好的优势,但是还存在模态混叠和端点效应的问题[3]。如果添加的白噪声幅值不宜,增加计算量的同时还会使固有模态函数中存在虚假分量。变分模态分解是比EMD、EEMD更优越的信号自适应分解方法[4],且具有更坚实的数学理论基础。自提出以来就被广泛应用于故障诊断与时间序列的预测中[5-8]。与EMD、EEMD相比,VMD利用非递归方法实现信号分解,能够分离两个频率接近的信号,此外,VMD本质为若干个自适应维纳滤波组,具有较强的鲁棒性及泛化能力。排列熵计算比较方便,抗噪能力强,将多尺度与排列熵相结合,可以实现多维度特征提取,序列信息得到充分分析。李振壁等[9]提出了一种基于VMD-近似熵的两相接地故障诊断方法,克服EMD在分解信号中模态混叠的难点,有较好的实用性。邹瑛珂等[10]提出一种VMD分解的MFCC/GFCC无人机噪音混合特征提取方法,实现了对无人机噪声的正确识别。张燕霞等[11]通过VMD分解机械振动信号,进行信号的重构,提取重构信号奇异值作为特征向量,将其输入到SVM中,实现了旋转机械的故障辨识。
基于以上分析,采用VMD-多尺度排列熵与SVM相结合的故障诊断方法,将振动信号进行VMD分解,并利用互相关系数筛选出敏感模态分量并将其多尺度排列熵做为特征向量输入SVM中实现船用空压机的故障识别。
1 VMD和多尺度排列熵 1.1 变分模态分解(VMD)VMD是一种抗干扰能力强、新型自适应信号处理方法,在处理非线性、非平稳信号时有较强的鲁棒性。VMD将原始时间序列数据分解为若干个固有模态分量(intrinsic mode function, IMF),每个IMF分量都为调频调幅子序列。通过乘法交替方向法迭代搜索一个受约束的变分模型最优解,求出每个调频调幅子信号的中心频率及带宽[2]。VMD可分为构造变分问题和求解变分问题[12]。
1.1.1 构造变分问题调频调幅子信号
| $ {U_k}\left( t \right) = {A_k}\left( t \right)\cos \left[ {{\varphi _k}\left( t \right)} \right] $ | (1) |
式中:Ak(t)——瞬时幅值,且Ak(t)≥0;
构造变分问题主要包含三个步骤:
对
| $ \left( {\delta \left( t \right) + \frac{{\text{j}}}{{{\text{π}}t}}} \right)*{U_k}\left( t \right) $ | (2) |
式中:
*——卷积。
中心频率
| $ \left[ {\left( {\delta \left( t \right) + \frac{{\text{j}}}{{{\text{π}}t}}} \right)*{U_k}\left( t \right)} \right] \times {{\text{e}}^{ - {\text{j}}{\omega _k}t}} $ | (3) |
获取每个IMF的带宽,得到约束变分问题的构造模型,如下式所示。其中,f为原始信号序列。
| $ \left\{ \begin{array}{l} \min\limits _{\left\{u_{k}\right\}\left\{\omega_{k}\right\}}\left(\displaystyle\sum_{k} \left\| \partial_{t} \left\{\left[\delta(t)+\dfrac{\mathrm{j}}{\pi t}\right] *U_{k}(t)\right\} \mathrm{e}^{-\mathrm{j} \omega_{k} t} \right\| _{2}^{2}\right) \\ \text { s.t. } \displaystyle\sum_{k} U_{k}=f \end{array}\right. $ | (4) |
在求最优解时,需要把约束变分问题转为非约束变分问题,此时需要引入二次惩罚因子
| $ \begin{split} &L\left(\left\{U_k\right\},\left\{\omega_k\right\}, \lambda\right)= \alpha \sum_k\left\|\partial_t\left[\left(\delta(t)+\frac{\mathrm{j}}{\pi t}\right) * U_k(t)\right] \mathrm{e}^{-\mathrm{j} \omega_k(t)}\right\|_2^2+\\ & f(t) - \sum_k\Big\|U_k(t)\Big\|_2^2 + \left\langle\lambda(t), f(t) - \sum_k U_k(t)\right\rangle\\[-1pt] \end{split} $ | (5) |
运用乘法交替方向法(alternating direction method of multipliers,ADMM)不断更新
排列熵算法是由BANDT等[14]提出的一种衡量一维时间序列复杂程度的概率算法,常应用于故障特征的提取。原始信号单一尺度上排列熵值不能完全反映故障的本质[15]。本文为了提高分析准确率,在排列熵基础上,引入多尺度排列熵进行分析。将时间序列进行多尺度粗粒化,然后计算不同尺度下粗粒化序列的排列熵[2]。计算流程如图1所示,计算过程如下:
|
| 图 1 技术路线与流程图 |
对长度为l的时间序列X={xi, i=1,2,…,l}进行粗粒化,即:
| $ {y_{s,j}} = \frac{1}{s}\mathop \sum \limits_{i = \left( {j - 1} \right)s + 1}^{js} {x_i},\quad 1 \leqslant j \leqslant \frac{l}{s} $ | (6) |
其中s和
对
| $ {Y_{s,t}} = \left\{ {{y_{s,t}},{y_{s,t + \tau }}, \cdots ,{y_{s,t + \left( {m - 1} \right)\tau }}} \right\} $ | (7) |
式中:m——嵌入维数;
t——第t个重构分量。
升序排列式(7),即:
| $ {y_{s,t + \left( {{j_1} - 1} \right)\tau }} \leqslant {y_{s,t + \left( {{j_2} - 1} \right)\tau }} \leqslant \cdots \leqslant {y_{s,t + \left( {{j_m} - 1} \right)\tau }} $ | (8) |
将时间序列中各元素原始位置索引进行重构[16]:
| $ {\pi _j} = \left\{ {{j_1},{j_2}, \cdots ,{j_m}} \right\} $ | (9) |
共有m!种排列,假设每种排列出现D次,各尺度下时间序列的概率为:
| $ {P_{s,l}} = \frac{D}{{n / s - m + 1}} $ | (10) |
可得MPE,即:
| $ {H_{s,p}} = - \mathop \sum \limits_{l = 1}^{m!} {P_{s,l}}{\text{ln}}\left( {{P_{s,l}}} \right) $ | (11) |
当
| $ {h_{s,p}} = {H_{s,p}}/{\text{ln}}\left( {m!} \right) $ | (12) |
熵值越接近1,信号随机性越大,非平稳程度也越高[17]。
1.3 技术路线基于VMD多尺度排列熵与SVM的船用空压机故障诊断方法的具体流程如图1所示,详细步骤如下:
Step1:采集6种工况下的振动信号。
Step2:通过VMD对振动信号进行分解,得到固有模态分量。
Step3:求出各固有模态分量的互相关系数,筛选出敏感分量。
Step4:计算特征向量的多尺度排列熵。
Step5:将特征向量输入SVM中,实现故障分类。
Step6:本文所使用方法与EMD、EEMD、MEEMD进行准确率对比分析。
2 空压机故障模拟实验为了对空压机不同故障进行诊断,实验选用WP135型船用往复式空压机,工作参数分别为:额定转速970 r/min,轴功率23.5 kW,容积流量118 m3/h,排气压力3.0 MPa。测试仪器和软件分别为:ICP型振动传感器、INV3602数据采集仪和DASP-V10振动分析软件。采样频率为20.48 kHz,采样样本长度为4096,频率分辨率2.5 Hz。将4个加速度传感器分别安装到缸盖顶端(1#)、机身右侧(2#)、机身左侧(3#)、底座(4#),如图2所示。

|
| 图 2 加速度传感器安装位置 |
模拟工况有二级活塞环故障(故障一)、一级活塞环故障(故障二)、二级进气阀片故障(故障三)、二级排气阀片故障(故障四)、地脚螺栓松动(故障五)、正常,共6种。对于活塞环故障,模拟方法为分别拆掉一级、二级两道活塞环。对于进排气阀片故障,分别将二级进、排气阀片进行断裂处理。故障模拟方法如图3~图5所示。

|
| 图 3 二级进气阀片故障 |

|
| 图 4 模拟二级排气阀片故障 |

|
| 图 5 模拟活塞环故障 |
3 实验数据分析 3.1 热工参数和频谱分析
对正常、活塞环故障以及进排气阀片故障状态下的热工参数分别进行记录,结果如表1所示。
| 序号 | 工况 | 热工参数 | |||||
| 进气 温度/℃ | 一级 排温/℃ | 二级 排温/℃ | 二级 排压/MPa | 缸盖 温度/℃ | 缸壁 温度/℃ | ||
| 1 | 正常 | 14.5 | 24.0 | 29.3 | 0.42 | 26.0 | 26.0 |
| 2 | 故障一 | 14.5 | 22.1 | 28.0 | 0.22 | 30.0 | 29.0 |
| 3 | 故障二 | 14.5 | 23.0 | 26.0 | 0.20 | 30.0 | 23.4 |
| 4 | 故障三 | 14.5 | 23.4 | 26.4 | 0.24 | 29.3 | 24.1 |
| 5 | 故障四 | 14.5 | 24.2 | 22.0 | 0.22 | 30.0 | 23.0 |
从表1中可以看出:当活塞环密封不良时,一级排压和二级排压明显降低,高温气体的泄漏会造成机身和缸盖温度的上升,但上升不明显;模拟二级进排气阀片断裂时,二级排压由正常0.42 MPa分别降低至0.24 MPa、0.22 MPa,但是温度变化并不明显。由此可见,只依靠热工参数对空压机系统进行故障诊断是不准确的。
3.2 故障产生机理 3.2.1 活塞环失效考虑活塞环故障机理,应在动态载荷、静态载荷以及人为因素方面考虑。以下从断裂、磨损、腐蚀等方面来查找活塞环失效的故障机理,如表2所示。
| 故障形式 | 故障原因 | 故障机理 |
| 活塞环故障 | 端面间隙、天地间隙的存在使活塞环产生泵油作用,此外缸内高温会使润滑油变质,造成积碳 | 疲劳磨损 磨粒磨损 |
| 活塞环材料硬度低造成环的弹性降低,环与环槽之间会发生相对滑动 | 粘着磨损 疲劳磨损 | |
| 活塞环断裂,使得局部发生严重磨损 | 断裂表面疲劳磨损 | |
| 活塞环与缸壁和活塞之间润滑不良,会发生磨损 | 粘着磨损 |
3.2.2 阀片失效
阀片失效主要是由于频繁的撞击引起的阀片断裂,此外阀片的材料以及磨损也是引起阀片失效的原因。
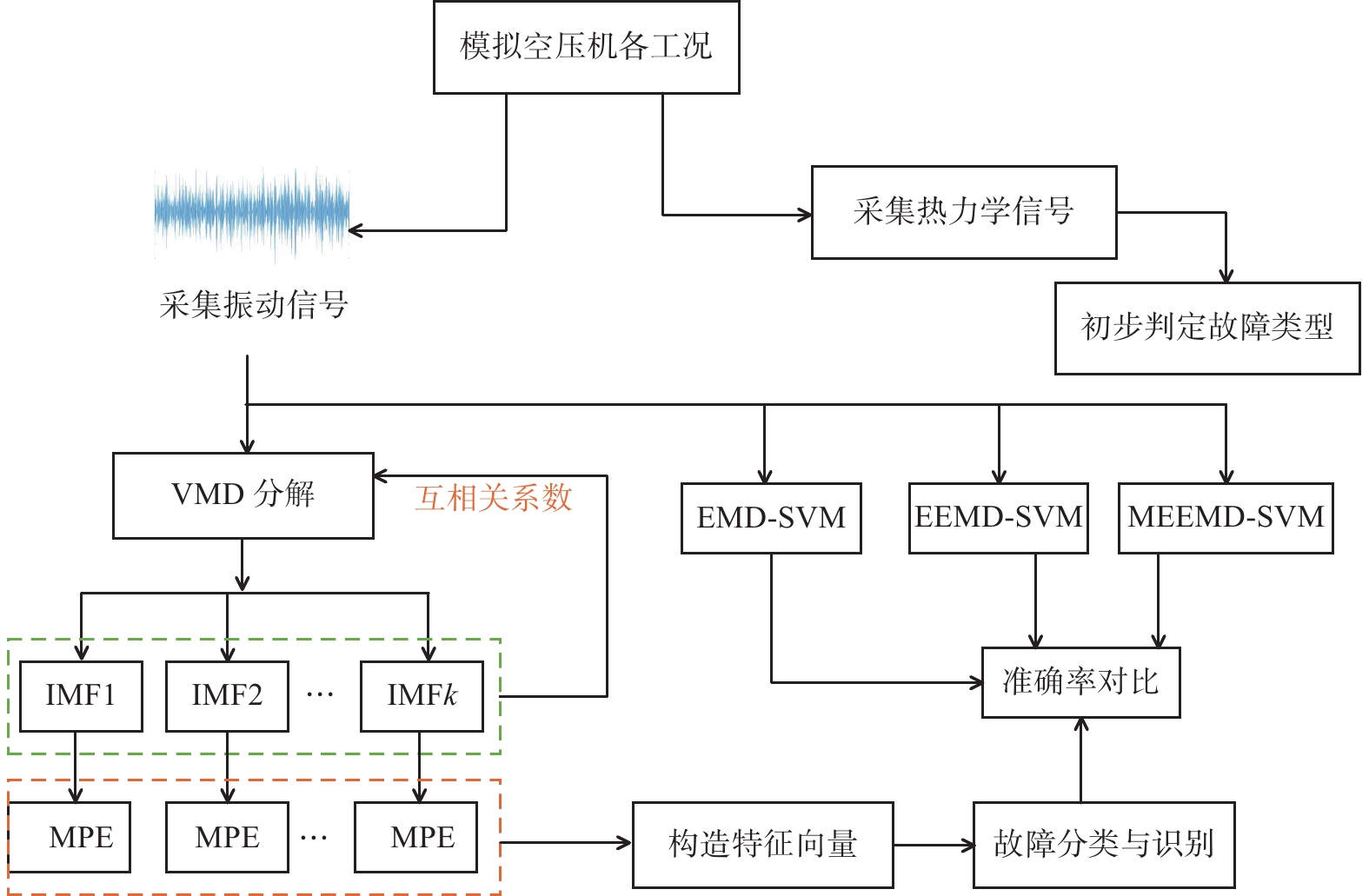
阀片运动形式主要取决于缸内压力、气阀弹簧、阀片升程、阀片自身质量等综合作用的结果,阀片的运动规律如图6所示。
|
| 图 6 阀片运动规律曲线 |
h为阀片的升程,t1为阀片开启过程时间,t2为阀片全开时间,t3为阀片关闭过程时间,t4为阀片开启至撞击阀档时间。
阀片启闭的平均速度分别为:
| $ {v_4} = \frac{h}{{{t_4}}} \text{,}{v_3} = \frac{h}{{{t_3}}} $ |
曲线的斜率代表瞬时运动速度:
| $ v = \frac{{\Delta h}}{{\Delta t}} $ |
运动速度可以反映出阀片启闭是否及时、缸内是否有压力脉动、流通性是否完好等,分析运动规律有利于查明阀片故障原因以及选择合适的气阀弹簧。
3.3 振动信号的VMD分解为增强振动信号特征的提取能力,利用VMD对各工况振动信号分解,分解出相应的固有模态分量,求其各尺度下排列熵值,并筛选敏感IMF分量,将其多尺度排列熵作为特征向量输入 SVM中,进行空压机工况的识别。
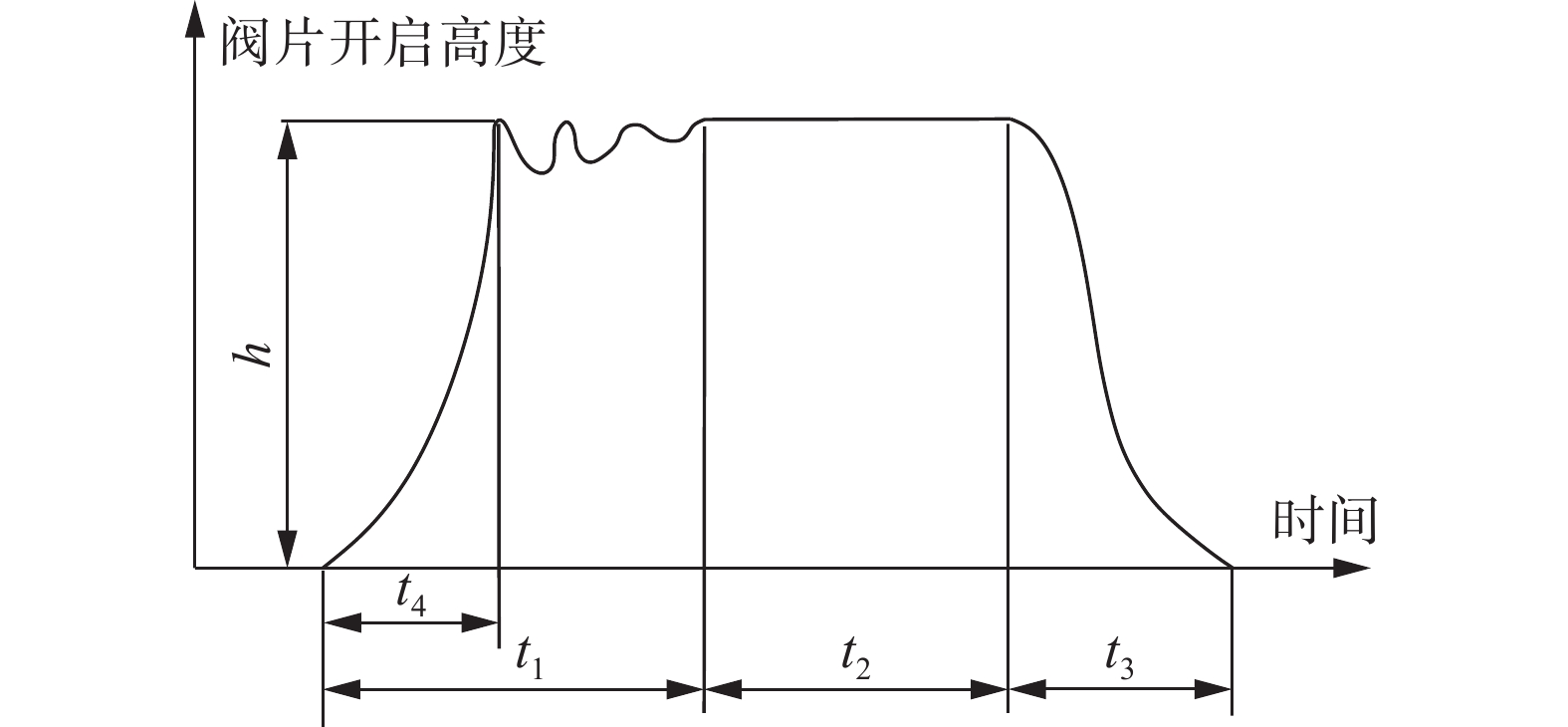
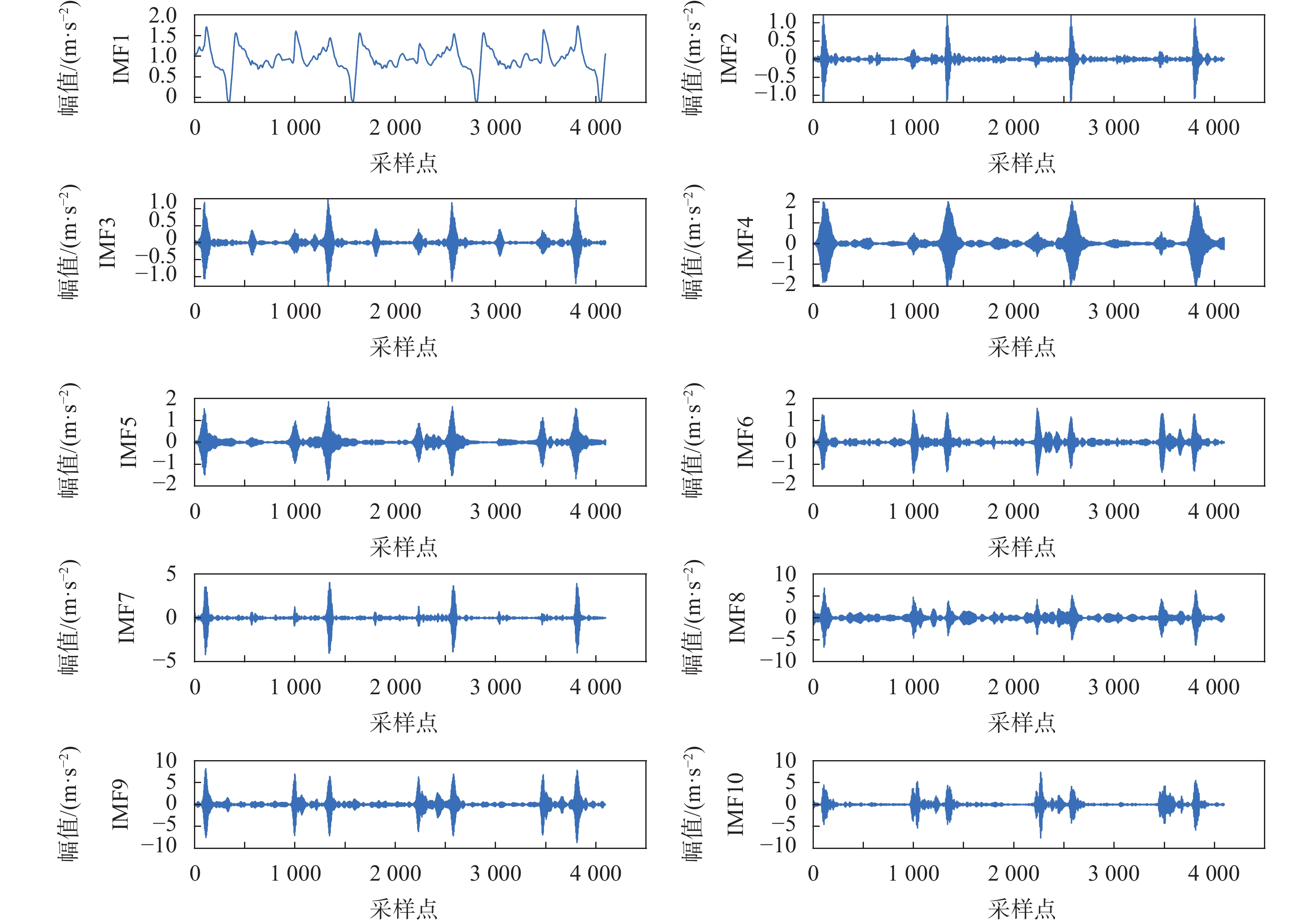
设定K=10,
|
| 图 7 IMF分量 |

|
| 图 8 各IMF分量的频谱图 |
在图8中可以看出:VMD分解的各IMF分量的频谱成分较简单,并且能够比较均匀的分布在各个频率上,各IMF所占的频率段相对较窄。通过对比发现,各IMF分量的频谱图与原始信号频谱图对应性良好。不仅改进了EMD模态混叠的不足,而且也不会使IMF波形失真,保证分解结果的准确性。
计算固有模态分量的MPE前,应确定好m、

|
| 图 9 IMF分量在各尺度下排列熵值(故障一) |
当尺度s=1时,为原始振动信号的排列熵[15]。由图9可知,尺度为1时熵值相差不大,无法区别分压机处于哪种工况,故需要进行多个尺度的分析。随着尺度因子的增加,各分量排列熵的离群值变小,体现出多尺度排列熵的稳定性。MPE方法可以估算不同尺度的时间序列的复杂度,可以有效地克服信号中的噪声影响[18]。虽然有些尺度排列熵值相对接近,但是得益于多尺度排列熵多维分析的优势,多个尺度结合总能对分量进行区分,大大提高对信号的识别能力[19]。由此可见,MPE能有效地获取多维度故障特征信息,能准确地反映出空压机系统的复杂程度以及变化规律。
为了筛选出包含主要特征信息的固有模态分量,文章引入互相关系数来选取敏感固有模态分量。在实际工程中,一般认为相关系数大于0.05的分量为真实分量[20]。空压机各工况下IMF分量与原始信号的互相关系数如表3所示。根据表3可知,可选取IMF1~IMF8分量为敏感固有模态分量,将IMF9、IMF10舍弃。
| 序号 | 工况 | 相关系数 | |||||||||
| 1 | 正常 | 0.8791 | 0.7657 | 0.4765 | 0.3893 | 0.2574 | 0.2342 | 0.1688 | 0.1427 | 0.0365 | 0.0181 |
| 2 | 故障一 | 0.8668 | 0.6921 | 0.5401 | 0.4037 | 0.3645 | 0.2943 | 0.2165 | 0.1586 | 0.0243 | 0.0036 |
| 3 | 故障二 | 0.9451 | 0.7359 | 0.6218 | 0.3958 | 0.3341 | 0.3122 | 0.2354 | 0.1939 | 0.0197 | 0.0231 |
| 4 | 故障三 | 0.8347 | 0.6852 | 0.6019 | 0.5549 | 0.4301 | 0.3954 | 0.3129 | 0.1472 | 0.0089 | 0.0027 |
| 5 | 故障四 | 0.9067 | 0.8108 | 0.5397 | 0.4468 | 0.3986 | 0.2769 | 0.1991 | 0.1032 | 0.0041 | 0.0035 |
| 6 | 故障五 | 0.8237 | 0.7649 | 0.5813 | 0.4937 | 0.3461 | 0.2573 | 0.1359 | 0.1469 | 0.0129 | 0.0241 |
3.4 空压机的故障诊断
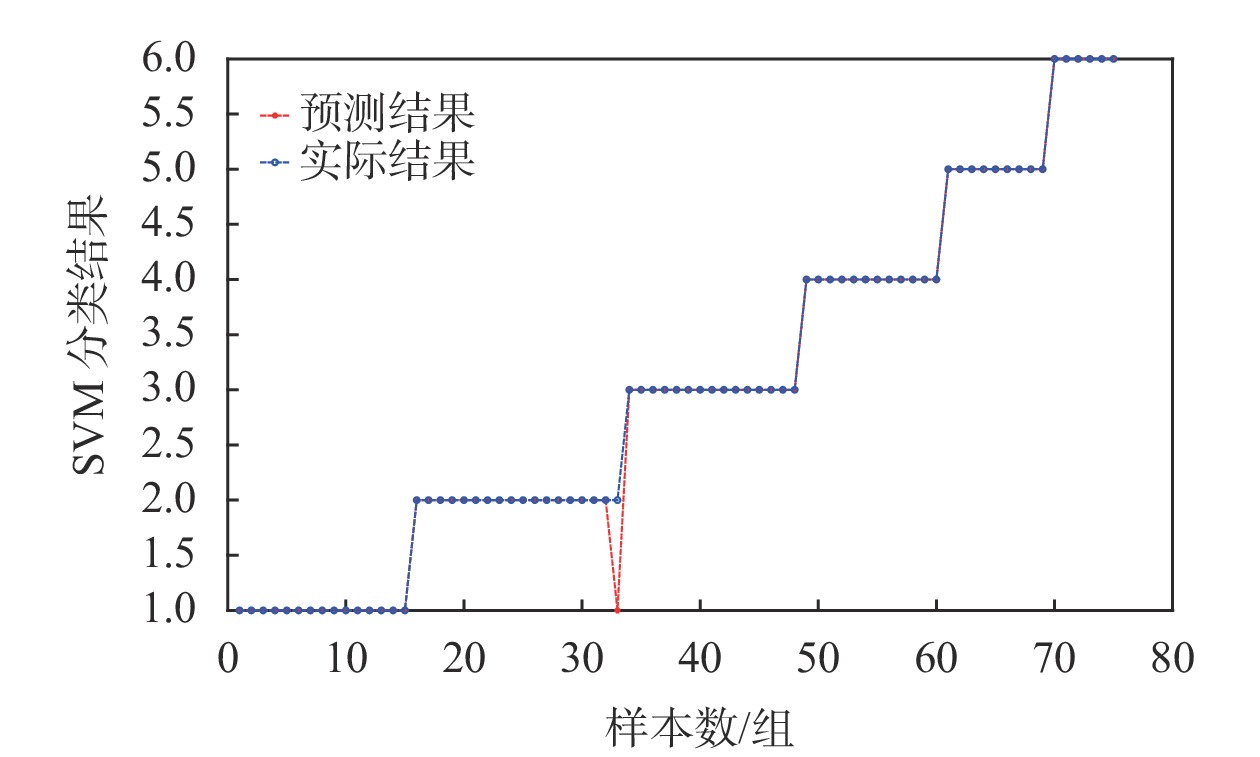
将采集的样本数据用VMD-MPE进行处理,随机抽取各工况下150组样本数据作为已知样本数据,各工况剩余样本数据为待识别样本。求出各工况下敏感量的MPE值,作为特征向量,将其输入到SVM中,诊断结果和准确率如图10和表4所示。
|
| 图 10 SVM诊断结果 |
| 序号 | 工况 | 训练组数 | 测试组数 | 准确率/% |
| 1 | 正常 | 15 | 15 | 100 |
| 2 | 故障一 | 18 | 17 | 94.4 |
| 3 | 故障二 | 18 | 12 | 100 |
| 4 | 故障三 | 12 | 12 | 100 |
| 5 | 故障四 | 10 | 10 | 100 |
| 6 | 故障五 | 9 | 9 | 100 |
只有故障一的一组样本在诊断过程中出现误差,出现误差的原因可能是由于训练样本较少或系统误差等。为进一步说明此方法的有效性,将所使用的方法与EMD、EEMD、MEEMD进行准确率对比,结果如图11所示。各方法的平均诊断精度分别为98.6%、69.6%、75.8%、88.4%。在图中可以看出,文中所提方法在各工况下都有较高的准确精度且更加平稳,说明本文所提方法具有较高的鲁棒性和泛化能力。

|
| 图 11 准确率对比图 |
4 结束语
针对空压机振动信号的非平稳性和非先线性问题,文章使用VMD-MPE与SVM相结合的故障诊断方法,主要结论如下:
1)只利用热工参数和频谱分析不能全面地了解空压机的运行状况。
2)本文使用VMD-MPE和SVM融合的船用空压机故障诊断方法,克服了EMD在信号分解过程中模态混叠的缺陷。利用互相关系数的方法筛选出敏感IMF分量,并将其多尺度排列熵作为特征向量,输入到SVM中进行故障辨识,提高了空压机故障识别的准确性。
3)以VMD-MPE和SVM故障辨别为主、热工参数为辅的空压机状态监测方法,可以为轮机维修人员提供理论和技术参考。
4)在接下来的研究工作中,将会采集实船空压机更多复杂工况进行研究,并改进VMD和SVM的相关参数,以便提高VMD运行速度和SVM的诊断精度。
| [1] |
杨丰源, 宋辉, 程序, 等. 基于改进EEMD和Cohen类的局部放电信号联合时频分析[J].
高电压技术, 2016, 42(7): 2345-2352.
YANG F Y, SONG H, CHENG X, et al. Analysis of joint time-frequency analysis on partial discharge signal based on improved EEMD and Cohen's class[J].
High Voltage Engineering, 2016, 42(7): 2345-2352.
|
| [2] |
陈东宁, 张运东, 姚成玉, 等. 基于变分模态分解和多尺度排列熵的故障诊断[J].
计算机集成制造系统, 2017, 23(12): 2604-2612.
CHEN D N, ZHANG Y D, YAO C Y, et al. Fault diagnosis method based on variational mode decomposition and multi-scale permutation entropy[J].
Computer Integrated Manufacturing Systems, 2017, 23(12): 2604-2612.
|
| [3] |
谢棕, 张丽萍. 基于参数优化VMD和多尺度排列熵的齿轮故障诊断[J].
机械制造与自动化, 2021, 50(6): 114-117.
XIE Z, ZHANG L P. Gear fault diagnosis based on parameter optimization VMD and multi-scale permutation entropy[J].
Machine Building & Automation, 2021, 50(6): 114-117.
|
| [4] |
唐蕾, 黄天立, 万熹. 基于变分模态分解和同步提取变换识别时变结构瞬时频率[J].
振动与冲击, 2022, 41(6): 197-205.
TANG L, HUANG T L, WAN X. Instantaneous frequency identification of time-varying structures using variational mode decomposition and synchroextracting transform[J].
Journal of Vibration and Shock, 2022, 41(6): 197-205.
|
| [5] |
WANG D Y, LUO H Y, GRUNDER O, et al. Multi-step ahead wind speed forecasting using an improved wavelet neural network combining variational mode decomposition and phase space reconstruction[J].
Renewable Energy, 2017, 113: 1345-1358.
DOI:10.1016/j.renene.2017.06.095 |
| [6] |
HAN T, JIANG D X. Rolling bearing fault diagnostic method based on VMD-AR model and random forest classifier[J]. Shock and Vibration, 2016(6): 5132046.
|
| [7] |
SUN W, GAO Q. Short-term wind speed prediction based on variational mode decomposition and linear-nonlinear combination optimization model[J].
Energies, 2019, 12(12): 1-27.
|
| [8] |
LI J C, ZHU S W, WU Q Q. Monthly crude oil spot price forecasting using variational mode decomposition[J].
Energy Economics, 2019, 83: 240-253.
DOI:10.1016/j.eneco.2019.07.009 |
| [9] |
李振璧, 张坤, 姜媛媛, 等. 基于变分模态分解与近似熵的输电线路两相接地故障诊断[J].
科学技术与工程, 2018, 18(5): 70-75.
LI Z B, ZHANG K, JIANG Y Y, et al. Two-phase grounding fault diagnosis of transmission lines based on variational mode decomposition and approximate entropy[J].
Science Technology and Engineering, 2018, 18(5): 70-75.
|
| [10] |
邹瑛珂, 李祖明, 刘晓宏, 等. 基于VMD分解的MFCC+GFCC无人机噪音混合特征提取方法[J].
中国测试, 2021, 47(11): 141-146.
ZOU Y K, LI Z M, LIU X H, et al. Hybrid feature extraction method of MFCC + GFCC UAV noise based on VMD decomposition[J].
China Measurement & Test, 2021, 47(11): 141-146.
DOI:10.11857/j.issn.1674-5124.2021040122 |
| [11] |
张燕霞, 户文刚. 基于VMD-SVD和SVM的旋转机械故障诊断研究[J].
机电工程, 2022, 39(3): 324-329.
ZHANG Y X, HU W G. Fault diagnosis of rotating machinery based on VMD-SVD and SVM[J].
Mechanical & Electrical Engineering Magazine, 2022, 39(3): 324-329.
DOI:10.3969/j.issn.1001-4551.2022.03.006 |
| [12] |
杜佳耘, 雷勇, 李永凯, 等. 基于参数优化变分模态分解的混合储能功率分配策略[J].
现代电力, 2021, 38(1): 51-59.
DU J Y, LEI Y, LI Y K, et al. Hybrid energy storage strategy based on parameter optimized variational mode decomposition[J].
Modern Electric Power, 2021, 38(1): 51-59.
|
| [13] |
卢鹏, 年圣全, 邹国良, 等. 基于变分模态分解和注意力机制的浪高预测[J].
海洋测绘, 2021, 41(2): 34-39.
LU P, NIAN S Q, ZOU G L, et al. Wave height prediction based on variational mode decomposition and attention mechanism[J].
Hydrographic Surveying and Charting, 2021, 41(2): 34-39.
|
| [14] |
BANDT C, POMPE B. Permutation entropy: A natural complexity measure for time series[J].
Physical Review Letters, The American Physiological Society, 2002, 88(17): 174102.
DOI:10.1103/PhysRevLett.88.174102 |
| [15] |
郑近德, 程军圣, 杨宇. 多尺度排列熵及其在滚动轴承故障诊断中的应用[J].
中国机械工程, 2013, 24(19): 2641-2646.
ZHENG J D, CHENG J S, YANG Y. Multi-scale permutation entropy and its applications to rolling bearing fault diagnosis[J].
China Mechanical Engineering, 2013, 24(19): 2641-2646.
DOI:10.3969/j.issn.1004-132X.2013.19.017 |
| [16] |
姚文坡, 刘铁兵, 戴加飞, 等. 脑电信号的多尺度排列熵分析[J].
物理学报, 2014, 63(7): 427-433.
DOI:10.7498/aps.63.078704 |
| [17] |
王伯昕, 杨海涛, 王清, 等. 基于补充改进集合经验模态分析法-多尺度排列熵分析桥梁振动信号优化滤波方法[J].
吉林大学学报(工学版), 2020, 50(1): 216-226.
WANG B X, YANG H T, WANG Q, et al. Bridge vibration signal optimization filtering method based on improved CEEMD-multi-scale permutation entropy analysis[J].
Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 216-226.
DOI:10.13229/j.cnki.jdxbgxb20190013 |
| [18] |
赵建岗, 宁静, 宁云志, 等. 基于多尺度排列熵和线性局部切空间排列的机械故障诊断特征提取[J].
振动与冲击, 2021, 40(13): 136-145.
ZHAO J G, NING J, NING Y Z, et al. Feature extraction of mechanical fault diagnosis based on MPE-LLTSA[J].
Journal of Vibration and Shock, 2021, 40(13): 136-145.
DOI:10.13465/j.cnki.jvs.2021.13.018 |
| [19] |
王泽, 王红军. 基于多尺度排列熵的滚动轴承故障特征提取[J].
组合机床与自动化加工技术, 2020(8): 30-34.
WANG Z, WANG H J. Fault feature extraction of rolling bearings based on multi-scale entropy[J].
Modular Machine Tool & Automatic Manufacturing Technique, 2020(8): 30-34.
DOI:10.13462/j.cnki.mmtamt.2020.08.008 |
| [20] |
蔡波, 黄晋英, 杜金波, 等. 基于MEEMD多特征融合与LS-SVM的行星齿轮箱故障诊断[J].
中国测试, 2021, 47(9): 126-132.
CAI B, HUANG J Y, DU J B, et al. Planetary gearbox fault diagnosis based on MEEMD multi-feature fusion and LS-SVM[J].
China Measurement & Test, 2021, 47(9): 126-132.
|
 2024, Vol. 50
2024, Vol. 50