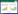文章信息
- 王智慧, 廖锐全, 程阳, 冯笑雅, 袁旭, 张兴凯
- WANG Zhihui, LIAO Ruiquan, CHENG Yang, FENG Xiaoya, YUAN Xu, ZHANG Xingkai
- 重力场中油滴运动速度及聚合规律研究
- Study on the velocity of oil droplet motion and aggregation law under the action of the gravitational field
- 中国测试, 2024, 50(6): 10-19
- CHINA MEASUREMENT & TEST, 2024, 50(6): 10-19
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022120132
-
文章历史
- 收稿日期: 2022-12-21
- 收到修改稿日期: 2023-03-17
2. 中国石油天然气集团公司采油采气重点实验室长江大学分室,湖北 荆州 434023;
3. 中国石油气举试验基地多相流研究室,湖北 武汉 430100;
4. 油气钻采工程湖北省重点实验室,湖北 武汉 430100;
5. 西安长庆化工集团有限公司,陕西 西安 710021
2. CNPC Key Laboratory of Oil and Gas Productions in Yangtze University, Jingzhou 434023, China;
3. CNPC Multiphase Flow Laboratory of Gas Lift Innovation Center, Wuhan 430100, China;
4. Key Laboratory of Drilling and Production Engineering for Oil and Gas, Wuhan 430100, China;
5. Xi’an Changqing Chemical Group Co., Ltd., Xi’an 710021, China
在采油井生产中后期,为保持或恢复油层压力,使油藏具备很强的驱动力,注水开发技术得到广泛应用。注水开发技术对注入水的水质要求较高,这对采出水中的油水分离效率提出更高的要求。现有的分离技术已不能达到满意的效果,不仅增加了采出水处理成本,又造成环境污染。油水分离技术的落后归根结底是缺乏对油水两相运动规律的深入认识。高效的油水分离不仅能够净化地层,减少环境污染,还能提高油井产出液的计量精度。
现有的采出水分离主要是静置分离法,针对静置分离过程中油滴聚合动态的研究主要以理论分析为主[1-3],将现场试验作为验证理论模型准确性的方法。Goncharov等[4]通过对数学模型和现场试验结果进行分析发现油滴的尺寸对其上浮速度有显著的影响。油滴的释放速度越快,产生的油滴尺寸越小。通常,计算粒子上浮速度最常用的是Stokes法则,但是这种方法只局限于球状的刚性粒子。为增加Stokes法则的普适性,Zheng和Yapa[5]在Cliff等人研究的基础上进行改进,提出了一种新的近似方法。Premathilake[6]发现气泡在向上运动过程中与周围流体之间存在滑移速度,对Yapa等人给出的气泡上升速度公式进行了修正,并将实验数据与理论公式进行对比,二者吻合良好。基于实验数据和理论分析建立了气泡上升的速度数学模型,为研究油滴在重力场中的运动奠定了理论基础。
Wu等[7]的研究表明,在重力场中油滴以球形或椭球型两种形式分布。其中,椭球型油滴在上升过程中轨迹呈螺旋形。球形油滴的上升速度小于椭球型的上升速度,这种速度差异主要是由连续相与分散相之间的密度差决定的[8],而油滴在上升过程中的形状变化主要受表面张力的影响。研究表明,随着表面张力增大,油滴在运动过程中形状基本不发生改变,只会发生周期性振动形变,且振动周期和振幅随着表面张力减小而增加[9]。当多个油滴同时产生时,在上升过程中会发生油滴的相互碰撞与合并。吕宇玲[10]的研究结果表明,液滴形成过程存在剪切破碎和碰撞聚结同时发生的现象。其中,液滴破碎的时间为0.008~0.02 s,碰撞又弹开的时间约为0.006 s,液滴合并时间约为0.002 s,表明液滴碰撞和合并的时间非常短暂。液滴碰撞之后会发生聚并还是破碎,取决于韦伯数大小[11-12],其中在除油的过程中,碰撞聚并是研究者所期望的。
为了研究油滴之间的聚结时间,需要捕捉油水界面的变化型态。实验中通过高速摄像机较难实现相界面的精细描述。李会雄等[13]采用Level Set 方法对两相流体界面的波动特性进行数值模拟,研究发现表面张力能够抑制界面的波动性,给出了界面变化特征。通过Level Set方法[14]和VOF方法[15]对油水界面进行追踪,结果表明油滴发生变形主要是压差作用引起的,其变化规律符合黏弹性矩阵方程。使用Level Set方法网格分辨率低,很难精确描述相界面,采用AMR技术和Level Set相结合的方法能够解决这一难题[16]。两种技术的结合有效提高了界面追踪精度,扩大了Level Set方法的适用范围。随着有限元模拟技术的快速发展,Fluent软件被广泛应用于多相流场的仿真模拟[17-18]。有限元模拟的优势在于能够根据需求自定义油滴直径、数量以及连续相物性,实现油滴运动速度和聚并动态的精细化研究。
前人的研究主要集中在油滴的变形及其界面运移规律等理论方面,对影响油滴变形的各个因素未进行详细的实验研究。实际上,控制外因对油滴运动的干扰,能够有效提高油水分离的效率。本文通过理论分析、室内实验和数值模拟等方法对油滴在重力场中的运移和聚并规律进行研究。从油滴的运动规律出发,研究油滴聚结、分裂动态及其上升速度。为确定油滴在静水中的分离时间提供参考依据,实现油水分离流程高效运行。
1 油滴运动理论油滴处于不同深度时静水压力不同,其上下表面形成的压力差被称为浮力。浮力使油滴产生向上的运动趋势,这种运动趋势也受到自身重力的阻碍。油滴在静态水中上升过程中,其表面和水接触并产生相对运动,水对油滴运动产生的阻力作用,称为曳力。若油滴以某个速度进入水中时,具有一定的初始动量,产生惯性力作用。油滴获得的惯性力能够推动周围的液体作加速运动,同时也受到液体的阻力作用。由于分子内聚力的作用,油滴表面能承受微小张力,具有收缩其表面积的趋势,这种作用力称为表面张力。但表面张力作用只是保持油滴原有形态,不能为油滴提供动力。因此,在重力场中油滴上浮主要受到重力、浮力、曳力的共同作用。油滴受力图如图1所示。
|
| 图 1 油滴受力分析图(沿y轴正方向运动) |
基于阿基米德原理,油滴受到浮力(
| $ {F_{\mathrm{f}}} = {\rho _{\mathrm{w}}}g{V_{\mathrm{o}}} $ | (1) |
重力(G)和浮力的方向相反,当油水密度差越小时,重力越接近浮力。通过下式计算重力大小:
| $ G = {\rho _{\mathrm{o}}}g{V_{\mathrm{o}}} $ | (2) |
式中:
在油滴运动过程中,不同深度处的压力差造成油滴变形。深度逐渐增加,油滴由球形变成椭球形。假设椭球型油滴的焦点在x轴,油滴出发点在(0,0),沿着y轴正方向运动。油滴体积是计算浮力的关键参数,因此油滴的体积使用下式计算:
| $ {V_{\mathrm{o}}} = \pi \int_{ - a}^a {\left({b^2} - \frac{{{b^2}}}{{{a^2}}}{x^2}\right){\text{ }}} {\mathrm{d}}x = \frac{{4\pi a{b^2}}}{3} $ | (3) |
当油滴的长轴和短轴相同时,即a=b,按照球体计算油滴体积,即
油滴的曳力(Fd)主要来源于连续相的黏性阻力。连续相在静置状态下,油滴所受曳力可用下式计算:
| $ {F_{\mathrm{d}}} = \frac{{\pi ab}}{2}\xi {\rho _{\mathrm{w}}}u_{\mathrm{o}}^2 $ | (4) |
式中:
a、b——椭圆形油滴的长半轴和短半轴。
根据不同雷诺数(
| $ \xi = \left\{ \begin{gathered} \frac{{24}}{{{{{Re}}} }} \qquad {10^{{{ - }}4}} < {Re} < 0.4 \\ \frac{{18.5}}{{{{{{{Re}}} }^{0.6}}}} \qquad 2 < {{{Re}}} \leqslant 500 \\ 0.44 \qquad 500 < {{{Re}}} < 2 \times {10^5} \\ \end{gathered} \right. $ | (5) |
根据动量定理,油滴在上行过程中的动量方程可以写成:
| $ m\frac{{{\mathrm{d}}u}}{{{\mathrm{d}}t}} = {F_{\mathrm{f}}} - {F_{\mathrm{d}}} - G $ | (6) |
将公式(1)、(2)、(3)、(4)代入公式(6)中可得:
| $ \frac{{{\mathrm{d}}{{u}}}}{{{\mathrm{d}}{{t}}}} = \frac{g}{{{\rho _{\mathrm{o}}}}}\left({\rho _{\mathrm{w}}} - {\rho _{\mathrm{o}}} - \frac{{3\xi {\rho _{\mathrm{w}}}u_{_{\mathrm{o}}}^2}}{{8bg}}\right) $ | (7) |
当油滴在水中匀速上升时,加速度为零,油滴速度计算公式为:
| $ {u_{\mathrm{o}}} = \sqrt {\frac{{8gb\Delta \rho }}{{3\xi {\rho _{\mathrm{w}}}}}} $ | (8) |
在油滴上升过程中,由于不同深度的压力不同,导致油滴变形。本研究中使用变形系数研究油滴的变形规律。油滴在变形过程中,纵横比发生变化,变形系数E定义为椭圆短轴与长轴的比值[19],由图1可知:E=b/a。E为无量纲数。
2 实验设计与介绍本实验系统由水槽、高速摄像机、激光器、精密助推器、注射器、速度控制器组成。为测量油滴在水中的上升速度、聚并动态、运动轨迹以及变形系数。在透明的长方体容器底部安装精密助推器,通过推进速度控制器给定注入油滴的频率。实验中使用的油品为工业级白油,使用增黏剂调整油品黏度。实验所用的油品性质见表1,注射针头使用不锈钢平口针头注入油滴,型号见表2。高速摄像机记录油滴在水中的运动轨迹和变形规律。实验设备如图2所示。通过图像处理软件对实验数据进行处理,得到不同直径的油滴实时速度及变形规律。
| 参数 | 8G | 10G | 11G | 12G | 13G | 14G | 16G | 18G | 19G | 20G | 21G |
| 内径(DI)/mm | 3.43 | 2.69 | 2.39 | 2.16 | 1.80 | 1.60 | 1.19 | 0.84 | 0.69 | 0.58 | 0.51 |
| 外径(DE)/mm | 4.57 | 3.45 | 3.05 | 2.77 | 2.41 | 2.11 | 1.65 | 1.27 | 1.07 | 0.91 | 0.81 |

|
| 图 2 实验设备 |
3 数值模拟
建立二维物理模型,使用volume of fraction (VOF)模型计算油滴在重力场作用下的运动规律。系统的温度为25℃,压力8 kPa,油品物性见表1。基于压力求解器计算油滴变形及聚并的瞬态过程,设置油滴初始速度为零。使用phase couple SIMPLE压力-速度耦合算法。为保证油水之间的清晰界面,打开Phase Localized Discretization选项。主相设置为水,第二相为油。通过求解油水两相的连续性方程跟踪相界面。对第i相,连续性方程如下:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho {\boldsymbol{v}}) = 0 $ | (9) |
| $ \rho = {\alpha _{\mathrm{w}}}{\rho _{\mathrm{w}}} + {\alpha _{\mathrm{w}}}(1 - {\rho _{\mathrm{o}}}) $ | (10) |
式中:
在进行计算之前初始化模型,对油滴的大小和位置进行定义。本文中设置油滴数量为2、3、5,油滴直径分别为3、5、10 mm,分析不同油滴直径和数量在重力场中的运动轨迹和聚并时间。
4 分析与讨论 4.1 油滴型态及运动规律油滴形状主要依靠表面张力维持,油滴总有缩小其表面积的倾向。油滴脱离针头的瞬间,在表面张力作用下形成球形油滴。油滴开始上升时,上下表面的压力差使油滴变成椭球型。油滴生长和上浮过程如图3所示。

|
|
图 3
不同时刻油滴的生长和变形(DI=1.19 mm, |
实验结果显示,当油滴达到最大速度,油滴开始匀速运动,处于动态平衡状态。可得到油滴的直径和针头内径的相关性[9]如下:
| $ d = {\left[ {\frac{{6\sigma {d_{\mathrm{k}}}}}{{({\rho _{\mathrm{w}}} - {\rho _{\mathrm{o}}})g}}} \right]^{1/3}} $ | (11) |
式中:
使用Image pro plus 7.0软件对实验数据处理,得到不同油滴直径变化规律。从图4(a)中可知,油滴直径随针头内径的增加而增加。通过实验结果和理论值的对比分析,理论计算所得油滴直径的平均误差均控制在3%以内,其中分散相黏度较低时误差更小(2.17%)。

|
| 图 4 油滴直径及变形系数变化规律 |
根据前人的研究发现[20-21],高黏油形成的油滴变形系数较大,在运动过程中不易发生变形。低黏油形成的油滴在上升过程中变形系数逐渐减小最后趋于稳定。由图4(b)可知,油滴的变形系数随着油滴直径的增大而逐渐减小,油滴直径和变形系数之间符合线性变化关系。因此,大直径的低黏度油滴最容易发生变形。油滴形状在运动过程中处于动态变化,越靠近液面,变形系数越大,油滴越接近球形。
通过精密助推器将油滴注入水中,注射器推进速度小,认为油滴在离开针头时无初始动量。曳力主要来自于油滴周围水的摩擦阻力,油滴的上升速度越大,受到的曳力越大。由公式(6)可知,油滴主要依靠浮力、重力和曳力的合力提供加速度。计算发现大直径的油滴所受的曳力大于小直径油滴,但曳力远小于重力和浮力。在油滴脱离针头瞬间,
| $ \frac{{8gr}}{3}({\rho _{\mathrm{w}}} - {\rho _{\mathrm{o}}}) = \xi {\rho _{\mathrm{w}}}{u_{\mathrm{o}}}^2 $ | (12) |
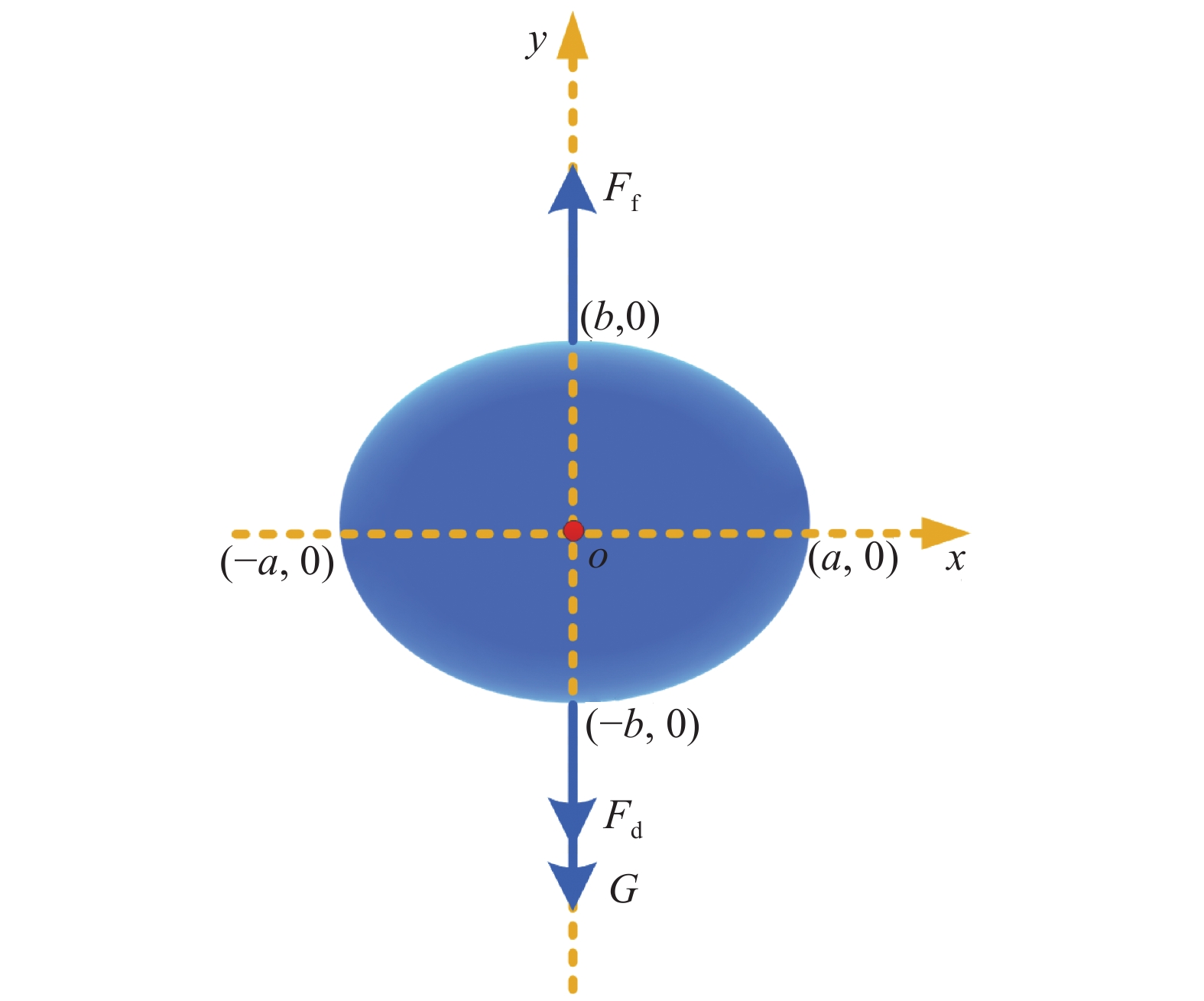
由图5可知,当
|
| 图 5 不同直径油滴的速度曲线 |
4.2 油滴聚并动态
按照发生顺序,油滴聚并过程可分为两个阶段:油膜排水和油膜破裂[22-23]。因此,油膜和油水界面的性质在聚结过程中起着重要作用[24]。其中,油膜排水的速率将会影响两个油滴的聚并时间。实验发现,两个大小不一的油滴接触的瞬间不会立即聚合,由图6(a)可知,油滴之间的距离逐渐缩小但未发生油膜的融合,而是处于油膜排液阶段。研究表明,连续相黏度对油膜排液速率有着巨大的影响,油膜面积(油滴尺寸)对油膜减薄速率至关重要:较小的油滴会缩短油膜减薄时间[25]。由图6(b)可知,重力场中处于同一条垂直线上的两个油滴,下方的油滴易受上方油滴的尾流影响导致其速度增加。Ruzicka等[26]认为尾流是导致油滴发生碰撞聚结最主要的原因。一方面,上方油滴的尾部产生的尾流加速了后面油滴的运动,使得下方的油滴速度增大,加速靠近上方油滴;另一方面,由于油滴和连续相的表面张力具有差异性,马兰戈尼效应[27]促进油滴的聚合。通过实验和模拟两种结果的对比(图6)发现,油滴的聚合过程基本相同,两者间具有较高的吻合度。

|
|
图 6
油滴之间的聚并过程( |
图6(b)显示,在0.76 s时两者即将接触,两油滴之间的液膜开始向四周排液,逐渐建立液桥。随着时间推移,在0.78 s时油膜破裂并逐渐开始聚合。在0.8 s后两个油滴的表面膜完全融合,由于惯性导致两个油滴完成聚并时发生短暂的变形,油滴由球形变为椭球形(t=0.94 s)。当聚并后的油滴靠近油水界面时,由于上下表面的压力差增大,导致油滴再次变为椭球形。油滴接触油层界面会出现短暂的液桥,随后瞬间与之融合。实验观察到在竖直方向上油滴刚接触到油层表面时,油滴具有较大的动能,对油层产生向上的冲击力,使油层表面向上隆起。随着油滴进入油层,受到界面张力作用,油滴周围流体产生向下凹陷的波纹[19]。
4.3 油滴聚并影响因素油滴之间或者油滴和油层间的聚合受到油滴间相对位置、液滴形状、连续相黏度、界面张力大小等因素的影响。本文重点分析了油滴间相对位置以及介质黏度对油滴聚合过程的影响。
4.3.1 油滴间相对位置由于油水界面张力作用,分散在水中的油滴本身具有一定的能量,当油滴表面膜被破坏使其破裂。模拟结果显示,小油滴与大油滴之间的聚并时间较小油滴之间的聚并提前发生。浮力为油滴提供了较大的动力,使得大油滴的速度大于小油滴,造成小油滴被大油滴吞并;另一方面,较大的油滴质量较大,在水中稳定性较强,不易受到小油滴运动的影响,因此,在两油滴的表面膜破裂的瞬间小油滴被大油滴快速吸收。
如图7(a)所示,分散的小油滴位于大油滴的45°处,大油滴在上升过程中与小油滴合并,形成“U”形的油滴。由于油的表面张力作用,其形状逐渐由“U”形变成球帽形最后变为椭球形,直至与上部油层融合。当分散的油滴与大油滴平行时(图7(b)),油膜相互融合,形成新的油膜为内部的流体提供了流动通道,小油滴和大油滴产生相向运动。主要原因是两种油滴之间的存在表面张力梯度,油膜破裂后,为保持油滴内部压力平衡,大油滴和小油滴同时向低压区移动。由于惯性、重力以及浮力共同作用,新合成的油滴成锥体。当大油滴周围有小油滴时(图7(c)),小油滴在向上运动的同时也向大油滴靠近。由于底部的小油滴具有向上运动的趋势,其首先和大油滴合并。每两个油滴之间都有一个低压区,小油滴都向大油滴靠近加速油滴聚合。虽油滴之间布局不同,最终形成的油滴都会在表面张力作用下变成椭球型。不同的是,油滴之间的分布位置将会影响油滴上升的速度。
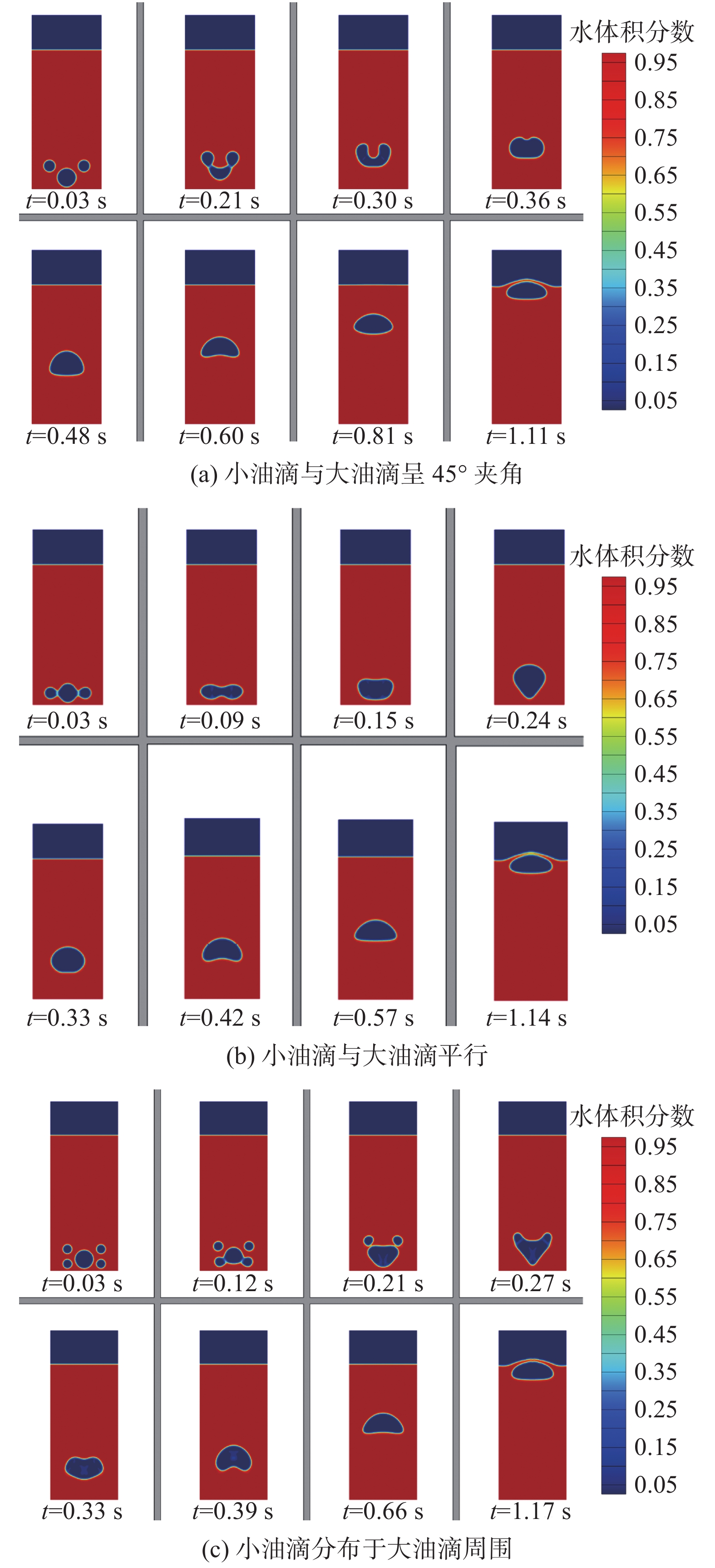
|
| 图 7 不同分布位置的油滴聚并及形状变化过程 |
4.3.2 连续相黏度
由于连续相的表面张力较大,在两个分散的油滴之间形成表面张力梯度。在表面张力梯度的作用下油滴相互靠近,油滴之间的连续相逐渐被排出,油滴表面膜相互融合。当连续相的黏度增加,导致液膜排水困难,增加了油滴聚结时间。由图8可知,连续相黏度等于300 mPa·s时液膜排液过程在0.04 s内基本完成,但连续相黏度等于500 mPa·s时液膜排液时间明显增加。油滴上升过程中与连续相产生的曳力随其黏度增加而增大。由图9可知,连续相黏度从100 mPa·s增加到500 mPa·s时,相同时间内油滴上升的位移明显减小。由于油滴与周围流体产生相对运动,在浮力和摩擦力作用下油滴形状随着黏度增加而逐渐接近球形。
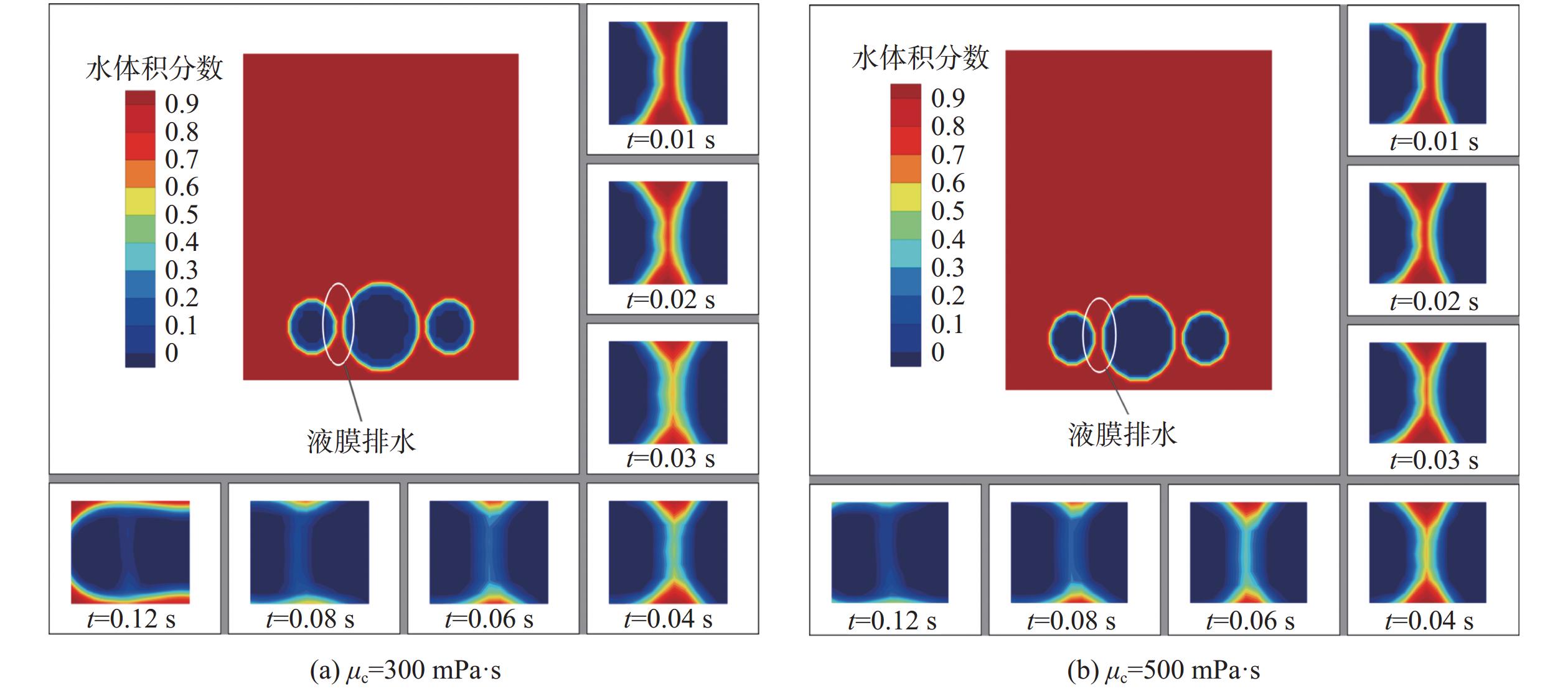
|
| 图 8 不同连续相黏度对油滴聚合的影响 |

|
| 图 9 不同黏度的连续相中油滴形状及其位移(t=0.57 s) |
4.3.3 离散相黏度
由图10可知,当油的黏度由48 mPa·s增加到150 mPa·s时,在0.57 s对应的油滴速度分别为0.0152 m/s、0.0149 m/s、0.0142 m/s,油滴的形状基本保持不变。油的黏度增加对油滴的运动速度影响较小,黏度由80 mPa·s增加到150 mPa·s时对应的速度变化量为0.0007 m/s。油滴的黏度增加使其表面切线方向受到的曳力增大[28],导致油滴的速度略有减小。油滴形状的变化主要受到连续相的浮力和自身重力的共同作用,由于形状不变,油滴的上下面受到的压力差也保持不变。综上,在油滴上浮过程中,连续相的黏度是影响油滴速度及形状的主要因素,而油滴聚合时间主要受到油滴不同分布位置的影响。

|
| 图 10 不同黏度的油滴在连续相中的形状(t=0.57 s) |
5 油滴上升速度模型
通过实验和数值模拟研究发现,油滴的上浮速度主要受到连续相黏度和油滴形状的影响。在重力、浮力、曳力及张力的共同作用下形成了油滴上升、变形的规律。现有的油滴速度计算模型的预测结果较实测值偏小(图5),其主要原因是未考虑表面张力对油滴变形的直接影响。根据前文分析发现实测值和预测值的差值与油滴直径大小相关,通过实验数据拟合可得:
| $ \Delta u = {u_{{\mathrm{ot}}}} - {u_{\mathrm{o}}} = - 0.076\ln d + 0.689\;2 $ | (13) |
通过实验研究得到油滴直径和针头内径存在明显的函数关系,新建立的关联式与公式(8)相似,即,
| $ {d_{\mathrm{k}}} = {\left[ {\frac{d}{{3\;624}}} \right]^{0.272}} $ | (14) |
将公式(14)代入式(11)得到新的油滴直径预测模型:
| $ d = \frac{{197}}{{500}}{\left[ {\frac{\sigma }{{\left( {{\rho _{\mathrm{w}}} - {\rho _{\mathrm{o}}}} \right)g}}} \right]^{0.4}} $ | (15) |
将公式(15)代入公式(13),结合公式(8)可得稳定状态下油滴速度预测新模型如下:
| $ {u_{{\mathrm{ot}}}} = \sqrt {\frac{{8Eag}}{{3\xi }}} - 19\left\{ {\frac{1}{{625}}\ln B + \frac{1}{{25}}} \right\} $ | (16) |
式中,
| $ {u_{{\mathrm{ot,s}}}} = \sqrt {\frac{{{B^{0.4}}g}}{\xi }} - J\left( {\frac{{\ln B}}{{625}} + \frac{1}{{25}}} \right) $ | (17) |
式中,
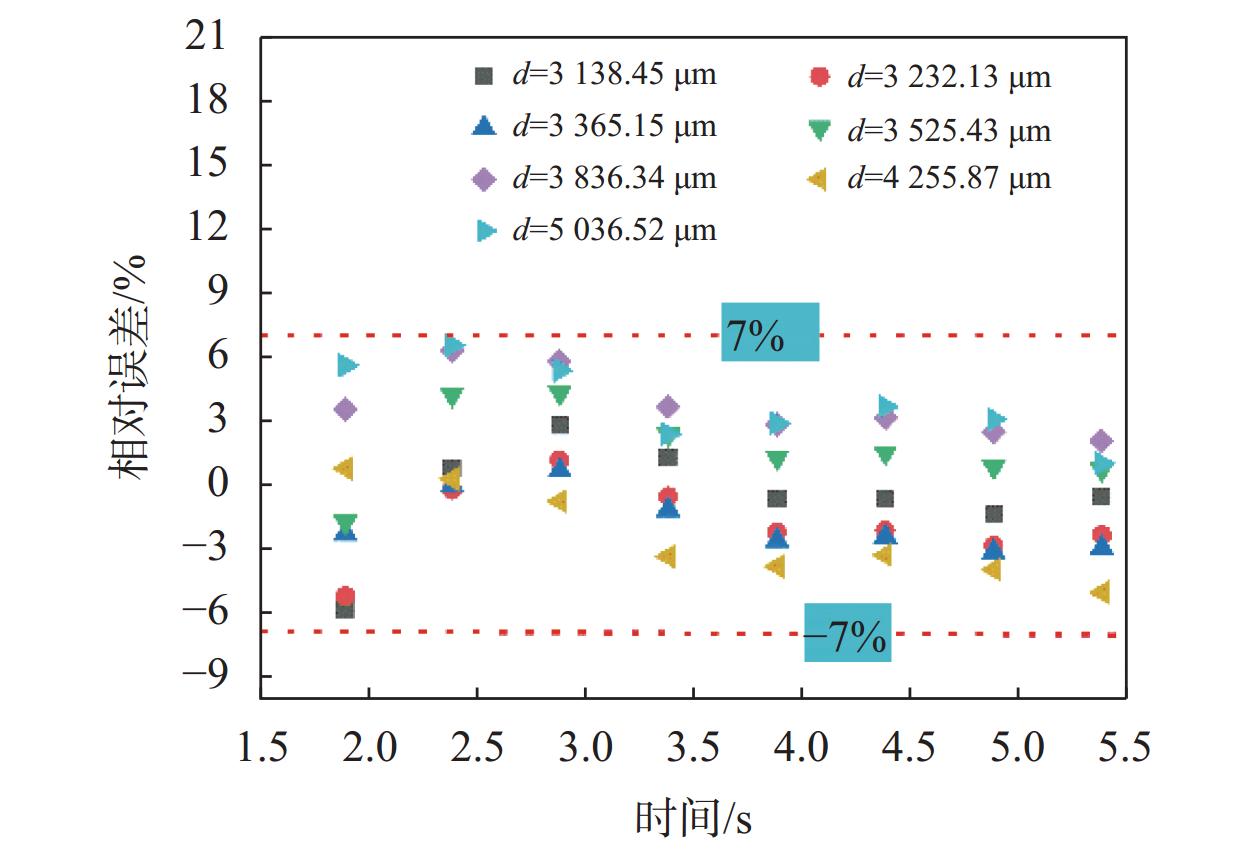
|
| 图 11 油滴速度预测误差分析 |
6 结束语
本文基于有限元计算方法,对油滴的聚合、变形及运动速度进行建模仿真。通过实验与有限元模拟结果对比发现,模拟的油滴动态聚并过程与实验吻合度极高,并通过模拟结果分析了油滴合并过程中液膜的变形与融合。对实验和模拟结果分析得出以下结论:
1)直径较大的油滴在上升过程中受到的合力大于小直径油滴,其速度曲线提前出现拐点,最早达到速度峰值。油滴初始的分布位置只影响其聚合过程中的形态变化。马兰戈尼效应能够有效促进油滴的聚合,但容易受到连续相的黏度影响。
2)初始状态下,处于不同深度的油滴能够相互接触,其主要动力来源于前面的液滴运动产生的尾流对后面液滴的加速。由于表面张力作用,相互接触的油滴不能瞬间聚合,液膜之间的相互融合取决于连续相的黏度和液膜的排液速率。
3)连续相的黏度是油滴的上升速度的主要控制因素。连续相黏度从100 mPa·s增加到500 mPa·s时,相同时间内油滴上升的位移明显减小。连续相黏度较大时,液膜的融合时间明显变长。
4)新建的油滴速度计算模型增加了表面张力对油滴形状的影响,计算值相对误差保持在
本文通过对油滴的运动规律的影响因素的研究,能够为油水分离技术提供可靠的理论基础。为油水分离装置的设计提供理论依据的同时,也将优化油水分离工艺,有效促进油水分离技术的进步。
| [1] |
WANG F C, FENG J T, ZHAO Y P. The head-on colliding process of binary liquid droplets at low velocity: High-speed photography experiments and modeling[J].
Journal of Colloid and Interface Science, 2008, 326(1): 196-200.
DOI:10.1016/j.jcis.2008.07.002 |
| [2] |
WANG F C, YANG F, ZHAO Y P. Size effect on the coalescence-induced self-propelled droplet[J].
Applied Physics Letters, 2011, 98(5): 988.
|
| [3] |
肖杰. 海底管线微孔泄漏油滴尺寸与上升速度研究[D]. 大连: 大连理工大学, 2007.
XIAO J. Theresearch on the size and the ascending velocity of oil drops spilling from tiny holes of seabed pipelines[D]. Dalian: Dalian University of Technology, 2007.
|
| [4] |
GONCHAROV V K, KLEMENTIEVA N Y. Forecasting of the ecological after-effects of the oil and natural gas escapes on the sea environments from pipelines located on seabed[C]//Proc. 6 th Int. Conf. ‘Remote Sensing for Marine and Coastal Environments’, Charleston, 2000, 1: 194-201.
|
| [5] |
ZHENG L, YAPA P D. Buoyant velocity of spherical and nonspherical bubbles/droplets[J].
Journal of Hydraulic Engineering, 2000, 126(11): 852-854.
DOI:10.1061/(ASCE)0733-9429(2000)126:11(852) |
| [6] |
PREMATHILAKE L T, YAPA P D, NISSANKA I D, et al. Modeling the flow regime near the source in underwater gas releases[J].
Journal of Marine Science and Application, 2016, 15(4): 433-441.
|
| [7] |
WU M, GHARIB M. Experimental studies on the shape and path of small air bubbles rising in clean water[J].
Physics of Fluids, 2002, 14(7): L49-L52.
DOI:10.1063/1.1485767 |
| [8] |
许明. 小管径多相流特性及流动参数测量研究[D]. 合肥: 中国科学技术大学, 2012.
XU M. Study of multiphase flow characteristics and parameters measurement in small diameter pipe[D]. Hefei: University of Science and Technology of China, 2012.
|
| [9] |
丁思源, 王瑞祥, 徐荣吉, 等. 表面张力对自由落体液滴形变的影响[J].
化工学报, 2016, 67(6): 2495-2502.
DING S Y, WANG R X, XU R J, et al. Effect of surface tension on deformation of free falling drops[J].
CIESC Journal, 2016, 67(6): 2495-2502.
|
| [10] |
吕宇玲, 何利民, 丁慎圆. 油水两相流管道内液滴形成过程研究[J].
化工进展, 2014, 33(3): 558-562.
LV Y L, HE L M, DING S Y. Droplets formation process of oil-water dispersed flows in pipeline[J].
Chemical Industry and Engineering Progress, 2014, 33(3): 558-562.
|
| [11] |
李枫, 熊峰, 刘彩玉, 等. 油滴聚并破碎行为对水力旋流器分离性能的影响[J]. 石油机械, 2019(6): 73-78.
LI F, XIONG F, LIU C Y, et al. Effect of oil droplet coalescence and breakup behavior on separation performance of hydrocyclone[J]. China Petroleum Machinery, 2019(6): 73-78.
|
| [12] |
张敏霞, 刘涛, 安明明, 等. 油田采出水中油滴的聚结技术与设备[J].
工业水处理, 2022, 42(3): 33-40.
ZHANG M X, LIU T, AN M M, et al. Coalescence technology and equipment of oil droplets in oil field produced water[J].
Industrial Water Treatment, 2022, 42(3): 33-40.
|
| [13] |
李会雄, 杨冬, 陈听宽, 等. Level Set 方法及其在两相流数值模拟研究中的应用[J].
工程热物理学报, 2001, 22(2): 233-236.
LI H X, YANG D, CHEN T K, et al. A formulation for the level set method and its applications in gas-liquid two-phase flow simulations[J].
Journal of Engineering Thermophysics, 2001, 22(2): 233-236.
|
| [14] |
王琳琳, 田辉, 李国君. 基于 Level Set 方法对油水和气水两相界面的数值模拟[J].
应用力学学报, 2010(2): 298-302.
WANG L L, TIAN H, LI G J. Numerical simulation of oil-water and air-water two-phase flow based on level set methods[J].
Chinese Journal of Applied Mechanics, 2010(2): 298-302.
|
| [15] |
CHINYOKA T, RENARDY Y Y, RENARDY M, et al. Two-dimensional study of drop deformation under simple shear for Oldroyd-B liquids[J].
Journal of Non-Newtonian Fluid Mechanics, 2005, 130(1): 45-56.
DOI:10.1016/j.jnnfm.2005.07.005 |
| [16] |
宫翔飞, 张树道, 江松. 界面捕捉 Level Set 方法的 (AMR) 数值模拟[J].
计算物理, 2006, 23(4): 391.
GONG X F, ZHANG S D, JIANG S. Numerical simulation of fluid interfaces with the adaptive mesh refinement method,the ghost fluid method and the Level Set method[J].
Chinese Journal of Computational Physics, 2006, 23(4): 391.
|
| [17] |
高清军. 多种海况下的水下溢油数值模拟[D]. 大连: 大连海事大学, 2008.
GAO Q J. Numerical simulation of the underwater oil spill under a variety of sea conditions[D]. Dalian: Dalian Maritime University, 2008.
|
| [18] |
李隆键, 张磊, 朱文冰, 等. 基于 VOSET 方法模拟并排气泡的上升过程[J].
计算物理, 2015, 32(5): 545.
LI L L, ZHANG L, ZHU W B, et al. Simulation of a pair of bubbles rising side by side using VOSET method[J].
Chinese Journal of Computational Physics, 2015, 32(5): 545.
|
| [19] |
王雪丽. 水中油滴运动实验与模拟研究[D]. 河北工业大学, 2017.
WANG X L. Experimentaland simulation study on oil droplet upward movement in water[D]. Tianjin: Hebei University of Technology, 2017.
|
| [20] |
WELLEK R M, AGRAWAL A K, SKELLAND A H P. Shape of liquid drops moving in liquid media[J].
AIChE Journal, 1966, 12(5): 854-862.
DOI:10.1002/aic.690120506 |
| [21] |
郭烈锦. 两相与多相流动力学[M]. 西安: 西安交通大学出版社, 2002.
|
| [22] |
BINKS B P, LUMSDON S O. Pickering emulsions stabilized by monodisperse latex particles: effects of particle size[J].
Langmuir, 2001, 17(15): 4540-4547.
DOI:10.1021/la0103822 |
| [23] |
AVEYARD R, BINKS B P, CLINT J H. Emulsions stabilised solely by colloidal particles[J].
Advances in Colloid and Interface Science, 2003, 100: 503-546.
|
| [24] |
LUO X, HUANG X, YAN H, et al. An experimental study on the coalescence behavior of oil droplet in ASP solution[J].
Separation and Purification Technology, 2018, 203: 152-158.
DOI:10.1016/j.seppur.2018.04.028 |
| [25] |
ABEYNAIKE A, DAVIDSON J F, MACKLEY M R. The experimental observation and modelling of film thinning and film retraction during the interfacial coalescence of biodiesel and glycerol droplets[J].
Journal of the American Oil Chemists' Society, 2013, 90: 1049-1062.
DOI:10.1007/s11746-013-2253-9 |
| [26] |
RUZICKA M C. On bubbles rising in line[J].
International Journal of Multiphase Flow, 2000, 26(7): 1141-1181.
DOI:10.1016/S0301-9322(99)00078-6 |
| [27] |
ZHANG Y, LIU Y, JI R, et al. Discussion of the drop rest phenomenon at millimeter scale and coalescence of droplets at micrometer scale[J].
Journal of dispersion science and technology, 2012, 33(12): 1700-1707.
DOI:10.1080/01932691.2011.645704 |
| [28] |
许玲丽. 单气泡运动特性分析及曳力模型修正[D]. 徐州:中国矿业大学, 2015.
XU L L. Motion characteristics analysis and drag model correction of single bubble movement[D]. Xuzhou: China University of Mining and Technology, 2015.
|
 2024, Vol. 50
2024, Vol. 50