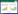文章信息
- 李远茂, 刘桂雄
- LI Yuanmao, LIU Guixiong
- 动力锂离子电池关键参数估计方法研究进展
- Research progress of key parameter estimation methods for power lithium-ion batteries
- 中国测试, 2024, 50(6): 1-9, 34
- CHINA MEASUREMENT & TEST, 2024, 50(6): 1-9, 34
- http://dx.doi.org/10.11857/j.issn.1674-5124.2024040060
-
文章历史
- 收稿日期: 2024-04-10
- 收到修改稿日期: 2024-05-06
纯电动驱动是电动汽车主要形式,动力电池、驱动电机和电控系统等是关键组成部分[1-4]。动力电池作为重要组件[5],与电动汽车安全性能息息相关。为促进新能源汽车广泛应用,需对动力电池关键性能参数进行测试、评估。目前常用动力电池包括锂离子电池(lithium ion battery, LIB)、镍氢电池等,LIB以高能量密度、长寿命、小体积和快速充电等特点成为新能源汽车首选电池类型,镍氢电池主要用于混合动力车辆,具有低成本、无重金属、宽工作温度范围、能量密度较低、充电速度较慢等特点,本文以LIB作为评述对象。尽管新能源汽车市场份额、需求不断增加,但LIB仍然面临着荷电状态估计不准[6]、容量衰减[7]和热失控安全[8]等方面挑战,大多数性能参数可通过标准测试,但LIB安全性能测试中的热失控测试属于破坏性试验,且会出现起火、爆炸等危险现象,可通过限元法(finite element method, FEM)对热失控行为进行仿真建模研究[9-10];LIB荷电状态(state of charge, SOC)参数[11-12]、电化学模型(electrochemical model, EM)参数[13-14]等无法通过设备直接测试或需进行破坏性试验,可通过数值计算方法实现相关参数估计。下面围绕热失控测试、电化学模型(EM)参数及SOC等关键性能估计参数展开评述。
1 LIB热失控热扩散建模方法根据建模原理不同,目前主要有热滥用模型[15-20]、电化学-热耦合模型[21-24]等。
1.1 LIB热滥用模型热滥用模型是指LIB在热滥用条件下(内部温度升高,温度上升至热失控临界温度,热失控副反应出现并释放大量热量),导致不同副反应相继发生,并出现连锁反应导致LIB温度不可控升高的动力学反应模型[25]。如文献[15](2001)构建基于Arrhenius方程的LIB热滥用一维模型,并通过烤箱试验证明所提模型与实际测试相比具有一致性、准确性;文献[16](2007)在文献[15]所提模型基础上,进一步研究LIB三维热滥用模型,可更加全面、清晰地研究LIB的热失控行为特性;文献[17](2015)对热滥用模型进行改进,研究固定功率加热下LIB热失控行为仿真建模,并通过实际实验验证其有效性,并探索外界对流条件、LIB结构设计、电解液等LIB热扩散特性的影响;文献[18](2016)等提出热失控数对LIB热失控状态进行估计,该参数与外部热传递、产热率、温度等相关,并通过实验证明仿真模型正确性,且该仿真模型可估计LIB结构中的安全、不安全区域,为LIB安全优化设计提供重要参考;文献[19](2019)通过5个LIB热失控副反应建立热滥用模型,探索外部加热、热耗散系数、加热面积等对隔膜影响,仿真试验表明控制散热系数可减少LIB热失控发生概率,但使隔膜温度分布不均匀;文献[20](2021)构建LIB三维热滥用模型,探索LIB材料、加热和散热等对LIB热扩散行为特性的影响,图1为6000 W·m−2加热条件下LIB温度分布云图,试验表明电池底部进行加热将增加LIB出现热失控的概率,且提高空气流速、降低外部温度可减少热失控发生概率。
热滥用模型能反映LIB在热滥用条件下,LIB内部材料在不同临界温度时出现分解副反应、产生大量热量过程,模型基于Arrhenius反应动力学反应构建,能直观体现LIB热失控机理,LIB不同层级均适用。
1.2 LIB电化学-热耦合模型LIB电化学-热耦合模型是指将电化学模型、传热模型通过热量、温度进行耦合构建的模型[26]。电化学模型描述LIB在充放电过程产热,包括Li+迁移导致的可逆热、不可逆热,其中不可逆热包含欧姆热、极化热。因此,可将电化学模型中由于电化学反应产生的可逆热、不可逆热,通过热传导、热对流和热辐射等传播方式进行扩散,同时这些热力学行为对电化学模型的反应速率、产物、条件等产生作用,相互耦合、共同作用,形成电化学-热耦合模型。如文献[21] (2017)建立LIB电化学-热耦合三维模型,利用数值仿真技术,探索LIB产热分布特点,试验表明电化学反应过程中电流分布不均匀,电化学产热多数集中在LIB正极片附近;文献[22](2019)研究圆柱形电池的电化学-热耦合模型,探索不同温度、放电速率下LIB热传播行为,研究适用回归模型对电池在不同放电倍率、放电深度下热行为;文献[23](2021)研究软包电池的三维电化学-热耦合模型,分析其在自然对流条件下热传播行为,试验表明电极平均粒子大小与LIB放电时的发热率直接相关,且最大局部电流密在放电过程中从极耳周围扩散到电池底部,其中电池厚度方向温度梯度较其他方向小;文献[24](2022)研究圆柱形电池的电化学-热耦合模型对比八种简化电池模型在不同放电倍率、传热系数下热特性差异,图2为不同简化模型的等温线示意图,可以看出简化模型1、6~8在不同放电倍率、传热系数下电池的温度云图类似,与完整三维耦合模型(模型5)不同,说明完整模型能更全面描述LIB产热情况,但其计算资源需求更高。除上述应用外,电化学-热耦合模型还可结合热滥用模型,用于探索LIB在正常工作状态下,因外部热滥用条件出现热失控状态的热传播行为研究。如文献[27](2018)结合电化学-热耦合、热滥用模型构建LIB数值模型,探索单体在不同高倍率充放电条件下热行为特性,试验表明热释放条件、充放电倍率对LIB热扩散特性影响较大,且提高放电倍率会明显改变LIB热失控进程,并指出在高充放电倍率条件下,等效传热系数应>2.2 W·m–2·K–1可有效减少热失控出现概率。
电化学-热耦合模型能直观反映电化学模型产热、热模型传热相互关系,准确描述LIB在正常工作状态下热特性,但该耦合模型复杂、非线性较强,需要消耗较高计算资源,目前仅应用于单体或较小模组层级。
综合上述,可得到如下结论:①热滥用模型、电化学-热耦合模型在建模机理、应用对象上存在差异,热滥用模型可通过反应动力学方程描述LIB在热滥用条件下,由于不同临界温度下发生不同副反应,从而导致LIB出现温度不可控现象;电化学-热耦合模型则反映电化学反应、传热模型相互关系,电化学模型由于反应产热,其热量通过耦合传热模型进行热传导、热对流和热辐射反作用于电化学模型,直接影响电化学反应速率、电化学变量和反应产物等。②热滥用模型能准确描述LIB热失控机理,对LIB单体、模组和系统等不同层级均适用,目前大部分研究停留在单体或较少单体构成模组上,在实际测试中需进行车辆层级上测试,其成本极高、危险性较大,可探索电池包层级仿真技术,分析其热扩散特性,对优化电池热管理系统设计具有重要作用。
2 LIB电化学模型参数估计方法电化学模型(EM)是基于电化学机理[28]构建,其模型参数能直观反映LIB老化以及健康状态、SOC、剩余寿命等状态,具有强非线性、参数较多、难以直接求解,但能准确描述LIB内部电化学性质,研究EM对提高电池管理系统评估性能有重要作用,但EM参数估计是该领域难点之一。常用EM参数估计方法有:应用元启发式算法估计、应用元启发式算法+深度学习网络估计等。
2.1 应用元启发式算法的EM参数估计元启发式算法通过遗传算法(genetic algorithm, GA)、粒子群优化算法(particle swarm optimization, PSO)等计算智能机制对优化问题进行求解方法。如文献[29](2016)对EM参数进行灵敏度分析,通过GA算法实现伪二维(pseudo-two-dimensions, P2D)简化模型8个参数估计,试验表明所提方法在不同放电倍率下具有有效性;文献[30](2020)通过体积平均法、伽辽金投影法研究P2D降阶模型,利用PSO算法对26个EM参数进行估计,在18个不同动态工况数据下证明该方法准确性;文献[31] (2020)应用有限体积法(finite volume method, FVM)求解P2D模型,通过进化算法(evolutionary algorithm, EA)、分步方式对11个EM参数进行估计,表明在40A (26.6C)高倍率条件下该方法具有较好的估计效果;文献[32] (2022)通过改进布谷鸟算法(cuckoo search algorithm, CSA)提出基于数据驱动的多目标多步EM参数估计框架,并通过有限差分法(finite difference method, FDM)、FVM简化P2D模型求解,完成24个EM参数估计,试验证明该方法有效性;文献[33](2022)研究一种代理模型辅助的分步估计方法(图3为其示意图),对降阶P2D模型进行估计参数预筛选,通过数据驱动模型完成6个EM参数估计,计算效率高,能克服模型过拟合、部分参数可观测性低等缺点。
2.2 应用元启发式算法+深度学习的EM参数估计
应用元启发式算法+深度学习方法首先通过深度学习网络研究LIB可测量数据、EM参数的映射关系,再利用元启发式算法对EM参数进行估计。如文献[34](2019)研究基于深度贝叶斯神经网络(bayesian neural network, BNN)+改进和声搜索(harmony search, HS)算法的EM参数估计方法,采用FEM对P2D模型进行求解,完成6个EM参数估计,与GA、PSO、Levenberg-Marquardt等算法对比,表明该方法计算效率更高、EM参数估计误差更低;文献[35](2022)研究EM参数快速估计方法(图4为其示意图),通过正交配置法实现P2D模型简化后,通过MATLAB求解模型,研究参数敏感度并进行分类,采用长短期记忆网络(LSTM, long short-term memory)对14个参数实现初步估计,并将其作为初值,再利用GA算法在恒流工况下实现Ⅰ、Ⅱ类参数估计,最后在动态工况下通过集成卡尔曼滤波(ensemble Kalman filtering, EnKF)算法估计Ⅲ类参数,模型估计电压的均方根误差(root mean square error, RMSE)小于14 mV。
表1总结上述EM参数估计方法,可以看出上述EM参数估计均采用P2D或其简化模型,每个方法估计参数个数不同,且均在恒定倍率或动态工况下进行。
综合上述,可得到如下结论:①由于电化学模型结构复杂、参数多且非线性强,常通过简化P2D模型后进行求解,这将降低模型精度,同时在EM参数估计中选取合适工况进行,通过灵敏度分析确定可估计参数;②深度学习网络已在EM参数估计中得到应用,但常结合元启发式算法进行使用,选用合适元启发算法仍有待加强研究。
3 LIB的SOC参数估计方法SOC用于描述LIB的剩余电量数量,可直观揭示LIB续航里程,SOC的精确评估对优化充放电控制策略、完善均衡技术具有积极作用[36]。目前常用的SOC参数估计方法包括:查表法[37]、安时积分法[38]、电池模型+状态观测器估计法[39-43]、基于数据驱动模型估计法[44-50]等。其中,查表法指构建SOC和开路电压(open circuit voltage, OCV)的关系表,利用查找表的方式进行SOC估计,但OCV测定需要LIB保持长时间静置获得,因此该方法难以在电池管理系统中实现实时在线应用[51];安时积分法指对LIB电流采用积分方法求得容量变化,从而实现SOC估计,但安时积分法需要首先获取SOC初始值,并定期对LIB容量进行标定、测量[52]。目前针对查表法、安时积分法应用研究逐渐减少,更多集中在电池模型+状态观测器估计法、基于数据驱动模型估计法等方法上。
3.1 应用电池模型+状态观测器的SOC估计法应用电池模型+状态观测器的SOC估计法是指首先构建等效电路模型或电化学模型(EM),然后采用卡尔曼滤波器、非线性观测器等状态观测器形成闭环系统,通过LIB模型状态反馈,调整SOC估计值,最终实现SOC准确估计。图5为应用电池模型+状态观测器的SOC估计流程图[53],EM建模难度高、不易求解且计算量较大,难以直接应用于SOC在线估计,需要简化处理,故该方法一般使用等效电路模型。
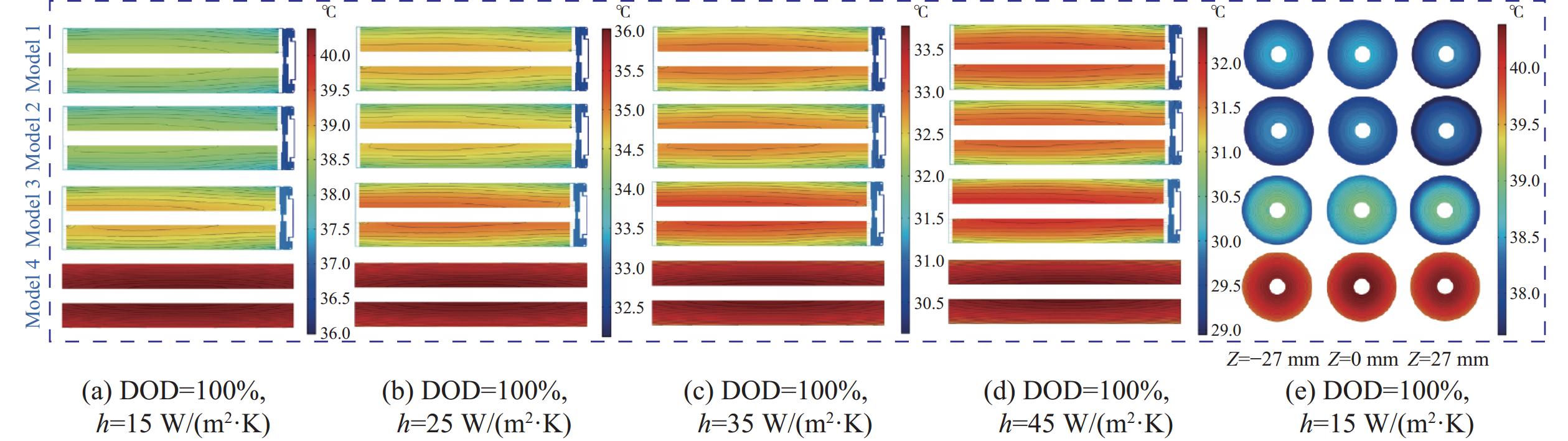
如文献[39](2017)采用二阶RC模型+增益非线性观测器方法,通过PSO算法搜索观测器参数最优解,试验证明其有效性、鲁棒性;文献[40] (2021)研究二阶RC模型+双遗忘因子改进的自适应扩展卡尔曼滤波器方法,同时完成SOC、能量状态(state of energy, SOE)估计(图6为其流程图),结果表明该方法在不同动态工况下SOC估计的RMSE小于0.85%,且在初始误差较大情况下仍能实现SOC精确估计;文献[41](2021)研究Thevenin模型+智能自适应扩展卡尔曼滤波器(AEKF)方法,可减少LIB建模及AEKF线性近似引起的误差,通过试验证明该方法的准确性、鲁棒性,并且与传统AEKF相比,该方法估计SOC的RMSE、平均绝对误差(mean absolute error, MAE)分别可提高43.34%、55.80%;文献[42] (2022)研究二阶RC模型+扩展非线性状态观测器方法,并分析该非线性状态观测器的稳定性及收敛速度,通过试验对比无迹卡尔曼滤波器(unscented Kalman filter, UKF)、滑模观测器,结果表明该方法的SOC估计精度更高、性能更佳;文献[43](2023)研究分数阶LIB模型+非相称分数阶观测器方法,通过改进PSO估计该电池模型参数,试验证明该方法SOC估计的RMSE、最大误差分别为0.62%~1.26%、1.50%~2.69%。
3.2 基于数据驱动模型的SOC估计法
数据驱动模型方法通常采用深度学习网络进行训练,探索电池电流、电压等可测信息与SOC之间关系,在训练好模型中输入该数据,即可实现SOC估计值输出。如文献[44](2020)研究LSTM+UKF方法(图7为其流程框图),通过输入LIB电压、电流和温度等,LSTM即可实现SOC估计,利用UKF对该SOC估计值滤波,进一步提升估计性能,并在0~50 ℃下证明其SOC估计具有较高精度;文献[45](2020)研究LSTM+注意力模型,通过注意力机制弥补LSTM长时间遗忘的不足,提出差分进化算法搜索LSTM网络的最优超参数,测试证明该方法估计SOC的准确性及泛化能力;文献[46](2021)研究PSO算法优化LSTM网络方法,通过自动调参方法提高效率,并在输入层加入随机噪声,提高该方法鲁棒性,试验表明该方法具有较高SOC估计精度;文献[47](2021)研究自监督Transformer模型,在不需要标记特征条件下即可实现SOC估计值输出,在不同环境温度验证其SOC估计RMSE、MAE分别可达1.19%、0.7%,并将训练好的网络直接应用不同材料电池上,可得到类似估计性能;文献[48](2022)提出双向LSTM网络+贝叶斯优化算法方法,双向网络可使获取信息更完整、时序依赖性更强,通过贝叶斯优化算法实现网络超参数自动调参,试验证明该方法估计SOC的RMSE<1%;文献[49](2022)研究基于门控循环单元的SOC多步估计方法,综合环境、驾驶行为等因素影响,采用多层次相关性分析、随机失活方法,从采集数据中提取有效特征,利用6组车辆运行数据证明SOC最大误差仅为0.86%;文献[50](2022)研究LSTM+改进粒子滤波器方法,通过LIB电压、电流、温度等作为LSTM网络输入,实现SOC初步估计,在利用改进粒子滤波器对该SOC估计值进行滤波修正,试验表明该方法在不同温度、电池和工况下SOC估计的RMSE<1%、最大误差<2%。
表2为基于数据驱动模型的SOC估计法汇总表,目前LSTM、门控循环单元等循环神经网络已在LIB的SOC估计得到较多应用,通过使用状态观测器辅助深度学习网络,或采用元启发式算法搜索网络超参数的最优解,有利于提高SOC估计精度;通过不同环境温度、不同动态工况数据对深度学习网络进行训练,有利于提高SOC估计性能。
| 序号 | 模型 | 辅助方法 | 环境温度 | 工况/数据集 | 文献 |
| 1 | LSTM | UKF | 0 ℃、10 ℃、20 ℃、30 ℃、40 ℃、50 ℃ | 动态压力测试(DST)、激烈驾驶工况(US06)、 美国联邦城市驾驶工况(FUDS) |
[44] |
| 2 | LSTM+注意力机制 | 差分进化算法 | 0 ℃、25 ℃、45 ℃ | CALCE数据集松下18650PF Mendeley数据集 | [45] |
| 3 | LSTM | PSO算法 | 25 ℃ | 城市道路循环(UDDS) | [46] |
| 4 | Transformer | --- | –20 ℃、–10 ℃、0 ℃、10 ℃、25 ℃、40 ℃ | LG18650数据集松下18650PF Mendeley数据集 | [47] |
| 5 | 双向LSTM | 贝叶斯优化 | 0 ℃、25 ℃、45 ℃ | CALCE数据集 | [48] |
| 6 | 门控循环单元 | 双随机失活 | --- | 6组车辆实际运行数据 | [49] |
| 7 | LSTM | 改进粒子滤波器 | 10 ℃、25 ℃、40 ℃、50 ℃ | CALCE数据集 | [50] |
综合上述,可得到如下结论:①电池模型+状态观测器估计方法可降低外部噪声对SOC估计效果影响,由于电化学模型复杂且求解困难,常采用简化模型或者等效电路模型,但两者均存在建模误差,并且该方法需要状态观测器具有较强非线性估计性能;②数据驱动模型可有效捕捉LIB可测量数据与SOC之间非线性关系,无须研究LIB内部电化学、物理特性,其中LSTM、门控循环单元等循环神经网络及Transformer等注意力模型已在SOC估计得到应用;③深度学习网络+注意力机制、深度学习网络+状态观测器、元启发式算法优化网络超参数、不同温度下不同动态工况数据等方法均有利于提升SOC估计性能。
4 结束语1) 热滥用模型、电化学-热耦合模型在建模机理及应用对象上存在差异。其中,热滥用模型通过反应动力学方程描述LIB在热滥用条件下发生副反应,进而使LIB出现温度不可控的现象;电化学-热耦合模型则反映电化学反应、传热模型之间关系,通过耦合的传热模型直接影响电化学反应速率和其他变量;热滥用模型能准确描述LIB热失控机理,适用于不同层级的LIB,但目前主要研究集中在单体或少量单体构成的模组上;在实际测试中,进行车辆层级测试成本高且危险,可考虑电池包层级仿真技术,有助于分析电池包的热扩散特性,对电池热管理系统设计优化具有重要作用。
2)电化学模型(EM)在参数估计中仍具有结构复杂、参数众多且非线性强等困难。常采用简化P2D模型求解,但会降低模型精度;在EM参数估计中,其中一个关键为选择合适工况,通过灵敏度分析确定可估计参数;同时,深度学习网络在电池EM参数估计中得到应用,目前通常需要结合元启发式算法,但选择合适的元启发算法仍需要深入研究、加强。
3)通过电池模型+状态观测器SOC估计方法,可有效减小噪声对SOC估计影响。鉴于电化学模型复杂、难以求解,常采用简化模型或等效电路模型,但均会造成建模误差,同时对状态观测器非线性估计性能要求较高;数据驱动模型能够有效地捕捉LIB可测量数据与SOC之间非线性关系,其中LSTM、门控循环单元等循环神经网络及Transformer等注意力模型均已得到应用;综合采用深度学习网络+注意力机制、深度学习网络+状态观测器、使用元启发式算法优化网络超参数及使用不同温度下动态工况数据等方法,均为提升SOC估计性能重要方法。
| [1] |
于智斌, 田易之. 由MIEKPF-EKPF算法协同估计锂离子电池SOC与SOH[J].
电池, 2023, 53(2): 160-164.
YU Z B, TIAN Y Z. Collaborative estimation of SOC and SOH of Li-ion battery by MIEKPF-EKPF algorithm[J].
Battery Bimonthly, 2023, 53(2): 160-164.
|
| [2] |
李杰, 贾长旺, 成林海, 等. 随机路面下轮毂电机偏心对电动汽车平顺性影响[J].
东北大学学报(自然科学版), 2022, 43(8): 1113-1119.
LI J, JIA C W, CHENG L H, et al. Influence of in-wheel motors' eccentricity on ride comfort of electric vehicles on random roads[J].
Journal of Northeastern University( Natural Science), 2022, 43(8): 1113-1119.
DOI:10.12068/j.issn.1005-3026.2022.08.007 |
| [3] |
张雷, 刘青松, 王震坡. 基于鲁棒积分滑模的四轮轮毂电机驱动电动汽车电液复合制动防抱死控制研究[J].
机械工程学报, 2022, 58(24): 243-253.
ZHANG L, LIU Q S, WANG Z B. Research on electro-hydraulic composite ABS control for four-wheel-independent-drive electric vehicles based on robust integral sliding mode control[J].
Journal of Mechanical Engineering, 2022, 58(24): 243-253.
|
| [4] |
蔡家富, 刘桂雄. 动力锂电池模组多工位多电性能参数测试调度方法研究[J].
中国测试, 2022, 48(1): 9-13.
CAI J F, LIU G X. Research on multi station and multi electric performance parameter test scheduling method of power lithium battery module[J].
China Measurement & Test, 2022, 48(1): 9-13.
|
| [5] |
高韶君, 刘伟峰, 符冬菊, 等. 废旧动力锂离子电池全组分回收技术研究进展(英文)[J].
新型炭材料, 2022, 37(3): 435-460.
GAO S J, LIU W F, FU D J, et al. Research progress on recovering the components of spent li-ion batteries[J].
New Carbon Materials, 2022, 37(3): 435-460.
DOI:10.1016/S1872-5805(22)60605-X |
| [6] |
文茹馨, 刘惠颖, 梁言贺, 等. Vi-RNN算法储能电池在线SOC估计[J].
中国测试, 2023, 49(5): 117-122.
WEN R W, LIU H Y, LIANG Y H, et al. Online SOC estimation of energy storage lithium battery based on Vi-RNN algorithm[J].
China Measurement & Test, 2023, 49(5): 117-122.
DOI:10.11857/j.issn.1674-5124.2021090138 |
| [7] |
赵沁峰, 蔡艳平, 王新军. 基于WOA-ELM的锂离子电池剩余寿命间接预测[J].
中国测试, 2021, 47(9): 138-145.
ZHAO Q F, CAI Y P, WANG X J. WOA-ELM based indirect prediction of remaining useful life of lithium-ion battery[J].
China Measurement & Test, 2021, 47(9): 138-145.
DOI:10.11857/j.issn.1674-5124.2020120089 |
| [8] |
魏仁川, 许金鑫, 丁炯. 锂离子电池热参数快速测量方法研究 [J/OL]. 中国测试, 1-7[2024-06-11]. http://kns.cnki.net/kcms/detail/51.1714.TB.20230804.1026.014.html.
WEI R C, XU J X, DING J. Research on rapid measurement of thermal parameters of lithium-ion battery[J/OL]. China Measurement and Test, 1-7[2024-06-11]. http://kns.cnki.net/kcms/detail/51.1714.TB.20230804.1026.014.html.
|
| [9] |
朱晓庆, 王震坡, WANG H, 等. 锂离子动力电池热失控与安全管理研究综述[J].
机械工程学报, 2020, 56(14): 91-118.
ZHU X Q, WANG Z P, WANG H. Review of thermal runaway and safety management for lithium-ion traction batteries in electric vehicles[J].
Journal of Mechanical Engineering, 2020, 56(14): 91-118.
|
| [10] |
张亚军, 王贺武, 冯旭宁, 等. 动力锂离子电池热失控燃烧特性研究进展[J].
机械工程学报, 2019, 55(20): 17-27.
ZHANG Y J, WANG H B, FENG X N, et al. Research progress on thermal runaway combustion characteristics of power lithiumion batteries[J].
Journal of Mechanical Engineering, 2019, 55(20): 17-27.
|
| [11] |
OYEWOLE I, CHEHADE A, KIM Y. A controllable deep transfer learning network with multiple domain adaptation for battery state-of-charge estimation[J]. Applied Energy, 2022, 312.
|
| [12] |
王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J].
电力系统自动化, 2022, 46(14): 193-207.
WANG Y J, ZUO X. A Review of charging state estimation methods and application scenarios of lithium-ion batteries[J].
Automation of Electric Power Systems, 2022, 46(14): 193-207.
DOI:10.7500/AEPS20211124005 |
| [13] |
赵杨梅, 时玮, 张雪楠, 等. 考虑石墨嵌锂平台的磷酸铁锂电池电化学参数辨识[J/OL]. 电源学报, 1-14[2024-06-11].http://kns.cnki.net/kcms/detail/12.1420.TM.20220223.1844.009.html.
ZHAO Y M, SHI W, ZHANG X N, et al. Identification of electrochemical parameters of lithium iron phosphate battery considering lithium insertion platform of graphite[J/OL]. Journal of Power Supply, 1-14[2024-06-11].http://kns.cnki.net/kcms/detail/12.1420.TM.20220223.1844.009.html.
|
| [14] |
陈洪涛. 锂电池电化学模型参数辨识研究[D]. 北京: 北京交通大学, 2019.
CHEN H T. Study on parameters identification of electrochemical model of lithium battery[D]. Beijing: Beijing Jiaotong University, 2019.
|
| [15] |
HATCHARD T D, MACNEIL D D, BASU A, et al. Thermal model of cylindrical and prismatic lithium-ion cells[J]. Journal of The Electrochemical Society, 2001, 148(7): A755-A761.
|
| [16] |
KIM G H, PESARAN A, SPOTNITZ R. A three-dimensional thermal abuse model for lithium-ion cells[J].
Journal of Power Sources, 2007, 170(2): 476-489.
DOI:10.1016/j.jpowsour.2007.04.018 |
| [17] |
LOPEZ C F, JEEVARAJAN J A, MUKHERJEE P P. Characterization of Lithium-ion battery thermal abuse behavior using experimental and computational analysis[J].
Journal of The Electrochemical Society, 2015, 162(10): A2163-A2173.
DOI:10.1149/2.0751510jes |
| [18] |
SHAH K, CHALISE D, JAIN A. Experimental and theoretical analysis of a method to predict thermal runaway in Li-ion cells[J].
Journal of Power Sources, 2016, 330: 167-174.
DOI:10.1016/j.jpowsour.2016.08.133 |
| [19] |
LEI Z, MAO T Z, XIAO M X, et al. Thermal runaway characteristics on NCM lithium-ion batteries triggered by local heating under different heat dissipation conditions[J]. Applied Thermal Engineering, 2019, 159: 113847.
|
| [20] |
KONG D P, WANG G Q, PING P, et al. Numerical investigation of thermal runaway behavior of lithium-ion batteries with different battery materials and heating conditions[J]. Applied Thermal Engineering, 2021, 189: 116661.
|
| [21] |
GHALKHANI M, BAHIRAEI F, NAZRI G A, et al. Electrochemical–thermal model of pouch-type lithium-ion batteries[J]. Electrochimica Acta, 2017, 247: 569-587.
|
| [22] |
CHIEW J, CHIN C, TOH W, et al. A pseudo three-dimensional electrochemical-thermal model of a cylindrical LiFePO4/graphite battery[J].
Applied Thermal Engineering, 2019, 147: 450-463.
DOI:10.1016/j.applthermaleng.2018.10.108 |
| [23] |
HE C X, YUE Q L, WU M C, et al. A 3D electrochemical-thermal coupled model for electrochemical and thermal analysis of pouch-type lithium-ion batteries[J]. International Journal of Heat and Mass Transfer, 2021, 181: 121855.
|
| [24] |
HE T, ZHANG T, WANG Z, et al. A comprehensive numerical study on electrochemical-thermal models of a cylindrical lithium-ion battery during discharge process[J].
Applied Energy, 2022, 313: 118797.
DOI:10.1016/j.apenergy.2022.118797 |
| [25] |
金星, 苗西朋. 锂离子动力电池充放电热跟踪系统设计[J].
中国测试, 2024, 50(1): 122-127.
JIN X, MIAO X P. Design of heat tracking system for charge and discharge of lithium-ion power battery[J].
China Measurement & Test, 2024, 50(1): 122-127.
|
| [26] |
李伟, 刘桂雄. 电化学与热滥用耦合模型的锂电池局部热扩散仿真试验技术[J].
中国测试, 2021, 47(12): 157-162.
LI W, LIU G X. Lithium battery local thermal dispersion simulation test technology based on coupled electrochemical and thermal abuse models[J].
China Measurement & Test, 2021, 47(12): 157-162.
|
| [27] |
DONG T, PENG P, JIANG F M. Numerical modeling and analysis of the thermal behavior of NCM lithium-ion batteries subjected to very high C-rate discharge/charge operations[J].
International Journal of Heat and Mass Transfer, 2018, 117: 261-272.
DOI:10.1016/j.ijheatmasstransfer.2017.10.024 |
| [28] |
牛凯, 李静如, 李旭晨, 等. 电化学测试技术在锂离子电池中的应用研究[J].
中国测试, 2020, 46(7): 90-101.
NIU K, LI J R, LI X C, et al. Research on the applications of electrochemical measurement technologies in lithium-ion batteries[J].
China Measurement & Test, 2020, 46(7): 90-101.
DOI:10.11857/j.issn.1674-5124.2020060014 |
| [29] |
JOKAR A, RAJABLOO B, DÉSILETS M, et al. An inverse method for estimating the electrochemical parameters of lithium-ion batteries[J].
Journal of The Electrochemical Society, 2016, 163(14): A2876-A2886.
DOI:10.1149/2.0191614jes |
| [30] |
FAN G. Systematic parameter identification of a control-oriented electrochemical battery model and its application for state of charge estimation at various operating conditions[J].
Journal of Power Sources, 2020, 470: 228153.
DOI:10.1016/j.jpowsour.2020.228153 |
| [31] |
KOSTETZER L, NEBL C, STICH M, et al. Physicsbased modeling and parameter identification for lithium ion batteries under high current discharge conditions[J]. Journal of The Electrochemical Society, 2020, 167(14): 140549.
|
| [32] |
LI W, DEMIR I, CAO D, et al. Data-driven systematic parameter identification of an electrochemical model for lithium-ion batteries with artificial intelligence[J].
Energy Storage Materials, 2022, 44: 557-570.
DOI:10.1016/j.ensm.2021.10.023 |
| [33] |
SHUI Z Y, LI X H, FENG Y, et al. Combining reduced-order model with data-driven model for parameter estimation of lithium-ion battery[J].
IEEE Transactions on Industrial Electronics, 2023, 70(2): 1521-1531.
DOI:10.1109/TIE.2022.3157980 |
| [34] |
KIM M, CHUN H, KIM J, et al. Data-efficient parameter identification of electrochemical lithium-ion battery model using deep Bayesian harmony search[J]. Applied Energy, 2019, 254: 113644.
|
| [35] |
XU L, LIN X, XIE Y, et al. Enabling high-fidelity electrochemical P2D modeling of lithium-ion batteries via fast and non-destructive parameter identification[J].
Energy Storage Materials, 2022, 45: 952-968.
DOI:10.1016/j.ensm.2021.12.044 |
| [36] |
李泓沛, 刘桂雄. 加窗LSTM网络的动力电池SOC预测优化算法[J].
中国测试, 2021, 47(12): 87-91.
LI H P, LIU G X. SOC prediction optimization algorithm for power battery based on LSTM network with window function[J].
China Measurement & Test, 2021, 47(12): 87-91.
DOI:10.11857/j.issn.1674-5124.2020050013 |
| [37] |
王子毅, 朱承治, 周杨林, 等. 基于动态可重构电池网络的OCV-SOC在线估计[J].
中国电机工程学报, 2022, 42(8): 2919-2929.
WANG Z Y, ZHU C Z, ZHOU Y L, et al. OCV-SOC estimation based on dynamic reconfigurable battery network[J].
Proceedings of the CSEE, 2022, 42(8): 2919-2929.
|
| [38] |
邢厚超. 基于修正开路电压-安时积分法的电池管理系统研究[D]. 盐城: 盐城工学院, 2022.
XING H C. Research on battery management system based on modified open circuit voltage-ampere hour integration method[D]. Yancheng: Yancheng Institute of Technology, 2022.
|
| [39] |
TIAN Y, LI D, TIAN J, et al. State of charge estimation of lithium-ion batteries using an optimal adaptive gain nonlinear observer[J].
Electrochimica Acta, 2017, 225: 225-234.
DOI:10.1016/j.electacta.2016.12.119 |
| [40] |
SHRIVASTAVA P, SOON T K, IDRIS M Y I B, et al. Combined state of charge and state of energy estimation of lithium-ion battery using dual forgetting factor-based adaptive extended Kalman filter for electric vehicle applications[J].
IEEE Transactions on Vehicular Technology, 2021, 70(2): 1200-1215.
DOI:10.1109/TVT.2021.3051655 |
| [41] |
SUN D, YU X, WANG C, et al. State of charge estimation for lithium-ion battery based on an Intelligent Adaptive Extended Kalman Filter with improved noise estimator[J].
Energy, 2021, 214: 119025.
DOI:10.1016/j.energy.2020.119025 |
| [42] |
SAKILE R, SINHA U K. Lithium-ion battery state of charge estimation using a new extended nonlinear state observer[J]. Advanced Theory and Simulations, 2022, 5(3): 2100552.
|
| [43] |
CHEN L P, GUO W L, LOPES A M, et al. State-of-charge estimation for lithium-ion batteries based on incommensurate fractional-order observer[J]. Communications in Nonlinear Science and Numerical Simulation, 2023, 118.
|
| [44] |
YANG F, ZHANG S, LI W, et al. State-of-charge estimation of lithium-ion batteries using LSTM and UKF[J]. Energy, 2020, 201.
|
| [45] |
MAMO T, WANG F K. Long short-term memory with attention mechanism for state of charge estimation of Lithium-Ion batteries[J].
IEEE Access, 2020, 8: 94140-94151.
DOI:10.1109/ACCESS.2020.2995656 |
| [46] |
REN X, LIU S, YU X, et al. A method for state-of-charge estimation of lithium-ion batteries based on PSO-LSTM[J]. Energy, 2021, 234.
|
| [47] |
HANNAN M A, HOW D N T, LIPU M S H, et al. Deep learning approach towards accurate state of charge estimation for lithium-ion batteries using self-supervised transformer model[J].
Scientific Reports, 2021, 11(1): 19541.
DOI:10.1038/s41598-021-98915-8 |
| [48] |
YANG B, WANG Y, ZHAN Y. Lithium battery state-of-charge estimation based on a Bayesian optimization bidirectional long short-term memory neural network[J]. Energies, 2022, 15(13).
|
| [49] |
LI R, WANG H, DAI H, et al. Accurate state of charge prediction for real-world battery systems using a novel dual-dropout-based neural network[J]. Energy, 2022, 250.
|
| [50] |
YAN X, ZHOU G, WANG W, et al. A hybrid data-driven method for state-of-charge estimation of Lithium-ion batteries[J].
IEEE Sensors Journal, 2022, 22(16): 16263-16275.
DOI:10.1109/JSEN.2022.3188845 |
| [51] |
李泓沛, 刘桂雄, 邓威. 基于LSTM+UKF融合的动力锂电池SOC估算方法[J].
中国测试, 2022, 48(8): 22-28.
LI H P, LIU G X, DENG W. LSTM+UKF fusion-based SOC estimation method for powered Lithium batteries[J].
China Measurement & Test, 2022, 48(8): 22-28.
|
| [52] |
李小虎, 王军. 基于改进无迹卡尔曼滤波器的锂电池荷电状态估计[J].
中国测试, 2023, 49: 105-110+130.
LI X H, WANG J. SOC estimation of Lithium battery based on improved unscented Kalman filter[J].
China Measurement & Test, 2023, 49: 105-110+130.
|
| [53] |
高铭琨, 徐海亮, 吴明铂. 基于等效电路模型的动力电池SOC估计方法综述[J].
电气工程学报, 2021, 16(1): 90-102.
GAO M K, XU H L, WU M B. Review of SOC estimation methods for power battery based on equivalent circuit model[J].
Journal of Electrical Engineering, 2021, 16(1): 90-102.
DOI:10.11985/2021.01.013 |
 2024, Vol. 50
2024, Vol. 50