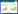文章信息
- 范晓龙, 闫鹏庆, 赵箫宇, 宋婉琪
- FAN Xiaolong, YAN Pengqing, ZHAO Xiaoyu, SONG Wanqi
- 基于高阶滑模算法的飞机架水平控制方法研究
- Aircraft leveling control method based on high-order sliding mode algorithm
- 中国测试, 2024, 50(5): 174-179
- CHINA MEASUREMENT & TEST, 2024, 50(5): 174-179
- http://dx.doi.org/10.11857/j.issn.1674-5124.2023110129
-
文章历史
- 收稿日期: 2023-11-30
- 收到修改稿日期: 2024-01-06
2. 西北工业大学机电学院,陕西 西安 710072
2. School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China
飞机架水平工作在飞行试验过程中是十分必要和经常进行的地面试验工作。首先,飞机的重量重心与气动力焦点有密切的联系,重量重心与焦点匹配与否会对飞机的安全性、操纵性、飞行性能及经济性产生直接影响[1-3],飞机的重量重心位置也是飞行试验过程中最重要的状态参数之一,一般在飞机出厂与飞行试验研究过程中都是通过架水平称重方法获取飞机的重量重心位置[4-6],并且在飞行试验过程中经常对其进行调节,因此面向千斤顶称重的飞机架水平控制是十分必要和经常的地面操作过程。其次,在飞机的强度和载荷试飞过程中也需要及时开展飞机架水平,并且进行全机水平测量操作;此外,在飞行试验过程中飞机的起落架标定和检查、航电设备标校等过程也都需要开展飞机架水平工作。传统飞机架水平工作操作过程比较繁琐,至少需要3组人员同时操作3台飞机千斤顶同步顶升,整个操作过程人力需求大、工作效率不高,还会存在顶升过程人为观察飞机姿态不平,导致千斤顶滑出顶窝的恶性安全问题。因此,在开展飞机架水平工作过程中,为了解决其引起的大量重复性人工操作问题,需要研发一种高效安全的自动化飞机架水平系统。
面向千斤顶称重的飞机架水平自动化,基于自动调平技术,对飞机架水平自动化系统进行了研究与设计,采用液压驱动系统作为动力源,针对飞机载荷较大的问题设计了一套支撑装置。为了实现自动化控制,减少操作人员工作量,基于现有的手动架水平设备设计了一套基于高阶滑模算法的电控系统,包括主控制器、液压控制器、控制面板、传感器等,实现了飞机姿态的自动化测量与高精度调整。
1 系统原理与结构设计 1.1 系统工作原理飞机调平控制系统由数字化测量系统、液压驱动控制系统、飞机千斤顶、控制器组成。平台姿态调整使用三点调平机构,首先通过数字化测量系统获取调平对象当前姿态,其中角度误差由传感器测量反馈,位置误差由数字化激光测量装置反馈。然后飞机根据传感器数据自动解算飞机3个顶点之间的高度差,以飞机后顶点高度为基准,将位置误差信号输入到高阶滑模算法中进行补偿计算,由系统控制器得出系统控制量。最后通过输出系统控制量对电机转速进行调整,进而通过液压驱动系统分别控制各支点顶升或下降,使飞机的姿态达到目标要求。对于飞机架水平过程来说,其外部干扰较小,对抗倾覆的能力要求不高。基于上述原因使用三点调平方式,3个顶升支撑点由独立的作动机构调整,通过对各点的高度进行控制来实现飞机姿态的改变。调平控制分为角度误差控制与位置误差控制。在飞机整体抬升阶段使用角度误差控制方式以缩短调节周期,在最终调整阶段使用位置误差控制方式以提高调节精度。运八飞机架水平三点调平控制系统原理图见图1。飞机整体姿态调整选取的3个顶升支点位置如图1中支点1、支点2、支点3所示,分别为右顶、左顶、后顶。图2为飞机调平机构顶升支点的具体结构图,支撑装置结构为专用千斤顶结构。
|
| 图 1 运八飞机自动调平控制系统原理图 |

|
| 图 2 运八飞机调平机构支点结构图 |
控制系统由主控制器、液压控制器、控制面板、倾角传感器等组成,同时还需与三维数字化测量系统通信以获取飞机姿态数据。主控制器运行人机交互与总控模式程序,通过modbusTCP协议与各顶升机构处的液压控制器通信。液压控制器负责顶升装置内各阀门动作、伺服电机驱动控制、传感器数据采集。支撑装置由3条支腿支撑,支腿间通过连接杆连接,每条支腿底部均配有一个底盘和一个车轮,装置顶部为液压千斤顶,其与支腿通过连接杆和销钉可靠连接。支撑装置底盘采用了可滑动式结构,可以保证可靠触地,增强机构整体抗倾覆能力,以减少甚至消除飞机千斤顶称重过程中侧向力的影响。
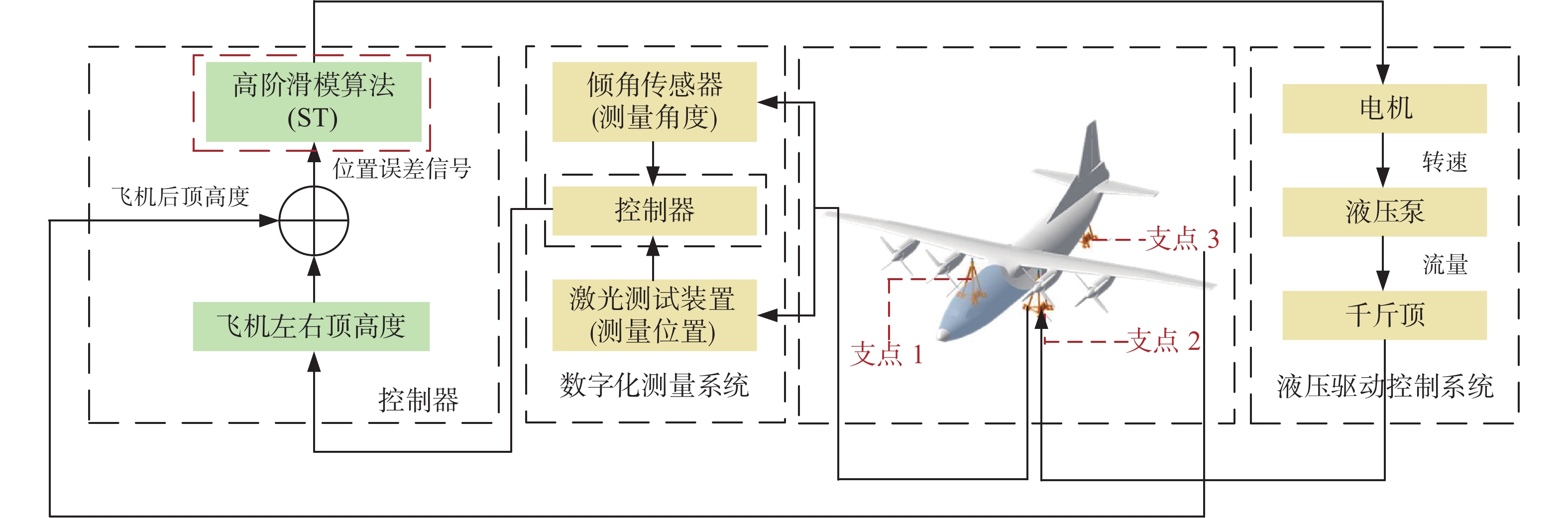
结合实际情况,如图3所示,液压驱动系统中液压缸为单作用液压缸,顶升时采用泵控,节流截止阀3打开,节流截止阀8和截止式换向阀7截止;当系统顶升到位,调平工作结束后,操作人员控制节流截止阀3关闭来锁定液压缸,下降时节流截止阀3和截止式换向阀7打开,调节其开度控制各支撑点下落速度。流量传感器用于采集液压缸进出流量,系统根据该流量监测液压缸动作,计算千斤顶行程[7-8]。
|
| 图 3 运八飞机调平机构液压驱动结构图 |
2 系统建模仿真设计
飞机调平系统整体控制结构如图4所示。基于高阶滑模算法设计控制系统以及滑模控制器[9-11]。本文对系统支撑装置、驱动电机、电动泵以及千斤顶、控制器进行了具体的数学建模分析。

|
| 图 4 飞机自动调平系统控制架构 |
2.1 支点位置误差建模
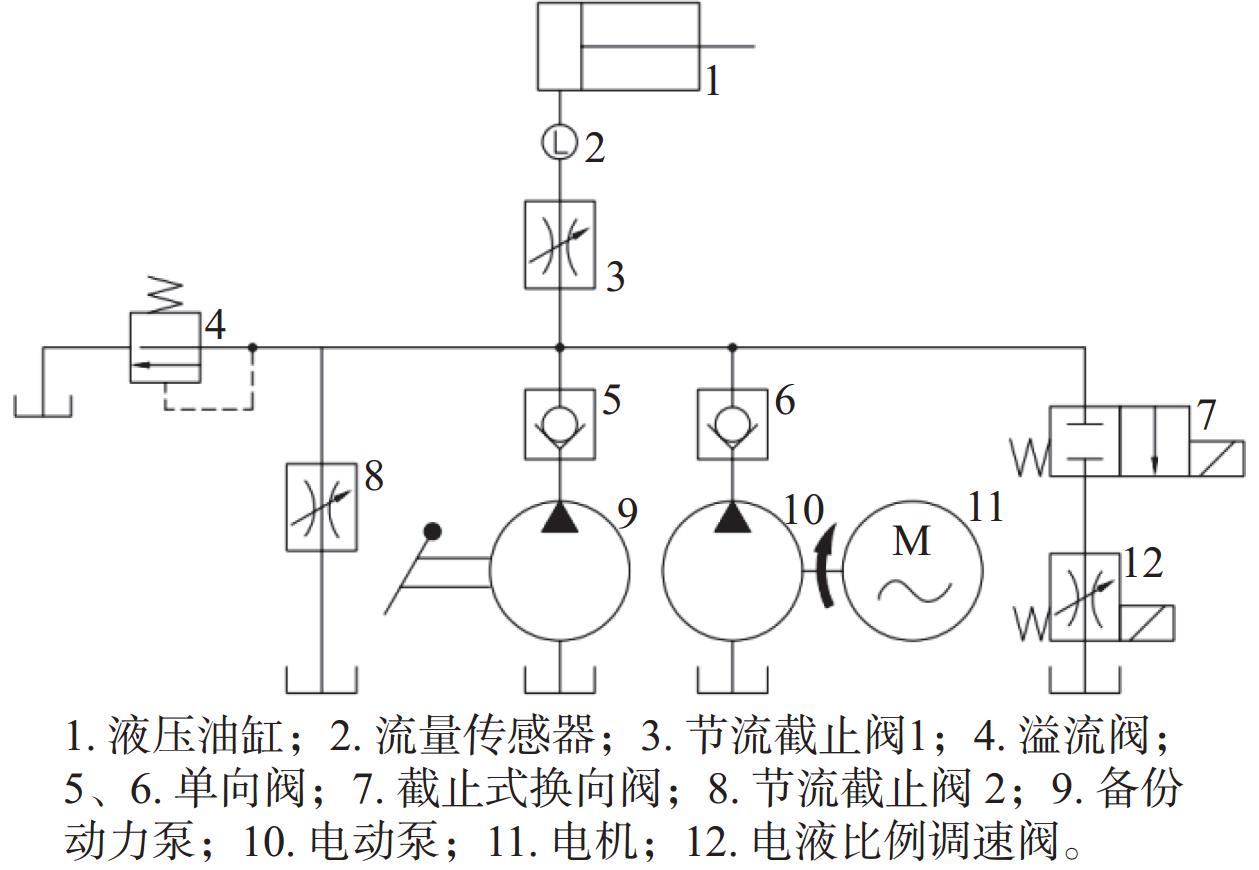
飞机调平系统采用的是三点调平法,根据飞机倾角计算出各个支撑点的高度差,调节3个点的位置,使飞机姿态达到水平。建立坐标系,以后顶顶点C为原点,OX平行于水平面指向前方(机头方向);OY垂直于OX指向右翼;OZ在飞机对称面内,垂直于水平面指向下方。
设飞机左右顶点A、B在Y轴方向间距为a,左右顶点A、B在X轴方向上距离为b,在Z轴方向上距离为c,则水平状态下三支点坐标分别为A:(b,–a/2,c),B:(b,a/2,c),C:(0,0,0),建立的坐标如图5所示。
|
| 图 5 飞机坐标系定义 |
由于飞机调平仅要求与地面水平,并不关心飞机绕Z轴旋转运动的情况,因此可以认为绕Z轴旋转的角度恒为0°。定义
| $ \begin{aligned} {{\boldsymbol{R}}_{\boldsymbol{X}}}({\boldsymbol{\alpha }}){\boldsymbol{ = }}&\left[ {\begin{array}{*{20}{c}} {\text{1}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\cos \alpha }&{ - \sin \alpha } \\ {\text{0}}&{\sin \alpha }&{\cos \alpha } \end{array}} \right]{\boldsymbol{}}\\ {{\boldsymbol{R}}_{\boldsymbol{Y}}}({\boldsymbol{\beta }}){\boldsymbol{ = }}&\left[ {\begin{array}{*{20}{c}} {\cos \beta }&{\text{0}}&{\sin \beta } \\ {\text{0}}&{\text{1}}&{\text{0}} \\ { - \sin \beta }&{\text{0}}&{\cos \beta } \end{array}} \right] \end{aligned} $ | (1) |
将两个旋转矩阵相乘,可得欧拉旋转矩阵:
| $ {\boldsymbol{R = }}\left[ {\begin{array}{*{20}{c}} {\cos \beta }&{\sin \beta \sin \alpha }&{\sin \beta \cos \alpha } \\ {\text{0}}&{\cos \alpha }&{ - \sin \alpha } \\ { - \sin \beta }&{\cos \beta \sin \alpha }&{\cos \beta \cos \alpha } \end{array}} \right] $ | (2) |
由此可得出,当飞机在X、Y轴倾斜角分别为
| $ \left\{ {\begin{array}{*{20}{c}} {{H_a} = - b\sin \beta - \dfrac{a}{{\text{2}}}\sin \alpha \cos \beta + c\cos \beta \cos \alpha } \\ {{H_b} = - b\sin \beta + \dfrac{a}{{\text{2}}}\sin \alpha \cos \beta + c\cos \beta \cos \alpha } \end{array}} \right. $ | (3) |
当飞机处于水平状态时A、B两点与C点的高度差应均为c,故用于调平控制的位置误差为
| $ \left\{ {\begin{array}{*{20}{c}} {{H_{ac}} = - b\sin \beta - \dfrac{a}{{\text{2}}}\sin \alpha \cos \beta + c\cos \beta \cos \alpha - c} \\ {{H_{bc}} = - b\sin \beta + \dfrac{a}{{\text{2}}}\sin \alpha \cos \beta + c\cos \beta \cos \alpha - c} \end{array}} \right. $ | (4) |
无刷直流电机是同步电机的一种,具有结构简单、运行可靠、维护方便、调速性能好等优势。
无刷直流电机的动态数学模型表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{U_{\text{c}}} = E + L\dfrac{{{\text{d}}i}}{{{\text{d}}t}} + Ri} \\ {E = {K_{\text{c}}}\omega {\text{ }}} \\ {{T_{\text{e}}} = {K_{\text{t}}}i{\text{ }}} \\ {{T_{\text{e}}} = J\dot \omega + {T_{\text{l}}}{\text{ }}} \end{array}} \right. $ | (5) |
式中:
泵组件由电动机带动,输入为转速
不考虑柱塞泵的脉动效应,泵的理论排量为:
| $ V = 0.25\pi {d^2}ZD\tan \theta $ | (6) |
式中:V——泵的排量;
D——柱塞分布圆直径;
d——柱塞直径;
θ——斜盘倾角;
Z——柱塞数。
泵组件输出流量表示为
| $ {q_{\text{m}}} = V \cdot n \cdot {\eta _{\text{v}}} $ | (7) |
其中
当液压油从缸体底部的油口进出时,活塞杆在油压作用下向上或向下运动。千斤顶数学模型可以表示为:
| $ l(t) = {l_{\text{0}}} + \int {{q_{\text{m}}}{\text{d}}} {{t}}/{S_{\text{k}}} $ | (8) |
式中:
其中,飞机后顶点电机参考转速由操作人员设定,在运行过程中,飞机根据倾角传感器数据自动解算飞机3个顶点之间的高度差,以飞机后顶点高度为基准,将位置误差信号输入到滑模算法Super-Twisting中进行补偿计算,得出系统控制量,对电机转速进行调整,进而通过液压驱动系统调节飞机左右顶点上升位移,调整飞机平衡。
传统控制环节主要采用PID控制方式,然而PID控制系统的响应速度较慢,且抗扰动能力不足[12],PID参数的计算选取需要对控制系统建立较为准确的模型,对实际情况下由液压泵加工误差所带来的工作参数变化和系统内各阀门的微量泄露等不可控因素带来的扰动影响无法完全消除。相比之下,滑模控制具有快速动态特性,对于系统内由机械摩擦、磁滞阻力、液压管路流动阻力等非线性因素引起的不确定性具有强鲁棒性,且对控制系统的模型精度要求较低。考虑到传统滑模控制中存在的抖振现象,可能会严重影响系统的动静态性能,因此本文基于高阶滑模算法Super-Twisting(ST) 设计了位置控制器。通过对滑模面以及滑模面导数进行约束,在保证快速动态特性的基础上,抑制了传统滑模控制中存在的抖振问题。此外,ST算法只需要知道滑模面的信息,不依赖于精确的系统模型,有效解决了液压驱动系统在流体域建模困难的问题[13-14],是一种更有优势的控制方式。
ST算法可表示为:
| $ u(t) = {u_1}(t) + {u_2}(t) $ | (9) |
| $ {\dot u_1} = \left\{ {\begin{array}{*{20}{c}} { - u}&{|u| > {u_{\max }}} \\ { - W{\text{sign}}(s)}&{|u| \leqslant {u_{\max }}} \end{array}} \right. $ | (10) |
| $ {u_2} = \left\{ {\begin{array}{*{20}{c}} { - \lambda {{\left| {{s_0}} \right|}^\rho }{\text{sign}}(s)}&{|s| > {s_0}} \\ { - \lambda |s{|^\rho }{\text{sign}}(s)}&{|s| \leqslant {s_0}} \end{array}} \right. $ | (11) |
式中:
W、ρ、λ、s0——调节参数。
根据李雅普诺夫理论,当满足以下条件时,系统可以在有限时间内收敛:
| $ \left\{\begin{array}{l}W > \dfrac{\phi }{{\textit{Γ}}_{M}} \\ {\lambda }^{2}\geqslant \dfrac{4\phi {\textit{Γ}}_{M}(W+\phi )}{{\textit{Γ}}_{M}^{3}(W-\phi )} \\ 0 < \rho \leqslant 0.5 \end{array} \right.$ | (12) |
当控制系统的相对阶大于1时,ST算法可进一步简化为:
| $ \left\{ \begin{gathered} u = {u_1} + {u_2} \\ {{\dot u}_1} = - W{\text{sign}}(s) \\ {u_2} = - \lambda |s{|^\rho }{\text{sign}}(s) \\ \end{gathered} \right. $ | (13) |
因此,对于飞机自动调平测试系统,系统滑模面可以定义为
| $ {s}_{a}(x)={H}_{a\text{ }}-{H}_{c\text{ }},{s}_{b}(x)={H}_{b\text{ }}-{H}_{c\text{ }} $ | (14) |
左右两个支点的滑模控制率表示为
| $ \left\{ \begin{gathered} {u_a} = \smallint - W{\text{sign}}({s_a}){\text{d}}t - \lambda |{s_a}{|^\rho }{\text{sign}}({s_a}) \\ {u_b} = \smallint - W{\text{sign}}({s_b}){\text{d}}t - \lambda |{s_b}{|^\rho }{\text{sign}}({s_b}) \\ \end{gathered} \right. $ | (15) |
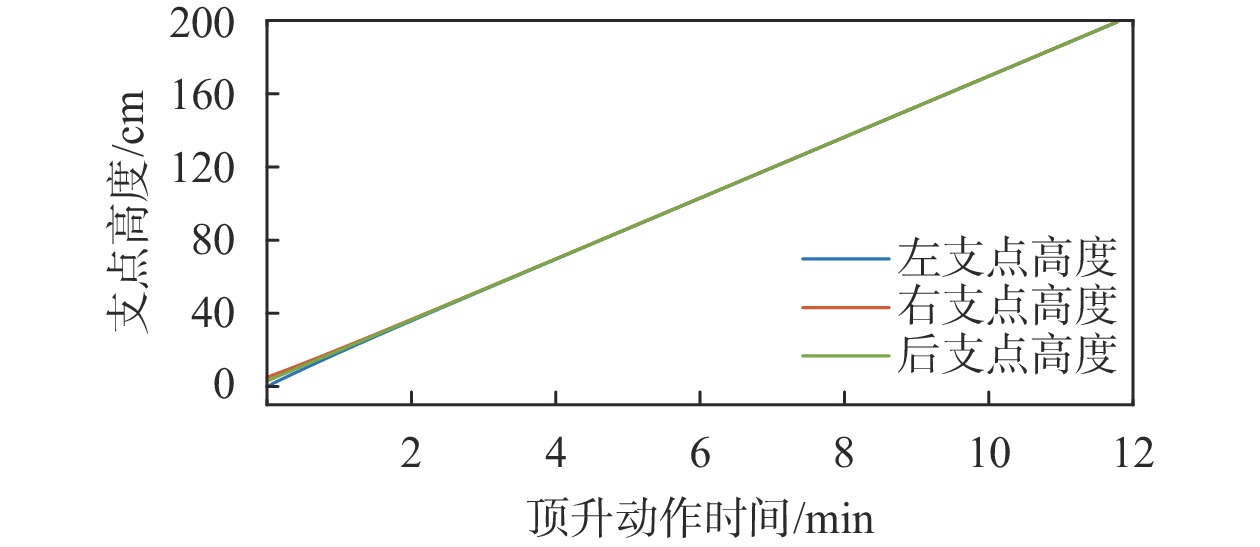
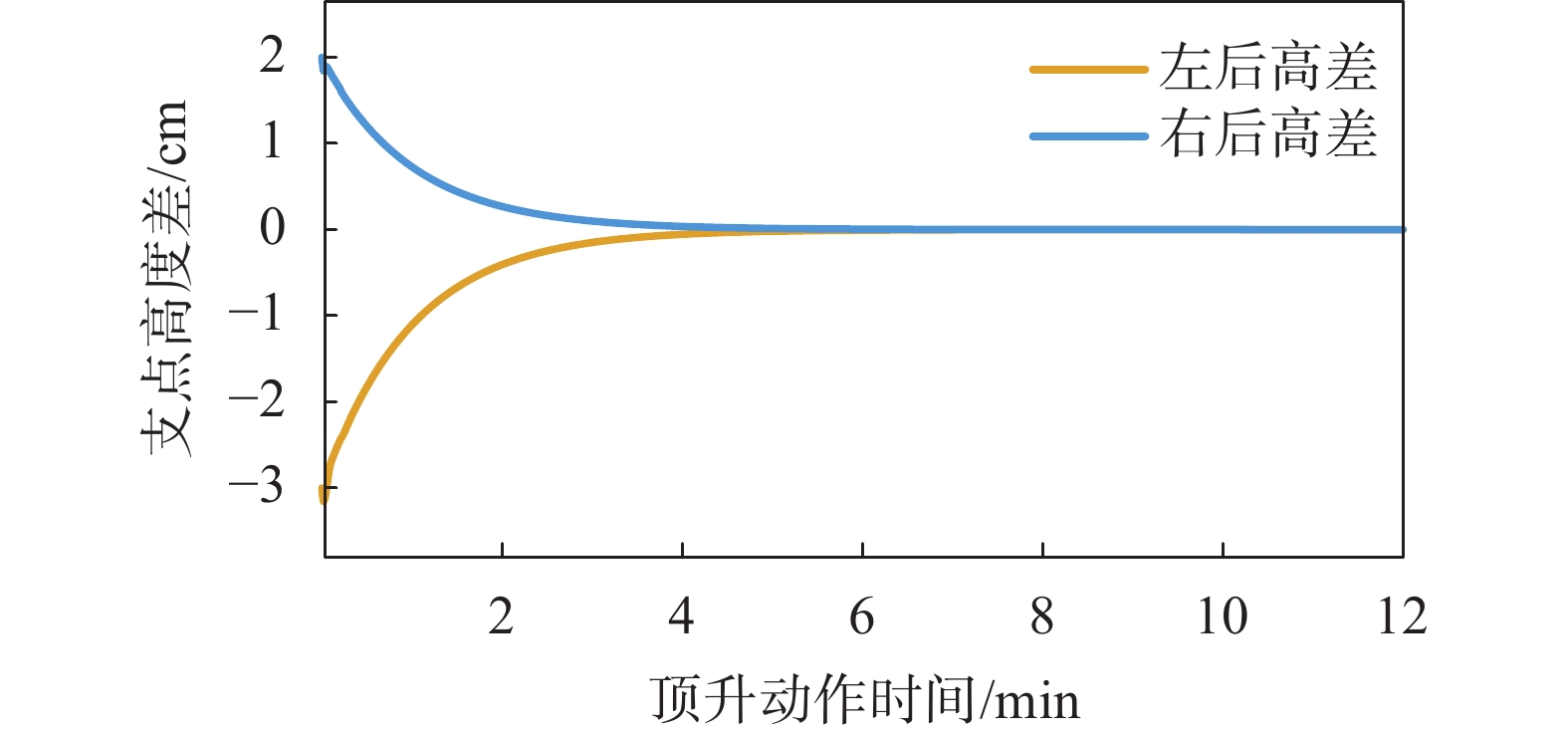
基于设计的控制器搭建仿真模型进行验证,设定左支点低于后支点3 cm,右支点高于后支点2 cm,后支点顶升速度维持不变。其支点高度变化如图6所示,支点间高度差变化如图7所示。
|
| 图 6 支点顶升阶段高度变化 |
|
| 图 7 支点顶升阶段高度差变化 |
仿真结果表明,系统的顶升速度可以达到16.92 cm/min,满足设计要求的15 cm/min,系统运行过程中可对高度偏差进行修正,依据前后支点间距离计算飞机姿态角度,在顶升动作过程中维持在0.5°范围内。
3 系统试验测试及分析在实验测试中,要求系统在高速顶升时,顶升速度不低于15 cm/min,顶升过程中设备倾角不大于0.5°;下降过程中设备倾角不大于5°,最终调平后左右支点与后支点位置误差为0.5 mm。
将设备安装到位后上电,启动主控制器软件并执行自检功能,确认系统不存在故障后进行测试。测试结果如表1所示。表中序号1实验的飞机姿态变化如图8所示。测试结果表明,系统升降及调平运行正常,相关功能指标满足要求,经过对比,实际运行测试结果与仿真结果误差较小,系统顶升速度与仿真结果相比误差为1.9%。系统测试时,顶升过程中设备倾角均不大于0.5°;下降过程中设备倾角均不大于5°,未出现超出控制要求的姿态,满足要求,不对飞机的安全造成影响。
| 参数 | 序号 | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 顶升前设备倾角/(°) | 0.034 | 0.025 | 0.039 | 0.026 | 0.033 |
| 顶升速度/(cm·min–1) | 15.68 | 15.70 | 16.59 | 16.38 | 15.93 |
| 顶升过程中设备最大倾角/(°) | 0.089 | 0.096 | 0.090 | 0.092 | 0.093 |
| 下降过程中设备最大倾角/(°) | 3.446 | 4.251 | 3.598 | 3.551 | 3.652 |
| 调平结束后左右顶 最大位置误差/mm |
0.4 | 0.3 | 0.4 | 0.4 | 0.3 |

|
| 图 8 顶升过程中飞机倾角变化 |
试验测试结果存在的误差主要由架水平的对象飞机本身变形引起。在进行试验验证时,由于飞机自身并非刚体且各处刚度不同,在地面进行校准的倾角传感器测得的倾角与真值相比会产生一定的偏差。为消除该误差,后续可以建立起飞机自身的简化刚度模型,通过该模型选择倾角传感器安装位置,同时根据刚度模型计算不同倾角时的补偿值,对倾角测量结果进行补偿,以减小飞机变形带来的倾角测量误差。
4 结束语针对飞机架水平过程的自动控制,本文以运八飞机为研究目标,搭建了以液压驱动系统作为动力源的自动架水平系统,针对支撑装置设计了滑动式地盘结构,以削弱飞机侧向力对系统的影响。在对系统传动机构进行详细建模的基础上,提出了一种用于运八飞机自动调平的高阶滑模控制方法。实验结果表明,系统能够实现预期目标,主要功能均可以正常运行,调平精度满足技术要求。
| [1] |
陈惠蓉. 基于性能的飞机配载平衡研究[J].
民航学报, 2023, 7(6): 81-84.
CHEN H R. Research on aircraft weight and balance based on performance[J].
Journal of Civil Aviation, 2023, 7(6): 81-84.
|
| [2] |
颜巍, 黄灵恩. 重心位置对不同布局飞机尾旋特性的影响[J].
民用飞机设计与研究, 2018(4): 29-35.
YAN W, HUANG L E. Effect of C. G. location on spin characteristics of different layout aircraft[J].
Civil Aircraft Design & Research, 2018(4): 29-35.
|
| [3] |
ZHAO X, YUAN Y, DONG Y, et al. Optimization approach to the aircraft weight and balance problem with the centre of gravity envelope constraints[J].
IET Intelligent Transport Systems, 2021, 15(10): 1269-1286.
DOI:10.1049/itr2.12096 |
| [4] |
贾恒信, 张志刚, 李明波, 等. 飞机重量及重心测量系统的应用及发展[J].
衡器, 2015, 44(4): 5-9.
JIA H X, ZHANG Z G, LI M B, et al. Application and development of aircraft center of gravity measuring system[J].
Weighing Instrument, 2015, 44(4): 5-9.
|
| [5] |
付鹏, 王利光, 谭春林. 重量与重心测量装置及测量方法: CN109632062A[P], 2023-11-15.
|
| [6] |
唐震宇,张云. 多传感器数据融合的四轴飞行器姿态角解算[J].
自动化与信息工程, 2023, 44(1): 33-38.
TANG Z Y, ZHANG Y. Multi-sensor data fusion for attitude angle calculation of four axis aircraft[J].
Automation & Information Engineering, 2023, 44(1): 33-38.
|
| [7] |
李文超. 数字式静液压传动系统动力特性及其控制策略研究[D]. 吉林:吉林大学, 2023.
LI W C. Research on the power characteristics of digitalhydrostatic transmission system and its control strategy[D]. Jilin: Jilin University, 2023.
|
| [8] |
张贻哲, 李跃松, 李阁强, 等. 单杆液压缸电液位置伺服系统物理建模与分析[J].
指挥控制与仿真, 2023, 45(6): 96-101.
ZHANG Y Z, LI Y S, LI G Q, et al. Physical modelling and analysis of electro-hydraulic position servo systems for single rod hydraulic cylinders[J].
Command Control & Simulation, 2023, 45(6): 96-101.
|
| [9] |
赵紫寅, 孔繁星, 孙皓章, 等. 光学芯轴测量台四点自动调平方法研究[J].
化工自动化及仪表, 2023, 50(2): 238-244.
ZHAO Z Y, KONG F X, SUN H Z, et al. Research on four-point auto- eveling method for optics mandre measuring table[J].
Control and Instruments in Chemical Industry, 2023, 50(2): 238-244.
|
| [10] |
刘丽媛, 邢然, 李道平, 等. 新一代运载火箭12点调平控制策略设计及优化[J].
导弹与航天运载技术, 2021(1): 99-104.
LIU L Y, XING R, LI D P, et al. Design and optimization of 12-piont leveling control strategy for the new generation carrier rocket[J].
Missiles and Space Vehicles, 2021(1): 99-104.
|
| [11] |
黄成成, 金海, 鲁文其. 基于Super-Twisting无位置滑膜观测器的永磁同步电机控制[J].
电子科技, 2023, 36(11): 8-13.
HUANG C C, JIN H, LU W Q. Permanent magnet synchronous motor control based on super-twisting sliding film observer[J].
Electronic Science and Technology, 2023, 36(11): 8-13.
|
| [12] |
赵回, 王雪梅, 许哲, 等. 一种转台伺服系统干扰补偿控制方法研究[J]. 中国测试, 2019, 45(3): 139-145.
ZHAO H, WANG X M, XU Z, et al. Research on a method of turntable servo system disturbance compensated control[J], China Measurement & Test, 2019, 45(3): 139-145.
|
| [13] |
ZHANG T, CHEN G, YAN G, et al. Research on the nonlinear characteristic of flow in the electro-hydraulic servo pump control system[J].
Processes, 2021, 9(5): 814.
DOI:10.3390/pr9050814 |
| [14] |
于涛, 王益博, 杨昆, 等. 球杆系统基于二阶滑模的分级滑模控制[J].
中国测试, 2019, 45(11): 114-119.
YU T, WANG Y B, YANG K, et al. Hierarchical sliding mode control of a ball and beam systembased on second order sliding mode[J].
China Measurement & Test, 2019, 45(11): 114-119.
DOI:10.11857/j.issn.1674-5124.2018090039 |
 2024, Vol. 50
2024, Vol. 50