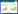文章信息
- 王海元, 郭光, 李恺, 尹晓博, 邵喜瑞, 温和
- WANG Haiyuan, GUO Guang, LI Kai, YIN Xiaobo, SHAO Xirui, WEN He
- 计及白噪声与谐波影响的复频域插值频率估计方法
- Complex frequency domain interpolation frequency estimation method considering white noise and harmonic effects
- 中国测试, 2024, 50(5): 167-173
- CHINA MEASUREMENT & TEST, 2024, 50(5): 167-173
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022050102
-
文章历史
- 收稿日期: 2022-05-16
- 收到修改稿日期: 2022-07-27
2. 智能电气量测与用电技术湖南省重点实验室,湖南 长沙 410000;
3. 湖南大学电气与信息工程学院,湖南 长沙 410082
2. Hunan Province Key Laboratory of Intelligent Electrical Measurement and Electricity Technology, Changsha 410000, China;
3. College of Electrical and Information Engineering,Hunan University , Changsha 410082, China
随着工业的发展,大量的电子设备和非线性负载接入电路,电力系统出现噪声以及谐波干扰等问题,影响电力系统保护控制的稳定性以及电能计量的准确性[1-2]。在存在噪声和谐波的情况下,频率准确测量是确保电力系统安全稳定运行的重要基础[3]。
国内外众多学者提出了许多频率估计方法,可以分为两大类:参数方法和非参数方法[4-6]。参数方法,包括过零检测法、最大似然估计、Prony算法、MUSIC算法等,需要大量的数学计算来确定算法模型。非参数方法主要是基于傅里叶变换(discrete Fourier transform,DFT)的方法,计算量小,准确率高,因此,被广泛应用于电力系统频率估计。然而,DFT存在频率泄漏和栅栏效应的问题,会降低频率估计准确度[7]。为了解决上述问题,提出了加窗插值DFT算法(windowed interpolated DFT,WIpDFT),来降低频谱泄漏和栅栏效应的影响。
经典的插值DFT(interpolated DFT,IpDFT)算法使用频谱中最大的两条或三条谱线的幅值进行插值计算实现频率测量。在文献[8-10]中,介绍了典型的基于两谱线IpDFT的频率估计方法。除此之外,国内外学者也提出了众多基于三谱线IpDFT的算法[11-12]。但是,在上述算法中,负频率的影响均被忽略不计,因此,当采样信号的周期个数很少的时候,频率测量准确度下降。
近年来,一些考虑负频谱影响的IpDFT方法已经被提出[11,13-16],进一步提升频率估计算法的性能。比如:文献[11]使用复频谱进行加窗三谱线插值,即使信号的测量时间在2.5个周期内,也能实现精确的频率估计。在文献[13]中,提出了基于尺度因子的IpDFT算法来减小负频谱的干扰。文献[17]使用信号频谱的实部和虚部来进行插值计算,消除了负频谱对频率估计的影响。
本文提出了一种可以克服白噪声和谐波影响的基于矩形窗的三谱线IpDFT频率估计算法,该方法使用复数频谱来进行插值处理,考虑了负频率的影响,在测量窗口很小的时候,也能实现精确的频率估计。本文推导了频率估计公式,建立了噪声影响下的频率估计理论方差模型,并通过仿真验证了模型的准确性。最后,通过仿真和实际测量实验验证了在测量窗口小于1.2个基波周期时,该算法性的抗噪性和抗谐波性优于其他算法。
1 频率估计方法在高斯白噪声和谐波影响下,以采样率fs采集电网信号,可得到离散信号s(n):
| $ \begin{split}s(n)= & A_0\cos\left(2\text{π }nf_0/f{_{\rm s}}\text{ + }\theta_0\right)+ \\ & \sum\limits_{h=1}^HA_h\cos\left(2\text{π }nf_h/f{_{\rm s}}\text{ + }\theta_h\right)+q(n)\end{split} $ | (1) |
式中,f0、A0和θ0——基波的频率、幅值和相位;
fh、Ah和θh——h次谐波的频率、幅值和相位,h=1,2,3
n=0,1,2,3
q(n)——方差为σ2的高斯白噪声。
在进行公式推导的过程中,忽略高斯白噪声和谐波的干扰,仅考虑基波分量,可得离散信号s(n)的表达式:
| $ s(n)=A_0\cos\left(2\pi f_0n/f{_{\rm s}}+\theta_0\right)\text{ = }A_0\cos\left(w_0n+\theta_0\right) $ | (2) |
式中:w0——角频率,w0=2πf0/fs=2πλ/N;λ——采样信号的周期个数,λ=k0+b,k0为λ的整数部分,b为λ的小数部分。
当信号为整周期采样时,k0与离散谱线重合,小数部分b等于0;当信号为非整周期采样时,k0位于最高谱线k1与次高谱线k2之间,小数部分b不等于0,如图1所示。在实际应用中,很难实现整周期采样,通常为非整周期采样。
|
| 图 1 非同步采样时的离散频谱 |
采用矩形窗w(n)对信号(2)进行加权,并对加权后的信号进行傅里叶变换,如式(3)所示:
| $ S(k) = \sum\limits_{n = 0}^{N - 1} {{A_0}\cos \left( {{w_0}n + {\theta _0}} \right)} w(n){{\rm e}^{ - {\rm j}2\pi kn/N}} $ | (3) |
式中,矩形窗w(n)=1,n=0,1
| $ S(k) = \frac{1}{2}{A_0}{{\rm e}^{{\rm j}{\theta _0}}}\frac{{1 - {{\rm e}^{{\rm j}N{w_0}}}}}{{1 - {{\rm e}^{ - {\rm j}\left( {\frac{{2\pi }}{N}k - {w_0}} \right)}}}} + \frac{1}{2}{A_0}{{\rm e}^{{\rm j}{\theta _0}}}\frac{{1 - {{\rm e}^{ - {\rm j}N{w_0}}}}}{{1 - {{\rm e}^{ - {\rm j}\left( {\frac{{2\pi }}{N}k + {w_0}} \right)}}}} $ | (4) |
为了简化表达式,引入中间变量v、u、wk,其表达式如下所示。
| $ \left\{ \begin{gathered} v = {A_0}{{\rm e}^{{\rm j}{\theta _0}}}(1 - {{\rm e}^{{\rm j}N{w_0}}})/2 \\ u = {{\rm e}^{{\rm j}{w_0}}} \\ {w_k} = {{\rm e}^{ - {\rm j}2\pi k/N}} \\ \end{gathered} \right. $ | (5) |
式中,u+u*=2cos(w0),uu*=1。则公式(4)可简化为:
| $ S(k)=\frac{v}{1-{w}_{k}u}+\frac{{v}^{*}}{1-{w}_{k}{u}^{*}}=\frac{(v+{v}^{*})-(v{u}^{*}+{v}^{*}u){w}_{k}}{1-\mathrm{cos}({w}_{0}){w}_{k}+{\left({w}_{k}\right)}^{2}}$ | (6) |
令v+v*=a,vu*+v*u=b。在频域内搜索最高谱线k2以及左右两根谱线k1和k3,可建立下式所示的三元一次方程组:
| $ \left\{ \begin{gathered} S({k_1})\left( {1 - \cos ({w_0}){w_{{k_1}}} + {{\left( {{w_{{k_1}}}} \right)}^2}} \right) = a - b{w_{{k_1}}} \\ S({k_2})\left( {1 - \cos ({w_0}){w_{{k_2}}} + {{\left( {{w_{{k_2}}}} \right)}^2}} \right) = a - b{w_{{k_2}}} \\ S({k_3})\left( {1 - \cos ({w_0}){w_{{k_3}}} + {{\left( {{w_{{k_3}}}} \right)}^2}} \right) = a - b{w_{{k_3}}} \\ \end{gathered} \right. $ | (7) |
式中wk1,wk2,wk3分别表示中间变量wk在k取k1,k2,k3时的表达式。方程组(7)含a、b、w0三个未知数,可使用消元法消去未知数a和b,求得w0的解,如下所示。
| $ \cos ({w_0}) = \frac{{{\alpha _1}S({k_3}) - {\alpha _2}S({k_2}) - {\alpha _3}S({k_1}) + {\alpha _4}S({k_2})}}{{{\beta _1}(S({k_2}) - S({k_1})) - {\beta _2}(S({k_2}) - S({k_3}))}} $ | (8) |
根据公式(8),可以得到角频率w0的表达式,如公式(9)所示:
| $ {w_0} = \arccos \left( {\frac{{{\alpha _1}S({k_3}) - {\alpha _2}S({k_2}) - {\alpha _3}S({k_1}) + {\alpha _4}S({k_2})}}{{{\beta _1}(S({k_2}) - S({k_1})) - {\beta _2}(S({k_2}) - S({k_3}))}}} \right) $ | (9) |
公式(9)中的六个系数α1、α2、α3、α4、β1、β2如下式所示:
| $ \left\{ \begin{gathered} {\alpha _1}{\text{ = }}\left( {{w_{{k_2}}} - {w_{{k_1}}}} \right){w_{{k_2}}}\left[ {1 + {{\left( {{w_{{k_3}}}} \right)}^2}} \right] \\ {\alpha _2}{\text{ = }}\left( {{w_{{k_2}}} - {w_{{k_1}}}} \right){w_{{k_3}}}\left[ {1 + {{\left( {{w_{{k_2}}}} \right)}^2}} \right] \\ {\alpha _3}{\text{ = }}\left( {{w_{{k_2}}} - {w_{{k_3}}}} \right){w_{{k_2}}}\left[ {1 + {{\left( {{w_{{k_1}}}} \right)}^2}} \right] \\ {\alpha _4}{\text{ = }}\left( {{w_{{k_2}}} - {w_{{k_3}}}} \right){w_{{k_1}}}\left[ {1 + {{\left( {{w_{{k_2}}}} \right)}^2}} \right] \\ {\beta _1}{\text{ = 2}}\left( {{w_{{k_2}}} - {w_{{k_3}}}} \right){w_{{k_1}}}{w_{{k_2}}} \\ {\beta _2}{\text{ = 2}}\left( {{w_{{k_2}}} - {w_{{k_1}}}} \right){w_{{k_2}}}{w_{{k_3}}} \\ \end{gathered} \right. $ | (10) |
根据角频率与频率之间的关系式:w0=2πf0/fs,可以得到基波频率f0的表达式:
| $ {f_0} = \frac{{{f{_{\rm s}}}}}{{2\pi }}\arccos \left( {\frac{{{\alpha _1}S({k_3}) - {\alpha _2}S({k_2}) - {\alpha _3}S({k_1}) + {\alpha _4}S({k_2})}}{{{\beta _1}(S({k_2}) - S({k_1})) - {\beta _2}(S({k_2}) - S({k_3}))}}} \right) $ | (11) |
在电力系统实际应用中,不可避免的受到高斯白噪声干扰,对参数估计造成影响,导致频率测量结果出现一定的随机性。因此,有必要开展白噪声影响下频率测量准确度的分析,确定随机白噪声对频率测量结果的影响。
在电力系统信号处理领域,研究噪声对参数估计的影响通常使用高斯白噪声模型。高斯白噪声是指概率分布是正态函数的白噪声,均值为0,方差为σ2,其概率密度函数可以表示为:
| $ P(x) = \frac{1}{{\sqrt {2\pi } \sigma }}{{\rm e}^{ - \frac{{{x^2}}}{{2{\sigma ^2}}}}} $ | (12) |
对于一个幅值为A的实正弦信号,信噪比(signal noise ratio,SNR)的表达式为:
| $ {\text{SNR}} = \frac{{{A^2}}}{{2{\sigma ^2}}} $ | (13) |
接下来,根据测量不准确度传播定则,采用统计学方法推导本文提出的算法的理论方差表达式,建立白噪声影响下的频率估计方差模型。为了方便表达,令x1=S(k1),x2=S(k2),x3=S(k3)。由文献[12]可知,x1、x2、x3的方差为:
| $ {\text{var}}\left[ {{x_1}} \right] = {\text{var}}\left[ {{x_2}} \right] = {\text{ var}}\left[ {{x_2}} \right] = {\sigma ^2}\sum\limits_{n = 0}^{N - 1} {{{\left[ {w(n)} \right]}^2}} $ | (14) |
式中,σ2为高斯白噪声的方差。任意两根频谱之间的协方差表达式为:
| $ {{\rm{cov}}} \left[ {{x_1},{x_2}} \right] = {{\rm{cov}}} \left[ {{x_2},{x_3}} \right] = {\sigma ^2}W(1) $ | (15) |
| $ {{\rm{cov}}} \left[ {{x_1},{x_3}} \right] = {\sigma ^2}W(2) $ | (16) |
式中,W(k)的表达式为:
| $ W(k) = \sum\limits_{n = 0}^{N - 1} {{w^2}(n){{\rm e}^{ - {\rm j}2\pi kn/N}}} $ | (17) |
本文中使用的窗函数为矩形窗,可知w(n)=1,将w(n)代入公式(14)可得:
| $ {\rm var}\left[ {{x_1}} \right] = {\rm var}\left[ {{x_2}} \right] = {\text{ }}{\rm var}\left[ {{x_2}} \right]{\text{ = }}N{\sigma ^2} $ | (18) |
同理,由公式(15)和(16)可得:
| $ {{\rm{cov}}} \left[ {{x_1},{x_2}} \right] = {{\rm{cov}}} \left[ {{x_2},{x_3}} \right]{\text{ = }}{{\rm{cov}}} \left[ {{x_1},{x_3}} \right]{\text{ = }}0 $ | (19) |
根据不确定度传播原则,由公式(8)可知,cos(w0)的方差可以表示为:
| $ \begin{split} {\rm{var}} \left[ {\cos ({w_0})} \right] = &{\left[ {\frac{{\partial \eta }}{{\partial {x_1}}}} \right]^2}{\rm{var}} \left( {{x_1}} \right) + {\left[ {\frac{{\partial \eta }}{{\partial {x_2}}}} \right]^2}{\rm{var}} \left( {{x_2}} \right)+ \\ & {\text{ }} {\left[ {\frac{{\partial \eta }}{{\partial {x_3}}}} \right]^2}{\rm{var}} \left( {{x_3}} \right){\text{ + 2}}\left[ {\frac{{\partial \eta }}{{\partial {x_1}}}} \right]\left[ {\frac{{\partial \eta }}{{\partial {x_2}}}} \right] \\ &{\rm{cov}} \left[ {{x_1},{x_2}} \right]+ {\text{ }} {\text{2}}\left[ {\frac{{\partial \eta }}{{\partial {x_1}}}} \right]\left[ {\frac{{\partial \eta }}{{\partial {x_3}}}} \right]{\rm{cov}} \left[ {{x_1},{x_3}} \right]+\\ &{\text{ 2}}\left[ {\frac{{\partial \eta }}{{\partial {x_2}}}} \right]\left[ {\frac{{\partial \eta }}{{\partial {x_3}}}} \right]{\rm{cov}} \left[ {{x_2},{x_3}} \right] \\[-18pt] \end{split} $ | (20) |
令公式(8)中分子为μ1,分母为μ2,即:
| $ \left\{ \begin{gathered} {\mu _1} = {\alpha _1}x({k_3}) - {\alpha _2}x({k_2}) - {\alpha _3}x({k_1}) + {\alpha _4}x({k_2}) \\ {\mu _2} = {\beta _1}(x({k_2}) - x({k_1})) - {\beta _2}(x({k_2}) - x({k_3})) \\ \end{gathered} \right. $ | (21) |
则公式(20)中三个偏导数的表达式为:
| $ \left\{ \begin{gathered} \frac{{\partial \eta }}{{\partial {x_1}}} = \frac{{ - {\alpha _3}{\mu _2} + {\beta _1}{\mu _1}}}{{\mu _2^2}} \\ \frac{{\partial \eta }}{{\partial {x_1}}} = \frac{{\left( {{\alpha _4} - {\alpha _2}} \right){\mu _2} + {{\left( {{\beta _2} - \beta } \right)}_1}{\mu _1}}}{{\mu _2^2}} \\ \frac{{\partial \eta }}{{\partial {x_1}}} = \frac{{{\alpha _1}{\mu _2} - {\beta _2}{\mu _1}}}{{\mu _2^2}} \\ \end{gathered} \right. $ | (22) |
将公式(18)和公式(19)和(22)代入公式(20),可得:
| $ {{\rm{var}}} \left[ {\cos ({w_0})} \right] = N{\sigma ^2}\left[ \begin{gathered} \frac{{\alpha _1^2 + \alpha _3^2 + {{\left( {{\alpha _4} - {\alpha _2}} \right)}^2}}}{{\mu _2^2}} - \\ 2{\mu _1}\frac{\begin{gathered} {(\alpha _1}{\beta _2} + {\alpha _3}{\beta _1} + \\ \left( {{\alpha _4} - {\alpha _2}} \right)\left( {{\beta _1} - {\beta _2}} \right)) \\ \end{gathered} }{{\mu _2^3}} + \\ \mu _1^2\frac{{\beta _1^2 + \beta _2^2 + {{\left( {{\beta _1} - {\beta _2}} \right)}^2}}}{{\mu _2^4}} \\ \end{gathered} \right] $ | (23) |
同理,角频率w0的方差可以表示为:
| $ {{\rm{var}}} \left[ {{w_0}} \right] = \frac{{N{\sigma ^2}}}{{{{\sin }^2}({w_0})}}\left[ \begin{gathered} \frac{{\alpha _1^2 + \alpha _3^2 + {{\left( {{\alpha _4} - {\alpha _2}} \right)}^2}}}{{\mu _2^2}} - \\ 2{\mu _1}\frac{\begin{gathered} ({\alpha _1}{\beta _2} + {\alpha _3}{\beta _1} \\ + \left( {{\alpha _4} - {\alpha _2}} \right)\left( {{\beta _1} - {\beta _2}} \right)) \\ \end{gathered} }{{\mu _2^3}} + \\ \mu _1^2\frac{{\beta _1^2 + \beta _2^2 + {{\left( {{\beta _1} - {\beta _2}} \right)}^2}}}{{\mu _2^4}} \\ \end{gathered} \right] $ | (24) |
根据公式(13)信噪比SNR与方差σ2之间的关系式,式(24)可以表示为:
| $ {{\rm{var}}} \left[ {{w_0}} \right] = \frac{{NA_0^2}}{{2{{\sin }^2}({w_0}){\text{SNR}}}}\left[ \begin{gathered} \frac{{\alpha _1^2 + \alpha _3^2 + {{\left( {{\alpha _4} - {\alpha _2}} \right)}^2}}}{{\mu _2^2}} - \\ 2{\mu _1}\frac{\begin{gathered} ( {\alpha _1}{\beta _2} + {\alpha _3}{\beta _1} + \\ \left( {{\alpha _4} - {\alpha _2}} \right)\left( {{\beta _1} - {\beta _2}} \right)) \\ \end{gathered} }{{\mu _2^3}} + \\ \mu _1^2\frac{{\beta _1^2 + \beta _2^2 + {{\left( {{\beta _1} - {\beta _2}} \right)}^2}}}{{\mu _2^4}} \\ \end{gathered} \right] $ | (25) |
角频率w0与频率f0之间的关系式:w0=2πw f0/fs,故根据不确定度传播原则,频率f0的理论方差表达式为:
| $ {{\rm{var}}} \left[ {{f_0}} \right] = \frac{{NA_0^2f_s^2}}{{8{\pi ^2}{{\sin }^2}({w_0}){\text{SNR}}}}\left[ \begin{gathered} \frac{{\alpha _1^2 + \alpha _3^2 + {{\left( {{\alpha _4} - {\alpha _2}} \right)}^2}}}{{\mu _2^2}}- \\ 2{\mu _1}\frac{\begin{gathered} ( {\alpha _1}{\beta _2} + {\alpha _3}{\beta _1} + \\ \left( {{\alpha _4} - {\alpha _2}} \right)\left( {{\beta _1} - {\beta _2}} \right)) \\ \end{gathered} }{{\mu _2^3}}+ \\ \mu _1^2\frac{{\beta _1^2 + \beta _2^2 + {{\left( {{\beta _1} - {\beta _2}} \right)}^2}}}{{\mu _2^4}} \\ \end{gathered} \right] $ | (26) |
式(26)即为高斯白噪声影响下的频率f0的估计方差模型,可用于评估信噪比SNR、窗函数长度N、采样频率fs对频率估计方差的影响。根据公式可知,频率估计方差与高斯白噪声信噪比SNR成反比,即叠加的噪声越强,信噪比SNR越小,频率估计方差越大。频率估计方差与窗函数长度N成正比,即窗函数长度N越大,频率估计方差越大。频率估计方差与采样频率fs的平方成正比,因此,随着采样频率fs的增加,频率估计方差呈逐渐增大的趋势。
3 仿真分析 3.1 噪声影响仿真为了验证频率估计理论方差表达式(26)(26)的正确性,进行了仿真实验。实验参数设置如下:基波幅值A0=220,基波相位φ0=π/12,采样频率fs=5000 Hz,采样点数N=128。我国电力系统频率相关标准要求电力系统频率偏差值不能超过±0.5 Hz,因此基波频率f0设置为49.5~50.5 Hz,步长为0.1 Hz。在计算实际方差时,在保证所有参数相同的条件下,运行3000次。
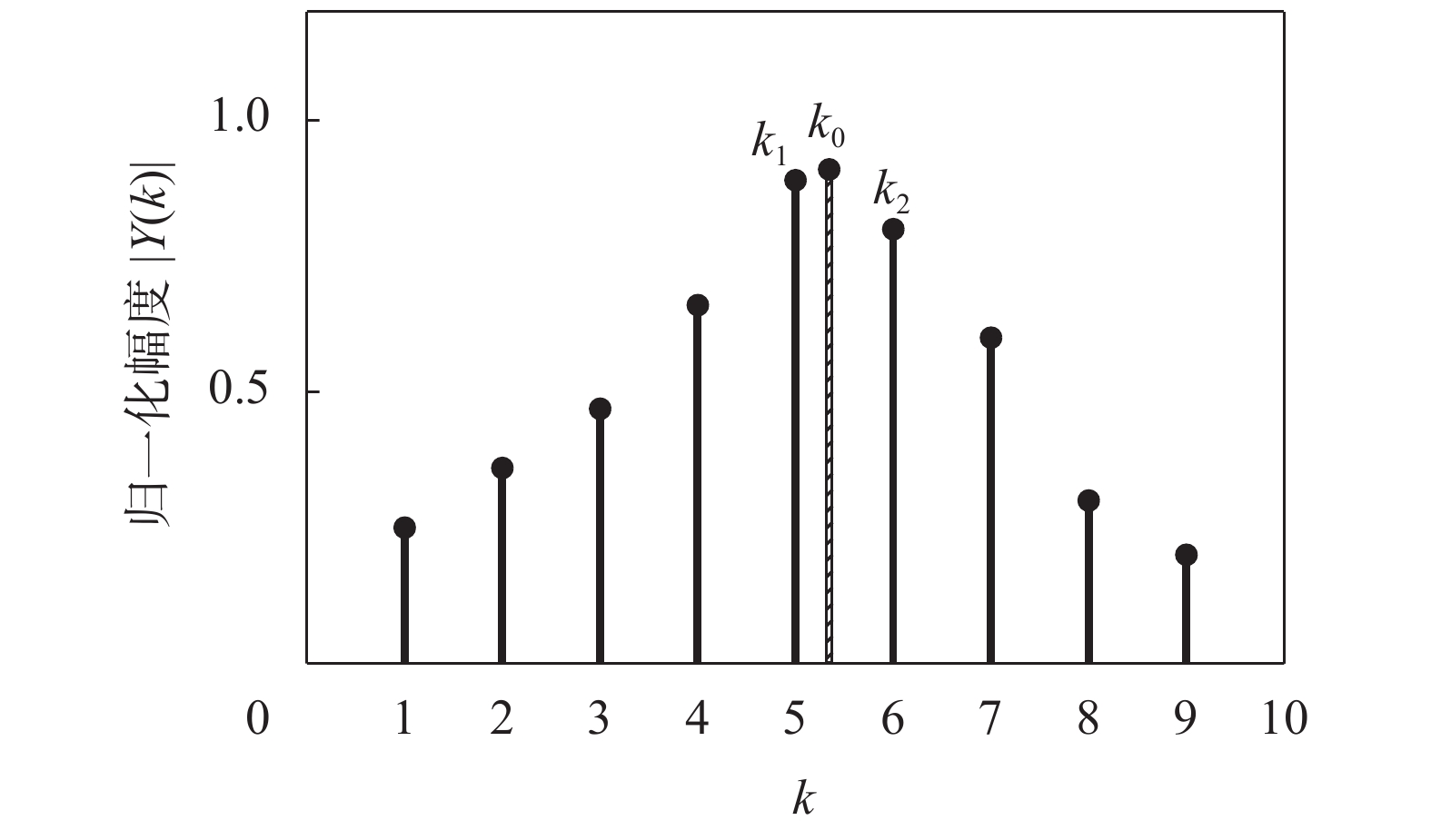
频率估计方差的仿真结果如图2所示,理论方差与实际方差吻合,验证了公式的正确性和有效性。在信噪比为20 dB时,频率估计方差最大;在信噪比为80 dB时,频率估计方差最小,符合理论方差表达式(26)的变化规律。
|
| 图 2 频率估计方差的理论和实际结果 |
接下来,通过仿真实验来验证在噪声影响下本文算法的性能,与文献[11-13]中提出的方法进行对比研究(表中IpDFT为本文方法)。上述实验参数保持不变,信噪比范围为0 ~ 100 dB,步长为10 dB。仿真结果如表1所示,频率估计方差与高斯白噪声信噪比成反比。在该实验环境下,本文提出的频率估计算法的方差最小,文献[12]中提出的算法方差最大,验证了本文算法具有更好的参数估计精度。
| SNR/dB | IpDFT | IpDFT[11] | IpDFT[12] | IpDFT[13] |
| 0 | –77.54 | –76.47 | –68.83 | –69.99 |
| 10 | –100.4 | –99.83 | –92.18 | –93.13 |
| 20 | –123.3 | –122.4 | –114.8 | –115.8 |
| 30 | –146.6 | –145.8 | –138.2 | –139.2 |
| 40 | –169.5 | –168.9 | –161.2 | –162.2 |
| 50 | –192.5 | –191.4 | –184.0 | –184.9 |
| 60 | –215.2 | –214.3 | –206.7 | –207.7 |
| 70 | –238.3 | –237.4 | –229.8 | –230.8 |
| 80 | –261.4 | –260.3 | –252.8 | –253.9 |
| 90 | –284.7 | –283.7 | –276.0 | –277.0 |
| 100 | –307.5 | –306.7 | –298.9 | –299.9 |
3.2 谐波对频率分析的影响
在电力系统实际应用中,也不可避免的存在谐波,影响频率估计的准确性。因此,要在包含谐波的情况下,验证算法的性能。在这一章节中,我们通过仿真实验试验算法的抗谐波性能。
本节所采用的仿真信号幅值和相位参数如表2所示。基波频率f0设置为49.5~50.5 Hz,步长为0.1 Hz,采样频率fs设置为5000 Hz。
需要注意的是,噪声的影响是产生随机误差的主要原因。但是在文献[12-13]的算法中,虚部的频谱干扰会产生系统误差,即偏差。方差和偏差联合使用才能真正反映频率估计结果的性能,单独使用偏差和方差是不能准确反映估计性能的。因此,在本章节中,引入均方误差的概念,既包含了估计量的偏差信息也包含了估计量的方差信息,来评价所提出的估计器和其他算法的性能。具体如下:
| $ \mathrm{MSE}\text{ = }10{\rm lg}\left[\frac{1}{M}\sum\limits_{i=1}^M\left(f(i)-\text{mean}(f)\right)^2\right] $ | (27) |
式中,mean(f)为f(i)的算数平均值。
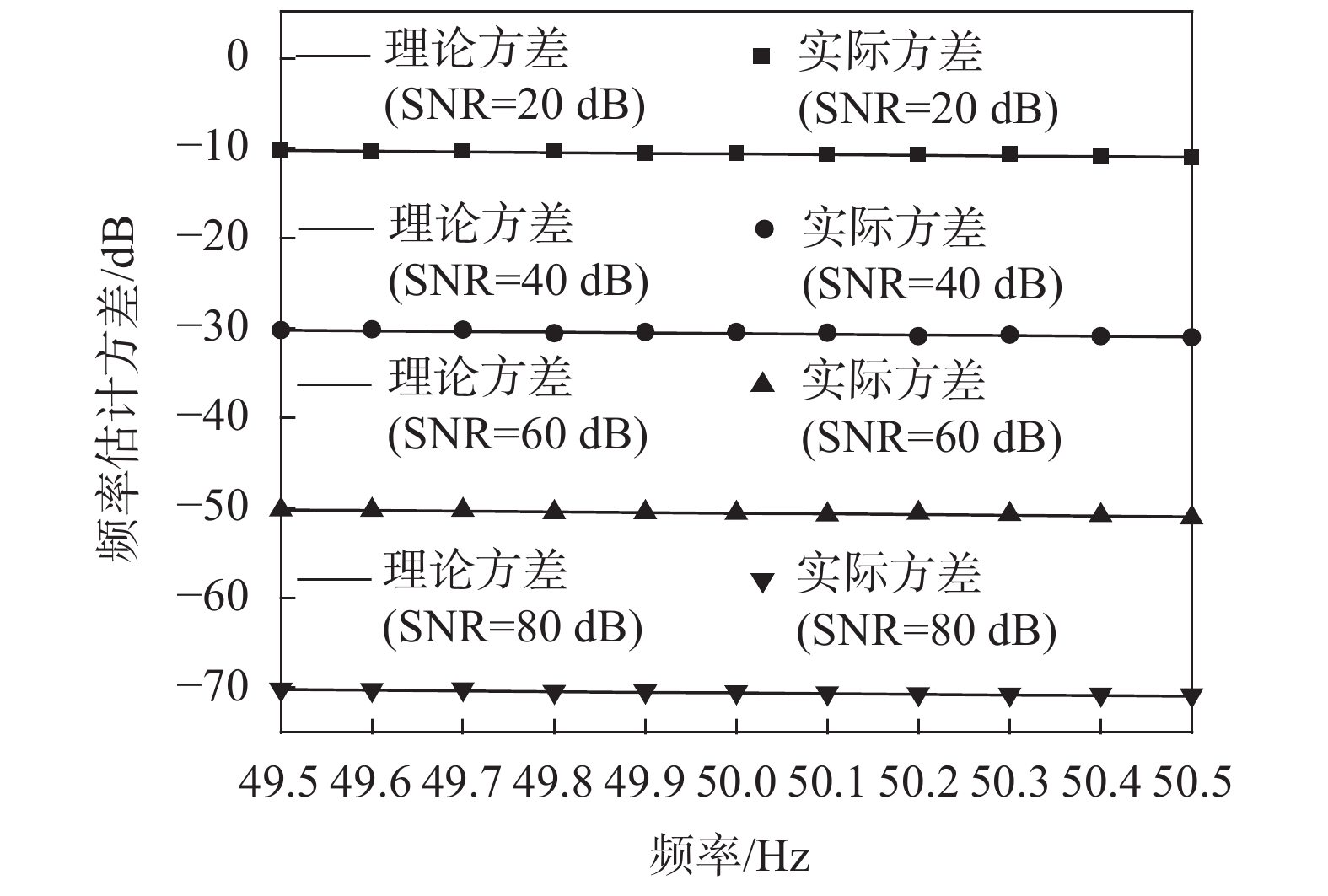
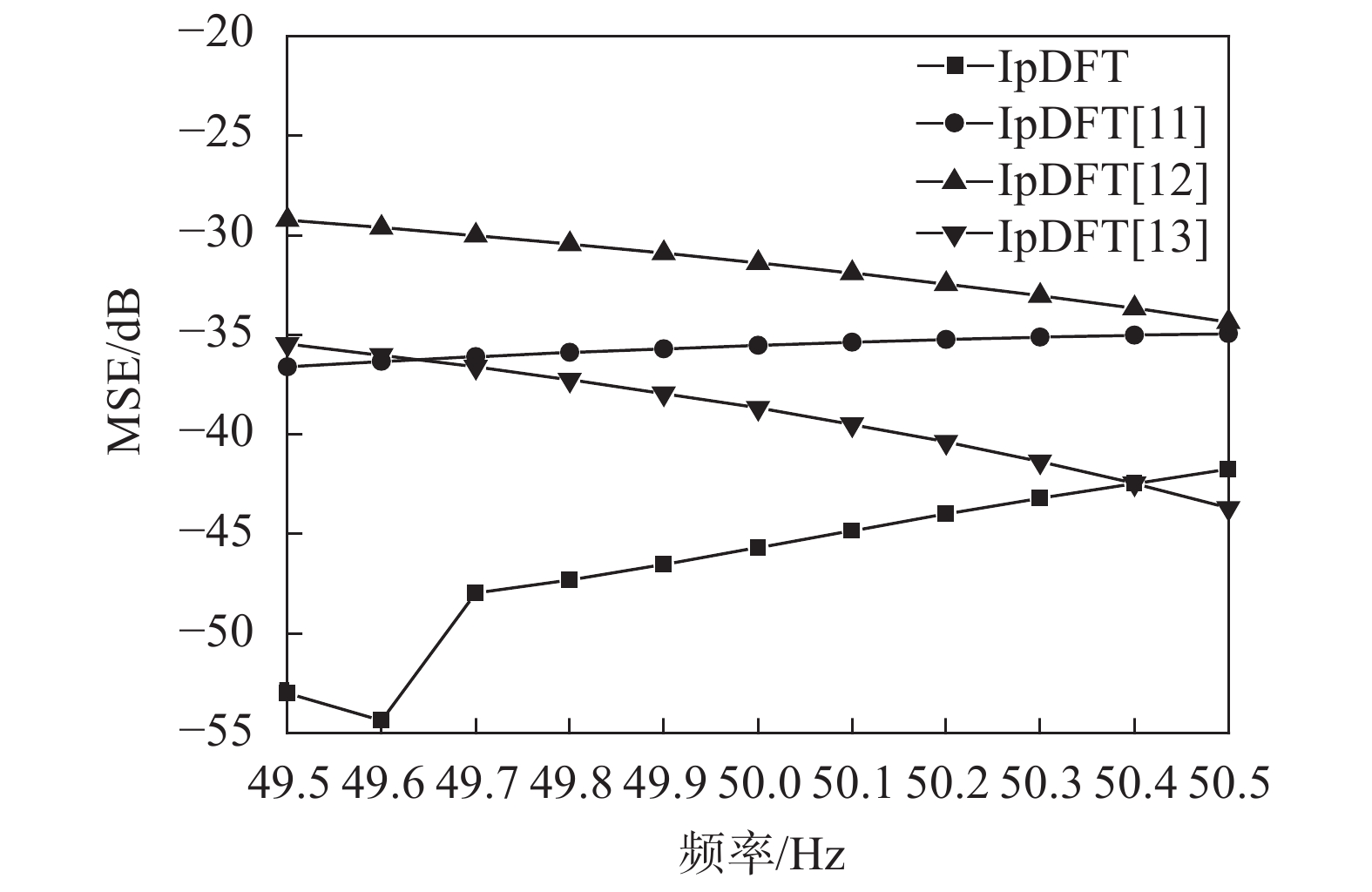
在本节的仿真中,信噪比设置为50 dB。试验分别在采样点数N=128和N=256两种情况下进行,实验结果如图3和图4所示。由图3和图4可知,两种情况下均为本文提出的算法精度最高,具有良好的抗谐波性能。在N=128时,文献[11]提出的算法精度较低。在N=256时,文献[12]提出的算法性能较差。
|
| 图 3 N=128、SNR=50 dB时,基波频率均方误差变化情况 |
|
| 图 4 N=256,SNR=50 dB时,基波频率均方误差变化情况 |
3.3 测量窗口长度的影响仿真
本节研究测量窗口长度对频率估计精度的影响。仿真模型参数如表2所示,采样点数N=512,信噪比SNR=50 dB,测量窗口长度设置为0.5~1.2个周期,步长为0.1。
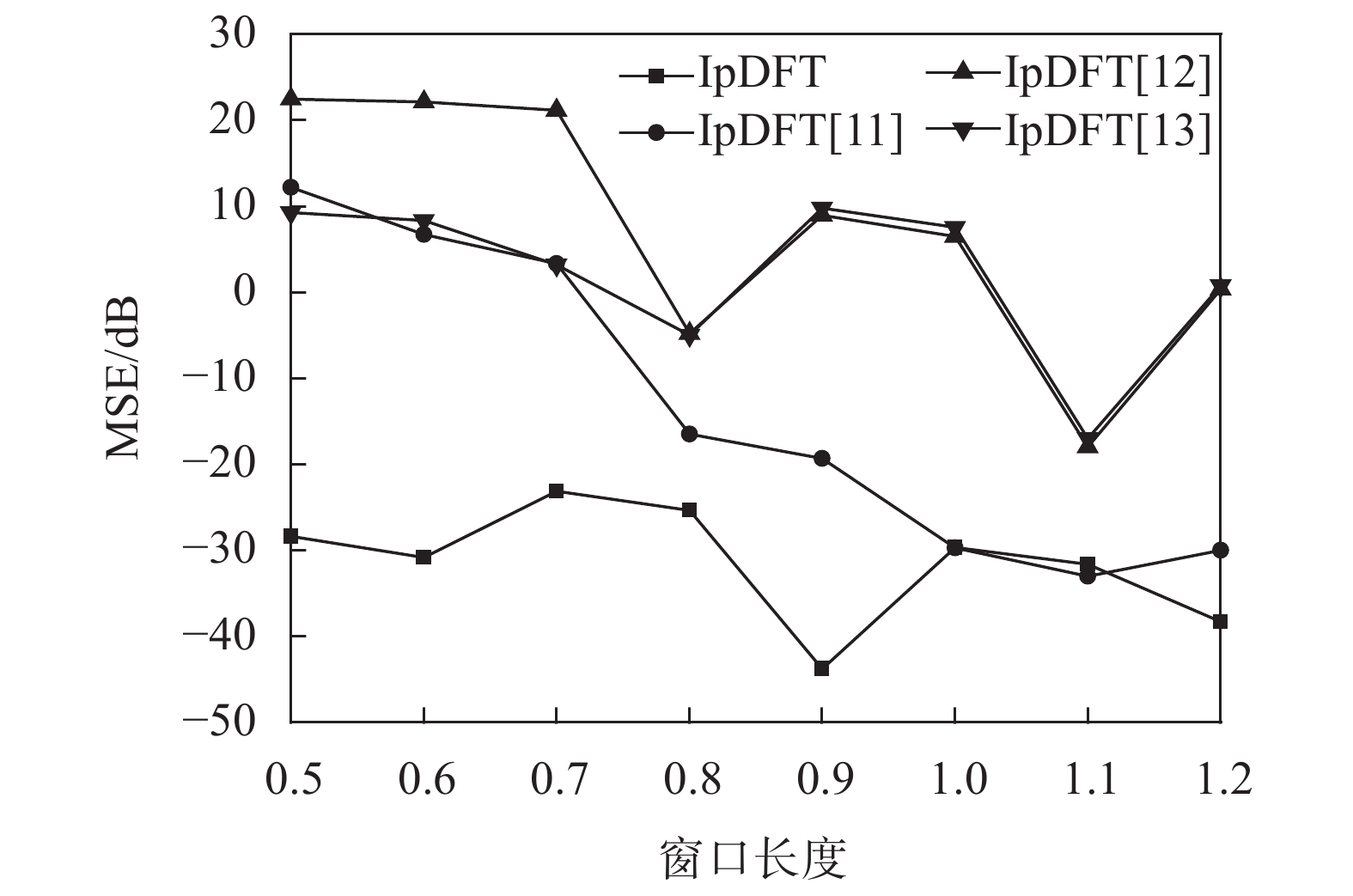
基波频率均方误差随测量窗口长度变化情况如图5所示。在测量窗口长度为0.5~1.0以及1.2个周期时,本文提出的算法频率估计精度最高,明显优于其他三种插值算法。在测量窗口长度为1.1个周期时,文献[11]提出的算法基波频率估计精度最高。文献[12-13]提出的算法基波频率估计精度较低,均方误差比本文提出的算法大了几个数量级。文献[11]提出的算法随着窗口长度增加,基波频率均方误差呈逐渐减小的趋势。
|
| 图 5 基波频率均方误差随测量窗口长度变化情况 |
4 实际测量实验
本节通过实际测量实验验证本文提出的频率估计算法的准确性和有效性。产生的正弦信号由标准功率源Fluke 6105A提供。所产生的信号由包括电压传感器的采样模块和数据采集板采集。采集板的采样频率fs设置为6.4 kHz。正弦信号的幅值A0设置为220 V,初相位φ0设置为0 rad。基波频率f0变化范围为49.5~50.5 Hz。
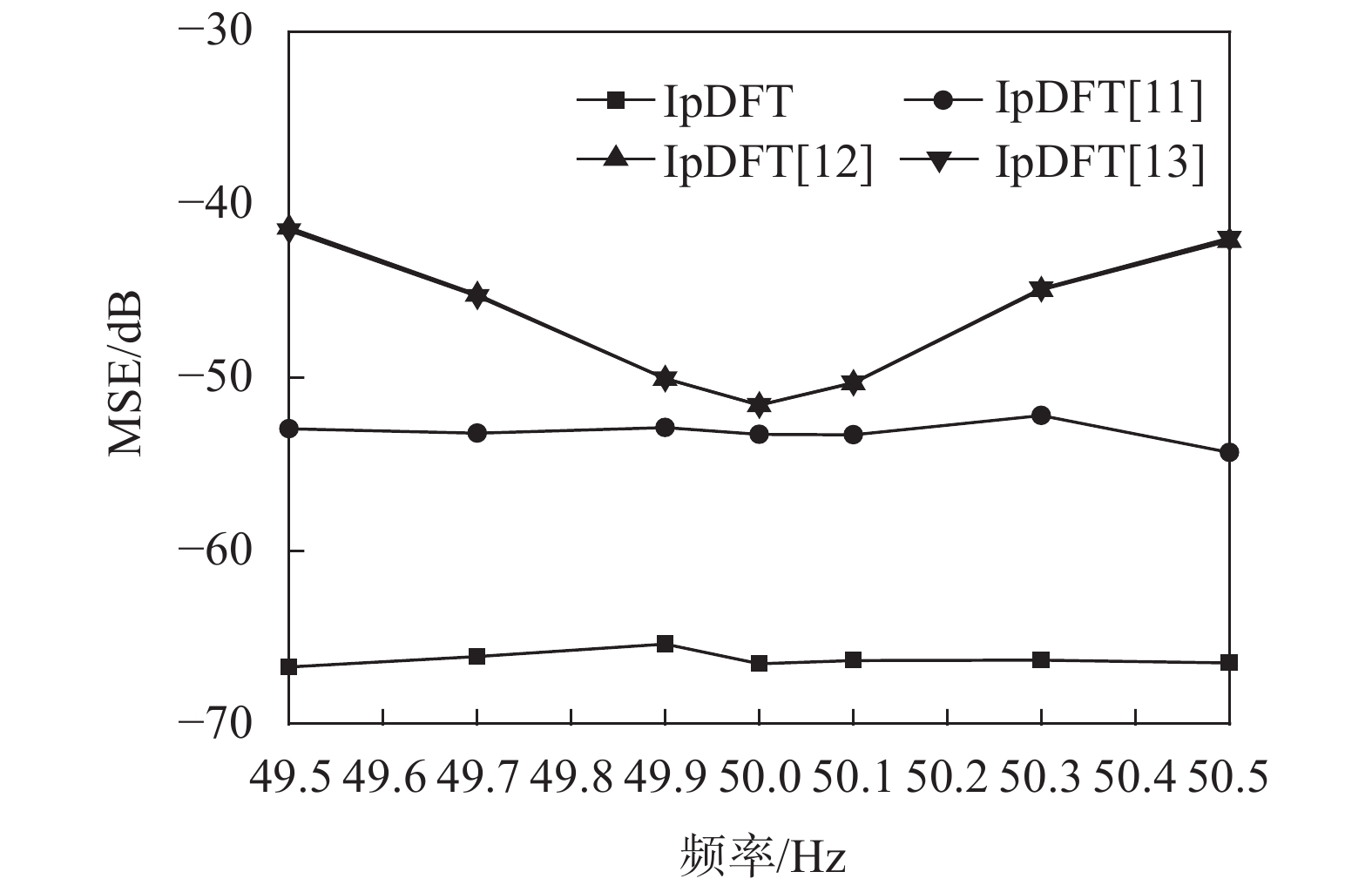
首先采集标准正弦信号,采集约15 s的数据。在处理信号并进行算法性能对比实验的时候,设置采样点数N=256,即约2个周期的离散信号。在每个基波频率下,进行3000组测试。实验结果如图6所示,本文提出的算法基波频率估计均方误差最小,文献[11]提出的算法频率估计均方误差次之,文献[12]和文献[13]中提出的算法频率估计均方误差最大。
|
| 图 6 正弦信号时,基波频率均方误差变化情况 |
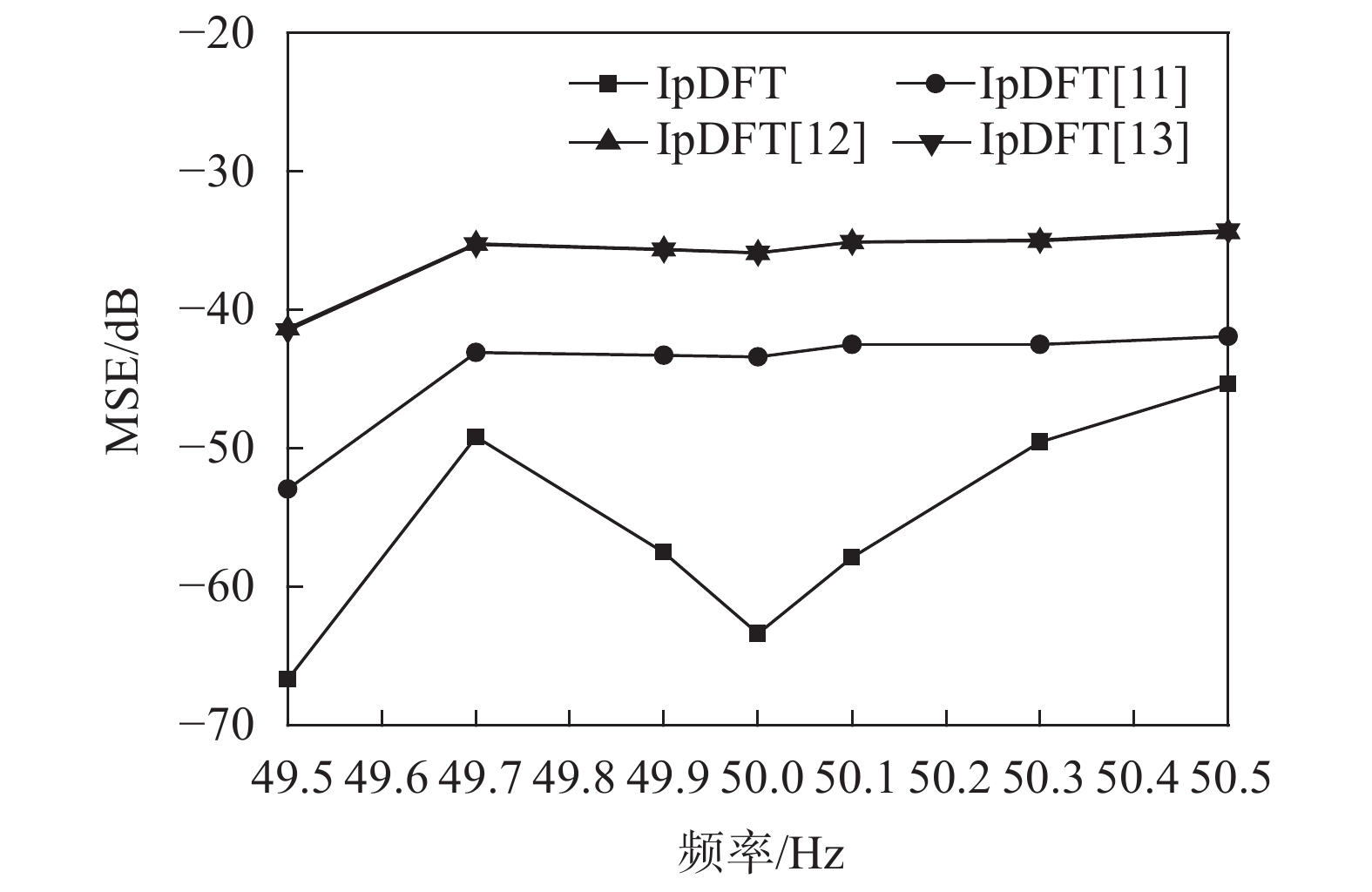
接下在添加2次谐波时,验证基波频率均方误差变化情况。基波参数保持不变,2次谐波幅值A1设置为0.1,相角φ1设置为0 rad。采样频率fs和采样点数N保持不变,试验结果如图7所示。由于在短周期测量,谐波幅值较小的条件下,负频成分导致长程频谱泄露造成的影响远大于谐波成分造成的影响,本文方法基于包含负频谱部分的无偏估计模型,完全消除负频干扰,且采用的矩形窗具有最小等效噪声带宽,因此基频频率的估计精度更高,与文献[11-13]的方法相比,本文的算法提供的频率估计均方根误差最小,表明算法可实现在噪声、频偏和谐波影响等情况下的频率准确估计。
|
| 图 7 添加2次谐波时,基波频率均方误差变化情况 |
5 结束语
针对强噪声和谐波干扰情况下传统频率测量算法精度不高的问题,本文提出了一种新的基于复频谱的三谱线插值DFT算法,同时进行了噪声影响下的频率估计不确定度分析。提出算法具有以下优点:1)推导过程基于包含负频谱部分的无偏估计模型,完全消除了频谱泄漏和栅栏效应的影响;2)与其他窗函数相比,提出算法采用的矩形窗具有最小等效噪声带宽使本算法具有最优抗噪性能;3)推导的频率估计方差模型能为算法的实际工程应用提供理论指导。仿真和实验结果证明,该算法在测量窗口小于1.2个周期的时候,算法的抗噪声抗谐波性能优于其他算法,具有一定的工程应用价值。
| [1] |
田正其, 欧阳曾恺, 周超, 等. 基于迭代滤波的电网基波与谐波动态频率测量技术[J].
电测与仪表, 2021, 58(4): 165-170.
|
| [2] |
李恺, 向鑫, 卜文彬, 等. 基于频谱分辨率自适应的双插值DFT谐波分析方法[J].
电测与仪表, 2021, 58(754): 92-97.
|
| [3] |
杨静, 熊德智, 王智, 等. 谐波与间谐波对电能计量误差影响研究[J].
中国测试, 2021, 47(3): 43-48.
|
| [4] |
舒骁骁, 祝君剑, 朱亮, 等. 计及噪声影响的高准确度迭代滤波电网频率测量方法[J].
中国测试, 2020, 46(7): 54-59.
|
| [5] |
王雅丽, 虞莉娟, 张华军等. 基于自适应陷波器的电网频率估计方法[J].
电测与仪表, 2018, v.55(701): 121-127.
|
| [6] |
徐子翼, 张忠立, 王灿, 等. 正弦压力信号数据处理方法研究[J].
中国测试, 2020, 46(9): 19-25.
XU Z Y, ZHANG Z L, WANG C, et al. Study on processing methods of sinusoidal pressure signal data[J].
China Measurement & Test, 2020, 46(9): 19-25.
|
| [7] |
陈勇, 李鹏, 宋树平, 等. 五项最小旁瓣窗插值方法电力谐波参数估计[J].
自动化仪表, 2017, 38(4): 46-49.
|
| [8] |
王娟, 张尔东, 于广艳. 基于加窗FFT和HWT算法的谐波检测系统设计[J].
电测与仪表, 2021, 58(7): 189-194.
|
| [9] |
黄瑞, 肖宇, 刘谋海, 等. 复频谱插值DFT的电力系统低频振荡信号测量方法[J].
湖南大学学报(自然科学版), 2021, 48(10): 170-177.
|
| [10] |
WANG K, WEN H, XU L, et al. Two points interpolated DFT algorithm for accurate estimation of damping factor and frequency[J].
IEEE Signal Processing Letters, 2021(99): 1.
|
| [11] |
BORKOWSKI J, KANIA D, MROCZKA J. Interpolated-DFT-based fast and accurate frequency estimation for the control of power[J].
IEEE Transactions on Industrial Electronics, 2014, 61(12): 7026-7034.
DOI:10.1109/TIE.2014.2316225 |
| [12] |
WEN H, LI C, YAO W. Power system frequency estimation of sine-wave corrupted with noise by windowed three-point interpolated DFT[J].
IEEE Transactions on Smart Grid, 2018, 9(5): 5163-5172.
DOI:10.1109/TSG.2017.2682098 |
| [13] |
BELEGA D, PETRI D, DALLET D. Frequency estimation of a sinusoidal signal via a three-point interpolated DFT method with high image component interference rejection capability[J].
Digital Signal Processing, 2014, 24: 162-169.
DOI:10.1016/j.dsp.2013.09.014 |
| [14] |
张金平, 李建立, 段晨. 计及负频率影响的新能源发电低频间谐波检测方法[J].
电测与仪表, 2020, 57(2): 95-100.
|
| [15] |
刘型志, 周全, 张淮清, 等. 基于负频率频谱干扰消除的高精度低频间谐波检测算法[J].
重庆大学学报, 2020, 43(2): 50-59.
|
| [16] |
SUN Y, CHUNGANG Z, XIONG Z. A switch-based interpolated DFT for the small number of acquired sine wave cycles[J].
IEEE Transactions on Instrumentation and Measurement, 2016, 65: 1-10.
DOI:10.1109/TIM.2016.2522838 |
| [17] |
JIUFEI L, HOU S, LI X, et al. Generalization of interpolation DFT algorithms and frequency estimators with high image component interference rejection[J]. EURASIP Journal on Advances in Signal Processing, 2016, 2016.
|
 2024, Vol. 50
2024, Vol. 50