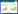文章信息
- 徐晓, 张鹏飞, 郝文秀, 郑兴莲, 朱常志
- XU Xiao, ZHANG Pengfei, HAO Wenxiu, ZHENG Xinglian, ZHU Changzhi
- 尾波干涉法检测混凝土应力损伤状态试验研究
- Experimental study on detecting stress damage state of concrete by coda interferometry
- 中国测试, 2024, 50(5): 153-159
- CHINA MEASUREMENT & TEST, 2024, 50(5): 153-159
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022040153
-
文章历史
- 收稿日期: 2022-04-23
- 收到修改稿日期: 2022-06-28
2. 保定职业技术学院,河北 保定 071051
2. Baoding Vocational and Technical College, Baoding 071051, China
混凝土中不断发生折射所形成的尾波由于其传播路径较长,可以较为准确地对混凝土结构的损伤状态进行检测,并准确评估其使用性能[1]。尾波普遍定义为超声波波形图中直达波后较长的波列,美国学者Snieder[2]首次提出尾波干涉技术的定义并利用尾波干涉技术分析了尾波波速变化,但采用的计算方法所得出的结果误差较大。Arnaud等[3]提出了直达波干涉技术(DWI),对直达波的时间轴进行拉伸求得波速变化率进行检测,与尾波干涉技术相比,实现了对结构的长久性监测,但对于判别结构内部的微小损伤不敏感。郑罡等[4-5]运用Matlab软件建立了一套时域数据的处理方法,对钢筋混凝土T梁进行尾波应力测试试验,但仅分析了T梁在小应力状态下的损伤。蒋含莞等[6-7]应用尾波干涉技术对桥梁进行检测,证明尾波波速变化与桥梁的应力和损伤具有相关性,但并未提出尾波波速变化率与应力状态的理论模型。Claub[8]对钢筋混凝土梁进行四点弯曲试验,建立钢筋应变与尾波波速变化的关系,但并未对比分析钢筋应变与混凝土应变之间的联系。
目前国内外学者并未对混凝土柱展开尾波干涉试验,因此本文基于超声波尾波对于混凝土内部变化更加敏感的特点,对4种不同强度的混凝土试块和短柱进行递增加载条件下的尾波干涉试验,对比混凝土试块和短柱的尾波波速变化率曲线,根据曲线斜率构造应力状态模型对混凝土在承受荷载过程中的应力区间及损伤状态进行分析、研究。
1 试验研究 1.1 试验仪器及试件制作本次递增加载条件下的尾波干涉试验主要由5000 kN压力试验机、Ritec非线性高能超声测试系统、RIGOL MSO2202A数字示波器和DH3818静态应变测试仪组成,如图1所示。试验时激发电压为200 V,超声波信号频率为50 kHz,声波检测频带宽度设为45~55 kHz,数据之间采样间隔2 μs。
|
| 图 1 试验装置图 |
本次试验根据JGJ 55—2011《普通混凝土配合比设计规程》设计了4组不同强度的150 mm的立方体试块和150 mm×150 mm×550 mm的混凝土短柱,如图2所示,强度等级为C20、C25、C30、C40,混凝土试块基本参数见表1,初始波速为无荷载状态下的超声波波速。

|
| 图 2 混凝土试件 |
| 强度 等级 | 水泥/ (kg∙m–3) | 水/ (kg∙m–3) | 砂/ (kg∙m–3) | 石子/ (kg∙m–3) | 抗压强度/ (N∙mm–2) | 初始波速/ (m∙s–1) |
| C20 | 290 | 185 | 725 | 1180 | 24.8 | 4513 |
| C25 | 345 | 185 | 670 | 1195 | 31.1 | 4678 |
| C30 | 380 | 185 | 648 | 1198 | 35.5 | 4745 |
| C40 | 460 | 185 | 590 | 1210 | 40.4 | 4916 |
1.2 试验方法 1.2.1 尾波干涉试验适宜参数确定
尾波干涉试验前需确定非线性高能超声测试系统多项试验参数,本文从超声波的激发频率、激发电压等条件研究尾波干涉试验适宜参数。先固定激发频率和发射周期,在试验仪器允许的范围内分别选择100 V、200 V、300 V的激发电压进行试验,接收端波形图如图3所示。比较3条不同的波形图可以发现,在200 V激发电压条件下的尾波波形整体信号质量较好且杂波较少,尾波发育更好,在尾波干涉试验中更具有代表性,因此本次试验选用200 V的激发电压。

|
| 图 3 不同激发电压下接收端波形 |
由于混凝土材料的非均质性,较低的激发频率更有利于尾波发育,而随着超声波信号的频率越大,散射衰减造成的能量损失就越大。因此为了保证信号强度较高,同时也为了增加尾波在混凝土中传播的距离,在选定200 V激发电压后,分别选择50 kHz、100 kHz、150 kHz的激发频率进行研究,接收波波形图如图4所示。比较3条波形图可以发现,在50 kHz条件下,所接收到的尾波波形幅值最大,尾波发育得最好。
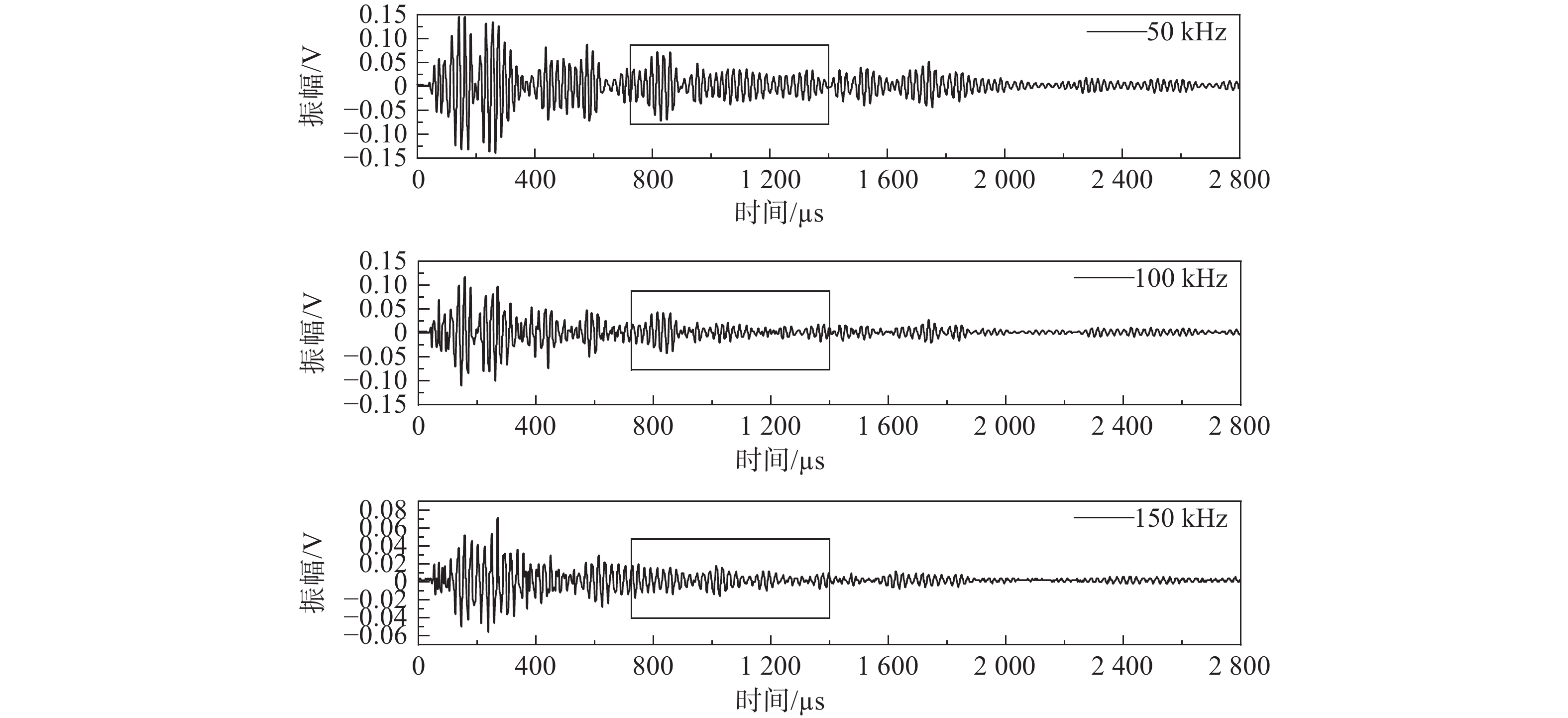
|
| 图 4 不同激发频率下接收端波形 |
1.2.2 尾波干涉试验过程
尾波干涉技术是对不同荷载状态下采集到的尾波波形进行互相关计算从而求得尾波波速变化率,一般适用于检测介质内部较小的变化。若施加荷载过大,混凝土试件内部产生较大裂缝,超声波尾波传播路径发生较大的改变,使接收到的波形发生较大的变化,从而造成试验误差[9]。加载前对传感器进行固定,防止试验过程中发生脱落等现象,通过压力试验机对混凝土试件逐级施加荷载,以1 kN/s的速率进行加载直至试件破坏,每隔20 kN进行持荷,持荷完成后由超声波检测系统发射超声波信号来获得高精度的波速变化信息[10]。采集的尾波波形数据是示波器经过多次平均以后的结果,可保证原始波形具有较好的信噪比,降低试验误差。
2 数据处理及试验结果 2.1 试验数据处理尾波干涉技术对混凝土进行检测时,主要研究参数为尾波波速变化率(dv/v)。根据直达波波速可以得出超声波在混凝土试件中传播一次需要33 µs左右,为了选取信号质量好、传播路径较长的尾波波形,本次尾波干涉试验选取[0.65,1.35] ms范围内共700 µs长的尾波波形进行分析计算。通过波形伸缩技术,利用Matlab编程对相邻两个荷载状态下的尾波波形进行互相关系数计算得到单次荷载步下的尾波波速变化率,再通过叠加法建立整个尾波波速变化率曲线,其中代表两列波形相似程度的互相关函数
| $ \quad \quad {R_{\text{k}}}(\varepsilon ) = \frac{{\displaystyle \int_0^T {u'(t)u(t){\rm d}t} }}{{\sqrt {\displaystyle \int_0^T {u{'^2}(t){\rm d}t\int_0^T {{u^2}(t){\rm d}t} } } }} $ | (1) |
式中:
T——尾波波形的长度;
根据试验过程中应变采集仪所采集的应变建立不同强度混凝土试块和短柱的应力-应变(σ-ε)曲线,如图5所示。从应力-应变曲线图中可以发现,当混凝土承受应力较小时,变形为线弹性变形,根据此时图中曲线的斜率通过公式

|
|
图 5
不同强度混凝土试块与短柱 |
| N/mm2 | ||||
| 参数 | C20 | C25 | C30 | C40 |
| 试块弹性模量 | 2.87×104 | 3.02×104 | 3.15×104 | 3.18×104 |
| 短柱弹性模量 | 2.46×104 | 2.54×104 | 2.80×104 | 3.06×104 |
| 规范弹性模量 | 2.55×104 | 2.80×104 | 3.00×104 | 3.25×104 |
2.2.2 混凝土尾波波速变化率-应力曲线
根据GB 50010—2010《混凝土结构设计规范》中混凝土受压状态下的应力-应变曲线中的公式对混凝土的应力进行计算,并建立尾波波速变化率-应力(dv/v-σ)曲线,如图6所示。x轴为公式所求得的应力,y轴为混凝土的尾波波速变化率。

|
|
图 6
不同强度混凝土试块与短柱dv/v- |
| $ \begin{gathered} \sigma = (1 - {d_{\text{c}}}){E_{\text{c}}}\varepsilon \end{gathered} $ | (2) |
| $ {d_{\text{c}}} = \left\{ \begin{gathered} 1 - \frac{{{\rho _{\text{c}}}n}}{{n - 1 + {x^{{n}}}}} \qquad \quad x \leqslant 1 \\ 1 - \frac{{{\rho _{\text{c}}}}}{{{\alpha _{\text{c}}}{{(x - 1)}^2} + x}} \qquad x \geqslant 1 \\ \end{gathered} \right. $ | (3) |
| $ {\rho _{\text{c}}} = \frac{{{f_{{\text{c,r}}}}}}{{{E_{\text{c}}}{\varepsilon _{{\text{c,r}}}}}} $ | (4) |
| $ n = \frac{{{E_{\text{c}}}{\varepsilon _{{\text{c,r}}}}}}{{{E_{\text{c}}}{\varepsilon _{{\text{c,r}}}} - {f_{{\text{c,r}}}}}} $ | (5) |
| $ x = \frac{\varepsilon }{{{\varepsilon _{{\text{c,r}}}}}} $ | (6) |
式中:
| 参数 | C20 | C25 | C30 | C40 |
| εc,r /10–6 | 1470 | 1560 | 1640 | 1790 |
| 0.74 | 1.06 | 1.36 | 1.94 | |
| 2.55×104 | 2.80×104 | 3.00×104 | 3.25×104 |
图6中,混凝土试块与混凝土短柱尾波波速变化率-应力曲线主要分为3部分:OA段(快速增长)、AB段(缓慢增长至峰值点)、BC段(下降段),对图6中A点、B点所对应的应力值进行统计并与极限抗压强度进行比较,如表4、表5所示。其中混凝土试块尾波波速变化率曲线中A点所对应的应力值
| 强度 等级 | (N∙mm–2) | (N∙mm–2) | (N∙mm–2) | ||
| C20 | 19.99 | 7.85 | 39.3% | 14.11 | 70.5% |
| C25 | 24.99 | 9.63 | 38.5% | 18.59 | 74.4% |
| C30 | 29.99 | 12.02 | 40.1% | 22.94 | 76.5% |
| C40 | 39.99 | 17.53 | 43.8% | 29.30 | 73.3% |
| 强度 等级 | (N∙mm–2) | (N∙mm–2) | (N∙mm–2) | ||
| C20 | 19.99 | 9.35 | 46.7% | 14.65 | 73.3% |
| C25 | 24.99 | 10.76 | 43.0% | 18.59 | 74.4% |
| C30 | 29.32 | 11.51 | 39.3% | 20.06 | 68.4% |
| C40 | 39.64 | 13.68 | 34.5% | 26.03 | 67.7% |
现根据表4、表5中对尾波波速变化率-应力曲线中A、B两点的应力值统计结果为条件构造混凝土受压状态下尾波波速变化率与应力状态模型,如图7所示。

|
| 图 7 波速变化率-应力状态模型 |
| $ \dfrac{\text{d}v}{v}=\left\{\begin{array}{l}{k}_{1}\cdot \dfrac{\sigma }{{\sigma }_{C}} \ \qquad \qquad \qquad \quad{k}_{1} > 0\text{,}\dfrac{\sigma }{{\sigma }_{C}} < 0.4\\ {k}_{2}\cdot \left(\dfrac{\sigma }{{\sigma }_{C}}-0.4\right)+a \qquad \ \ {k}_{2} > 0\text{,}0.4 < \dfrac{\sigma }{{\sigma }_{C}} < 0.7\\ {k}_{3}\cdot \left(\dfrac{\sigma }{{\sigma }_{C}}-0.7\right)+b \qquad \quad{k}_{3} < 0\text{,}0.7 < \dfrac{\sigma }{{\sigma }_{C}} < 1\end{array} \right.$ | (7) |
式中:
a、b——常数项。
所建立的模型将尾波波速变化率曲线分为3段,均用直线进行拟合,其中上升区分为两段,斜率分别为
分别对4种强度混凝土试块与混凝土短柱的尾波波速变化率-应力曲线中的
| 强度等级 | |||
| C20试块 | 4.88×10–3 | 0.45×10–3 | −6.3×10–3 |
| C20短柱 | 2.41×10–3 | 0.30×10–3 | −3.07×10–3 |
| C25试块 | 3.94×10–3 | 0.76×10–3 | −5.16×10–3 |
| C25短柱 | 2.25×10–3 | 0.45×10–3 | −3.58×10–3 |
| C30试块 | 3.58×10–3 | 0.78×10–3 | −5.25×10–3 |
| C30短柱 | 2.46×10–3 | 0.48×10–3 | −3.89×10–3 |
| C40试块 | 4.30×10–3 | 0.51×10–3 | −5.86×10–3 |
| C40短柱 | 1.83×10–3 | 0.4×10–3 | −3.03×10–3 |
1)应力状态模型
此时混凝土处于初始裂缝闭合阶段,随着荷载的不断增加,混凝土里面微裂缝和空气被压缩进入线弹性阶段,尾波波速变化率快速增大,混凝土所处应力区间为0~0.4
2)应力状态模型
随着混凝土所承受的应力继续增加,混凝土内部开始产生微小裂缝,颗粒之间的相对位置不再发生改变,试件表面并未产生破坏、开裂,曲线斜率逐渐减少至0,尾波波速变化率达到最大值,混凝土所处应力区间为0.4
3)应力状态模型
尾波波速变化率曲线随着应力的逐渐增加开始下降,混凝土内部微小裂缝逐渐扩展变大,表面开始产生新的裂缝,此时混凝土的应力区间为0.7
本文通过对4种强度等级的混凝土试块和短柱同时进行递增加载条件下的尾波干涉试验,主要结论总结如下:
1)适宜的激发电压和激发频率可以获得信号质量较好的原始波波形,从中选取相对靠后、波形区间较宽的尾波波形进行分析计算是此次尾波干涉法检测混凝土内部应力损伤试验成功的关键。
2)由于超声波尾波在混凝土中传播时会产生折射等现象,可以对混凝土内部微小裂缝进行放大,且随着应力的递增,混凝土试块与混凝土短柱的尾波波速变化率曲线变化趋势基本一致,因此尾波干涉技术可以作为新的检测混凝土内部应力损伤状态的方法。
3)可以将建立的尾波波速变化率-应力状态模型分为3部分:0~40%极限抗压强度、40%~70%极限抗压强度、70%极限抗压强度至破坏,分别代表混凝土在承受荷载过程中不同的应力区间及内部损伤状态,可以更加精确的判断混凝土产生裂缝的关键点。
| [1] |
肖卓, 高原. 尾波干涉原理及其应用研究进展综述[J].
地震学报, 2015, 37(3): 516-526.
XIAO Z, GAO Y. A review on the theory of coda wave interferometry and its research progress[J].
Acta Seismologica Sinica, 2015, 37(3): 516-526.
|
| [2] |
SNIEDER R. Coda wave interferometry and the equilibration of energy in elastic media.[J].
Physical Eeview. E, Statistica, Nonlinear, and Soft Matter Physics, 2002, 66(4): 046615.
|
| [3] |
ARNAUD D, CEDRIC D. Embedding ultrasonic transducers in concrete: A lifelong monitoring technology[J].
Construction and Building Materials, 2019, 194: 42-50.
DOI:10.1016/j.conbuildmat.2018.11.013 |
| [4] |
郑罡, 吴俊葶, 黎志谋, 等. T梁在三点弯曲荷载作用下的超声测试[J].
北京工业大学学报, 2020, 46(2): 162-168.
ZHENG G, WU J T, LI Z M, et al. Ultrasonic testing of t-beam under three-point bending load[J].
Journal of Beijing University of Technology, 2020, 46(2): 162-168.
|
| [5] |
郭增伟, 田川, 郑罡, 等. 混凝土工字梁三点弯曲荷载超声测试[J].
重庆大学学报, 2019, 42(11): 88-97.
GUO Z W, TIAN C, ZHENG G, et al. Three-point bending load ultrasonic test of concrete I-beam[J].
Journal of Chongqing University, 2019, 42(11): 88-97.
|
| [6] |
JIANG H, ZHAN H, ZHANG J, et al. Diffusion coefficient estimation and its application in interior change evaluation of full-size reinforced concrete structures[J].
Journal of Materials in Civil Engineering, 2019, 31(3): 04018398.
DOI:10.1061/(ASCE)MT.1943-5533.0002609 |
| [7] |
ZHAN H, JIANG H, ZHUANG C, et al. Estimation of stresses in concrete by using coda wave interferometry to establish an acoustoelastic modulus database[J].
Sensors, 2020, 20(14): 4031.
DOI:10.3390/s20144031 |
| [8] |
CLAUB F. Correlation of load-bearing behavior of reinforced concrete members and velocity changes of coda waves[J].
Materials, 2022, 15(3): 738-738.
DOI:10.3390/ma15030738 |
| [9] |
赵元明, 郭怀攀. 基于尾波干涉法反演结构微小损伤[J].
测试技术学报, 2019, 33(2): 110-115.
ZHAO Y M, GUO H P. Inverse structure damage based on tail wave interference[J].
Journal of Test and Measurement Technology, 2019, 33(2): 110-115.
|
| [10] |
郝绍菊, 马竞. 混杂纤维协同增强轻骨料混凝土力学性能试验研究[J].
中国测试, 2022, 48(6): 128-133.
HAO S J, MA J. Hybrid fiber synergistic reinforcement of the mechanical properties of lightweight aggregate concrete[J].
China Measurement & Test, 2022, 48(6): 128-133.
|
 2024, Vol. 50
2024, Vol. 50