0 引　言

金属材料作为科技社会发展的重要物质基础，在航空航天、军工制造、特种设备等领域具有广泛的应用。为保障人民能够安全地生产生活，需要对劣质、仿造的金属物品进行严格筛除。一些传统的金属辨识方法如外观测试、火花测试以及硬度测试，不仅对工作人员的经验要求高，还会对样品造成破坏^[1] 。现代的X射线荧光分析法(XRF)和光学发射光谱法(OES)可以通过读取金属样品元素百分比的含量来确定其成分和合金等级标识^[2-3] 。但由于其技术复杂以及检测仪器的造价较高、体型较大，同样存在辨识过程繁琐、辨识成本高昂的问题。

超声检测作为一种方便快捷且应用广泛的无损检测技术，大多用于检测和表征样品中的缺陷。值得注意的是，超声波在多晶材料中传播时，会与材料的晶粒结构相互作用发生散射、反射、折射和透射效应，从而造成声波能量的损失和声衰减系数的变化。MASON W等^[4] 最先指出，晶界处的声阻抗失配是多晶材料内部超声散射和衰减的主要来源，体现了多晶材料对超声波的吸收作用。基于上述原理，国内外不少学者将超声衰减与材料的微观结构信息联系起来^[5] ，实现了对金属材料的无损评价^[6] 。本课题组依托该背景，提出了多种不同方法对金属材料的晶粒尺寸进行评价研究^[7] 。并在此基础上，利用衰减系数谱法成功实现了三个性能相近金属样品的辨识区分^[8] 。随着不法分子伪造手段的不断提升，仿制品与真品间的差异已经越来越小，以往的辨识技术手段在实际应用中面临着极大的挑战。

本文结合现今工业检测中常用的超声相控阵技术，采用更加科学合理的阈值计算方法，对成分相近甚至成分完全相同的金属样品进行辨识区分。避免了以往辨识方法中受极端值影响而造成错误辨识的情况。特别的，提出金属样品“超声指纹”这一概念。不同的金属样品由于其显微组织和晶粒结构等特征的不同^[9] ，都拥有其自身独一无二的“超声指纹”。利用超声相控阵检测系统，对已知的标准样品进行信号采样，获取其“超声指纹”，将改进曼哈顿距离作为指纹特征，结合高斯分布原理和三倍标准差法计算辨识阈值。后续对相混的待辨识样品同样进行采样并提取指纹特征，通过将其与辨识阈值比较便可知它是否为之前的标准样品，达到金属样品防伪辨识的目的。

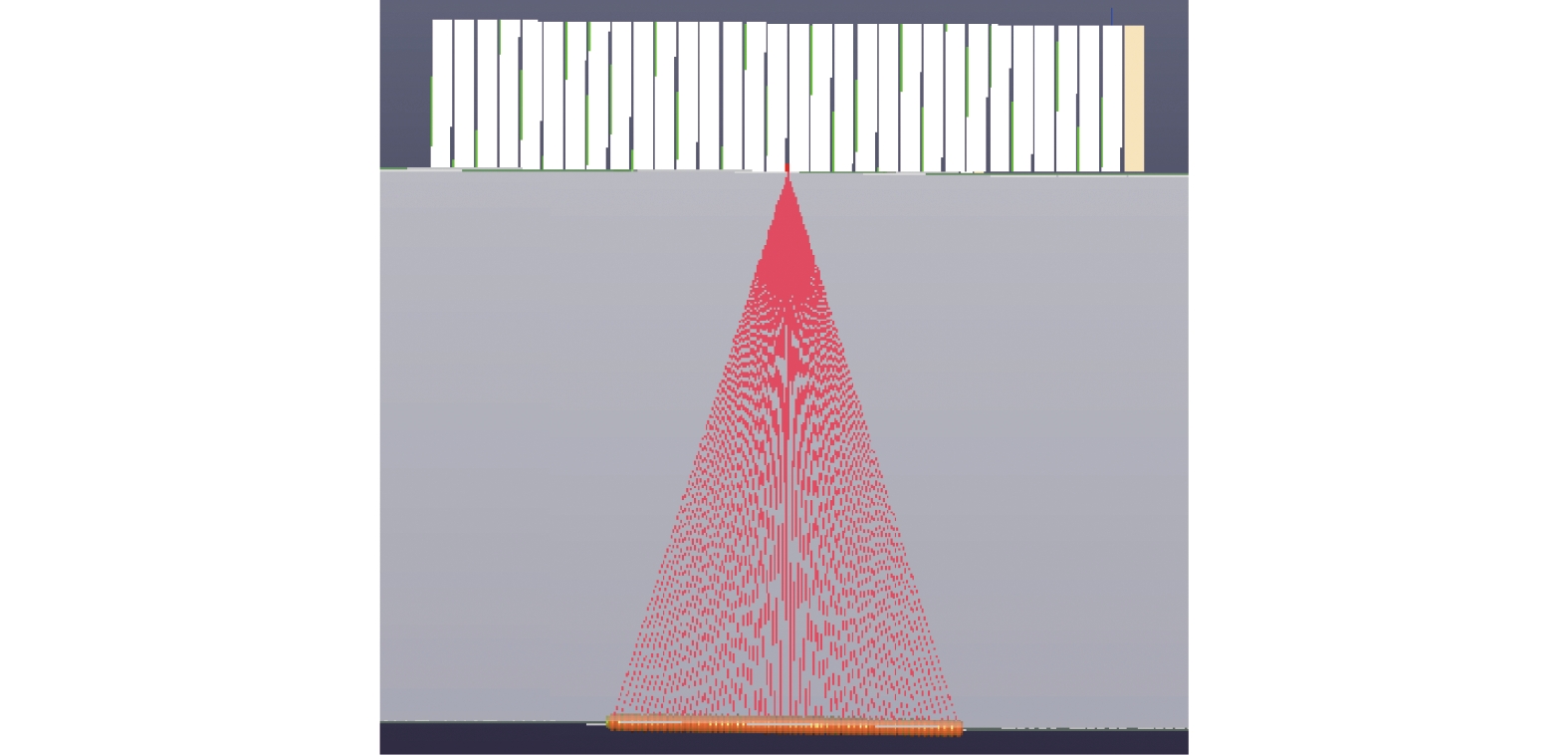
1 实验装置及信号的获取

将相控阵超声检测技术（PAUT）应用于金属样品的辨识工作中，相较于文献[8] 中使用的常规超声检测技术（UT），主要优势体现在可以实现多阵元、多角度的检测方式。结合扇形扫查方式，声束可大面积覆盖被测样品，使得样品的可检测区域变得更广，可检测角度变得更宽^[10] ，以展现出样品更多的微观结构信息。

如图1所示，超声相控阵主机（UT-Studio）一端连接相控阵探头，一端通过屏蔽网线与计算机相连，进行数据传输。利用计算机中的软件控制主机发射脉冲信号于探头，该探头的中心频率为5MHz，包含有32个阵元。如图2所示，设定相控阵探头的扫查方式为扇形扫查方式，角度范围为[−15°，15°]，角度步进为1°。在每个角度上各个阵元按照设定的延时法则发射脉冲信号，在接收时同样按照延时法则进行信号叠加。超声相控阵系统在工作时能够实现一次信号采集同时得到多个采样信号，即每个角度上都能够接收到叠加后的多个A扫描信号。相控阵系统的采样率为100 MHz，设置采样时间为20 μs，则每个A扫描信号包含2000个采样数据点。

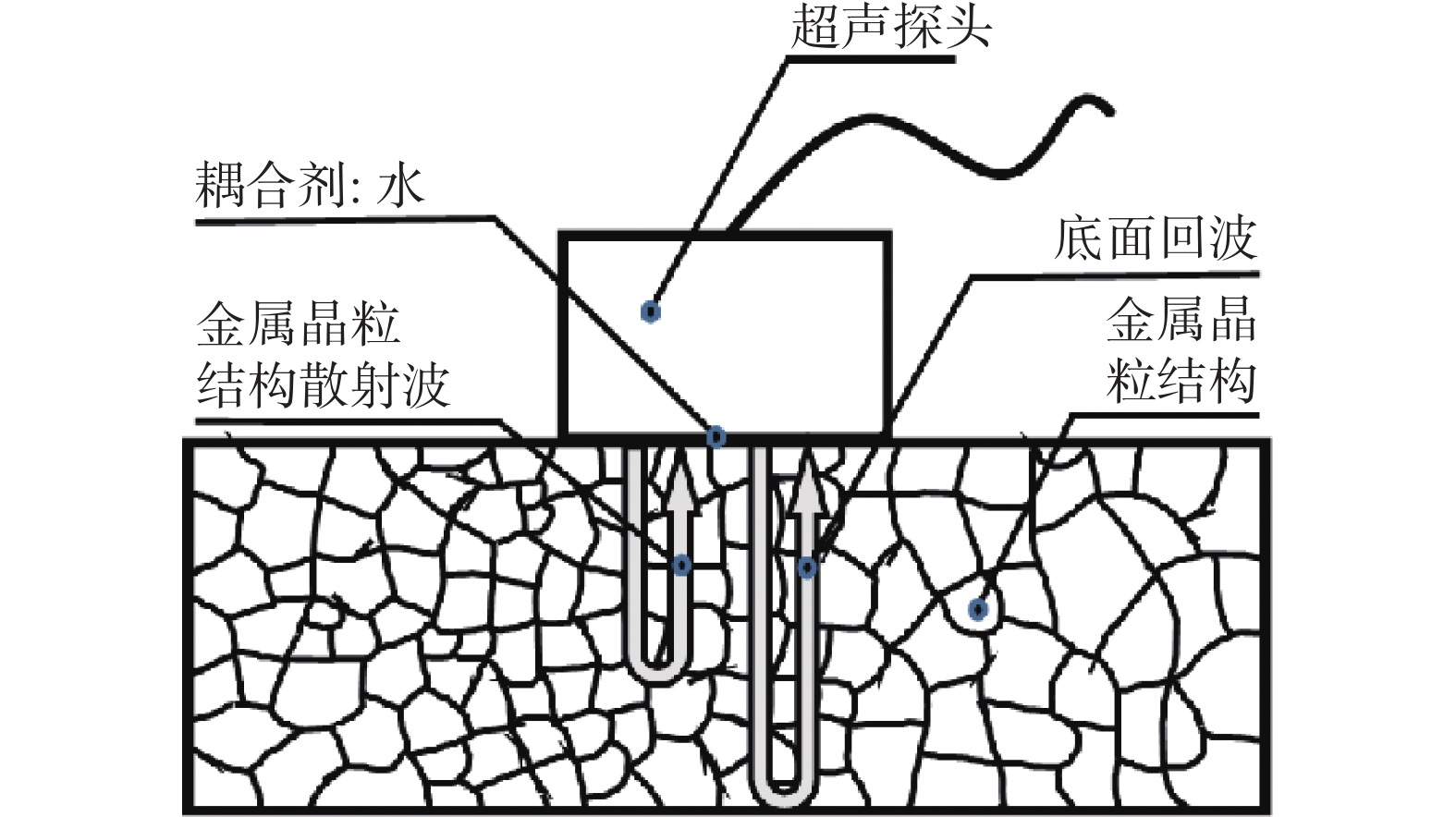
如图3所示，以水作为耦合剂，探头发射的超声波脉冲在金属样品中传播，声波遇到金属晶粒结构相互作用并发生散射效应，产生散射信号。当声波传至底面时，由于金属与空气声阻抗的巨大差异，声波在金属底面会发生反射，产生回波信号。最终散射信号和回波信号都会被探头接收。

如图4所示，选取牌号为2Cr13、3Cr13、Cr17Ni2的不锈钢金属圆柱体各7个作为实验样品，它们的厚度为15 mm，直径为47.1 mm，从外观上看不出任何差别。按次序对它们进行分类编号，记作x-y #样品（如第2排3Cr13的第2个样品记为2-2#样品）。实验时，为提高实验的可重复性，保证每次采集的信号都是稳定有效的。如图5（a）所示，仿照之前提出的探头固定方法^[11] ，使用自主研制的相控阵探头固定器固定探头，确保探头与样品表面严密贴合并且探头每次受到的压力是相同的。又如图5（b）所示，选用强度高、韧性好、易于加工成型ABS热塑型材料通过SBS胶粘剂固定在实验样品表面，通过这种直角位置固定器来对采样点位进行标记，确保每次采集信号的位置一致。

在扇形扫描方式下，超声相控阵系统0°角度上所采集到的金属样品时域信号如图6所示，包含有始波、散射波以及各次回波信号。可以看出，随着传播距离的增加，由于金属晶粒结构对声波的散射衰减以及底面对声波的反射吸收衰减，导致声波能量逐渐损失，信号的幅值不断下降^[7] 。

2 辨识方法 2.1 基于IMD的特征提取

为实现对不同的金属样品的辨识区分，需要对所采集到的超声信号进行特征提取。曼哈顿距离（Manhattan distance, MD）是衡量两点或两个向量之间距离的常用方法。设n维数据空间中有两点坐标x、y，则MD的定义为：

其中，x_u和y_u分别为坐标x、y中的第u个元素。与MD不同，改进曼哈顿距离(improved Manhattan distance, IMD)衡量的是两个矩阵之间的距离。假设有两个m×n阶的矩阵X、Y，在计算它们的IMD之前，首先需要计算各个对应行向量之间的MD，然后再将它们的平均值作为两个矩阵的IMD。具体计算公式为^[12] ：

其中，X_lu和Y_lu分别为矩阵X、Y中第l行u列的元素。通过（2）式便能够衡量两次采集信号之间的相关度。另外值得注意的是，在实际获得的超声信号中，回波信号幅值的波动程度要比散射信号幅值的波动程度大得多，在计算IMD时，回波信号的贡献会占有更大的权值。为了消除这种影响，在计算之前将信号进行对数变换。在未改变信号性质和相关关系的基础上，使回波信号和散射信号占有相当的权值，同时也使信号更加平稳，削弱了模型的共线性、异方差性等。因此，在（2）式的基础上进行对数变换，得到本文的IMD计算公式为：

2.2 辨识阈值的计算

金属中超声信号的形成受多种因素影响（如金属晶粒等散射体的散射、底面的反射、介质的吸收以及其它噪声干扰等），具有明显的不确定性和非线性特性。根据中心极限定理，这种受多种因素影响所形成的信号可以看作是服从高斯分布的^[13] 。从统计学上说，当一组测量数据服从高斯分布时，根据三倍标准差法，数据点位于均值为中心，正负三倍标准差范围之外的概率很小，仅有0.3%，而在此范围之内都认为是正常值^[14] 。

基于上述原理，本文中的辨识阈值具体计算过程为：首先对标准样品进行多次采样测试，记为$ {A}_{i} $，i表示第i次信号，求出多次标准信号的平均值作为基准信号，记为$ \bar{A} $，然后利用（3）式计算基准信号$ \bar{A} $与各次标准信号$ {A}_{i} $的改进曼哈顿距离${D}_{\rm imd}\left(\bar{A},{A}_{i}\right)$，最后利用（4）式计算阈值：

其中，$\overline {{D_{\rm imd}}} = \frac{{\mathop {\displaystyle\sum \nolimits}_{i = 1}^N {D_{\rm imd}}}}{N}$与$\sigma = \sqrt {\frac{{\mathop {\displaystyle\sum \nolimits}_{i = 1}^N {{\left( {\overline {{D_{\rm imd}}} - {D_{\rm imd}}} \right)}^2}}}{N}}$分别为标准信号IMD的平均值和标准差，N为标准信号的采集次数。根据大数定律，对测试个体进行多次重复性的研究，才能从数量上反映其变化的规律性^[15] 。所以从理论上来讲，N取得越大越能够体现出阈值的准确性，结合实际情况，本文中N只取20。

相较于文献[8] 中的阈值计算方法：对标准样品多次测试后，求得其衰减自相关系变化范围为$ {r}_{a} \sim{r}_{b} $，阈值定义为$ \varDelta =\left|{r}_{b}-{r}_{a}\right|/2 $。不难发现，该阈值是由端点值$ {r}_{a}、{r}_{b} $计算所得，易受极端值的影响。倘若某次标准信号采集不准确，与其余标准信号的相关度较低，使得该次信号计算得到的自相关系数偏小（即$ {r}_{a} $偏小），则会导致阈值过大，出现错误辨识的情况。本文基于高斯分布原理和三倍标准差法提出的阈值计算方式很好地避免了这个问题，将多次采集的信号融合计算，即使出现了个别信号采集不准确的情况，也不会对阈值造成太大的影响。

2.3 辨识流程

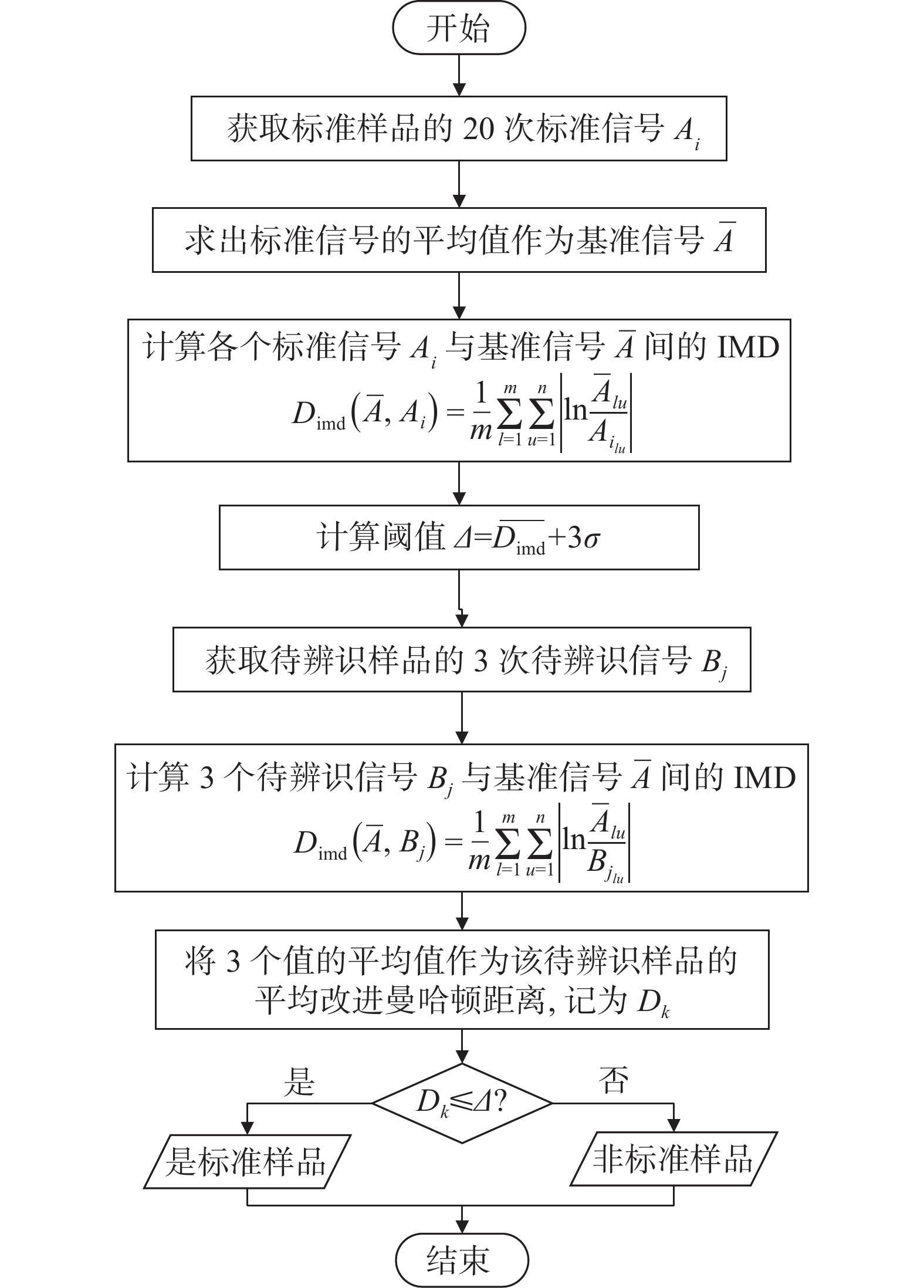
通过（4）式计算得到标准样品的辨识阈值后，需要对待辨识样品进行采样测试，为避免人为操作不当而产生采集误差，对每个待辨识样品采集3次待辨识信号，记为$ {B}_{j} $。将这3次待辨识信号与基准信号$ \bar{A} $计算所得IMD的平均值作为该待辨识样品的平均改进曼哈顿距离，记为$ {D}_{k} $。如图7所示，最终的辨识准则为：若$ {D}_{k}\leqslant \varDelta $，则认为该待辨识样品“是标准样品”，否则认为该待辨识样品“非标准样品”。具体的辨识流程如图8所示，按照图8中的辨识流程，可以完成单个角度上的辨识工作，将扇形区域内所有角度逐一辨识，通过计算机统计辨识为“是标准样品”与“非标准样品”的次数来确定最终的辨识结果。

3 辨识实验 3.1 实验结果及结果分析

按照上述的辨识流程，分别进行“成分相近金属样品”及“成分相同金属样品”的辨识实验。其中“成分相近金属样品”指的是每个样品的化学成分相近但却不同，即2Cr13、3Cr13、Cr17Ni2之间的辨识（以1-1#样品、2-1#样品和3-1#样品的辨识为例）；“成分相同金属样品”指的每个样品的化学成分完全相同，即同一型号下7个样品的辨识（以1-1#样品至1-7#样品的辨识为例）。两类实验中，统一将1-1#样品作为标准样品。

图9为相控阵扇形扫查方式下各个角度的阈值$ \varDelta $与待辨识样品平均改进曼哈顿距离$ {D}_{k} $的比较。表1中详细给出了标准样品（0°角度）阈值的相关计算数据。对应的，表2中给出了各个待辨识样品（0°角度）的辨识过程及辨识结果。

从表1中可以看出，在0°角度上，各次标准信号与基准信号的IMD别是2.6068、1.9680、1.7860、1.1584、1.9320、2.6928、2.4840、1.6148、1.6200、1.7176、1.2540、1.6180、2.5608、2.3644、1.3736、1.6488、1.7356、0.8792、2.0424、1.9536，平均值${\bar{D}_{\rm imd}}$=1.8505，标准差σ=0.5007，由（4）式计算所得的阈值$ \varDelta $=3.3527。表2“成分相近金属”的辨识实验中，1-1#样品各次待辨识信号与基准信号的IMD分别为2.7564、2.6850、2.4726，平均值$ {D}_{k} $=2.6830，小于阈值$ \varDelta $=3.3527，故其辨识结果为“是标准样品”；2-1#样品的IMD分别为12.8458、11.5734、11.7758，平均值$ {D}_{k} $=12.0650，大于阈值$ \varDelta $，故其辨识结果为“非标准样品”；3-1#样品的IMD分别为13.0315、12.9807、13.8500，平均值$ {D}_{k} $=13.2874，大于阈值$ \Delta $，故其辨识结果也为“非标准样品”。“相同成分金属”的辨识实验同理，这里不再赘述。

从图9（a）中可以看出，在所有角度上，1-1#样品的平均改进曼哈顿距离$ {D}_{k} $都在阈值范围内，故其最终的辨识结果为“是标准样品”，而1-2#样品和1-3#样品的平均改进曼哈顿距离$ {D}_{k} $都远超出了阈值范围，所以它们最终的辨识结果为“非标准样品”。在图9（b）的“成分相同金属”辨识实验中，各个角度上依旧能够将1-1#样品辨识为“是标准样品”；对于其余的待辨识样品，在某些角度上有部分样品的平均改进曼哈顿距离$ {D}_{k} < \varDelta $（如1-3#样品的−9°角度），究其原因，可能是在这些角度上，待辨识样品与标准样品的晶粒结构或显微组织极为接近，导致所采集的超声信号并无太大差别，从而在这些角度上出现错误辨识的情况。但综合所有的角度来判断，依旧能够实现准确辨识。

对于以往的辨识方法^[8] ：由表1中的数据计算得到阈值$ \varDelta = \left|{r}_{b}-{r}_{a}\right|/2 $=$ \left|2.692\;8-0.879\;2\right|/2=0.906\;8 $，自相关系数中间值$ {\bar{r}_{{\textit{z}}}}=({r}_{a}-{r}_{b})/2=1.786\;0 $。对于表2中“成分相同金属”的辨识，1-1#样品的$ {\bar{r}_{h}}=2.760\;0 $（即本文中的$ {D}_{k} $）。$ \left|{\bar{r}_{{\textit{z}}}}-{\bar{r}_{h}}\right|=0.9740 > \varDelta =0.906\;8 $。故辨识结果为“非标准样品”。显然，这与事实相悖，出现了错误辨识的情况。通过以上的辨识数据和结果分析可以看出，对比以往方法中存在某些辨识不准确的情况，使用本文所提出的辨识方法能够很好地将成分相近甚至成分完全相同的金属样品辨识区分。

3.2 适应性研究

在实际的金属辨识工作中，对已知标准样品提取“超声指纹”并作留存后。往往并不会立即对其进行采样辨识，而是经过较长时间的运输或贮存后再对该样品进行待辨识工作（如危险化学品的出入运输、核容器的贮存监测以及文物的外借归还等情形）。随着时间的推移和环境温度等因素的改变，采集标准信号时的测试条件与采集待辨识信号时的测试条件总会存在些许偏差，从而使得待辨识信号与基准信号之间产生更大的差异，导致平均改进曼哈顿距离$ {D}_{k} $变大，超出阈值范围，出现“自身辨识”错误的情况。

为结合实际应用，避免“自身辨识”错误的情况出现。对上述实验样品进行相关的适应性研究，主要包括时间推移和测试温度变化这两大因素对辨识结果的影响。以1-1#样品为例，图10中给出了不同变化因素对其“自身辨识”结果的影响。

从图10（a）中可以看出，在其他测试条件尽量保持一致的前提下，对于间隔多天后再采集的待辨识信号，1-1#样品依旧能够实现自身的正确辨识。尽管有少量阵元计算的平均改进曼哈顿距离超出了阈值范围，但绝大多数阵元依旧在阈值范围内，所以1-1#样品的辨识结果为“是标准样品”。又从图10（b）中发现，当样品温度为−20 ℃和60 ℃时，1-1#样品的平均改进曼哈顿距离$ {D}_{k} $超出了阈值范围，出现自身错误辨识的情况。究其原因，一方面可能是由于样品表面的高温（或低温）导致相控阵探头性能发生改变，影响超声信号的发射与接收；另一方面，样品温度的改变也会使样品本身的物理特性发生变化，与其相互作用超声波的声学参量，如声速、衰减系数也会有所改变，因此出现错误辨识的情况。但对于测试温度在−10 ~40 ℃的情形，各个金属样品依旧能够实现正确的“自身辨识”，说明本文的方法能够在一定的温度波动范围内进行金属辨识工作。

4 结束语

超声波在金属中传播时，与金属晶粒结构相互作用会产生散射衰减，遇到底面会发生反射衰减。通过将超声波信号与金属样品的显微组织和晶体结构联系起来，提出金属样品“超声指纹”这一概念。不同的金属样品都有其自身独一无二的“超声指纹”。利用这一特点实现了金属样品的防伪辨识。

本文以3类成分相近的金属样品以及每类7个成分相同的金属样品为例，利用超声相控阵的扇形扫查方式对它们进行信号采样。将改进曼哈顿距离作为指纹特征，结合高斯分布原理和三倍标准差法计算标准样品的辨识阈值。相较于文献[8] 中提出的阈值计算方法，新的阈值计算方法更加科学合理，不易受极端值的影响。测试结果表明，基于本文提出的方法不仅能够实现成分相近金属样品的准确辨识，还能够将成分相同的金属样品辨识区分。同时为了贴合实际，还探究了时间推移和测试温度变化对辨识结果的影响，进一步说明了本文提出的金属物品辨识方法具有较好的鲁棒性。

为方便实际应用，本课题组正在将该防伪辨识技术研制成一自动测试仪器，利用机械装置替代手动操作，避免由于人为操作不当而产生采集误差。将该技术往自动化、便携化和智能化的方向发展。超声防伪辨识技术作为一种安全无损、方便快捷的探测技术，在工业领域、军事领域、特种领域以及文物鉴定等领域具有良好的应用前景，同时还在一定程度上促进了超声应用技术的发展。