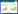文章信息
- 孙芳锦, 邓富河, 贺伟盼, 曾倩, 张大明
- SUN Fangjin, DENG Fuhe, HE Weipan, ZENG Qian, ZHANG Daming
- 基于大涡模拟的大型风力机在剪切来流条件下的尾流研究
- Study on the wake of large wind turbines under shear flow conditions based on large eddy simulation
- 中国测试, 2024, 50(5): 130-137
- CHINA MEASUREMENT & TEST, 2024, 50(5): 130-137
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022010050
-
文章历史
- 收稿日期: 2022-01-12
- 收到修改稿日期: 2022-05-24
2. 广西嵌入式技术与智能系统重点实验室,广西 桂林 541006;
3. 桂林理工大学信息科学与工程学院,广西 桂林 541006
2. Guangxi Key Laboratory of Embedded Technology and Intelligent System, Guilin 541006, China;
3. School of Information Science and Engineering, Guilin University of Technology, Guilin 541006, China
随着科学技术的快速变更,资源的合理利用受到更多的关注,不可再生能源的缺点,使可再生能源优势更突出,风能作为一种可再生能源,受到很多学者的青睐。风力机使得风能转换为电能,大功率的风力机转化效率突出,经济效益高,大功率风力机比小功率风力机优势更明显。风电场中当来流风速经过旋转的叶片,受到旋转叶片的粘性阻碍,空气在叶片附近流动,进而被吸收发生能量损耗,造成速度损失,湍流度变强,涡能量损耗,造成尾流效应。根据贝兹理论极限值,风能转化为59.3%,实际工程中,这一数值会更低,此外尾流效应带来的湍流度增强也造成下游风力机叶片疲劳,影响风力机使用寿命,因此研究风力机尾流有其重要的意义,可为风电场地资源的合理利用和提高风能利用率提供参考。风力机尾流分布存在近尾流区和远尾流区,近尾流区流动情况复杂,远尾流区是除了近尾流区外的区域,主要受到风力机尾流的相互作用以及尾流效应带来的湍动能变化等。
以往很多学者研究风力机的方法主要分为实验研究法和数值模拟法两种,实验研究是通过风洞实验,给定流场条件,研究风力机在风洞中的各种湍流特性。在早期,李万润等[1] 就通过实地测算风场中尾流的实际速度数值,对风力机的尾流进行分析;随着计算机技术的快速发展,数值模拟方法越来越受到欢迎。在数值模拟方面,杨立国等[2] 结合风洞试验与数值模拟,两者数据结果对比,得出数值模拟的正确性;孙芳锦等[3] 用CFD方法对单台风力机不同变桨角度的尾流特性进行定性分析;刘智益等[4] 通过对串列与错列风力机模型,修正尾流区域膨胀系数来验证模型准确性。王兵等[5] 用大涡模拟比较了六种亚格子模型,分析了六种亚格子模型在湍流运动中瞬时场的压力和粘性大小的分布情况,定性给出了六种亚格子模型选取的导向;张亚光[6] 用大涡模拟结合致动线风力机几何模型,对单台风力机的尾流特性进行分析。致动线是一种将风力机等效为沿叶片径向分布的体积力,以线表达的一种技术,致动线几何模型极大减少网格数量,节省计算资源,一般结合大涡模拟运用,但致动线几何模型会忽略叶片翼型细节,是一种简化模型,不符合实际情况,故本文采用未简化风力机几何模型,结合大涡模拟进行尾流特性研究;在尾流研究方面,杨瑞等[7] 对水平轴风力机尾流研究揭示尾流产生平面机理及在叶片末端膨胀发展和向下游风力机扩散的机理;钟宏民[8] 耦合大涡模拟与致动线的技术研究了风力机尾流湍流运动的变化情况;温文等[9] 利用数值模拟对2 MW风力机串列下不同间距尾流进行分析,得到2 MW风力机不同间距下尾流的影响,间距越大,影响越小,但是目前主要趋势是针对大功率风力机进行研究,提高经济效益。
本文采用数值模拟的方法,构建风力机模型及流场空间,结合陈荣盛等[10] 提出的相似准则,对大功率NREL-5 MW风力机模型按1∶10比例缩小,解决因流域大导致计算机资源浪费的问题。对单个风力机模型进行不同风速下风力机功率和水平推力验证,同美国可再生实验室风洞实验做对比,分析了不同风速下模型的功率和水平推力数据,验证模型的可行性。并以此为基础,在风速入口采用UDF函数输入剪切风模型,对风力机采用正对串列的形式,控制了上下游风力机的间距,采用大涡模拟湍流模型,分析不同间距下5 MW大功率风力机的尾流特性变化。
1 CFD数值模拟 1.1 风力机模型模型采用美国可再生实验所给出的翼型数据,在Solidworks建模软件中,调整翼型坐标,对各个翼型建立一个翼型平面,组合成风力机单叶片,最终结合轮毂生成三叶片模型。基本参数见表1,叶片及风力机模型见图1和图2。5 MW风力机直径为126 m,额定风速为11.4 m/s,切入风速3 m/s,切出风速25 m/s,额定转速12.1 r/min,轮毂高度为90 m。
| 截面编号 | 截面距/ m | 安装扭角/ (°) | 展长/ m | 弦长/ m | 翼型类别 |
| 1 | 2.8667 | 13.308 | 2.7333 | 3.542 | Cylinder1 |
| 2 | 5.6000 | 13.308 | 2.7333 | 3.854 | Cylinder1 |
| 3 | 8.3333 | 13.308 | 2.7333 | 4.167 | Cylinder2 |
| 4 | 11.7500 | 13.308 | 4.1000 | 4.557 | DU40_A17 |
| 5 | 15.8500 | 11.480 | 4.1000 | 4.652 | DU35_A17 |
| 6 | 19.9500 | 10.162 | 4.1000 | 4.458 | DU35_A17 |
| 7 | 24.0500 | 9.011 | 4.1000 | 4.249 | DU30_A17 |
| 8 | 28.1500 | 7.795 | 4.1000 | 4.007 | DU25_A17 |
| 9 | 32.2500 | 6.544 | 4.1000 | 3.748 | DU25_A17 |
| 10 | 36.3500 | 5.361 | 4.1000 | 3.502 | DU21_A17 |
| 11 | 40.4500 | 4.188 | 4.1000 | 3.256 | DU21_A17 |
| 12 | 44.5500 | 3.125 | 4.1000 | 3.010 | NACA64_A17 |
| 13 | 48.6500 | 2.319 | 4.1000 | 2.764 | NACA64_A17 |
| 14 | 52.7500 | 1.526 | 4.1000 | 2.518 | NACA64_A17 |
| 15 | 56.1667 | 0.863 | 2.7333 | 2.313 | NACA64_A17 |
| 16 | 58.9000 | 0.370 | 2.7333 | 2.086 | NACA64_A17 |
| 17 | 61.6333 | 0.106 | 2.7333 | 1.419 | NACA64_A17 |

|
| 图 1 风力机单叶片 |

|
| 图 2 三叶片风力机模型 |
1.2 计算域与网格划分
计算域为长方体流域,流域入口处两侧距风力机轮毂中心为1.5D,风力机轮毂处距底部9 m(未缩放实际高度为90 m),即轮毂高度,轮毂距上部对称壁面为2D,上游风力机距入口为1.5D,上下游风力机间距设为
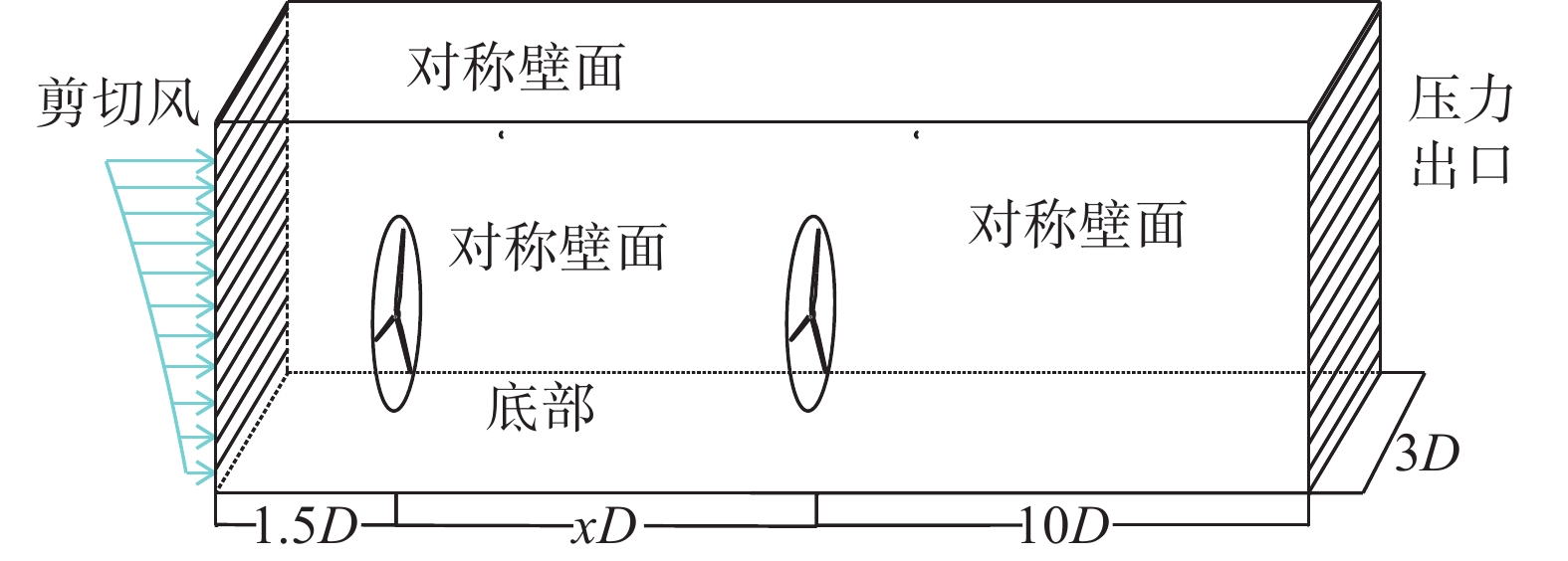
|
| 图 3 风场计算域图 |
网格划分对计算结果有着重要的影响,采用 ICEM软件对流域进行网格处理,大涡模拟对网格要求很高,考虑到结构化网格精度更高更好计算,但由于风力机表面比较复杂,较难生成结构化网格,基于外网格跟内网格分块思想,分成两个块,内网格块采用非结构网格,做法为风力机表面过渡到外空间部分逐层加密,边界层网格Y+小于1,边界层网格划分5层,保证捕抓到精细的流场变化,由于外流场分布均匀,故外网格采用更高质量的结构化网格。综上所述,用结构化外网格混合非结构内网格,形成混合网格的结构形式,如图4所示。

|
| 图 4 风力机网格划分 |
1.3 大涡模拟湍流模型
目前,湍流数值模拟方法分为直接数值模拟法(DNS)、雷诺平均模拟法(RANS)和大涡模拟法三种方法,直接模拟法用不可压缩流动的连续性N-S方程求解湍流运动中湍流细节,雷诺平均法是用时均N-S方程求解时均运动,小的脉动忽略,得到接近平均的结果,但很难准确预测尾流内的详细湍流特性[11-13] ,且对比LES,RANS的计算精度较低,综合考虑,本文采用大涡模拟,大涡模拟是一种介于DNS和RANS方法的一种方法。大涡模拟的整体思想是认为大涡被流场影响较大,小涡认为是各向同性,因此将湍流运动紊流涡的空间平均,通过滤波函数将大尺度的涡与小尺度的涡过滤,大涡直接用方程模拟,小涡通过亚格子直接模拟。大涡模拟的控制方程如下式所示:
| ∂ρ˜ui∂xj=0 | (1) |
| ∂∂t(ρ˜ui)+∂∂xj(ρ˜ui˜uj)=∂∂xj(μ∂˜ui∂˜uj)−∂˜p∂xi−∂τij∂xj+Fi | (2) |
式中:
其中亚格子应力
| τij=−2μt˜Sij+13τkkδij | (3) |
式中:
| ˜Sij=12(∂˜ui∂xj+∂˜uj∂xi) | (4) |
为实现大涡模拟,还应该具有亚格子应力模型,本文大涡模拟研究采用的是动态Smagorinsky-Lilly模型,利用Smagorinsky-Lilly模型来求解亚格子湍流粘度
| μt=ρL2s|˜S|=ρL2s√2˜Sij˜Sij | (5) |
其中
| Ls=min(κδ,CSV1/3) | (6) |
式中:
本文流场的入口条件设置为速度入口,速度采用UDF程序输入剪来流风,产生的风速随着高度而变化,即x方向的速度随着z方向高度变化而变化,出口边界为压力出口边界,风力机计算域上部与左右部壁面采用对称边界条件,为现实叶轮旋转,叶轮旋转区域建立旋转域,旋转域表面跟外流域交界面采用interface面静动网格交界面,设定旋转域旋转,叶轮相对于旋转域静止以实现叶轮转动,故风力机叶轮采用无滑移壁面,底部也设定无滑移壁面。具体如图3所示,采用大涡模拟湍流模型,亚格子模型采用动态Smagorinsky-Lilly模型,算法采用simple算法对速度跟压力方程进行耦合计算,扩散项用中心差分格式,时间步长采用风力机旋转3°所用的时间即0.04 s,收敛精度为0.001,先进行稳态计算,为瞬态流场提供良好的初始流场信息,在进行瞬态大涡模拟计算,每种工况计算20 s。
在地表附近,由于空气会形成一系列不规则的涡流,形成湍流,对空气流动造成很大的阻碍作用,由于受到近地层的阻碍作用,风速随着高度会呈现出指数函数形式变化,即高度越高,风速越大,一定高度后风速会趋于常数,这种现象被称为风剪切,本文采用FLUENT中UDF功能,编写风速函数程序,形成垂直风剪切来流,具体如图5所示,入口处的风速随着高度变大,风速也变大,在轮毂处形成额定风速,具有明显的速度分层,相对于均匀来流,符合实际的入流条件,具体公式为:

|
| 图 5 速度来流风剪切速度分布 |
| UZ=U0(Z/Z0)α | (7) |
式中:U0——轮毂处的风速,取11.4 m/s;
Z0——轮毂处的高度为90 m,模型缩小为1/10,取9 m;
Z——速度入口边界任意高度;
A类地貌取0.12,具体为沙漠、海岛等;B类地貌取0.16,具体为田野、乡村、丛林、丘陵以及房屋比较稀疏的乡镇和城市郊区。本文针对B类粗糙度系数进行模拟,取
陈荣盛等[10] 以流体机械理论为基础,提出了风力机械相似准则,具体为风力机模型与风力机原型在空气能量传递过程与风流经过风力机过程中流动过程相似,包括几何相似,运动相似,力相似。风力机械相似准则将风力机特性用相关参数将模型和原型风力机联系起来,其中功率,水平推力之间的联系表现在比例因子
| PSPM=α2 | (8) |
| TSTM=α2 | (9) |
式中:P——功率;
T——水平推力;
本文采用原型风力机大小与模型大小比例为10的比例因子,先求出模型风力机的力矩,用比例因子求出原型风力机的力矩,进一步通过力矩与功率的关系求出风力机的功率。
1.6 网格无关性验证采用瞬态计算不同数量的网格在额定风速下功率,提取不同数量网格与不同时间点的功率数据,如图6所示,结果表明:同一时间点上,当437万网格至766万之间,功率相比较437万之前越来越趋于平缓。同一数量网格上,437万网格相比较530万跟766万网格三条曲线的点较拟合,说明在10~20 s时间段功率较为平稳,综合考虑可认为437万网格之后,网格数量对功率影响变小,且在时间段上平稳,故本文采用437万网格进行模拟,保证网格无关性的同时提高计算效率。
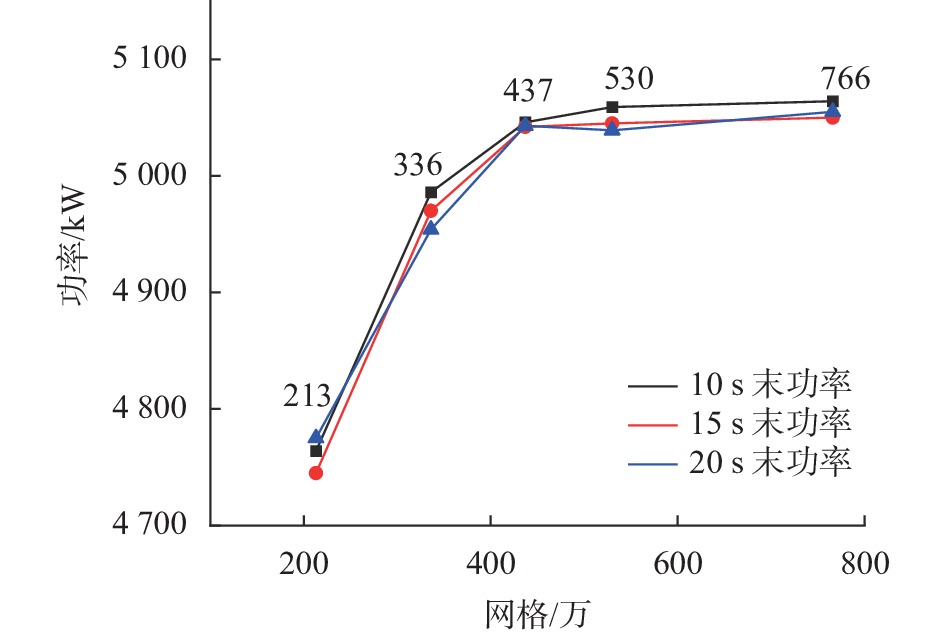
|
| 图 6 不同数量网格在不同时间点功率图 |
1.7 功率和水平推力验证
本文用功率和水平推力参数进行模型验证。以单台风力机创建流场域,布置流场,采用稳态计算,对模型导入Fluent求解不同风速下5 m/s,8 m/s,11.4 m/s(额定风速),20 m/s风轮对旋转轴的转矩,计算风力机模型的功率和水平推力,依据美国可再生实验给出的5 MW风力机功率和水平推力,验证模型的可靠性。当风速变化时,特别是超过额定风速后,调整叶片的角度,实现变桨,控制风力机功率,在本文中,对超过额定风速的功率验证工况做改变风力机变桨角度的处理,具体变桨过程如图7所示。
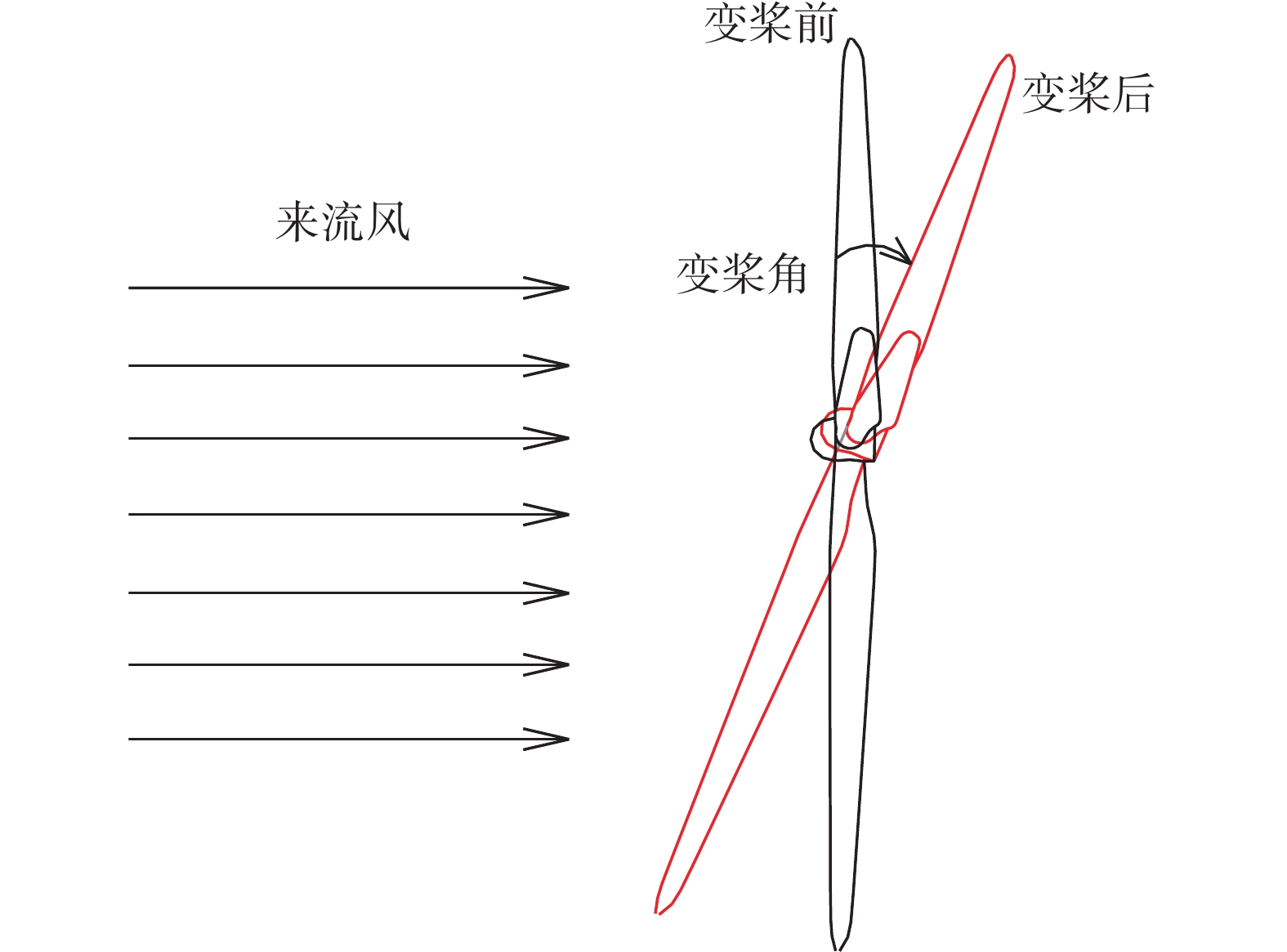
|
| 图 7 变桨示意图 |
依据文献[10],得出了风力机对旋转轴力矩跟功率之间的公式关系。如下式:
| P=2πMnΩ60 | (10) |
式中:
经Fluent模拟,整个过程对旋转轴的力矩趋于稳定,模拟结果收敛后,求得风轮对x轴的力矩。依据式(8)、式(9)相似准则,力矩为缩小模型后的风轮对x旋转轴的力矩,原型风力机力矩需依据比例因子
|
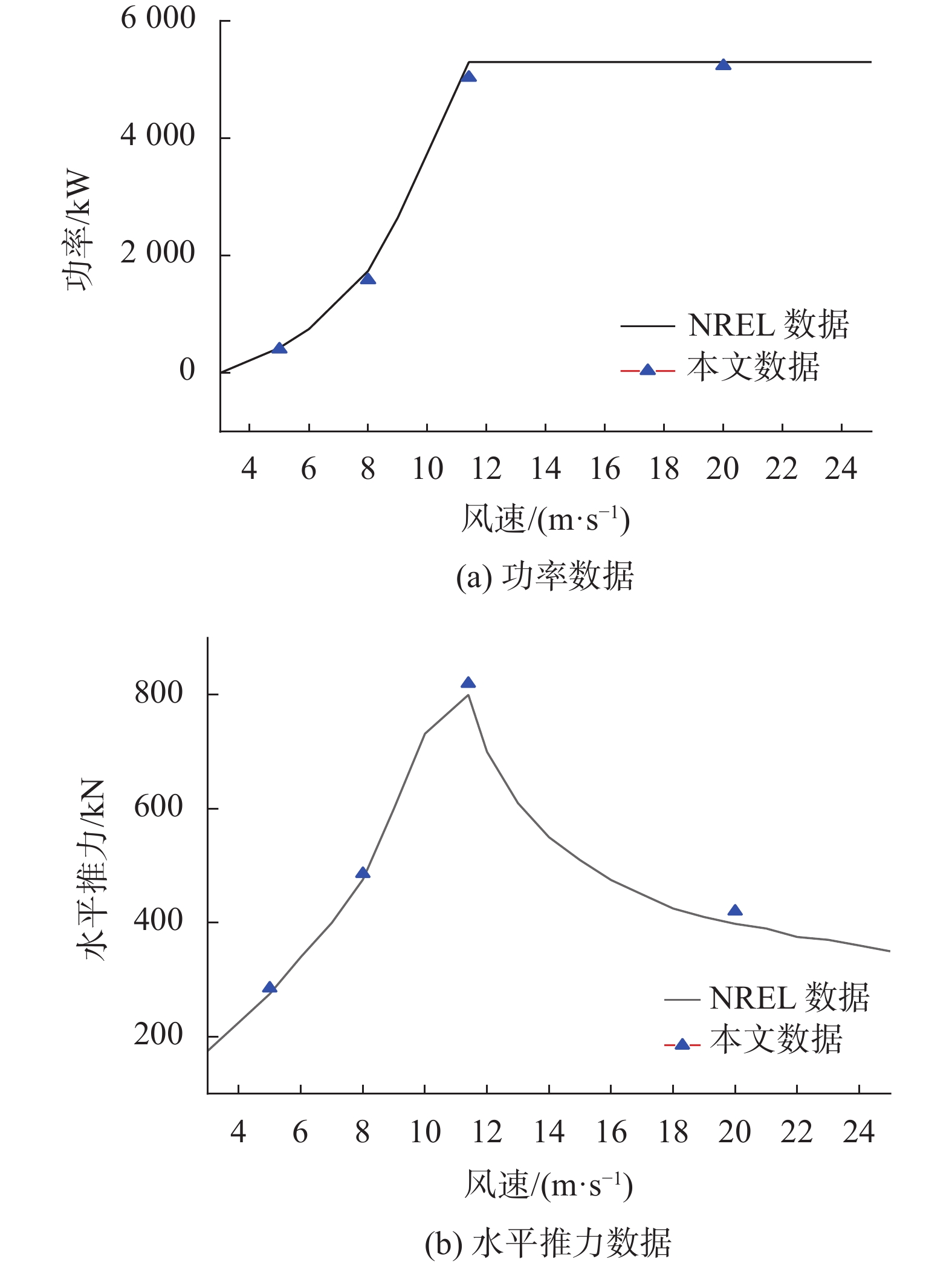
| 图 8 功率与水平推力验证 |
根据上图数据,结果表明,风力机功率数据与实验数据具有很小的误差,水平推力跟实验数据均偏大一些,五种具有代表性的风速工况下,均能满足风力机经过Fluent求解后的要求,五种风速下,整体误差都控制在10%内,产生误差的可能原因为风力机叶片表面翼型弯曲复杂,生成的非结构网格造成网格质量存在一定缺陷,未考虑风力机叶片截面的约束,都可能会造成误差,但误差控制在可接受的20%内,保证模型的有效性。
2 结果分析 2.1 工况设置为研究不同间距对大型风力机尾流效应的影响,设置如下工况:大功率风力机采用串列方式,分别置于5D、8D、11D三种间距下的工况,其中D为风力机直径,尾流速度衰减在尾流发展4D~6D,设置最短间距5D开始,每一个工况间隔3D[14] 。图9~图11分别表示5D、8D、11D下游风力机旋转区域的压力云图。图12~图14分别表示两台风力机在串列下前后距离为5D、8D、11D的速度云图,工况布置见表2。
|
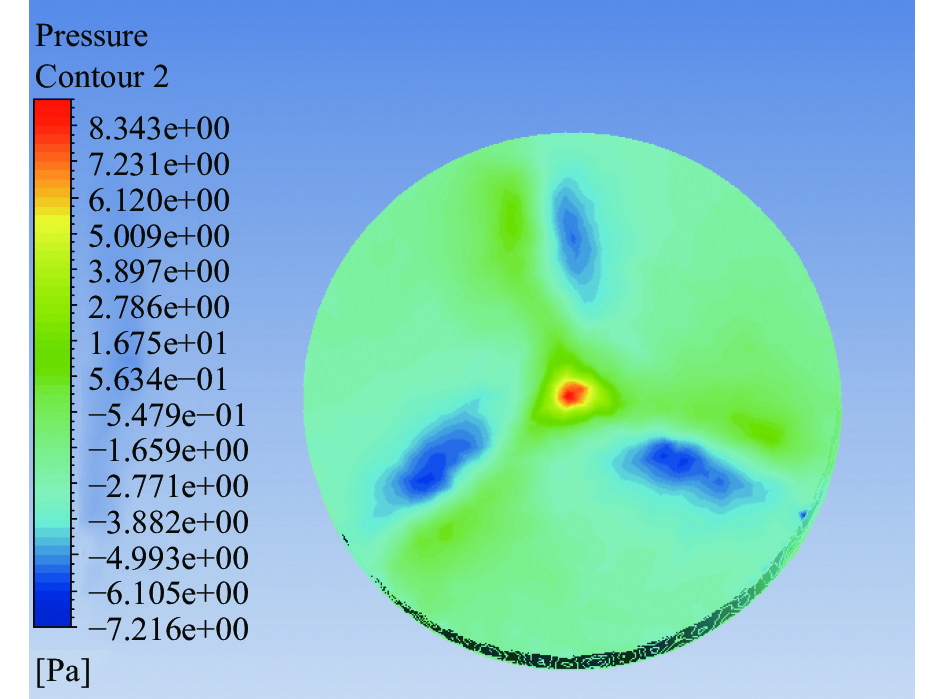
| 图 9 5D下游风力机旋转域压力云图 |

|
| 图 10 8D下游风力机旋转域压力云图 |
|
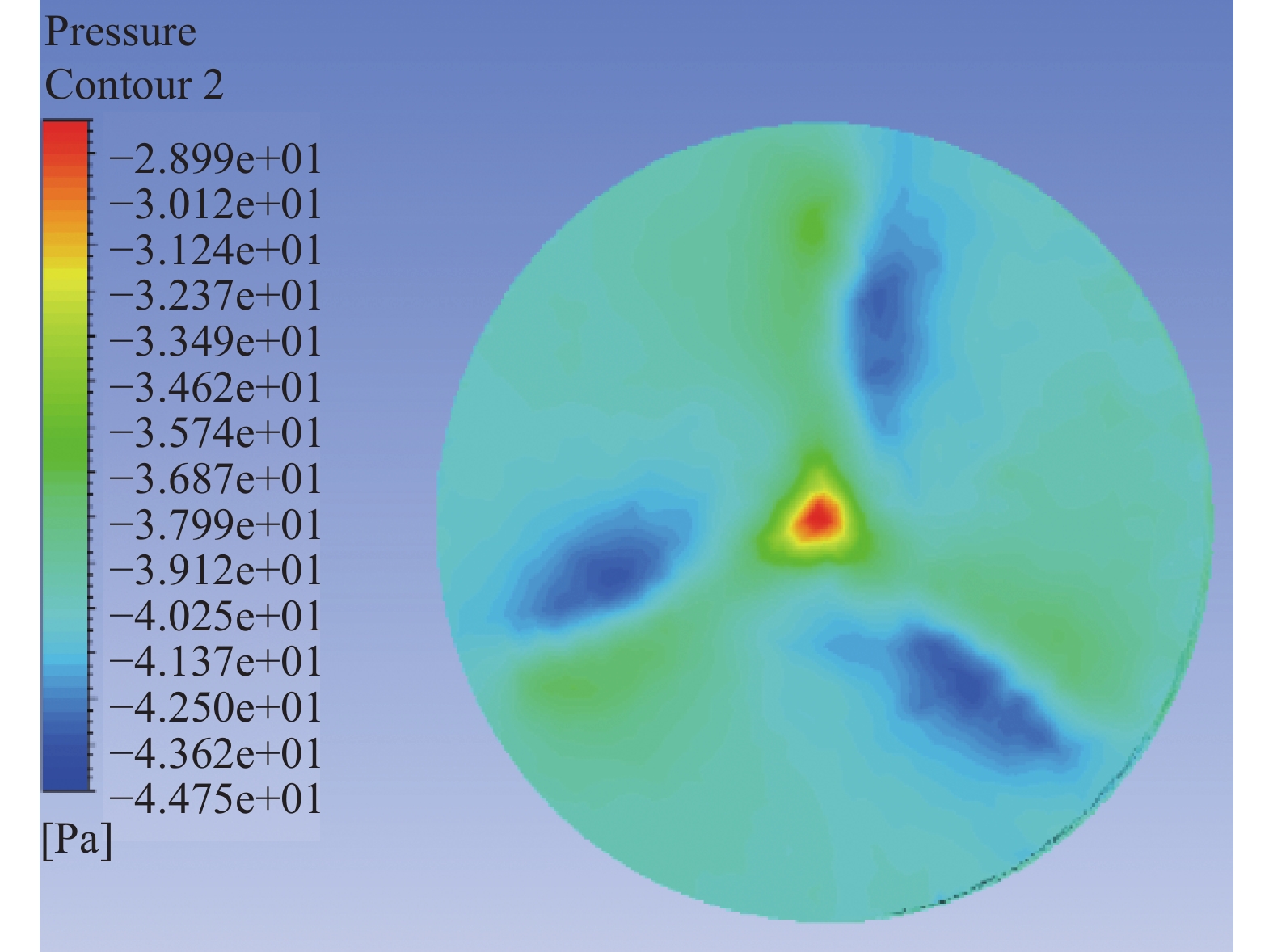
| 图 11 11D下游风力机旋转域压力云图 |

|
| 图 12 5Dxz面尾流速度云图 |
|
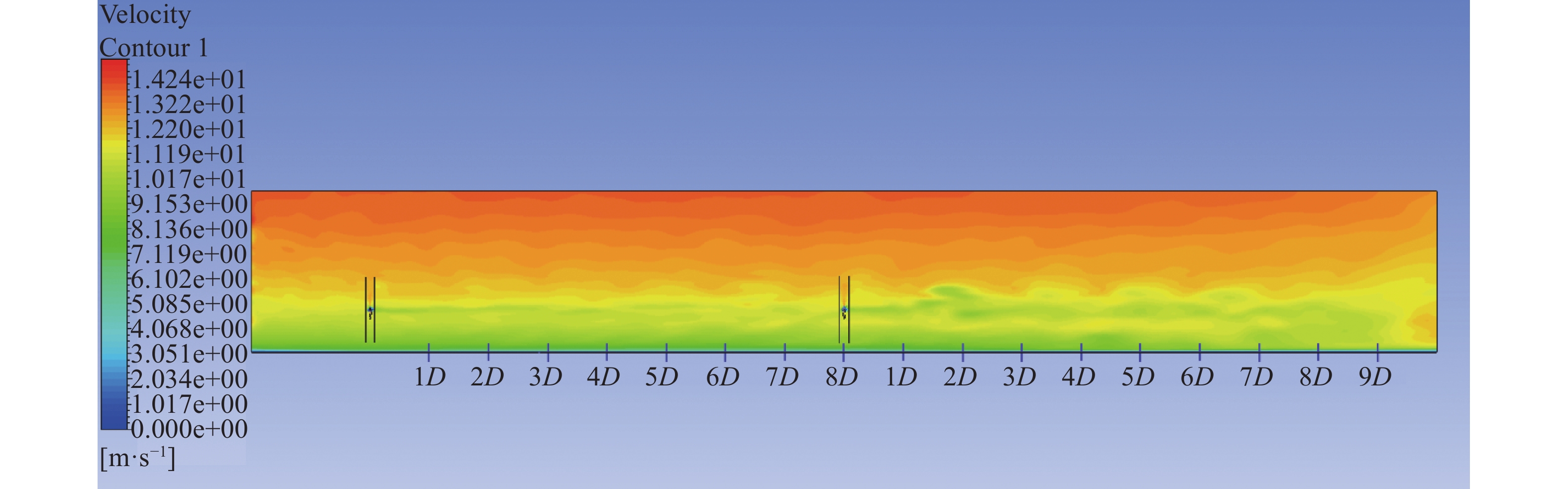
| 图 13 8Dxz面尾流速度云图 |
|
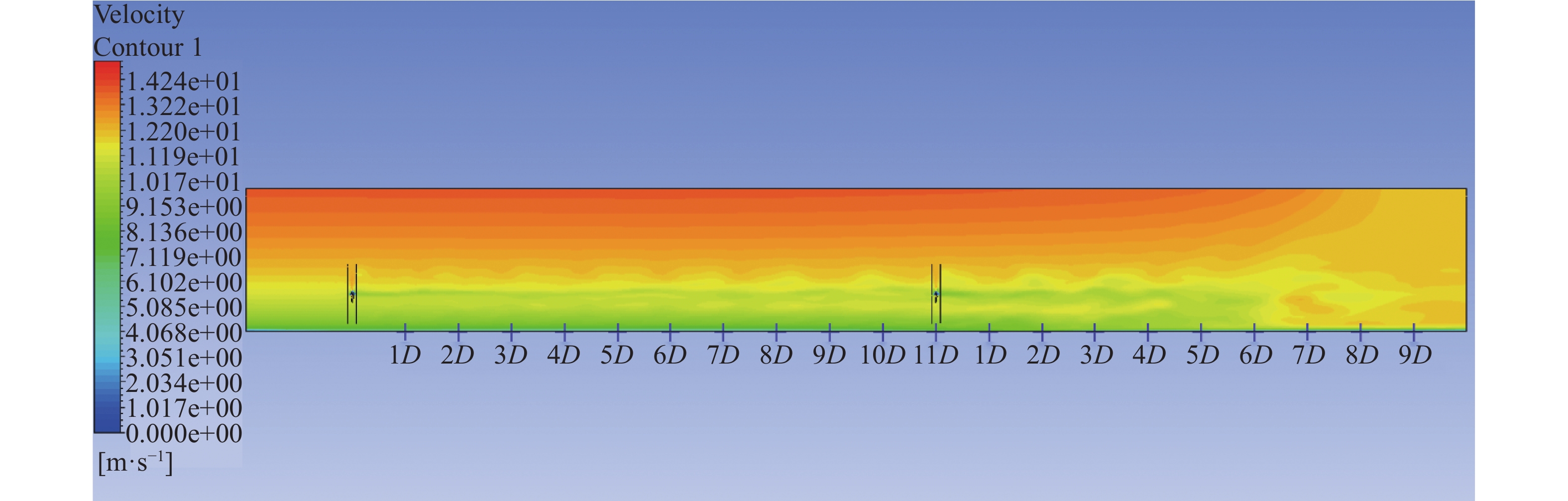
| 图 14 11Dxz面尾流速度云图 |
2.2 下游旋转域压力分析
风场流入剪切来流风后,形成不同高度的风速层。从图9~图11可知来流风在经过有旋转速度的风力机后,形成类似于叶片形状的压力轮廓,有着明显的压力分层,形成这种现象的原因为风力机对风气流有一定的阻碍和扰动作用,扰动作用会使风力机叶片两面形成压力差,这种压力差和粘性力作用会造成风力机表面形成阻力,由于这种阻力一旦脱离风力机叶片,会使得粘性力在风力机表面损失,形成流动损失,使得下游风力机的尾流区速度亏损且持续发生剪切作用,进一步造成速度损失;相比于11D的间距,5D和8D受到上游风力机的气流扰动和压力影响更大,说明间距越小,这种压力影响作用越大;在11D的工况下,下游风力机入流扰动相比5D和8D更加趋于平缓;此外,三种工况下,共同特点是风力机轮毂处的压力大于叶表面,由于压差阻力之和大于其他部分,造成压力较大,导致轮毂处的能量转换比较强烈。
2.3 侧面速度云图分析真实的风场中,存在差异性较大的速度梯度,进而形成湍流较强的剪切层;为了研究在剪切来流风情况下串列风力机不同间距对尾流特性的影响,因此截取两台风力机间距为5D、8D、11D三种工况下xz面,变量随着高度z变化的速度云图。由图12和图13对比可知:5D对比8D下,下游风力机入流处风速还在受到上游风速损失的影响,恢复不明显,来流速度的损失会影响下游风力机入流风速大小,同时下游风力机处于自身与上游风力机产生的湍流叠加区域,导致下游尾流形成膨胀流,虽然风力机间距大小不同,但是轮毂处的压强差很大,能量交换剧烈,导致中心处尾流损失较为明显;下游风力机6D之后由于不同梯度的速度的剪切层,尾流恢复区与未恢复区域的上层与下层区能量交换比较明显,会形成速度分离,与不同层速度梯度混合,最终速度趋于平缓,尾流恢复处(下游风力机速度损失恢复到来流环境的位置)发生在10D之后;从图13可得知:8D下游风力机的入流速度明显高于5D,下游风力机由于受到流动损失小于5D,导致了8D下游风力机尾流恢复处发生在9D左右,对比图12~图14得知:随着间距的增大,下游风力机受到的影响减小;综上所述:随着风力机上下游间距的增大,下游风力机受到上游风力机速度影响会越来越小,导致下游风力机在剪切层环境下,尾流恢复处发生的位置会越来越近,趋于正常的剪切层会越来越快。
3 结束语1)使用剪切风入流,风速会随着高度变化而变化,风经过风力机扰动,会在风力机叶片形成压力分层,且这种压力扰动随着上下游风力机间距增大会越来越小。
2)风力机间距不同,但是共同特点是轮毂处压力大,能量转换强烈,使得轮毂后速度损失比叶轮其他地方严重,这一处速度损失应进一步加强研究。
3)基于大涡模拟,在剪切来流风下两台风力机采用串列方式布置,随着间距增大,尾流恢复处越近,说明间距越大,下游风力机受到上游风力机尾流速度影响越来越小。因此在风电场布置中,可建议参考尾流恢复处的距离来合理布置风力机间的距离。
| [1] |
李万润, 栾雪涛, 王雪平, 等. 基于实测数据的西北地区风电场风场及尾流特性分析[J].
东南大学学报(自然科学版), 2018, 48(4): 699-705.
LI W R, LUAN X T, WANG X P, et al. Analysis of wind field and wake characteristics of wind farm in Northwest China based on measured data[J].
Journal of Southeast University(Natural Science Edition), 2018, 48(4): 699-705.
|
| [2] |
杨立国, 严亚林, 李宏海. 某滑雪场复杂山地地形风场的风洞试验与数值模拟研究[J].
建筑结构, 2020, 50(11): 135-140.
YANG L G, YAN Y L, LI H H. Wind tunnel test and numerical simulation of complex mountainous terrain wind field in a ski resort[J].
Building Structure, 2020, 50(11): 135-140.
|
| [3] |
孙芳锦, 贺伟盼, 邓富河, 等. 大型风力机变桨角度对尾流特性影响的研究[J]. 中国测试, 2022, 48(8): 9-16.
SUN F J, HE W P, DENG F H, et al. Research on the effect of pitch angle of large wind turbine on wake characteristics[J]. China Measurement & Test, 2022, 48(8): 9-16.
|
| [4] |
刘智益, 陈瑶, 高晓霞, 等. 多风力机尾流干扰模型特性研究与分析[J]. 中国测试, 2021, 47(5): 136-144.
LIU Z Y, CHEN Y, GAO X X, et al. Study and analysis of wake disturbance model characteristics of multi-wind turbine[J]. China Measurement & Test, 2021, 47(5): 136-144.
|
| [5] |
王兵, 张会强, 王希麟, 等. 不同亚格子模式在后台阶湍流流动大涡模拟中的应用[J].
工程热物理学报, 2003, 24(1): 157-160.
WANG B, ZHANG H Q, WANG X L, et al. Large eddy simulation of backward-facing step turbulent flow using different sgs models[J].
Journal of Engineering Thermophysics, 2003, 24(1): 157-160.
|
| [6] |
张亚光. 基于大涡模拟的单台大型风力机尾流特性研究[D]. 兰州: 兰州理工大学, 2019.
ZHANG Y G. Study of wake characteristics of single large scale wind turbine based on large-eddy simulation[D]. Lanzhou: Lanzhou University of Technology, 2019.
|
| [7] |
杨瑞, 王小丽, 许世海, 等. 水平轴风力机尾流场的特性分析[J].
兰州理工大学学报, 2016, 42(2): 57-61.
YANG R, WANG X L, XU S H, et al. Analysis of wake flow field characteristics of horizontal-axis wind turbine[J].
Journal of Lanzhou University of Technology, 2016, 42(2): 57-61.
|
| [8] |
钟宏民. 综合Lagrangian动力大涡模拟与致动线法的风力机尾流数值模拟研究[D]. 成都: 电子科技大学, 2015.
ZHONG H M. Lagrangian dynamic large-eddysimulation of wind turbine wakescombined with an actuator linemethod[D]. Chengdu: University of Electronic Science and Technology of China, 2015.
|
| [9] |
温文, 邓胜祥. 不同串列布置间距下2 MW风力机尾流的研究[J].
太阳能, 2019(1): 57-60.
|
| [10] |
陈荣盛, 张礼达, 任腊春. 基于相似理论的风力机力特性分析[J].
水力发电, 2008, 34(6): 92-94.
CHEN R S, ZHANG L D, REN L C. Characteristic analysis of wind turbine based on similarity theory[J].
Water Power, 2008, 34(6): 92-94.
|
| [11] |
SCRENSEN N N, BECHMANN A, RETHORE P E, et a1. Near wake Reynolds-averaged Navier-Stokes predictions of the wake behind the MEXICO rotor in axial and yawed flow conditions[J].
Wind Energy, 2014, 17(1): 75-86.
|
| [12] |
MO J O, CHOUDHRY A, ARJOMANDI M, et a1. Effects of wind speed changes on wake instability of a wind turbine in a virtual wind tunnel using large eddy simulation[J].
Journal of Wind Engineering and Industrial Aerodynamics, 2013, 117: 38-56.
|
| [13] |
OKA S, ISHIHARA T. Numerical study of aerodynamic characteristics of a square prism in a uniform flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 97(11-12): 548-559.
|
| [14] |
高晓霞, 王腾渊, 赵飞, 等. 基于激光雷达扫描数据的湍流强度影响下风力机尾流特性研究[J].
太阳能学报, 2019, 40(12): 3645-3650.
GAO X X, WANG T Y, ZHAO F, et al. Study on influence of turbulence intensity on wind turbine wake characteristics using lidars scanning data[J].
Acta Energiae Solaris Sinica, 2019, 40(12): 3645-3650.
|
 2024, Vol. 50
2024, Vol. 50