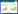文章信息
- 张明皓, 宋睿, 张鋆, 周晨媛, 王俊元, 李运甲
- ZHANG Minghao, SONG Rui, ZHANG Jun, ZHOU Chenyuan, WANG Junyuan, LI Yunjia
- 面向电力设备的T型梁电磁式振动能量采集器设计
- Design of electromagnetic vibratory energy harvester with T-type beam for power grid equipment
- 中国测试, 2024, 50(5): 114-121
- CHINA MEASUREMENT & TEST, 2024, 50(5): 114-121
- http://dx.doi.org/10.11857/j.issn.1674-5124.2021100097
-
文章历史
- 收稿日期: 2021-10-23
- 收到修改稿日期: 2022-03-06
2. 西安交通大学电气工程学院,陕西 西安 710049
2. Department of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China
导线、变压器等输变电设备支撑着电网安全稳定运行。随着超特高压电网的持续建设,电网输送容量不断上升,运维人员工作压力持续增大。提高各类输变电设备的运行可靠性,推动设备运维工作转型成为重中之重。
当前,电力物联网建设工作持续开展,多种类传感器迭代应用到电网场景中,支撑着输变电设备运维从定期检修向状态检修逐步过渡[1]。经过十多年的发展,在线监测技术也逐步向微型化、网络化、智能化演进,不断为设备状态评估及检修决策提供可靠数据来源。
在各类电力传感器中,供电单元的可靠性是制约其持续大规模应用的关键问题之一[2]。例如,对于输电线路的在线监测系统,并不存在可直接使用的直流电。同时,输电线路多处于环境复杂的野外,设备在严格密封的条件下,电池的更换也难以实现。同时,相关高校、企业等机构也持续在环境能量收集与转化中开展研究工作[3]。
在电力系统常见的振动场景如导线振动、电机振动以及变压器、电抗器的振动等。其中电机的额定工作频率为50 Hz,并且电机的谐波所对应的振动频率为基频(50 Hz)的整数倍。变压器的谐振频率主要为100 Hz,部分变压器的谐振频率为200 Hz或300 Hz。电抗器本体的谐振频率主要是以100 Hz的基频为主,同时包含少量倍频信号[4]。线缆的固有振动频率的基频主要是在105 ~150 Hz左右,并且其他各阶模态为其基频的整数倍[5]。对这些振动形式的微能量进行有效获取的同时,也可辨识出异常振动会对设备造成不利影响。因此,恰当利用电网设备上述振动特性,进行振动能量有效采集,并供给在线监测设备应用,进而用于监测设备振动状态[6],可有效保障电网设备安全稳定运行。
根据能量转化机理不同,振动能量收集技术可分为静电式、压电式、电磁式及磁致伸缩式等技术[7]。其中,针对静电式、压电式和电磁式三种形式的振动能量采集器的相关研究较为深入。相较其他二者,电磁式振动能量采集器不需要其他外接电源作为启动电压,制造材料也易于获得。虽然其输出电压需通过器件优化进一步提高,但是输出电流较大,输出功率较高,容易快速实现产品化应用。
1995年,英国谢菲尔德大学的Williams等人首次提出电磁式振动能量采集器模型[8]。2004年,美国密歇根大学Kulah等人提出了一种线圈磁铁同振型电磁式振动能量采集器[9]。该器件通过线圈与磁铁振动模态的差别将低频振动转化为高频形式,进而获取更多低频能量[10]。2014年,北京大学微电子实验室Han等人基于磁铁阵列设计了一种电磁式振动能量采集器[11]。其磁铁振动方向为面内振动,磁铁不再是手工粘贴在振动膜上,而是直接通过电镀CoNiMnP硬磁合金批量制造。折叠梁的制作降低了系统固有频率,磁铁阵列结构和面内振动方式加大了器件的输出性能。该器件在环境振动频率48 Hz时达到最大峰值输出电压0.98 mV。
经过二十几年的发展,电磁式振动能量采集器已经有成熟的理论模型,类型发展出了包括动铁式、动圈式传统线性电磁式振动能量采集器以及线圈磁铁同振式、旋转式、流磁体式、磁悬浮式、高磁导率悬臂梁式等多种非线性形式[12]。近几年,电磁式振动能量采集器的研究朝着器件的优化方向发展。然而,目前很多研究的采集器需要把磁铁手工粘贴在易损坏的硅梁上,操作难度大,导致产品良率较低,且成本很高,不适合商品化。除了针对能量采集器本体的研究,重庆大学[13]等单位也开展了振动能量收集电路的相关优化,驱动了无线传感器节点的周期性工作。
本文为监测电力设备振动特征对于电磁式振动能量采集器展开深入研究,其能量采集器主要是采用由聚酰亚胺材料所制造的T型梁结构的拾振梁,可以进一步降低采集器固有频率,有利于对振动能量的采集。并且该采集器的线圈选用平面线圈,从而实现器件的低成本并批量生产,但存在限制线圈匝数的弊端,因此,线圈匝数的提高与高密度生产工艺将是平面线圈的一大优化方向。
1 器件系统原理 1.1 模型建立电磁式振动能量采集器是以电磁感应为基本原理,包括拾振结构和换能结构的装置。拾振结构主要为弹簧梁和质量块,把环境中的振动转换为线圈和磁铁的相对运动。换能结构包括线圈和磁铁,根据电磁感应定律,把相对运动转换为线圈两端的电压,连接负载时继而产生输出功率。
本文采用弹簧-质量块-阻尼模型对线圈和磁铁的相对运动进行分析。支撑框架和外界环境振动保持一致,拾振系统受支撑框架的运动发生强迫振动。
m为质量块的质量,x0为质量块的绝对振动位移,c为系统阻尼,x1为外围环境和系统外框的绝对振动位移,x01为质量块与系统外框的相对振动位移。k为弹簧梁的弹性系数,与弹簧梁的结构和材料有关。
由电磁感应定律可知,在磁场中导体所产生电动势的大小可以写为:
| $ {e} = - \frac{{{\text{d}}\psi }}{{{\text{d}}t}} = - N\frac{{{\text{d}}\phi }}{{{\text{d}}t}} $ | (1) |
式中:e——导体两端产生的电动势;
ψ——导体所处回路的全磁通;
N——导体匝数;
ϕ——每匝导体的平均磁通。
电动势的方向与磁通量变化率方向相反。回路中磁通量的大小可以由有效磁感应强度(垂直导体回路平面的磁感应分量)在其面上的积分计算,即:
| $ \phi = \int\limits_S {B{\text{d}}S} $ | (2) |
式中:B——有效磁感应强度;
S——导体回路围成的面积。
由此,随着器件中平面线圈与磁铁在振动过程中位置的相对变化,将在线圈中产生磁通量变化。将线圈中磁感应强度的变化速率记为:
| $ \frac{{{\text{d}}B}}{{{\text{d}}t}} = \frac{{{\text{d}}B}}{{{\text{d}}x}} \cdot \frac{{{\text{d}}x}}{{{\text{d}}t}} $ | (3) |
式中,x为线圈与磁铁的相对位移,结合公式(2)和公式(3)可以得能量采集器产生的感应电压为:
| $ {e} = - N\int\limits_S {\frac{{{\text{d}}B}}{{{\text{d}}x}} \cdot \frac{{{\text{d}}x}}{{{\text{d}}t}}{\text{d}}S} $ | (4) |
从公式(4)可以看出,要增大能量采集器的输出电压,可以增加N,即线圈的匝数,增加S,即有效磁感应强度和线圈重叠面积,增加dB/dx,即增加有效磁感应强度在振动方向上的梯度,增加dx/dt即增加磁铁与线圈的相对运动速度。其中,N的优化可以通过线圈的匝数设计来实现,S的增加可以通过增加磁体和线圈在垂直振动方向上的面积实现,但这会增大能量采集器的体积,dx/dt的优化可以通过拾振结构的优化设计来实现。dB/dx的优化加可以通过换能结构的优化设计来实现。
1.2 梁材质的选择本文设计制作的采集器除了采用组合线圈结构来提高能量采集器的输出功率外,还拟使用聚酰亚胺材料制作弹簧梁。由分析可知,系统固有频率

|
| 图 1 不同材料悬臂梁固有频率计算仿真 |
仿真中使用材料的杨氏模量、泊松比、密度以及最小固有频率的仿真计算结果如表1所示。
| 材料 | 杨氏模量/GPa | 泊松比 | 密度/(kg·m–3) | 最小固有频率/Hz |
| 硅 | 190 | 0.23 | 2330 | 860.92 |
| 铜 | 130 | 0.34 | 8960 | 670.17 |
| 镍 | 210 | 0.31 | 8900 | 846.23 |
| 聚酰亚胺 | 3.9 | 0.42 | 1440 | 140.95 |
从图1和表1可以看出,在相同弹簧梁结构的条件下,聚酰亚胺材料的使用可以大大降低系统的固有频率。金属铜、镍相比硅材料来说也都有不同程度降低固有频率的效果。且聚酰亚胺作为一种柔性印刷电路板的材料,具有制作工艺成熟、价格低廉的优点。总的来说,采用聚酰亚胺材料制作系统的弹簧梁可以达到降低系统固有频率,降低成本,批量制造的效果。
2 器件结构设计及制备电磁式T型梁振动能量采集器的结构分解图如图2所示。器件主要由聚酰亚胺T型梁、平面线圈及质量块和磁铁组成。

|
| 图 2 T型梁能量采集器在不同振动模态示意图 |
对于平面线圈而言,线圈密度越大,输出电压越高。但考虑到以PCB工艺加工线圈的分辨率限制,同时需要降低线圈内阻以提高振动能量采集器供电效率,最终选定线圈匝数为20匝,线圈宽度为 0.25 mm,并设置线圈间距为线圈宽度的2倍以降低线圈由于过密而发生短路的可能性。
进而对能量采集器的拾振部分进行仿真,得出利用刚柔结合工艺所制造的T型梁能量采集器不同阶次的振动模态及相应的谐振频率。在模态一中,频率为140.95 Hz时,器件拾振系统中心质量块将垂直于安装表面振动,此时横梁将受力产生纯弯曲形变。在模态二和三中外界振动频率达到 231.36 Hz和231.84 Hz时,该拾振部件将以通过线圈中心的水平横梁为轴出现垂直方向的扭转振动。扭转模态的引入不仅增加了梁的柔性,提高了振动幅度,更进一步降低了拾振系统的固有频率,更好满足电力设备振动频带要求。仿真结果如图3所示。

|
| 图 3 T型梁不同参数与各振动模态谐振频率的关系曲线 |
由于T型梁长度与宽度都是能量采集器拾振部分中振动响应的关键参数。因而本文在仿真过程中,分别通过调整T型梁的长度与宽度并依次进行仿真,可分别得到能量采集器的各阶次谐振频率与T型梁的长度和宽度的关系图,结果如图3所示。
由图3所得,能量采集器的各阶次谐振频率会跟随T型梁梁长的长度增加而降低。并且在T型梁的长度不断增加的情况下,相邻模态下的谐振频率之间的差值也是逐渐减小的,可以得出在高频情况下,T型梁能量采集器的工作带宽会随着T型梁长度增加而扩宽,但T型梁梁长也会受到能量采集器整体尺寸大小的制约。因此,在T型梁的设计过程中,为了尽可能地增加T型梁的长度,将T型梁的设计位置处于器件平面的对角线处。最终其T型梁梁长设计参数为2.60 mm。
同时由图所得,能量采集器的谐振频率会随着T型梁的宽度增加而增加,并且高频段振动环境中,随着横梁宽度增加,其相邻模态谐振频率逐渐接近。因此可通过合理设计横梁宽度实现高频振动下器件工作带宽的扩大。但是由于本文所研究的能量采集器面向于电力系统振动取能的应用,其谐振频率应位于低频区域,因而对于其T型梁的宽度在保证可靠性的前提下尽量减小。综合上述情况,本文研究的能量采集器的T型梁宽设计为1.00 mm。
对于磁铁而言,目前常用的磁体材料有铝镍钴、钐钴、铁氧体、钕铁硼等[14]。其中钕铁硼材料在剩磁、矫顽力、最大磁能积上均具有较大优势,但其最高工作温度较低。针对电力系统振动取能的场景而言,对于温度要求不高。综合考虑后磁体材料选用钕铁硼材料,并因此综合加工成本、器件输出及尺寸大小等因素,将磁铁直径设计与线圈相同,磁铁厚度选定为5 mm。
最终,T型梁电磁式振动能量采集器结构分解图如图4所示。
|
| 图 4 T型梁电磁式振动能量采集器结构分解 |
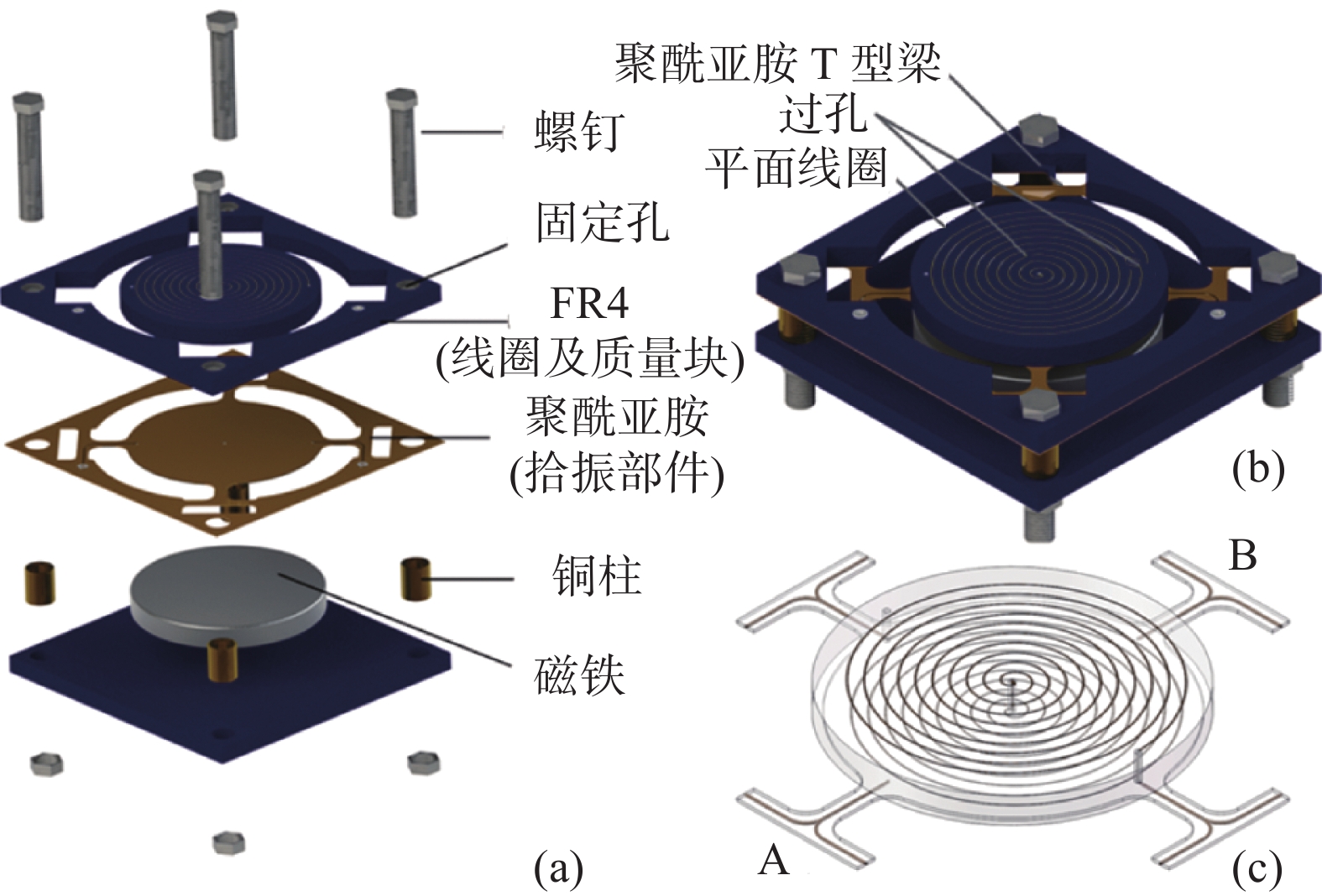
螺母穿过平面线圈外围的四个孔把平面线圈、聚酰亚胺T型梁以及粘附磁铁的FR4板固定为一个整体。聚酰亚胺T型梁通过四个横梁连接中心线圈,其中两个横梁内布有铜线内接线圈两个端点,外连焊盘以方便能量采集器和负载连接,另外两个横梁内也布有铜线以保证其机械对称性。在外界振动的激励下,磁铁与线圈间将产生相对位移,通过线圈产生振动的方式,在线圈上产生感应电压。器件组装图如图5所示,参数如表2所示。针对每个均匀分布的T型梁,其参数注解如图6所示。

|
| 图 5 电磁式T型梁振动能量采集器组装图 |
| 参数 | 设计参数 | 实际参数 |
| 器件尺寸(L×W×H) / (mm×mm×mm) | 25.4×25.4×1.65 | 25.55×25.40×1.72 |
| 横梁长度l1 /mm | 2.60 | 2.57 |
| 横梁长度l2 /mm | 5.6 | 5.51 |
| 竖梁宽w1/mm | 1.00 | 1.00 |
| 横梁宽w2/mm | 1.00 | 1.00 |
| 横梁厚度/mm | 0.10 | 0.10 |
| 拾振线圈PCB直径/mm | 16.00 | 16.50 |
| 拾振线圈PCB厚度/mm | 1.60 | 1.60 |
| 拾振线圈PCB质量 /g | 0.65 | 0.70 |
| 线圈匝数 | 20 | 20 |
| 磁铁直径/mm | 16.00 | 15.96 |
| 磁铁厚度/mm | 5.00 | 4.75 |
| 磁铁线圈间隙/mm | 2.00 | – |
|
| 图 6 T型横梁参数注解图 |
3 器件测试 3.1 测试环境搭建
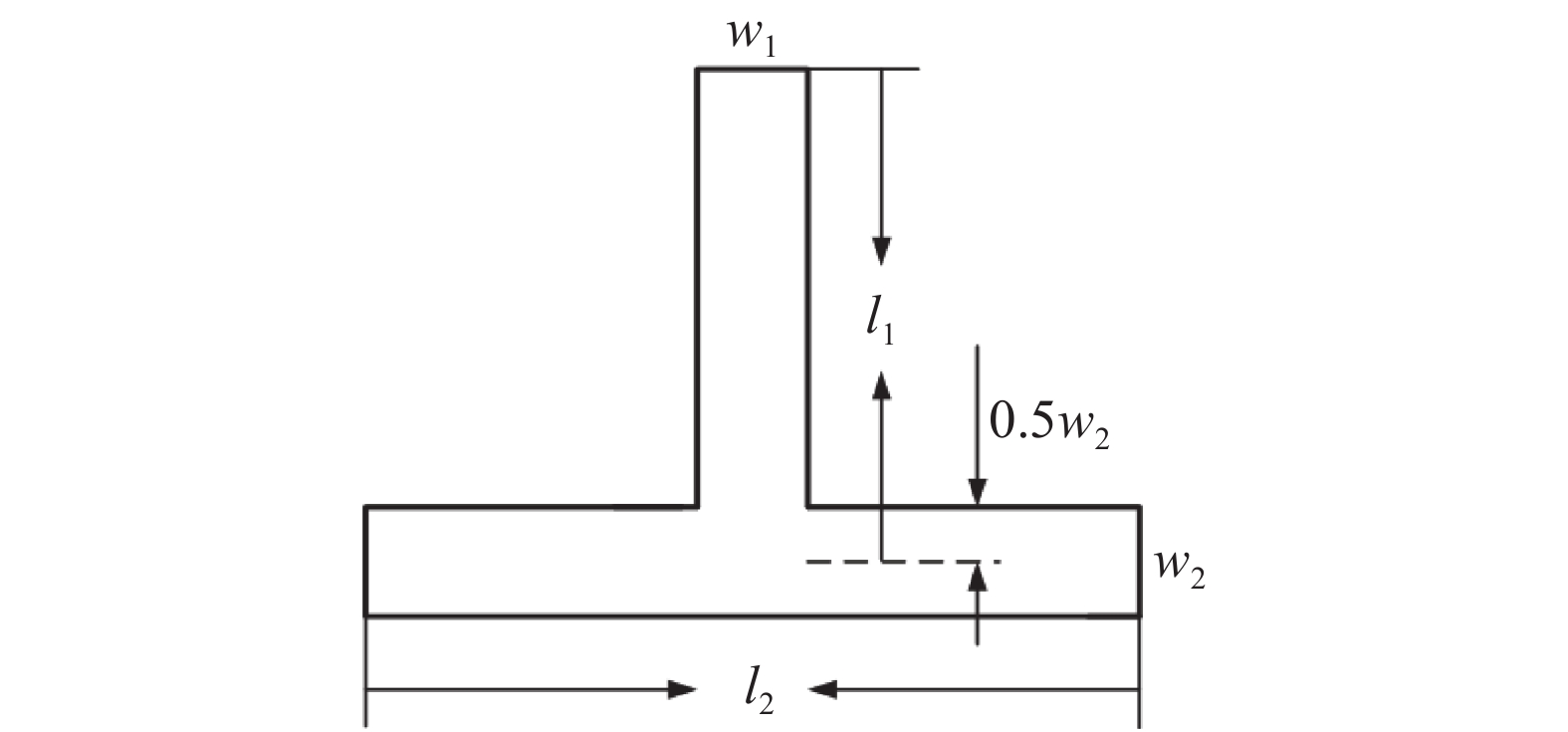
电磁式T型梁振动能量采集器的测试系统如图7所示。由图中拓扑关系可知,首先通过信号发生器产生一个正弦激励信号输入到功率放大器中,经信号放大后接入到激振台,作为激振台的标准激励信号。同时,选择一只标准加速度计,与所设计的振动能量采集器一并固定于激振台上,作为振动信号的输出依据。系统启动后,标准加速度计及振动能量采集器的输出全部由数据采集卡进行获取,并接入到上位机便于后续分析计算。测试系统选用的实验设备及型号如表3所示。
|
| 图 7 测试系统 |
| 设备型号 | 重要参数 |
| JZK-2激振台 | 最大振幅:±3 mm; 最大加速度:20 g; 频率范围:DC~15 kHz |
| AFG-2112信号发生器 | 分辨率:0.1 Hz; 正弦波方波频率范围: 0.1~12 MHz |
| SINOCERA YE 5871A功率放大器 | 频率响应:0~50 kHz |
| CT1050LC加速度计 | 电压灵敏度:0.5 V/g; 频率范围:0.2~ 2500 Hz; 量程:10 g |
| NI USB-6211数据采集卡 | 最小灵敏度:91.6 μV |
该测试系统可以提供最大振幅峰峰值为6 mm,在正弦波频率范围内的激励条件下,加速度传感器有效测量范围0.2~2500 Hz,高于这一范围振动环境可以提供,但是测量数据不能保证准确性;同理测量加速度量程为10 g,高于这一值激振台可以工作,但加速度传感器测量不能保证准确性。鉴于绝大部分电力振动场景为低频振动,因此该测试环境可以满足器件测试需求。
同时,上位机采用LabVIEW软件对测得的电压数据进行进一步分析。具体地,采集利用DAQ助手将原始数据读入;并采用内置的巴特沃斯四阶滤波器进行滤波;计算利用内置的均方根、峰峰值函数对采集的数据进行计算处理;显示采用内置示波器窗口,对采集处理的数据进行实时波形显示;储存利用内置的写txt模块将采集处理的数据储存写入txt文档中,便于后续进行数据观察。
3.2 磁铁和线圈气隙对输出电压的影响本文研究的能量采集器基于法拉第电磁感应定律设计,因此能量采集器中线圈的输出与永磁体外表面的磁场变化强度相关。同时器件的能量输出对应于输出电压,进而表征本征定律下的感应电动势,因此能够正确反映其将振动能转化为电能的能力。
通常而言,线圈距离永磁体越远,其所处位置的磁场强度越小。但如果二者距离过近或线圈靠近永磁体边缘,磁场容易产生畸变,因而对于线圈与磁铁的距离并不是越近越好。因此,本文通过实验的方式,在保证能量采集器的输出最高的情况下确定磁铁与线圈的最佳距离。设定激振台输出加速度固定为±1g,对所设计的振动微能量采集器通过组装不同高度的铜柱来改变磁铁和线圈的距离。通过采集输出电压,磁铁和线圈间距离d与输出电压峰峰值的变化曲线如图8所示。由图中可以看出,随着磁铁与线圈距离d的增大,该T型梁振动能量采集器输出电压呈现先增后减的趋势。当磁铁与线圈距离增至0.93 mm时,线圈输出最大感应电压峰峰值9.40 mV,其后随着d的增大,采集器输出电压逐渐降低。因此,后续应用将把该距离固定在0.93 mm处后进行其他参数的测定及优化。

|
| 图 8 磁铁和线圈距离d与输出电压峰峰值的关系图 |
3.3 激励频率对输出电压的影响
对该T型梁振动能量采集器进行电阻测量,其测量电阻值为2.13 Ω。在负载值为2.13 Ω附近进行电阻匹配实验,当匹配电阻为2.31 Ω时,系统输出功率达最大。
保持激振台的振动加速度为±1 g,改变不同激振频率,观察器件的输出电压。图9是不同激励频率下,器件开路时输出电压峰峰值和外接匹配电阻2.31 Ω时的负载电压峰峰值及功率之间的关系。

|
| 图 9 器件输出电压及功率与激励频率的关系图 |
图9中器件的输出电压峰峰值及功率均能真实反映出能量采集器的输出。由于能量采集器的输出波形近似为正弦波形,因而输出功率与电压峰峰值之间存在正相关性,也可从图中看出器件的输出电压峰峰值与功率的变化趋势大致相同。具体而言,峰峰值输出电压随激励频率的变化为先增大到最大值后减小。当激振台的工作频率距离所设计器件的谐振频率较远时,器件几乎没有输出电压,且随着激振频率的增加,电压的增加并不明显;当激励频率与器件的谐振频率逐步接近至重合时,其输出电压显著提升。当激励频率跨过器件固有频率后,峰峰值输出电压便减小很多,由此可知该能量采集器的带宽较小。在激振频率为140 Hz时,器件的输出开路电压9.40 mV,匹配2.31 Ω电阻后,其输出端电压为4.67 mV,计算可得功率为4.71 μW。
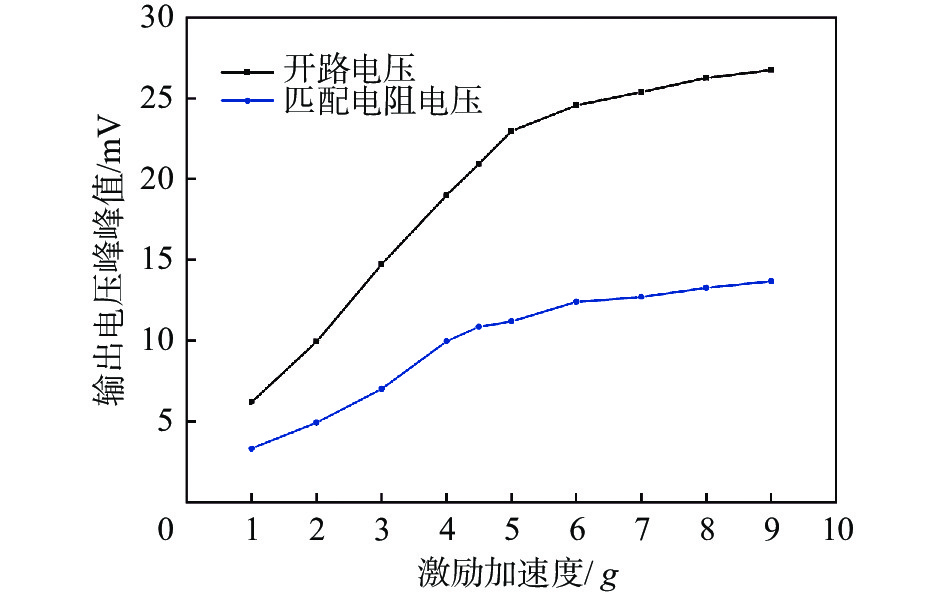
3.4 振动加速度对输出电压的影响进一步地,考察不同加速度下输出电压的变化。将频率控制在采集器的谐振频率140 Hz,通过调整激振台至不同加速度1~9 g,观测采集器输出电压在不同振动加速度下的变化情况。图10是不同加速度下的器件输出电压的时域响应曲线。随着激振台加速度增加,T型梁振动能量采集器输出电压峰峰值不断增加。图11是不同加速度下器件的开环输出电压和外接匹配电阻时的负载电压的图像。从激振台加速度从1~5 g时,输出开路电压成线性增加,当激振台加速度超过5 g,开路电压增加速率不断减小,分析是由于通过线圈的磁通量变化逐渐降低。当激振台提供加速度为(1± 0.5) g时,系统输出电压峰峰值为6.09 mV,当系统提供加速度到达(9±0.5) g时,系统输出电压峰峰值26.75 mV。

|
| 图 10 不同加速度下输出电压的时域响应曲线 |
|
| 图 11 器件输出电压与激励加速度的关系图 |
4 结束语
本文针对输变电设备振动能量获取需求,面对低频振动特征,设计了一种电磁式振动能量采集器。基于刚柔结合理念设计了T型梁结构,拾振部分采用聚酰亚胺进行梁的制备,利用FR4制造拾振平面线圈,可在低环境振动下实现较高的振幅和能量采集效率。通过系列测试,验证了器件设计的有效性,T型梁振动能量采集器件的谐振频率为140Hz,其谐振频率处于低频区域,位于电力系统中变压器,线缆与电抗器的振动频率的频率区间内,从而可以看出其器件可用于之后为电力系统实现振动取能的可能性。并且该器件在±1 g加速度下,固有频率为140 Hz,可输出电压9.40 mV,外接匹配电阻2.31 Ω后,输出功率为4.71 μW。未来会对于器件设计进行优化处理,以进一步将能量采集器的谐振频率与电力系统中常见振动的振动频率精确对应。同时面对于本文所研究的能量采集器的工艺设计上,也将保留低成本且可批量生产的特点,进一步增加线圈匝数并且实现高密度生产工艺,从而提高能量采集器的输出。后续结合恰当的能量存储设计,该器件的应用可为电力传感器的可靠供电提供有效补充,为电力传感器的广泛部署提供有利基础。
| [1] |
张记飞. 智能变电站一次设备在线监测系统研究和设计[D]. 济南: 山东大学, 2017.
|
| [2] |
朱永灿, 黄新波, 张冠军, 等. 输电线路在线监测设备供电电源应用分析[J].
高压电器, 2018, 54(7): 231-236.
ZHU Y C, HUANG X B, ZHANG G J, et al. Application research of the power supply for transmission line on-line monitoring devices[J].
High Voltage Apparatus, 2018, 54(7): 231-236.
DOI:10.13296/j.1001-1609.hva.2018.07.032 |
| [3] |
彭喜英, 崔丹丹, 赵强松. 基于能量收集的高压电力线监测设备供电电源[J].
机械工程与自动化, 2017(2): 192-194.
PENG X Y, CUI D D, ZHAO Q S. Energy collection based power supply for monitoring equipment on transmission line[J].
Mechanical Engineering and Automation, 2017(2): 192-194.
DOI:10.3969/j.issn.1672-6413.2017.02.081 |
| [4] |
葛德馨. 特高压并联电抗器铁心振动研究及仿真分析[D]. 济南: 山东大学, 2017.
|
| [5] |
朱瑞环. 振动应力下线缆电磁兼容特性的不确定性分析[D]. 哈尔滨: 哈尔滨工业大学, 2020.
|
| [6] |
邸永峰, 汤宝平, 蔡巍巍. 面向机械振动监测的无线传感器网络节点的设计[J].
中国测试, 2012, 38(3): 105-108.
QIU Y F, TAGN B P, CAI W W. Design of wireless sensor network node for mechanical vibration monitoring[J].
Chian Measurement and Test, 2012, 38(3): 105-108.
|
| [7] |
穆锦标. 面向自供电监测系统的复合振动能量采集器设计与试验研究[D]. 太原: 中北大学, 2021.
|
| [8] |
WILLIAMS C B, YATES R B. Analysis of a micro-electric generator for microsystems[C]// Proceedings of the International Solid-state Sensors and Actuators Conference - Transducers '95, 1995.
|
| [9] |
KULAH H, NAJAFI K. An electromagnetic micro power generator[J]. 17th IEEE International Conference on Micro Electro Mechanical Systems, 2004, : 237-240.
|
| [10] |
KULAH H, NAJAFI K. Energy scavenging from low-frequency vibrations by using frequency up-conversion for wireless sensor applications[J].
IEEE Sensors Journal, 2008, 8(3): 261-268.
DOI:10.1109/JSEN.2008.917125 |
| [11] |
HAN M, LI Z, SUN X, et al. Analysis of an in-plane electromagnetic energy harvester with integrated magnet array[J].
Sensors and Actuators, A:Physical, 2014, 219: 38-46.
DOI:10.1016/j.sna.2014.08.008 |
| [12] |
孙诗. 电磁式振动能量采集器非线性拓频方法研究[D]. 上海: 上海交通大学, 2018.
|
| [13] |
李俊, 汤宝平, 舒云龙, 等. 自供电无线振动传感器网络的双模组振动能量收集与管理方法[J].
中国测试, 2019, 45(09): 76-83.
LI J, TANG B P, SHU Y L, et al. Method of dual modules energy harvesting and management for self-powered wireless vibration sensor network[J].
China Measurement & Test, 2019, 45(09): 76-83.
DOI:10.11857/j.issn.1674-5124.2019030011 |
| [14] |
邵玮. 电磁式振动能量采集结构的优化[D]. 南京: 南京航空航天大学, 2012.
|
 2024, Vol. 50
2024, Vol. 50