文章信息
- 陈辉, 刘建湖
- CHEN Hui, LIU Jianhu
- 舰船水平向冲击环境测量仪研制
- Instrument development for measuring horizontal shock environment of ships
- 中国测试, 2024, 50(5): 100-105
- CHINA MEASUREMENT & TEST, 2024, 50(5): 100-105
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022030147
-
文章历史
- 收稿日期: 2022-03-23
- 收到修改稿日期: 2022-06-02
在舰船实船及模型水下爆炸试验研究中,舰船设备的冲击环境测量是整个试验任务的一项重要内容,通常有两种方法测量冲击环境 [1]:1) 用冲击加速度测试系统测量得到的时程信号处理为冲击环境数据,这在计算机上已经有成熟的处理方法和处理程序[2-7];2) 用簧片仪、中/低频振子等冲击环境测量仪测量得到冲击环境数据。
加速度测试系统能够准确地获取数十赫兹以上的中高频段冲击环境数据,但由于强冲击造成的零漂,导致20 Hz以下的低频段容易偏离实际情况,需要冲击环境测量仪得到的数据对其测量结果进行验证和补充。将加速度测试系统和冲击环境测量仪二者配合使用,也可以提升试验数据的准确度和可信度[8]。随着近年来簧片仪电测技术等的建立[9],冲击环境测量仪的自动化程度和测试准确度均得到了极大的提升。
簧片仪、中/低频振子都可以看作是一组自振频率不同的单自由度振子组成的装置,各个振子相对于基础输入载荷的响应和对应频率下的冲击环境成正比关系,通过测量振子的响应即可得到基础的冲击环境数据,这样的设计与冲击环境频域图谱——冲击谱的概念是相对应的[10]。通过大量实船及模型水下爆炸试验的检验,冲击环境测量仪可以得到准确的垂向冲击谱数据,通过与加速度测量冲击环境的相互验证,确保了2~20 Hz频段冲击环境数据的可靠性。
然而,目前要获取可靠的水平向冲击环境数据仍是一个难题,现有的做法是使用悬吊的簧片进行水平向冲击环境的测量[11],但无法消除垂向载荷(重力、冲击载荷等)与水平向载荷的耦合作用,与加速度测试系统相比测量结果往往偏低。为此,本文从合理适配测量装置垂向与水平向刚度的角度出发,开展水平向冲击环境专用测量仪的设计工作,以实现水下爆炸冲击载荷在测量装置上的解耦,从而保证水平向冲击环境参数测量的可靠性。
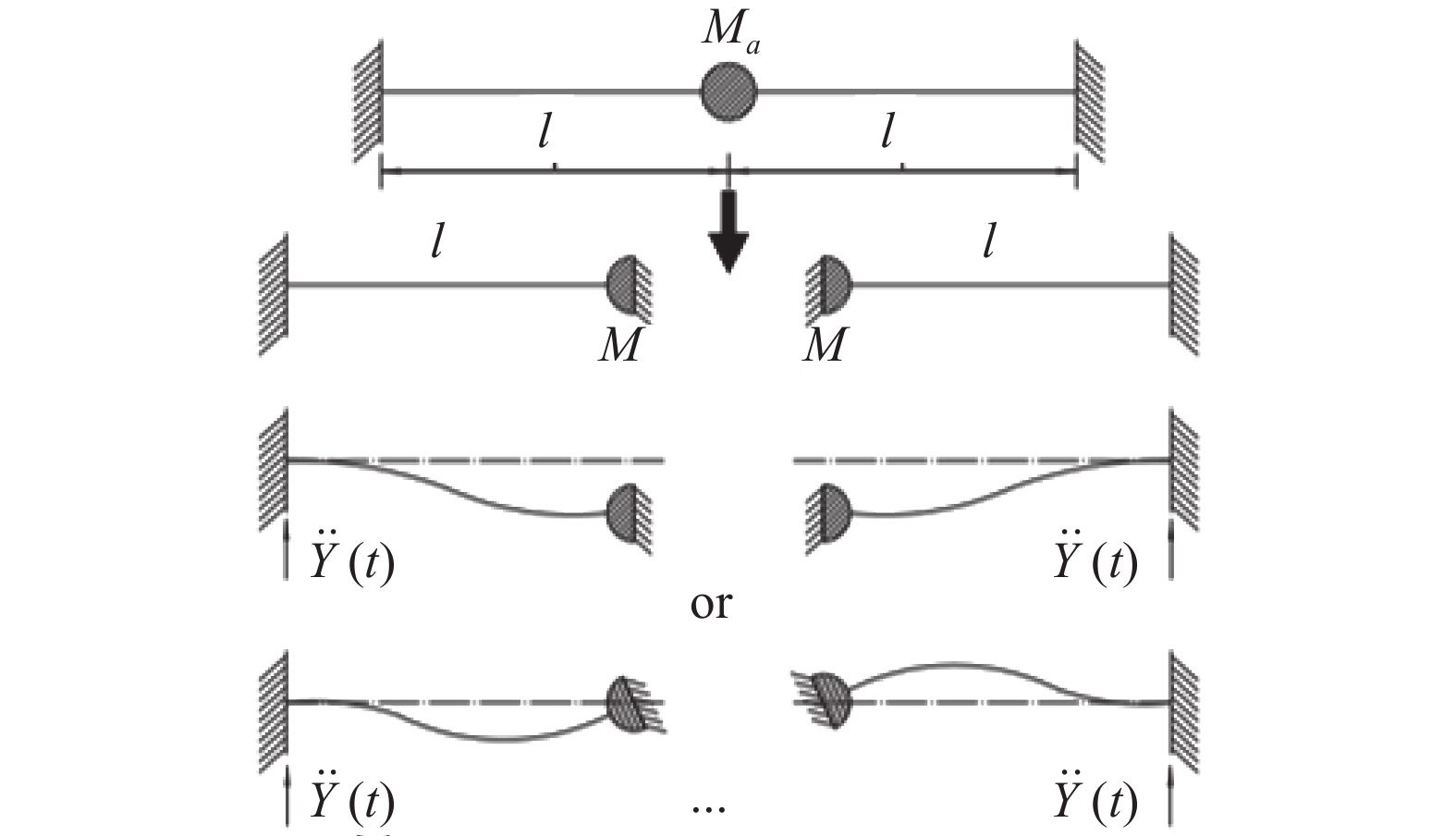
1 水平向冲击环境测量仪设计原理 1.1 两端固支梁式测量仪的设计将装置设计成截面为矩形、中间有集中质量、两端固支的簧片,调节簧片截面尺寸可以很容易地使簧片垂向弯曲刚度远大于水平向,从而实现垂向和水平向冲击响应的解耦。将两端固支簧片等效为一个基础受到激励载荷作用的单自由度弹簧-质量系统,如图1所示。图中同时给出了系统的第一、二阶振型。
|
| 图 1 水平向冲击环境测量仪设计原理图 |
冲击载荷作用下,将簧片用
| $ {M}_{ei}{\ddot{\xi }}_{i}\left(t\right)+{C}_{ei}{\dot{\xi }}_{i}\left(t\right)+{K}_{ei}{\xi }_{i}\left(t\right)=-{\lambda }_{i}\ddot{Y}\left(t\right) $ | (1) |
式中:
令:
| $ {2n}_{i}=\frac{{C}_{i}}{{M}_{ei}} \text{,} {p}_{i}^{2}=\frac{{K}_{i}}{{M}_{ei}} \text{,} {\alpha }_{i}=\frac{{n}_{i}}{{p}_{i}} $ |
系统初始状态为静止时,通过杜哈曼积分得到公式(1)的振型响应表达式:
| $\begin{split} {\xi }_{i}\left(t\right)=&\left[\frac{{\lambda }_{i}}{{M}_{ei}}\right]\left\{-\frac{1}{{p}_{i}\sqrt{1-{\alpha }_{i}^{2}}}\cdot {\int }_{0}^{t}{\rm e}^{-{\alpha }_{i}{p}_{i}\left(t-\tau \right)}\cdot \mathrm{sin}{p}_{i}\cdot\right.\\ &\left.\sqrt{1-{\alpha }_{i}^{2}}\left(t-\tau \right)\ddot{Y}\left(\tau \right){\rm d}\tau \right\} \end{split}$ | (2) |
其中方程右端的第二项为单自由度系统的冲击位移谱响应。那么,簧片任意位置
| $ {y}_{i{\rm{max}}}\left(x,t\right)={X}_{i}\left(x\right)\cdot {\xi }_{i{\rm{max}}}\left(t\right) $ | (3) |
式(3)表明簧片的各阶挠度响应与该阶频率下的冲击位移谱成正比关系。因此,可以通过测量簧片的冲击挠度响应来推算出簧片安装基础部位冲击环境的量值。
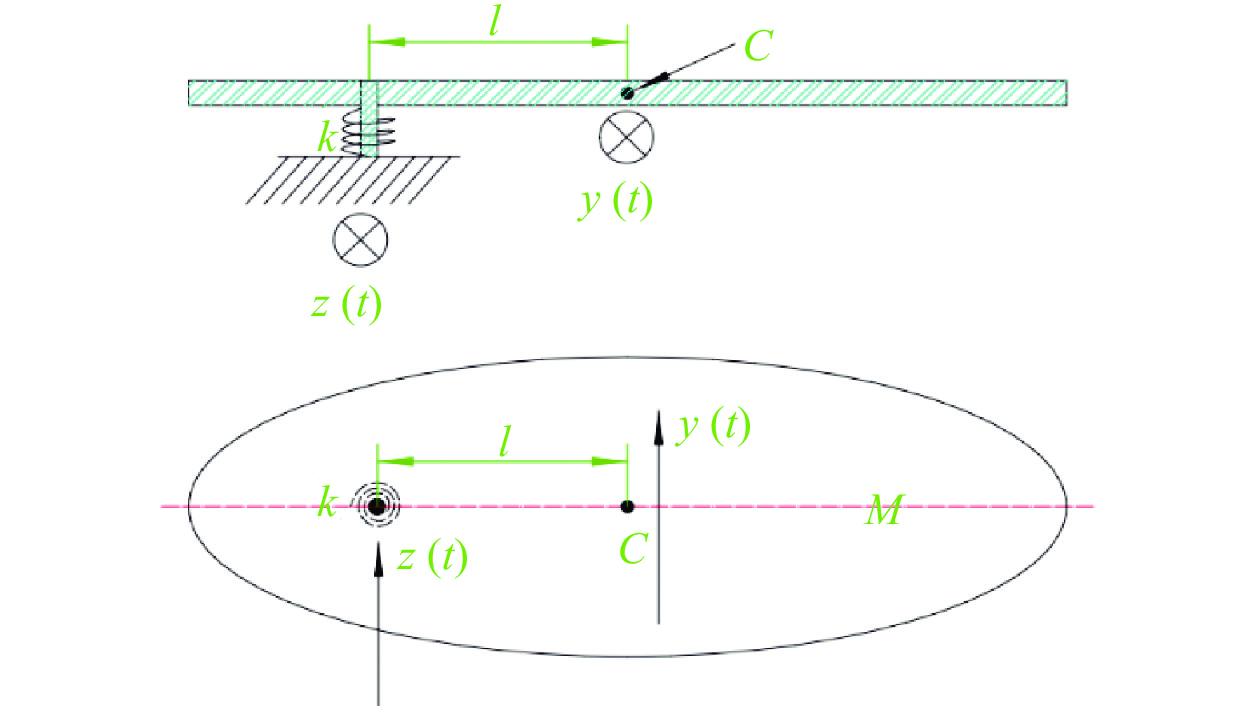
1.2 偏心轮式测量仪的设计将装置设计成如图2所示的物理摆形式,椭圆形簧片通过偏心安装轴水平布置在基础上,同时在安装轴上布置扭簧,簧片和扭簧构成了一个单自由度弹簧-质量系统。当簧片具备足够的结构强度时,可以不考虑簧片的垂向冲击响应,同时忽略扭簧、转动轴承等构成的系统阻尼影响,则冲击载荷作用下,建立簧片运动方程:
|
| 图 2 水平向冲击环境测量仪设计原理图 |
| $ M\cdot \ddot{y}\left(t\right)\cdot l+k\cdot \left[{\rm{arcsin}}\left(\frac{y\left(t\right)-{\textit{z}}\left(t\right)}{l}\right)\right]=-{J}_{\rm O}\cdot \ddot{\varphi }\left(t\right) $ | (4) |
式中:
取簧片的相对位移
| $ \varphi \left(t\right)={\rm{arcsin}}\left(\frac{y\left(t\right)-{\textit{z}} \left(t\right)}{l}\right)\approx \frac{y\left(t\right)-{\textit{z}}\left(t\right)}{l}=\frac{x\left(t\right)}{l} $ | (5) |
当簧片转角不超过10°时,式(5)近似计算引起的偏差小于0.51%,式(4)化简为:
| $ \ddot{x}\left(t\right)+{\mathrm{\omega }}^{2}\cdot x\left(t\right)=-\frac{M\cdot {l}^{2}}{{J}_{{\textit{z}}}}\cdot \ddot{{\textit{z}}}\left(t\right) $ | (6) |
式中:
系统初始状态为零时,对式(6)进行杜哈曼积分,得到:
| $ x\left(t\right)=\frac{M\cdot {l}^{2}}{{J}_{{\textit{z}}}}\left[-\frac{1}{\omega }{\int }_{0}^{t}\ddot{{\textit{z}}}\left(t\right){\rm{sin}}\omega \left(t-\tau \right){\rm d}\tau \right] $ | (7) |
式(7)为簧片的位移响应,方程右端第二项为单自由度系统的冲击位移谱。将式(7)代入式(5),则簧片的转角响应
| $ \varphi \left(t\right)=\frac{M\cdot {l}^{2}}{l\cdot {J}_{{\textit{z}}}}\left[-\frac{1}{\omega }{\int }_{0}^{t}\ddot{{\textit{z}}}\left(t\right){\rm{sin}}\omega \left(t-\tau \right){\rm d}\tau \right] $ | (8) |
从式(8)可以看到,簧片的转角响应与冲击位移谱成正比关系。因此,可以通过测量簧片的转角响应来推算出簧片安装基础部位冲击环境的量值。
2 水平向冲击环境测量仪测量需求分析根据簧片仪的设计经验,冲击环境测量仪的测量频率分布过低会造成结构尺寸的增加,过高则会带来测量实施的困难。对于水平向冲击环境测量仪的频率分布,主要参考现有的低频簧片仪,设计为5~20 Hz,应能满足舰船实船及模型水下爆炸试验的需求[12],对于5 Hz以下极低频冲击环境的测量,则考虑使用低频振子等装置[13]。
使用环境的量值决定了簧片的测量范围(挠度、转角等)、结构强度限值等参数,均与测量仪的结构尺寸密切相关。以现有的水平式强碰撞冲击机考核冲击环境作为簧片的使用环境指标开展水平向冲击环境测量仪的结构设计。水平式强碰撞冲击机可用于质量不超过8 t的舰船设备水平冲击条件下的安全性考核和动力响应特性研究[14],其最大冲击输入为谱加速度200 g、谱速度5.5 m/s、谱位移100 mm,如图3所示。从水平式强碰撞冲击机的考核环境曲线来看,对于安装频率8.75 Hz以下的簧片,应以簧片变形不小于100 mm为设计上限;安装频率8.75 Hz以上的簧片,则以速度谱5.5 m/s为设计上限[15-16]。

|
| 图 3 水平式强碰撞冲击机考核环境曲线 |
3 水平向冲击环境测量仪的设计 3.1 两端固支梁式簧片结构尺寸的设计
采用文献[9]给出的簧片振型求解方法及簧片结构尺寸开展两端固支梁式簧片的设计,如表1所示。一端固支和两端固支簧片分别对应簧片仪和水平向冲击环境测量仪。两端固支簧片一阶振动频率为一端固支簧片的2倍,而结构的对称性使两种簧片的二阶振动频率一致,计算结果合理。进一步计算可知,一阶设计振动频率为5.27 Hz的两端固支簧片尺寸为:长583.28 mm、宽10 mm、厚1.44 mm。
| 长度/ mm |
厚度/ mm |
宽度/ mm |
集中质 量比 |
振型 | 一端固支簧 片频率/Hz |
两端固支簧 片频率/Hz |
| 291.64 | 1.44 | 10 | 1.510 | 1 | 5.270 | 10.15 |
| 2 | 64.34 | 64.34 | ||||
| 211.78 | 1.46 | 10 | 2.052 | 1 | 8.857 | 17.21 |
| 2 | 122.6 | 122.6 | ||||
| 151.00 | 1.40 | 10 | 2.393 | 1 | 15.59 | 30.38 |
| 2 | 230.4 | 230.4 |
使用Abaqus有限元软件对两端固支簧片进行强度校核,20 mm冲击变形下振动频率5.27 Hz的簧片应力响应达到1 126 MPa,已接近弹簧钢等高弹性合金的屈服极限。要达到100 mm冲击变形只能进一步放大簧片尺寸,但必然造成装置使用及装配的困难,且簧片的结构稳定性也很难保证。设计结果表明,两端固支梁式水平向冲击环境测量仪难以达到设计指标,但刚度适配的装置设计思路仍具有参考价值。
3.2 偏心轮式簧片结构尺寸的设计 3.2.1 安装频率8.75 Hz以下簧片的设计考虑小转角条件下计算偏差的影响,取试验时簧片最大转角为10°(0.175 rad)、谱位移100 mm,将相关参数代入式(8),有如下限定条件:
| $ \frac{M\cdot {l}^{2}}{l\cdot {J}_{{\textit{z}}}}\times 0.1\leqslant 0.175 $ | (9) |
取椭圆形簧片的半长轴
| $ a=18 l;b=12 l $ |
| $ {J}_{\rm O}=\frac{M}{4}\left({a}^{2}+{b}^{2}\right)=\frac{468 M\cdot {l}^{2}}{4} $ | (10) |
可以得到:
| $ l\geqslant\frac{1}{1.75}\times\dfrac{M\cdot l^2}{\dfrac{468 M\cdot l^2}{4}+M\cdot l^2}\text{,}l\geqslant0.004\; 84\; \text{m} $ | (11) |
取
| 簧片尺寸(长×短轴×厚)/ (mm×mm×mm) |
簧片质量/ kg |
转动惯量/ (kg·m2) |
簧片安装 频率/Hz |
| 216×144×25 | 1.722 | 0.00732 | 5.263 |
| 216×144×20 | 1.378 | 0.00585 | 5.884 |
| 216×144×15 | 1.033 | 0.00439 | 6.794 |
| 216×144×10 | 0.689 | 0.00293 | 8.321 |
3.2.2 安装频率8.75 Hz以上簧片的设计
等速度段不同频率下谱位移的变化使各安装频率簧片对应的式(9)限定条件出现变化,如表3所示。以表3给出的限定条件,取扭簧刚度为8.0
| 谱速度/ (m·s-1) |
安装频率/ Hz |
谱位移/ mm |
簧片转角/ (°) |
|
| 5.5 | 9.0 | 97.3 | 0.175 | 1.799 |
| 5.5 | 12.0 | 72.9 | 0.175 | 2.401 |
| 5.5 | 15.0 | 58.4 | 0.175 | 2.997 |
| 5.5 | 18.0 | 48.6 | 0.175 | 3.601 |
| 5.5 | 20.0 | 43.8 | 0.175 | 3.995 |
| 簧片尺寸(长×短轴× 厚)/(mm×mm×mm) |
簧片质量/ kg |
转动惯量/ (kg·m2) |
安装频率/ Hz |
限定条件与 限值对比 |
| 207×138×10 | 0.633 | 0.002470 | 9.057 | 1.537<[1.799] |
| 180×120×10 | 0.478 | 0.001417 | 11.96 | 2.026<[2.401] |
| 159×106×10 | 0.373 | 0.000865 | 15.30 | 2.588<[2.977] |
| 144×96×10 | 0.306 | 0.000584 | 18.62 | 3.145<[3.601] |
| 138×92×10 | 0.281 | 0.000494 | 20.26 | 3.418<[3.995] |
3.2.3 簧片垂向刚度及强度校核
通过有限元仿真可得到尺寸216 mm×144 mm×25 mm的簧片垂向安装频率为317.6 Hz,落在图3所示考核环境的高频等加速度段,试验时簧片垂向响应以高频冲击加速度响应为主,可以很容易地与水平向的低频特征信号区分开,垂向冲击响应不会对水平向冲击测量结果造成影响。同时,冲击峰值200 g条件下簧片冲击响应在几十兆帕量级,簧片也具备足够的冲击强度。
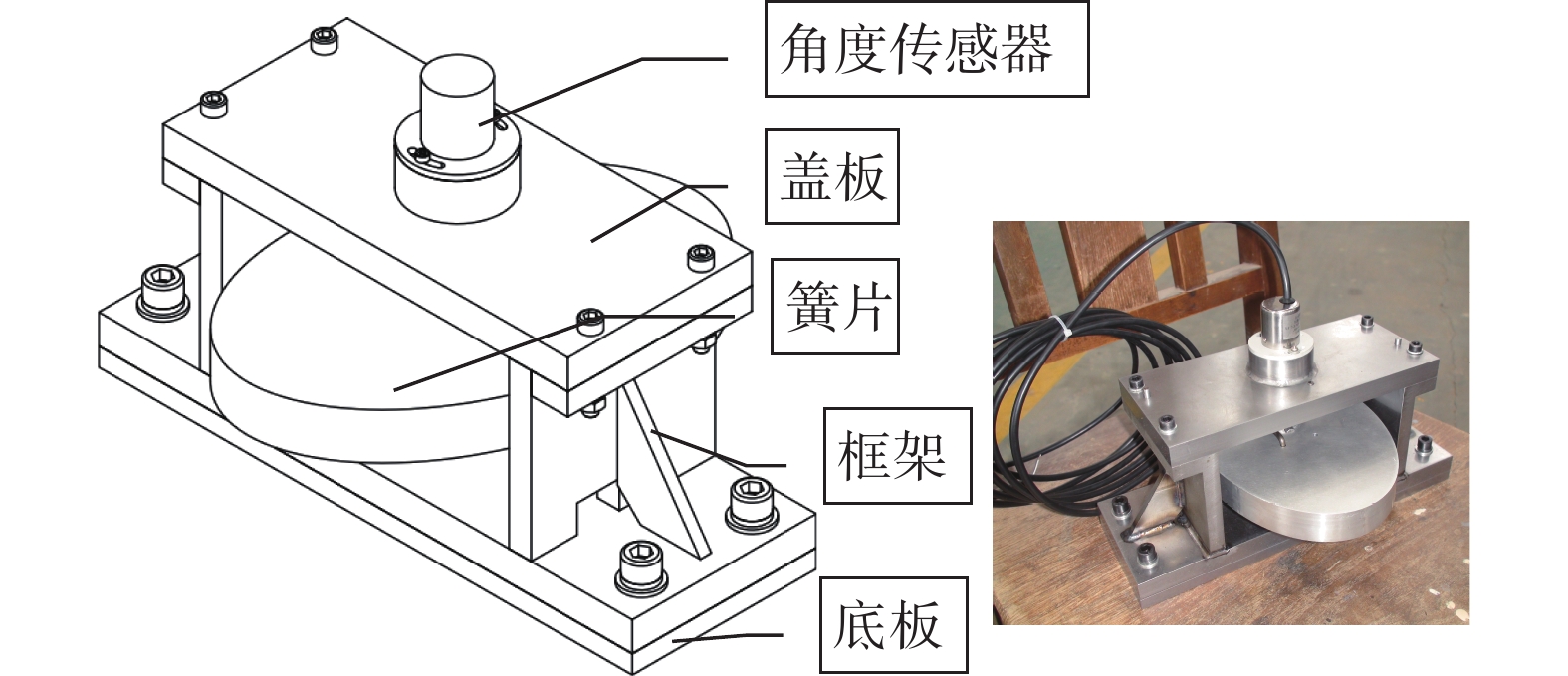
3.3 测量仪结构及试验参数测试方法偏心轮式水平向冲击环境测量仪样机如图4所示。主体结构由底板、安装框架、固定轴套、顶板、转轴、簧片等部件构成,其他部件包括扭转弹簧以及用于摆动角度测量的角度传感器等。簧片垂向刚性固定,测量仪承受的垂向冲击载荷通过框架传递到簧片上,但其垂向高频冲击响应通过滤波等手段即可与水平向的低频特征信号区分开。测量仪受水平向冲击时,簧片可以绕固定轴套旋转,并由扭转弹簧提供恢复力,从而实现簧片在平衡位置的摆动。同时,通过与簧片同轴安装的角度传感器测量簧片的旋转角度,并根据式(8)换算为冲击环境数据。
|
| 图 4 水平向冲击环境测量仪样机图片 |
4 水平向冲击环境测量仪样机试验检测
图4中水平向冲击环境测量仪样机簧片尺寸为216 mm×144 mm×25 mm。用手拨动组装好的样机簧片,记录角度传感器拾取的簧片摆动信号,实测簧片安装频率为5.504 Hz,与表2给出的设计安装频率5.263 Hz相比,相对偏差为4.58%,表明理论设计是正确的。
在水平式强碰撞冲击机上开展水平向冲击环境测量仪样机的试验检测,并与加速度测试冲击环境数据进行比对,以考察测量仪的测试精度。布置在冲击机台面上的装置如图5所示。布置了ENDEVCO2270型1只、B&K4369型1只、B&K4371型2只,共计4只加速度计,水平向冲击环境测量仪布置在4只加速度计中间位置。ENDEVCO2270通常用作检定参考加速度计,具备非常高的测量精度;B&K4369、B&K4371工作加速度计也在试验室成熟运用多年,已积累了丰富的测量应用经验[18]。
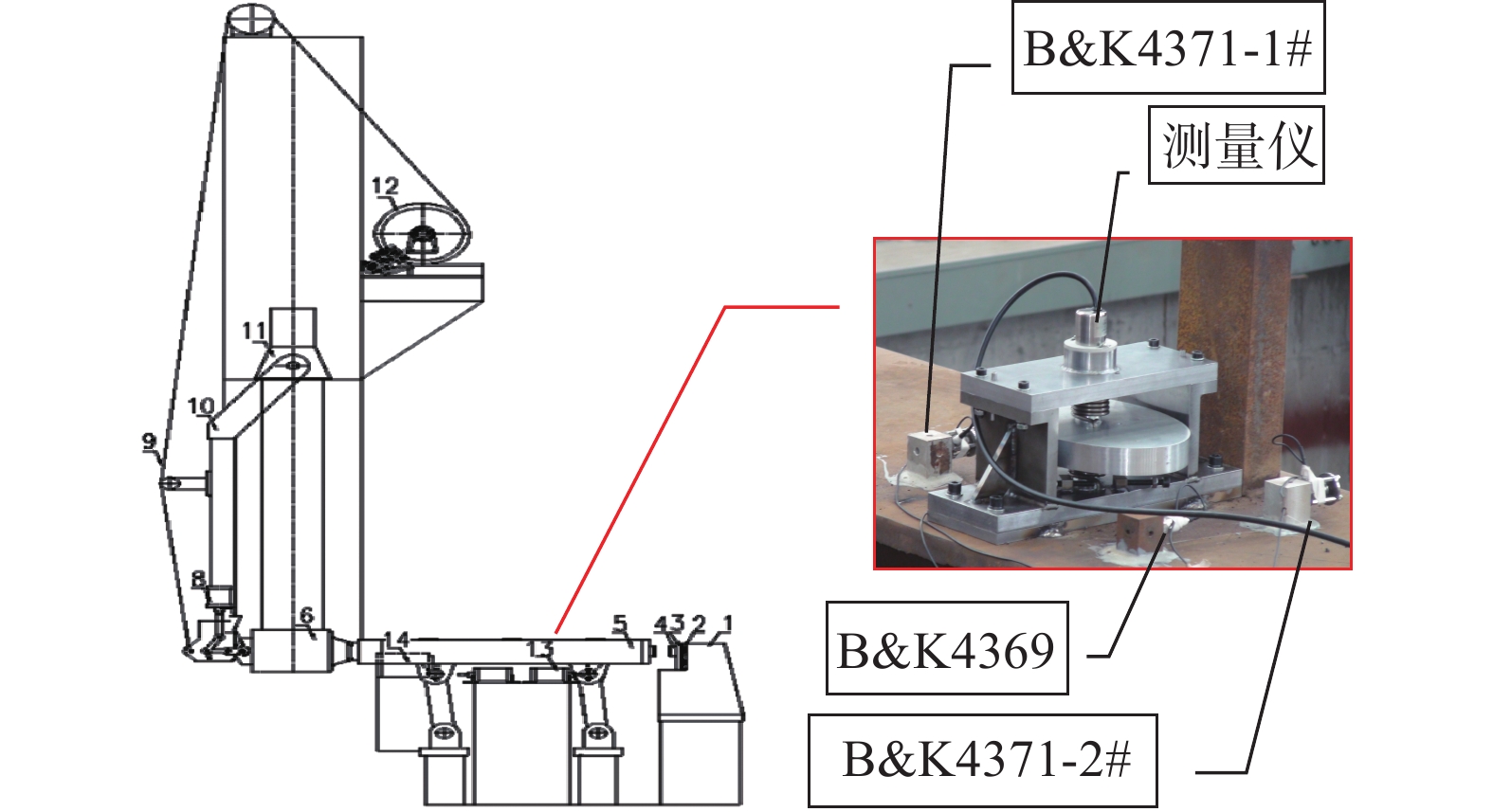
|
| 图 5 水平向冲击环境测量仪样机冲击试验示意图 |
将试验测量得到的簧片摆动角度代入式(8),计算得出簧片安装频率下的谱位移值,并将该数据放入加速度计算冲击谱曲线中进行对比,如图6所示。从图中可以看到,水平向冲击环境测量仪测量结果与加速度测试冲击谱非常接近。将测量数据折算成谱速度值,并与加速度计测量结果进行对比,如表5所示。两种测量结果的最大相对偏差仅为8.53%。对比结果表明,不同测量装置获取的试验数据可以进行相互验证,同时也表明试验获取的5.504 Hz下的冲击环境数据是准确可信的。

|
| 图 6 加速度计与水平向冲击环境测量仪测量结果对比图 |
| 测量通道 | 谱速度值/(m·s–1) | 与水平向冲击环境测量 仪相对偏差/% |
| ENDEVCO2270 | 0.8229 | 8.38 |
| B&K4369 | 0.8407 | 6.40 |
| B&K4371-1# | 0.8216 | 8.53 |
| B&K4371-2# | 0.8358 | 6.94 |
| 水平向冲击环境测量仪 | 0.8982 | – |
5 结束语
本文以实现水下爆炸冲击载荷在测量装置上的解耦为目标,从适配测量装置的垂向与水平向振动刚度角度出发,参照现有低频簧片仪安装频率分布,并以水平式强碰撞冲击机考核冲击环境为指标,开展两端固支梁式、偏心轮式水平向冲击环境测量仪的设计工作。在此基础上,推导水平向冲击载荷作用下的簧片动力响应理论公式,设计系列满足安装频率分布要求的簧片,并加工水平向冲击环境测量仪原理样机。通过水平式强碰撞冲击机试验检测,水平向冲击环境测量仪与加速度测试系统获取的冲击环境数据最大相对偏差仅8.53%,两种测量装置的测量结果可以相互验证,表明水平向冲击环境测量仪设计是合理有效的。
| [1] |
C. M. 哈里斯, C. E. 克瑞德. 冲击和振动手册[M]. 北京: 科学出版社, 1990: 417-436.
|
| [2] |
谢浩, 冯麟涵, 吴静波, 等. 舰船冲击谱若干计算方法比较研究[J].
噪声与振动控制, 2017, 37(4): 115-120.
XIE H, FENG L H, WU J B, et al. Comparative study on several calculation methods for ship's shock spectra[J].
Noise and Vibration Control, 2017, 37(4): 115-120.
DOI:10.3969/j.issn.1006-1355.2017.04.023 |
| [3] |
SMALLWOOD D O. Shock response spectrum at low frequencies[J].
Shock and Vibration Bulletin, SAVIAC, 1986, 1: 279-288.
|
| [4] |
杜志鹏, 汪玉, 杨洋, 等. 舰艇水下爆炸冲击信号拟合及应用[J].
噪声与振动控制, 2010, 29(3): 182-184.
DU Z P, WANG Y, YANG Y, et al. Curve fit method for naval underwater explosion shock signal and its application[J].
Journal of Vibration and Shock, 2010, 29(3): 182-184.
|
| [5] |
GABERSON H A, CHALMERS R H. Modal velocity as a criterion of shock severity[J].
Shock and Vibration Bulletin, 1969, 40(2): 31-49.
|
| [6] |
DATIG M, SCHLUMANN T. Perfoemance and limitations of Hibert-Huang transformation (HHT) with an application to irregular water waves[J].
Ocean Engineering, 2004, 31(14): 1783-1834.
|
| [7] |
邹瑛珂, 贾云飞, 刘素芸. 一种基于改进EMD分解人车地震动信号识别算法[J].
中国测试, 2022, 48(4): 85-94.
ZOU Y K, JIA Y F, LIU S Y. Improved EMD decomposition based recognition algorithm for pedestrian and vehicle ground motion signals[J].
China Measurement & Test, 2022, 48(4): 85-94.
|
| [8] |
陈辉, 潘建强, 唐佳炜,等. 水下非接触爆炸条件下舰船冲击环境测试相关技术研究[J].
计算机测量与控制, 2011, 19(11): 2635-2640.
CHEN H, PAN J Q, TANG J W, et al. Researches of metrical technique of shock environment UNDEX of warships[J].
Computer Measurement & Control, 2011, 19(11): 2635-2640.
DOI:10.16526/j.cnki.11-4762/tp.2011.11.023 |
| [9] |
潘建强, 唐佳炜, 张克明. 簧片式冲击谱测量仪电测技术研究[J].
应用科技, 2010, 37(11): 14-17.
PAN J Q, TANG J W, ZHANG K M. The electromotive technology based on sheet metal-spring which is used to measure shock spectrum[J].
Applied Science and Technology, 2010, 37(11): 14-17.
DOI:10.3969/j.issn.1009-671X.2010.11.004 |
| [10] |
RUDOLPH J S, HENRY C P. 舰船冲击分析与设计[M]. 哈尔滨:哈尔滨工程大学出版社, 2006: 43-46.
|
| [11] |
曾泽璀, 闫明, 赵鹏铎, 等. 中低频冲击响应谱测量技术综述[J].
造船技术, 2016, 4: 30-33,41.
ZENG Z C, YAN M, ZHAO P D, et al. Review on measurement technology of middle-low frequency shock response spectrum[J].
Marine Technology, 2016, 4: 30-33,41.
DOI:10.3969/j.issn.1000-3878.2016.03.006 |
| [12] |
潘建强, 陈辉, 刘建湖, 等. 实船和模型水下非接触爆炸条件下舰船冲击环境测量方法: CB20075-2012[S]. 北京: 中国船舶工业综合技术经济研究院, 2013.
|
| [13] |
张磊, 杜志鹏, 吴静波, 等. 200 t级浮动冲击平台水下爆炸试验低频冲击响应数据分析[J].
中国舰船研究, 2018, 13(3): 60-65.
ZHANG L, DU Z P, WU J B, et al. Low-frequency shock response data analysis of underwater explosion test of 200-ton class floating shock platform[J].
Chinese Journal of Ship Research, 2018, 13(3): 60-65.
DOI:10.19693/j.issn.1673-3185.01149 |
| [14] |
潘建强, 刘建湖, 杨云川, 等. 水平式强碰撞冲击机冲击动响应分析[C]//第十届全国冲击动力学学术会议, 2011.
|
| [15] |
EDWARD A J. Shock response spectrum [J]. Sound and Vibration, 2009, 43(6): 6-15.
|
| [16] |
GABERSON H A. Using the velocity shock spectrum to predict shock damage [J]. Sound and Vibration, 2003, 37(9): 5-6.
|
| [17] |
毛谦德, 李振清. 袖珍机械设计师手册[M]. 2版.北京: 机械工业出版社, 2002: 270, 1106-1107.
|
| [18] |
陈辉, 江楠. 用于冲击加速度测量的机械滤波器设计[J].
中国测试, 2018, 44(10): 107-114.
CHEN H, JIANG N. Design of mechanical filter for shock acceleration measuring[J].
China Measurement & Test, 2018, 44(10): 107-114.
DOI:10.11857/j.issn.1674-5124.2018.10.018 |
 2024, Vol. 50
2024, Vol. 50