文章信息
- 赵兴华, 唐韵, 徐尹杰, 邢鲁, 贺云
- ZHAO Xinghua, TANG Yun, XU Yinjie, XING Lu, HE Yun
- 基于内压法的锆合金薄壁管泊松比试验研究
- Experimental study on Poisson’s ratio of zirconium alloy thin-walled tube based on internal pressure method
- 中国测试, 2024, 50(5): 42-46, 61
- CHINA MEASUREMENT & TEST, 2024, 50(5): 42-46, 61
- http://dx.doi.org/10.11857/j.issn.1674-5124.2023020069
-
文章历史
- 收稿日期: 2023-02-12
- 收到修改稿日期: 2023-03-27
泊松比作为描述材料横向变形的弹性常数,在材料的结构力学或弹性力学行为分析中扮演重要角色,尤其是对一些特殊材料的泊松比研究,例如负泊松比超材料的研究[1-3],近年更是被广泛涉及。获得材料泊松比的试验方法多种多样[4],包括静态法[5]、动态法[6]、干涉法等[7],其中传统静态法因其简单、高效、精度高等优点被广泛应用于各种材料的泊松比测试中,特别是高温下材料的泊松比试验[8-10]。
锆合金包壳管等薄壁管大量应用于核电领域,作为反应堆核燃料组件的核心部件,对核电安全起到重要作用。在锆合金包壳管实际使用过程中,受内外压力及燃料棒的影响,存在长度和直径的变化,而无论是包壳管的直径变化还是长度变化,都可能导致管材破裂、燃料泄漏,影响反应堆的正常运行。因此,为了更好地评价锆合金包壳管等管材受内压时的变形性能,给燃料组件的设计、计算、验证提供参考,并与传统拉伸法得到的泊松比试验结果进行相互验证,设计基于内压法的泊松比测试方法十分必要。如此可以量化包壳管轴向和径向的变形关系,更好地明确包壳管的受力状态,确保反应堆的正常运转。
国内对于锆合金薄壁管力学性能领域的试验研究相对较少[11-14],其中对锆合金薄壁管泊松比试验方法的研究更是鲜有涉及。目前已有的试验方法是通过拉伸法得到材料泊松比,但该方法与管件实际受力状况存在差异。因此,本文旨在尽可能模拟薄壁管受力状况的条件下,寻求一种新的薄壁管泊松比试验方法,还原锆合金薄壁管真实受力状态,获得更加接近真实服役状态下锆合金薄壁管的泊松比。
本文通过压力容器受内压时的弹性力学分析,建立了通过内压试验测定薄壁管泊松比的理论依据,进而发展了测定N36锆合金薄壁管泊松比的内压试验方法,为薄壁管试样的泊松比研究提供了一种新的技术途径。
1 受内压薄壁管泊松比的理论公式根据弹性力学,受内压的薄壁管,其壁厚任意位置,极坐标系下周向和轴向的内应变表达式如下:
| $ \left\{ \begin{aligned} {\varepsilon _{\mathrm{\theta}} } =& \frac{{(1 - 2\nu )}}{{{E_1}}}\frac{{{P_{{\text{in}}}}R_{{\text{in}}}^2 - {P_{\text{o}}}R_{\text{o}}^2}}{{R_{\text{o}}^2 - R_{{\text{in}}}^2}} + \frac{{({P_{{\text{in}}}} - {P_{\text{o}}})R_{{\text{in}}}^2 \cdot R_{\text{o}}^2(1 + \nu )}}{{{E_1}(R_{\text{o}}^2 - R_{{\text{in}}}^2) \cdot {r^2}}} \\ {\varepsilon _{\textit{z}}} =& \frac{{(1 - 2\nu )}}{{{E_1}}}\frac{{{P_{{\text{in}}}}R_{{\text{in}}}^2 - {P_{\text{o}}}R_{\text{o}}^2}}{{R_{\text{o}}^2 - R_{{\text{in}}}^2}} \end{aligned}\right. $ | (1) |
式中:
由于薄壁管的内压试验中只有内压力
| $\left\{ \begin{aligned} {\text{d}}{\varepsilon _\theta } = &\frac{{(1 - 2\nu )}}{{{E_1}}}\frac{{{\text{d}}{P_{{\text{in}}}} \cdot R_{{\text{in}}}^2}}{{R_{\text{o}}^2 - R_{{\text{in}}}^2}} + \frac{{{\text{d}}{P_{{\text{in}}}} \cdot R_{{\text{in}}}^2 \cdot (1 + \nu )}}{{{E_1}(R_{\text{o}}^2 - R_{{\text{in}}}^2)}} \\ {\text{d}}{\varepsilon _{\textit{z}}} = &\frac{{(1 - 2\nu )}}{{{E_1}}}\frac{{{\text{d}}{P_{{\text{in}}}} \cdot R_{{\text{in}}}^2}}{{R_{\text{o}}^2 - R_{{\text{in}}}^2}} \end{aligned}\right.$ | (2) |
令,
| $ K = \frac{{{\text{d}}{\varepsilon _{\textit{z}}}}}{{{\text{d}}{\varepsilon _\theta }}} $ | (3) |
将式(2)代入式(3)可得:
| $ K = \frac{{{\text{d}}{\varepsilon _{\textit{z}}}}}{{{\text{d}}{\varepsilon _\theta }}} = \frac{{(1 - 2\nu ) \cdot {\text{d}}{P_{{\text{in}}}}}}{{(1 - 2\nu ) \cdot {\text{d}}{P_{{\text{in}}}} + (1 + \nu ) \cdot {\text{d}}{P_{{\text{in}}}}}} = \frac{{1 - 2\nu }}{{2 - \nu }} $ | (4) |
所以,
| $ \nu = \frac{{1 - 2K}}{{2 - K}} $ | (5) |
又,
| $ \left\{ \begin{aligned} {K_1} = &{\text{d}}{\varepsilon _{\textit{z}}} \\ {K_2} =& {\text{d}}{\varepsilon _\theta } \end{aligned}\right. $ | (6) |
则,根据式(5)和式(6)可得到薄壁管泊松比的最终表达式为:
| $ \nu = \frac{{1 - 2\dfrac{{{K_1}}}{{{K_2}}}}}{{2 - \dfrac{{{K_1}}}{{{K_2}}}}} $ | (7) |
试验中采用高温径向引伸计测量薄壁管直径方向的变形量,用2
| $ {U_\theta } = 2\pi \left( {{R_{\text{o}}} + {U_{{r}}}} \right) - 2\pi {R_{\text{o}}} = 2\pi {U_{{r}}} $ | (8) |
式(8)除以周长进一步可得到周向应变的表达式:
| $ {\varepsilon _\theta } = \frac{{{U_\theta }}}{{2\pi {R_{\text{o}}}}} = \frac{{2\pi {U_{{r}}}}}{{2\pi {R_{\text{o}}}}} = \frac{{{U_{{r}}}}}{{{R_{\text{o}}}}} $ | (9) |
试验材料为某锆合金薄壁管材,外壁半径4.74 mm,内壁半径4.17 mm,长度300 mm。试样上端使用油管卡套进行密封;试样下端用三通卡套密封,三通与油管和Ф10 mm不朽钢圆柱连接,用以增压和试验机夹持。试验装配示意图如图1所示。

|
| 图 1 试验装配示意图 |
内压试验在MTS810电液伺服试验系统上完成,控制系统为Flextest60,试验机的静载荷按照JJG 556要求进行校准,其系统误差不大于±0.5%,偏差不大于0.5%。采用手动油泵对试样施加内压,使用0.4级精度的压力表指示压力[15]。
加热设备为大气高温炉,炉膛均温区高度不低于80 mm,加热温度范围100~1000 ℃,满足试样工作段的均温区要求,温度控制偏差在±3 ℃以内。温度测量采用德图测温仪,其温度测试范围和精度满足试验要求,试验前将所有使用的热电偶[16]进行校准,测量精度为1 ℃。
室温轴向应变的测量采用634.31F-25引伸计,该引伸计标距20 mm,量程为±20%,精度为0.5级;高温轴向应变的测量采用MTS 632.53F-14 引伸计,该引伸计标距为12 mm,量程为±10%,精度为0.5级;径向应变采用MTS 632.61C-02 引伸计测量,该引伸计量程为0.5 mm,精度为0.5级。
3 试验方法实际测量中,
为使被测锆合金薄壁管试样内部产生可控的内压,使用卡套装置封闭试样一端,另一端接三通卡套与液压泵和0.4级压力表联通,压力表可以指示管道内的压力,应变数据的采集由MTS Flextest60控制器完成。由于引伸计安装位置的限制,轴向变形和径向变形不能同时测量,因此在每个温度环境下需要进行两次试验分别测量轴向变形和径向变形才能获得完整的试验数据。
分步测量要经过室温状态下的试验验证。室温状态下可以同时装卡两个引伸计,一次得到泊松比,同时也会得到弹性模量和径向参量(应力与径向应变之比);进行分步测量时,要在相同室温下进行弹性模量和径向参量(应力与径向应变之比)的验证,结果一致时方可开展后续高温试验。
试验前,先用无水酒精对试样进行清洗,去除表面杂质和油污;测量试样的外形尺寸并记录,使用直通液压卡套密封管试样的夹持端,三通型液压卡套连接施压油泵和压力表。将试样夹持端安装于试验机上并安装引伸计,室温试验采用空调调节室内温度,高温试验使用大气高温炉对试样进行加热,并用热电偶测量试样标距段的温度,达到规定温度后保温至少15 min开始试验。根据各温度下材料的屈服强度换算得到内压水平,分4~6级压力逐步加载至换算内压的50%,记录各级载荷下的内压值和应变数据,计算内压条件下的泊松比。
4 试验结果及分析 4.1 内压法试验结果试验分为20、100、200、300、350、400 ℃共6个温度工况,每个温度工况包含3个平行样。以室温试验数据处理过程为例,表1是内压试验下采集到的试验数据,以及根据式(9)计算得到的周向应变。
| 管内压力(Pin)/ MPa |
轴向应变(εz)/ (10–6 mm∙mm–1) |
径向变形(2Ur)/ (10–5 mm∙mm–1) |
周向应变(εθ)/ (10–6 mm∙mm–1) |
| 5 | 37 | 300 | 316.5 |
| 10 | 85 | 612 | 645.6 |
| 15 | 134 | 925 | 975.7 |
| 20 | 184 | 1240 | 1308.0 |
| 25 | 235 | 1557 | 1642.4 |
| 30 | 283 | 1865 | 1967.3 |
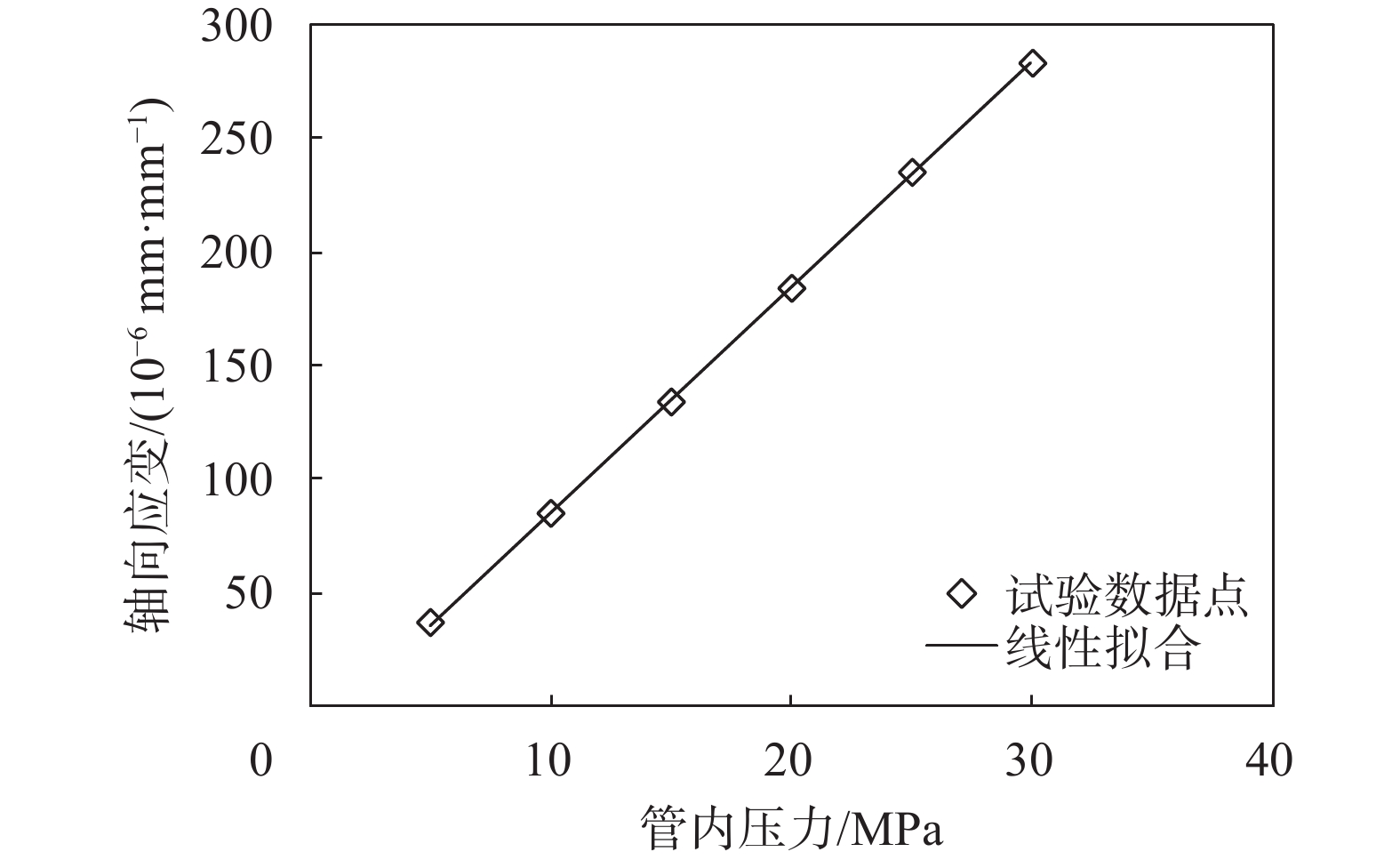
依据表1试验数据绘制曲线
|
|
图 2
|
|
|
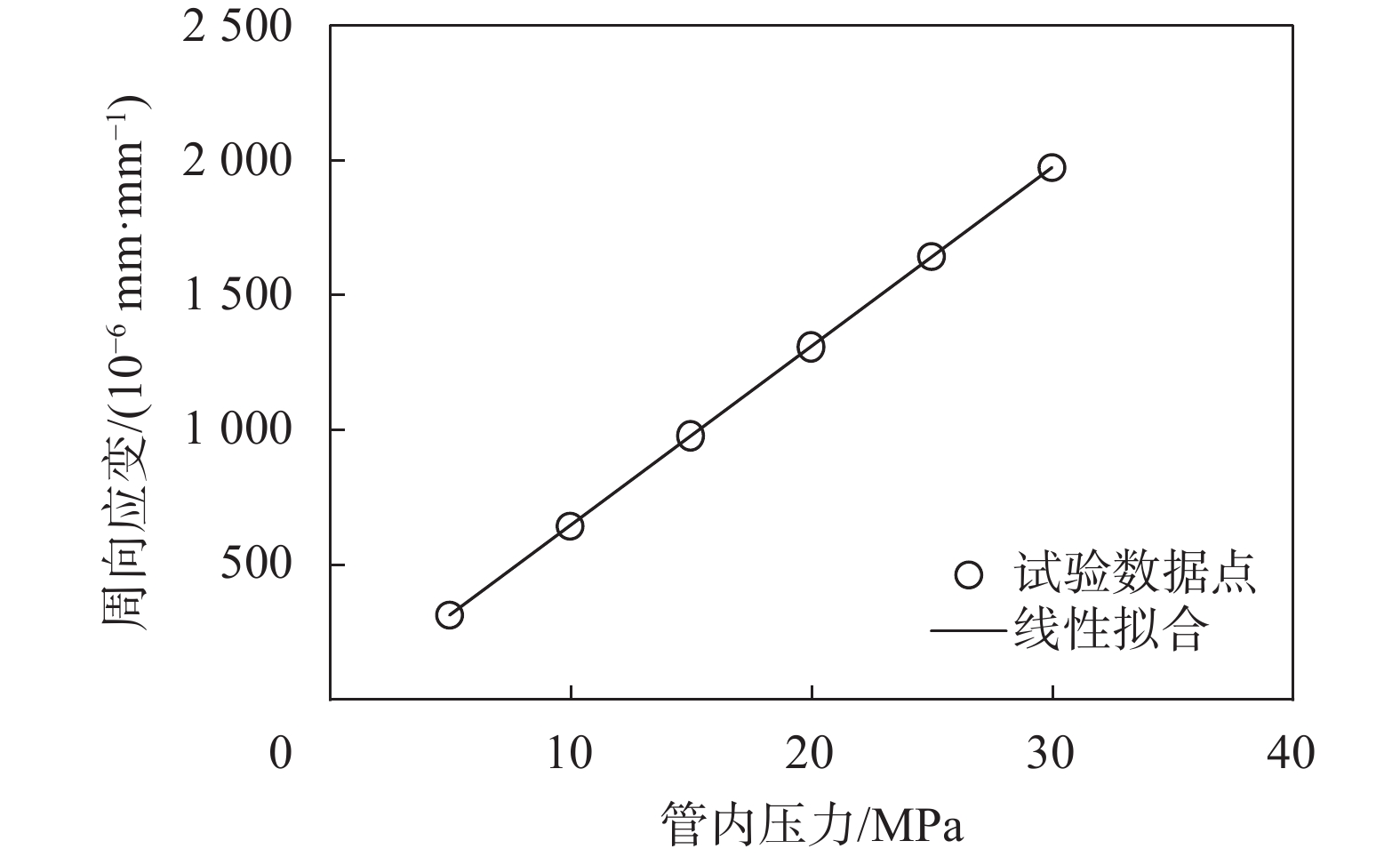
图 3
|
按上述方式分别对6种温度共18个样品的试验数据进行处理,可以得到表2所示所有样品的
| 试样编号 | 试验温度(T)/ ℃ |
K1/ MPa–1 |
K2/ MPa–1 |
泊松比(ν) | 泊松比均值 |
| 20-1 | 20 | 11.04 | 66.81 | 0.365 | 0.361 |
| 20-2 | 11.35 | 66.14 | 0.359 | ||
| 20-3 | 11.24 | 66.02 | 0.360 | ||
| 100-1 | 100 | 10.89 | 68.41 | 0.370 | 0.365 |
| 100-2 | 11.44 | 68.22 | 0.363 | ||
| 100-3 | 11.49 | 68.41 | 0.362 | ||
| 200-1 | 200 | 10.20 | 71.37 | 0.385 | 0.380 |
| 200-2 | 10.68 | 71.08 | 0.378 | ||
| 200-3 | 10.94 | 71.99 | 0.376 | ||
| 300-1 | 300 | 10.24 | 74.11 | 0.389 | 0.389 |
| 300-2 | 10.06 | 74.18 | 0.391 | ||
| 300-3 | 10.40 | 74.77 | 0.388 | ||
| 350-1 | 350 | 9.14 | 75.38 | 0.403 | 0.397 |
| 350-2 | 10.02 | 76.12 | 0.394 | ||
| 350-3 | 10.16 | 76.43 | 0.393 | ||
| 400-1 | 400 | 8.48 | 75.82 | 0.411 | 0.408 |
| 400-2 | 9.36 | 76.05 | 0.402 | ||
| 400-3 | 8.76 | 77.34 | 0.410 |
4.2 拉伸法试验结果
为了验证该内压法测试薄壁管泊松比的可行性,与传统的拉伸法进行对比验证,本文同时开展了该锆合金薄壁管同种温度下的拉伸法泊松比试验,试验结果如表3所示。
| 试样编号 | 试验温度/℃ | 泊松比 |
| L-1 | 20 | 0.358 |
| L-2 | 100 | 0.360 |
| L-3 | 200 | 0.375 |
| L-4 | 300 | 0.391 |
| L-5 | 350 | 0.399 |
| L-6 | 400 | 0.403 |
4.3 试验结果比对分析
由表2和表3可知,该锆合金薄壁管20~400 ℃的泊松比在0.35~0.41之间变化,且泊松比随温度的升高而增大。
图4为拉伸法和内压法所得泊松比试验结果的对比图。由图可知,两种试验方法得到的泊松比变化趋势一致,都是随温度增大而增大。
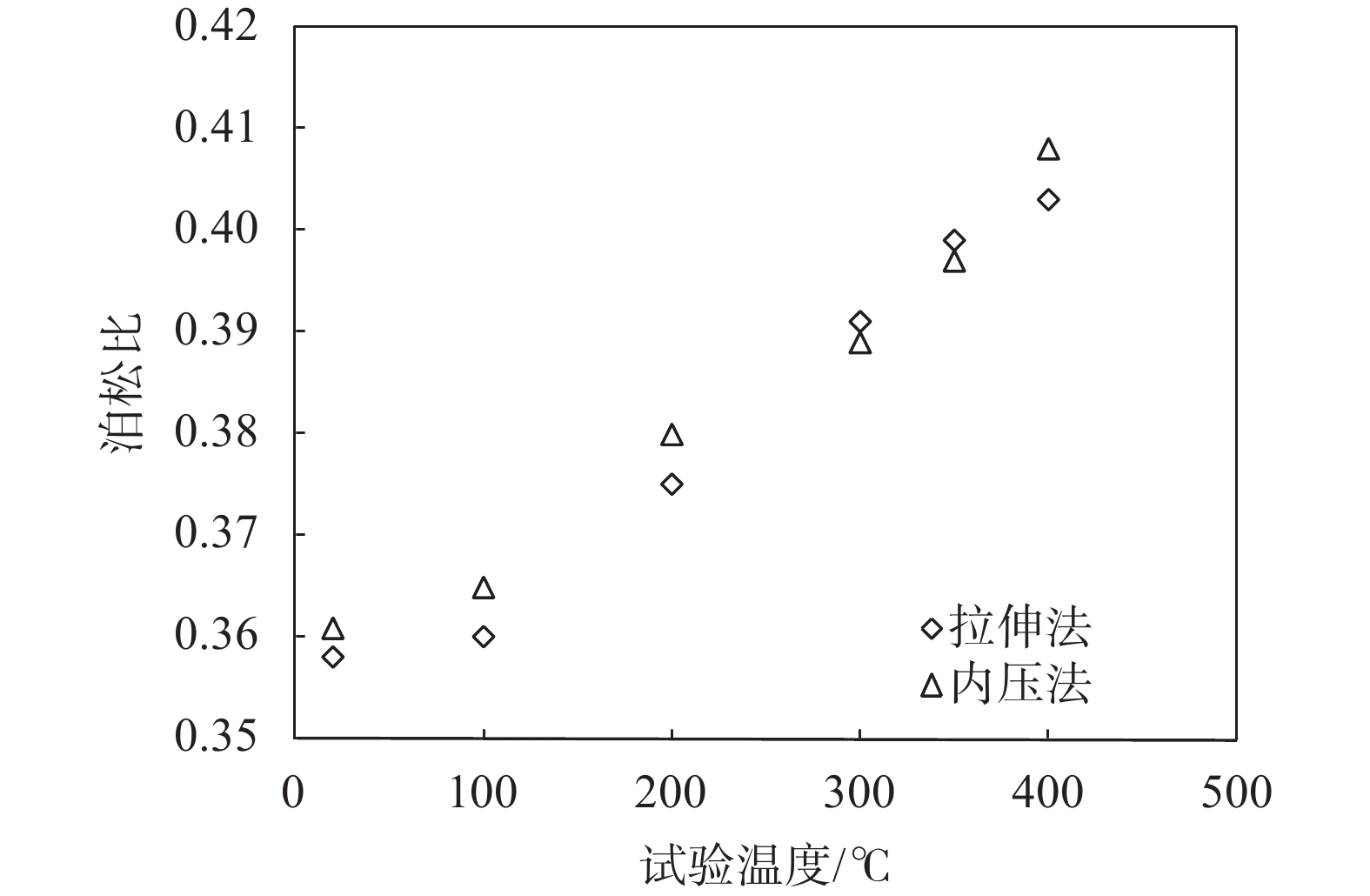
|
| 图 4 拉伸法和内压法泊松比试验结果对比 |
图5是内压法与拉伸法泊松比试验结果的误差。由图可见,内压法所得锆合金薄壁管的泊松比与拉伸法所得锆合金薄壁管的泊松比相对误差不超过2%,表明利用该内压试验方法进行锆合金薄壁管的泊松比测试合理可行。
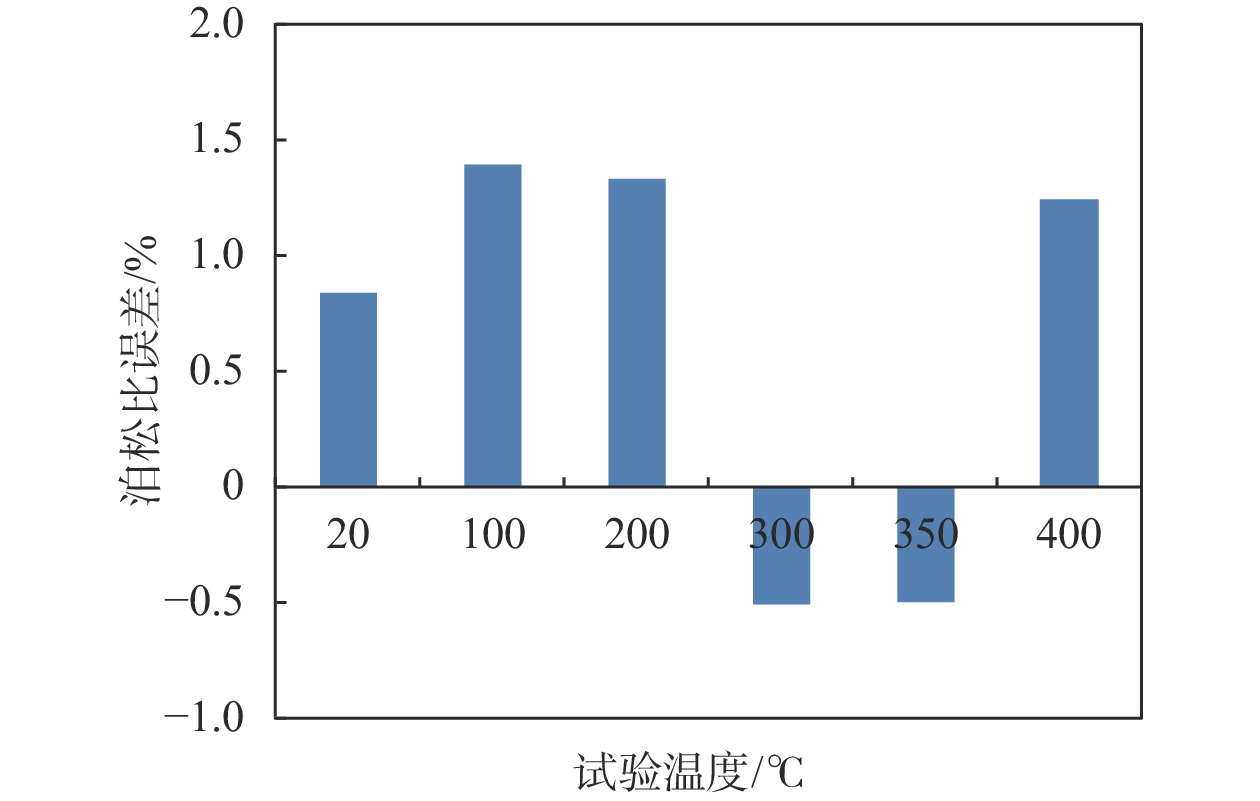
|
| 图 5 内压法与拉伸法泊松比试验结果误差 |
5 结束语
本文分析了受内压薄壁管泊松比的理论计算公式,建立了测定薄壁管泊松比的内压试验法。采用该方法对某锆合金薄壁管进行了从20~400 ℃的泊松比试验,得到各温度下锆合金的泊松比。采用常规拉伸法对该锆合金薄壁管进行了相同温度的试验,并将两种方法得到的泊松比进行了对比分析,得到以下结论:
1) 采用内压试验法可以有效测定锆合金金薄壁管试样的泊松比。
2) 该内压法和常规拉伸法得到的锆合金管泊松比吻合良好,相对误差均在2%以内。
3) 锆合金管的泊松比随温度的升高而增大。
| [1] |
任鑫, 张相玉, 谢亿民. 负泊松比材料和结构的研究进展[J].
力学学报, 2019, 51(3): 656-687.
REN X, ZHANG X Y, XIE Y M. Research progress in auxetic materials and structures[J].
Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(3): 656-687.
|
| [2] |
高玉魁. 负泊松比超材料和结构[J].
材料工程, 2021, 49(5): 38-47.
GAO Y K. Auxetic metamaterials and structures[J].
Journal of Materials Engineering, 2021, 49(5): 38-47.
|
| [3] |
于靖军, 谢岩, 裴旭. 负泊松比超材料研究进展[J].
机械工程学报, 2018, 54(13): 1-14.
YU J J, XIE Y, PEI X. State-of-art of metamaterials with negative Poisson’s ratio[J].
Journal of Mechanical Engineering, 2018, 54(13): 1-14.
|
| [4] |
单桂芳, 杨伟, 冯建民, 等. 材料泊松比测试方法的研究进展[J].
材料导报, 2006(3): 15-20.
SHAN G F, YANG W, FENG J M, et al. Advances in test methods for Poisson’s ratio of materials[J].
Materials Reports, 2006(3): 15-20.
|
| [5] |
王韵璐, 王正, 李敏敏, 等. MDF弹性模量、泊松比和剪切模量静态测试方法探讨[J].
北京林业大学学报, 2017, 39(10): 117-121.
WANG Y L, WANG Z, LI M M, et al. Discussion on static testing method of material MDF constants of elastic modulus, Poisson's ratio and shear modulus[J].
Journal of Beijing Forestry University, 2017, 39(10): 117-121.
|
| [6] |
赵澎涛, 于慧臣, 何玉怀. 单晶高温合金弹性模量和泊松比测试方法的现状分析[J].
航空材料学报, 2019, 39(3): 25-34.
ZHAO P T, YU H C, HE Y H. Current situation of research on test methods for elastic modulus and Poisson’s ratio of single crystal superalloys[J].
Journal of Aeronautical Materials, 2019, 39(3): 25-34.
|
| [7] |
李禾, 严超华, 李仁增, 等. 云纹干涉法测定高温材料弹性模量及泊松比[J].
机械强度, 2004(3): 302-306.
LI H, YAN C H, LI R Z, et al. Measuring elastic modulus and poisson ratio for high-temperature materials by moiré interferometry[J].
Journal of Mechanical Strength, 2004(3): 302-306.
|
| [8] |
李禾, 张少钦, 邓颖, 等. 高温泊松比测试方法与对比[J].
宇航材料工艺, 2011, 41(6): 28-31.
LI H, ZHANG S Q, DENG Y, et al. Methods for testing of Poisson’s ratio at elevated temperature[J].
Aerospace Materials & Technology, 2011, 41(6): 28-31.
|
| [9] |
余建新, 王晓鹏, 崔喜平. 高温环境下材料泊松比测试方法研究[J].
实验科学与技术, 2022, 20(1): 28-33.
YU J X, WANG X P, CUI X P. Material Poisson’s ratio measurement method at elevated temperatures[J].
Experiment Science and Technology, 2022, 20(1): 28-33.
|
| [10] |
王连庆, 王红缨, 马文江. 460 MPa耐火钢高温泊松比试验研究[J].
工业建筑, 2021, 51(3): 176-179.
WANG L Q, WANG H Y, MA W J. Experimental research on poisson’s ratios of 460 megapascal heat-resisting steel at high temperature[J].
Industrial Construction, 2021, 51(3): 176-179.
|
| [11] |
谢梦, 刘琼, 袁波, 等. 锆合金管氢化物应力再取向及其环向拉伸实验方法研究[J].
世界有色金属, 2022(13): 229-231.
XIE M , LIU Q, YUAN B, et al. Research on hydride reorientation of zircaloy tube and its hoop tensile test[J].
World Nonferrous Metals, 2022(13): 229-231.
|
| [12] |
闫萌, 彭倩, 王朋飞, 等. N36锆合金包壳管周向拉伸试验方法研究[J].
核动力工程, 2012, 33(S2): 13-16.
YAN M. PWNG Q, WANG P F, et al. Research on hoop tensile test method for N36 zirconium tube[J].
Nuclear Power Engineering, 2012, 33(S2): 13-16.
|
| [13] |
陆玉华. 薄壁锆合金管材组织与环向性能研究[D]. 西安: 西安建筑科技大学, 2019.
LU Y H. The research on microstructure and property of zirconium tube with thin-wall[D]. Xi’an: Xi’an University of Architecture and Technology, 2019.
|
| [14] |
张长义, 宁广胜, 佟振峰, 等. M5锆合金包壳管轴向和环向拉伸性能测试[J].
原子能科学技术, 2005(S1): 34-36.
ZHANG C Y, NING G S, TONG Z F, et al. Test on tension properties of M5 alloy[J].
Atomic Energy Science and Technology, 2005(S1): 34-36.
|
| [15] |
王洋. 基于光纤传感的管道和容器压力测量方法研究[J].
中国测试, 2022, 48(2): 41-48.
WANG Y. Rasearch on pressure measurement method of pipeline and vessel based on optical fiber sensor[J].
China Measurement & Test, 2022, 48(2): 41-48.
|
| [16] |
韩志鑫, 贾广成, 杨锐, 等. 校准300℃及以下廉金属热电偶自动测量系统的测试方法研究[J].
中国测试, 2022, 48(S1): 7-12.
HAN Z X, JIA G C, YANG R, et al. Research on test method of auto-measuring system for 300℃ & under base metal thermocouples[J].
China Measurement & Test, 2022, 48(S1): 7-12.
|
| [17] |
赵可沦, 江境宏, 邓进, 等. 基于遗忘因子递推最小二乘法的锂电池等效电路模型参数辨识方法[J].
电子测量技术, 2022, 45(23): 53-58.
ZHAO K L, DENG J H, DENG J, et al. Parameter identification method of lithium battery equivalent circuit model based on forgetting factor recursive least squares[J].
Electronic Measurement Technology, 2022, 45(23): 53-58.
|
 2024, Vol. 50
2024, Vol. 50


 ,
,